Thermal System Analysis and Optimization of Large-Scale Compressed Air Energy Storage (CAES)
Abstract
:1. Introduction
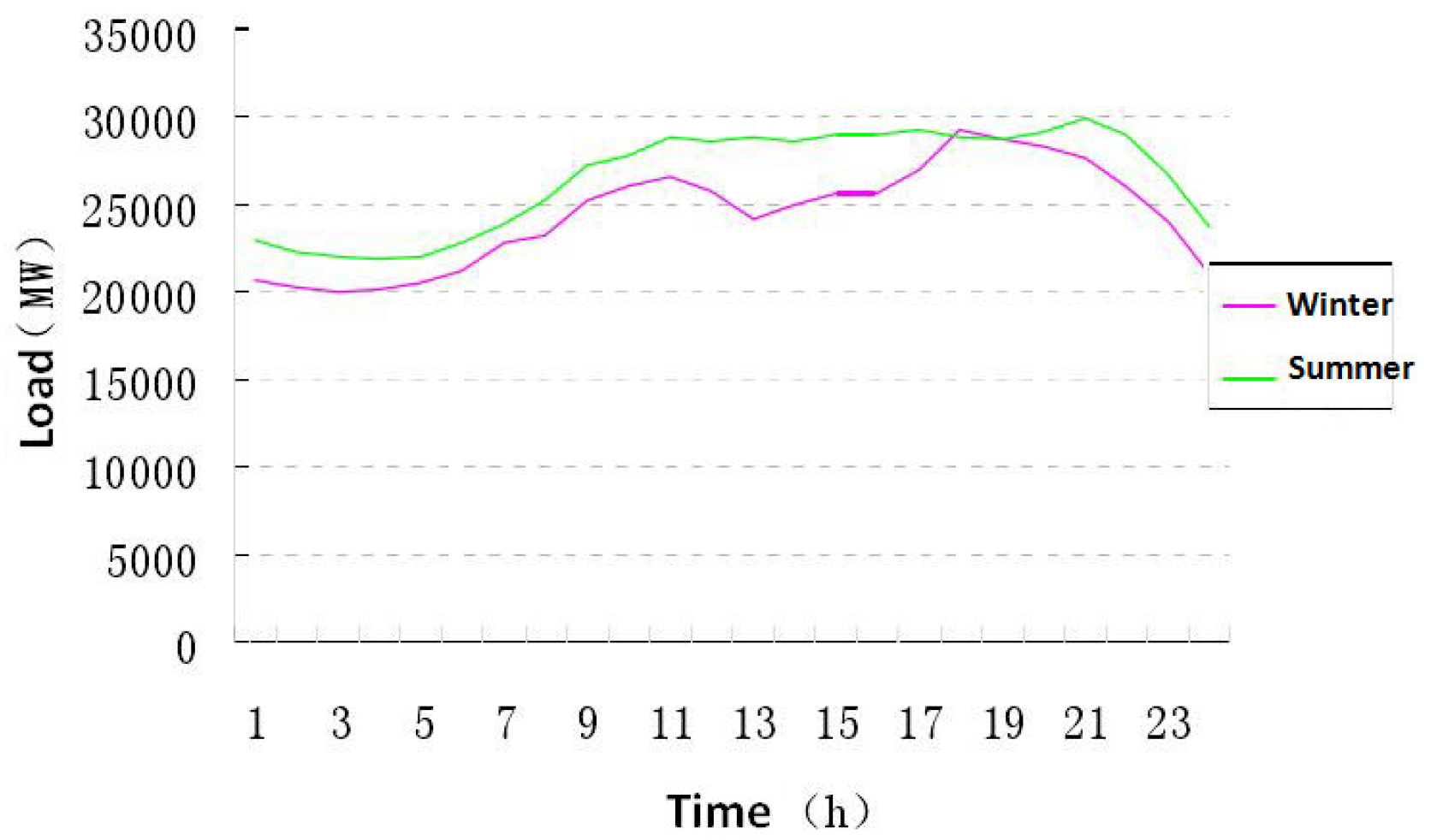
2. Technical Principles, Analysis, and Optimization of Compressed Air Energy Storage
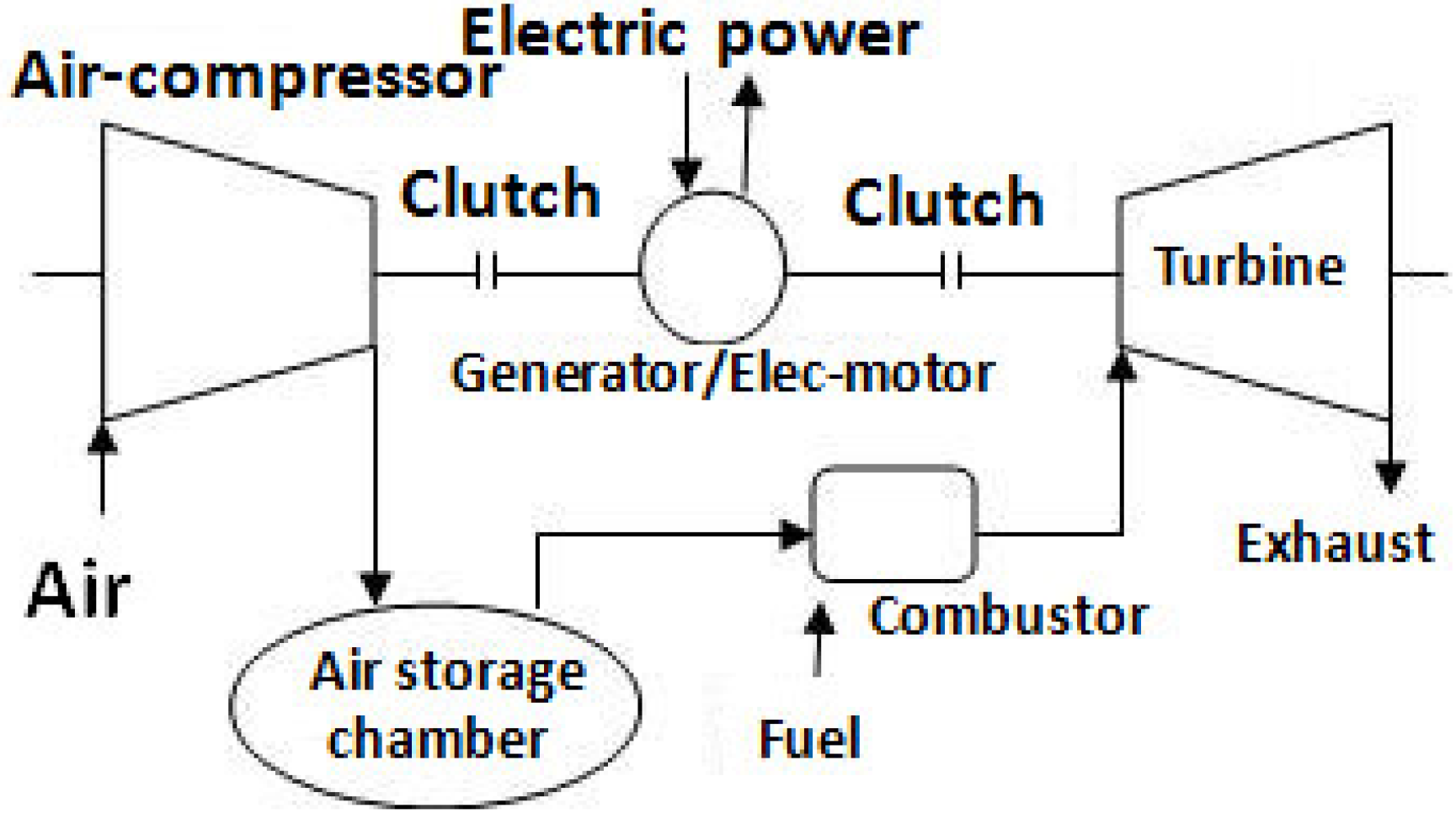
2.1. Characteristics of a Compressed Air Energy Storage Thermal System
- Compression pressure is high. The pressure of air that is compressed by the compressor and stored in the gas storage device can exceed 100 bar.
- Storage temperature in the gas-storing devices is low. At present, most gas storage devices are located in underground caves at room and even lower temperatures.
- Storage air pressure decreases linearly with the consumption of compressed air during power generation.
2.2. Analysis and Improvement of a Compressed Air Energy Storage Thermal System
2.2.1. Thermal System Calculation and Analysis of a Second-Generation Compressed Air Energy Storage Power System
| Parameters | Gas pressure | Flow Rate of Air | Pressure Ratio of a Gas Turbine | Inlet Temperature of a Turbine | Exhaust Temperature |
|---|---|---|---|---|---|
| Values | 100 bar | 600 kg/s | 15.4 | 1300 °C | 383.4 °C |
- When the pressure of the compressed air is high (above 100 bar), the exhaust temperature of the expander decreases if high-pressure energy is utilized further although air temperature increases after heat regeneration. Thus, expander efficiency is reduced.
- In the release system, the gas turbine circle belongs to the simple Brayton cycle. An efficient gas turbine and system can be generated by optimizing this cycle.
2.2.2. Improvement and Optimization of the Thermodynamic Cycle of a System
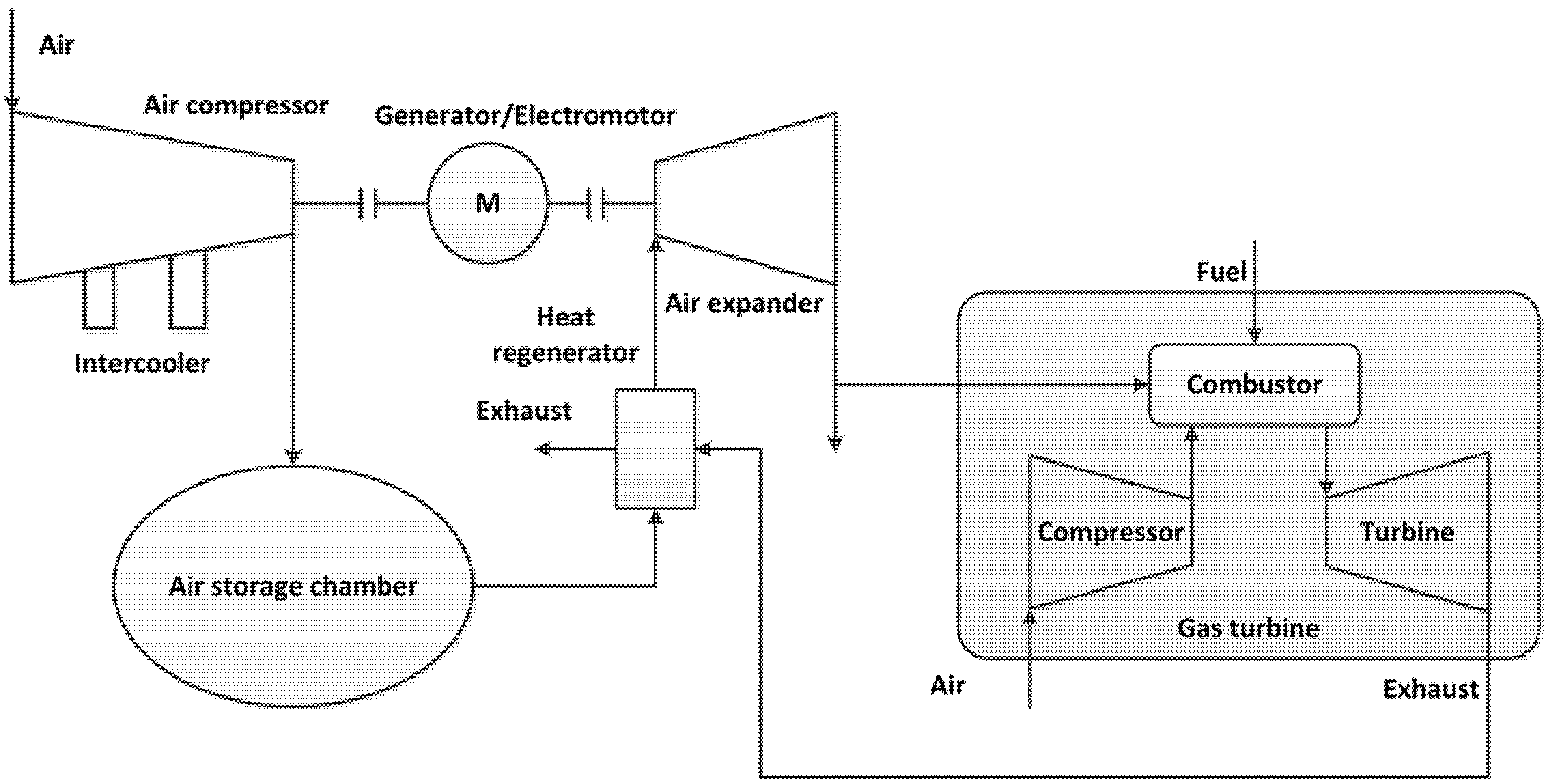
(1) Use of a new type of high-pressure reheat gas turbine
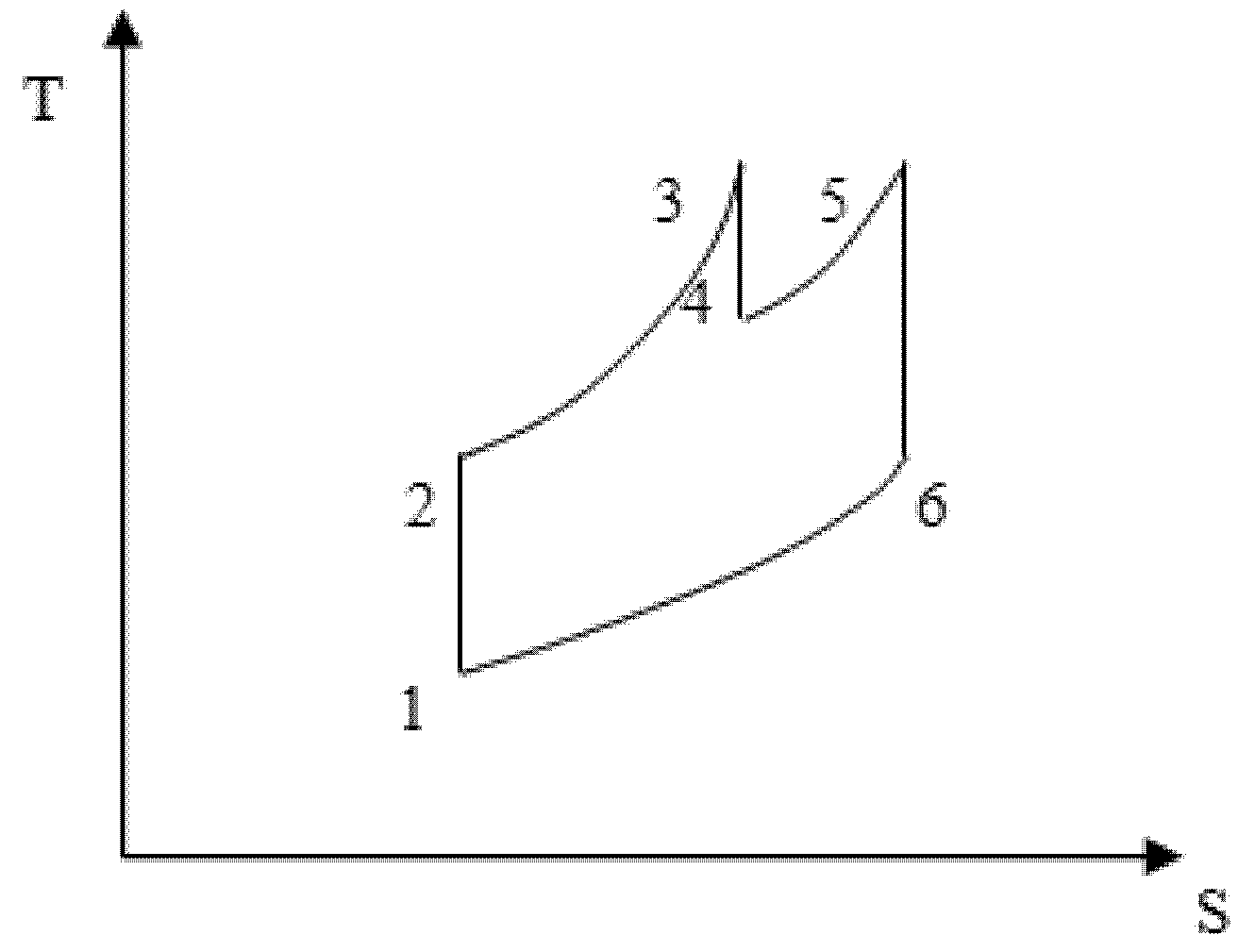
(2) Using the regenerative cycle
2.2.3. Improved System
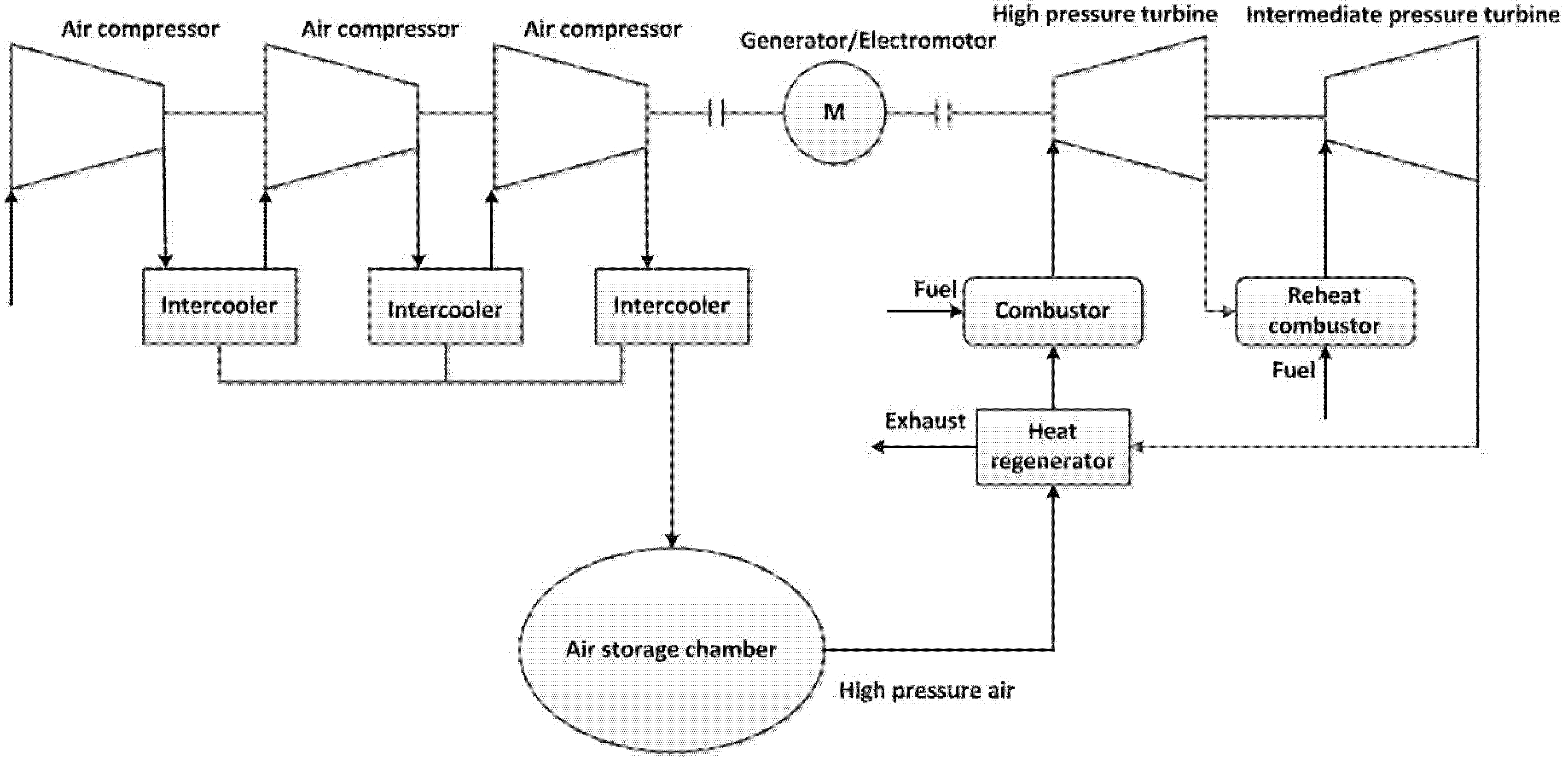
3. Results and Discussion
3.1. Effect of Pressure on Efficiency
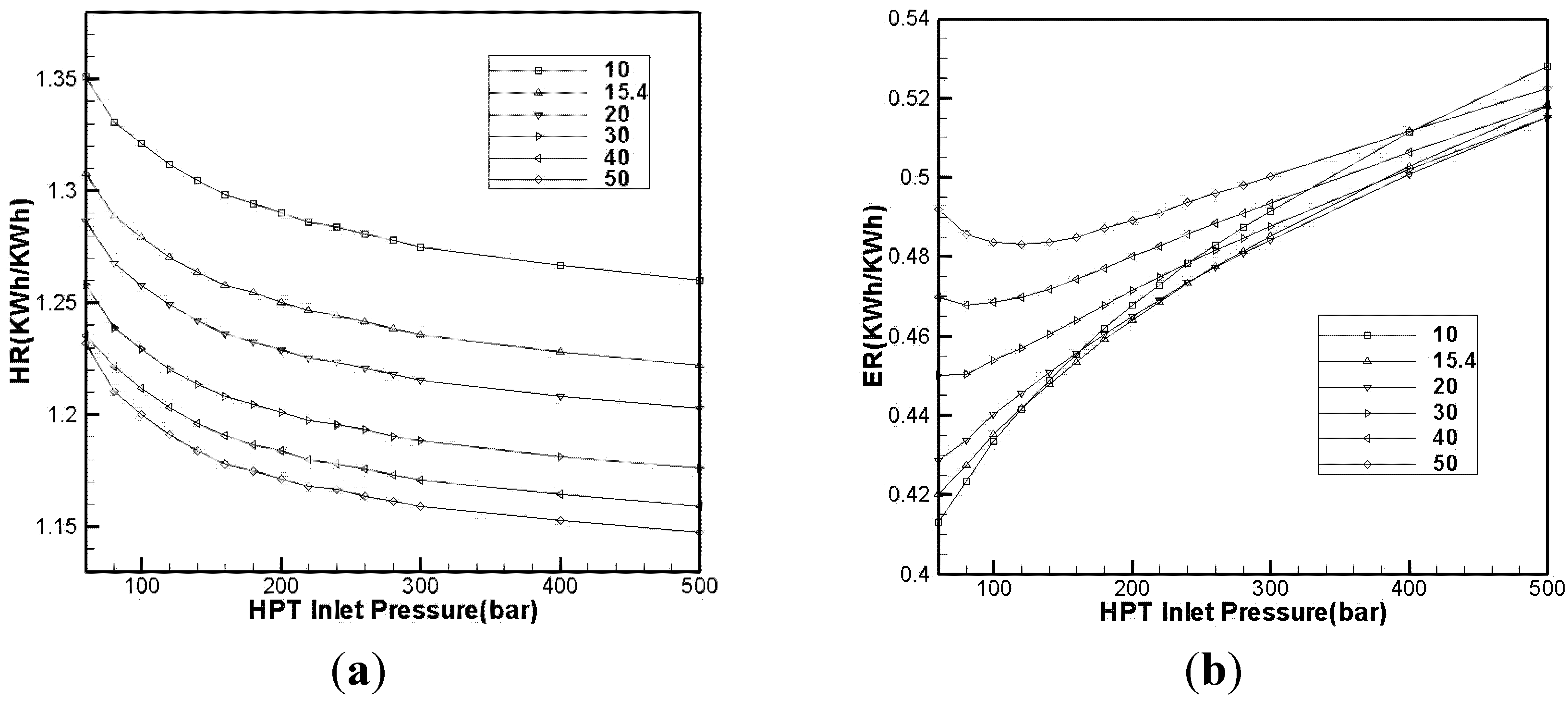
3.1.1. Effect of High-Pressure Turbine Inlet Pressure on Efficiency
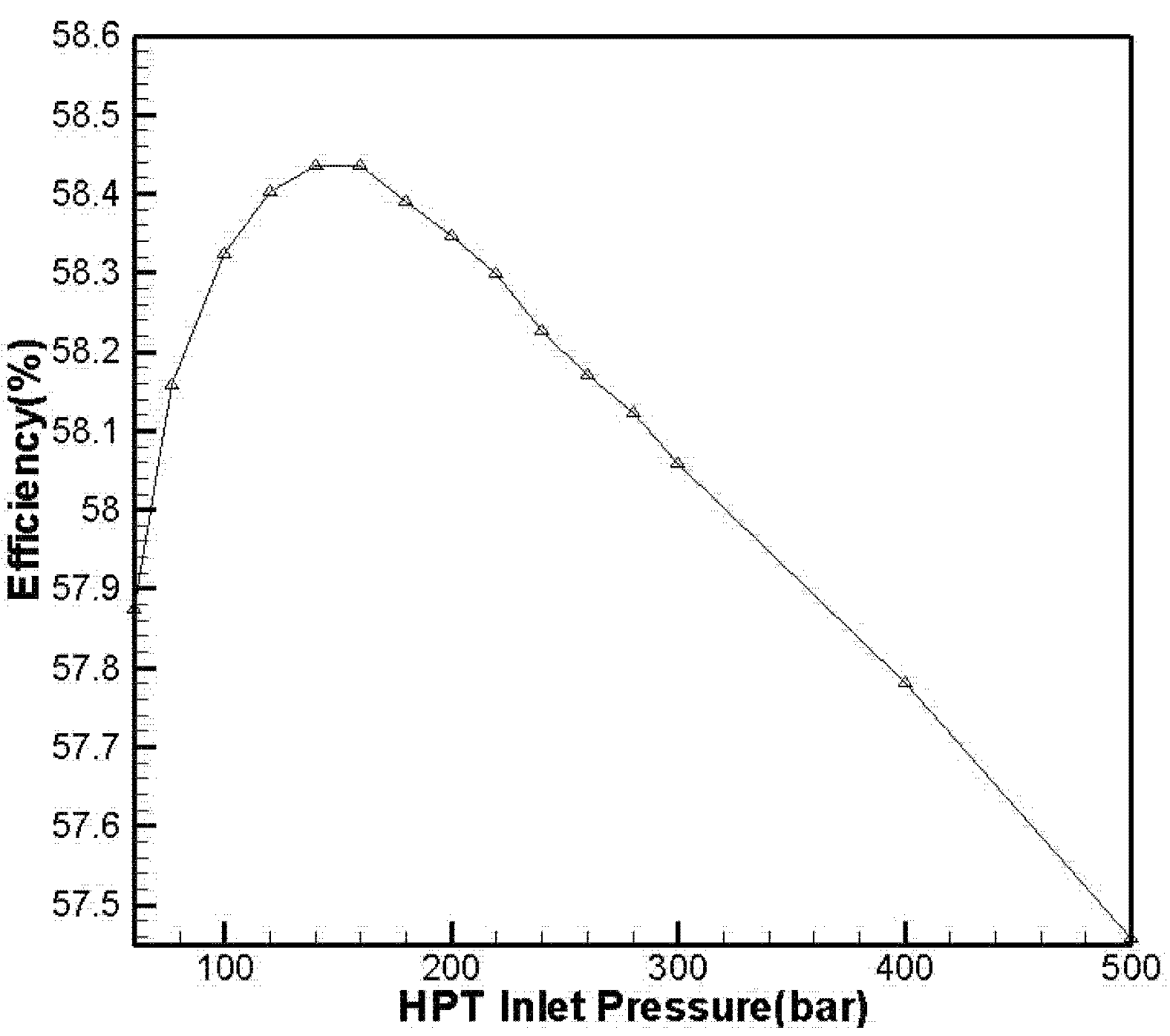
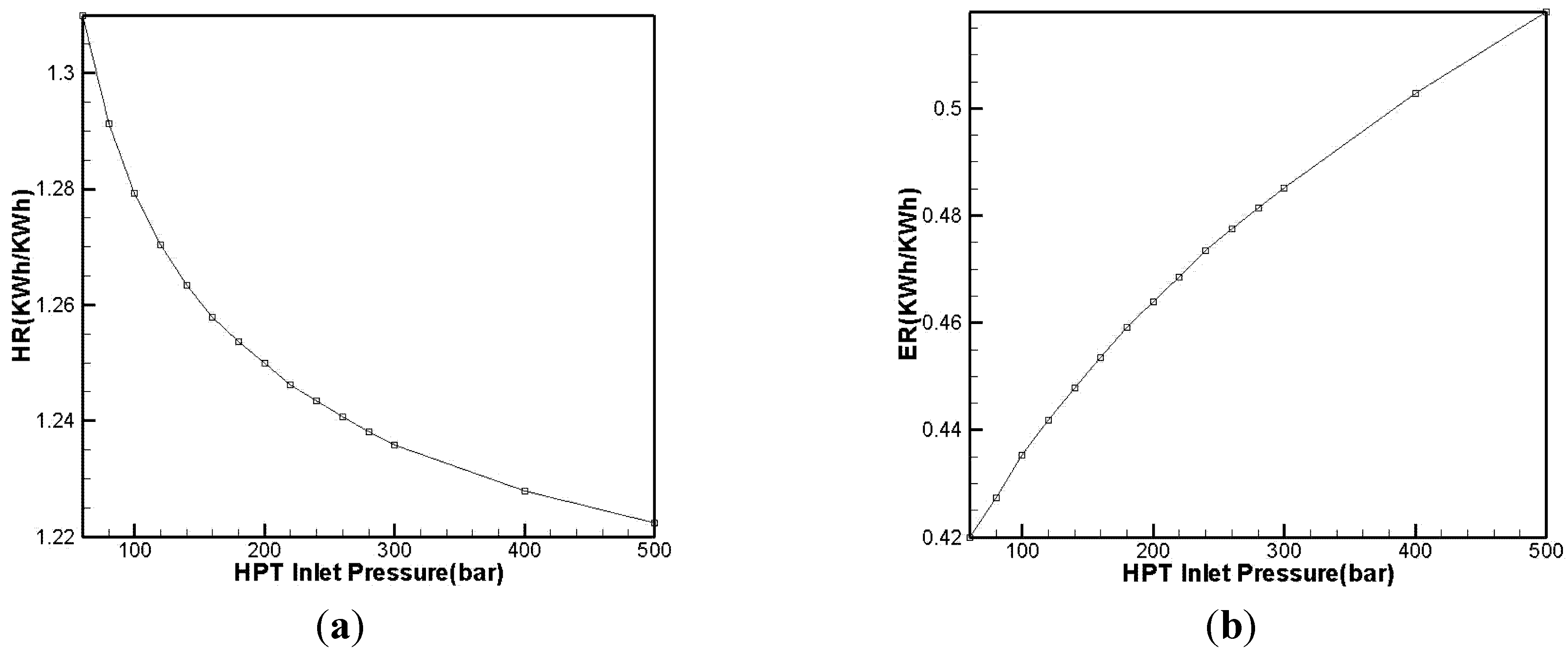

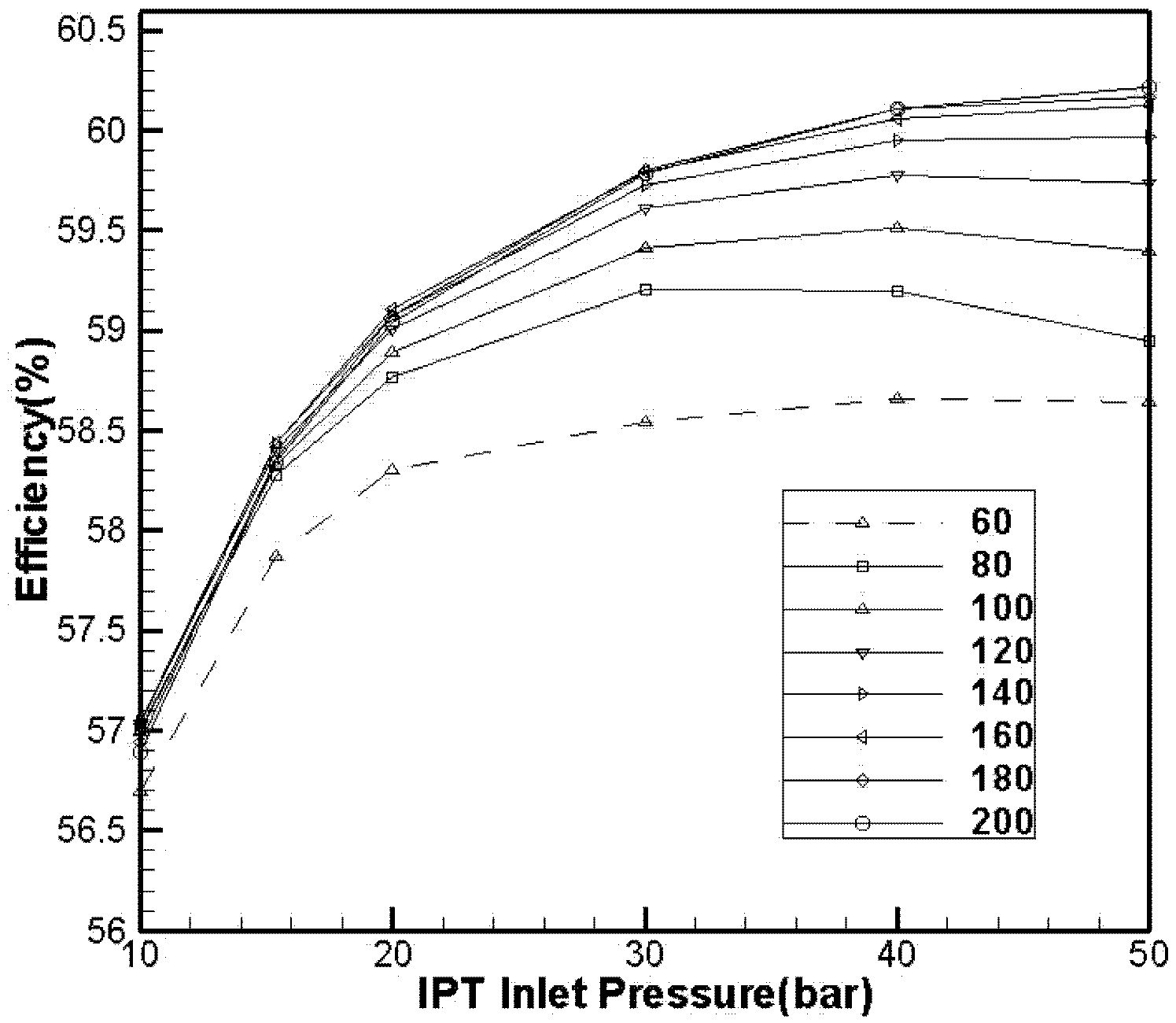
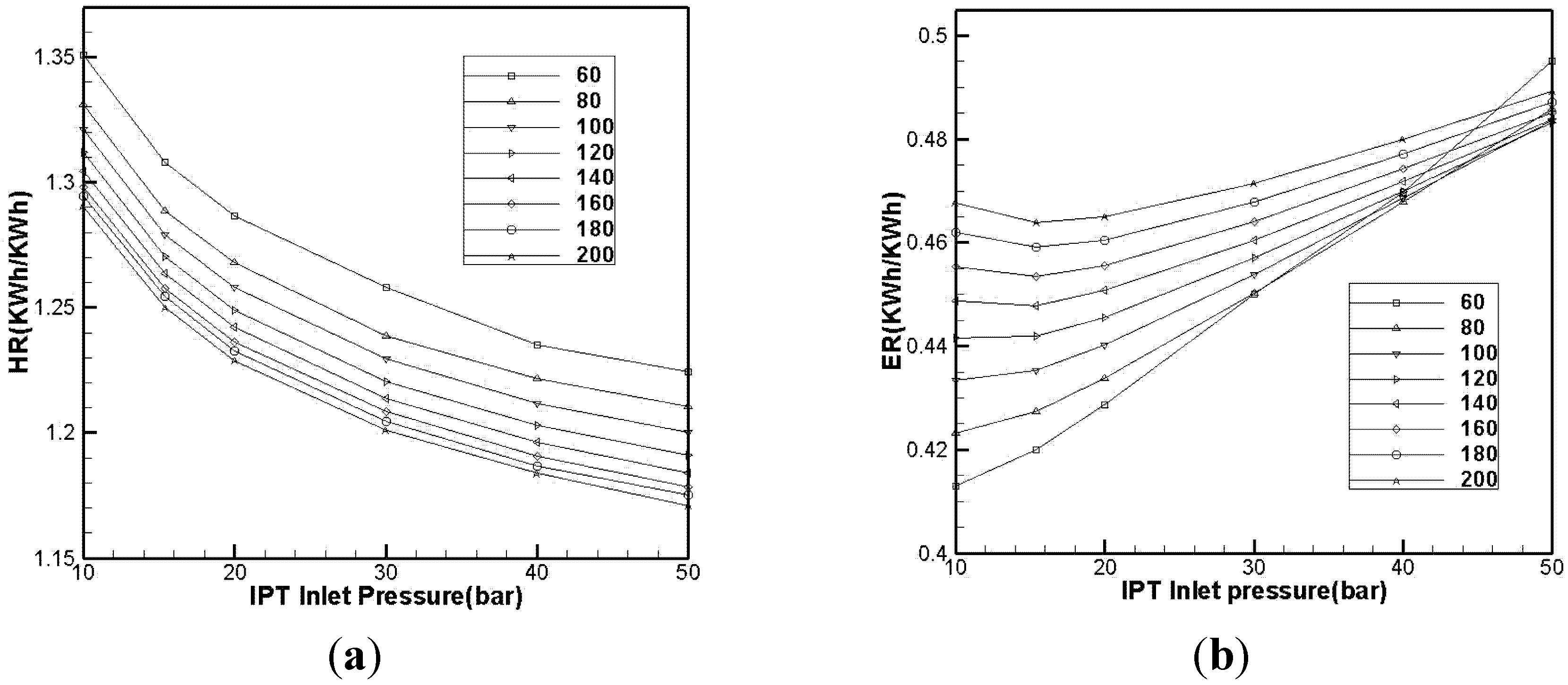
3.1.2. Effect of Intermediate-Pressure Turbine Inlet Pressure on Efficiency
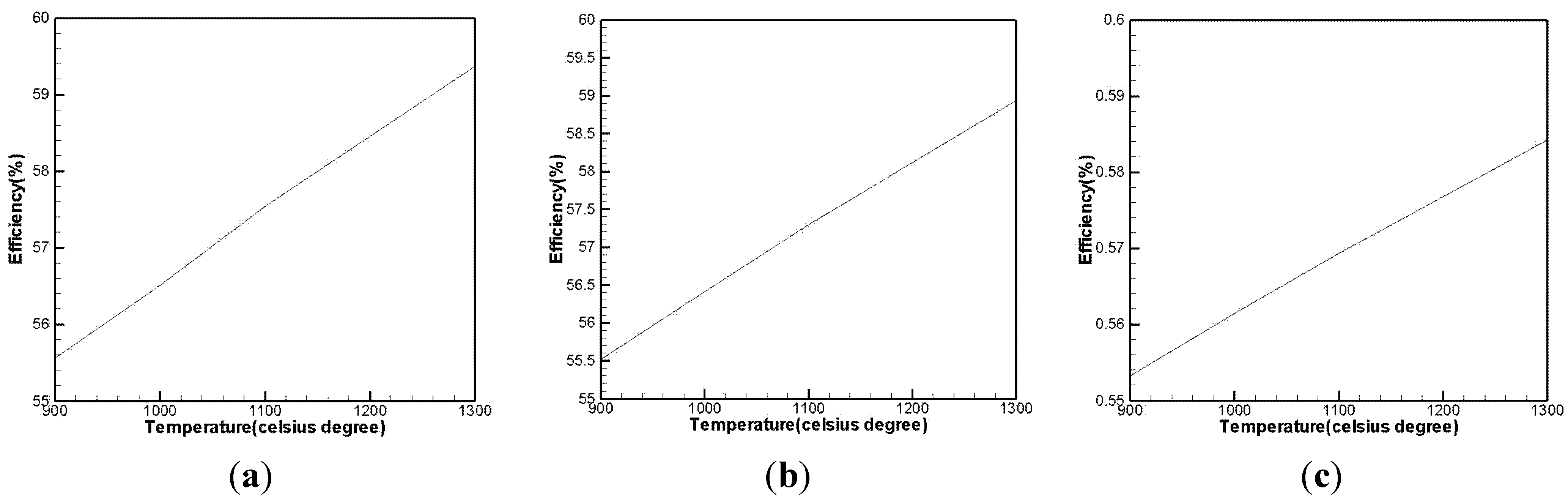
3.2. Effect of High-Pressure Turbine Inlet Temperature on Efficiency
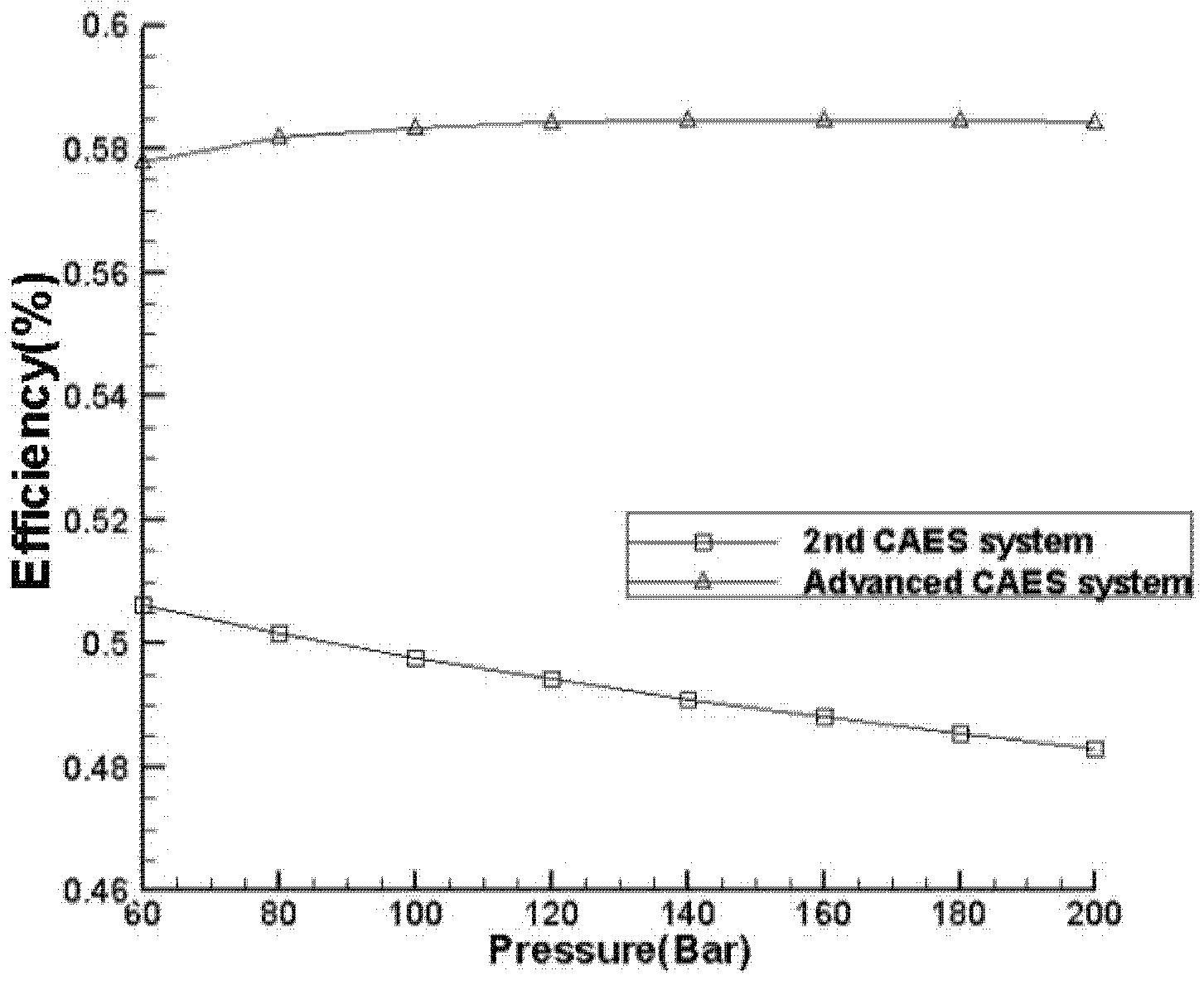
3.3. Performance Under Various Conditions
3.4. Calculation Results
| System/Parameters | Second-Generation CAES | Improved System | |
|---|---|---|---|
| Air storage chamber parameters | Pressure (bar) | 140 | |
| Temperature (°C) | 50 | ||
| Compressor outlet parameters | Pressure (bar) | 140 | |
| Temperature (°C) | 50 | ||
| Air flow (kg/s) | 600 | 600 | |
| Turbine expansion work (MW) | HPT (air turbine) | 157.3 | 396.6 |
| IPT (gas turbine) | 474.7 | 492.0 | |
| Compressor power consumption (MW) | 398 | 398 | |
| Turbine inlet pressure (bar)/temperature (°C) | HPT | - | 133/1300 |
| IPT (gas turbine) | 15.4/1300 | 15.4/1300 | |
| Flow rate of the fuel (kg/s) | 17.74 | 22.36 | |
| Power output (MW) | 632.0 | 888.6 | |
| Efficiency | 49.06% | 58.44% | |
| HR (kWh/kWh) | 1.410 | 1.265 | |
| ER (kWh/kWh) | 0.629 | 0.447 | |
3.5. Investment Estimation
| Project | Reference F-Class CAES Power Plant (2 MW × 600 MW) | Mature Reheating Combustion Equipment (2 MW × 800 MW) | New Reheat CAES Equipment (2 MW × 800 MW) |
|---|---|---|---|
| Electromechanical equipment | 153.4 | 271.08 | 355.55 |
| High-pressure gas turbine | - | 67.84 | 135.67 |
| Low-pressure gas turbine | 41.90 | 45.22 | 45.22 |
| Compressor | 17.08 | 17.08 | 32.55 |
| Gas turbine generator | 8.87 | 14.07 | 14.07 |
| Intercoolers | 2.66 | 2.66 | 2.66 |
| Instrument and control system | 3.91 | 5.86 | 7.03 |
| Spare parts fee + freight | 78.90 | 118.35 | 118.35 |
| Regenerator | 25.48 | 25.48 | 25.48 |
| Main transformer supply | 5.31 | 8.09 | 8.09 |
| 252 KV GIS supply | 2.09 | 3.18 | 3.18 |
| Gas pressure regulating station and gas replacement | 2.05 | 2.96 | 2.96 |
| Total equipment cost | 188.34 | 310.78 | 395.25 |
| Civil engineering cost and gas storage chamber | 398.21 | 495.60 | 566.51 |
| 252 KV GIS supply | 2.09 | 3.18 | 3.18 |
| Gas pressure regulating station and gas replacement | 2.05 | 2.96 | 2.96 |
| Total equipment cost | 188.34 | 310.78 | 395.25 |
| Civil engineering cost and gas storage chamber | 398.21 | 495.60 | 566.51 |
| Crew, including heating pipe network | 17.94 | 24.94 | 24.94 |
| Gas transmission pipeline | 17.73 | 25.59 | 25.59 |
| Static total investment | 622.22 | 865.90 | 1012.29 |
| Static investment per kW ($/KW) | 518 | 536 | 633 |
| Dynamic total investment | 691.36 | 952.12 | 1124.77 |
| Dynamic investment per kW ($/KW) | 576 | 595 | 703 |
4. Conclusions
- (1)
- The efficiency of the improved CAES system increased by 9% with the adoption of a high-pressure gas turbine that includes a reheat process and the utilization of heat energy in the inter-cooling process based on the second-generation CAES system.
- (2)
- In the improved system, efficiency is related to HPT inlet pressure. When pressure increases, efficiency increases at first and then decreases. An optimum value was thus obtained.
- (3)
- System efficiency increases initially and decreases eventually with an increase in IPT inlet pressure. Optimal pressure also increases with HPT inlet pressure.
- (4)
- Efficiency is related to HPT inlet temperature, and an increase in temperature can improve the thermal efficiency of a cycle to some extent.
- (5)
- System efficiency changes with air storage chamber pressure. Despite changes in pressure, the efficiency of the improved system is always significantly higher than that of the existing second-generation CAES system.
- (6)
- In the improved system, not only did the parameter values increase, but capacity increased as well. System capacity reached 800 MW, thus indicating that the system can be used on a large scale.
- (7)
- The costs of the F-class gas turbine equipment and the equipment for the improved system are estimated, and the cost per kW of the latter do not increase significantly.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| ξ | energy conversion coefficient |
| Pe | total system output power (MW) |
| Pc | compressor power consumption (MW) |
| Gf | flow rate of fuel (kg/s) |
| HR | heat consumption rate (kJ/kWh) |
| ER | power consumption rate (kWh/kWh) |
| PI | inlet pressure of IPT (bar) |
| PH | inlet pressure of HPT (bar) |
References
- Ouyang, C.Y. To attach great importance to the development of power grid peaking problems. Electr. Power Technol. Econ. 2002, 1, 10–15. (In Chinese) [Google Scholar]
- Grazzini, G.; Milazzo, A. Thermodynamic analysis of CAES/TES systems for renewable energy plants. Renew. Energy 2008, 33, 1998–2006. [Google Scholar] [CrossRef]
- Abbaspour, M.; Satkin, M.; Mohammadi-Ivatloo, B.; Lotfi, F.H.; Noorollahi, Y. Optimal operation scheduling of wind power integrated with compressed air energy storage (CAES). Renew. Energy 2013, 51, 53–59. [Google Scholar] [CrossRef]
- Li, C. Progress in renewable energy problem in China. Forum Sci. Technol. China 2008, 2, 111–120. (In Chinese) [Google Scholar]
- Jubeh, N.M.; Najjar, Y.S. Green solution for power generation by adoption of adiabatic CAES system. Appl. Therm. Eng. 2012, 44, 85–89. [Google Scholar] [CrossRef]
- Raju, M.; Khaitan, S.K. Modeling and simulation of compressed air storage in caverns: A case study of the Hundorf plant. Appl. Energy 2012, 89, 474–481. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Y.; Zhang, X.; Xin, Y. Present Situation and Development Trend of Compressed air energy storage (CAES) power plant. Shandong Electr. Power 2007, 2, 10–14. (In Chinese) [Google Scholar]
- Kushnir, R.; Dayan, A.; Ullmann, A. Temperature and pressure variations within compressed air energy storage caverns. Int. J. Heat Mass Transf. 2012, 55, 5616–5630. [Google Scholar] [CrossRef]
- Nakhamkin, M.; Chiruvolu, M. Available Compressed Air Energy Storage (CAES) Plant Concepts. Available online: http://espcinc.com/mobile/library/PowerGen_2007_paper.pdf (accessed on 18 August 2015).
- Proczka, J.J.; Muralidharan, K.; Villela, D. Guidelines for the pressure and efficient sizing of pressure vessels for compressed air energy storage. Energy Convers. Manag. 2013, 65, 597–605. [Google Scholar] [CrossRef]
- Crotogino, F.; Mohmeyer, K.U.; Scharf, R. Huntorf CAES: More than 20 Years of Successful Operation. In Proceedings of the Spring 2001 Meeting, Orlando, FL, USA, 15 April 2001.
- Van der Linder, S. The case for CAES. Modern Power Systems. Available online: http://www.modernpowersystems.com/features/featurethe-case-for-caes/ (accessed on 18 August 2015).
- Concept Screening of Coal Gasification CAES Systems; EPRI Research Report; Electric Power Research Institute: Palo Alto, CA, USA, May 1979.
- Schoenung, S.M. Utility energy storage applications studies. IEEE Trans. Energy Convers. 1996, 11, 658–664. [Google Scholar] [CrossRef]
- Thumann, A.; Mehta, D.P. Handbook of Energy Engineering, 5th ed.; The Fairmont Press Inc: Anaheim, CA, USA, 2001; pp. 391–418. [Google Scholar]
- Liu, W.Y.; Yang, Y.P.; Song, Z.P. Compressed air energy storage and performance simulation. In Proceedings of the China Engineering Thermophysics engineering thermodynamics and energy utilization Conference, Xi’an, China, 8 November 2004; pp. 288–296. (In Chinese)
- Liu, W.Y.; Yang, Y.P.; Song, Z.P. Optimization and Performance Simulation of Different CAES Systems. J. Eng. Thermophys. 2005, 6, 25–28. (In Chinese) [Google Scholar]
- Huang, Q.H. Steam Turbine and Gas Turbine Principles and Applications; Southeast University Press: Nanjing, China, 2005; pp. 190–205. (In Chinese) [Google Scholar]
- Kushnir, R.; Ullmann, A.; Dayan, A. Compressed air flow within aquifer reservoirs of CAES plants. Transp. Porous Media 2010, 81, 219–240. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Z.; Lu, K.; Zhu, Y. Thermal System Analysis and Optimization of Large-Scale Compressed Air Energy Storage (CAES). Energies 2015, 8, 8873-8886. https://doi.org/10.3390/en8088873
Fu Z, Lu K, Zhu Y. Thermal System Analysis and Optimization of Large-Scale Compressed Air Energy Storage (CAES). Energies. 2015; 8(8):8873-8886. https://doi.org/10.3390/en8088873
Chicago/Turabian StyleFu, Zhongguang, Ke Lu, and Yiming Zhu. 2015. "Thermal System Analysis and Optimization of Large-Scale Compressed Air Energy Storage (CAES)" Energies 8, no. 8: 8873-8886. https://doi.org/10.3390/en8088873
APA StyleFu, Z., Lu, K., & Zhu, Y. (2015). Thermal System Analysis and Optimization of Large-Scale Compressed Air Energy Storage (CAES). Energies, 8(8), 8873-8886. https://doi.org/10.3390/en8088873





