Application of Model Predictive Control to BESS for Microgrid Control
Abstract
:1. Introduction
2. MPC for BESS
2.1. Discrete-Time Model of Converter
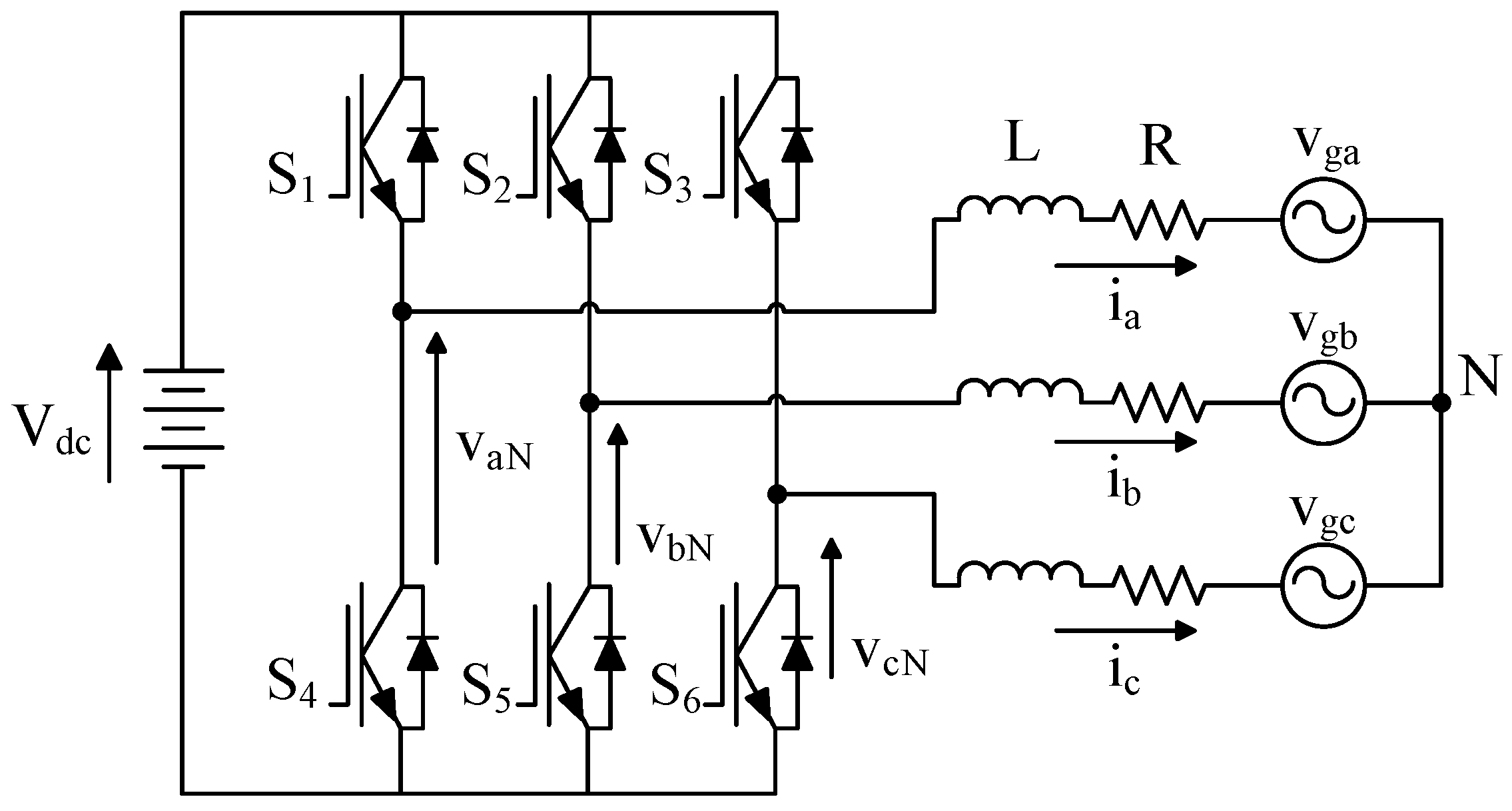
| x | Sa | Sb | Sc | Voltage vectors |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | v0 = 0 |
| 2 | 1 | 0 | 0 | |
| 3 | 1 | 1 | 0 | |
| 4 | 0 | 1 | 0 | |
| 5 | 0 | 1 | 1 | |
| 6 | 0 | 0 | 1 | |
| 7 | 0 | 1 | 1 | |
| 8 | 1 | 1 | 1 | v7 = 0 |
2.2. Principle of MPC
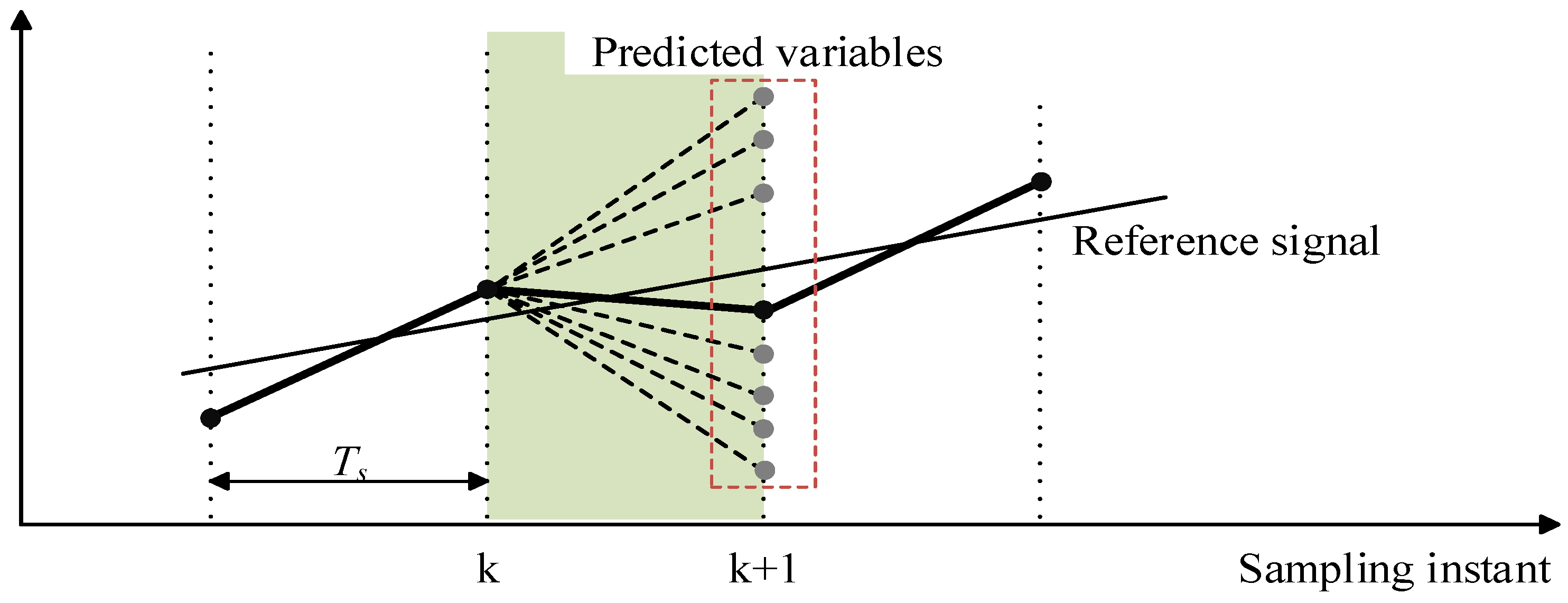
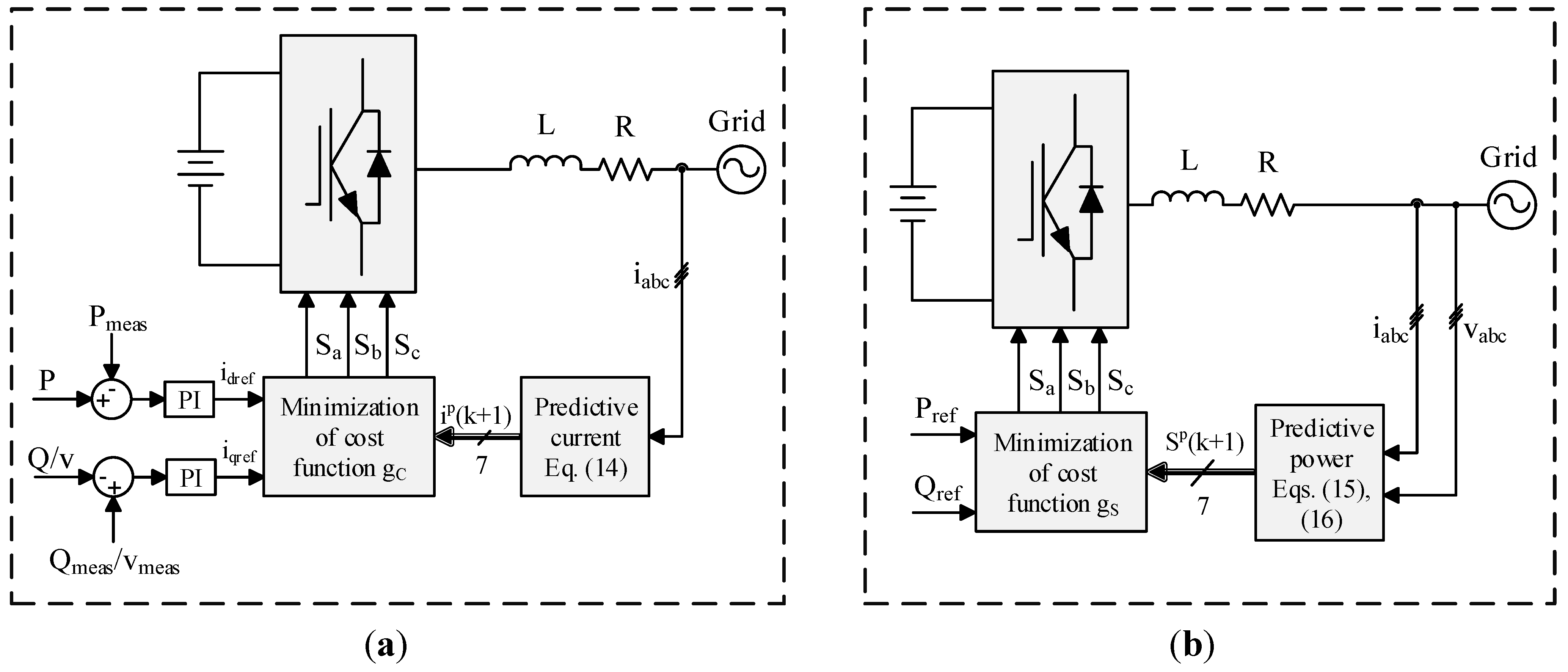
- (1)
- The three-phase current and voltage of the BESS are measured, and the values of reference signals are obtained from the outer control loop.
- (2)
- The discrete-time model of the converter is used to predict the values of current or real/reactive powers in the next sampling interval (k + 1) for each voltage vector according to Equations (14)–(16).
- (3)
- The cost function or based on Equations (17) and (18) is used to compute the errors between the reference and the predicted current or real/reactive powers for each voltage vector.
- (4)
- The minimum value of the cost function gives the minimum error between the reference and the measured signals. The voltage vector with respect to the minimum cost function is selected, and the corresponding switching state signals are generated to apply to the converter.
3. Test Microgrid
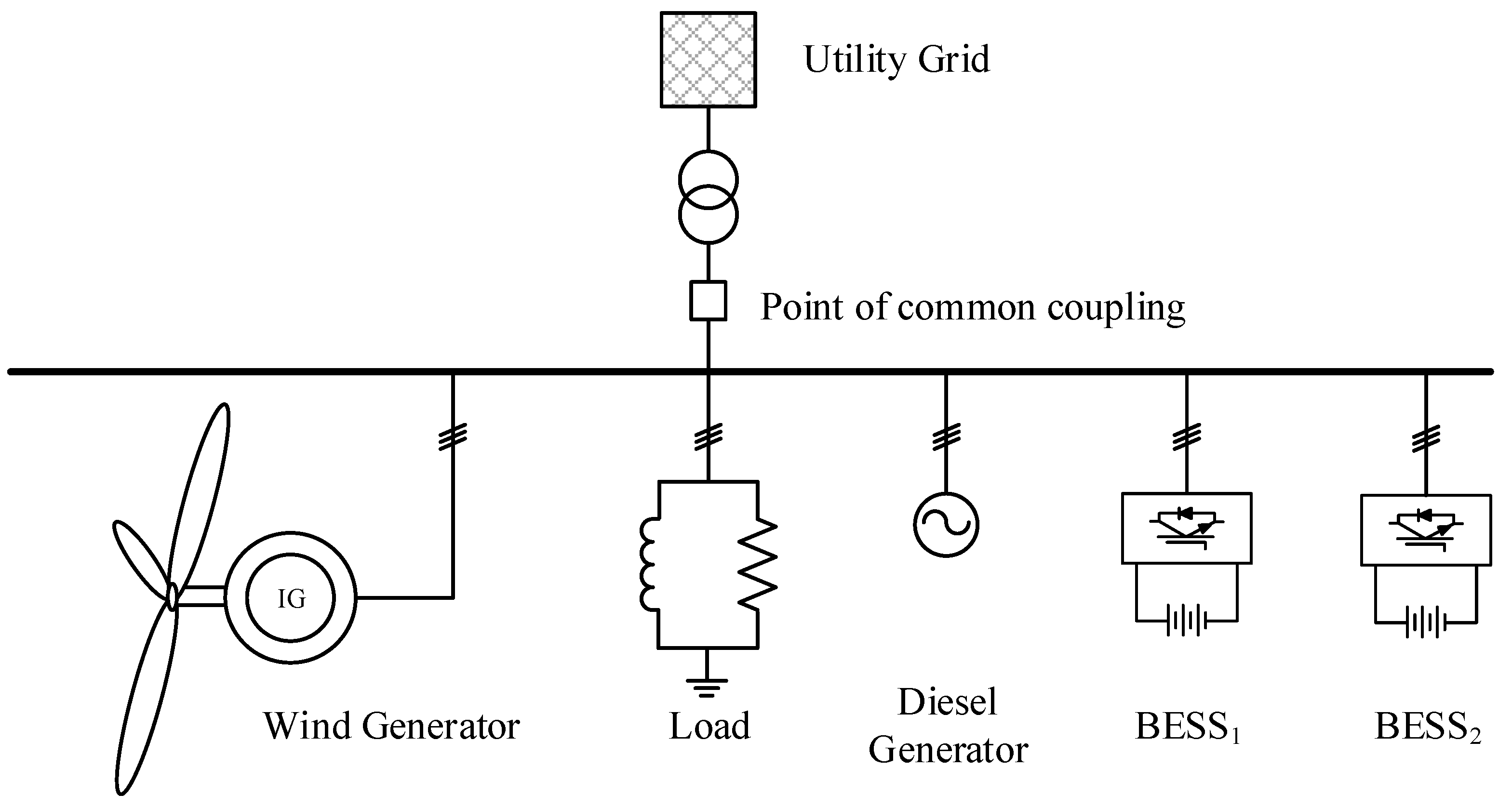
| Components | Rating |
|---|---|
| Wind generator | 150 kVA |
| BESS1 | 450 kWh |
| BESS2 | 200 kWh |
| Load | 500 kW; 100 kVAR |
| Diesel generator | 500 kVA |
| Mean wind speed | 9 m/s |
| System frequency | 60 Hz |
| Transformer | 700 kVA; 6.6 kV/380 V |
| Operation modes | BESS1 | BESS2 |
|---|---|---|
| Grid-connected | Tie-line powers at point of common coupling | Smoothing wind power |
| Islanded | Frequency control | Smoothing wind power |
| Reactive power at point of common coupling | Voltage control |
4. Control Performance of MPC Techniques
4.1. Comparison of Control Performance of MPC and PI Control Techniques
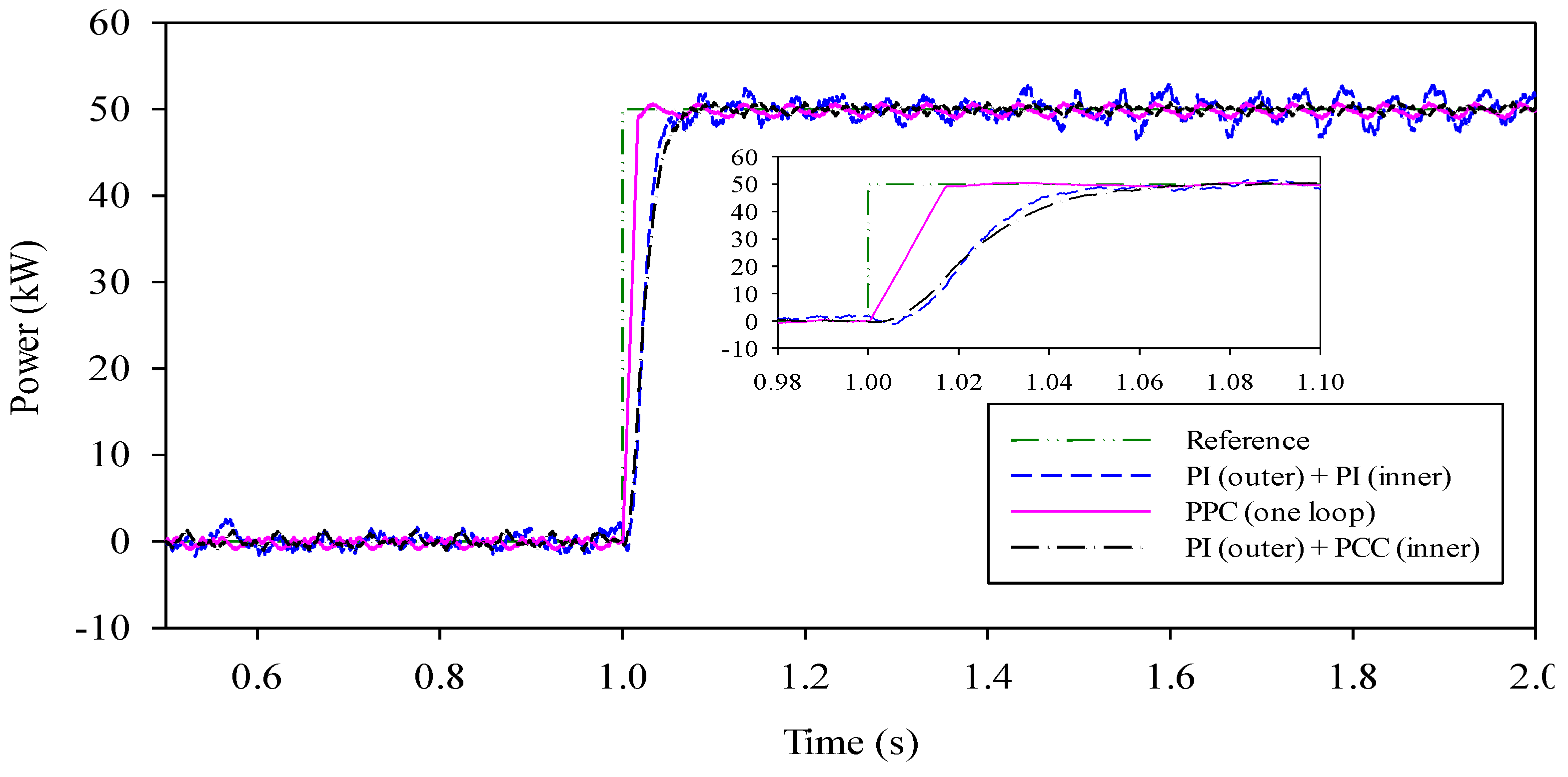
4.2. Effective Application of MPC Techniques to Microgrid Control
| Characteristics | PI (outer) + PI (inner) | PI (outer) + PCC (inner) | PPC (one loop) |
|---|---|---|---|
| Ability to control | P/Q, f/v | P/Q, f/v | P/Q |
| Response time | Long | Long | Short |
| Ripple | Large | Small | Small |
5. Simulation Results
5.1. Control Microgrid in Grid-Connected Mode
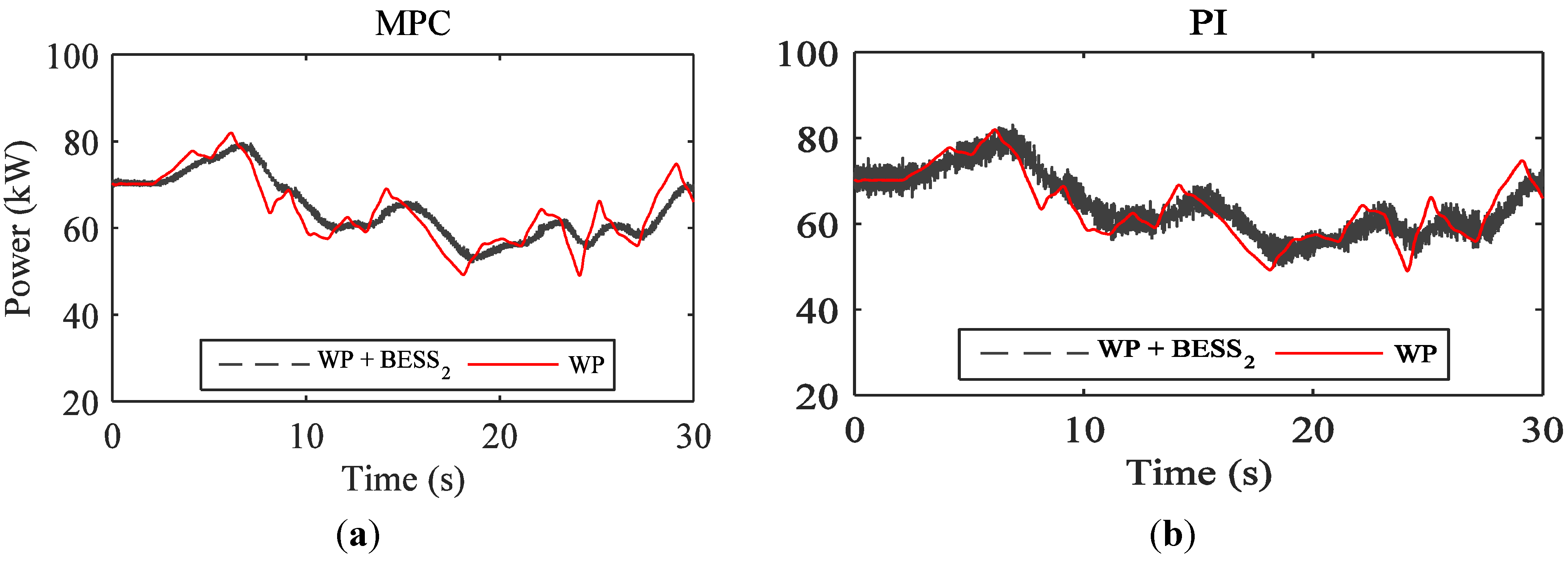
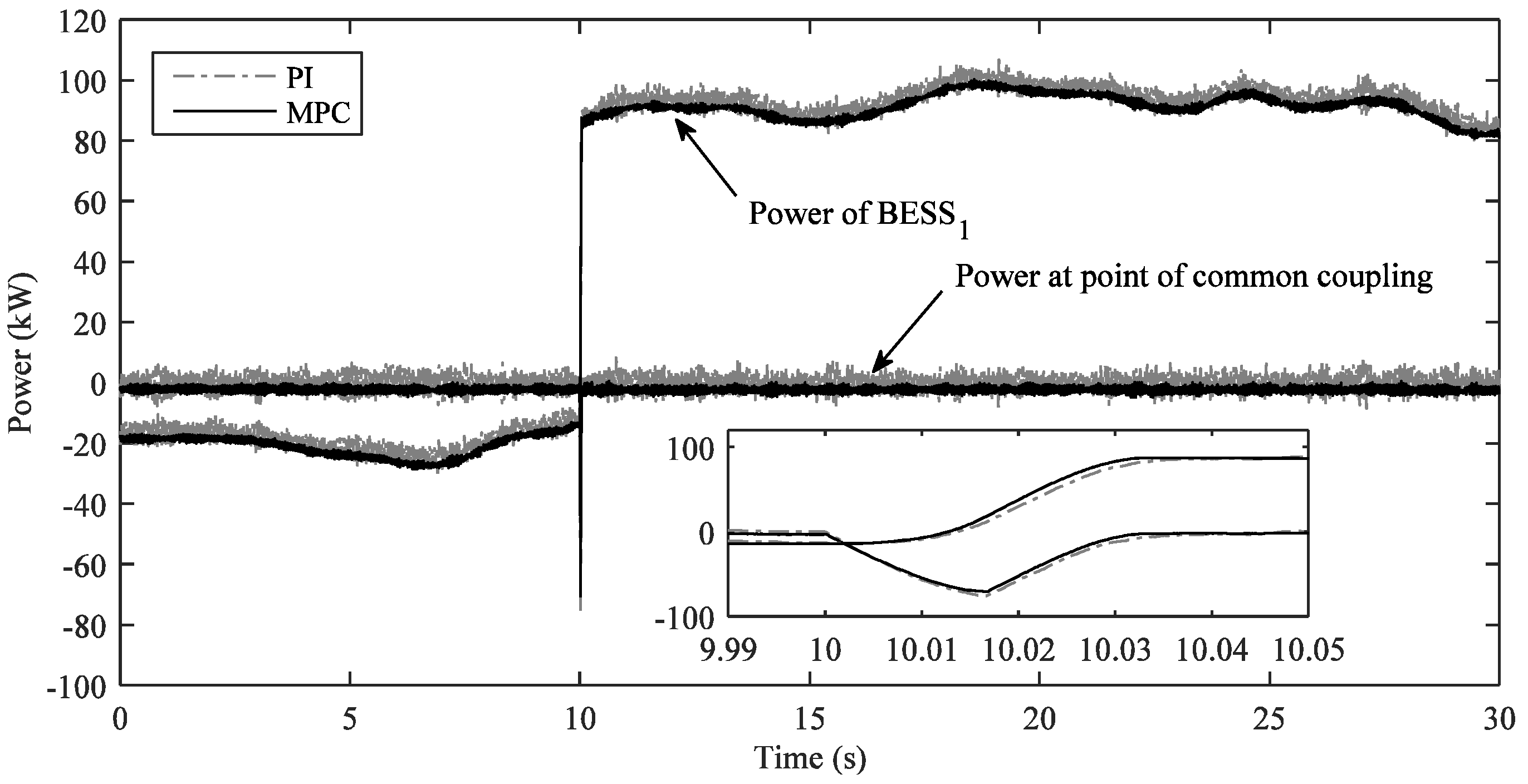
5.2. Control Microgrid in Islanded Mode
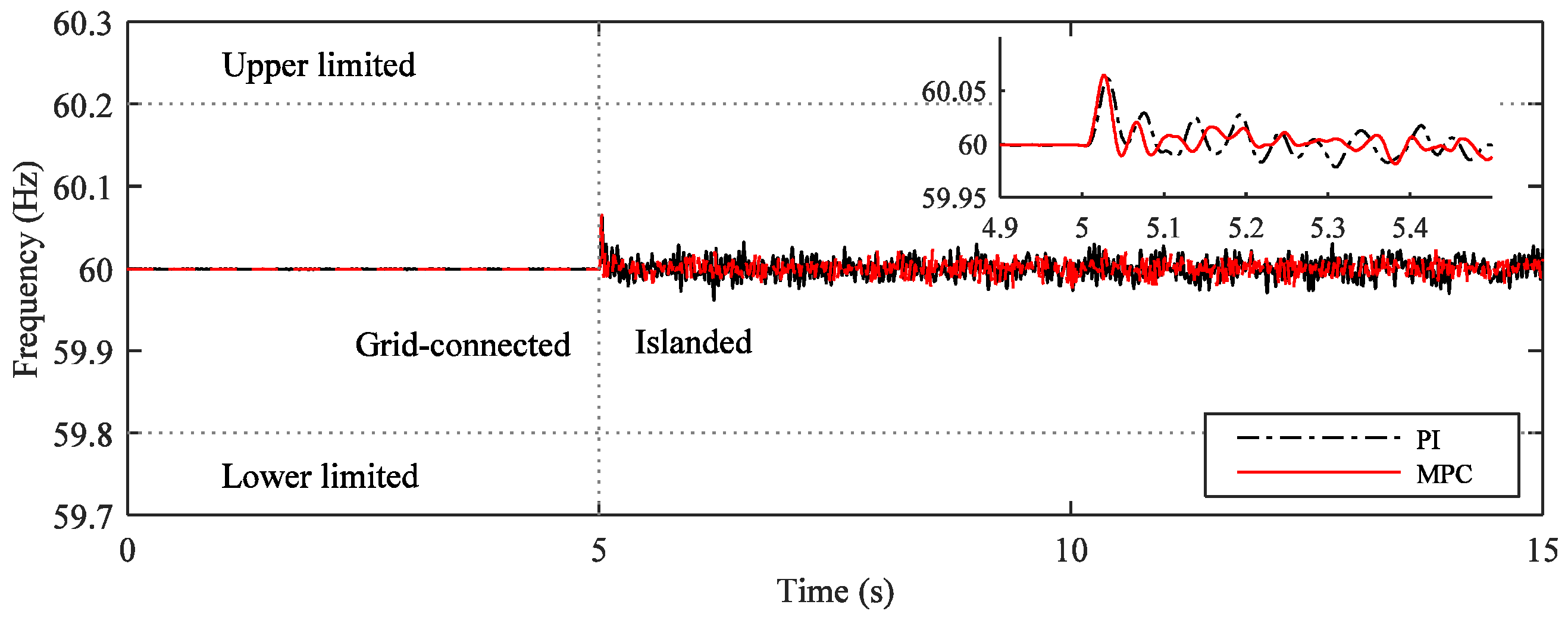
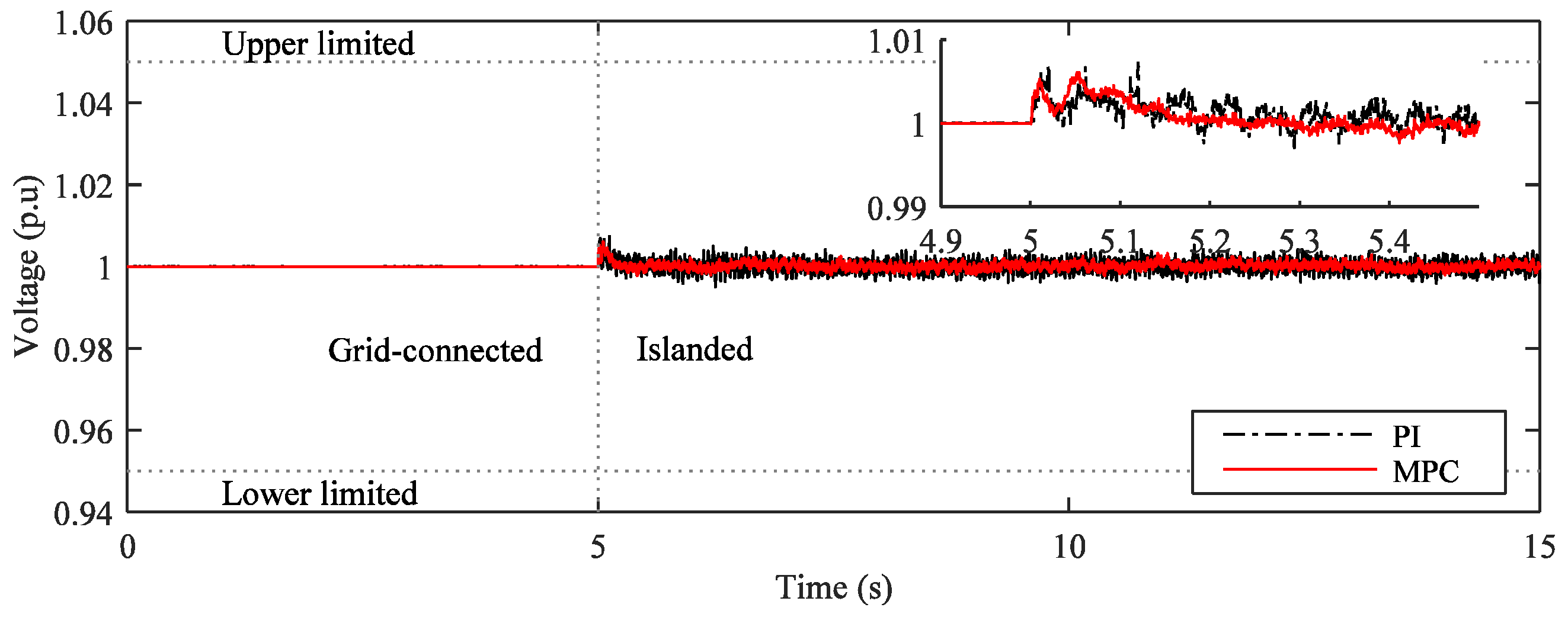
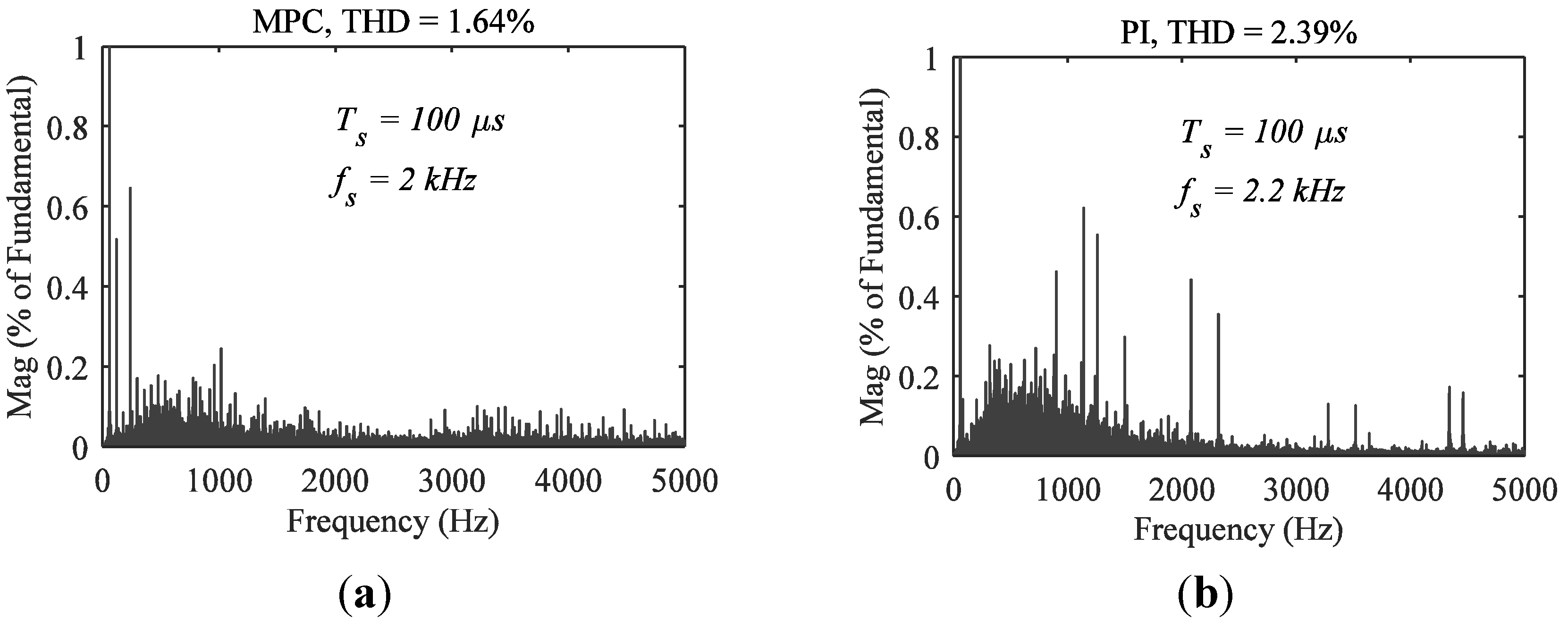
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mahmoud, M.S.; Hussain, S.A.; Abido, M.A. Modeling and control of microgrid: An overview. J. Frankl. Inst. 2014, 351, 2822–2859. [Google Scholar] [CrossRef]
- Hatziargyriou, N.D. Microgrids. IEEE Power Energy 2008, 6, 26–29. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Kim, H.-M.; Lim, Y.; Kinoshita, T. An intelligent multiagent system for autonomous microgrid operation. Energies 2012, 5, 3347–3362. [Google Scholar] [CrossRef]
- Kim, H.-M.; Kinoshita, T. A multiagent system for microgrid operation in the grid-interconnected mode. J. Electr. Eng. Technol. 2010, 2, 246–254. [Google Scholar] [CrossRef]
- Molina, M.G.; Mercado, P.E. Power flow stabilization and control of microgrid with wind generation by superconducting magnetic energy storage. IEEE Trans. Power Electron. 2011, 26, 910–922. [Google Scholar] [CrossRef]
- Inthamoussou, F.A.; Pegueroles-Queralt, J.; Bianchi, F.D. Control of a supercapacitor energy storage system for microgrid applications. IEEE Trans. Energy Conver. 2013, 28, 690–697. [Google Scholar] [CrossRef]
- Islam, F.; Al-Durra, A.; Muyeen, S.M. Smoothing of wind farm output by prediction and supervisory-control-unit-based FESS. IEEE Trans. Sustain. Energy 2013, 4, 925–933. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Yoo, H.-J.; Kim, H.-M. A flywheel energy storage system based on a doubly fed induction machine and battery for microgrid control. Energies 2015, 8, 5074–5089. [Google Scholar] [CrossRef]
- Chang, X.; Li, Y.; Zhang, W.; Wang, N.; Xue, W. Active disturbance rejection control for a flywheel energy storage system. IEEE Trans. Ind. Electron. 2015, 62, 991–1001. [Google Scholar] [CrossRef]
- Li, X. Fuzzy adaptive kalman filter for wind power output smoothing with battery energy storage system. IET Renew. Power Gener. 2012, 6, 340–347. [Google Scholar] [CrossRef]
- Li, X.; Hui, D.; Lai, X. Battery energy storage station (BESS)-based smoothing control of photovoltaic (PV) and wind power generation fluctuations. IEEE Trans. Sustain. Energy 2013, 4, 464–476. [Google Scholar] [CrossRef]
- Lawder, M.T.; Suthar, B.; Northrop, P.W.C.; De, S.; Hoff, C.M.; Leitermann, O.; Crow, M.L.; Santhanagopalan, S.; Subramanian, V.R. Battery energy storage system (BESS) and battery management system (BMS) for grid-scale applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- Duran, M.J.; Prieto, J.; Barrero, F.; Toral, S. Predictive current control of dual three-phase drives using restraned search techiniques. IEEE Trans. Ind. Electron. 2011, 58, 3253–3263. [Google Scholar] [CrossRef]
- Kouro, S.; Cortés, P.; Vargas, R.; Ammann, U.; Rodríguez, J. Model predictive control—A Simple and powerful method to control power converter. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Miranda, H.; Cortés, P.; Yuz, J.I.; Rodríguez, J. Predictive Torque control of induction machines based on state-space models. IEEE Trans. Ind. Electron. 2009, 56, 1916–1924. [Google Scholar] [CrossRef]
- Morel, F.; Xuefang, L.S.; Retif, J.M.; Allard, B.; Buttay, C. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive. IEEE Trans. Ind. Electron. 2009, 56, 2715–2728. [Google Scholar] [CrossRef]
- Bolognani, S.; Peretti, L.; Zigliotto, M. Design and implementation of model predictive control for electrical motor drives. IEEE Trans. Ind. Electron. 2009, 56, 1925–1936. [Google Scholar] [CrossRef]
- Cortés, P.; Rodríguez, J.; Antoniewicz, P.; Kazmierkowski, M. Direct power control of an AFE using predictive control. IEEE Trans. Power Electron. 2008, 23, 2516–2523. [Google Scholar] [CrossRef]
- Vargas, R.; Rodríguez, J.; Ammann, U.; Wheeler, P.W. Predictive current control of an induction machine fed by a matrix converter with reactive power control. IEEE Trans. Ind. Electron. 2008, 55, 4362–4371. [Google Scholar] [CrossRef]
- Abad, G.; Rodriguez, M.A.; Poza, J. Three-level NPC converter based predictive direct power control of the doubly fed induction machine at low constant switching frequency. IEEE Trans. Ind. Electron. 2008, 55, 4417–4429. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; Garcia, P.; Femadez, L.M.; Jurado, F. Predictive control for the energy management of a fuel-cell-battery-supercapacitor tramway. IEEE Trans. Ind. Electron. 2014, 10, 276–285. [Google Scholar] [CrossRef]
- Hredzak, B.; Agelidis, V.G.; Jang, M. A model predictive control system for a hybrid battery-ultracapacitor power source. IEEE Trans. Power Electron. 2014, 29, 1469–1479. [Google Scholar] [CrossRef]
- Akter, M.P.; Mekhilef, S.; Tan, N.M.L.; Akagi, H. Model predictive control of bidirectional AC-DC converter for energy storage system. J. Electr. Eng. Technol. 2015, 10, 165–175. [Google Scholar] [CrossRef]
- John, T.; Wang, Y.; Tan, K.T.; So, P.L. Model predictive control of distributed generation inverter in a microgrid. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies (ISGT Asia), Kuala Lumpur, Malaysia, 20–23 May 2014; pp. 657–662.
- Jafari, H.; Mahmodi, M.; Rastegar, H. Frequency control of micro-grid in autonomous mode using model predictive control. In Proceedings of the 2012 IEEE Iranian Conference on Smart Grids (ICSG), Tehran, Iran, 24–25 May 2012; pp. 1–5.
- Naeiji, N.; Hamzeh, M.; Rahimi Kian, A. A modified model predictive control method for voltage control of an inverter in islanded microgrids. In Proceedings of the 2015 IEEE Power Electronics, Drives Systems & Technologies Conference (PEDSTC), Tehran, Iran, 3–4 February 2015; pp. 555–560.
- Han, J.; Solanki, S.K.; Solanki, J. Coordinated predictive control of a wind-battery microgrid system. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 296–305. [Google Scholar] [CrossRef]
- Rodríguez, J.; Cortés, P. Predictive Control of Power Converter and Electrical Drives; John Wiley & Sons: West Sussex, UK, 2012. [Google Scholar]
- Xia, C.; Wang, M.; Song, Z.; Liu, T. Robust model predictive current control of three-phase voltage source PWM rectifier with online disturbance observation. IEEE Trans. Ind. Informat. 2012, 8, 459–471. [Google Scholar] [CrossRef]
- Antoniewicz, P.; Kazmierkowski, M.P. Virtual-flux-based predictive direct power control of AC/DC converters with online inductance estimation. IEEE Trans. Ind. Electron. 2008, 55, 4381–4390. [Google Scholar] [CrossRef]
- Rivera, M.; Yaramasu, V.; Rodriguez, J.; Wu, B. Model predictive current control of two-level four-leg inverters—Part II: Experimental implementation and validation. IEEE Trans. Power Electron. 2013, 28, 3469–3478. [Google Scholar] [CrossRef]
- Natesan, C.; Ajithan, S.; Mani, S.; Kandhasamy, P. Applicability of droop regulation technique in microgrid—A survey. Eng. J. 2014, 18, 23–35. [Google Scholar] [CrossRef]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2011; pp. 153–170. [Google Scholar]
- Yoo, H.-J.; Kim, H.-M.; Song, C.-H. A coordinated frequency control of lead-acid BESS and Li-ion BESS during islanded microgrid operation. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference (VPPC), Seoul, Korea, 9–12 October 2012; pp. 1453–1456.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-T.; Yoo, H.-J.; Kim, H.-M. Application of Model Predictive Control to BESS for Microgrid Control. Energies 2015, 8, 8798-8813. https://doi.org/10.3390/en8088798
Nguyen T-T, Yoo H-J, Kim H-M. Application of Model Predictive Control to BESS for Microgrid Control. Energies. 2015; 8(8):8798-8813. https://doi.org/10.3390/en8088798
Chicago/Turabian StyleNguyen, Thai-Thanh, Hyeong-Jun Yoo, and Hak-Man Kim. 2015. "Application of Model Predictive Control to BESS for Microgrid Control" Energies 8, no. 8: 8798-8813. https://doi.org/10.3390/en8088798







