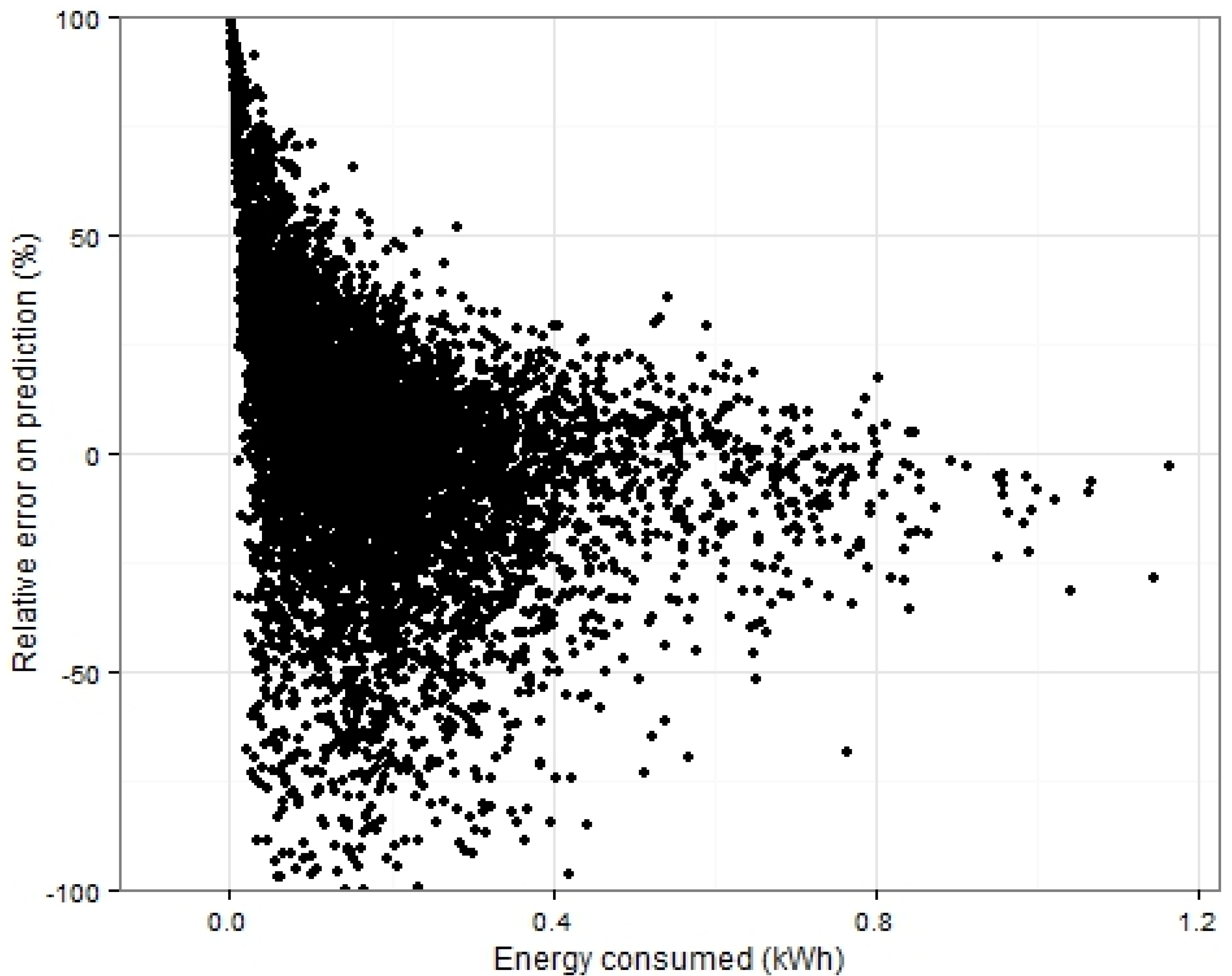
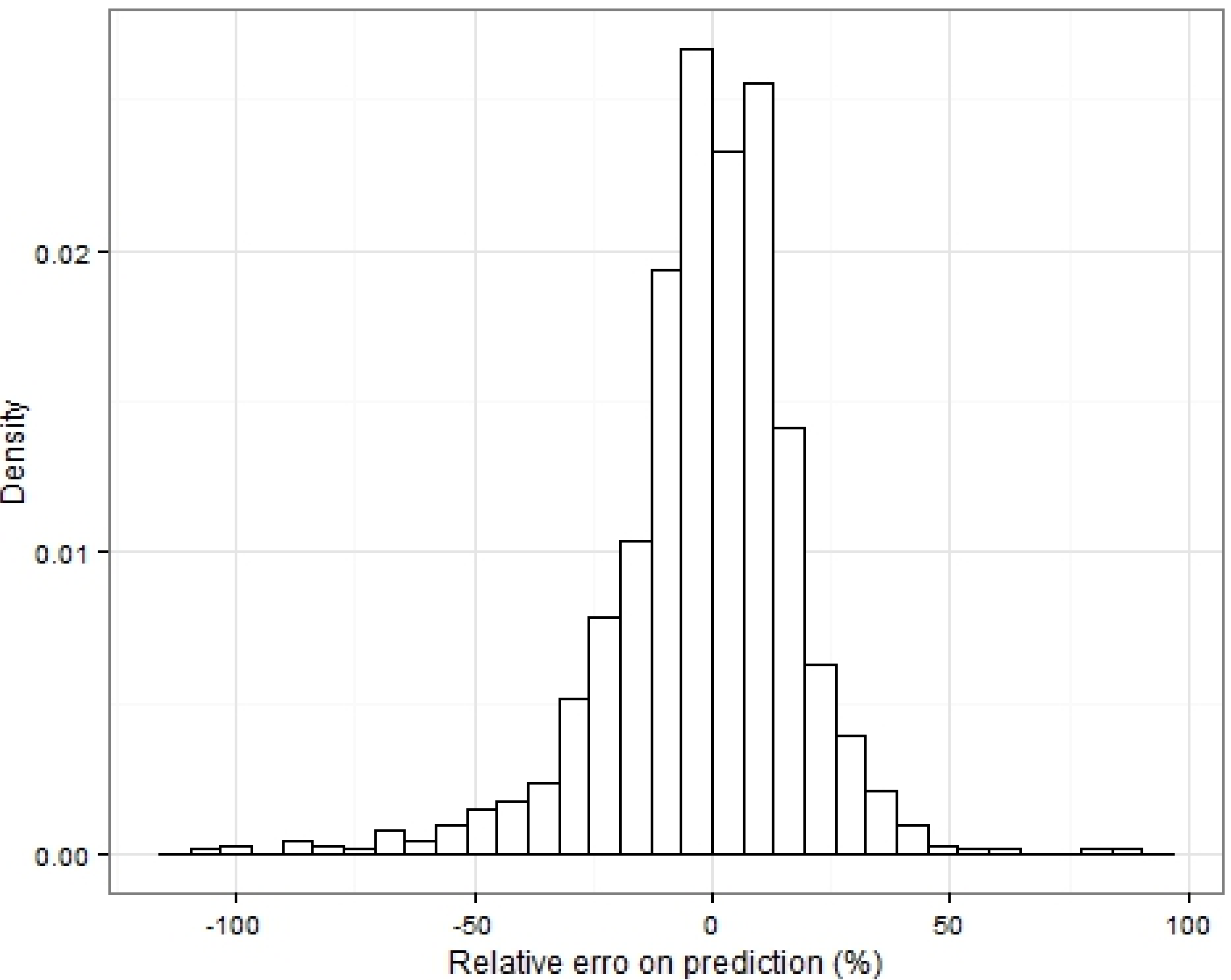
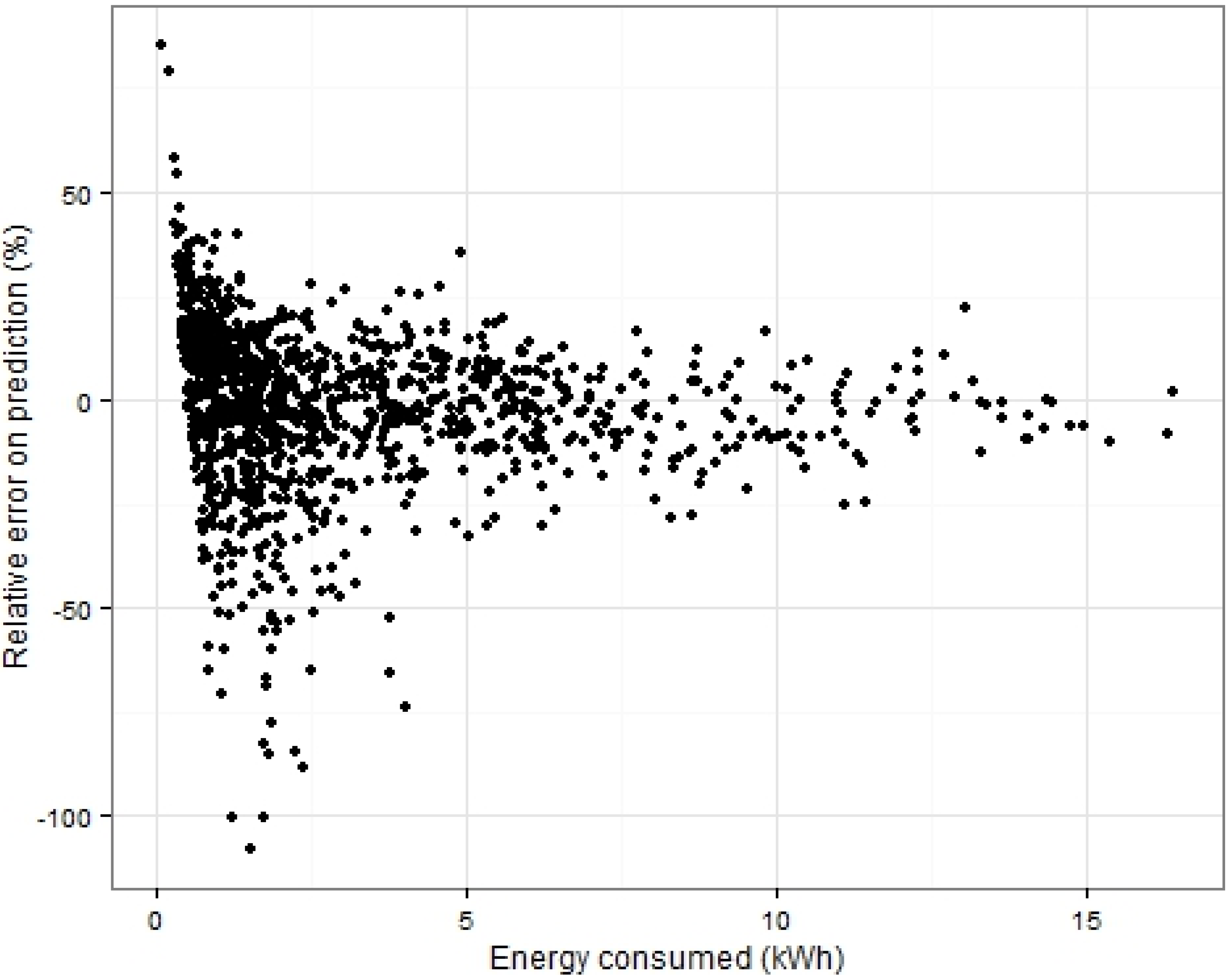
1. Introduction
The energy consumption of vehicles has been a widely assessed research topic. Until recent years, research was focused on fuel consumption of conventional vehicles, and how driving styles, ITS (Intelligent Transport System) systems, and other intelligent systems impact fuel consumption [
1]. Recently, these studies have been extended to the energy use of electric vehicles (EVs). EV energy consumption studies can generally be divided according to their purpose and model calculation methodology. Studies report the development of energy models for the purpose of EV drivetrain design and optimization [
2,
3], assessment of the influences on the energy consumption [
4,
5,
6], and global energy consumption or grid impact due to the introduction of EV or hybrid vehicles [
7,
8]. In some cases the energy model is used for an (all-electric) range prediction [
9]. The methodology for the calculation of energy consumption either consists of creating a vehicle model that simulates electrical parameters based on kinematic and dynamic requirements (backwards simulation) [
3,
5,
6,
7] or by means of statistical models based on measurements of the EV consumption, either from real-world data [
4,
9] or test cycles [
2]. Using real-world measurements has the advantage of predicting more realistic values for energy consumption, but relies on available data and statistical modeling and is often uncoupled from the vehicle dynamics and drivetrain behavior. In contrast, using a vehicle model gives you a direct link with the vehicle dynamics and drivetrain behavior, making the identification of influences of the drivetrain parameters on energy consumption more clear. Although Shankar
et al. [
4] and Neaimeh
et al. [
9] both use real-world measurements for the calculation of the energy consumption, only a limited number of external parameters are included in their models and the link with the vehicle dynamics is low. In Neaimeh
et al. [
9], the prediction was based on a simplified vehicle dynamics model and only included road inclination as an external influencing parameter, whereas Shankar
et al. [
4] use a purely statistical approach based on road type detection and its linked average consumption. This paper proposes to extend those models and fill this knowledge gap by including more external parameters while increasing the link with the vehicle dynamics. The goal here is to detect and quantify correlations between the kinematic parameters of the electric vehicle and its energy consumption using real-world data, in order to predict the real-world consumption of electric vehicles as an intermediate step towards range prediction. A model that uses real-world data compared to using cycle test values produces more realistic energy consumptions, and has added value for research topics relying on consumption data as input. Life Cycle Assessments (LCA) and Total Cost of Ownership (TCO) studies, for example, still use energy consumption based on the New European Drive Cycle (NEDC) [
10,
11,
12] or other standardized cycles.
2. Energy Models
The goal is to build up EV energy consumption models based on real-world measurements. The proposed models are statistical models based on the underlying physical principles of the vehicle dynamics and kinematics. As the ultimate goal of this study is all-electric range (AER) prediction for electric vehicles, the energy consumption considered in this paper is the energy consumption on a battery-to-wheel scope as defined in De Cauwer
et al. [
13] and corresponds to the energy drawn from the battery. Therefore, energy losses in the energy supply chain prior to the battery are not considered as they do not impact the range of the EV. As such, grid losses and charging losses are not included in this model. As De Cauwer
et al. [
13] argues, it does, however, influence real-world tank-to-wheel consumption and therefore the costs associated with real-world EV use. The battery-to-wheel consumption of an electric vehicle is a function of the required mechanical energy at the wheels, determined by the kinematic parameters over a trajectory, the drivetrain efficiency, and the energy consumption of auxiliaries. The total required mechanical energy at the wheels as a function of the kinematic parameters describing vehicle movement can be expressed in the vehicle dynamics equation:
where:
Equation (1) includes five terms, each describing a contribution to the energy consumption. These terms describe, respectively, the rolling resistance, potential energy, aerodynamic losses, kinetic energy, and energy for the acceleration of rotational parts. The aerodynamic losses and rolling resistances are pure energy losses. The potential and acceleration (kinetic) energy for EVs, unlike for conventional vehicles, can partly be recovered by regenerative braking. It is the EV battery that provides, through the numerous energy conversion steps of the drivetrain, the required energy for traction. Additionally, the EV battery also provides the energy to supply the auxiliaries. Heating and air-conditioning systems can make a significant contribution to the EV energy consumption and are ambient temperature dependent.
The proposed models are statistical models that correlate these kinematic parameters over a trajectory and the measured energy consumption at the battery, based on the vehicle dynamics equation. They are application specific, because different research topics do not necessarily have the same input data available for the model, nor do they require the same level of accuracy. Three models will be proposed here: one using the aggregated trip data, a second using aggregated trip data with additional acceleration data, and a third using shorter trip segments or “micro-trips” to calculate energy consumptions. These models have a direct link with the vehicle kinematics (vehicle speed, distance, altitude,
etc.) but do not yet allow extraction of secondary effects that impose kinematic constraints (such as traffic and weather), although this information is inherently included in the real-world data.The first energy model is a model based on macro trips,
i.e., uses aggregated values of the kinematic parameters that describe trips. These are the average vehicle speed, the distance driven, and the elevation. By applying multiple linear regression on the real-world measured values of the consumed energy and kinematic parameters for trips, a linear model is created based on the vehicle model presented above. The model presented in Lebeau
et al. [
14] used the vehicle dynamics equation to calculate the required mechanical energy and added a temperature- and time-dependent term to account for auxiliaries and temperature-dependent efficiencies. The difference here is that the prediction is purely statistical without any calculation based on theoretical values, and based on the underlying known relations between energy consumption and a number of independent variables presented in Equation (1). As such we must have a distance-dependent term describing rolling resistance, a speed-squared-dependent term describing aerodynamic losses, a height-dependent term describing potential energy, and a term describing auxiliary consumption. Two obvious factors influencing energy consumption that are present in the physical model,
i.e., acceleration and weight variation, are absent here. This approach is justified for applications where the input data for the prediction only contain aggregated values of the kinematic parameters (such as those presented in Lebeau
et al. [
14]). The weight factor cannot be extracted as this information was not in the available data. To describe the linear dependency of the auxiliary use and the energy consumption, we introduce a temperature-scaled, time-dependent term. To be able to introduce such a term into the linear regression, we reform the temperature scale to an absolute one, with 20 °C being the neutral temperature, and introduce the parameter
aux ∊ [0,1], with its value being the ratio of the time the auxiliaries are on. Now the independent variable in the regression analysis describing auxiliary consumption becomes:
The resulting formula using linear regression describing energy consumption in this simplified model then becomes:
Except for the temperature, the unit of each parameter does not matter as a linear relationship is assumed; it will only change the regression coefficients but not the result. This model will be referred to as the macro model. Using the average speed instead of the integration in the aerodynamic term
in Equation (3) (or sum because of the discrete nature of the data) introduces a (large) approximation because of the quadratic nature of the term. Moving towards a model that is no longer restricted by the available input data for prediction, the aerodynamic term in Equation (3) can be replaced by:
with:
where n is the number of recorded data points.
Similarly, the
can be used to include a term describing acceleration, so kinetic energy changes are calculated by the sum of the squared speed differences. If divided by the distance driven, this becomes a characteristic metric that is here called the constant motion factor (CMF) and describes the kinetic energy changes per unit distance:
Over a complete trip there will be as much positive change as negative change and the contributions of decelerations and accelerations to the CMF will be virtually equal. Including Equations (5) and (6) in Equation (3) gives:
This model uses non-averaged data of the speed and distance parameters and sums them up over the trip before performing the linear regression on the aggregated values. The model and its coefficients are still based on the aggregated trips but not yet based on micro-trips. Therefore we will refer to this model as the hybrid model.
Another option is to segment a trip into pieces of equal duration (micro-trips) and use the detailed measuring points to make a prediction on the micro trip consumption using linear regression. Thereafter the consumptions of the segments are integrated over the trip to predict the total consumed energy. Unlike for the macro trips, for the micro trips the contributions of the positive and negative speed changes to the CMF will not necessarily be equal and the CMF should be split in CMF+ and CMF− when vi+1 > vi and vi+1 < vi respectively.
In this model, Equation (7) evolves to:
This model has the potential to be the most accurate as it does not apply averaging and so more information resides in the values of the parameters. However, these detailed values of the kinematic parameters to be fed into the model for prediction are not necessarily readily available for any random trip, making prediction with this model impossible. To make this model applicable for the prediction of energy consumption of new trips, an additional correlation has to be done between characteristic values of these kinematic and physical (measured here) parameters and external factors so that their occurrence in the chosen trip can be predicted. This model will be referred to as the micro model.
3. Data Availability and Reliability
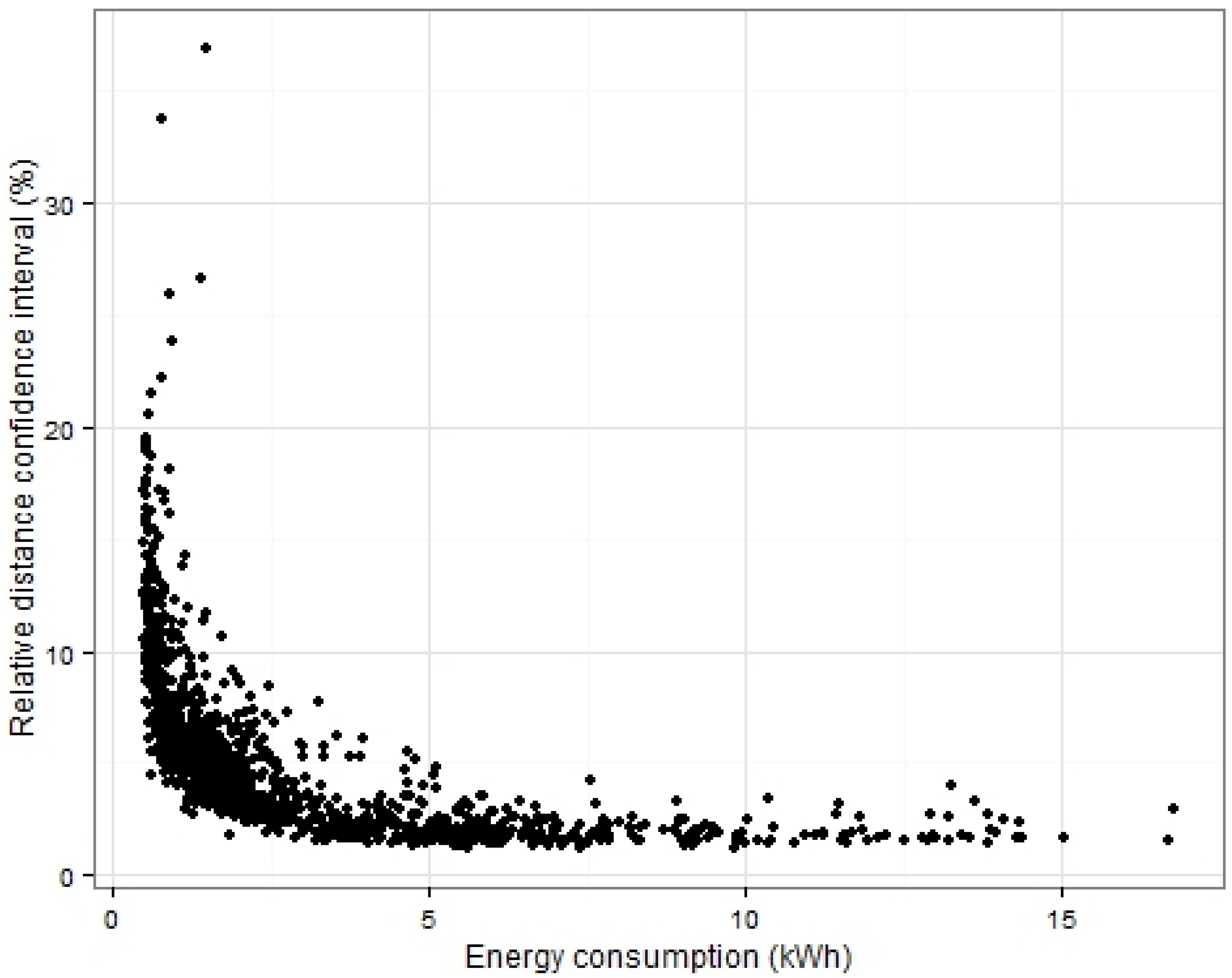
The available data were generated with a logger device recording the CAN bus signals of a 2012 Nissan Leaf (24 kWh Li-Ion battery, 80 kW electric motor, 1700 kg vehicle mass [
15]) during a two year period of 2013 and 2014. A CAN logger registered the battery current and voltage, the state-of-charge (SoC), the GPS coordinates, and the timestamp at a 1 Hz frequency. This provided a dataset containing 23,700 km distance covered, spread over the 261 days in 2013 and 312 days in 2014 when the vehicle was driven (out of a total of 730 days registered). The vehicle was driven by up to 10 individuals on a regular basis, with no restrictions of use, and was located in the outer region of the city of Brussels. This way most types of use and road topology (urban, highway, rural,
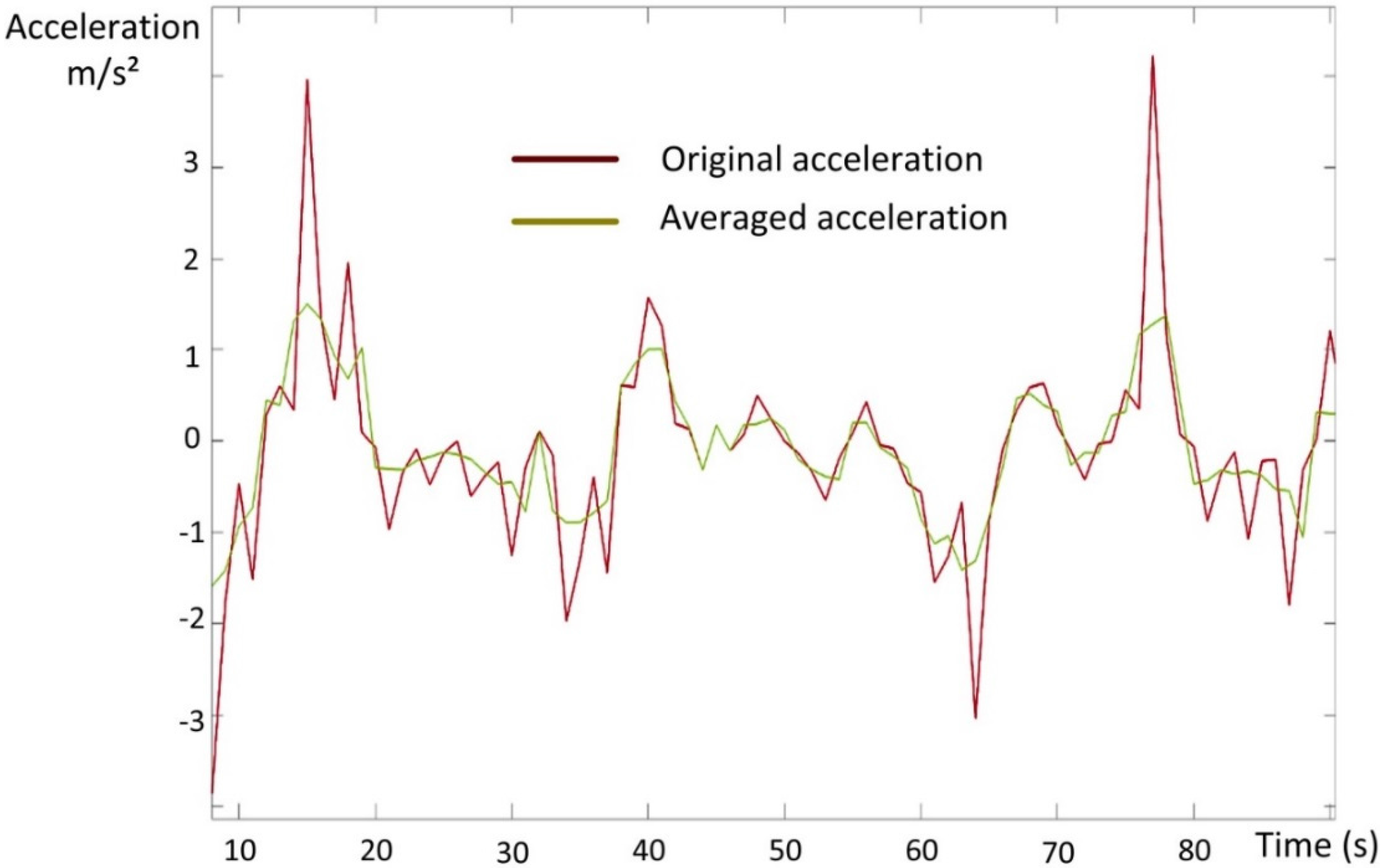
etc.) are represented in the data. However, because the data are generated by only one vehicle, the constructed models are drivetrain specific and potential differences in the impact of the external factors on real-world energy consumption for different EV types cannot be extracted from the data. The speed and acceleration values used are based on position coordinates; therefore an error exists on speed and especially acceleration. The acceleration often showed unrealistic acceleration peaks of over 2 m/s². Therefore, if the speed was monotonically increasing (positive acceleration) or decreasing (negative acceleration) over multiple measurement points, the acceleration was averaged up to a maximum of three measurement points (3 s). By increasing the duration over which the acceleration is calculated, the relative error of the acceleration decreases, but the acceleration is more averaged. The maximum of three measurement points (so 3 s) was chosen to have a balance between both. The acceleration peaks and the averaged values are illustrated in
Figure 1 by plotting the acceleration values for 2014 for a selection of data points.
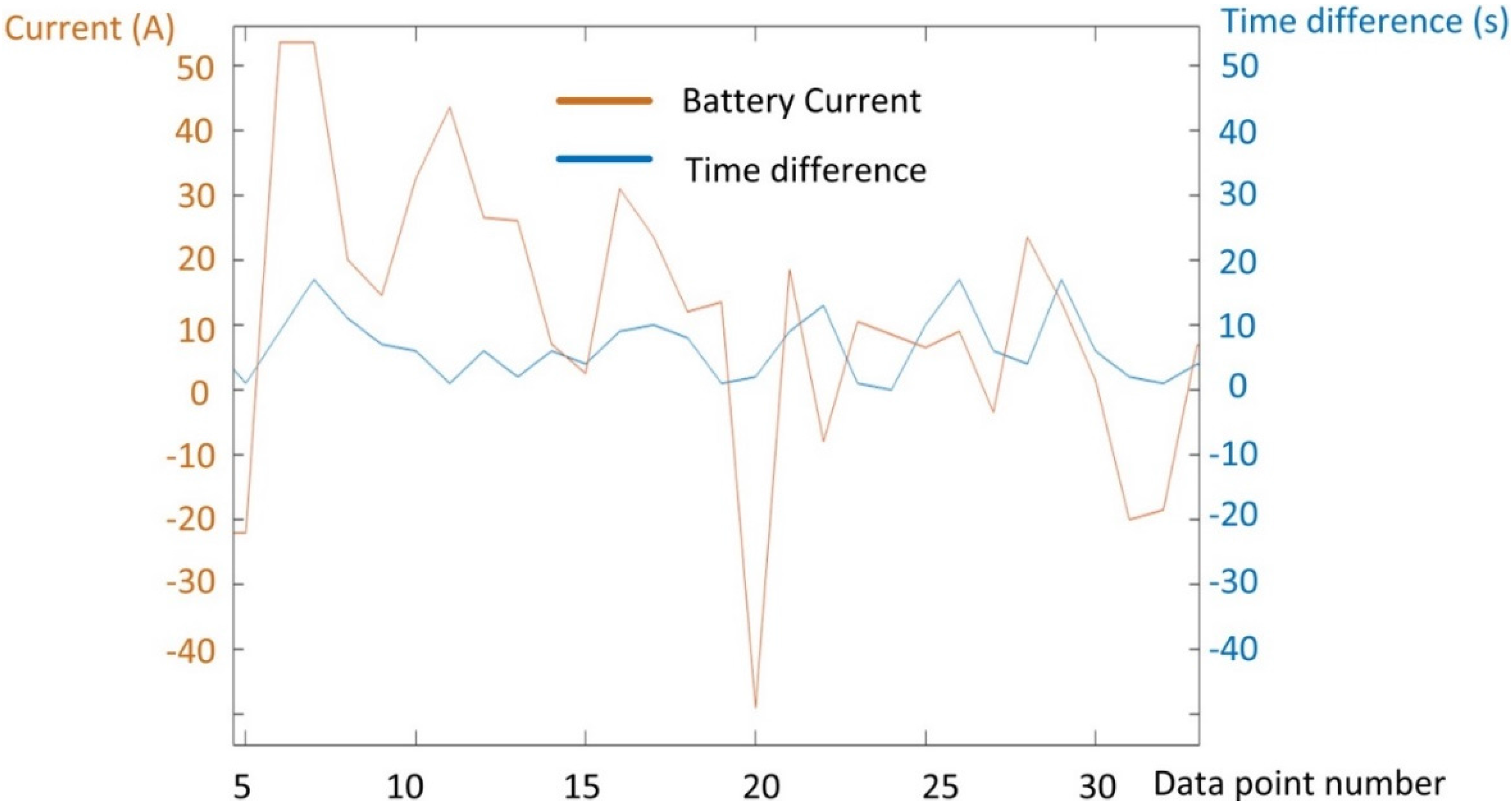
Occurrences of loss of satellite connection caused the data to “jump”,
i.e., divert from the 1 Hz data point registration. Because of this, the vehicle “jumps” to the next location, making the distance between the points the straight line distance, causing the distance and acceleration to be wrong. Moreover, as the energy consumption is calculated by integrating the battery voltage and current over time, decreasing the log frequency increases integration error. This effect can be considerable when driving into tunnels. Making a hard filter to eliminate all trips that recorded events of time lapses over 3 s resulted in only 15%–30% of the total available trips remaining. Investigation of these particular trips with time lapses showed they did not significantly alter the results of the models on a systematic basis. Therefore, when using the data structured under the form of trips, we decided not to use this hard filter but to eliminate individual cases (entire trips) after analysis using statistical post-processing tools: extreme values of the standard residuals (>2) and Cook’s distances (>1) were individually investigated and eliminated in the case of non-reliable data.
Figure 2 shows a part of a trip where time lapses are registered. It also shows the current value at those points to illustrate that data jumps at non-average current values lead to large energy errors due to the integration.
Figure 1.
Acceleration and averaged acceleration for a number of data points.
Figure 1.
Acceleration and averaged acceleration for a number of data points.
An additional problem was the occasional speed spike. The trips containing unrealistic high speed values were deleted a posteriori after detection of outliers through the same statistical post-processing tools. After the post-processing and filtering was applied, the remaining usable data for the model construction consisted of 21,300 driven kilometers. All the remaining usable data was used for the multiple linear regression and not split up into parts for model construction and model validation. The statistical nature of the model, the vast amount of measured data used, and post-processing sensitivity analysis justify this approach. However, for further improvement and usefulness of the model, the considered vehicle fleet could be extended and further validation of the individual contributions of external factors could be performed.
Figure 2.
Example of data point jumps and the current value at those points.
Figure 2.
Example of data point jumps and the current value at those points.
5. The Regenerative Braking Influencing Factors
Regenerative braking for EVs is an important part of the EV drivetrain efficiency [
16] and regenerative braking strategies are a topic of research [
16,
17,
18].
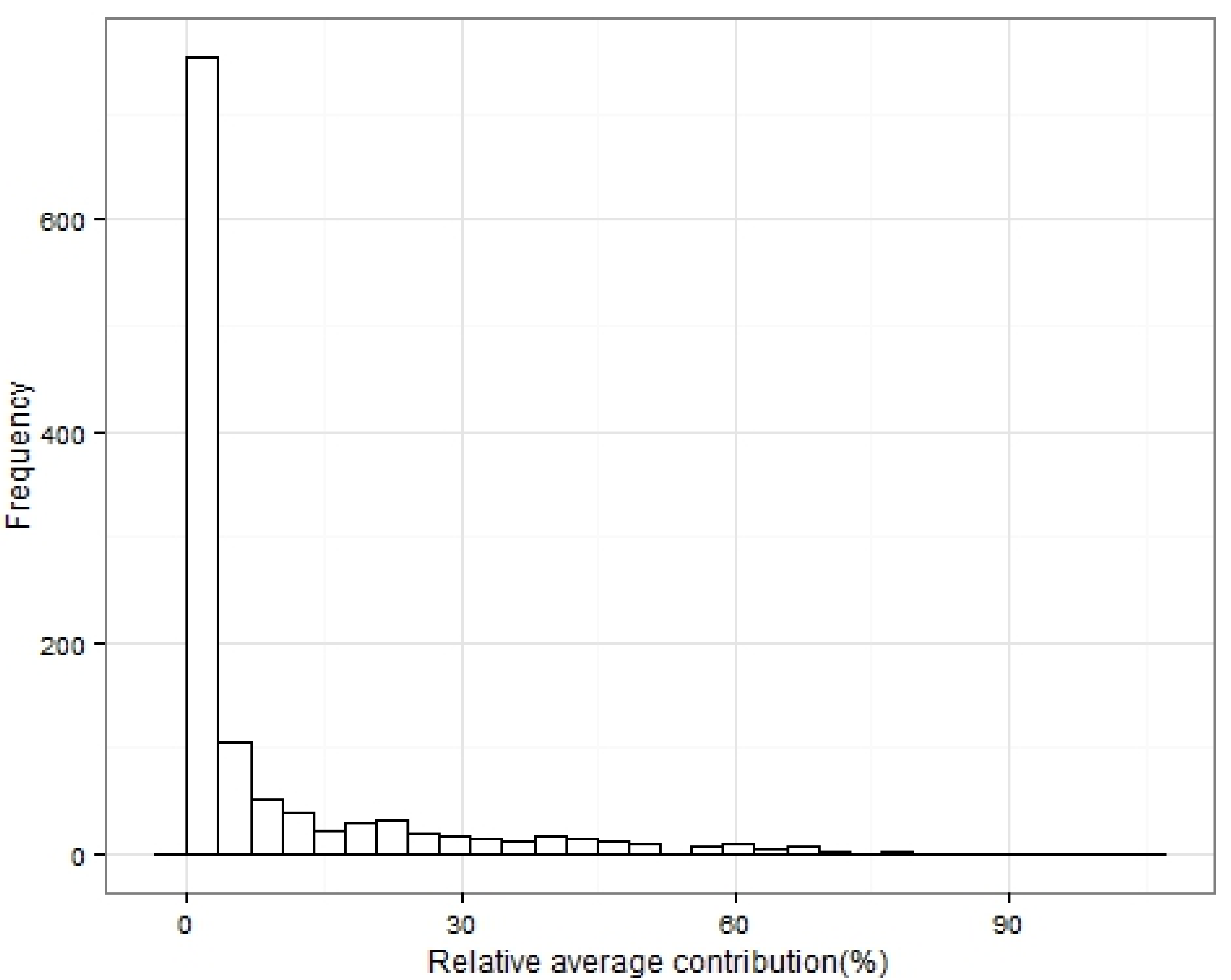
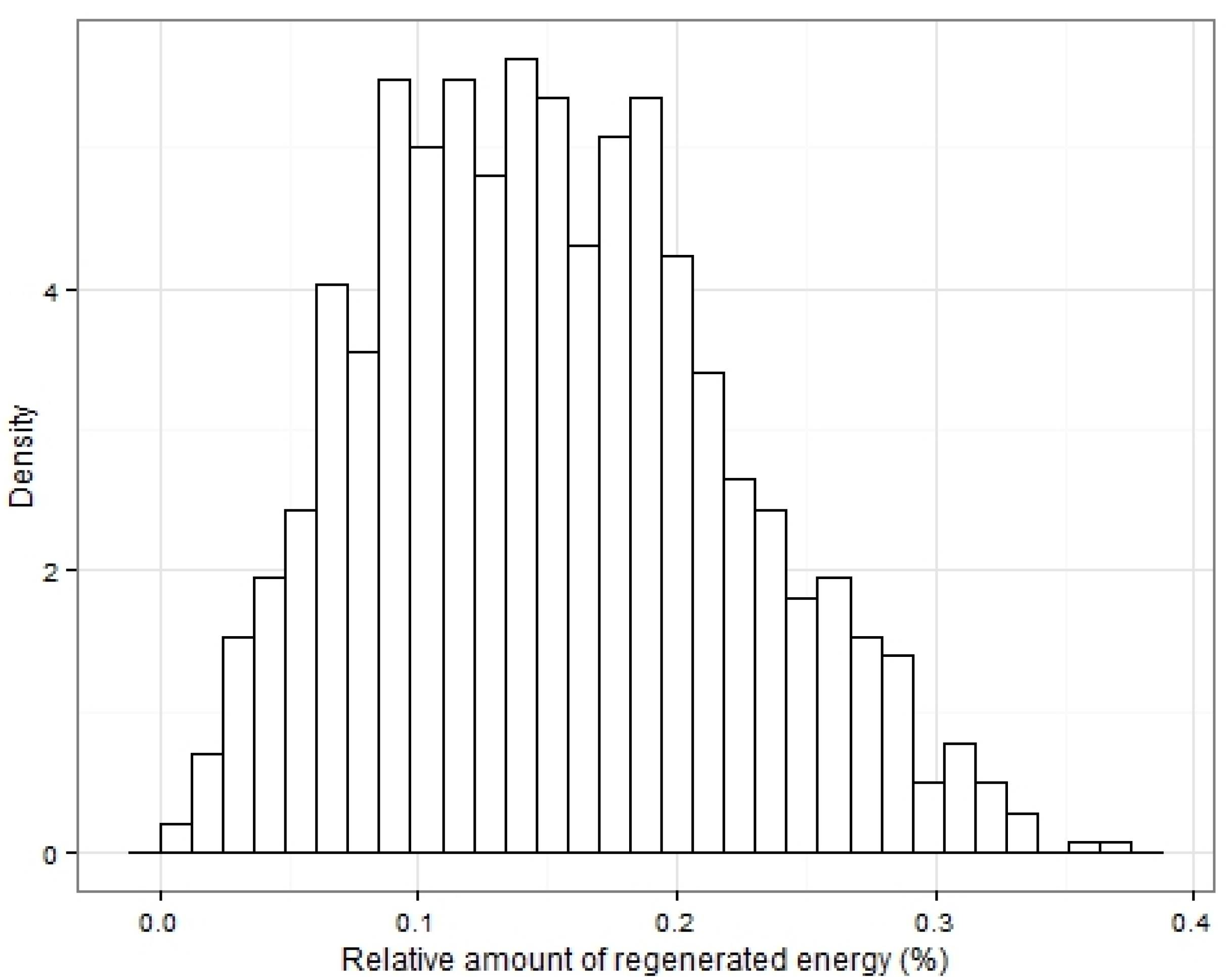
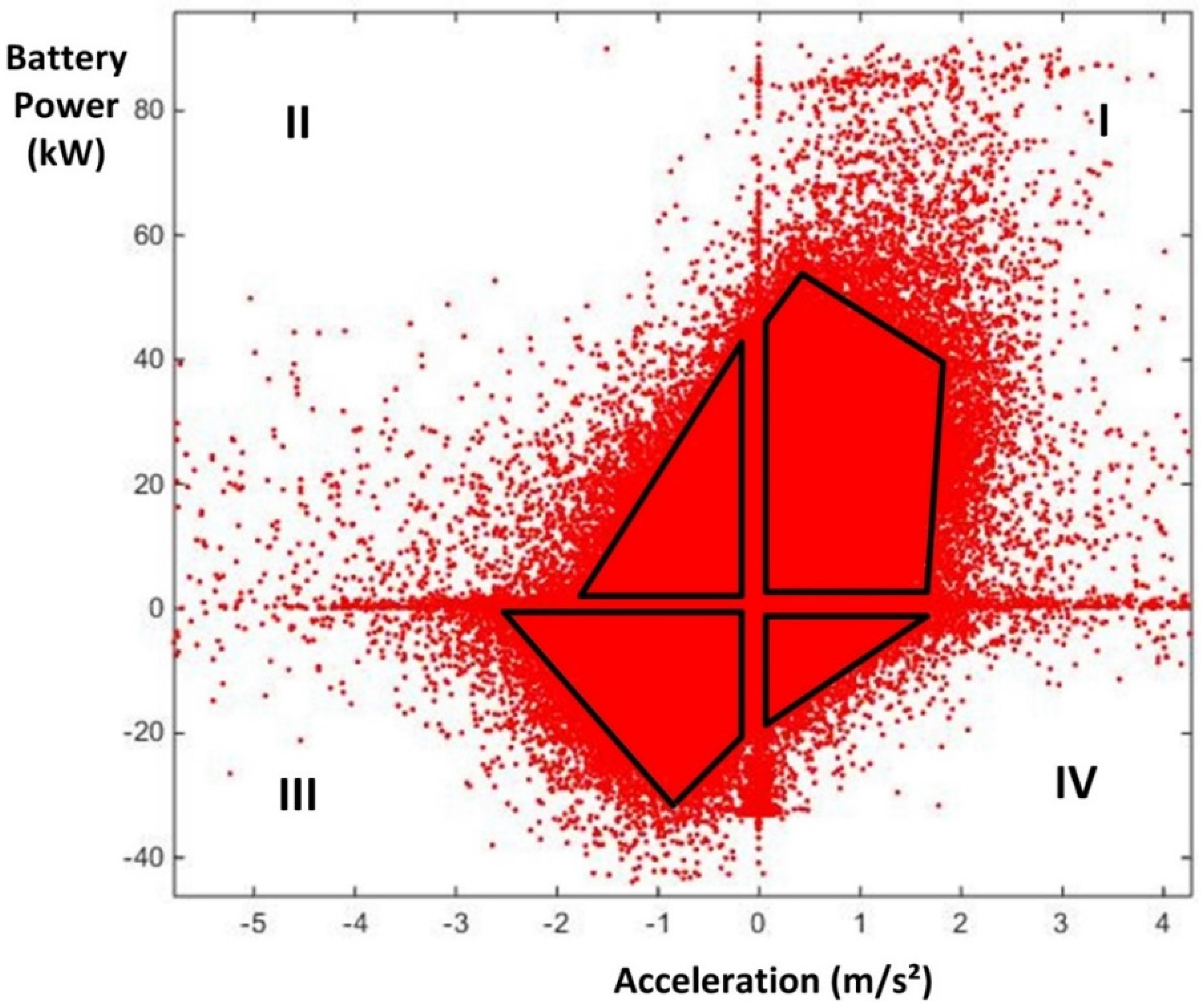
Figure 12 depicts the distribution of the relative amount of regenerated energy, defined as the ratio of the total amount of energy returned to the battery to the total amount of energy extracted from the battery.
Figure 12 shows that while the average percentage of regenerated energy is about 15%, regenerated percentages can go up to 40% in extreme cases.
Figure 12.
Distribution of regenerated energy percentage for all trips.
Figure 12.
Distribution of regenerated energy percentage for all trips.
Figure 13.
Four quadrant operation data points for the 2013 data.
Figure 13.
Four quadrant operation data points for the 2013 data.
The regenerative energy percentage is heavily dependent on the number of braking actions performed during a trip, which depends on road topology, traffic situation, and driving style, in combination with the regenerative braking strategy and drivetrain efficiency. This is shown in Mammosser
et al. [
17], where efficiency maps for regenerative braking are generated as a function of the braking force and vehicle speed using a vehicle simulation tool. In the second and third models, part of the use of the vehicle (braking actions) is represented in the CMF
+ and CMF
−, but these parameters do not include all effects. Regenerative braking only occurs within a torque and power window and driving style can have a further effect on efficient regenerative braking.
Figure 13 depicts all the 2013 data points in an
acceleration–battery power plane and illustrates the effect of driving style on regenerative braking. From
Figure 13 it is observed that the regenerative power does not exceed 40 kW and has its largest value at a specific deceleration (at about −1 m/s
2 here, but for more information on the accuracy of this value see
Section 3 (Data Availability and Reliability)). This highlights the non-linear principle of the regenerative braking energy and should be thoroughly investigated to further improve the model.
The battery power-vehicle acceleration plane can be divided into four quadrants. Quadrant one consists of actions using traction power for acceleration (so positive battery power and acceleration) and quadrant three for regenerative braking (negative power and acceleration). Less obvious are the actions residing in quadrant 2 and 4. Quadrant 2 has use of traction power but decreasing speed (negative acceleration), meaning traction power is still being used but not sufficiently to overcome resistive forces (for example, slowing down while climbing a hill). Quadrant 4 consists of actions where there is positive acceleration yet power is regenerated. This seems a very artificial condition, but the easiest example of a situation that would allow that to happen is driving steeply downhill. For ease of view, the bulk of the data in each of these quadrants are marked with a black cross section.
Figure 13 seems to have a great number of outliers or extreme values, but since more than 1 million data points are depicted, this is not abnormal. Although the arguments above show why further analysis is required to better model regenerative braking and driving style, the CMFs can be used to categorize the use of the vehicle and are important parameters in the linear regression models above.
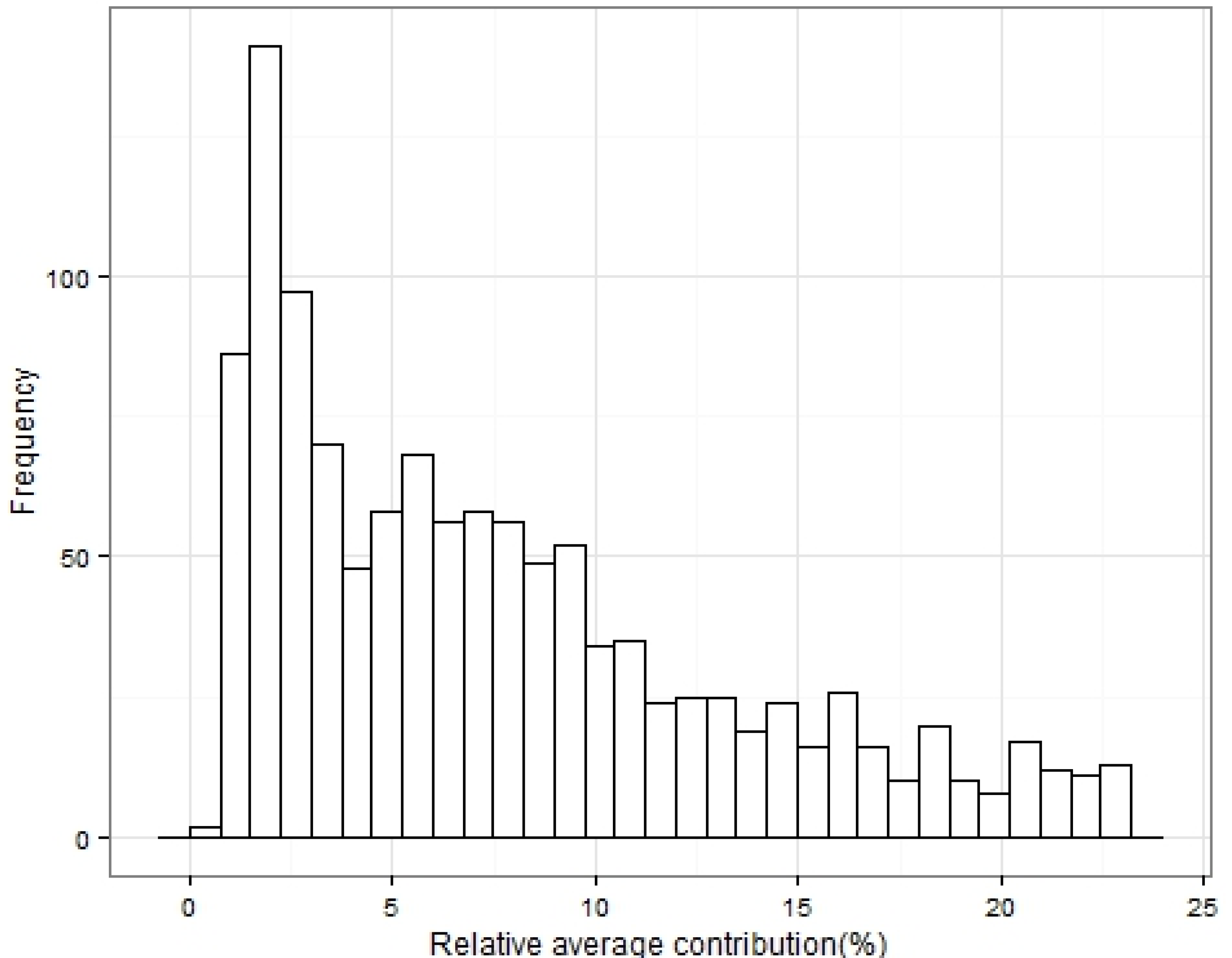
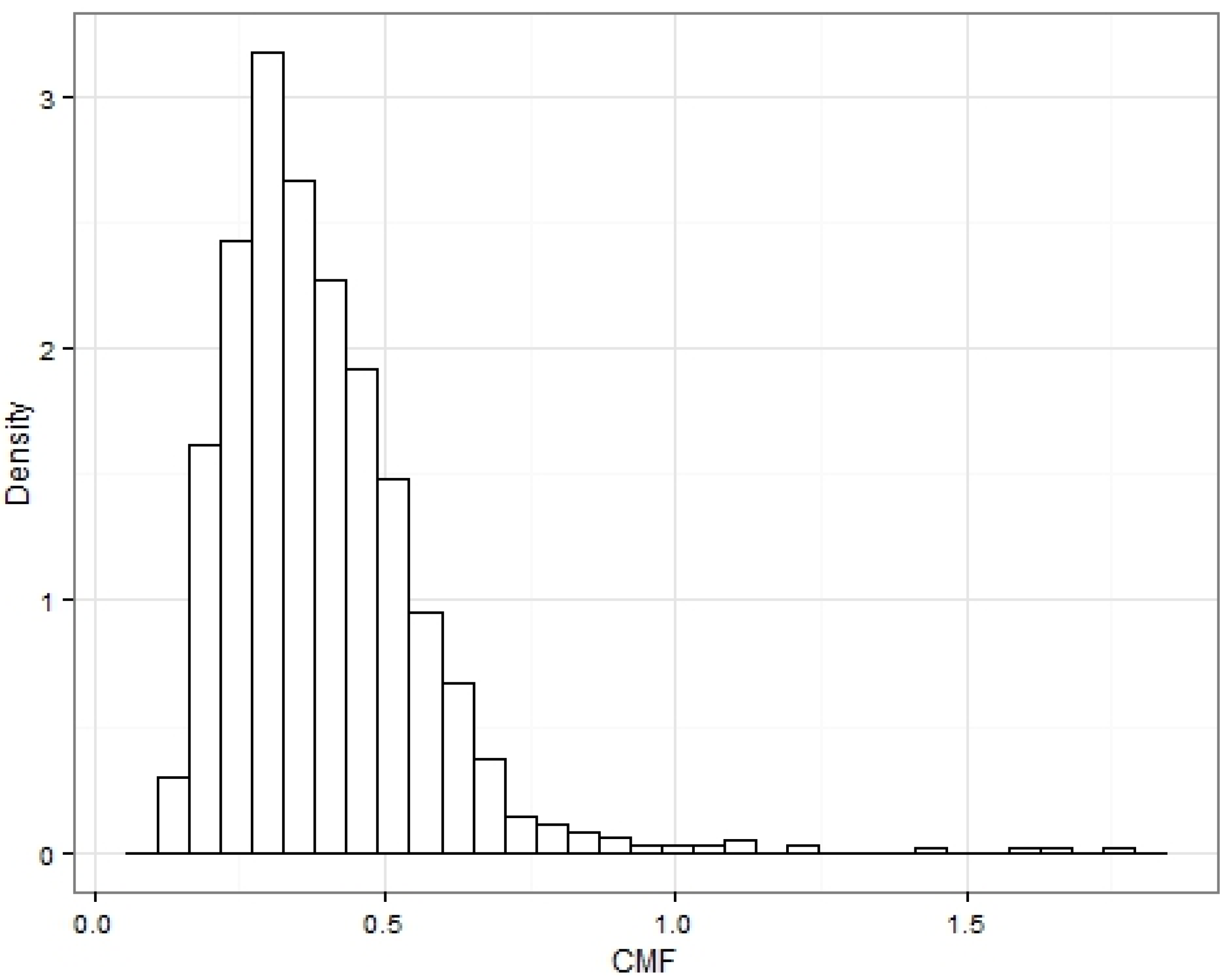
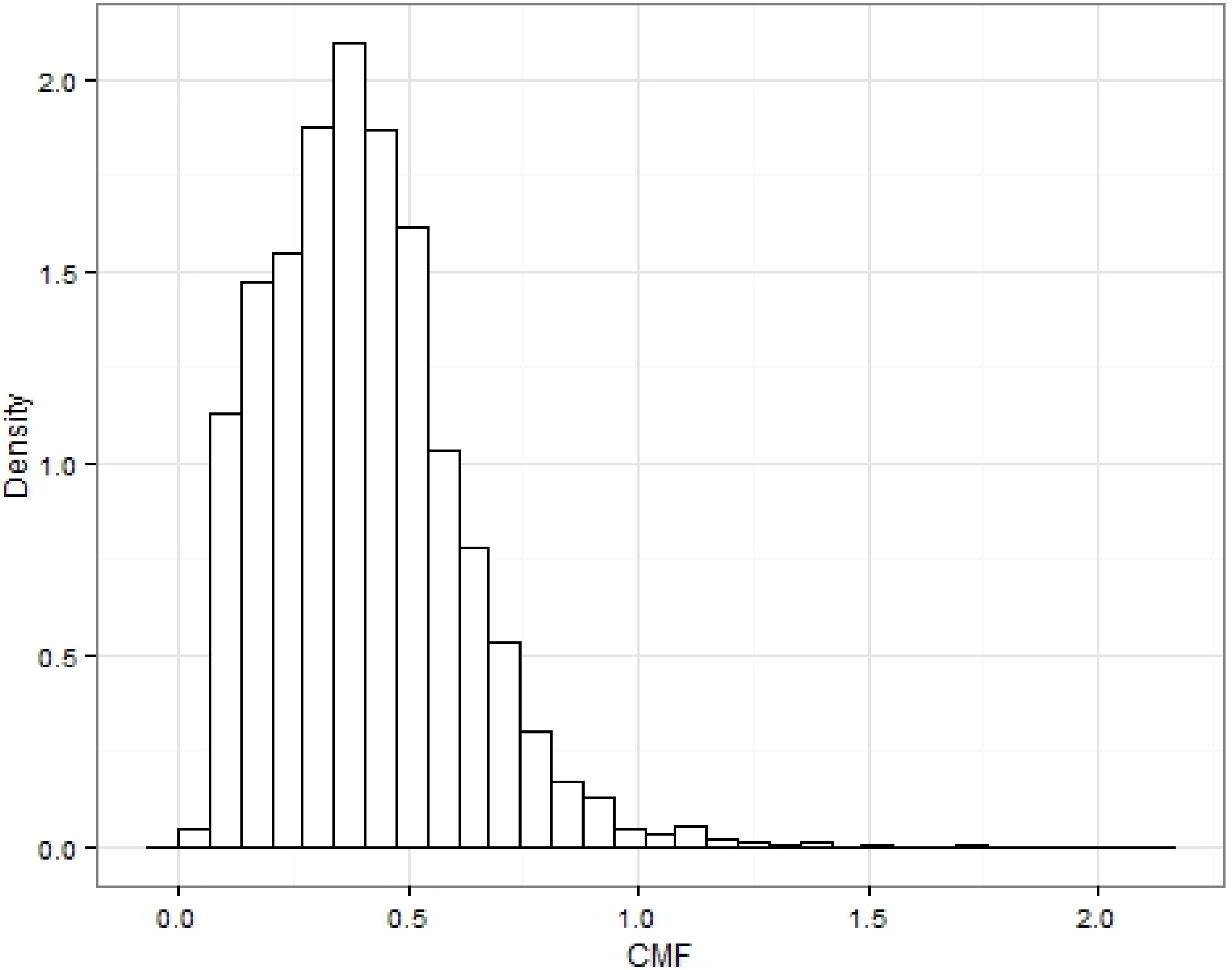
Figure 14 and
Figure 15 depict the distribution of the CMFs for macro-trips and micro-trips, respectively. Both show similar distributions and show that occurrences of CMFS greater than 1 are very rare and greater than 2 non-existent (macro trips did show CMFs greater than 2 but from statistical analysis these outliers were investigated and deleted from the sample because of the corrupted data). These CMFs are calculated from the speed in km/h and distance in km. Having a value varying between 0 and 1 is convenient for the characterization, as the CMF basically indicates the amount of kinetic energy change per km, which will vary according to the road topology/traffic situation and driving style.
Figure 14.
Histogram of the constant motion factor for the macro trips.
Figure 14.
Histogram of the constant motion factor for the macro trips.
Figure 15.
Histogram of the constant motion factor for the micro-trips.
Figure 15.
Histogram of the constant motion factor for the micro-trips.
Another parameter influencing regenerative braking is the weight of the vehicle. Increased mass results in an increased kinetic energy per unit speed. Moreover, this can shift the regenerative braking window. To investigate the influence of increased mass on vehicle consumption, during a three-month test phase in 2015 the vehicle was loaded with 200 kg. We expected to see shifted regression coefficients for the acceleration and elevation terms, as well as increased average consumption. This was not, in fact, observed, but a longer monitoring period might be required for the energy consumption to be significantly different.