A Uniform Voltage Gain Control for Alignment Robustness in Wireless EV Charging

Abstract

The efficiency of wireless power transfer is sensitive to the horizontal and vertical distances between the transmitter and receiver coils due to the magnetic coupling change. To address the output voltage variation and efficiency drop caused by misalignment, a uniform voltage gain frequency control is implemented to improve the power delivery and efficiency of wireless power transfer under misalignment. The frequency is tuned according to the amplitude and phase-frequency characteristics of coupling variations in order to maintain a uniform output voltage in the receiver coil. Experimental comparison of three control methods, including fixed frequency control, resonant frequency control, and the proposed uniform gain control was conducted and demonstrated that the uniform voltage gain control is the most robust method for managing misalignment in wireless charging applications.

1. Introduction

The world has witnessed a rapid growth of plug-in hybrid electric vehicles (PHEVs) and pure electric vehicles (EVs) over the past decade due to the increase in greenhouse gas emissions, environmental pollutants, and fossil-fuel price fluctuations. However, PHEVs and EVs still need to address range anxiety, high battery cost, and the inconvenience of charging before their widespread acceptance [1,2]. Wireless power transfer (WPT) has been an emerging research area for several years and could overcome the inconvenience of EV charging [1]. WPT allows power to transfer from a transmitter coil to a receiver coil over an air gap. Applications for WPT include mobile devices, household facilities, medical implants, and electric vehicles [1,2,3,4,5,6,7]. WPT is based on the principle of magnetic resonance couplings. The WPT system is mainly composed of a high-frequency power inverter, transmitter coil (also called “primary side”), receiver coil (also called “secondary side”), compensation capacitors, and rectification electronics. The alternating magnetic field generated by the primary side induces an alternating current in the secondary side. The rectifier converts the alternating current into direct current (DC), and then a DC-DC converter can be used to drive the desired load—for example, a battery. The compensation capacitors make up for the large inductance leakage and allow for a loose coupling, so power can transfer wirelessly across a large air gap.

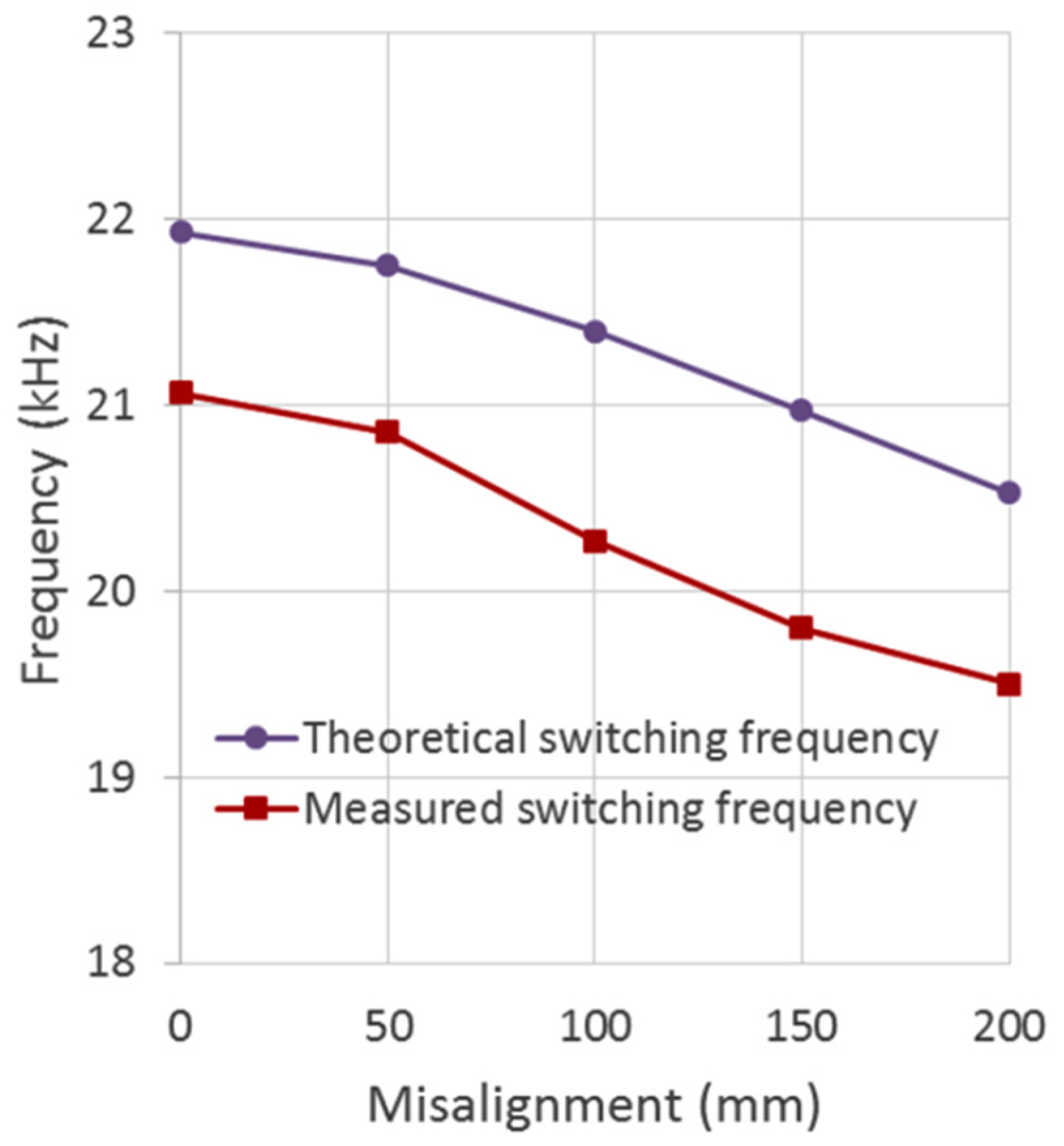
WPT systems are frequency-sensitive due to their use of magnetic resonance. Any change in the resonant components, such as inductance, capacitance or load, can influence the operating frequency of the system. Since WPT systems operate in a non-contact manner, the physical spacing between the two coils can vary, resulting in a change in magnetic coupling and eventually shifting the best switching frequency for WPT [8]. Often, EVs used in everyday life are not parked in the ideal position over the transmitter each time. The misalignment between the two coils influences the output voltage at the secondary side and hence changes the power delivery. Additionally, the chassis height might be different for different EVs, which can also influence the optimal switching frequency.

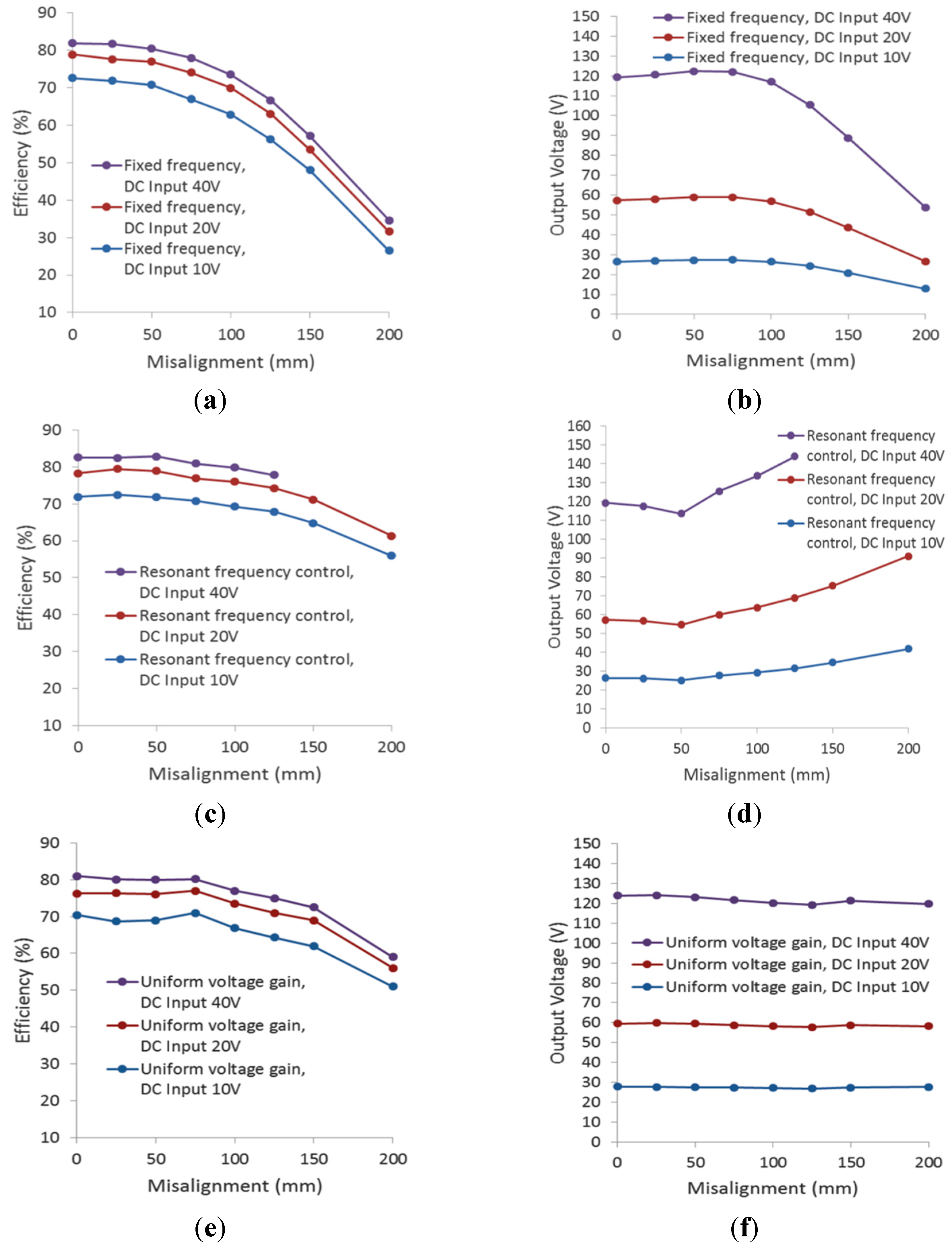
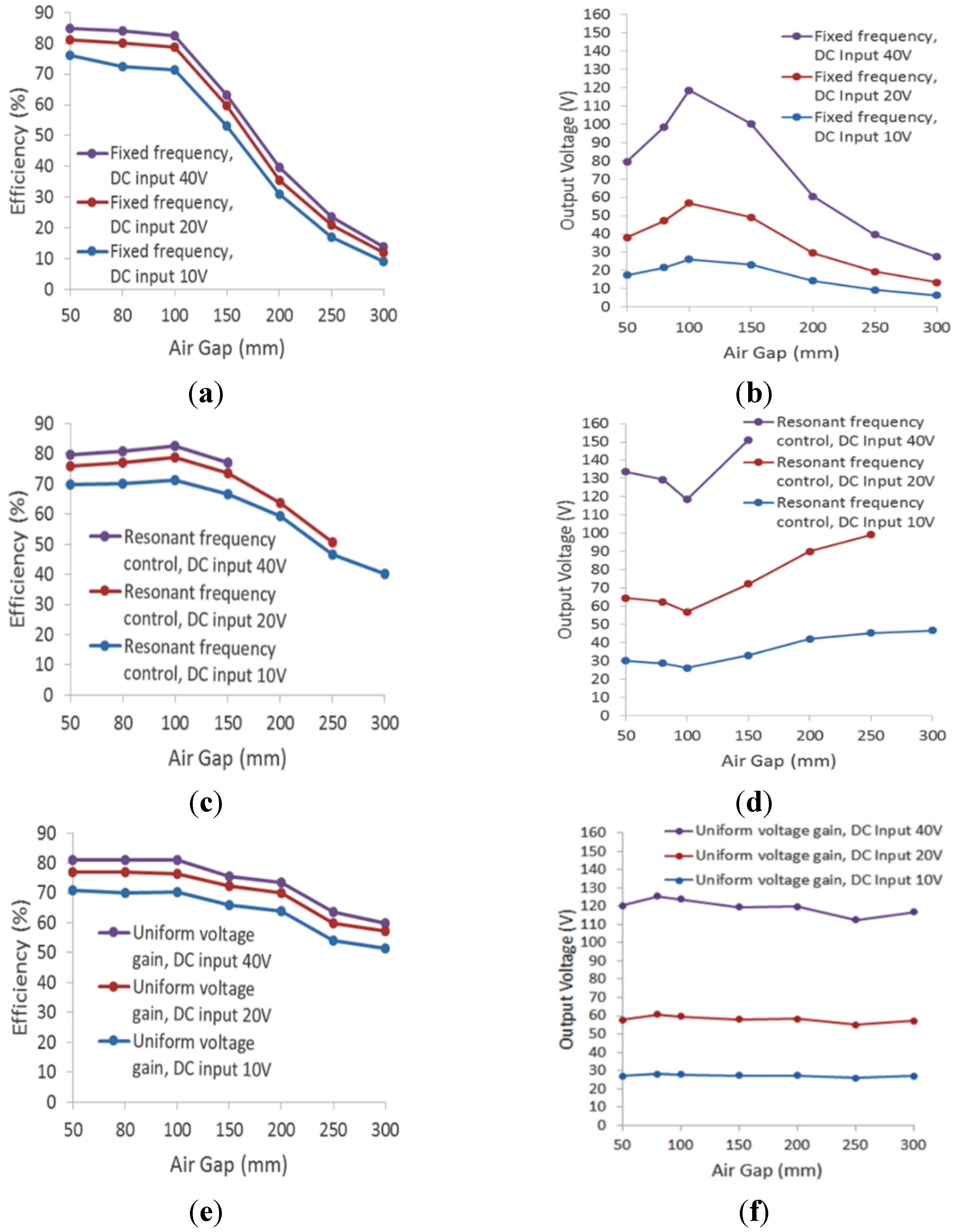
The body of this study focuses on a uniform voltage gain control method to address the frequency shift caused by misalignment and different air gaps while keeping the output voltage stable. A WPT system was developed to experimentally demonstrate the proposed frequency control under different coil alignments. There are four common resonant tank topologies for WPT based on different capacitor arrangements, including series-series (SS), series-parallel (SP), parallel-series (PS), and parallel-parallel (PP). A popular SP resonant tank is used as an example to demonstrate the frequency control in the experiment.

The WPT frequency controls fall into two categories: fixed frequency control and variable frequency control (also called “adaptive frequency control”). A fixed frequency control is normally operated under limited magnetic coupling variances, and a typical input voltage control is used to keep the charging voltage constant [9]. Resonant frequency control, which is a kind of variable frequency control, is designed to improve the WPT’s adaptability for coupling change. Resonant frequency control allows WPT to always operate at a zero phase angle between the output voltage and current in the primary inverters. However, this causes the circulating current for resonant control to be quite high. In some studies, soft switching techniques are used to minimize the power losses of switching devices where the phase angle is forced to shift to a small value, making the WPT under-coupled [1,8,10,11,12]. There are several different ways to provide resonant frequency control, such as adding auxiliary components to adapt to the variance of magnetic couplings and directly switching the frequency of gate signals. For example, Aldhaher et al. adjusted the operating frequency by using saturable reactors [13], and the WPT system developed by Han et al. can adjust a different resonant capacitor and then change the operating frequency [14]. Although these auxiliary resonant components help to switch the frequency indirectly, they increase the cost of wireless chargers, especially in high power applications, and the additional electronic elements make the WPT system bulky. An automatic frequency tuning system is proposed by Sample et al. and Kar et al., where the WPT is tuned and operated at its resonant frequency, resulting in a zero load phase angle [8,15]. Although the system is physically resonant, the output voltage at the secondary side is varied under different coil spacing, making it difficult to regulate power delivery to the battery. To address the influence of load variances on output voltage, a universal WPT was designed to charge different batteries [11,16]. However, the universal system did not compensate for misalignment issues. Moreover, a different hardware configuration was used to achieve variable frequency control for WPT. Most of the proposed variable frequency controllers calculate the voltage and current of the secondary side via wireless communications, which can increase the cost and overall system complexity.

Wireless charging systems could operate at an adaptive switching frequency with uniform voltage gain in order to compensate for misalignment. The frequency control proposed in this paper is based on voltage gain and impedance analysis across the frequency domain, and the uniform voltage gain control is achieved through phase angle feedback at the primary side.

2. Overview of the WPT System

The schematic diagram in Figure 1a illustrates the components of the WPT system with frequency control. The phase angle between output voltage and current of the inverter is measured before charging, and the digital signal processor (DSP) controller switches the frequency of pulse width modulation (PWM) signals to adjust the impedance of the system, thereby providing efficient wireless power transfer. The H-bridge inverter drives the transmitter coil to generate high-frequency electromagnetic fields. The voltage/current induced in the receiver is rectified to DC to power the load or charge a battery. Table 1 shows the parameters of the coils in the WPT system.

Figure 1b shows the power inverter packaged with liquid cooling. Two half-bridge, insulated gate bipolar transistor (IGBT) modules (FF100R12K4, Infineon) are employed to form the H-bridge controlled by a four-channel gate drive board. Since the IGBT can support a higher power rating with liquid cooling, the power inverter can be upgraded to a higher power level with minor changes. A resistor-capacitor-diode (RCD) snubber circuit is paralleled with each half-bridge switch to mitigate the undesirable spikes which can cause component failures and electromagnetic interference (EMI) issues. Moreover, these spikes can result in poor phase angle measurement, or even destroy the phase angle measurement circuit.

Figure 1. (a) Overview of the WPT system; (b) Inverter and control electronics.

Figure 1. (a) Overview of the WPT system; (b) Inverter and control electronics.

Table 1. Parameters of transmitter and receiver coils.

Specification	Primary	Secondary
Inductance (µH)	65.3	65.1
Tuning capacitor (µF)	1.0	1.0
Turns	12	12
Coil inside diameter (cm)	11	11
Coil outside diameter (cm)	56	56
Copper tube outside diameter (inch)	3/8	3/8
Copper tube inside diameter (inch)	1/4	1/4

Table 1. Parameters of transmitter and receiver coils.

Specification	Primary	Secondary
Inductance (µH)	65.3	65.1
Tuning capacitor (µF)	1.0	1.0
Turns	12	12
Coil inside diameter (cm)	11	11
Coil outside diameter (cm)	56	56
Copper tube outside diameter (inch)	3/8	3/8
Copper tube inside diameter (inch)	1/4	1/4

3. Phase Angle Measurement

The phase angle between the primary inverter’s output current and voltage can be used to calculate the WPT’s frequency. The operating frequency influences both the voltage gain and the phase angle. Thus, the phase angle must be measured in order to find and adjust the operating frequency to control the WPT system’s power delivery.

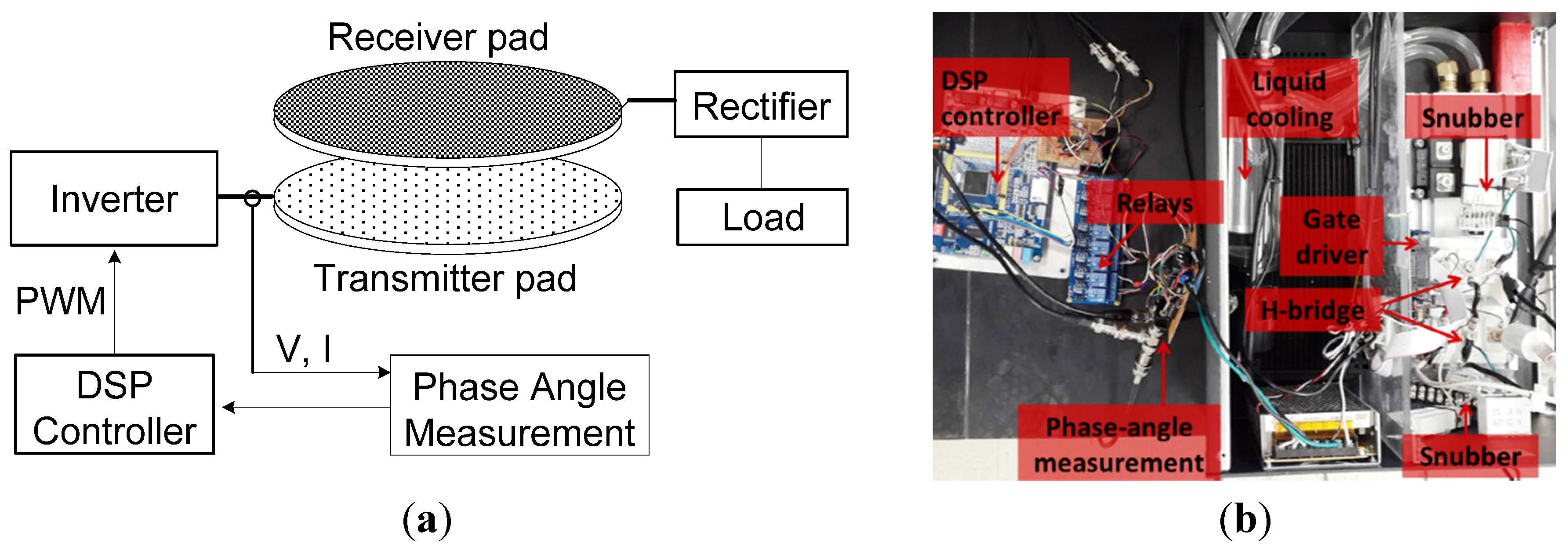
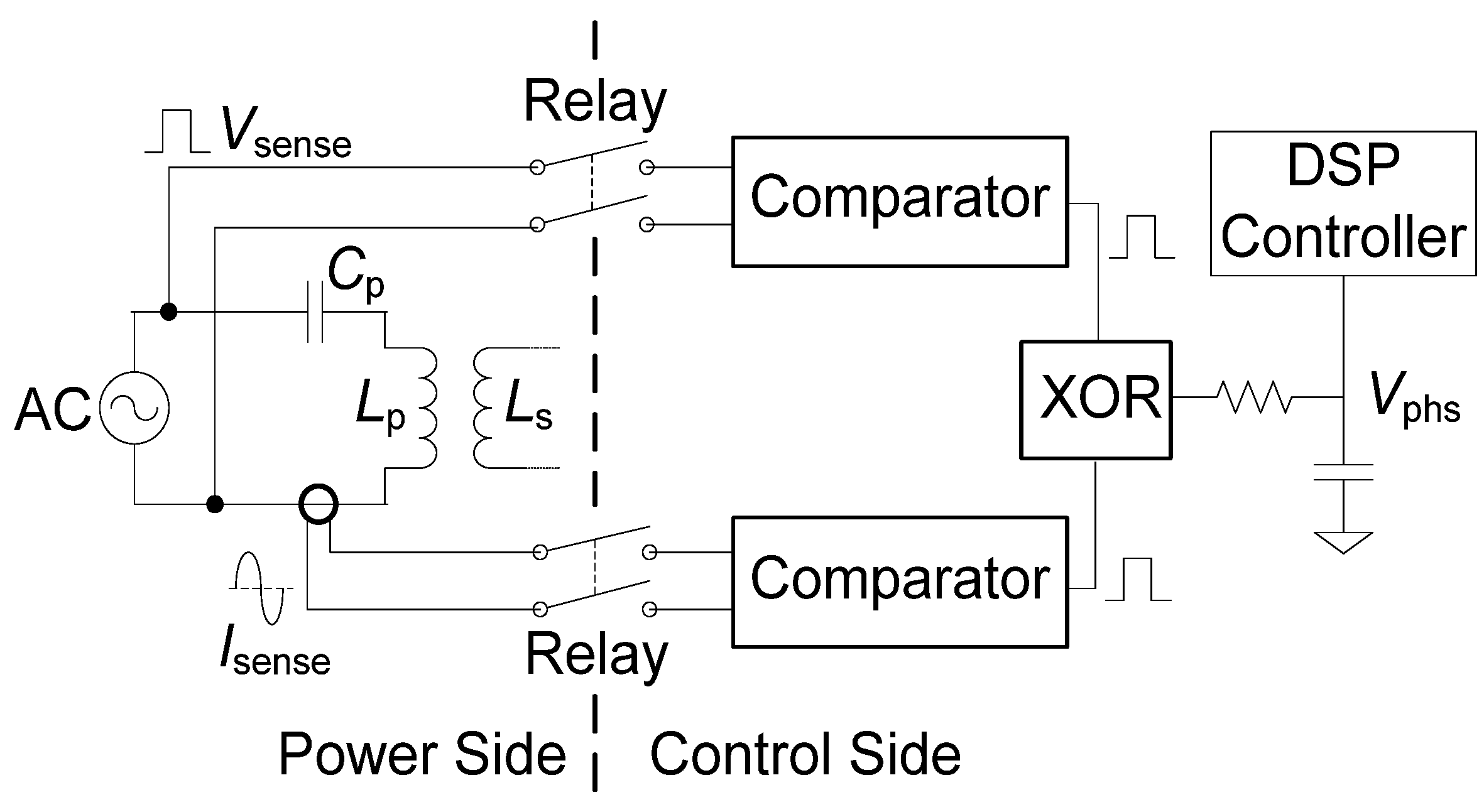
Figure 2 shows the schematic design of the phase angle measurement circuit. The output voltage (V_sense) and current (I_sense) signals from the power inverter (modeled as an AC source in Figure 2) are transformed into two square waveforms by comparators. An exclusive-OR gate (XOR) combines the two square waveforms to one pulse waveform whose width is equal to the phase delay between V_sense and I_sense. A low-pass filter converts the pulse into a DC signal V_phs, which can be acquired by the analog-to-digital converter (ADC) in the DSP controller. The DC output of the filter is proportional to the phase angle between V_sense and I_sense. Since the high power in the WPT system can destroy the comparators and control circuit, four relays were used to isolate the power and control sides, as shown in Figure 2.

Figure 2. Schematic of phase angle measurement.

Figure 2. Schematic of phase angle measurement.

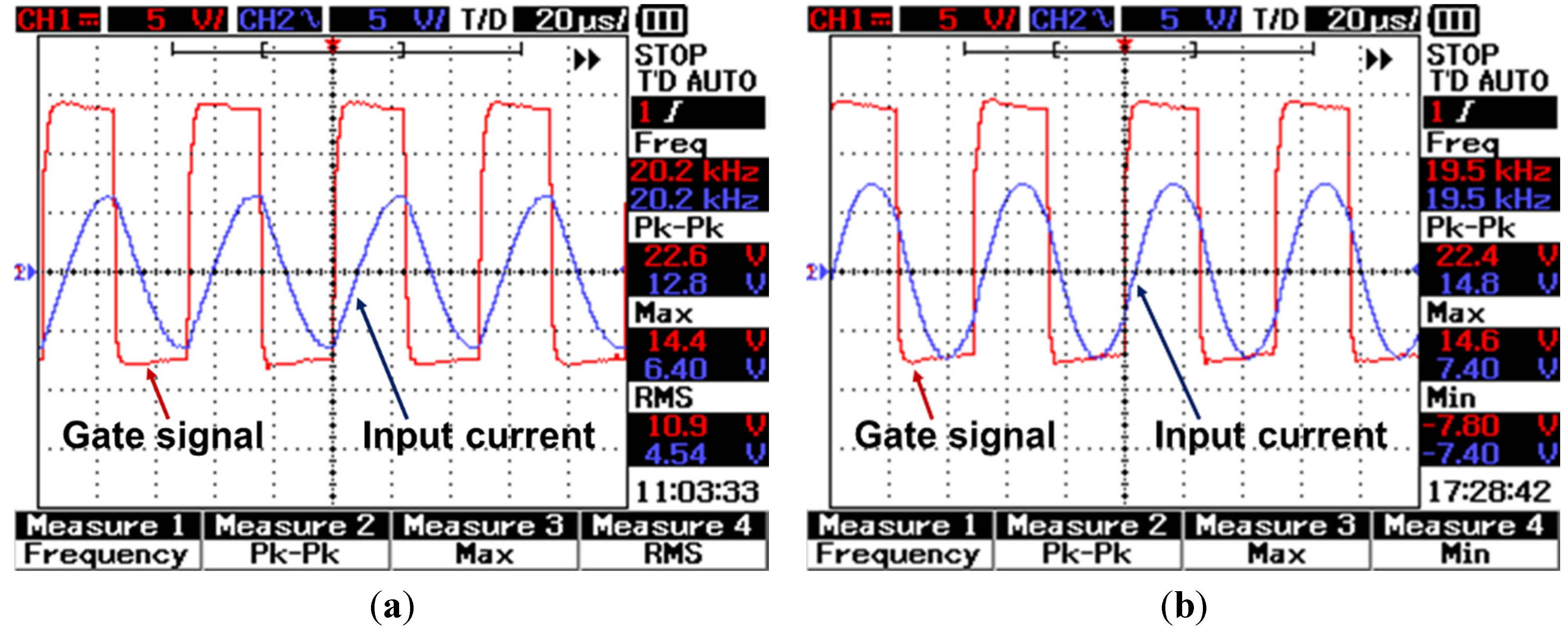
Because the switching frequency is greater than 10 kHz, and at times even 100 kHz, it is quite difficult for a commercialized hall-effect voltage sensor to pick up the high speed. The voltage probe is directly connected to the output of the power inverter and then to the comparator. A current transformer is used to measure the circulating current in the coil. Although discrete Fourier transform (DFT) can be programmed in the DSP for phase angle measurements, using an XOR and an RC filter greatly simplifies the embedded software development process and reduces the computational load of the DSP.

Once the phase angle has been measured, the switching frequency must be adjusted until uniform voltage gain is achieved. The DC input voltage is limited to 12 V during the frequency tuning process because lower voltage levels are much safer for the control circuit, and frequency tuning at high power levels would prolong the tuning time. Additionally, unreasonably fast variance of the frequency generates instability of output voltage and power emissions in high-power applications, which could damage the battery. Hence, frequency tuning is designed to occur at low power levels for both tuning speed and the safety of the circuit. After the switching frequency is well tuned, the WPT system operates at high power and starts charging.

4. Analysis and Simulation of WPT

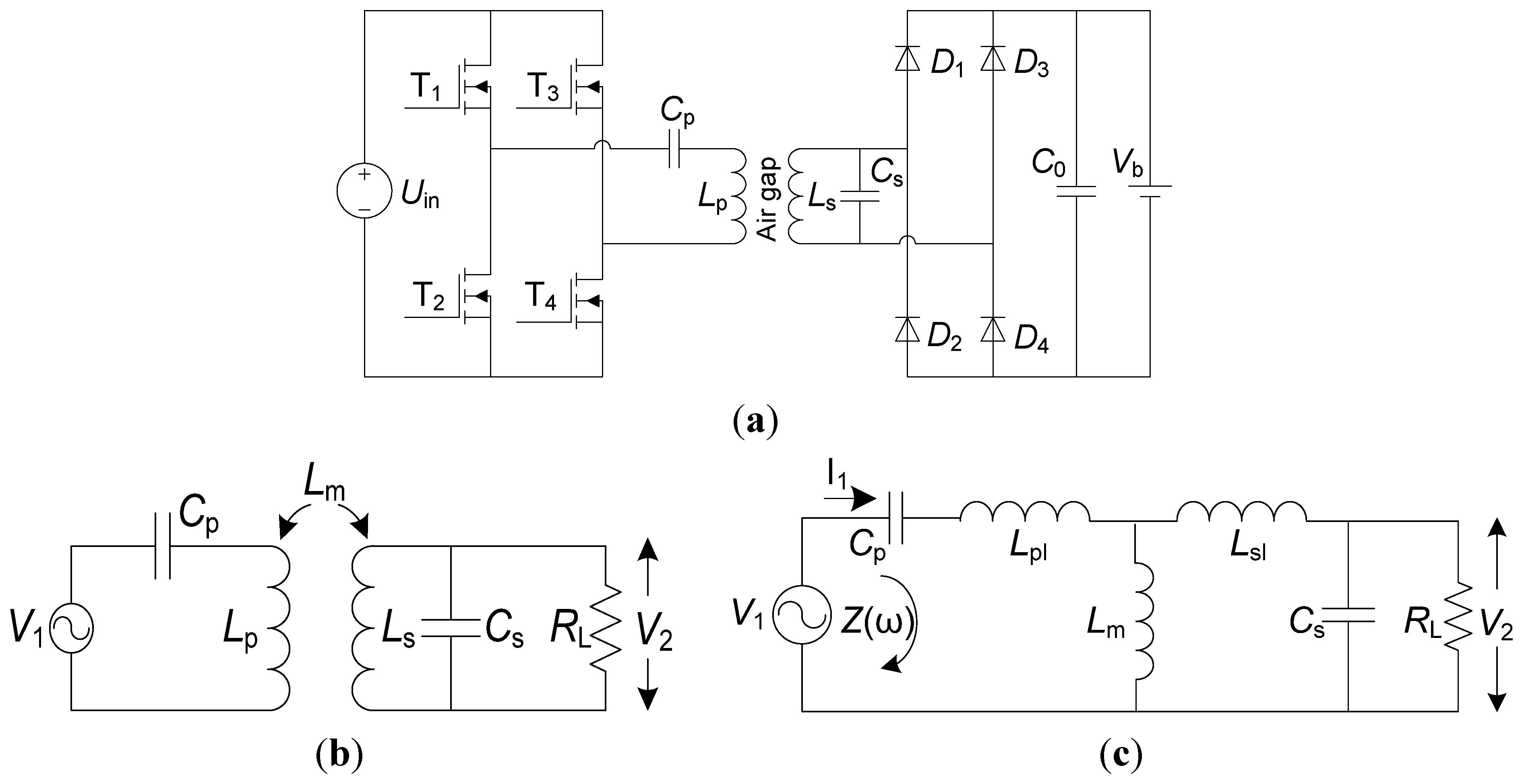
A full-bridge series-parallel WPT schematic is shown in Figure 3a. The four semi-conductors were driven by square waveform signals with a duty cycle close to but less than 50% to avoid make-before-break situations (momentary short circuit) in the inverter. Although the energy consumption of the rectifier can lower the system efficiency due to the inherent voltage drop, its simplicity makes it an ideal choice for industrial use where reliability and low cost are highly valued.

Figure 3b is a simplified series-parallel circuit diagram, and Figure 3c is the corresponding equivalent circuit. Equation (1) describes the circuit impedance (Z) in terms of the switching frequency (ω).

$$Z(\omega )=\frac{1}{j\omega C_p}+j\omega L_{pl}+j\omega L_m//\left(j\omega L_{sl}+\frac{1}{j\omega C_s}//R_L\right)$$

(1)

where C_p is the series tuning capacitance of the primary side and C_s is the tuning capacitance of the secondary side. C_p must equal C_s to achieve resonance. L_pl and L_sl are the leakage inductances of each coil. Since both coils are the same, L_pl equals L_sl. L_m is the mutual inductance. The leakage and mutual inductance can be experimentally measured. The battery is equivalent to a resistive load, R_L, which can be calculated using the delivered power and voltage across the battery. For a desired 1.4 kW/120 V battery charging condition, R_L is 20 Ω. j is the imaginary unit.

The coupling coefficient k is defined as

$$k=\frac{L_m}{\sqrt{L_p{L}_s}}$$

(2)

$$L_p=L_{pl}+L_m$$

(3)

$$L_s=L_{sl}+L_m$$

(4)

The voltage gain G is the ratio of output voltage V₂ over input voltage V₁ as shown in Figure 3c and is determined by

$$G=\left|\frac{{\omega }^2{L}_m{C}_p{R}_L}{{\omega }^4{L}_p{L}_s{C}_p{C}_s{R}_L(1-k^2)-{\omega }^2{R}_L(L_p{C}_p+L_s{C}_s)+R_L-j({\omega }^3{L}_p{L}_s{C}_p(1-k^2)-\omega L_s)}\right|$$

(5)

Figure 3. Circuit diagram of proposed WPT system: (a) SP topology for WPT; (b) Simplified SP topology; (c) Equivalent circuit of SP topology.

Figure 3. Circuit diagram of proposed WPT system: (a) SP topology for WPT; (b) Simplified SP topology; (c) Equivalent circuit of SP topology.

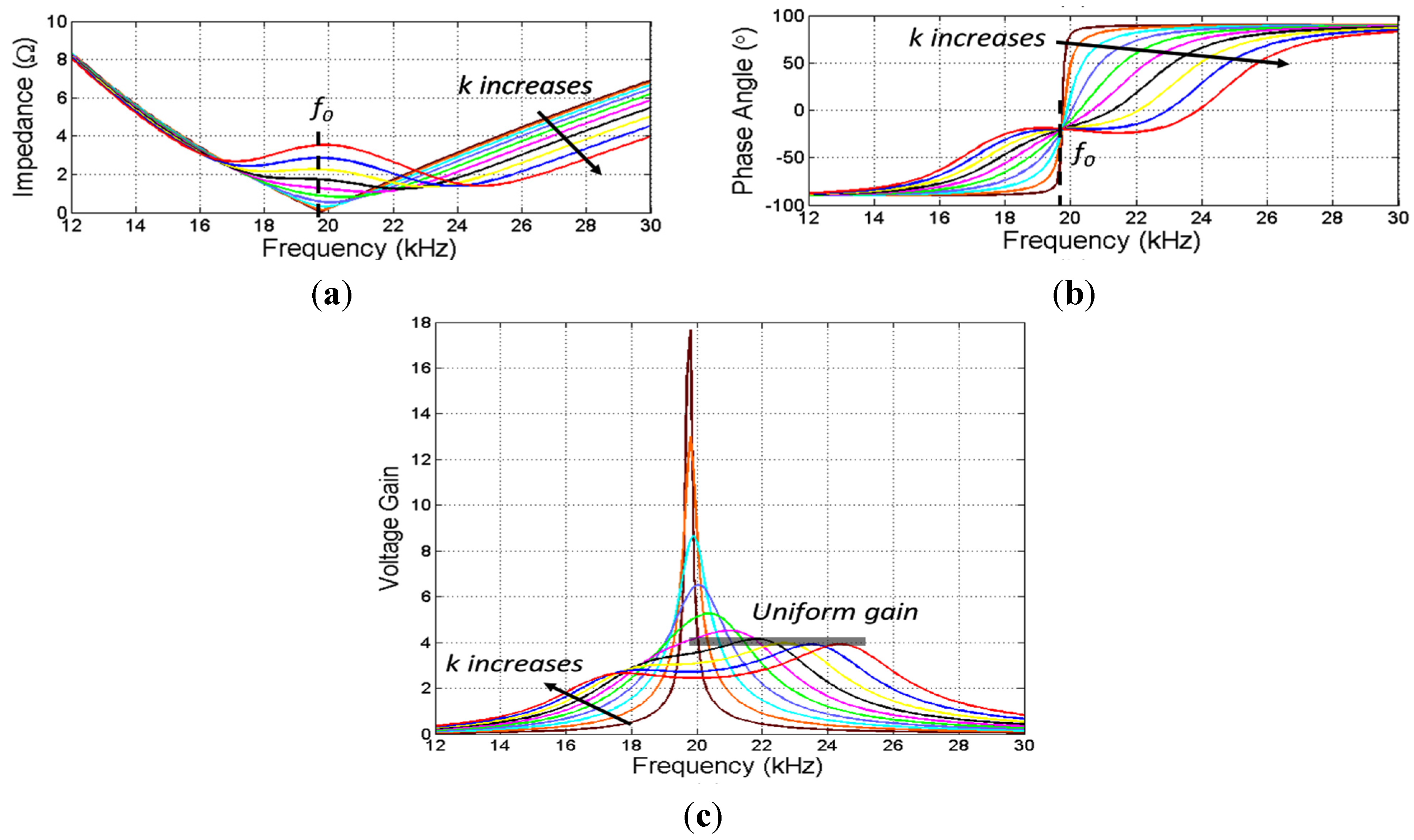
The mutual inductance changes with different coil alignments, which can cause a shift in the best switching frequency for WPT. Figure 4 is a simulation result of impedance and voltage gain against frequency performed in Simulink (MathWorks, Natrick, MA, USA). Figure 4a,b show that the resonant frequency of WPT varies due to different magnetic couplings. Figure 4c is the voltage gain curve in the frequency domain. Although the WPT system has purely resistive impedance if operating at the resonant frequency, the voltage gain can change dramatically with different couplings, meaning that misalignment can cause the voltage output and power delivery to be unstable. The output voltage at resonance can be extremely high even under a weak coupling.

Although voltage gain varies at a specific frequency according to different magnetic couplings, uniform voltage gain can be achieved for a given coupling by changing the switching frequency. In Figure 4b, each curve goes through one fixed phase angle value at frequency f₀. The phase angle is fixed at f₀ no matter how the coupling varies, but the voltage gain G and impedance magnitude are the most unstable at f₀, so the WPT system cannot operate at f₀. On the left side of f₀, uniform gain theoretically exists, but the corresponding phase angle is much lower than on the right side of f₀, showing that the overall efficiency will be low if the WPT system operates on the left side of f₀. Therefore, the frequency range marked in Figure 4c, on the right side of f₀, is seen as the uniform gain control area. In Figure 4c, the frequency range for uniform gain control decreases from 24.4 kHz to 20.2 kHz when the coupling becomes weaker, and the corresponding phase angle is 18° at 24.4 kHz and 90° at 20.2 kHz. The total impedance is inductive in this frequency domain where the input voltage leads the input current, which realizes zero-voltage switching (ZVS) operation of the inverter.

Figure 4. Impedance and voltage gain G in frequency domain. (a) Impedance magnitude; (b) Impedance phase characteristics; (c) Voltage gain in frequency domain. The simulation conditions were L_p = 65 μH, L_s = 65 μH, C_p = 1 μF, C_s = 1 μF, R = 20 Ω, and L_m = 2.5, 5, 7.5, 10, 12.5, 15, 17.5, 20, 22.5, and 25 μH.

Figure 4. Impedance and voltage gain G in frequency domain. (a) Impedance magnitude; (b) Impedance phase characteristics; (c) Voltage gain in frequency domain. The simulation conditions were L_p = 65 μH, L_s = 65 μH, C_p = 1 μF, C_s = 1 μF, R = 20 Ω, and L_m = 2.5, 5, 7.5, 10, 12.5, 15, 17.5, 20, 22.5, and 25 μH.

For each curve of the phase angle in Figure 4b, one zero-crossing point exists, which indicates the resonant frequency point. Therefore, the switching frequency can be shifted to some value higher than the resonant frequency in order to achieve uniform voltage gain by first detecting the phase angle. Since the phase angle measurement cannot detect polarity of angles, the first step is to find the resonant frequency, and then increase the frequency until the predetermined uniform gain is obtained. From Figure 4b,c the phase angle for a uniform voltage gain is around 18°–22° as long as the magnetic coupling (k) is relatively strong. The phase angle corresponding to the uniform voltage gain increases when the magnetic coupling becomes worse.

5. Control Loop Design

The main objective of this section is to explore the use of the proposed uniform gain control to generate a fixed output voltage regardless of any coil misalignment. The WPT is designed to automatically choose the optimal frequency after the EV is parked but before charging begins. A dummy resistor is required to simulate the battery status, as its equivalent resistive load can vary at different levels of charge.

The resonant frequency is the frequency that makes the load phase angle between the primary inverter’s input voltage and current zero. While the resonant frequency allows the system to transfer maximum power, the output voltage at the secondary side varies significantly, thus increasing the difficulty in designing a DC-DC converter that can ensure the charger voltage is stable. The non-zero phase angle between the primary inverter’s output voltage and current allows for the use of soft switches, decreasing the power losses caused by switching devices. The tuning process is as follows:

Firstly, the WPT system searches for the resonant frequency for a specific alignment condition. This resonant frequency is determined by the coil coupling, so it can be different each time a driver parks an EV. As shown in Figure 5, the resonant frequency is located through frequency shifting (∆fp) and phase angle comparison between current and previous angles (θ_current and θ_previous). As the polarity of the phase angle cannot be detected by the measurement circuit, a direction flag p is utilized in the firmware to determine whether to shift the frequency to larger or smaller frequencies. The phase-angle which corresponds to the resonant frequency is zero, but the phase angle read by the DSP at the resonant frequency is not exactly zero due to the measurement error of digital devices. Therefore, the resonant frequency is set when the current phase angle (θ_current) is lower than t, where t is a value within the range of acceptable measurement accuracy. Secondly, the WPT system determines the uniform gain frequency once the resonant frequency is known. The tuning program increases the frequency step by step (∆f) while measuring the load phase angle. The resonant frequency acquired in the first step determines the phase angle curve (Figure 4b) and the mutual inductance between the two coils can be calculated according to Equation (1). Once the mutual inductance is known, the phase angle (θ_uniform) for the uniform gain can be obtained using Equations (1) and (5). Then the DSP program increases the switching frequency step by step (∆f) while measuring the load phase angle until the phase angle is equal to θ_uniform. Finally, the WPT sets the switching frequency to the uniform gain frequency and raises the input DC voltage to begin charging the EV.

Figure 5. Flowchart of the uniform voltage gain control loop.

Figure 5. Flowchart of the uniform voltage gain control loop.

Theoretically, the calculation of the phase angle θ_uniform for a known coupling can be derived from Equations (1)–(5). However, a floating calculation could consume the computational resources of a 16-bit DSP dramatically and might influence the tuning speed as well. In addition, the theoretical value might have an error due to parasitic resistance and stray inductance in the electronic elements. Hence, the phase angle θ_uniform is calibrated for each increase (set 2 cm in our test) in misalignment and the coupling between two calibration points will linearly map the phase angle θ_uniform.

6. Experimental Validation

6.1. 3-Axis Platform for Alignment Study

Figure 6 shows a three-axis motorized platform which was used to set the alignment conditions for experimental study. The three-axis platform shown in Figure 6 is based on a CNC machine (Model DHC, PlasmaCAM, Inc., Colorado City, CO, USA). It has a width of 1.75 m, a height of 1.65 m, and a depth of 1.65 m. The maximum speeds are 25 m/min in the horizontal direction and 2 m/min in the vertical direction. The movable ranges are 1.2 m × 1.2 m in the horizontal plane and 0.6 m in the vertical direction (Figure 6). The speed and motion trail can be programmed in a computer interface. The misalignment test was only performed in a single direction in the horizontal plane since the coil shape is circular.

Figure 6. Experimental setup for misalignment study.

Figure 6. Experimental setup for misalignment study.

6.2. Experimental Results with Misalignment under a Constant Air Gap

While the air gap was kept at 100 mm, the efficiency and voltage gain (G) were measured with variance of misalignment in the horizontal plane. Figure 7 shows the efficiency and G curves under three frequency control methods, the fixed frequency, the resonant frequency, and the uniform gain control. The experiment was conducted using three input voltages: 10 V, 20 V, and 40 V, to show the influence of power losses of from switching devices on efficiency when the frequency and misalignment stay the same.

Figure 7. Experimental comparison in three control modes at a fixed air gap of 100 mm and different misaligned coil conditions. (a) Efficiency at a fixed frequency; (b) Voltage at a fixed frequency; (c) Efficiency at resonant frequencies (phase angle θ = 0); (d) Voltage at resonant frequencies (phase angle θ = 0); (e) Efficiency at uniform gain frequencies; (f) Voltage at uniform gain frequencies.

Figure 7. Experimental comparison in three control modes at a fixed air gap of 100 mm and different misaligned coil conditions. (a) Efficiency at a fixed frequency; (b) Voltage at a fixed frequency; (c) Efficiency at resonant frequencies (phase angle θ = 0); (d) Voltage at resonant frequencies (phase angle θ = 0); (e) Efficiency at uniform gain frequencies; (f) Voltage at uniform gain frequencies.

As shown in Figure 7a,c,e, the efficiency of resonant frequency and uniform gain control is better in misalignment than that of fixed frequency control. The efficiency at resonant frequency in different misalignment conditions is slightly higher than the uniform gain’s efficiency. For example, at a DC input voltage of 40 V, the efficiency of fixed frequency control dropped from 82% to 67% when the misalignment was changed from 0 to 125 mm, while the efficiency of resonance control dropped from 82% to 79%, and the efficiency of uniform gain control dropped from 81% to 77%. It was noted that the efficiency curve of 40 V input was unavailable after the misalignment exceeded 125 mm in Figure 7c. This is because the mutual inductance between two coils was too small, which led to a much smaller impedance under resonance. The DC supply could not support such a heavy load. From the efficiency curves in Figure 7a,c,e, the efficiency under different DC inputs is different even at the same misalignment value. This phenomenon occurs when the switching device’s loss occupies a relatively larger portion of the total consumed power when operating in a low power condition. The efficiency can still increase if the DC input is greater than 40 V.

According to the voltage gain characteristics in Figure 7b,d,f, the output voltage at the secondary side under fixed and resonant frequencies began to vary significantly at a misalignment of more than 100 mm. However, the output voltage gain (G = $V_b/V_{in}$, V_in is the DC input voltage of the inverter) was maintained at about 3.04 across the misalignment range up to 200 mm, which coincides well with the simulation result in Figure 4c. The DC output voltage V_b after the rectifier and the smoothing capacitor (Figure 3a) is the rectifier input RMS voltage V₂ multiplied by a constant value, specifically: V₂ = $\frac{\sqrt{3}}{2}$V_b [12]. The theoretical peak-peak voltage gain is 4.0 (Figure 4c); hence the theoretical DC output voltage over DC input is 3.27, which is quite close to the measured gain.

A stable output voltage for wireless charging helps to reduce the burden on the DC-DC converter to regulate the power flow. Although operating at resonance frequency has a slightly higher efficiency than the uniform gain control, it introduces a much more complex power regulation issue in comparison to the uniform gain control. Moreover, since the overall impedance under resonance frequency operation is very small for a large misalignment, the circulating current in the coils is extremely high and the power supply faces a huge challenge to drive the heavy load.

6.3. Experimental Results with Air Gap Variations under Zero Misalignment

When both the primary and secondary coils were in perfect alignment, the efficiency and voltage gain (G) were measured with a variance of air gaps. Similar to the misalignment experiment, Figure 8 shows the efficiency and G curves under three frequency control methods: fixed frequency, resonant frequency, and uniform gain control.

The experimental results for air gaps (Figure 8) followed the same trend in efficiency and voltage gain with the results shown in Figure 7, due to the fact that both misalignment and air-gap variation change the magnetic coupling. The relative error for output stability under the uniform voltage control was 2.0% for misalignment (Figure 7) and 4.7% for air gap variations (Figure 8). One interesting phenomenon is that the efficiency of uniform gain control (Figure 8e) dropped more gradually than that of the resonant control when the air gap was more than 100 mm. As the coils used for EV charging are relatively large in dimension, they are more tolerant to misalignments than air gap variations. Thus, an air gap variation causes a worse coupling compared with the same amount of misalignment in this case. The worse coupling represents a heavier overall load that needs a larger current from the inverter, which results in more conduction losses in switching devices and lowers the efficiency more quickly. Figure 8a,c,e demonstrates that the efficiency varies under different DC inputs but the same frequency method and misalignment condition. Since the switching device’s loss accounts for a higher percentage of the total consumed power when operating in a low power condition versus a high power condition, a lower DC input can make the WPT less efficient compared with a higher DC input. Figure 8b shows that the output voltage at an air gap of 50 mm is much lower than that of 100 mm. Since 100 mm is assumed a nominal operation gap for EV charging in our setup, the switching frequency is chosen based on the 100 mm gap for fixed frequency control. Therefore, although the wireless charging system has a stronger coupling at an air gap of 50 mm than 100 mm, the mistuned frequency causes the huge output voltage drop when the gap is 50 mm.

Figure 8. Experimental comparison in three control modes with different air gaps and no coil misalignment. (a) Efficiency at a fixed frequency; (b) Voltage at a fixed frequency; (c) Efficiency at resonant frequencies (phase angle θ = 0); (d) Voltage at resonant frequencies (phase angle θ = 0); (e) Efficiency at uniform gain frequencies; and (f) Voltage at uniform gain frequencies.

Figure 8. Experimental comparison in three control modes with different air gaps and no coil misalignment. (a) Efficiency at a fixed frequency; (b) Voltage at a fixed frequency; (c) Efficiency at resonant frequencies (phase angle θ = 0); (d) Voltage at resonant frequencies (phase angle θ = 0); (e) Efficiency at uniform gain frequencies; and (f) Voltage at uniform gain frequencies.

6.4. Accuracy of Frequency Tracking

Figure 9 shows the comparison between theoretical and actual operating frequencies. The theoretical switching frequencies were calculated with Matlab using Equation (5) and the acquired frequency was experimentally obtained by the proposed control method using a DSP controller. The difference between the theoretical and actual values ranged from 0.8 to 1.1 kHz, and all the acquired frequencies were lower than the theoretical ones. Since the inverter and rectifier were considered ideal switching devices in the circuit model and the equivalent resistance of coils was not considered, as shown in Figure 3c, the actual switching frequency is different from the theoretical one. Due to the error analysis of voltage gain as stated above, such frequency tracking error should be acceptable in a practical application.

Figure 9. The theoretical and acquired switching frequencies for uniform voltage gain control with various couplings (misalignment at an air gap of 100 mm).

Figure 9. The theoretical and acquired switching frequencies for uniform voltage gain control with various couplings (misalignment at an air gap of 100 mm).

6.5. Frequency Control at a Large Misalignment

Figure 10 shows the primary side’s circulating current and the gate drive signals when the misalignment is 200 mm and the air gap is set at 100 mm. These scope graphs are obtained under a DC input voltage of 40 V. Under these conditions, the circulating current of resonance operation is extremely high, which challenges the electronic devices and hinders heat dissipation, meaning resonant operation is impractical under severe misalignment. The phase angle between the two signals is around 56° for fixed frequency control (Figure 10a). Such a large phase angle results in a weak wireless power transfer capability. However, the current signal in Figure 10b lags slightly (about 29.3°) behind the switching signal which is also consistent with the inverter voltage. Thus, the soft-switching operation is used in the uniform gain control. The measured mutual inductance is 9.69 µH when the misalignment is 200 mm and the air gap is 100 mm. According to Figure 4b and Figure 9, the theoretical phase angle is 30.5°, which coincides well with the experimental value (about 29.3°).

Figure 10 also shows that the RMS current of fixed frequency control is 13% smaller than that of uniform gain control, while the efficiency of uniform gain control is 76.4% larger than that of fixed frequency control (Figure 7a,e). Therefore, the maximum allowed misalignment can be significantly extended with help of the uniform gain control. The power delivery of the uniform gain control performs much better than the fixed frequency control under severe misalignments while the resonance control cannot operate in such a weak coupling.

The current switching frequency band for light duty EV wireless chargers is 81.38 kHz–90 kHz according to the SAE-J2954 [17]. For heavy duty EV wireless chargers, the SAE currently has no such frequency recommendations due to the frequency properties of high power switching devices. As far as the authors know, the switching frequency of several commercialized wireless chargers is around 20 kHz. For instance, the Plugless wireless charging system from Evatran Group, Inc operates at 19.5 kHz [18]. Following the trend of SAE, our future demonstrations for light duty EVs will also focus on a nominal operating frequency of 85 kHz.

Figure 10. Switching signals and the inverter circulating current under two extreme conditions (misalignment = 200 mm, air gap = 100 mm) (a) Fixed frequency control (20.2 kHz); Sinusoidal current waveform: Max = 32 A, RMS = 22.7 A; (b) Uniform gain operation (19.5 kHz). Sinusoidal current waveform: Max = 37 A, RMS = 26.2 A. The voltage-current ratio of the current sensor is 0.2 V/A.

Figure 10. Switching signals and the inverter circulating current under two extreme conditions (misalignment = 200 mm, air gap = 100 mm) (a) Fixed frequency control (20.2 kHz); Sinusoidal current waveform: Max = 32 A, RMS = 22.7 A; (b) Uniform gain operation (19.5 kHz). Sinusoidal current waveform: Max = 37 A, RMS = 26.2 A. The voltage-current ratio of the current sensor is 0.2 V/A.

7. Conclusions

A uniform voltage gain control for wireless charging can generate a stable and controllable voltage to address the negative effects of misalignment and air gap variations in EV applications. Simulation and experimental validation were conducted in comparison with traditional fixed frequency and resonance frequency operation. The uniform voltage gain control offers certain advantages, as shown by the theoretical analysis and experimental demonstration. Firstly, the uniform gain control allows for operation under greater misalignment and is more robust under differing vehicle chassis heights. Since the proposed control method can operate under worse magnetic couplings, it can counteract the drawback of a common circular coupler, which is that the coupling coefficient drops relatively quickly. Secondly, although the WPT system does not operate at the resonance frequency under uniform control, it does not mean the overall efficiency is low. Lower current operation and use of soft switching can decrease the power loss caused by switching devices, and hence uniform gain control has a competitive or even higher efficiency compared to resonant operation. Thirdly, the stable voltage output under uniform gain operation can decrease the design requirements of a DC-DC converter on the secondary side. Potentially, a battery could be directly charged without the existence of the DC-DC converter using the proposed gain control plus duty-cycle regulation. This could decrease the amount of electronic components involved in wireless charging.