Investigation of Fault Permeability in Sands with Different Mineral Compositions (Evaluation of Gas Hydrate Reservoir)
Abstract
:1. Introduction
2. Materials and Experimental Section
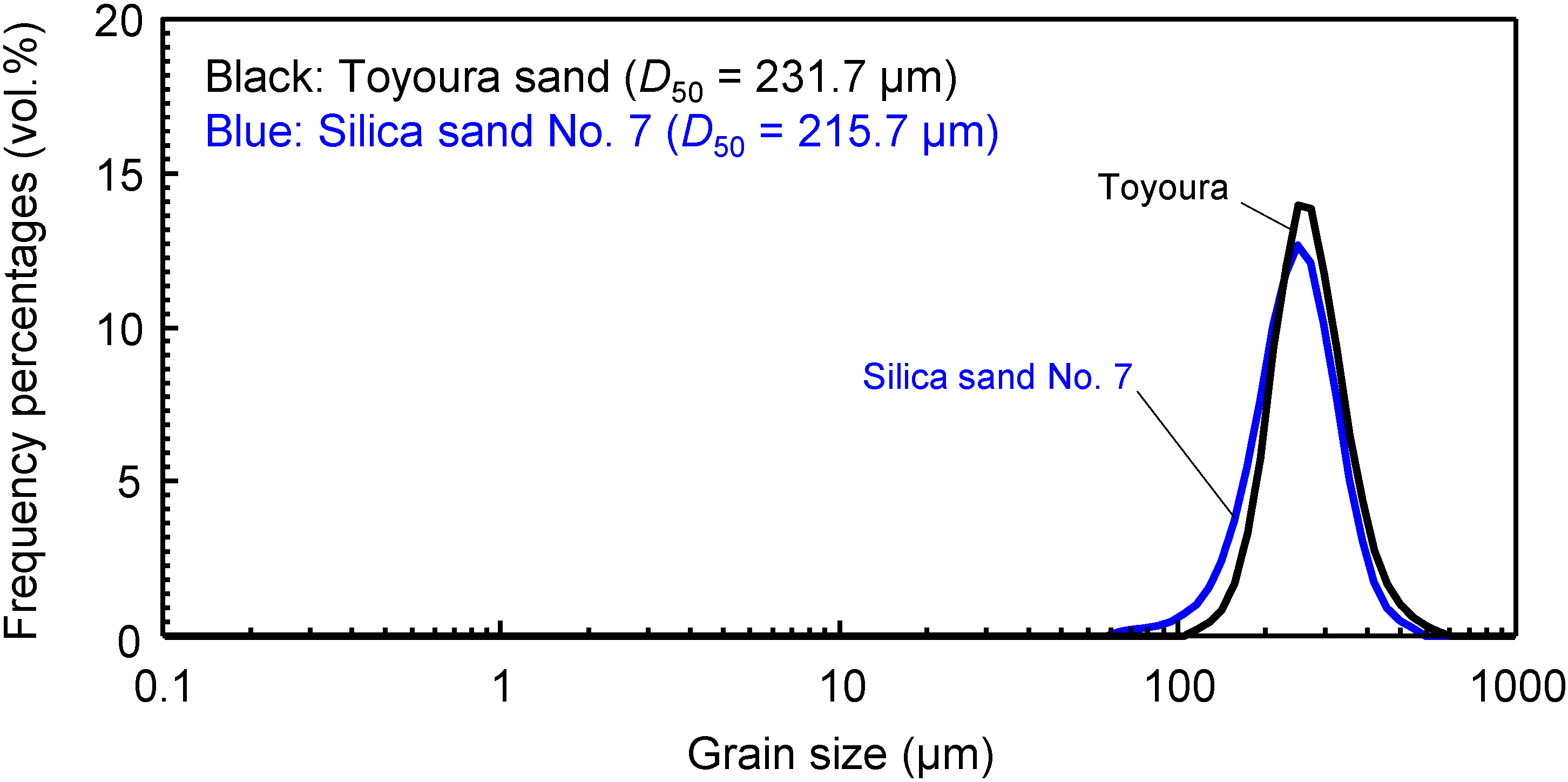
2.1. Samples


2.2. Ring-Shear Apparatus and Permeability Measurements

2.3. Analysis of Microstructure and Grain Size Distribution of Shear Zones
3. Results and Discussion
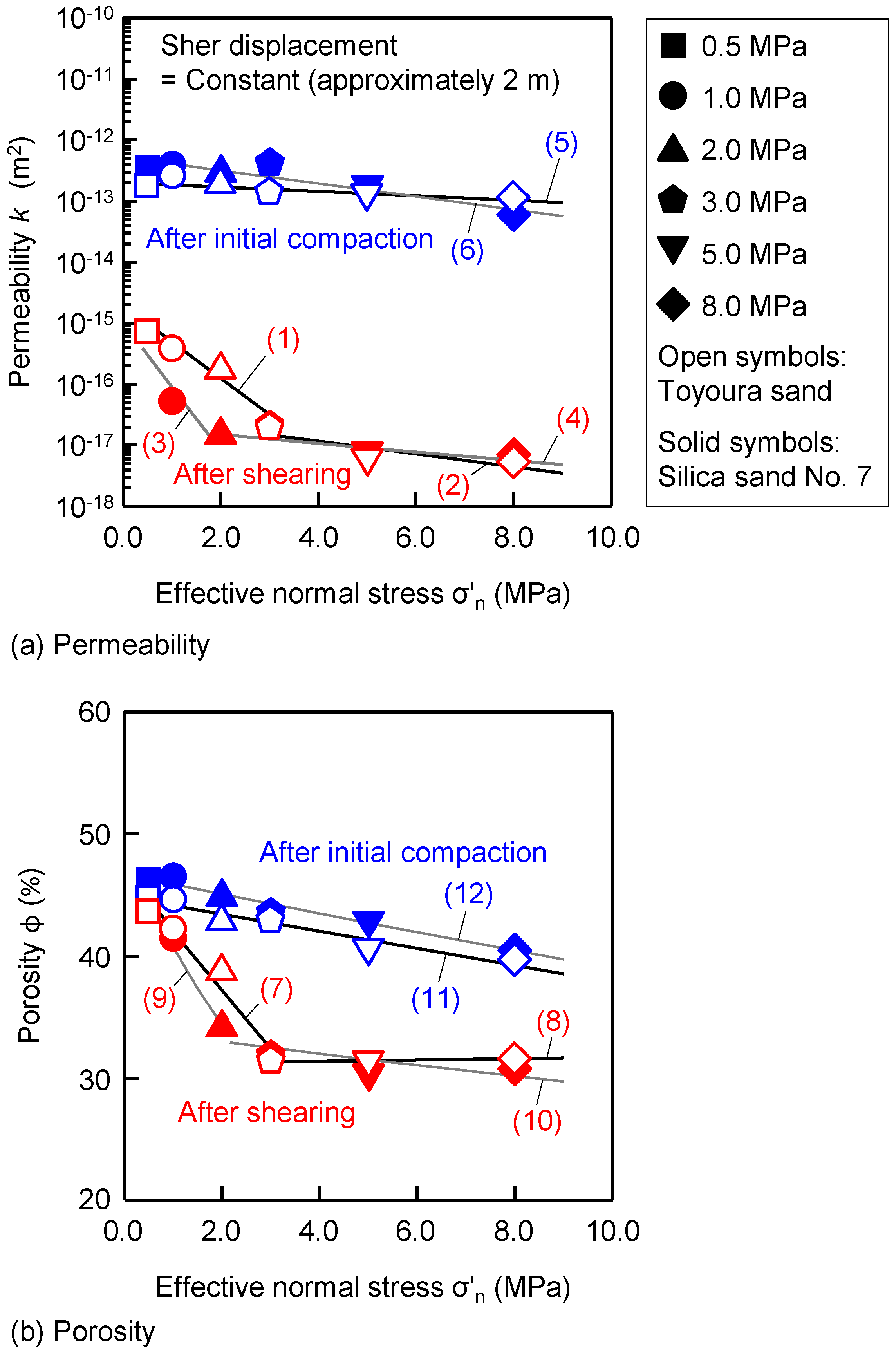
3.1. Permeability and Porosity Reduction versus Effective Normal Stress
| Effective Normal Stress during Shearing (MPa) | Permeability (m2) | Porosity (%) | Specimen Height (mm) | |||
|---|---|---|---|---|---|---|
| Initial Compaction | After Shearing | Initial Compaction | After Shearing | Initial Compaction | After Shearing | |
| σ′n | kic | kas | ϕic | ϕas | Hic | Has |
| Toyoura | ||||||
| 0.5 | 1.80 × 10−13 | 7.21 × 10−16 | 44.8 | 43.6 | 23.7 | 21.7 |
| 1.0 | 2.55 × 10−13 | 3.83 × 10−16 | 44.4 | 42.2 | 22.4 | 19.8 |
| 2.0 | 3.64 × 10−13 | 1.70 × 10−16 | 42.8 | 38.7 | 22.3 | 19.3 |
| 3.0 | 5.06 × 10−13 | 1.92 × 10−17 | 42.9 | 31.4 | 21.5 | 18.5 |
| 5.0 | 3.42 × 10−13 | 6.15 × 10−18 | 40.6 | 31.4 | 21.6 | 17.6 |
| 8.0 | 4.74 × 10−14 | 5.31 × 10−18 | 39.7 | 31.6 | 23.3 | 19.5 |
| Silica sand No. 7 | ||||||
| 0.5 | 3.51 × 10−13 | 7.38 × 10−16 | 46.2 | 43.7 | 21.1 | 20.2 |
| 1.0 | 3.88 × 10−13 | 5.19 × 10−17 | 46.5 | 41.5 | 21.3 | 19.4 |
| 2.0 | 2.83 × 10−13 | 1.42 × 10−17 | 44.8 | 34.1 | 22.9 | 19.2 |
| 3.0 | 4.10 × 10−13 | 2.02 × 10−17 | 43.5 | 31.8 | 22.4 | 18.5 |
| 5.0 | 1.82 × 10−13 | 7.73 × 10−18 | 42.9 | 30.4 | 22.0 | 18.0 |
| 8.0 | 5.71 × 10−14 | 6.89 × 10−18 | 40.5 | 30.8 | 21.2 | 18.2 |
| No. | Correlations | Statistical Fit | Sample * | Remarks |
|---|---|---|---|---|
| r | T or No. 7 | |||
| 1 | kas = 2.0 × 10−15 × exp (−1.3915 × σ′n) | 0.976 | T | kas, σ′n < 3.0 MPa |
| 2 | kas = 3.0 × 10−17 × exp (−0.2408 × σ′n) | 0.861 | T | kas, σ′n > 3.0 MPa |
| 3 | kas = 1.0 × 10−15 × exp (−2.4430 × σ′n) | 0.926 | No. 7 | kas, σ′n < 2.0 MPa |
| 4 | kas = 2.0 × 10−17 × exp (−0.1602 × σ′n) | 0.832 | No. 7 | kas, σ′n > 2.0 MPa |
| 5 | kic = 2.0 × 10−13 × exp (−0.0839 × σ′n) | 0.825 | T | kic, σ′n = 0.5–8.0 MPa |
| 6 | kic = 5.0 × 10−13 × exp (−0.2450 × σ′n) | 0.921 | No. 7 | kic, σ′n = 0.5–8.0 MPa |
| 7 | ϕas = 47.7362 × exp (−0.1297 × σ′n) | 0.969 | T | ϕas, σ′n < 3.0 MPa |
| 8 | ϕas = 31.2473 × exp (0.0012 × σ′n) | 0.993 | T | ϕas, σ′n > 3.0 MPa |
| 9 | ϕas = 48.2113 × exp (−0.1696 × σ′n) | 0.991 | No. 7 | ϕas, σ′n < 2.0 MPa |
| 10 | ϕas = 33.9440 × exp (−0.0149 × σ′n) | 0.758 | No. 7 | ϕas, σ′n > 2.0 MPa |
| 11 | ϕic = 44.9012 × exp (−0.0168 × σ′n) | 0.967 | T | ϕic, σ′n = 0.5–8.0 MPa |
| 12 | ϕic = 46.6999 × exp (−0.0181 × σ′n) | 0.981 | No. 7 | ϕic, σ′n = 0.5–8.0 MPa |
3.2. Microstructure and Grain Size Distribution of Shear Zones





| Effective Normal Stress during Shearing | Grain Size Distribution (%) | Median | Sorting | ||
|---|---|---|---|---|---|
| Clay | Silt | Sand | D50 | SO | |
| σ′n (MPa) | Sub-3.9-µm | 3.9–62.5 (µm) | 62.5–2000 (µm) | (µm) | |
| Toyoura | |||||
| Original | 0.0 | 0.0 | 100.0 | 231.7 | 0.37 |
| 0.5 | 0.0 | 0.0 | 100.0 | 225.8 | 0.31 |
| 1.0 | 0.0 | 0.0 | 100.0 | 219.5 | 0.35 |
| 2.0 | 3.2 | 3.6 | 93.2 | 211.7 | 0.71 |
| 3.0 | 13.2 | 10.2 | 76.6 | 184.2 | 2.49 |
| 5.0 | 33.4 | 25.0 | 41.6 | 18.1 | 3.03 |
| 8.0 | 37.7 | 30.3 | 32.0 | 8.8 | 2.96 |
| Silica sand No. 7 | |||||
| Original | 0.0 | 0.0 | 100.0 | 215.7 | 0.42 |
| 0.5 | 0.0 | 2.0 | 98.0 | 194.2 | 0.49 |
| 1.0 | 1.0 | 5.9 | 93.1 | 192.1 | 0.75 |
| 2.0 | 9.3 | 12.8 | 77.9 | 166.4 | 1.99 |
| 3.0 | 18.1 | 15.0 | 66.9 | 149.2 | 2.76 |
| 5.0 | 45.7 | 35.2 | 19.1 | 4.8 | 2.81 |
| 8.0 | 38.1 | 52.5 | 9.4 | 7.0 | 2.28 |
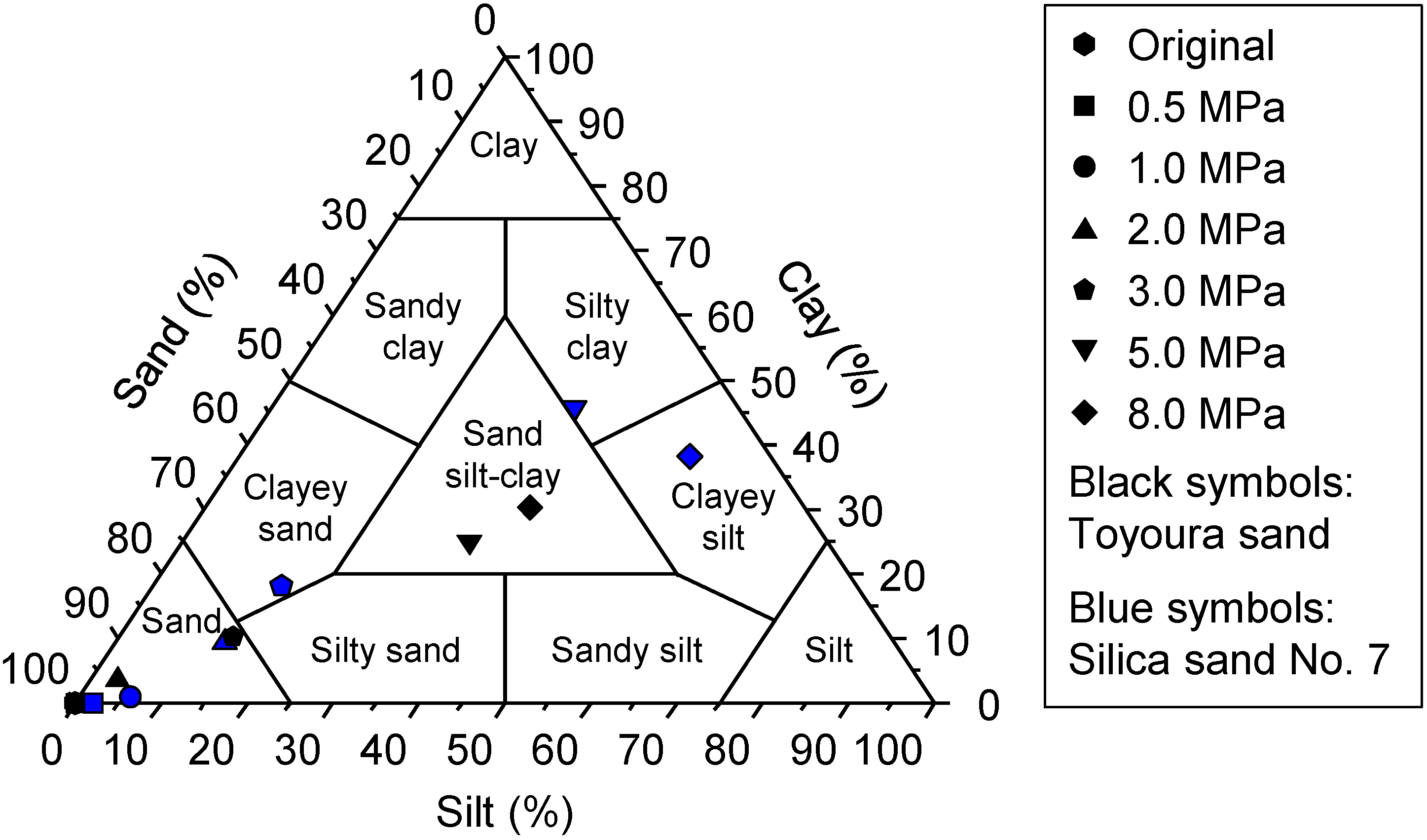
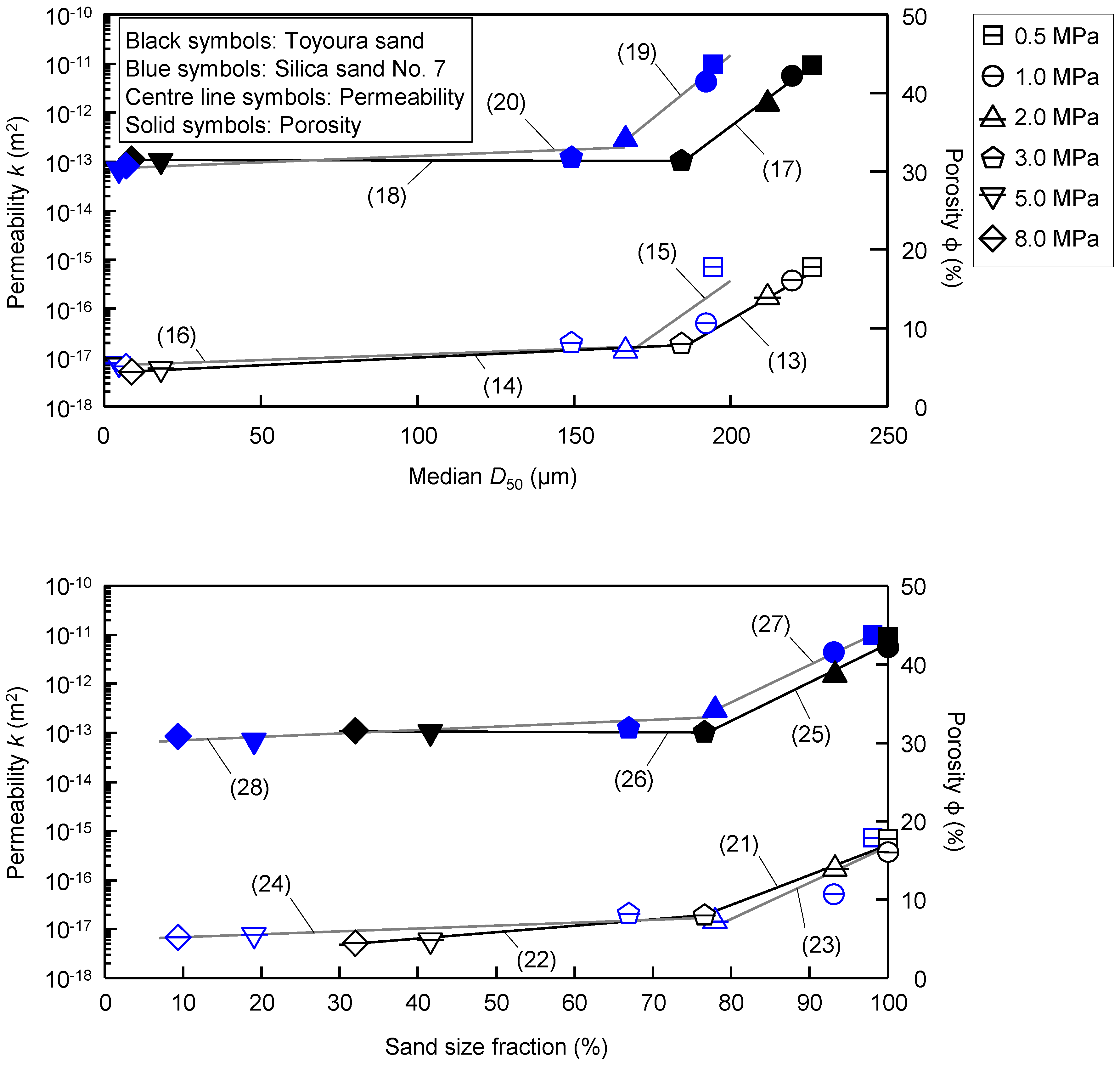
3.3. Effect of Grain Size Reduction of Shear Zone on Permeability/Porosity Reduction
| No. | Correlations | Statistical Fit | Sample * | Remarks |
|---|---|---|---|---|
| r | T or No. 7 | |||
| 13 | kas = 2.0 × 10−24 × exp (0.0862 × D50) | 0.998 | T | kas, D50 > 184.2 µm |
| 14 | kas = 5.0 × 10−18 × exp (0.00071 × D50) | 0.998 | T | kas, D50 < 184.2 µm |
| 15 | kas = 2.0 × 10−25 × exp (0.1033 × D50) | 0.795 | No. 7 | kas, D50 > 166.4 µm |
| 16 | kas = 7.0 × 10−18 × exp (0.0054 × D50) | 0.928 | No. 7 | kas, D50 < 166.4 µm |
| 17 | ϕas = 0.2978 × D50 − 23.6646 | 0.995 | T | ϕas, D50 > 184.2 µm |
| 18 | ϕas = −0.0008 × D50 + 31.5057 | 0.761 | T | ϕas, D50 < 184.2 µm |
| 19 | ϕas = 0.3204 × D50 − 19.2591 | 0.988 | No. 7 | ϕas, D50 > 166.4 µm |
| 20 | ϕas = 0.0166 × D50 + 30.4121 | 0.867 | No. 7 | ϕas, D50 < 166.4 µm |
| 21 | kas = 4.0 × 10−22 × exp (0.1411 × Sand) | 0.985 | T | kas, Sand > 76.6% |
| 22 | kas = 2.0 × 10−18 × exp (0.0298 × Sand) | 0.995 | T | kas, Sand < 76.6% |
| 23 | kas = 2.0 × 10−23 × exp (0.1701 × Sand) | 0.885 | No. 7 | kas, Sand > 77.9% |
| 24 | kas = 6.0 × 10−18 × exp (0.0136 × Sand) | 0.913 | No. 7 | kas, Sand < 77.9% |
| 25 | ϕas = 0.4921 × Sand − 6.5634 | 0.991 | T | ϕas, Sand > 76.6% |
| 26 | ϕas = −0.0036 × Sand + 31.6309 | 0.854 | T | ϕas, Sand < 76.6% |
| 27 | ϕas = 0.4793 × Sand − 3.2028 | 0.999 | No. 7 | ϕas, Sand > 77.9% |
| 28 | ϕas = 0.0431 × Sand + 29.9039 | 0.873 | No. 7 | ϕas, Sand < 77.9% |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pooladi-Darvish, M. Gas production from hydrate reservoirs and its modelling. J. Petrol. Technol. 2004, 56, 65–71. [Google Scholar] [CrossRef]
- Kawamura, T.; Sakamoto, Y.; Toon, J.; Ohtake, M.; Yamamoto, Y.; Komai, T.; Haneda, H. Dissociation behavior of hydrate core sample using thermodynamic inhibitor. Int. J. Offshore Polar Eng. 2006, 16, 5–9. [Google Scholar]
- Sakamoto, Y.; Komai, T.; Kawamura, T.; Minagawa, H.; Tenma, N.; Yamachi, T. Laboratory-scale experiment of methane hydrate dissociation by hot-water injection and numerical analysis for permeability estimation in reservoir: Part 1—Numerical study for estimation of permeability in methane hydrate reservoir. Int. J. Offshore Polar Eng. 2007, 17, 47–56. [Google Scholar]
- Sakamoto, Y.; Kakumoto, M.; Kawamura, T.; Minagawa, H.; Tenma, N.; Yamachi, T. Numerical study on dissociation of methane hydrate and gas production behavior in laboratory-scale experiments for depressurization: Part 3—Numerical study on estimation of permeability in methane hydrate reservoir. Int. J. Offshore Polar Eng. 2009, 19, 124–134. [Google Scholar]
- Nagakubo, S.; Kobayashi, T.; Saeki, T.; Shimoda, N.; Fujii, T.; Noguchi, S. The Relations between Methane Hydrate-bearing Formations and Seafloor Manifestations Accompanied by Methane Discharges in the Eastern Nankai Trough. J. Geogr. 2009, 118, 835–853, (In Japanese with English Abstract). [Google Scholar] [CrossRef]
- Biegel, R.L.; Sammis, C.G.; Dieterich, J.H. The frictional properties of a simulated gouge having a fractal particle distribution. J. Struct. Geol. 1989, 11, 827–846. [Google Scholar] [CrossRef]
- Marone, C.; Scholz, C.H. Particle-size distribution and microstructures within simulated fault gouge. J. Struct. Geol. 1989, 11, 799–814. [Google Scholar] [CrossRef]
- Morrow, C.A.; Byerlee, J.D. Experimental studies of compaction and dilatancy during frictional sliding on faults containing gouge. J. Struct. Geol. 1989, 11, 815–825. [Google Scholar] [CrossRef]
- Beeler, N.M.; Tullis, M.; Blanpied, J.D. Frictional behavior of large displacement experimental faults. J. Geophys. Res. 1996, 101, 8697–8715. [Google Scholar] [CrossRef]
- Tobari, A.; Braathen, A.; Cuisiat, F.; Fossen, H. Shear zones in porous sand: Insights from ring-shear experiments and naturally deformed sandstones. Tectonophysics 2007, 437, 37–50. [Google Scholar]
- Dewhurst, D.N.; Brown, K.M.; Clennell, M.B.; Westbrook, G.K. A comparison of the fabric and permeability anisotropy of consolidated and sheared silty clay. Eng. Geol. 1996, 42, 253–267. [Google Scholar] [CrossRef]
- Zhang, S.; Tullis, T.E. The effect of fault slip on permeability and permeability anisotropy in quartz gouge. Tectonophysics 1998, 295, 41–52. [Google Scholar] [CrossRef]
- Zhang, S.; Tullis, T.E.; Scruggs, V.J. Permeability anisotropy and pressure dependency of permeability in experimentally sheared gouge materials. J. Struct. Geol. 1999, 21, 795–806. [Google Scholar] [CrossRef]
- Zhang, S.; Tullis, T.E.; Scruggs, V.J. Implications of permeability and its anisotropy in a mica gouge for pore pressures in fault zones. Tectonophysics 2001, 335, 37–50. [Google Scholar] [CrossRef]
- Okada, Y.; Sassa, K.; Fukuoka, H. Excess pore pressure and grain crushing of sands by means of undrained and naturally drained ring-shear tests. Eng. Geol. 2004, 75, 325–343. [Google Scholar] [CrossRef]
- Kimura, S.; Kaneko, H.; Ito, T.; Minagawa, H. The effect of effective normal stress on particle breakage, porosity and permeability of sand: Evaluation of faults around methane hydrate reservoirs. Tectonophysics 2014, 630, 285–299. [Google Scholar] [CrossRef]
- Hvorslev, M.J. Torsion Shear Tests and Their Place in the Determination of Shearing Resistance of Soils. Proc. ASTM 1939, 39, 999–1022. [Google Scholar]
- La Gatta, D.P. Residual Strength of Clays and Clay-Shale by Rotation Shear Tests. Harvard Soil Mechanics Series (86). Ph.D. Thesis, Harvard University, Cambridge, MA, USA, June 1970. [Google Scholar]
- Bishop, A.W.; Green, G.E.; Garga, V.K.; Anderson, A.; Brown, J.D. A new ring shear apparatus and its application to the measurement of residual strength. Géotechnique 1971, 21, 273–328. [Google Scholar] [CrossRef]
- Bromhead, E.N. A Simple Ring Shear Apparatus. Ground Eng. 1979, 12, 40–44. [Google Scholar]
- Skempton, A.W. Residual strength of clays in landslides, folded strata and the laboratory. Géotechnique 1985, 35, 3–18. [Google Scholar] [CrossRef]
- Gibo, S.; Egashira, K.; Ohtsubo, M. Residual strength of smectite-dominated soils from the Kamenose landslide in Japan. Can. Geotech. J. 1987, 24, 456–462. [Google Scholar] [CrossRef]
- Stark, T.D.; Choi, H.; McCone, S. Drained shear strength parameters for analysis of landslides. J. Geotech. Geoenviron. 2005, 131, 575–588. [Google Scholar] [CrossRef]
- Nakamura, S.; Gibo, S.; Egashira, K.; Kimura, S. Platy layer silicate minerals for controlling residual strength in landslide soils of different origins and geology. Geology 2010, 38, 743–746. [Google Scholar] [CrossRef]
- Minagawa, H.; Egawa, K.; Sakamoto, Y.; Komai, T.; Tenma, N.; Narita, H. Characterization of hydraulic permeability and pore-size distribution of methane hydrate-bearing sediment using proton nuclear magnetic resonance measurement. Int. J. Offshore Polar Eng. 2012, 22, 306–313. [Google Scholar]
- Minagawa, H.; Nishikawa, Y.; Ikeda, I.; Miyazaki, K.; Takahara, N.; Sakamoto, Y.; Komai, T.; Narita, H. Characterization of sand sediment by pore size distribution and permeability using proton nuclear magnetic resonance measurement. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Egashira, K.; Matsuo, K.; Gibo, S.; Nakamura, S.; Zhou, Y.; Inoue, H.; Sasaki, K. Clay mineralogical approach to the slip-surface formation in the O’dokoro landslide. Clay Sci. 2000, 11, 107–113. [Google Scholar]
- Lupini, J.F.; Skinner, A.E.; Vaughan, P.R. The drained residual strength of cohesive soils. Géotechnique 1981, 31, 181–213. [Google Scholar] [CrossRef]
- Hungr, O.; Morgenstern, N.R. High velocity ring shear tests on sand. Géotechnique 1984, 34, 415–421. [Google Scholar] [CrossRef]
- Tika, T.E.; Vaughan, P.R.; Lemos, L.J.L.J. Fast shearing of pre-existing shear zones in soil. Géotechnique 1996, 46, 197–233. [Google Scholar] [CrossRef]
- Gibo, S.; Egashira, K.; Ohtsubo, M.; Nakamura, S. Strength recovery from residual state in reactivated landslide soils. Géotechnique 2002, 52, 683–686. [Google Scholar] [CrossRef]
- Sassa, K.; Fukuoka, H.; Wang, G.; Ishikawa, N. Undrained dynamic-loading ring-shear apparatus and its application to landslide dynamics. Landslides 2004, 1, 7–19. [Google Scholar] [CrossRef]
- Tiwari, B.; Marui, H. A new method for the correlation of residual shear strength of the soil with mineralogical composition. J. Geotech. Geoenviron. 2005, 131, 1139–1150. [Google Scholar] [CrossRef]
- Fukuoka, H.; Sassa, K.; Wang, G. Influence of shear speed and normal stress on the shear behavior and shear zone structure of granular materials in naturally drained ring shear tests. Landslides 2007, 4, 63–74. [Google Scholar] [CrossRef]
- Toyota, H.; Nakamura, K.; Sugimoto, M.; Sakai, N. Ring shear tests to evaluate strength parameters in various remoulded soils. Géotechnique 2009, 59, 649–659. [Google Scholar] [CrossRef]
- Iverson, N.R.; Mann, J.E.; Iverson, R.M. Effects of soil aggregates on debris-flow mobilization: Results from ring-shear experiments. Eng. Geol. 2010, 114, 84–92. [Google Scholar] [CrossRef]
- Vithana, S.B.; Nakamura, S.; Kimura, S.; Gibo, S. Effects of overconsolidation ratios on the shear strength of remoulded slip surface soils in ring shear. Eng. Geol. 2012, 131–132, 29–36. [Google Scholar] [CrossRef]
- Kimura, S.; Nakamura, S.; Vithana, S.B.; Sakai, K. Shearing rate effect on residual strength of landslide soils in the slow rate range. Landslides 2014, 11, 969–979. [Google Scholar] [CrossRef]
- Ito, T.; Minagawa, H. Selective dehydration during methane-hydrate dissociation in the eastern Nankai Trough sediments and its implications. J. Sediment. Soc. Jpn. 2013, 72, 3–12, (In Japanese with English Abstract). [Google Scholar] [CrossRef]
- Ito, T.; Iwamoto, H.; Kamiya, K.; Fukushima, T.; Kumon, F. Use of flood chronology for detailed environmental analysis: A case study of Lake Kizaki in the northern Japanese Alps, central Japan. Environ. Earth Sci. 2010, 60, 1607–1618. [Google Scholar] [CrossRef]
- Fukuoka, H.; Sassa, K.; Wang, G.; Sasaki, R. Observation of shear zone development in ring-shear apparatus with a transparent shear box. Landslides 2006, 3, 239–251. [Google Scholar] [CrossRef]
- Folk, R.L.; Ward, W.C. Brazos river bar: A study of significance of grain size parameters. J. Sediment. Petrol. 1957, 27, 3–26. [Google Scholar] [CrossRef]
- Shepard, F.P. Nomenclature based on sand-silty-clay ratios. J. Sediment. Petrol. 1954, 24, 151–158. [Google Scholar]
- Ito, T.; Komatsu, Y.; Fujii, T.; Suzuki, K.; Egawa, K.; Nakatsuka, Y.; Konno, T.; Yoneda, J.; Jin, T.; Kida, M.; et al. Lithological features of hydrate-bearing sediments and their relationship with gas hydrate saturation in the eastern Nankai Trough, Japan. Mar. Pet. Geol. 2015. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kimura, S.; Kaneko, H.; Ito, T.; Minagawa, H. Investigation of Fault Permeability in Sands with Different Mineral Compositions (Evaluation of Gas Hydrate Reservoir). Energies 2015, 8, 7202-7223. https://doi.org/10.3390/en8077202
Kimura S, Kaneko H, Ito T, Minagawa H. Investigation of Fault Permeability in Sands with Different Mineral Compositions (Evaluation of Gas Hydrate Reservoir). Energies. 2015; 8(7):7202-7223. https://doi.org/10.3390/en8077202
Chicago/Turabian StyleKimura, Sho, Hiroaki Kaneko, Takuma Ito, and Hideki Minagawa. 2015. "Investigation of Fault Permeability in Sands with Different Mineral Compositions (Evaluation of Gas Hydrate Reservoir)" Energies 8, no. 7: 7202-7223. https://doi.org/10.3390/en8077202
APA StyleKimura, S., Kaneko, H., Ito, T., & Minagawa, H. (2015). Investigation of Fault Permeability in Sands with Different Mineral Compositions (Evaluation of Gas Hydrate Reservoir). Energies, 8(7), 7202-7223. https://doi.org/10.3390/en8077202





