Unraveling the Mysteries of Turbulence Transport in a Wind Farm
Abstract
:1. Introduction
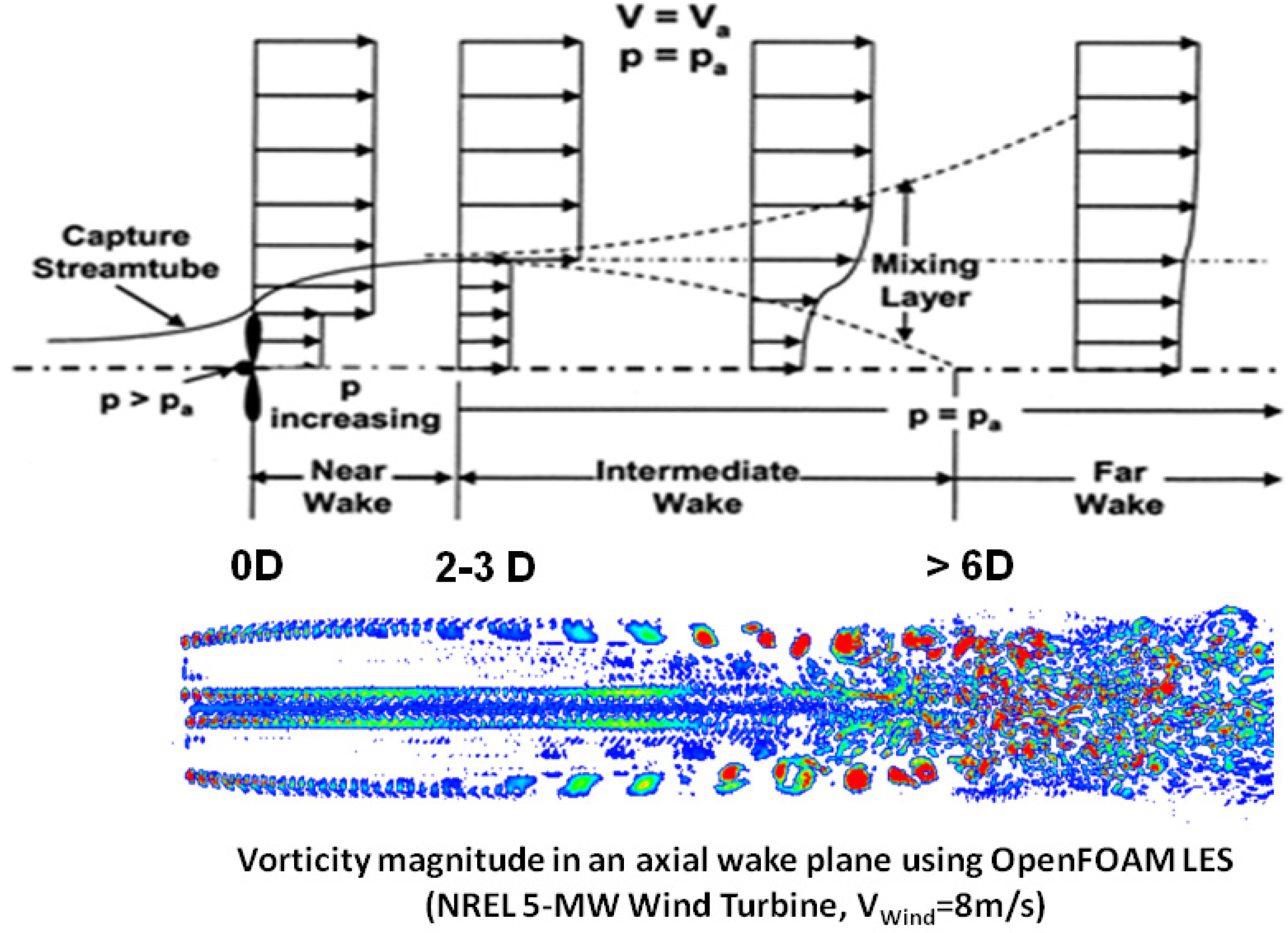
2. Numerical Methods
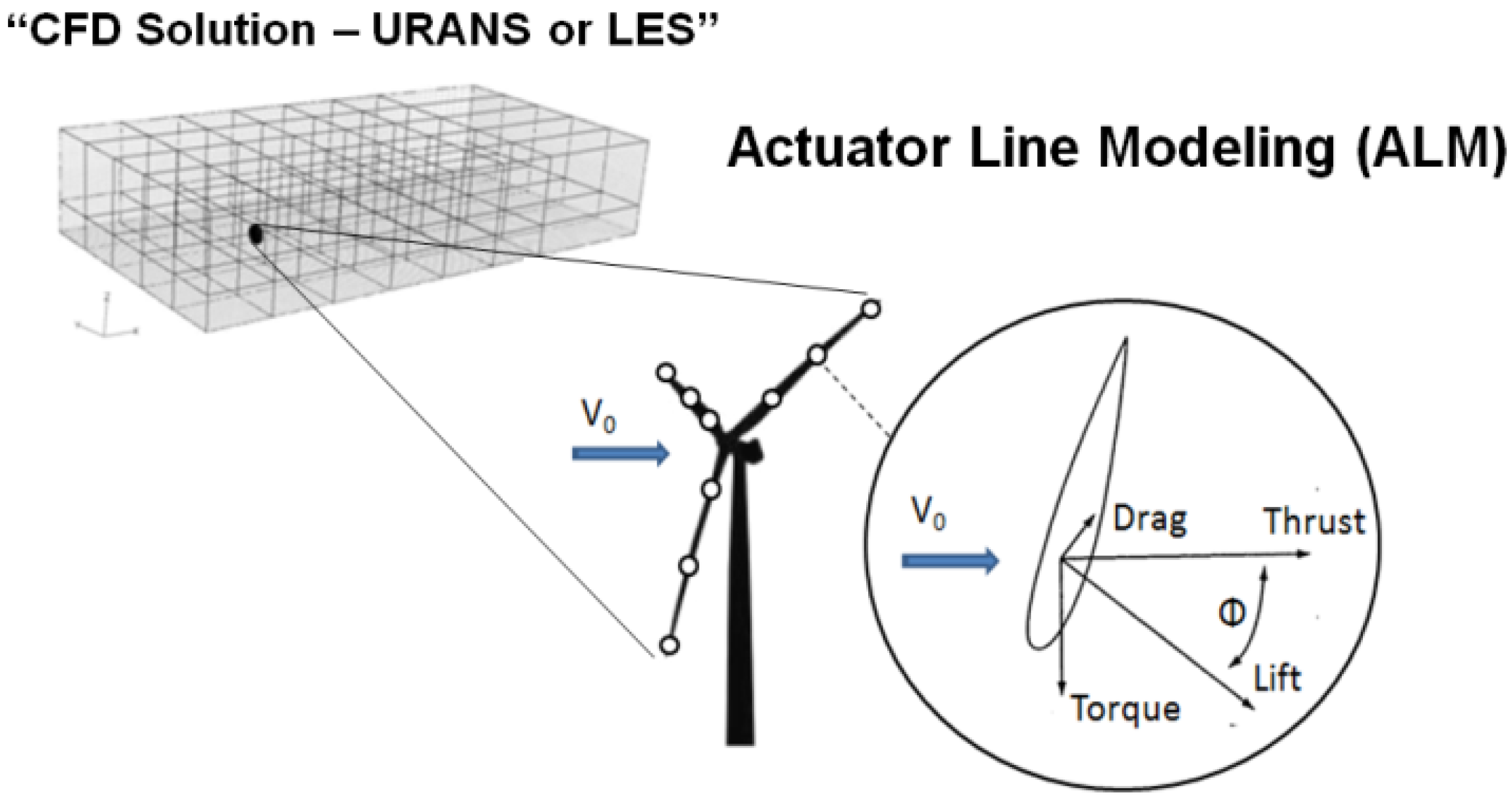
2.1. The Actuator Line Method
2.2. The ABLPisoSolver in OpenFOAM (OpenFOAM-LES)
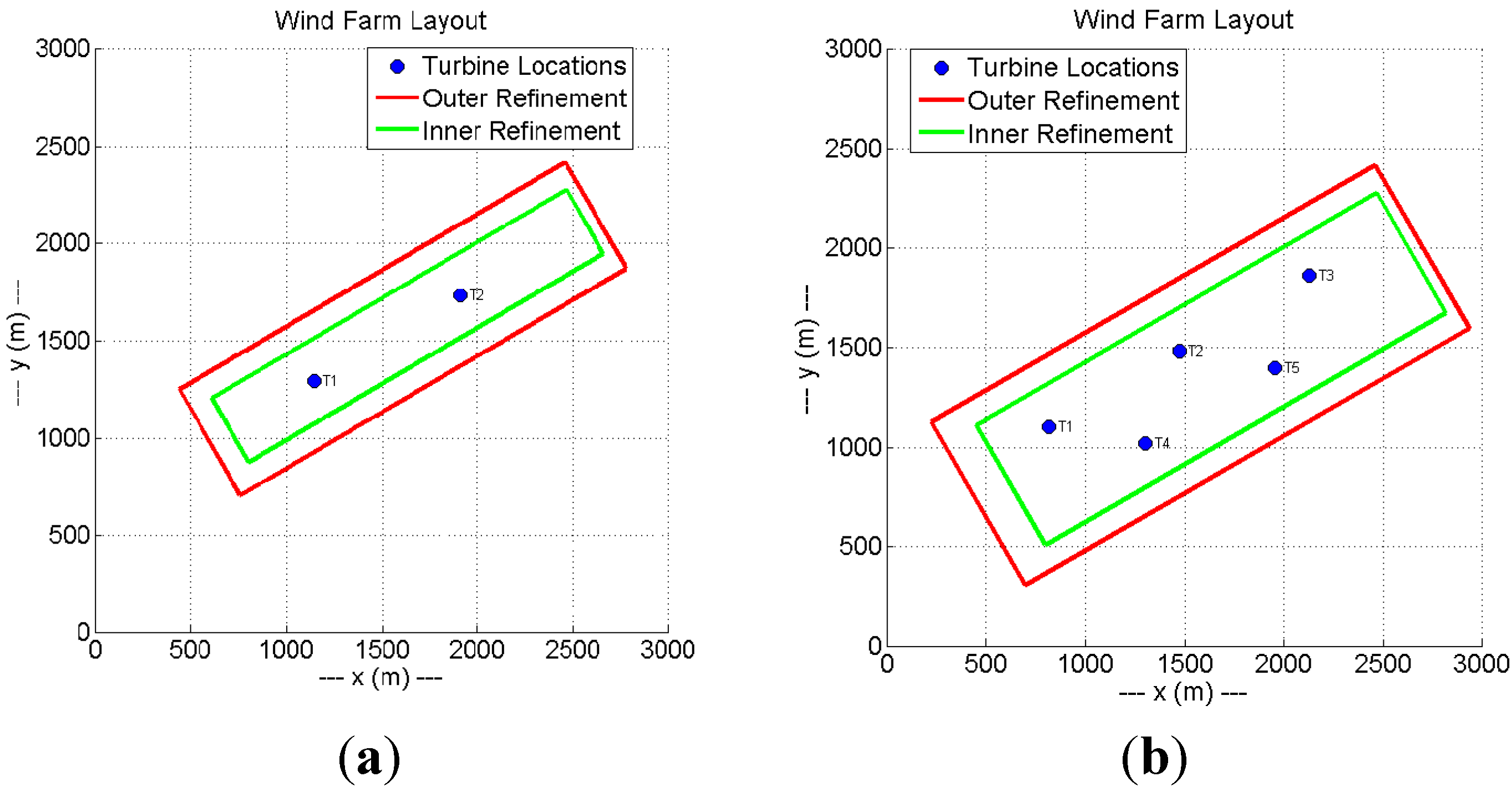
2.3. Computational Grids and Simulation Methodology
2.4. FieldView XDB Workflow
3. Results and Discussion
3.1. Atmospheric Boundary Layer Precursor Simulations (OpenFOAM-LES)
| Precursor Simulation | Stability | Ug (m/s) | Ih (%) | u* (m/s) | w* (m/s) | zi (m) | −zi/L | t* (min) |
|---|---|---|---|---|---|---|---|---|
| Turbine-Turbine Interaction (z0 = 0.001 m) | NBL | 9.1 | 4.9 | 0.27 | 0 | 755 | 0 | 46 |
| MCBL | 8.0 | 7.0 | 0.33 | 0.99 | 745 | 10.99 | 12 | |
| 5-Turbine Wind Farm (z0 = 0.2 m) | MCBL | 10.4 | 8.9 | 0.53 | 1.00 | 765 | 2.70 | 13 |
3.2. A Turbine-Turbine Interaction Problem (ALM OpenFOAM-LES)


3.2.1. Turbine Power
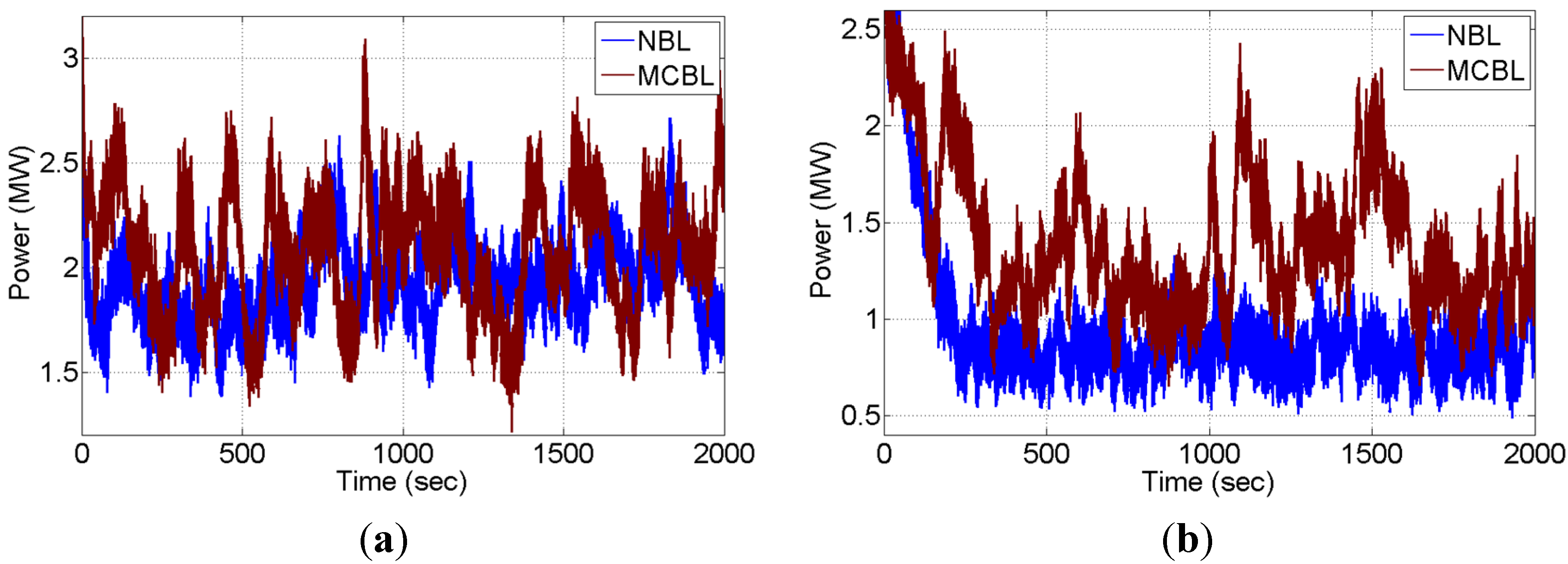
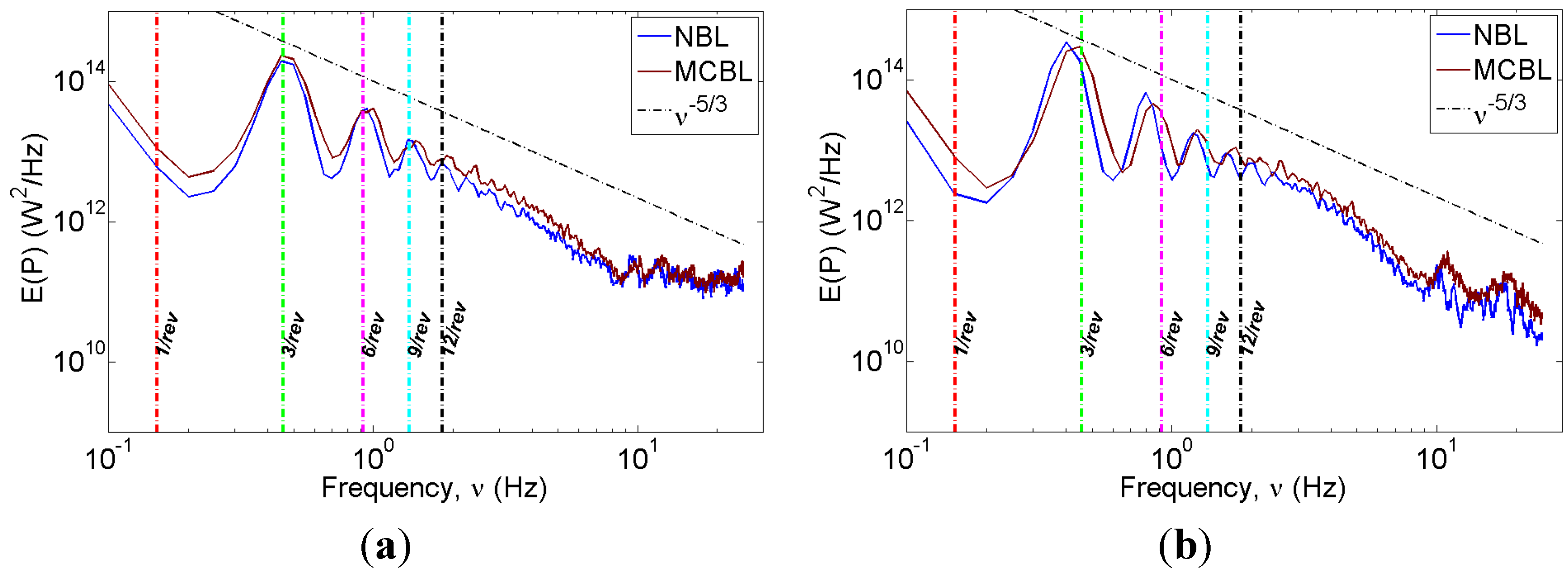
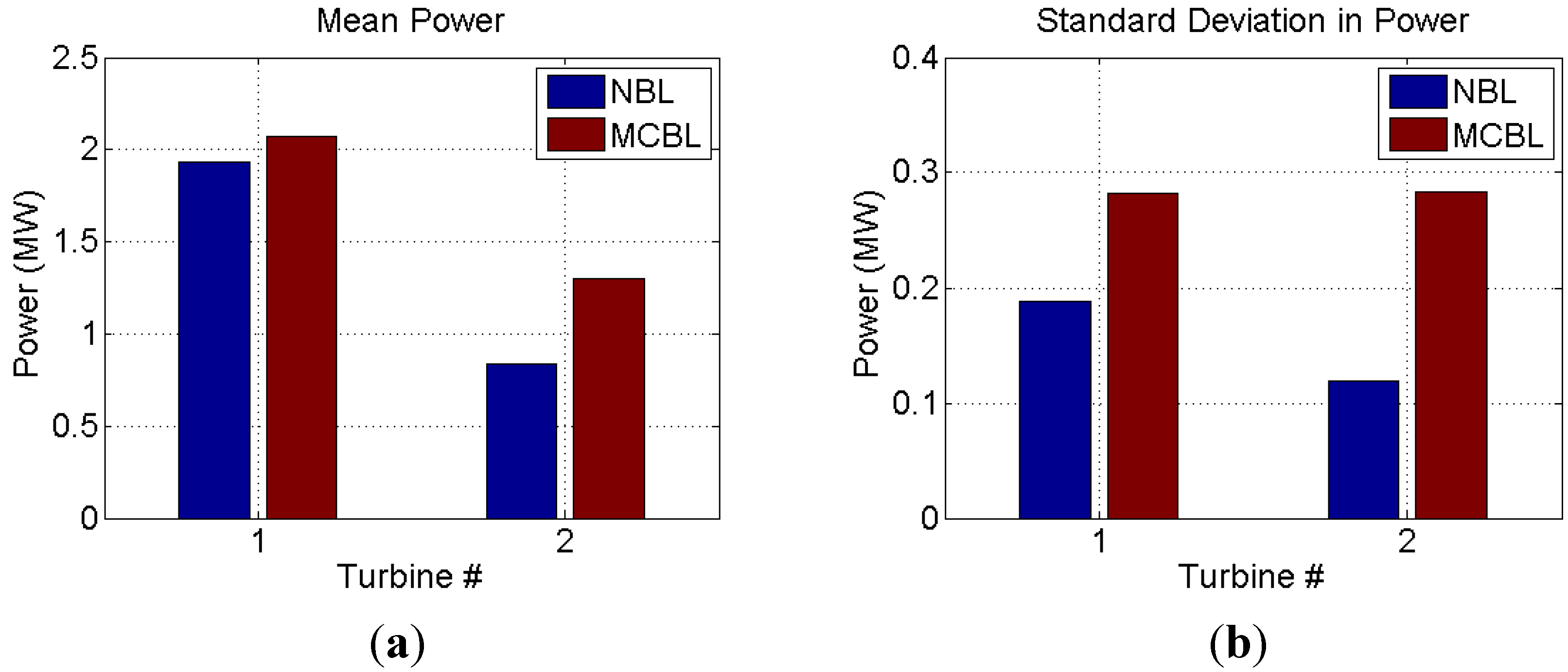
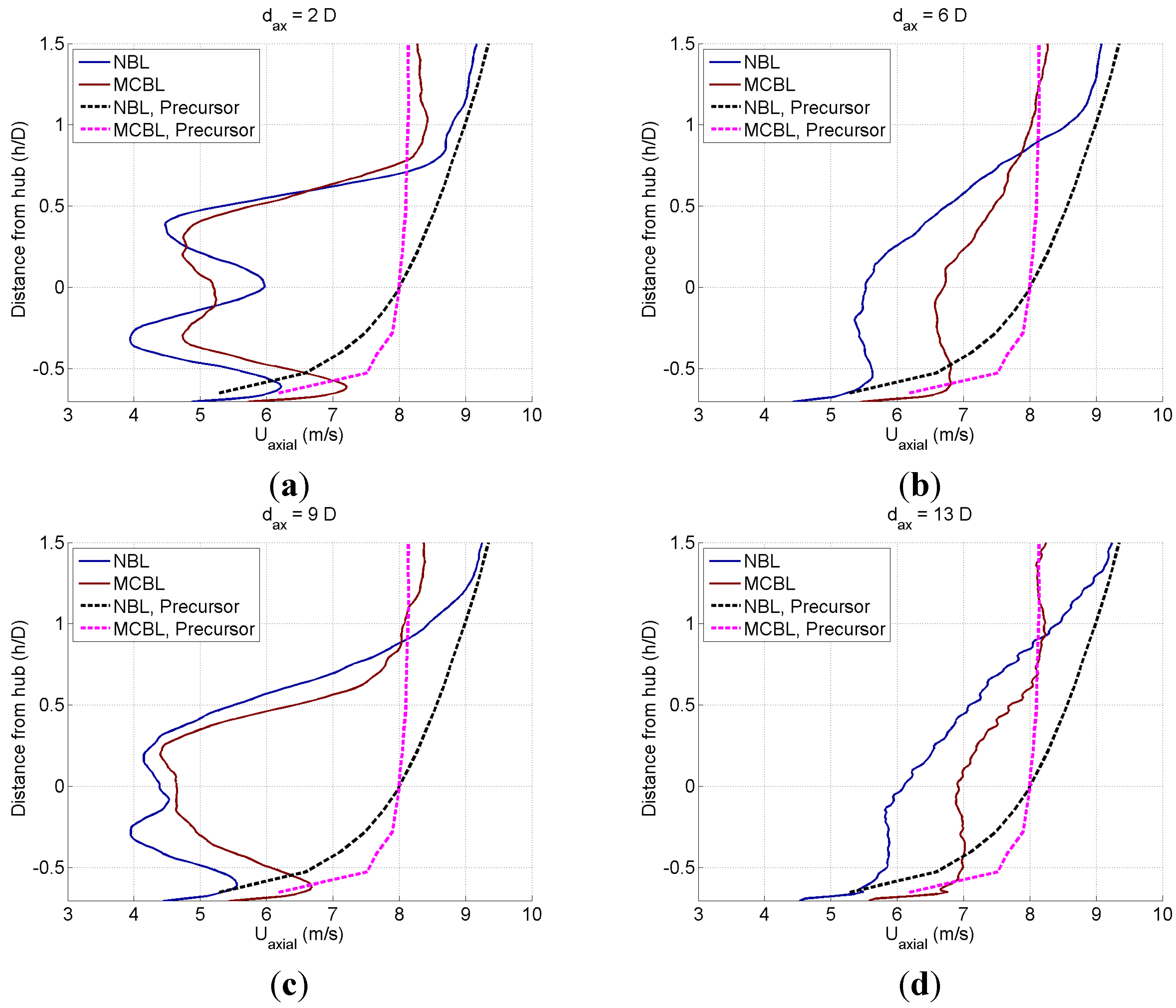
3.2.2. Wake Velocity Deficit
3.2.3. Wake Turbulence
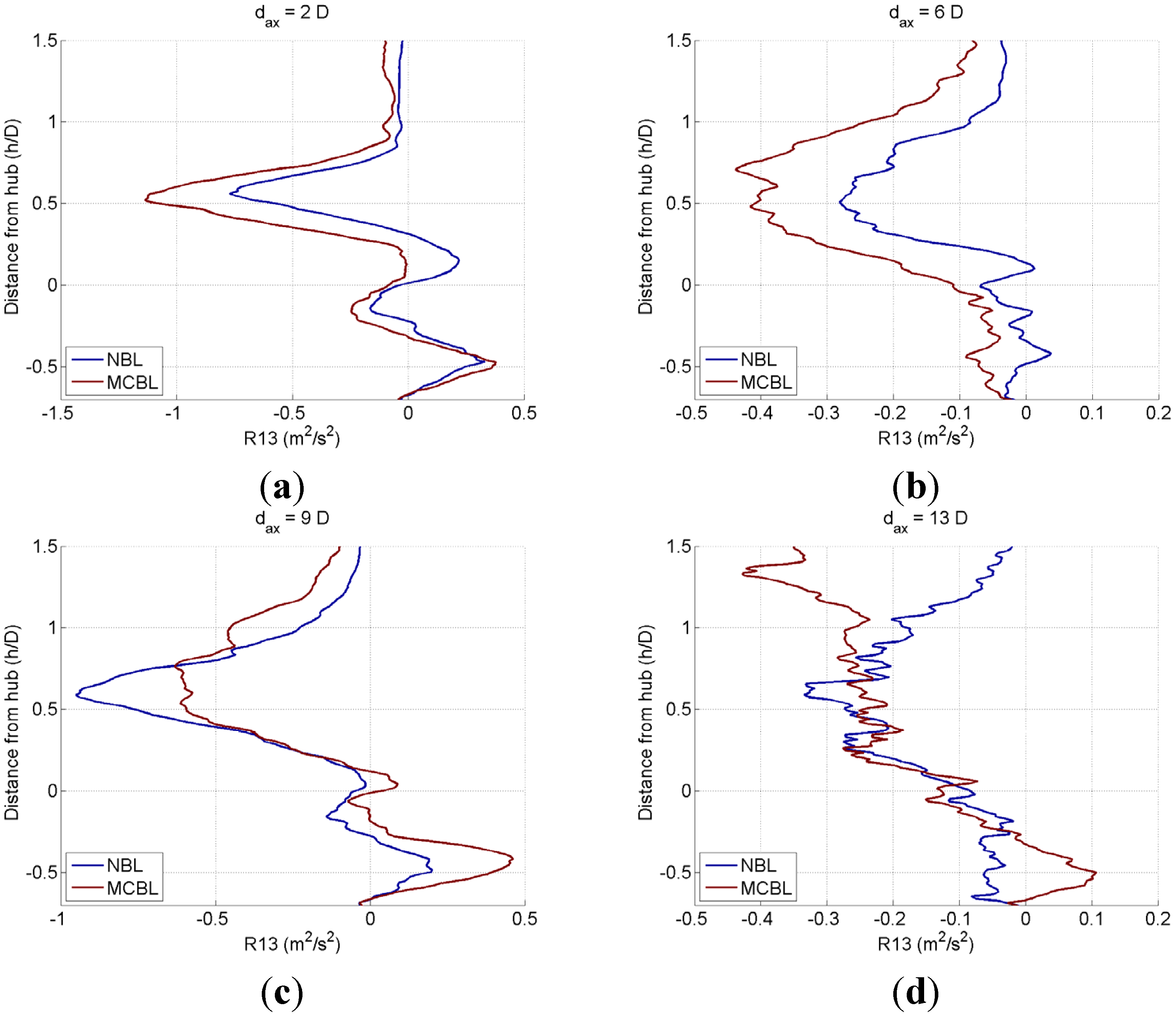
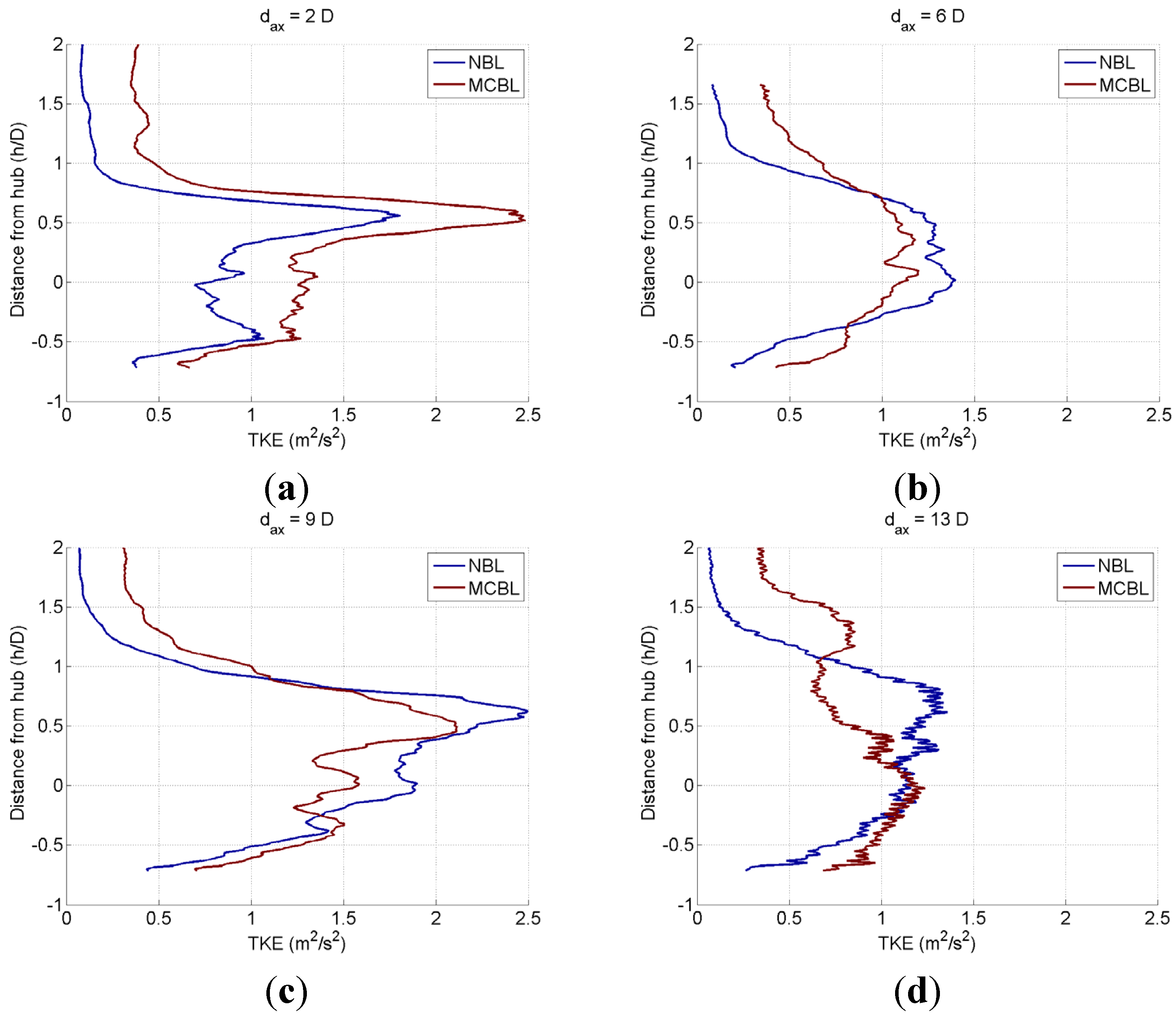
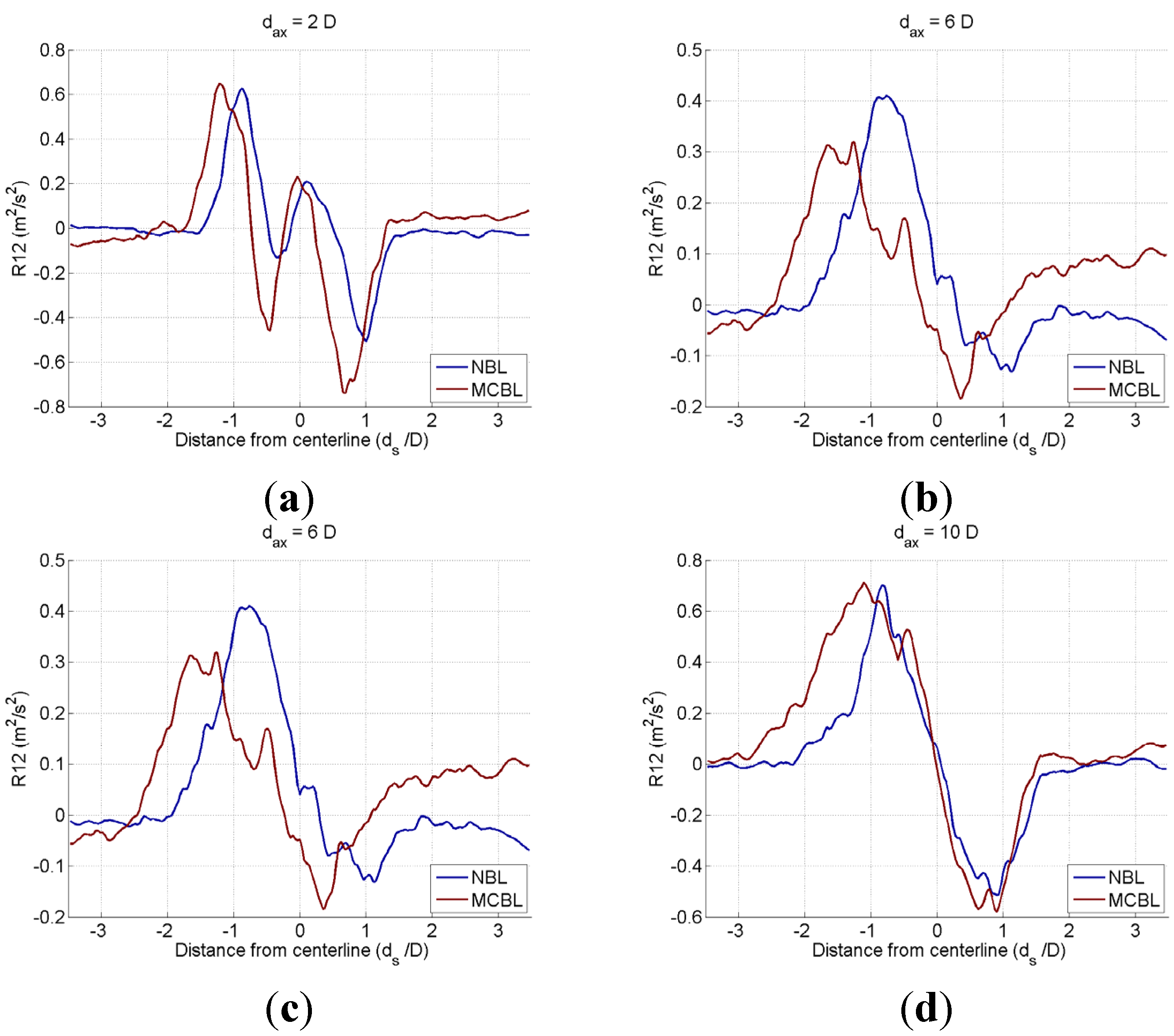
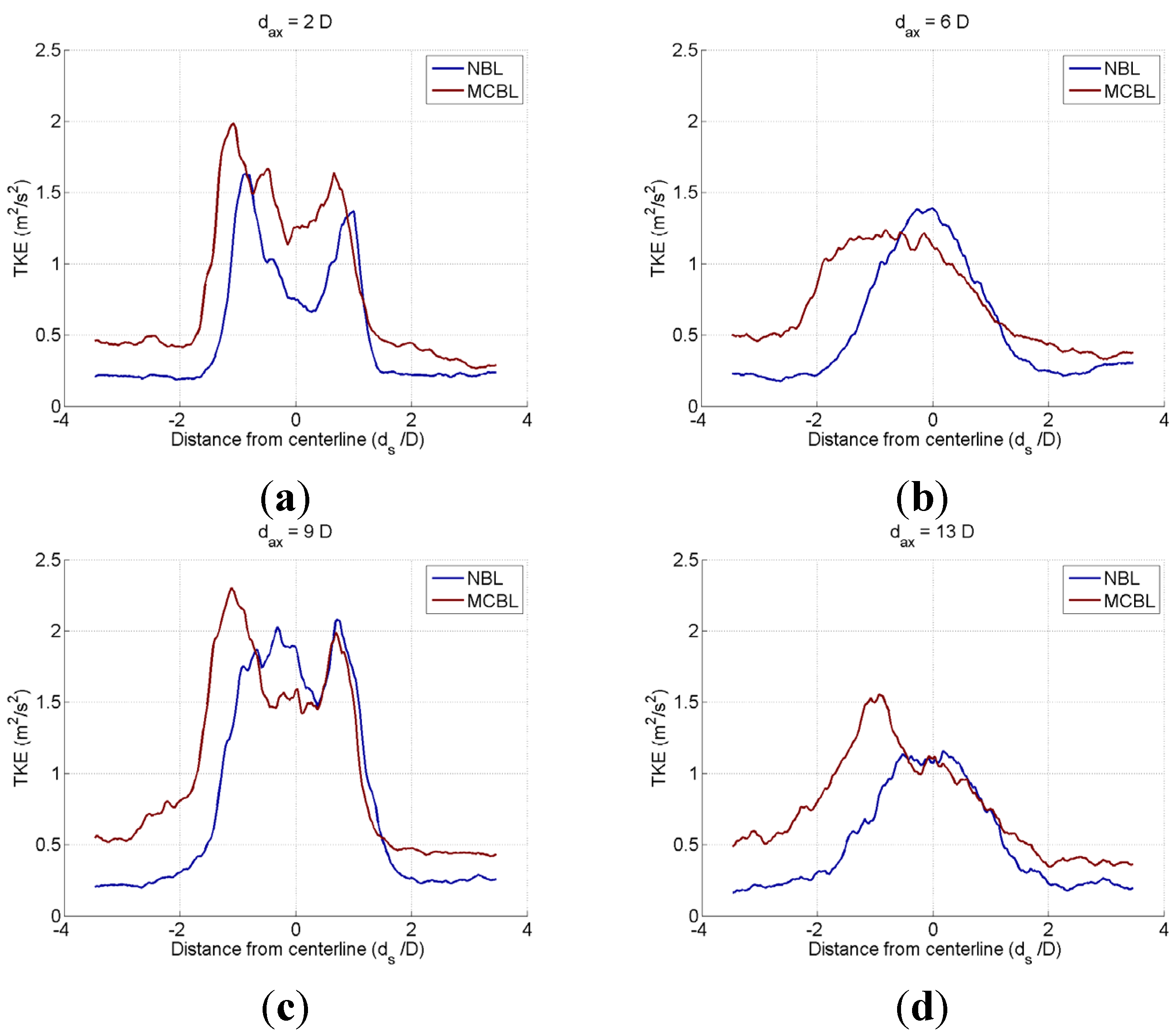
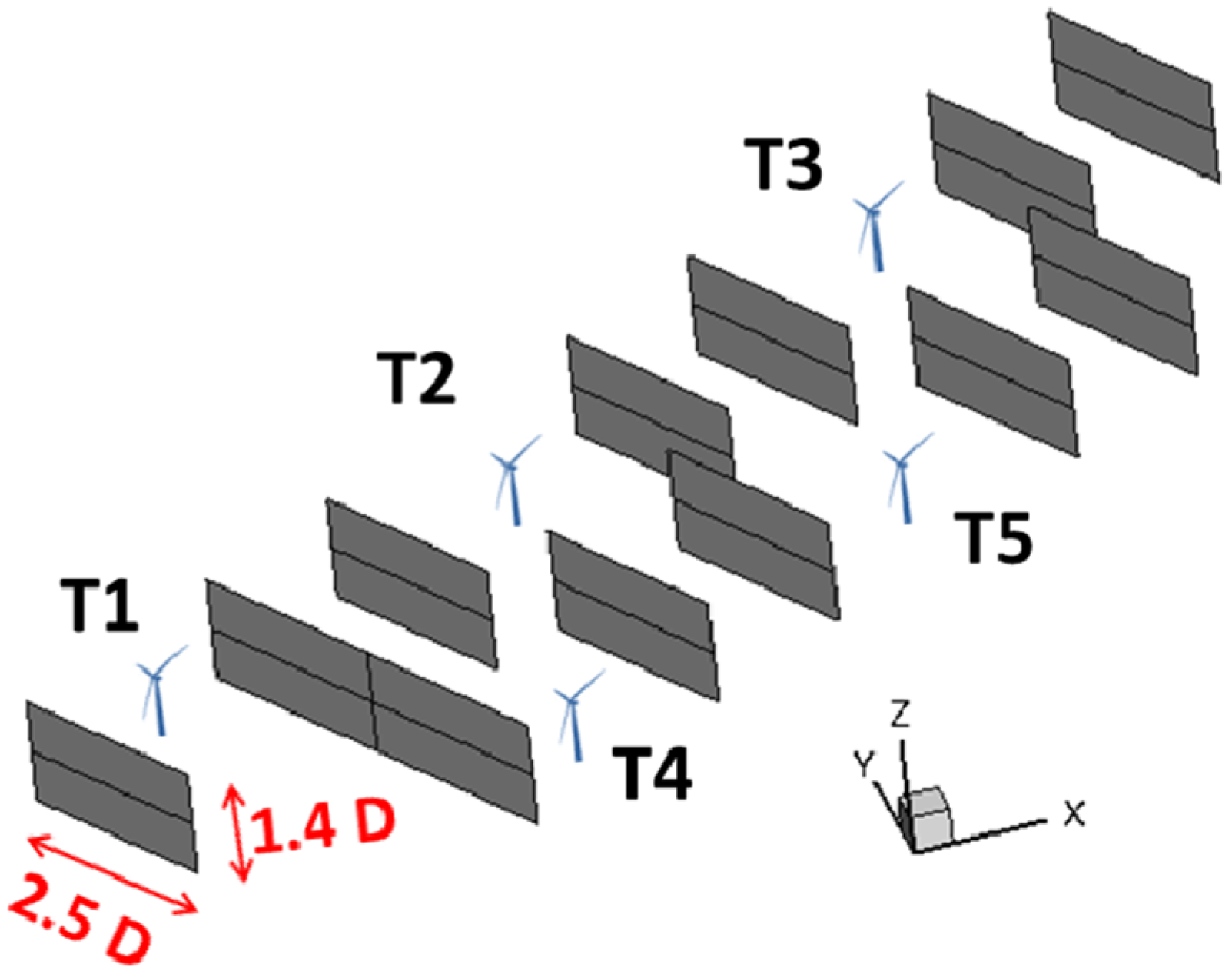
3.3. A Wind Farm Consisting of Five Wind Turbines (ALM OpenFOAM-LES)
3.3.1. Turbine Power
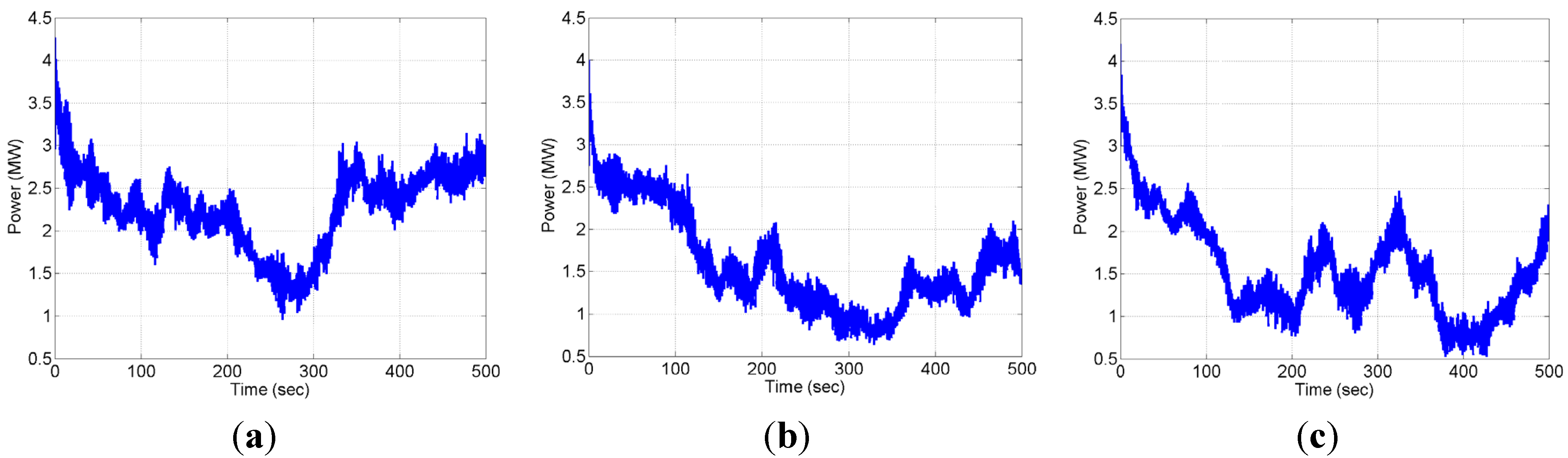
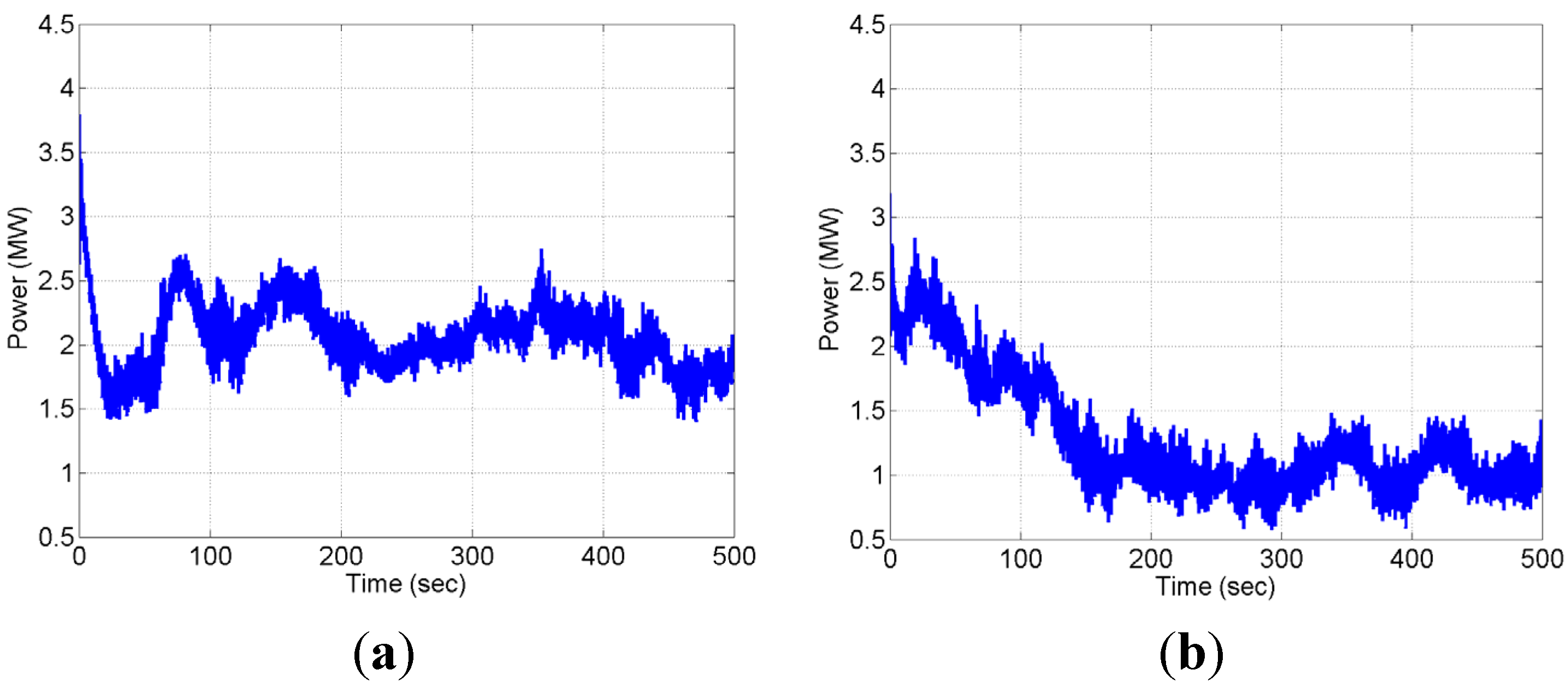
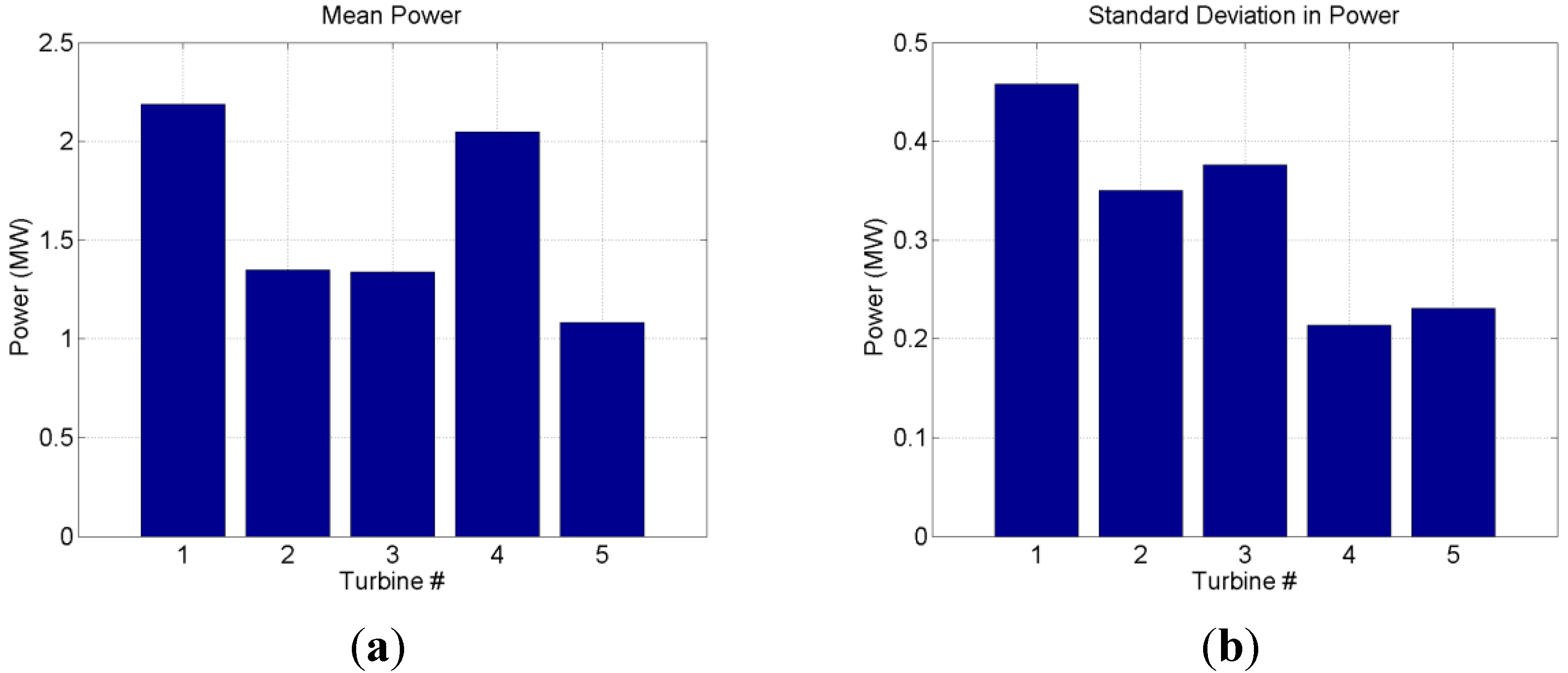
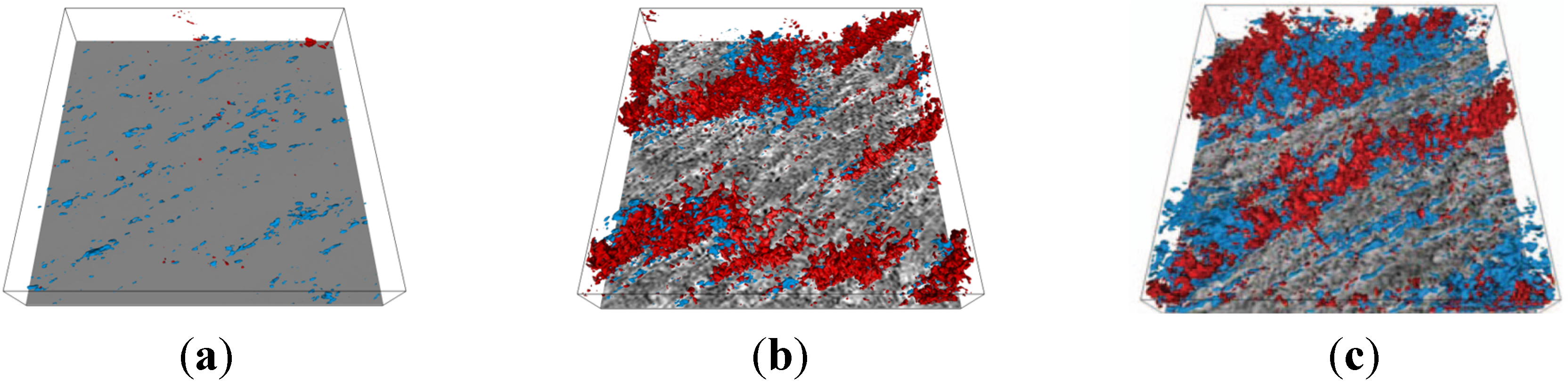
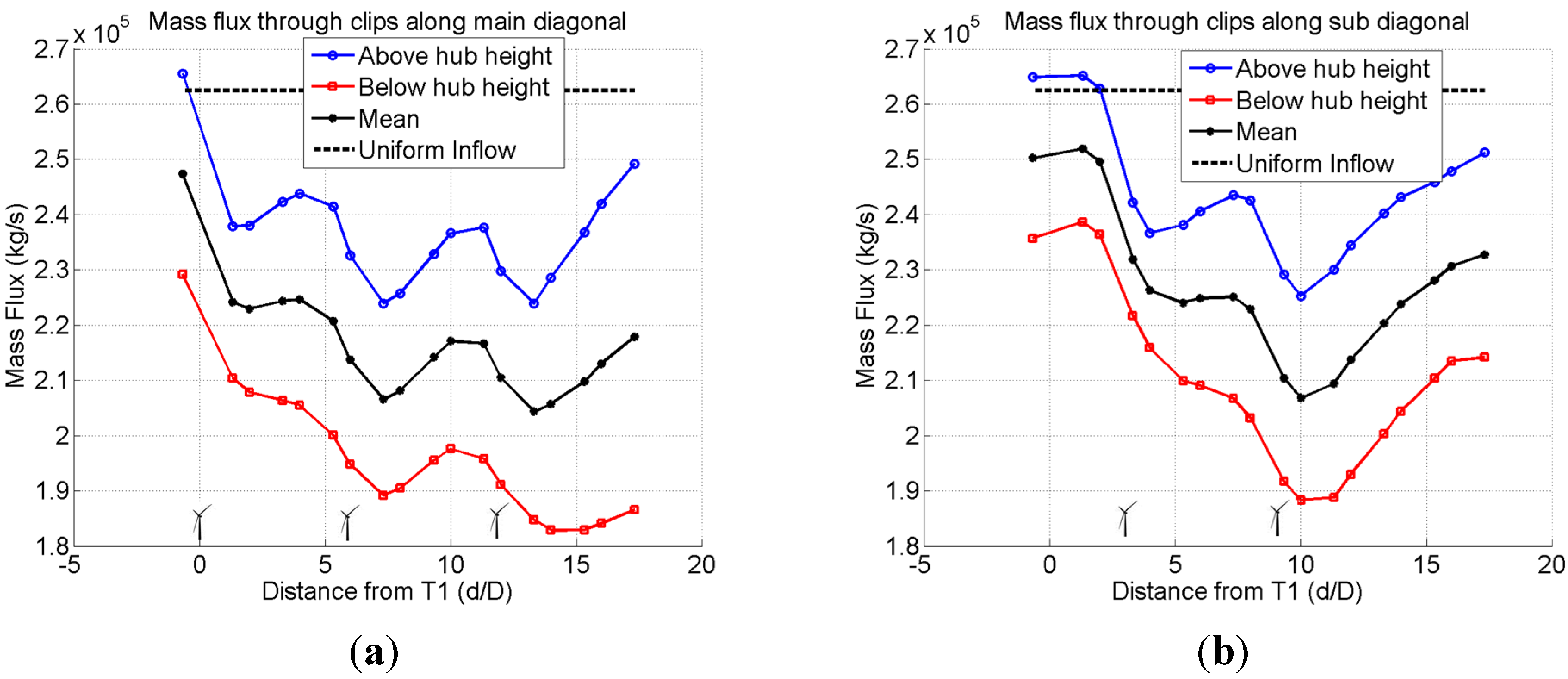
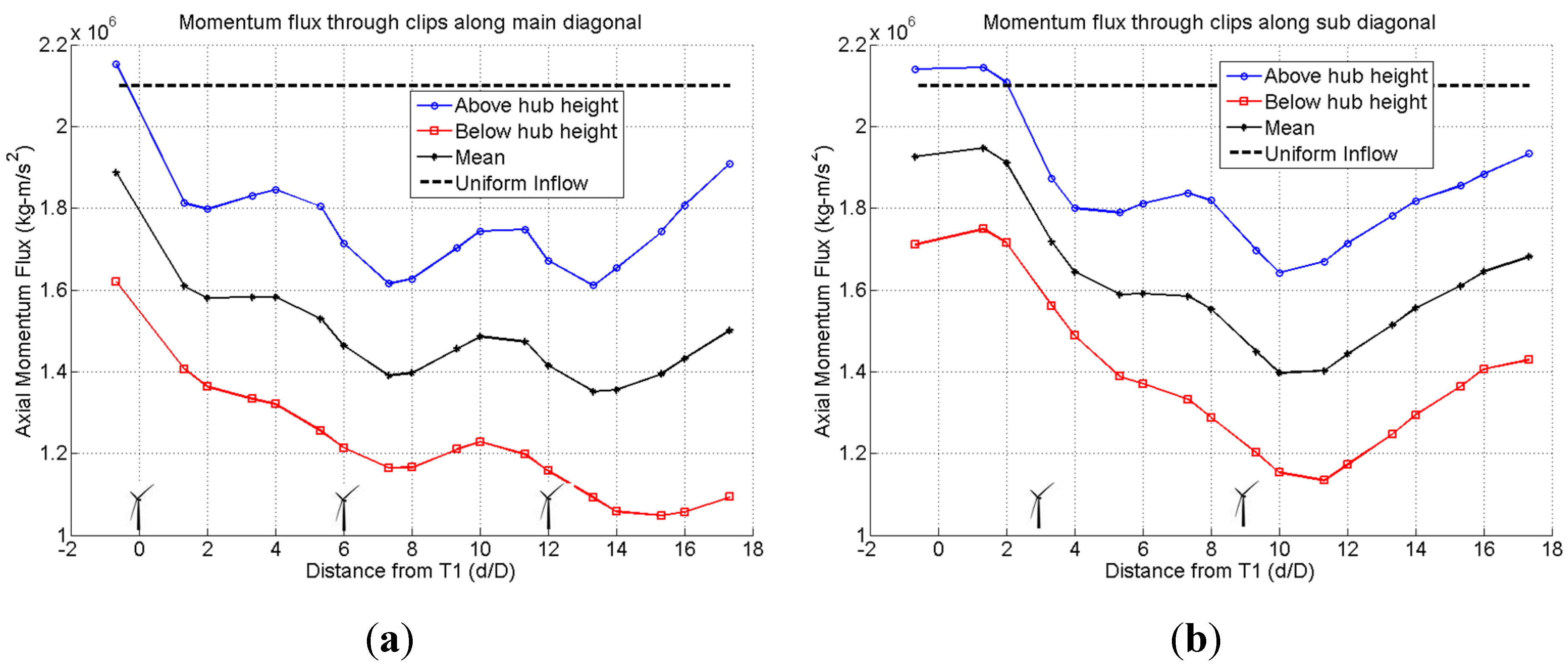
3.3.2. Dynamic Surface Clipping for Flux Analysis
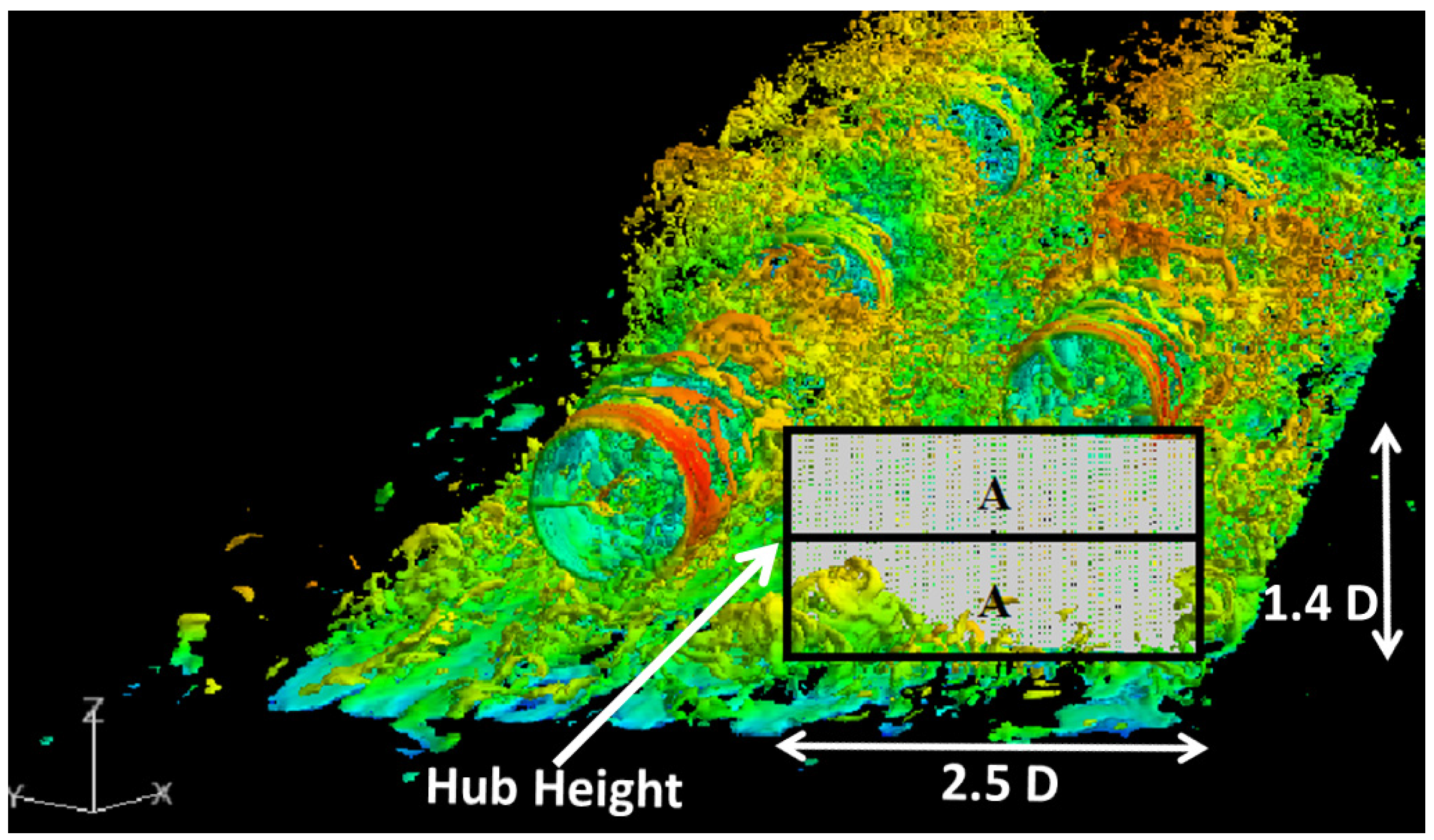
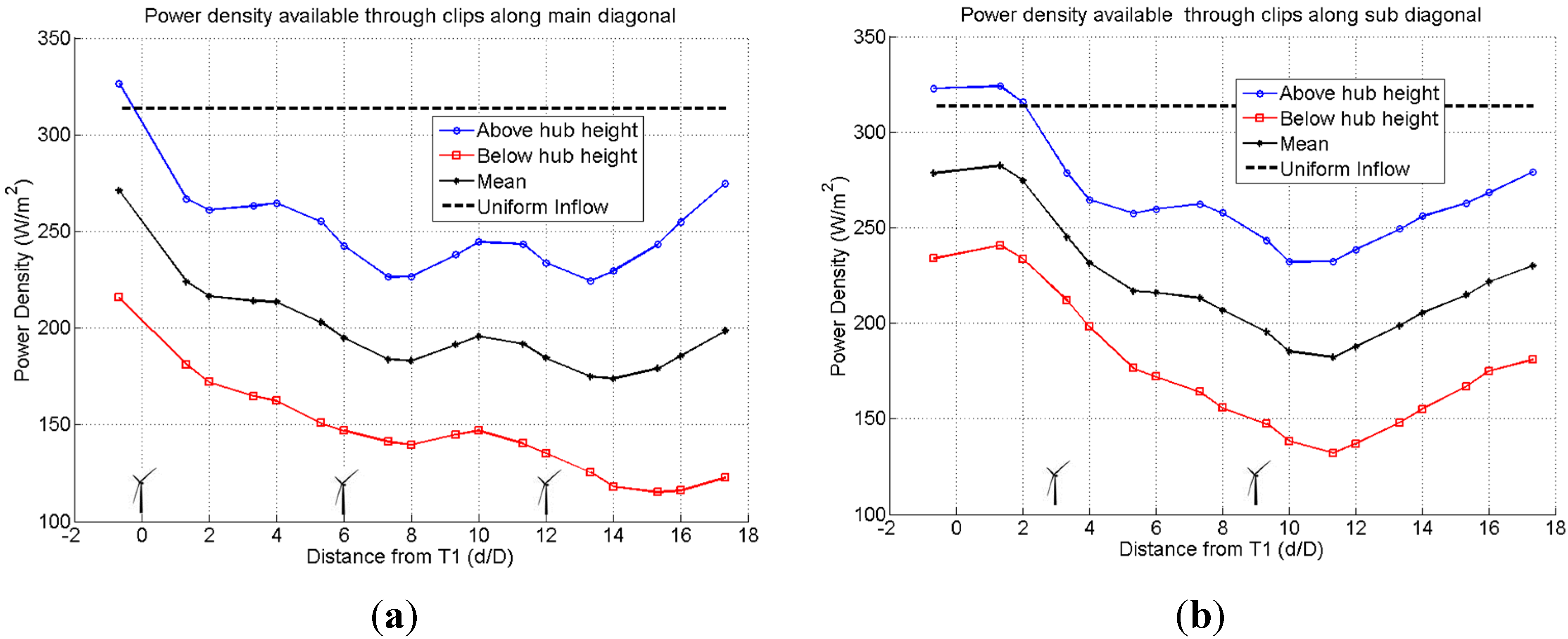
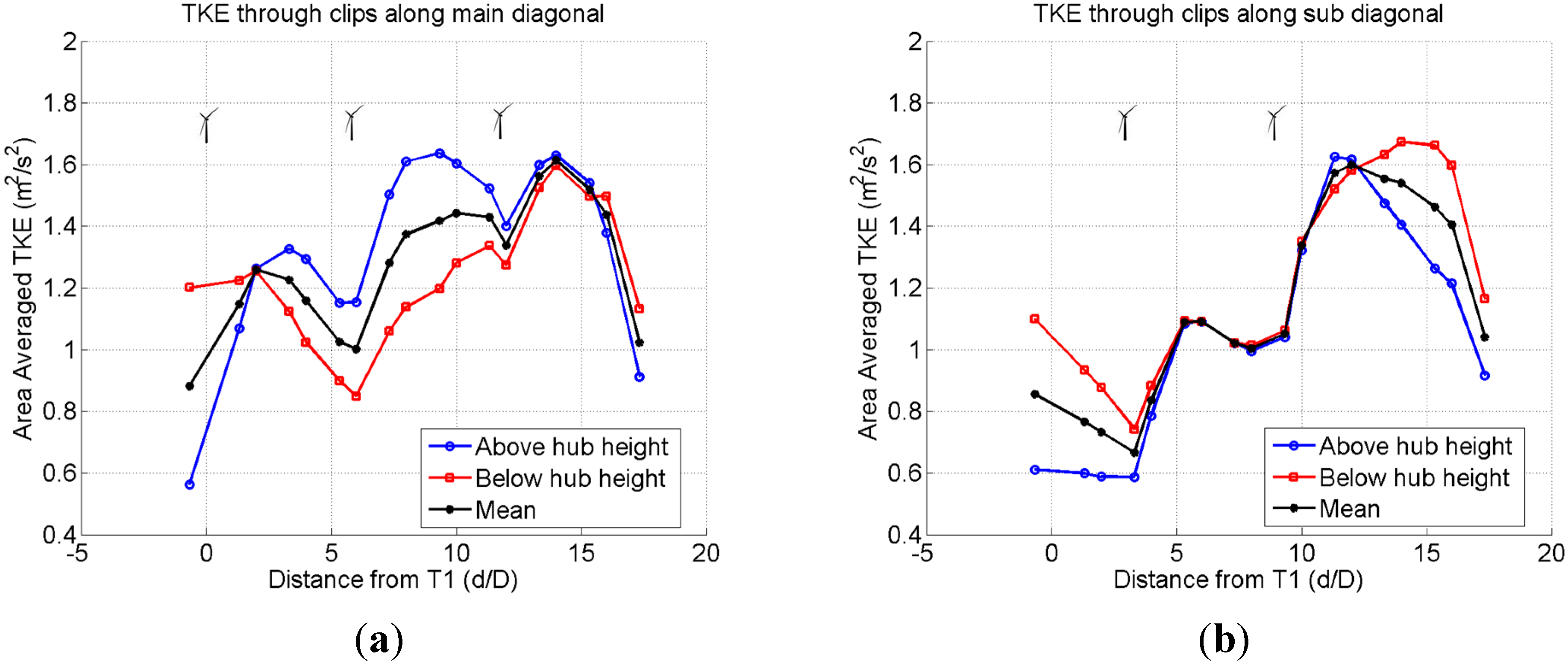
3.3.3. Integrated Quantities along “Dynamic Surface Clips” of Wake Surface Cutting Planes
4. Conclusions
- The ABL stability state defines the shear in the atmospheric boundary layer (ABL) and has a profound effect on the wake recovery and power production of wind turbine arrays.
- Array efficiency increases in a moderately-convective boundary layer (MCBL) compared to a neutral boundary layer (NBL), thus leading to a faster recovery of the wake momentum deficit. This is supported by R13 distributions along vertical lines.
- Higher turbulence levels in MCBL compared to NBL conditions also lead to higher fatigue loads, in particular for the downstream turbine in a turbine-turbine interaction problem, as supported by higher standard deviation of turbine power.
- The peak TKE occurs at the upper edge of the wake and on the sides of the wake at hub height due to the presence of a developing shear layer and tip vortices.
- The shear due to the wake is far more pronounced than the shear due to ABL.
- The TKE distribution is broadened due to wake rotation and ensuing turbulent mixing.
- For wind farms arranged in staggered arrays, the downstream array is affected by the wake of the upstream array, even for perfectly aligned wind conditions (zero yaw). This leads to a small power loss in the (downstream) staggered array; however, the standard deviation in power, and most probably fatigue loads, are reduced at a higher rate compared to the power loss. This may be of interest for future array planning.
- The observed fact from many wind farms that power production has leveled out by the third turbine in an array has been confirmed in the computations of this work in the example of a 5-turbine wind farm.
- The use of the “dynamic surface clipping” method in FieldView allowed to separate integrated fluxes of mass, momentum, power density, and TKE in wake surface cutting planes above and below hub height. It was discovered that the lower portion of a wake surface cutting plane lags in its recovery process by about one turbine spacing.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sørensen, J.N.; Shen, W.Z. Numerical modeling of Wind Turbine Wakes. ASME J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Troldborg, N.; Sørensen, J.N.; Mikkelsen, R. Actuator Line Simulation of Wake of Wind Turbine Operating in Turbulent Inflow. In Journal of Physics: Conference Series, The Science of Making Torque from Wind; Technical University of Denmark: Lyngby, Denmark, 2007. [Google Scholar]
- Troldborg, N. Actuator Line Modeling of Wind Turbine Wakes. Ph.D. Thesis, Technical University of Denmark, Copenhagen, Denmark, 2008. [Google Scholar]
- Troldborg, N.; Sørensen, J.; Mikkelsen, R. Numerical Simulations of Wake Characteristics of a Wind Turbine in Uniform Flow. Wind Energy 2010, 13, 86–99. [Google Scholar] [CrossRef]
- Jensen, L.E. Array Efficiency at Horns Rev and the Effect of Atmospheric Stability. In Proceedings of the 2007 European Wind Energy Conference, Milan, Italy, 7–10 May 2007.
- Rathmann, O.; Frandsen, S.T.; Barthelmie, R.J. Wake Modelling for Intermediate and Large Wind Farms. In Proceedings of the European Wind Energy Conference and Exhibition, Milan, Italy, 7–10 May 2007.
- Churchfield, M.J.; Moriarty, P.J.; Vijayakumar, G.; Brasseur, J.G. Wind Energy-Related Atmospheric Boundary-Layer Large-Eddy Simulation Using OpenFOAM; National Renewable Energy Laboratory: Golden, CO, USA, 2010; NREL/CP-500–48905. [Google Scholar]
- Churchfield, M.J. Wind Energy/Atmospheric Boundary Layer Tools and Tutorials. In Training Session at the 6th OpenFOAM Workshop; The Pennsylvania State University: University Park, PA, USA, 2011. [Google Scholar]
- Churchfield, M.J.; Lee, S.; Moriarty, P.J.; Martínez, L.A.; Leonardi, S.; Vijayakumar, G.; Brasseur, J.G. A Large-Eddy Simulation of Wind-Plant Aerodynamics. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, TN, USA, 9–12 January 2012.
- Martínez, L.A.; Leonardi, S.; Churchfield, M.J.; Moriarty, P.J. A Comparison of Actuator Disk and Actuator Line Wind Turbine Models and Best Practices for Their Use. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, TN, USA, 9–12 January 2012.
- Churchfield, M.J.; Lee, S.; Michalakes, J.; Moriarty, P.J. A Numerical Study of the Effects of Atmospheric and Wake Turbulence on Wind Turbine Dynamics. J. Turbul. 2012, 13, 1–32. [Google Scholar]
- Jha, P.K.; Churchfield, M.J.; Moriarty, P.J.; Schmitz, S. Accuracy of State-of-the-Art Actuator-Line Modeling for Wind Turbine Wakes. In Proceedings of the 51th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 7–10 January 2013.
- Jha, P.K.; Churchfield, M.J.; Moriarty, P.J.; Schmitz, S. Guidelines for Volume Force Distributions within Actuator Line Modeling of Wind Turbines on Large-Eddy Simulation-type Grids. ASME J. Sol. Energy Eng. 2014, 136. [Google Scholar] [CrossRef]
- Jha, P.K.; Churchfield, M.J.; Moriarty, P.J.; Schmitz, S. The Effect of Various Actuator-Line Modeling Approaches on Turbine-Turbine Interactions and Wake-Turbulence Statistics in Atmospheric Boundary-Layer Flow. In Proceedings of the 52th AIAA Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014.
- OpenFOAM, Ver. 2.0.x, ESI Group-OpenCFD. Available online: http://www.openfoam.org/git.php (accessed on 20 April 2015).
- Porté-Agel, F.; Wu, Y.; Chen, C. A Numerical Study of the Effects of Wind Direction on Turbine Wakes and Power Losses in a Large Wind Farm. Energies 2013, 6, 5297–5313. [Google Scholar] [CrossRef]
- Wu, Y.; Porté-Agel, F. Atmospheric Turbulence Effects on Wind-Turbine Wakes: An LES Study. Energies 2012, 5, 5340–5362. [Google Scholar] [CrossRef]
- Sim, C.; Basu, S.; Manuel, L. On Space-Time Resolution of Inflow Representations for Wind Turbine Loads Analysis. Energies 2012, 5, 2071–2092. [Google Scholar] [CrossRef]
- VerHulst, C.; Meneveau, C. Altering Kinetic Energy Entrainment in Large Eddy Simulations of Large Wind Farms Using Unconventional Wind Turbine Actuator Forcing. Energies 2015, 8, 370–386. [Google Scholar] [CrossRef]
- Bhaganagar, K.; Debnath, M. Implications of Stably Stratified Atmospheric Boundary Layer Turbulence on the Near-Wake Structure of Wind Turbines. Energies 2014, 7, 5740–5763. [Google Scholar] [CrossRef]
- Bhaganagar, K.; Debnath, M. The effects of mean atmospheric forcings of the stable atmospheric boundary layer on wind turbine wake. J. Renew. Sustain. Energy 2015, 7. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Porté-Agel, F. Turbulent Flow Inside and Above a Wind Farm: A Wind-Tunnel Study. Energies 2011, 4, 1916–1936. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Arndt, R.E.A.; Sotiropoulos, F. Turbulent Flow Properties Around a Staggered Wind Farm. Bound. Layer Meteorol. 2011, 141, 349–367. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Arndt, R.E.A.; Sotiropoulos, F. Reynolds number dependence of turbulence statistics in the wake of wind turbines. Wind Energy 2012, 15, 733–742. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Mikkelsen, R.F.; Henningson, D.S.; Ivanell, S.; Sarmast, S.; Andersen, S.J. Simulation of wind turbine wakes using the actuator line technique. Phil. Trans. R. Soc. A 2014, 373. [Google Scholar] [CrossRef] [PubMed]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Rhie, C.M.; Chow, W.L. Numerical Study of the Turbulent Flow Past an Airfoil with Trailing Edge Separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the Implicitly Discretized Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1985, 62, 40–65. [Google Scholar] [CrossRef]
- Intelligent Light. Available online: http://www.ilight.com (accessed on 20 April 2015).
- Bashioum, J.L.; Jha, P.K.; Schmitz, S.; Duque, E.P.N. Wake Turbulence of Two NREL 5-MW Wind Turbines Immersed in a Neutral Atmospheric Boundary-Layer Flow. American Physical Society Division of Fluid Dynamics. Available online: http://arxiv.org/abs/1310.3294 (accessed on 15 October 2013).
- Stull, R.B. Meteorology for Scientists and Engineers, 2nd ed.; Brooks/Cole: Florence, KY, USA, 2000. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL-TP-500–38060; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Lee, S.; Churchfield, M.J.; Moriarty, P.J.; Jonkman, J.; Michalakes, J. A Numerical Study of Atmospheric and Wake Turbulence Impacts on Wind Turbine Fatigue Loadings. ASME J. Sol. Energy Eng. 2013, 135. [Google Scholar] [CrossRef]
- Vijayakumar, G.; Brasseur, J.G.; Lavely, A.W.; Kinzel, M.P.; Paterson, E.G.; Churchfield, M.J.; Moriarty, P.J. Considerations in coupling LES of the atmosphere to CFD around wind turbines. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, TN, USA, 9–12 January 2012.
- Lavely, A.W.; Vijayakumar, G.; Brasseur, J.G.; Paterson, E.G.; Kinzel, M.P. Comparing Unsteady Loadings on Wind Turbines using TurbSim and LES Flow Fields. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, TN, USA, 9–12 January 2012.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jha, P.K.; Duque, E.P.N.; Bashioum, J.L.; Schmitz, S. Unraveling the Mysteries of Turbulence Transport in a Wind Farm. Energies 2015, 8, 6468-6496. https://doi.org/10.3390/en8076468
Jha PK, Duque EPN, Bashioum JL, Schmitz S. Unraveling the Mysteries of Turbulence Transport in a Wind Farm. Energies. 2015; 8(7):6468-6496. https://doi.org/10.3390/en8076468
Chicago/Turabian StyleJha, Pankaj K., Earl P. N. Duque, Jessica L. Bashioum, and Sven Schmitz. 2015. "Unraveling the Mysteries of Turbulence Transport in a Wind Farm" Energies 8, no. 7: 6468-6496. https://doi.org/10.3390/en8076468
APA StyleJha, P. K., Duque, E. P. N., Bashioum, J. L., & Schmitz, S. (2015). Unraveling the Mysteries of Turbulence Transport in a Wind Farm. Energies, 8(7), 6468-6496. https://doi.org/10.3390/en8076468






