Abstract
Recently, the optimization of power flows in portable hybrid power-supply systems (HPSSs) has become an important issue with the advent of a variety of mobile systems and hybrid energy technologies. In this paper, a control strategy is considered for dynamically managing power flows in portable HPSSs employing batteries and supercapacitors. Our dynamic power management strategy utilizes the concept of approximate dynamic programming (ADP). ADP methods are important tools in the fields of stochastic control and machine learning, and the utilization of these tools for practical engineering problems is now an active and promising research field. We propose an ADP-based procedure based on optimization under constraints including the iterated Bellman inequalities, which can be solved by convex optimization carried out offline, to find the optimal power management rules for portable HPSSs. The effectiveness of the proposed procedure is tested through dynamic simulations for smartphone workload scenarios, and simulation results show that the proposed strategy can successfully cope with uncertain workload demands.
1. Introduction
Recently, mobile technologies have advanced to a remarkable extent, and power consumption from mobile devices has become a serious concern in portable electronics such as smartphones, tablet PCs, and electric vehicles. The most widely used power-supply systems for portable electronic devices are electrochemical-battery-based. However, battery technology has progressed very slowly and suffers from several drawbacks such as the high current load that rapidly depletes the battery’s energy and its intrinsic low power density characteristic, resulting in inefficiency when handling high load fluctuations. One of the promising methods that can compensate for some of the battery’s drawbacks is based on the use of supercapacitors [1]. The supercapacitor is an emerging technology that is currently experiencing rapid development and is particularly attractive for portable systems. This is because the supercapacitor has a higher power density and faster charge/discharge capability compared to a power supply based only on batteries. Owing to the strengths of supercapacitors that can compensate for the weaknesses of batteries, portable hybrid power-supply systems (HPSSs) employing both batteries and supercapacitors are now considered to be an important alternative to conventional battery-only power supply systems [2,3]. Because the lifetime of an HPSS can be significantly extended by judiciously controlling the level of each component’s power consumption, optimization of the power flows in HPSSs is a key issue that should be solved for intelligent power management of HPSSs [4]. In this paper, the problem of dynamically managing power flows in portable HPSSs employing batteries and supercapacitors is considered, and we propose an approximate dynamic programming (ADP)-based solution. In recent years, stochastic optimal control theory has been applied to various engineering problems. As is well known, a general stochastic optimal control strategy can be derived, in principle, utilizing the concept of the state value function, which is defined as the minimum total expected cost achieved by an optimal control policy from the given state. This value-function-based method is called dynamic programming (DP) and provides an important theoretical foundation for various optimal control problems. However, most real-world optimal control problems cannot be solved by DP exactly, except in very simple cases, and many studies rely on ADP, which finds an approximate solution to the stochastic optimal control problem utilizing an approximate value function, in order to obtain a good suboptimal control policy [5,6,7,8,9]. The main objective of this paper is to consider an ADP-based solution to dynamic power management (DPM) for portable HPSSs employing batteries and supercapacitors. More specifically, we consider a mathematical formulation of DPM for an HPSS in the form of a stochastic optimal control problem and establish an ADP-based procedure for solving the resulting controller synthesis problem. Simulation results show that this procedure works well when applied to DPM for smartphones under various load profiles.
The remainder of this paper is organized as follows. In Section 2, a preliminary background is provided regarding the mathematical formulation of the DPM problem for portable HPSSs employing batteries and supercapacitors. In Section 3, we present the framework for stochastic optimal control and describe the ADP-based controller synthesis procedure for the DPM problem. In Section 4, the effectiveness of the ADP-based procedure is illustrated by using actual workload scenarios for mobile phones. Finally, in Section 5, concluding remarks are presented.
2. Problem Formulation
This section describes the portable HPSS, and presents a mathematical model in the form of a state-space description.
2.1. System Configuration and Related Background
Recently, the optimization of power flows in HPSSs has become an important issue for the purposes of energy savings, lifetime lengthening, and so forth. For the current state-of-the-art works on the subject, the reader is referred to papers such as [10,11,12,13,14,15]. Romaus et al. [10] addressed the problem of controlling the power flows of a hybrid energy storage system combining batteries and double layer capacitors, and proposed the use of self-optimization methods that can consider various operating conditions and take into account several partly conflicting objective functions. As an application domain, the reference paper [10] considered an autonomous rail-bound vehicle. Chen et al. [11] proposed a scheduling strategy for a hybrid energy storage system for a wind farm based on predictive wind speed and the particle swarm optimization (PSO) algorithm. The strengths of the proposed scheduling strategy are that the optimization results can not only satisfy the requirements of output power quality, but also have good prediction accuracy for the wind power output. Choi et al. [12] presented an optimal energy management scheme based on the so-called the multiplicative-increase-additive-decrease (MIAD) policy for hybrid energy storage systems with the objectives of minimizing the magnitude/fluctuation of the battery current, and minimizing the supercapacitor energy loss. Gee et al. [13] analyzed and implemented a battery lifetime extension strategy for a battery/supercapacitor hybrid energy storage system, in which current filtering using a low pass filter was proposed to divert the high-frequency component of the HPSS system charge/discharge current to the supercapacitor in real time. The results of [13] showed the potential improvement in battery lifetime of HPSS in a wind power system without applying any optimization methods. Blanes et al. [14] considered the implementation of a hybrid energy storage system using ultracapacitor, and investigated a simple FPGA control method with a bidirectional buck-boost converter for an electrical vehicle HPSS system. In the method in [14], the battery supplies the low frequency part and the supercapacitor supplies the high-frequency part of the motor current, which reduces the battery stress and softens the battery peak current. Min et al. [15] presented a linear programming (LP) based method to address the problem of minimizing the installation cost while meeting the grid connection requirement, together with a quadratic programming-based approach to transmit the optimal operational signals to battery energy storage system and electric double layer capacitor modules.
This paper is concerned with an ADP-based DPM of an HPSS employing batteries and supercapacitors, which are used for portable and low-power applications. A typical example is shown in Figure 1. In this example, the HPSS consists of a single battery, two supercapacitors, two DC-DC converters, and five bidirectional switches. As is well known, a battery is currently the most widely used device that supplies energy to portable systems and has a high-energy and low-power density. However, the intrinsic low-power density of a battery often results in inefficiency, especially when handling high load fluctuations. On the other hand, supercapacitors have a low-energy and high-power density. Thus, batteries and supercapacitors can compensate for each other’s weaknesses quite well [16]. In the portable HPSS in Figure 1, the battery and supercapacitors can operate in the charging and discharging modes, respectively, or all together. DC-DC converter #1 between the battery/supercapacitors and the load of the HPSS regulates the load voltage at a constant value. DC-DC converter #2 between the battery and the supercapacitors controls the charging current, which is calculated by the DPM unit. Because energy loss may occur during the process of DC-DC conversion, the converter topologies need be carefully selected [17]. Switches connect the components of the portable HPSS following the operation strategy provided by DPM. The DPM monitors the system at each sampling time step and determines the optimal decision to lengthen the lifetime of the HPSS, thus improving the energy conversion efficiency.
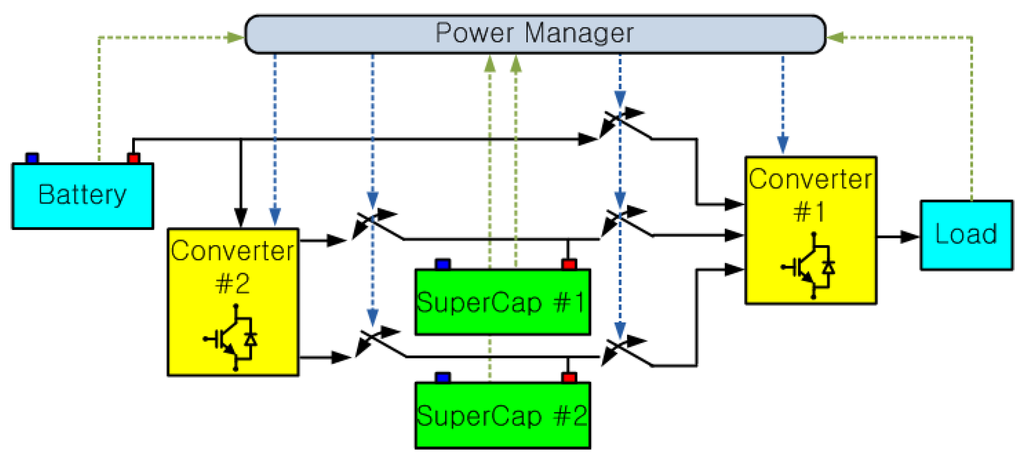
Figure 1.
Structure of a typical portable hybrid power supply system.
2.2. State Equation and Performance Index
In this section, we describe the DPM of a portable HPSS employing batteries and capacitors within the framework of a stochastic optimal control problem. Throughout this paper, we consider an HPSS with the structure shown in Figure 1, which has a single battery and two supercapacitors. Generalization of the model and the corresponding solution procedure for a case with any multiple number of batteries and supercapacitors is straightforward. The steps for deriving the state equation and the performance index (PI) for the system are based on the results of [18] with some modifications. The details of these modifications will be specified later in this section.
Generally, dynamical systems in discrete-time stochastic optimal control problems are described by the state-space model in the form of:
where x(t) ϵ X is the state vector, u(t) ϵ U is the control input vector; and w(t) is the external disturbance, all at time t. In the DPM problem presented in this paper, w(t) is the load demand during a single time interval (t, t + 1). The state vector that we consider for the DPM problem contains the amounts of charge of the supercapacitors and battery as well as the change in the battery’s charge, i.e.,
where rcap,i(t) is the charge state of the ith supercapacitor at time t, rbat(t) is the charge state of the battery at time t, and ∆rbat(t) = rbat(t − 1) − rbat(t) is the difference in the charge state of the battery. Note that in this paper, we assume that the state-of-charge (SOC) values of the supercapacitors and the battery are all available. In practical implementations, these SOC values can be estimated by e.g., extended Kalman filters [19]. The control input vector we consider for the DPM problem contains information regarding the proportion of the charge that each component (i.e., the ith supercapacitor or battery) supplies to meet the workload and the level of the battery charge transferred to each supercapacitor. As in [18], an upper bound Rth is placed on the amount of charge that can be transferred from a battery to each supercapacitor within a time interval so that the battery charge may not be exhausted during the process of charging the supercapacitors. More specifically, the control input vector consists of the following five entries, all in the range of [0,1]:
Here, aix(t), i = 1, 2, is the normalized level of the ith supercapacitor being charged by the battery; thus, the amount of charge transferred from the battery to the ith supercapacitor during the time interval (t, t + 1) is Rth·aix(t). The other entries, a1y(t), a2y(t), and abat(t), are the proportions of the charges that the two supercapacitors and battery supply to meet the workload w(t) in the time interval (t, t + 1). Because these entries are all proportions, they satisfy:
With the above definitions of the state and control inputs, the state transition from time step t to (t + 1) can be expressed as follows [18]:
Note that with the above definitions of the state vector and control input vector, these state transitions can be compactly written in the following state equation form:
where
and
In addition, note that u(t) should satisfy the following constraints from the definitions of the control inputs:
In real portable HPSS applications, exhausting the charge of any component during operation is not desirable. Considering this practical constraint, one can additionally place constraints on the operating ranges of the battery and supercapacitors as follows:
As mentioned before, the state equation is based on the HPSS model of Mirhoseimi and Koushanfar in [18]. The main differences between these two models are as follows:
- ∙
- In [18], it is assumed that the charge values of the batteries and supercapacitors take only discrete values. In this study, we omit this assumption; thus, rcap,i(t) and rbat(t) are all real-valued.
- ∙
- In the model in [18], supercapacitors are constrained to not be simultaneously charged by the battery and discharged by the load. In this paper, we omit this constraint.
- ∙
- In the model in [18], a decision for assigning the source to the workload is carried out such that only one electronic energy supply source can transfer the required charge to the load. Hence, the control inputs in [18] are all binary numbers, and only one member of aiy(t) and abat(t) is one. In this study, we omit this constraint. As a result, aiy(t) and abat(t) are nonnegative real numbers satisfying ∑iaiy(t) + abat(t) = 1.
- ∙
- In the model in [18], it is assumed that at most one supercapacitor can be charged by the battery. This assumption is omitted in this paper.
In order to solve the DPM problem within the framework of stochastic optimal control, we have to choose a PI that can ensure improved energy savings after optimization. A widely used choice for the PI in a stochastic optimal control problem is the expected sum of the discounted stage costs, i.e.,
where γ ϵ (0, 1) is the discount factor; l(·,·) is the stage cost function; and T is the final time whose value is ∞ in infinite-horizon problems. By minimizing this PI over all admissible state feedback control policies ϕt: X→U, the optimal control problem can be solved. For the performance index in the optimization of power flows for HPSSs, one may resort to some ad-hoc stage cost functions (e.g., [18]). However in this paper, it turns out that a traditional objective function which is more clear and widely used in the field of linear quadratic optimal control works well. More precisely, we derive an ADP-based solution to the dynamic power management of HPSSs with the purpose of minimizing the battery charge consumption rate and maintaining the charge level of supercapacitors while keeping the control efforts reasonably low. For the purpose, the stage cost function l(·,·) of the DPM task is chosen as follows:
where the weight values (w1, w2, w3, w4, and βbat) are obtained empirically via a tuning process. In the DPM in [18], the Q-learning method [20] was used to derive an approximation for the optimal power management strategy, and the stage function was defined as
Here, we adopt the main idea of this stage reward function with the following significant modifications. First, representing the stage costs in a quadratic form is important for solving the DPM problem in the context of constrained linear quadratic stochastic optimal control. Hence, our stage cost function utilizes second order polynomial terms instead of exponential functions. Second, in order to minimize the battery charge consumption rate and maintain the charge level of supercapacitors with the control efforts kept reasonably low, we employ the cost terms involving ∆rbat(t), (rcap,i(t) − 0.5)2, i = 1, 2, and the control-input-related quadratic terms, (t), (t), i = 1, 2, and (t). Finally, note that our stage cost Equation (19) deals with the control effort directly with weighted summation of the quadratic input terms, whereas in the objective Equation (20) of the reference paper [18], consideration of the control efforts can be treated indirectly via the expectation operation.
3. Approximate Dynamic Programming Approach to Dynamic Power Management
3.1. Preliminaries
General stochastic optimal control problems can be analyzed, in principle, utilizing the concept of a state value function. This value-function-based method is called DP, and a variety of topics on stochastic optimal control and DP are well-addressed by [5,6,7,8]. A large class of stochastic optimal control problems deal with the dynamics of the form in Equation (1) and are concerned with finding a state-feedback control policy:
that can optimize a given PI function. As mentioned before, a widely used choice for the PI is the expected sum of the discounted stage cost, i.e., . By minimizing this PI over all admissible control policies ϕt: X→U, the optimal value of J can be found. This minimal PI value is denoted J*, and the optimal state-feedback function achieving the minimal value is denoted by ϕ* t. The state value function is defined as the minimum total expected cost achieved by an optimal control policy from the given initial state x(0) = z, i.e.,
Note that when the initial condition x(0) is a fixed vector x0, the optimal PI value can be expressed as J* = V*(x0). According to stochastic optimal control theory [6,7], the state value function in Equation (23) is the fixed point of the Bellman equation:
In its operator form, the Bellman equation can be written as:
where T is the Bellman operator (see e.g., [5]), whose domain and codomain are both function spaces mapping X onto , defined as:
As is well known, the Bellman equation or its operator equation version cannot be solved exactly, except in simple special cases [5,6], and an alternative strategy when finding the exact state value function is the use of ADP relying on an approximate state value function . In the DPM problem discussed in this paper, we are concerned with an ADP solution utilizing convex quadratic functions. This class of quadratic functions is a good choice for the approximate state value function [5,8] because these functions are convenient and powerful for handling various optimization steps appearing in the ADP procedure.
3.2. ADP-Based Solution Procedure
From the above preliminary steps, the DPM of the portable HPSS can now be represented as the following dynamic stochastic control problem:
where l(·,·) is the quadratic stage cost function specified in Equation (19). To solve the above DPM problem for the portable HPSS, we propose an ADP-based solution procedure utilizing the approximate value function (AVF) policy approach of O’Donoghue, Wang, and Boyd [9]. In this AVF policy approach [9], the convex quadratic function:
is used for approximating the state value functions, and by letting the parameters (i.e., Pi, pi, and qi) satisfy the iterated Bellman inequalities:
with , it is ensured that is a lower bound of the optimal state value function V* [5,9]. Further, by optimizing this lower bound via convex optimization, the ADP approach finds a suboptimal approximate state value function and the corresponding ADP policies . In the following, we derive an ADP-based solution to the dynamic management problem for the portable HPSS.
First, note that our stage cost function at time t can be expressed using the state x(t) and input u(t) as follows:
Then, the general stage cost term can be written in the following matrix–vector form:
where
Next, we define the derived matrix variable Gi, i = 1, …, M to satisfy the following:
Note that the right hand side of Equation (37) is the expectation of the convex quadratic function evaluated at the next state. Since the expectation can be expressed as a quadratic function with respect to u and x, we use the derived matrix variable Gi [8] for notational convenience. Here, the expectation of the right-hand side of Equation (37) can be further expanded as follows:
Furthermore, by further evaluating the right-hand side of Equation (38), one can obtain
where
In Equations (40)–(42), and are the first and second moments of the external workload demands, respectively.
With the convex quadratic approximation , the Bellman inequalities for the DPM problem can be written as
where Si−1 is the matrix variable defined by
Note that the constraints in Equations (13)–(17) are all given in the form of an affine equality or affine inequalities with respect to the state and control inputs. Thus, these constraints can be compactly expressed via the affine form Du(t) + Fx(t) + H. More specifically, the equality constraint in Equation (13) can be written as
where and
Similarly, the remaining inequality constraints can be represented by
where
Note that these constraints can be further modified in accordance with the requirements considered in the design stage. One of the key steps in this solution procedure is to find satisfying the Bellman inequalities in Equation (28) under the constraints in Equations (46) and (48). For this, we resort to the S-procedure [21]. On the basis of the S-procedure, we can ensure that the Bellman inequalities be satisfied under the constraints in Equations (46) and (48) by requiring that the following linear matrix inequalities (LMIs) hold true:
where represents the S-procedure multipliers [21], and
By combining the above steps, one can obtain a DPM design procedure. The following show an illustrative design procedure:
Controller synthesis procedure:
Preliminary steps:
- Choose the parameters of the problem: γ, λ, M, Rth, , , and .
- Estimate the 1st and 2nd moments of the external load demands, and , from the training data.
Main steps:
- Initialize the decision-making time t = 0, and choose x(0)= x0.
- Compute the stage cost matrix in Equation (30) and the constant matrix in Equation (64).
- Define the LMI variables:
- (1)
- Define the basic LMI variables: Pi, pi, and qi in Equation (27).
- (2)
- Define the derived LMI variables: Gi in Equation (39) and Si−1 in Equation (47).
- (3)
- Define the S-procedure multipliers: in Equation (63).
- Find the approximate state value functions, , by solving the following convex optimization problem:
- Obtain the ADP controllers on the basis of
4. Simulation Results and Trajectories
In this section, we first describe a portable HPSS example to illustrate the proposed ADP-based DPM procedure. Afterwards, we conduct simulations and provide discussions for simulation results.
4.1. An Illustrative Example
We conducted simulations for a portable HPSS example [18] to illustrate the proposed ADP-based DPM procedure. For the example, we considered the workload scenarios of Figure 2, which are essentially based on the iPhone battery current measurements in [18,22]. The tasks considered in the scenarios include airplane mode (40 mA), default mode (100 mA), working internet with 3G network (310 mA), working game application “Tap-Tap” (220 mA), working 3D game application “GTI Racing” (400 mA), working application “YouTube” with WiFi (260 mA), working application “YouTube” (350 mA), and voice phone (170 mA) [18].
The portable HPSS in our example consists of two 200 [F] supercapacitors with = 400 [C] and a single 4 [V] battery with rbat(0) = 1000 [C]. The initial state conditions for the HPSS were assumed as follows:
Following the data treatment of [18], we rescaled the source and demand charges such that at each instant t, the load charge demand wload(t) was transformed into w(t) = wload(t)/10. We performed simulations based on the ten scenarios of Figure 2, and evaluated the resultant controllers. In the evaluation stage, we used a 10-fold cross-validation method for the iPhone workload data of Figure 2. For the simulation results, we considered all possible 10 different partitions of the training and test subsets. For the parameters of the problem, we chose the following:
where the weight values, w1, w2, w3, w4, and βbat were obtained empirically via a tuning process based on a subset of the training data. Simulation results show that the above set of weight values yielded reasonably good results. To develop a more disciplined design guideline for the weight values is an important topic that can be covered in follow-up works.
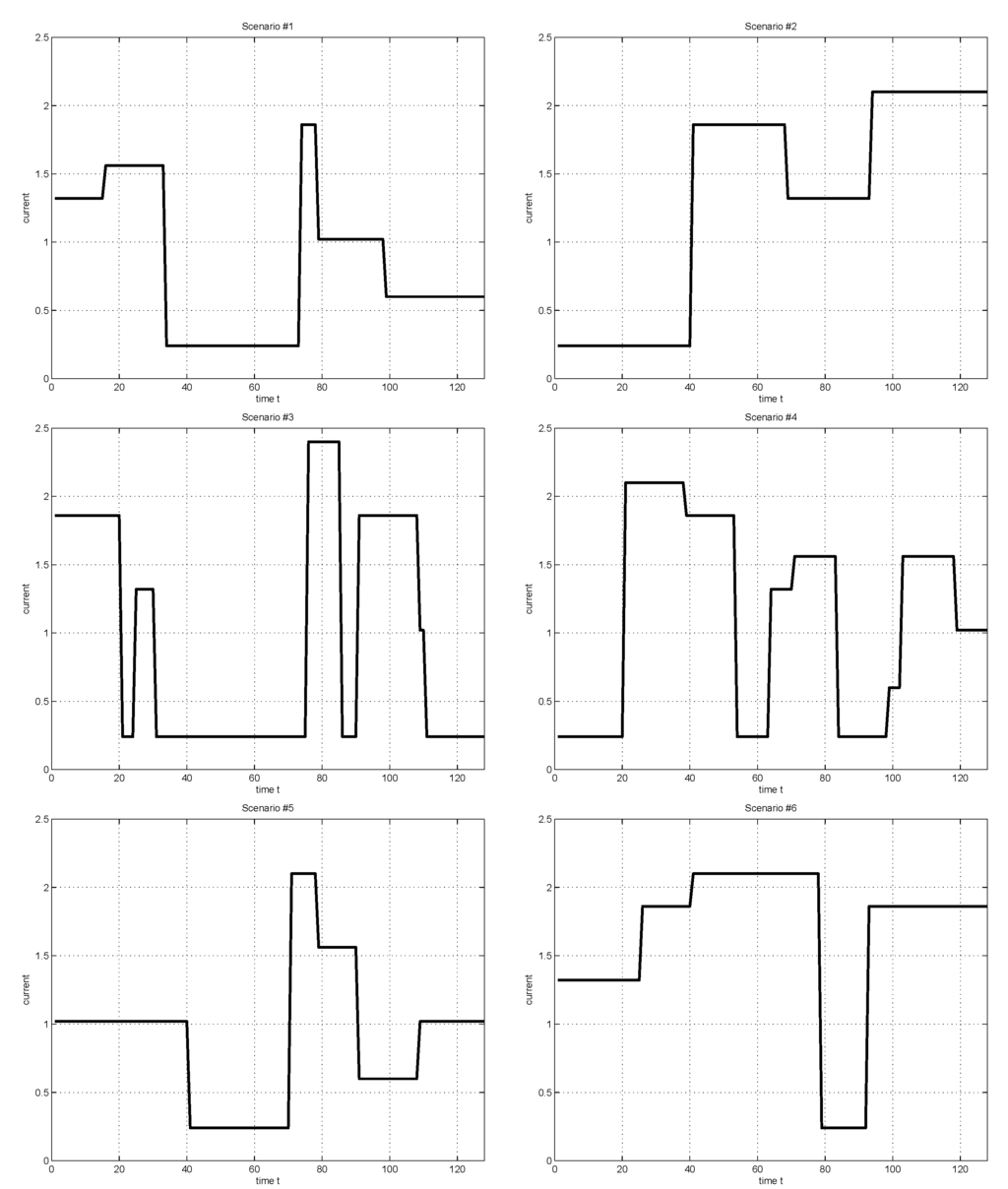
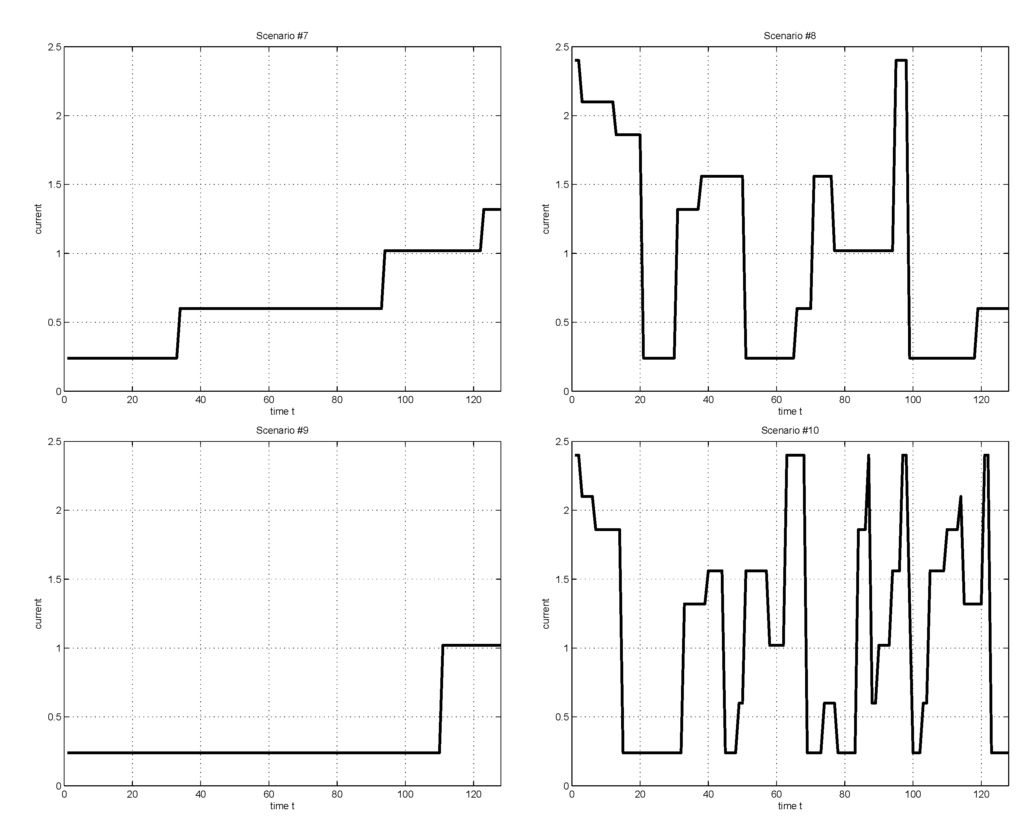
Figure 2.
Considered workload scenarios, which are essentially based on the iPhone battery current measurements of [18].
4.2. Discussions and Performance Comparison
Figure 3 is the simulation results of the 10-fold cross-validation, and describes the charge depletion patterns of the battery and the supercapacitors in the HPSS. The exact meaning of the pictures in the figure is as follows: the ith picture shows the charge-depleting patterns obtained by the proposed ADP-based DPM procedure for the ith numerical experiment, in which the ith workload scenario of Figure 2 was used as the test set, and the other nine workload scenarios were used as the training set for estimating the first and second moments of w(t). In the pictures, the solid line represents the charge value of the battery, rbat(t), and the dashed line is for the sum of supercapacitor charges, rcap,1(t) + rcap,2(t). Note that in the sixth picture, the scenario consists of heavy loads (such as playing games, browsing the Internet, and watching YouTube videos), and the charges in the battery and the supercapacitors were completely depleted before the end of the considered time horizon. Figure 3 shows that the proposed ADP-based DPM procedure resulted in reasonable dynamic charge management for the HPSS. From the simulation results, one can see that when the demand charge changed abruptly, then the control actions for the supercapacitors reacted promptly. It is well known that in general, the battery alone cannot handle the situation of rapidly changing loads effectively due to its low power density. By comparison, Figure 3 shows that the HPSS utilizing the ADP-based DPM was capable of handling such situation reasonably well. We believe that this capability is ensured by the stage cost function of Equation (19), which is defined with the purpose of minimizing the battery charge consumption rate and maintaining the charge level of supercapacitors appropriately for speedy reaction to fluctuating loads. Note that our ADP-based DPM procedure can be applied to a significantly larger class of stage cost functions as long as they are quadratic-program (QP) representable [23] (i.e., l(·,·) is convex quadratic plus a convex piecewise linear function, possibly including linear equality and inequality constraints).
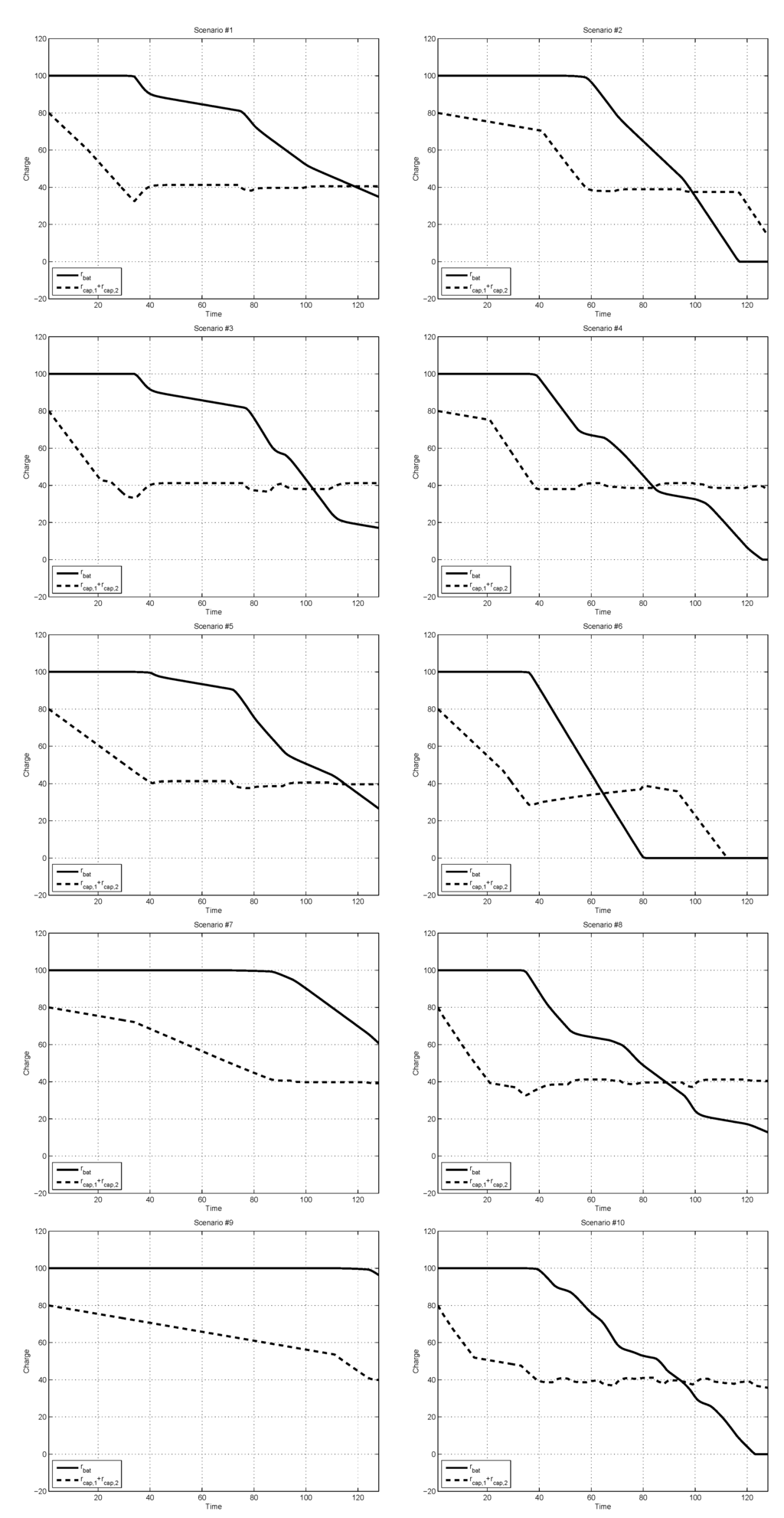
Figure 3.
Charge-depleting patterns of the battery and supercapacitors resulting from the ADP-based approach of this paper.
For the sake of performance comparison, we considered the reinforcement learning (RL) based DPM technique of the reference paper [18]. RL is a branch of machine learning which is related to stochastic optimal control. Recently, RL methods [20] have been successfully applied to various decision-making problems, including the field of DPM for HPSSs [18]. One of the main differences of the RL methods for stochastic optimal control is that in their solution procedures, they use the training data on the state transitions together with function approximation instead of exact mathematical analysis. In the reference paper [18], Q-learning [24], which is one of the most widely used value-function-based RL methods, was utilized to derive an RL-based DPM strategy. In Q-learning, given the state transition data (x(t), u(t), r(t), x(t + 1)), where r(t) is the reward signal defined as the negative cost (i.e., r(t) = −l(x(t), u(t))), the state-action value function Q [20,24] is updated via Q(x(t), u(t))←Q(x(t), u(t)) + α[r(x(t), u(t)) + Q(x(t+1),u) − Q(x(t), u(t))] In our numerical experiments for performance comparison, the discount rate of Q-learning was set to be the same (i.e., γ = 0.99). Function approximation for state-action value function Q was performed via the tile coding [20]. Also for the learning rate and the ε value for exploration via the ε-greedy policy [20], we used α =0.1 and ε = 0.1 (For detailed meaning of α and ε in Q-learning, the reader is referred to [20]). Figure 4 shows the learning curve (the solid line) resulting from Q-learning, which describes the average total cost vs. the iteration over a set of 10 simulation runs, together with the total cost of the proposed ADP-based DPM approach (the dashed line). As shown in the figure, Q-learning took about 500 iterations of training scenarios to have a convergent behavior. Figure 5 shows the simulation results of the Q-learning-based DPM strategy, and describes the charge depletion patterns of the battery and the supercapacitors in the HPSS. Also, Figure 6 reports the average stage cost sums over a set of ten simulation runs for the two methods. As shown in Figure 5 and Figure 6, the proposed ADP-based DPM strategy yielded better performance than the Q-learning-based DPM [18].

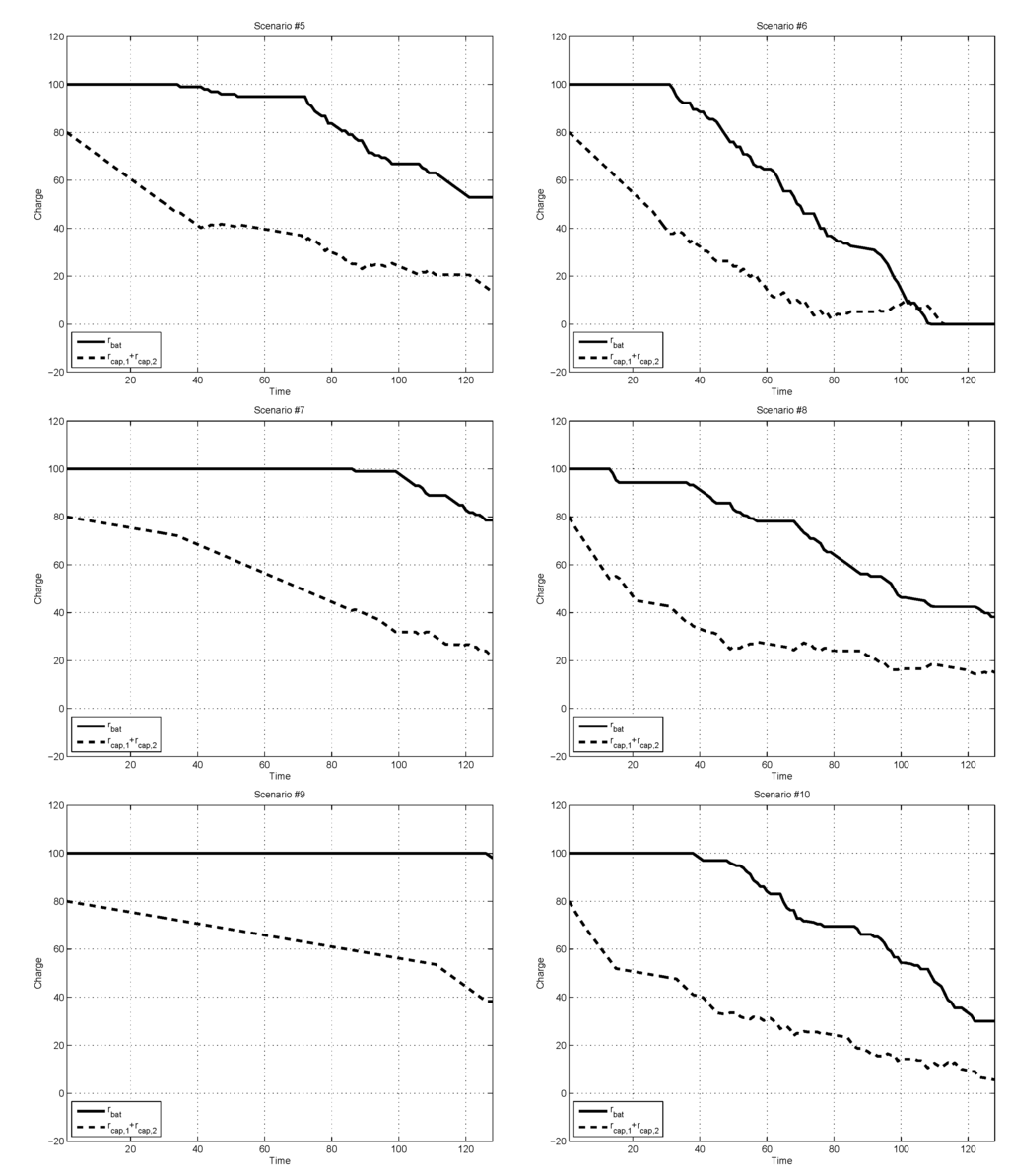
Figure 4.
Charge-depleting patterns of the battery and supercapacitors resulting from the Q-learning-based DPM.
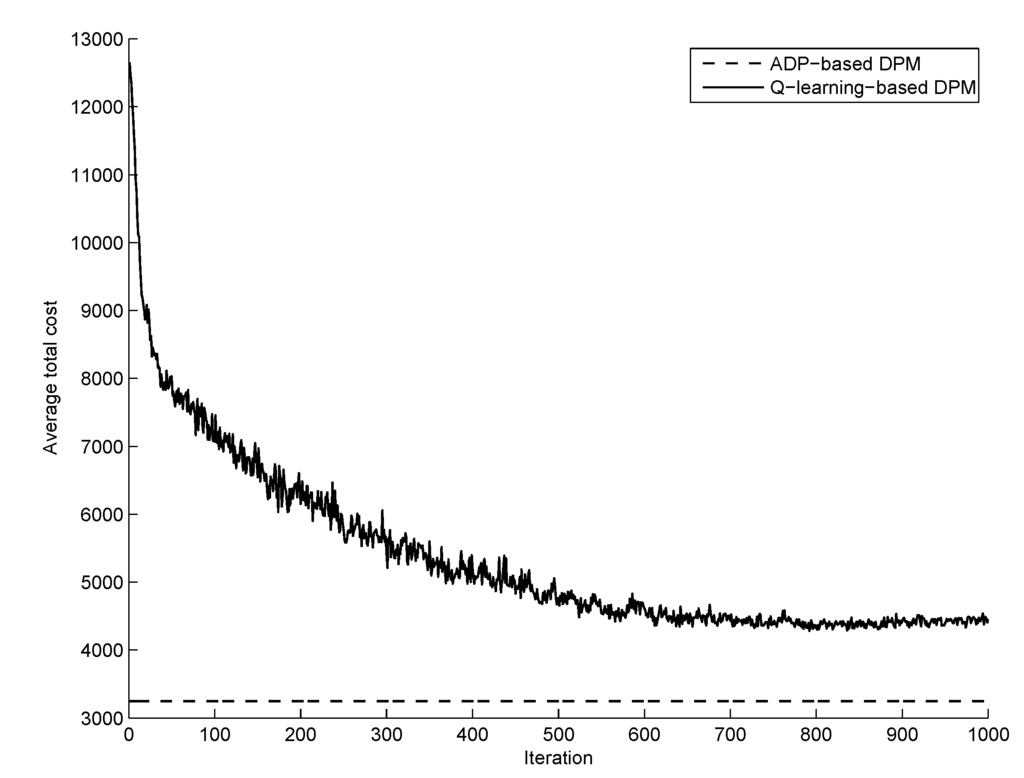
Figure 5.
Learning curve (the average total cost vs. the iteration over a set of 10 simulation runs): Q-learning (dashed) and ADP (solid).
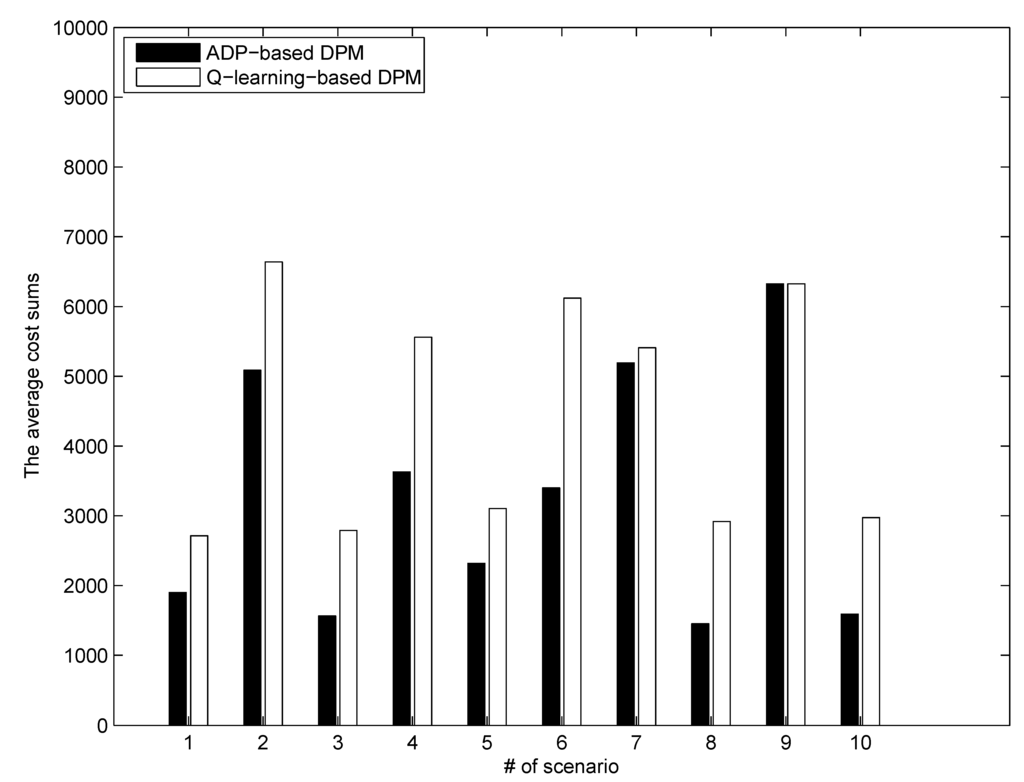
Figure 6.
Performance comparison for ADP and Q: Average total cost for each scenario.
Finally, we think that the main significance of the ADP-based DPM approach of this paper and the Q-learning-based approach is in their capacity for customization. More specifically, they can customize the DPM for a (similar) user group, affecting the dynamic power management policy based on the first and second moments of the workloads and/or the past workload scenarios. We expect that this aspect will be covered in future works with sufficiently large training data sets.
5. Conclusions
Managing power flows in portable HPSSs has become an important issue with the advent of a variety of mobile systems and hybrid energy technologies, particularly when supercapacitors are used, which can compensate for the various weaknesses of conventional battery-based power supplies. The problem of optimally managing the power flows for HPSSs thus becomes more complicated. In this paper, the DPM problem for portable HPSSs with combined supercapacitors and battery energy supplies was considered, and an ADP-based DPM strategy was presented. Simulation results show that the proposed ADP-based approach can find a DPM strategy that copes with uncertain workload demands well, and its performance is better compared to the conventional Q-learning-based DPM method. Our plans for future work include more detailed modeling. For example, in the current model of the paper, the losses in the storage systems and in the power converters were neglected, and we are planning to take into account such losses as well with a more detailed model. Also, we will perform more extensive simulation studies, which should reveal the strengths and weaknesses of ADP-based methods, and applications to other types of HPSSs.
Acknowledgments
This work was supported by a Korea University Grant.
Author Contributions
J.P. and G.C. conceived and designed the methodology of the paper; J.P., D.Y. and J.L. wrote the computer program and performed the numerical experiments; J.P. and G.C. wrote the paper.
Conflict of Interest
The authors declare no conflicts of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Burke, A. Ultracapacitors: Why, How, and Where is the Technology. J. Power Sources 2000, 91, 37–50. [Google Scholar] [CrossRef]
- Yap, H.T.; Schofield, N.; Bingham, C.M. Hybrid energy/power sources for electric vehicle traction systems. In Proceedings of the IEEE Power Electronics, Machines and Drives (PEMD) Conference, Edinburgh, UK, 31 March–2 April 2004; Volume 1, pp. 61–66.
- Miller, J.M.; Deshpande, U.; Dougherty, T.J.; Bohn, T. Power electronic enabled active hybrid energy storage system and its economic viability. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 190–198.
- Wang, L.; Liu, X.; Li, H.; Im, W.S.; Kim, J.M. Power electronics enabled energy management for energy storage with extended cycle life and improved fuel economy in a PHEV. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 3917–3922.
- Wang, Y.; Boyd, S. Approximate dynamic programming via iterated bellman inequalities. Int. J. Robust Nonlinear Control 2015, 25, 1472–1496. [Google Scholar] [CrossRef]
- Bertsekas, D. Dynamic Programming and Optimal Control: Volume 1; Athena Scientific: Belmont, MA, USA, 2005. [Google Scholar]
- Bertsekas, D. Dynamic Programming and Optimal Control: Volume 2; Athena Scientific: Belmont, MA, USA, 2007. [Google Scholar]
- O’Donoghue, D.; Wang, Y.; Boyd, S. Min-Max approximate dynamic programming. In Proceedings of the 2011 IEEE International Symposium on Computer-Aided Control System Design (CACSD), Denver, CO, USA, 20–23 September 2011; pp. 424–431.
- O’Donoghue, B.; Wang, Y.; Boyd, S. Iterated approximate value functions. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3882–3888.
- Romaus, C.; Bocker, J.; Witting, K.; Seifried, A. Optimal energy management for a hybrid energy storage system combining batteries and double layer capacitors. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), San Jose, CA, USA, 20–24 September 2009.
- Chen, G.; Bao, Z.J.; Yang, Q.; Yan, W.J. Scheduling strategy of hybrid energy storage system for smoothing the output power of wind farm. In Proceedings of the IEEE Control and Automation (ICCA), Hangzhou, China, 12–14 June 2013; pp. 1874–1878.
- Choi, M.E.; Kim, S.W.; Seo, S.W. Energy Management Optimization in a Battery/Supercapacitor Hybrid Energy Storage System. IEEE Trans. Smart Grid 2012, 3, 463–472. [Google Scholar] [CrossRef]
- Gee, A.M.; Robinson, F.V.P.; Dunn, R.W. Analysis of battery lifetime extension in a small-scale wind-energy system using supercapacitors. IEEE Trans. Energy Convers. 2013, 28, 24–33. [Google Scholar] [CrossRef]
- Blanes, J.M.; Gutierrez, R.; Garrigos, A.; Lizan, J.L.; Cuadrado, J.M. Electric vehicle battery life extension using ultracapacitors and an FPGA controlled interleaved buck-boost converter. IEEE Trans. Power Electron. 2013, 28, 5940–5948. [Google Scholar] [CrossRef]
- Min, S.W.; Kim, S.J. Optimized installation and operations of battery energy storage system and electric double layer capacitor modules for renewable energy based intermittent generation. J. Electr. Eng. Technol. 2013, 8, 238–243. [Google Scholar] [CrossRef]
- Gao, L.; Dougal, R.A.; Shengyi, L. Power enhancement of an actively controlled battery-ultracapacitor hybrid. IEEE Trans. Power Electron. 2005, 20, 236–243. [Google Scholar] [CrossRef]
- Mirzaei, A.; Farzanehfard, H.; Adib, E.; Jusoh, A.; Salam, Z. A fully soft switched two quadrant bidirectional soft switching converter for ultra capacitor interface circuits. J. Power Electron. 2011, 11, 1–9. [Google Scholar] [CrossRef]
- Mirhoseini, A.; Koushanfar, F. Learning to manage combined energy supply systems. In Proceedings of the IEEE/ACM International Symposium on Low-Power Electronics and Design, Fukuoka, Japan, 1–3 August 2011; pp. 229–234.
- Plett, G.L. Extended Kalman Filtering for Battery Management Systems of LiPB-based HEV Battery pack: Part 1. Background. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Boyd, S.; Ghaoui, L.E.; Feron, E.; Balakrishman, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Mirhoseini, A.; Koushanfar, F. HypoEnergy: Hybrid supercapacitor-battery power-supply optimization for energy efficiency. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition, Grenoble, France, 14–18 March 2012; pp. 1–4.
- Boyd, S.; Mueller, M.T.; O’Donoghue, D.; Wang, Y. Performance bounds and suboptimal policies for multi-period investment. Found. Trends Optim. 2014, 1, 1–69. [Google Scholar] [CrossRef]
- Watkins, C. Learning from Delayed Rewards. Ph.D. Thesis, Cambridge University, Cambridge, UK, 1989. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).