Hierarchical Load Tracking Control of a Grid-Connected Solid Oxide Fuel Cell for Maximum Electrical Efficiency Operation
Abstract
:1. Introduction
2. Determination of the Optimal Operating Condition of a Grid-Connected SOFC Using Nonlinear Programming
- (1)
- Hydrogen rich nature gas is converted to hydrogen (H2) through the external-reforming fuel processor. Like in [22], the carbon oxide (CO) shift reaction is ignored in the analysis. Only pure H2 is fed to the anode;
- (2)
- Oxygen in the air is used as the oxidant. The mole ratio of nitrogen (N2) to oxygen (O2) in the air is denoted as kc which is 3.762;
- (3)
- Both the fuel and air are preheated to the same temperature before they are transmitted to the cell stack. The detailed thermal management is not studied;
- (4)
- The cell stack is well-insulated and the energy losses caused by radiation, convection and conduction are negligible.
2.1. The SOFC Dynamic Model for Power System Studies
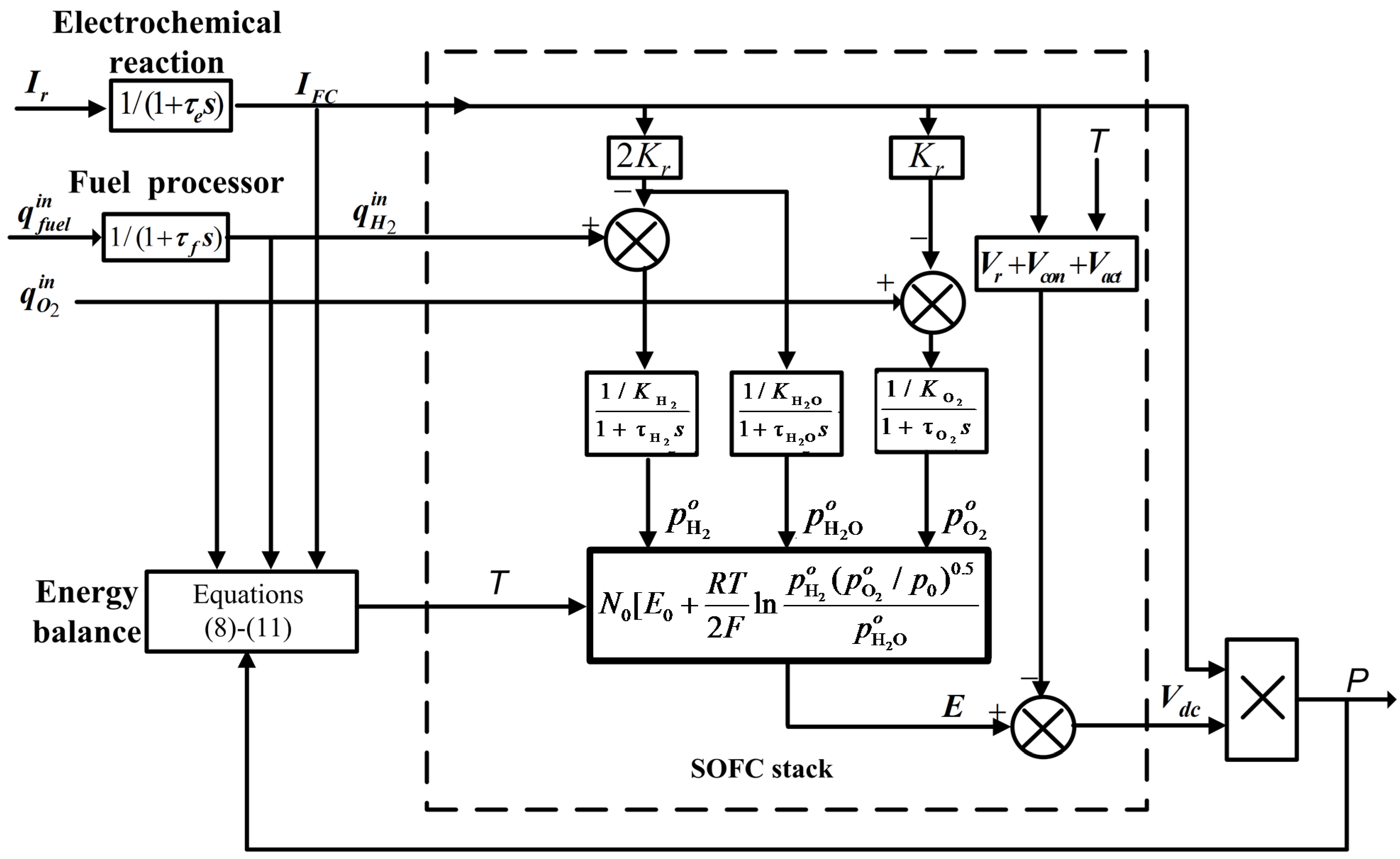
2.2. Power Regulation of a Grid-Connected SOFC
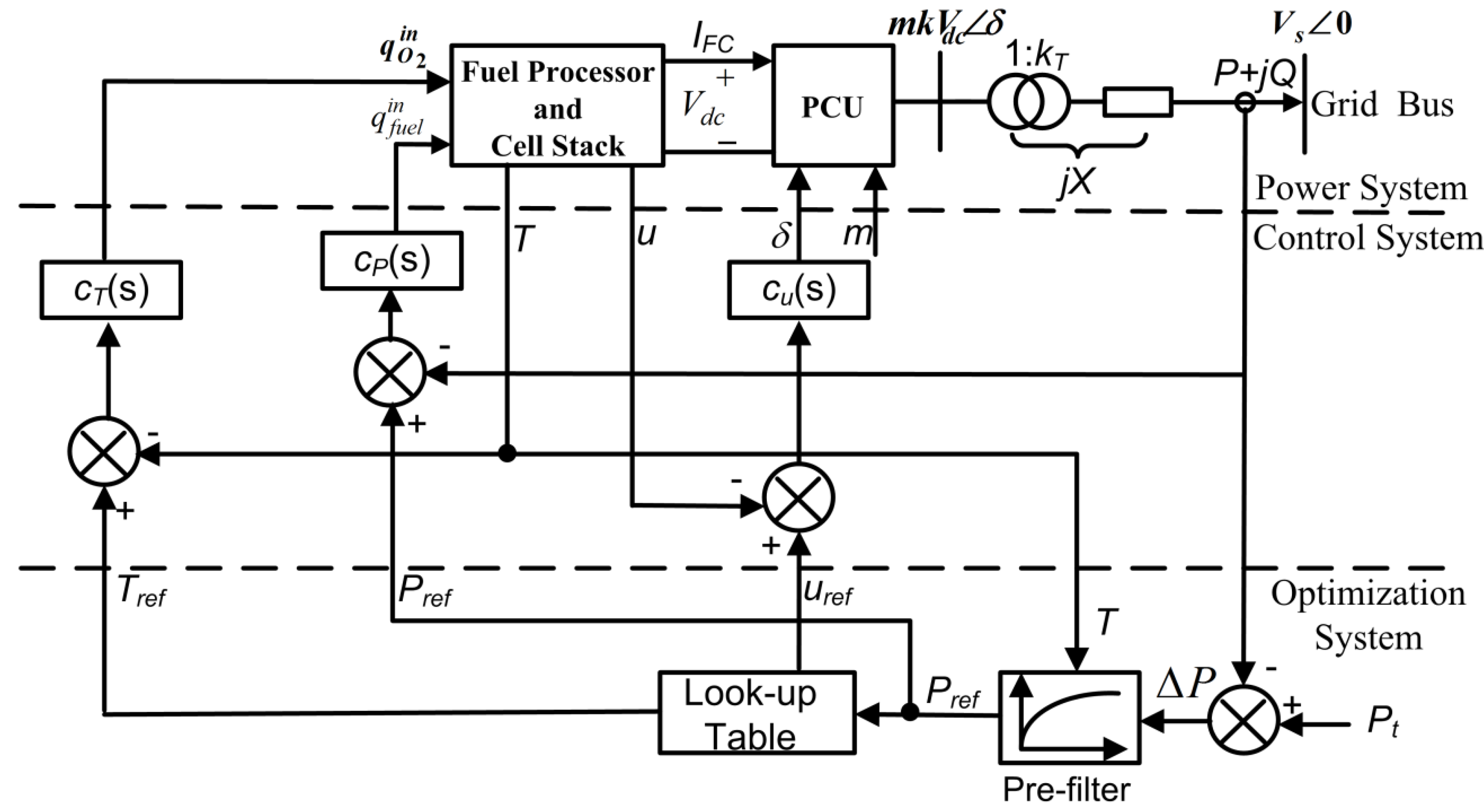
2.3. Operating Variables and Constraints
2.4. Determination of the Optimal Operating Condition
3. Hierarchical Load Tracking Control Scheme for the Grid-Connected SOFC
3.1. Analysis of the Open-Loop System Poles

3.2. The Hierarchical Load Tracking Control Scheme
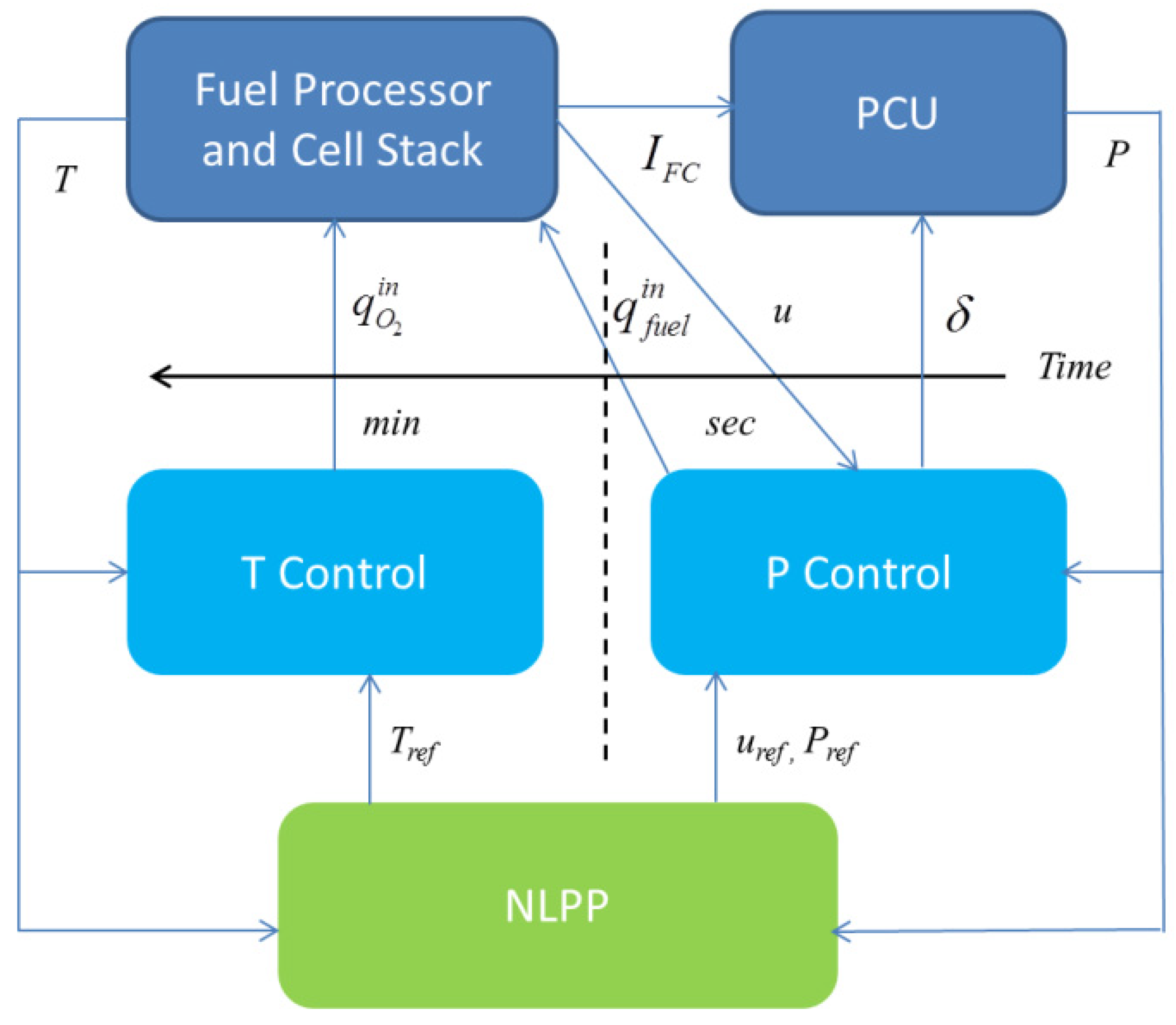
4. Design of the P and T Control Systems
4.1. SOFC Dynamic Model for the Design of P Controller
4.2. Selection of P Control Output-input Variables Pairs
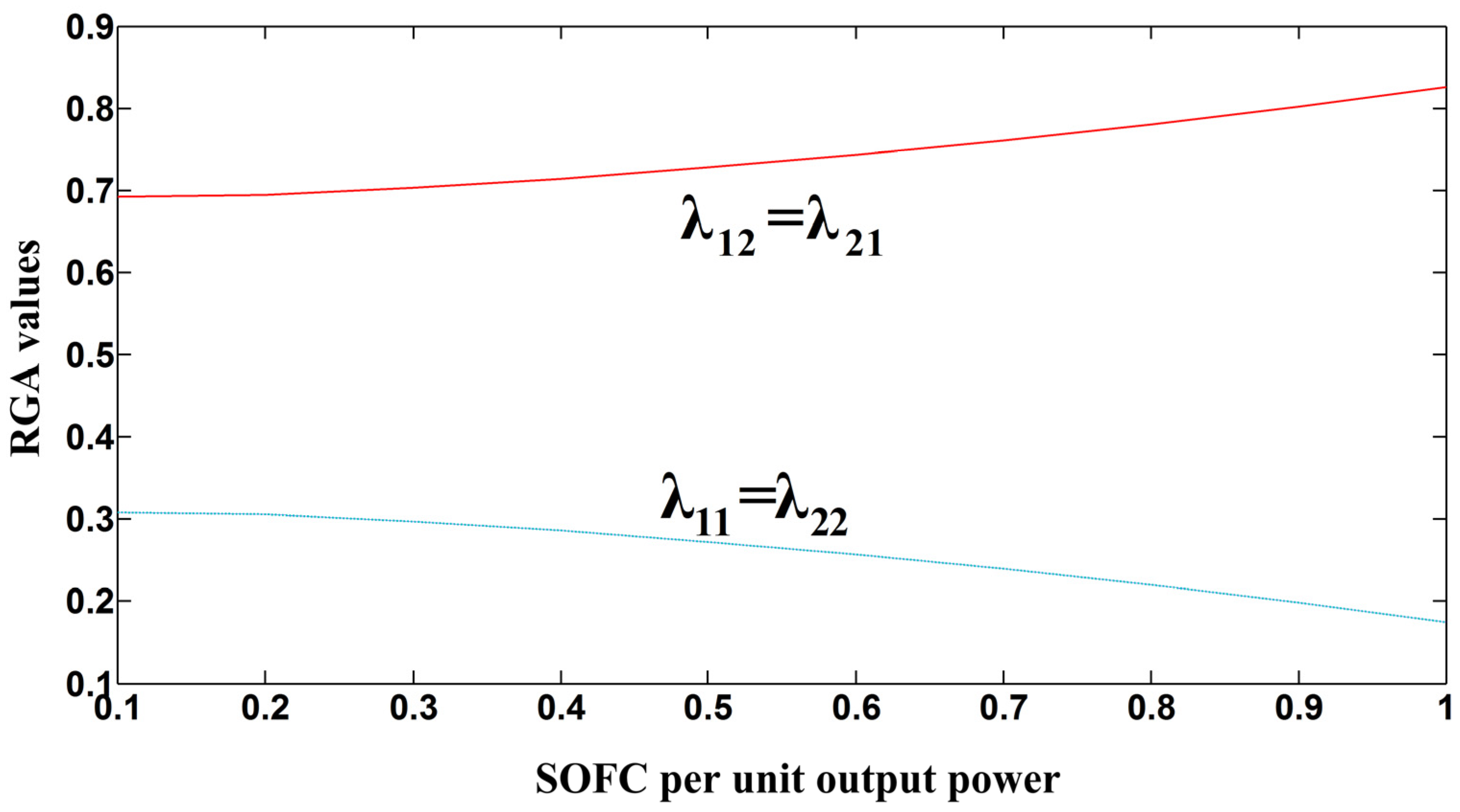
4.3. Design of the Decentralized P Controller
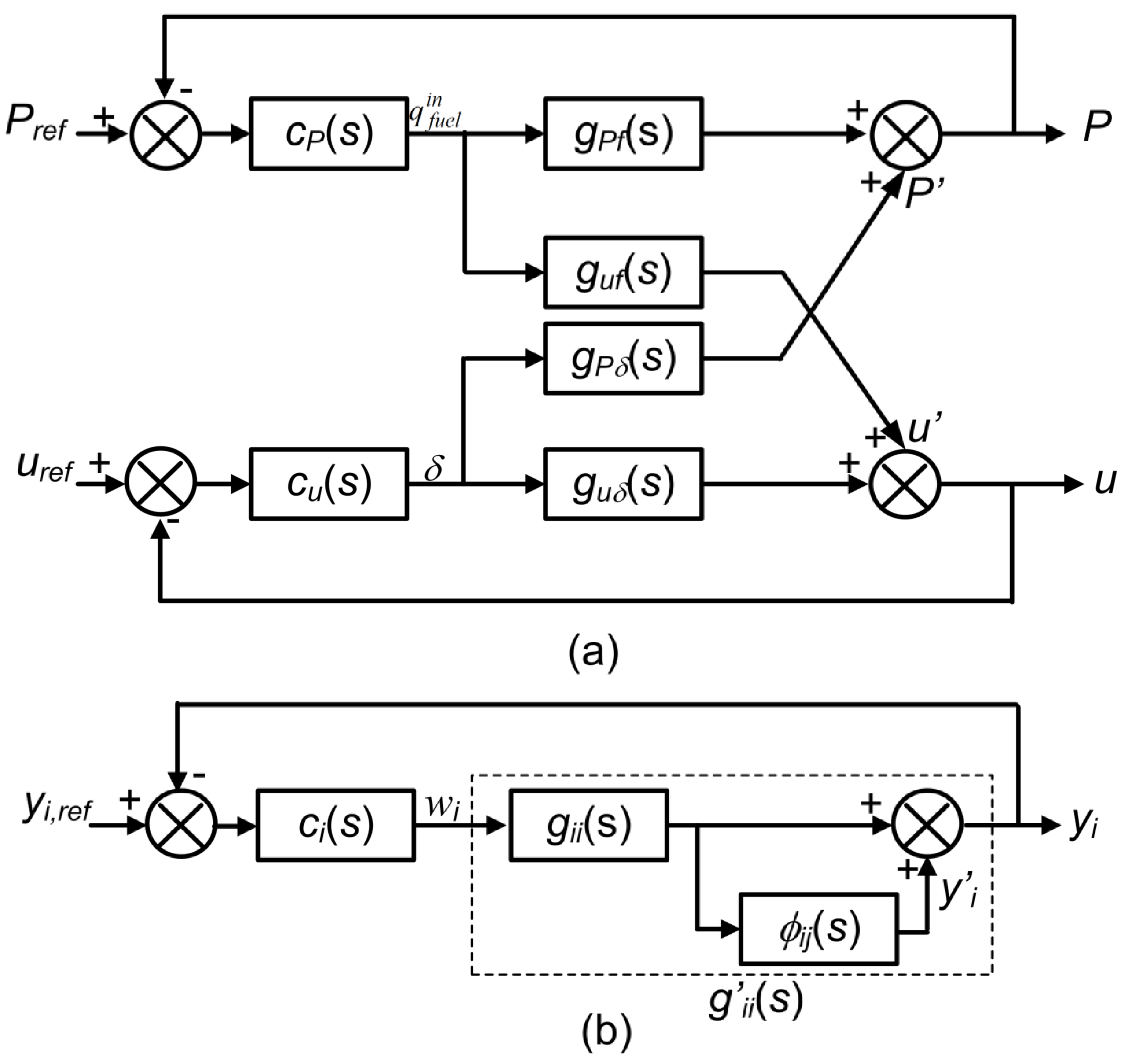
4.4. T Control System Design
4.5. Overall Load Tracking and Temperature Control Scheme
| Parameters | Value |
|---|---|
| Tin | 923 K |
| p | 0.15 MPa |
| N0 | 384 |
| msCps | 1.1 × 104 (J/K) |
| Kr | 9.95 × 10−4mol/(s.A) |
| KH2 | 8.32 × 10−6 mol/(s.Pa) |
| KH2O | 2.77 × 10−6 mol/(s.Pa) |
| KO2 | 2.49 × 10−5 mol/(s.Pa) |
| Va | 2.3 m3 |
| Vc | 0.76 m3 |
| τf | 5 s |
| τe | 0.8 s |
| α | 0.02 Ω |
| β | −2870 K |
| a | 0.05 V |
| b | 0.11 V |
| IL | 800 A |
| ηc | 0.7 |
5. Case Studies
5.1. Steady-State ηmax Operations
| P (kW) | Ploss (kW) | Vdc (V) | (mol/s) | (mol/s) | T (K) | u | ηmax | η1 |
|---|---|---|---|---|---|---|---|---|
| 10 | 1.514 | 269.31 | 0.082 | 0.208 | 1173 | 0.9 | 0.427 | 0.3904 |
| 30 | 4.438 | 272.06 | 0.244 | 0.610 | 1173 | 0.9 | 0.434 | 0.3973 |
| 50 | 7.560 | 269.49 | 0.410 | 1.040 | 1173 | 0.8998 | 0.428 | 0.3992 |
| 70 | 10.889 | 266.08 | 0.585 | 1.497 | 1173 | 0.8948 | 0.418 | 0.3988 |
| 90 | 14.416 | 261.51 | 0.771 | 1.982 | 1175 | 0.8885 | 0.406 | 0.3973 |
| 100 | 15.906 | 257.87 | 0.872 | 2.187 | 1184 | 0.8849 | 0.399 | 0.395 |
5.2. Controller Design
5.3. SOFC Load Tracking Dynamic Performance
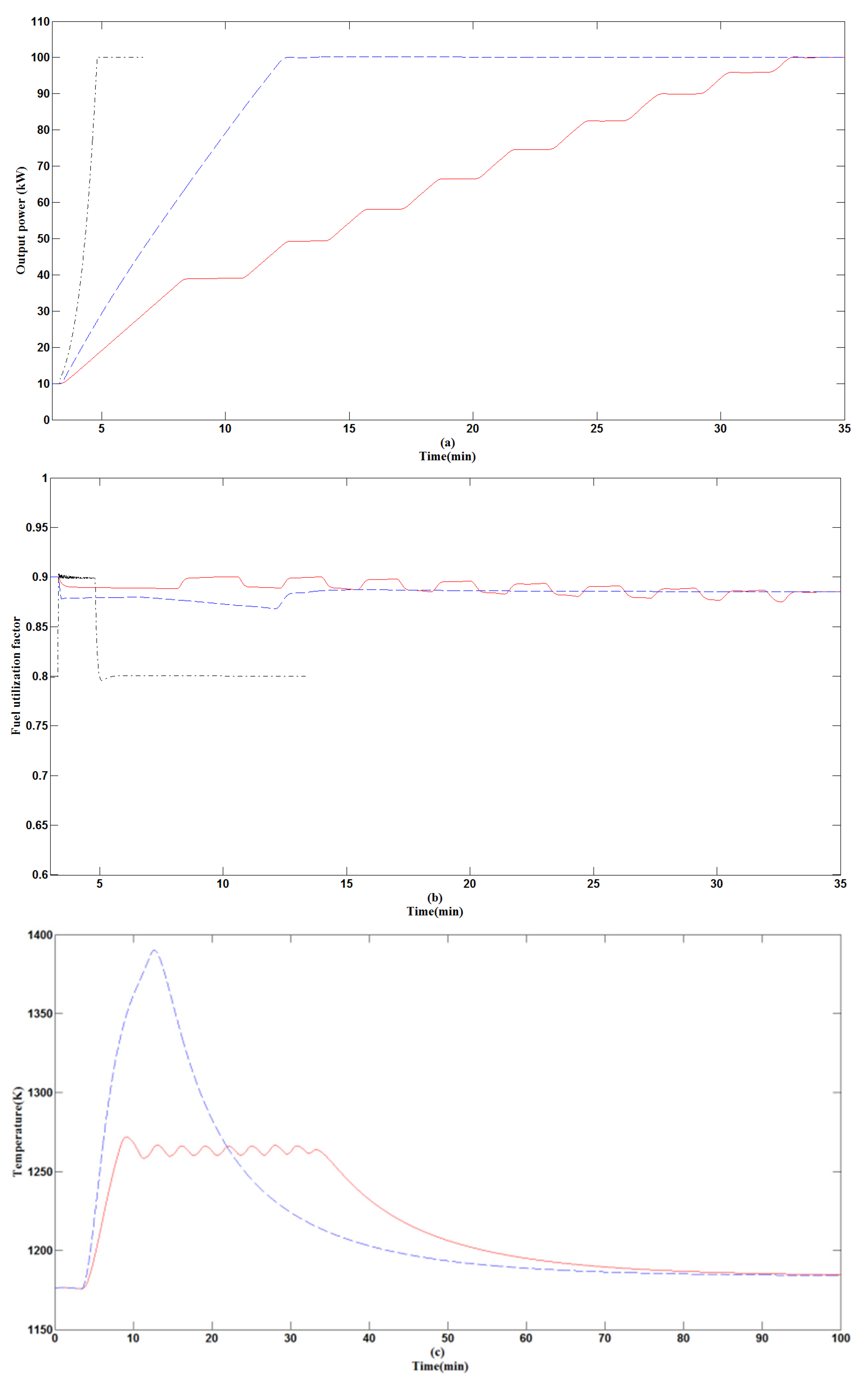
6. Conclusions
Nomenclature
| Symbols | ||
| a | V | Tafel constant |
| b | V | Tafel slope |
| ci(s) | The ith controller | |
| J·mol−1·K−1 | The ith gas average constant-pressure specific heat | |
| E0 | V | Nernst potential at standard pressure |
| E | V | Nernst potential |
| F | 96485 C·mol−1 | Faraday constant |
| g(s) | Transfer function | |
| J·mol−1 | The ith gas per mole enthalpy | |
| IFC | A | Stack current |
| IL | A | Limiting current |
| k | 3.762 | Mole ratio of nitrogen to oxygen in the air |
| Ki | mol·s−1·Pa−1 | The ith gas valve molar constant |
| m | Modulation index | |
| msCps | J·K−1 | Stack solid mass-specific product |
| N0 | Cell number in series | |
| N | Mole number | |
| p | MPa Stack operating pressure | |
| P | kW | Fuel cell output power |
| Ploss | kW | Power loss caused by the air compressor |
| q | mol·s−1 | Mole flow rate |
| R | 8.314 J·K−1·mol−1 | Universe gas constant |
| T | K | Temperature |
| u | Fuel utilization factor | |
| Vi | m3 | Anode or cathode volume |
| Vdc | V | Cell terminal voltage |
| Vs | V | Grid bus voltage |
| Greek letters | ||
| α | Ω | Ohmic resistant constant |
| β | K | Ohmic resistant constant |
| δ | rad | Phase shift angle |
| η | SOFC electrical efficiency | |
| ηc | Air compressor efficiency | |
| ρ | Multiplicate model factor | |
| τ | s | Time constant |
| φ | Dynamic Relative Index | |
| Subscripts | ||
| a | Anode | |
| act | Activation | |
| c | Cathode | |
| con | Concentration | |
| H2 | Hydrogen | |
| H2O | Water | |
| N2 | Nitrogen | |
| O2 | Oxygen | |
| r | Ohmic | |
| std | Standard | |
| Superscripts | ||
| in | Inlet | |
| r | Reacted | |
| out | Outlet | |
Author Contributions
Conflicts of Interest
References
- Larminie, J.; Dicks, A. Fuel Cell System Explained, 2nd ed.; John Wiley: New York, NY, USA, 2002. [Google Scholar]
- Singhal, S.C.; Kendall, K. High Temperature Solid Oxide Fuel Cells: Fundamentals, Design, and Applications; Elsevier: New York, NY, USA, 2003. [Google Scholar]
- Zhang, X.; Chan, S.H.; Li, G.; Ho, H.K.; Li, J.; Feng, Z. A review of integration strategies for solid oxide fuel cells. J. Power Sour. 2010, 195, 685–702. [Google Scholar] [CrossRef]
- Park, S.K.; Ahn, J.H.; Kim, T.S. Performance evaluation of integrated gasification solid oxide fuel cell/gas turbine systems including carbon dioxide capture. Appl. Energy 2011, 88, 2976–2987. [Google Scholar] [CrossRef]
- Razbani, O.; Wærnhus, I.; Assadi, M. Experimental investigation of temperature distribution over a planar solid oxide fuel cell. Appl. Energy 2013, 105, 155–160. [Google Scholar] [CrossRef]
- Zhu, G.R.; Loo, K.H.; Lai, Y.M.; Tse, C.K. Quasi-maximum efficiency point tracking for direct methanol fuel cell in dmfc-supercapacitor hybrid energy system. IEEE Trans. Energy Convers. 2012, 27, 561–571. [Google Scholar] [CrossRef]
- Kelouwani, S.; Adegnon, K.; Agbossou, K.; Dube, Y. Online system identification and adaptive control for pem fuel cell maximum efficiency tracking. IEEE Trans. Energy Convers. 2012, 27, 580–592. [Google Scholar] [CrossRef]
- Hong, W.T.; Yen, T.H.; Chung, T.D.; Huang, C.N.; Chen, B.D. Efficiency analyses of ethanol-fueled solid oxide fuel cell power system. Appl. Energy 2011, 88, 3990–3998. [Google Scholar] [CrossRef]
- Su, Y.; Chan, L.C.; Shu, L.; Tsui, K.L. Real-time prediction models for output power and efficiency of grid-connected solar photovoltaic systems. Appl. Energy 2012, 93, 319–326. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Rengaswamy, R. A reiview of solid oxide fuel cell (sofc) dynamic model. Ind. Eng. Chem. Res. 2009, 48, 6068–6086. [Google Scholar] [CrossRef]
- Wang, K.; Hissel, D.; Péra, M.C.; Steiner, N.; Marra, D.; Sorrentino, M.; Pianese, C.; Monteverde, M.; Cardone, P.; Saarinen, J. A review on solid oxide fuel cell models. Int. J. Hydrog. Energy 2011, 36, 7212–7228. [Google Scholar] [CrossRef]
- Huang, B.; Qi, Y.; Murshed, M. Solid oxide fuel cell: Perspective of dynamic modeling and control. J. Process Control 2011, 21, 1426–1437. [Google Scholar] [CrossRef]
- Spivey, B.J.; Edgar, T.F. Dynamic modeling, simulation, and mimo predictive control of a tubular solid oxide fuel cell. J. Process Control 2012, 22, 1502–1520. [Google Scholar] [CrossRef]
- Menon, V.; Janardhanan, V.M.; Tischer, S.; Deutschmann, O. A novel approach to model the transient behavior of solid-oxide fuel cell stacks. J. Power Sources 2012, 214, 227–238. [Google Scholar] [CrossRef]
- Gao, F.; Simoes, M.G.; Blunier, B.; Miraoui, A. Development of a quasi 2-D modeling of tubular solid-oxide fuel cell for real-time control. IEEE Trans. Energy Convers. 2014, 29, 9–19. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H. A physically based dynamic model for solid oxide fuel cells. IEEE Trans. Energy Convers. 2007, 22, 887–897. [Google Scholar] [CrossRef]
- Sorrentino, M.; Pianese, C.; Guezennec, Y.G. A hierarchical modeling approach to the simulation and control of planar solid oxide fuel cells. J. Power Sour. 2008, 180, 380–392. [Google Scholar] [CrossRef]
- Huo, H.B.; Wu, Y.X.; Liu, Y.Q.; Gan, S.H.; Kuang, X.H. Control-oriented nonlinear modeling and temperature control for solid oxide fuel cell. J. Fuel Cell Sci. Technol. 2010. [Google Scholar] [CrossRef]
- Hajimolana, S.A.; Tonekabonimoghadam, S.M.; Hussain, M.A.; Chakrabarti, M.H.; Jayakumar, N.S.; Hashim, M.A. Thermal stress management of a solid oxide fuel cell using neural network predictive control. Energy 2013, 62, 320–329. [Google Scholar] [CrossRef]
- Komatsu, Y.; Kimijima, S.; Szmyd, J.S. Numerical analysis on dynamic behavior of solid oxide fuel cell with power output control scheme. J. Power Sour. 2013, 223, 232–245. [Google Scholar] [CrossRef]
- Padulles, J.; Ault, G.W.; McDonald, J.R. An integrated sofc plant dynamic model for power systems simulation. J. Power Sour. 2000, 86, 495–500. [Google Scholar] [CrossRef]
- Zhu, Y.; Tomsovic, K. Development of models for analyzing the load-following performance of microturbines and fuel cells. Electr. Power Syst. Res. 2002, 62, 1–11. [Google Scholar] [CrossRef]
- Li, Y.H.; Choi, S.S.; Rajakaruna, S. An analysis of the control and operation of a solid oxide fuel-cell power plant in an isolated system. IEEE Trans. Energy Convers. 2005, 20, 381–387. [Google Scholar] [CrossRef]
- Li, Y.G.; Shen, J.; Lu, J.H. Constrained model predictive control of a solid oxide fuel cell based on genetic optimization. J. Power Sour. 2011, 196, 5873–5880. [Google Scholar] [CrossRef]
- Nayeripour, M.; Hoseintabar, M. A new control strategy of solid oxide fuel cell based on coordination between hydrogen fuel flow rate and utilization factor. Renew. Sustain. Energy Rev. 2013, 27, 505–514. [Google Scholar] [CrossRef]
- Sanandaji, B.M.; Vincent, T.L.; Colclasure, A.M.; Kee, R.J. Modeling and control of tubular solid-oxide fuel cell systems: II. Nonlinear model reduction and model predictive control. J. Power Sour. 2011, 196, 208–217. [Google Scholar] [CrossRef]
- Li, Y.H.; Rajakaruna, S.; Choi, S.S. Control of a solid oxide fuel cell power plant in a grid-connected system. IEEE Trans. Energy Convers. 2007, 22, 405–413. [Google Scholar] [CrossRef]
- Du, W.; Wang, H.F.; Zhang, X.F.; Xiao, L.Y. Effect of grid-connected solid oxide fuel cell power generation on power systems small-signal stability. IET Renew. Power Gener. 2012, 6, 24. [Google Scholar] [CrossRef]
- Sorrentino, M.; Pianese, C. Model-based development of low-level control strategies for transient operation of solid oxide fuel cell systems. J. Power Sour. 2011, 196, 9036–9045. [Google Scholar] [CrossRef]
- Vijay, P.; Tade, M.O.; Datta, R. Effect of the operating strategy of a solid oxide fuel cell on the effectiveness of decentralized linear controllers. Ind. Eng. Chem. Res. 2011, 50, 1439–1452. [Google Scholar] [CrossRef]
- Bunin, G.A.; Wuillemin, Z.; Francois, G.; Nakajo, A.; Tsikonis, L.; Bonvin, D. Experimental real-time optimization of a solid oxide fuel cell stack via constraint adaptation. Energy 2012, 39, 54–62. [Google Scholar] [CrossRef]
- Wang, Q.G.; Ye, Z.; Cai, W.J.; Hang, C.C. Pid Control for Multivariable Processes; Springer: Berlin, Germany, 2009. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wu, Q.; Zhu, H. Hierarchical Load Tracking Control of a Grid-Connected Solid Oxide Fuel Cell for Maximum Electrical Efficiency Operation. Energies 2015, 8, 1896-1916. https://doi.org/10.3390/en8031896
Li Y, Wu Q, Zhu H. Hierarchical Load Tracking Control of a Grid-Connected Solid Oxide Fuel Cell for Maximum Electrical Efficiency Operation. Energies. 2015; 8(3):1896-1916. https://doi.org/10.3390/en8031896
Chicago/Turabian StyleLi, Yonghui, Qiuwei Wu, and Haiyu Zhu. 2015. "Hierarchical Load Tracking Control of a Grid-Connected Solid Oxide Fuel Cell for Maximum Electrical Efficiency Operation" Energies 8, no. 3: 1896-1916. https://doi.org/10.3390/en8031896
APA StyleLi, Y., Wu, Q., & Zhu, H. (2015). Hierarchical Load Tracking Control of a Grid-Connected Solid Oxide Fuel Cell for Maximum Electrical Efficiency Operation. Energies, 8(3), 1896-1916. https://doi.org/10.3390/en8031896





