Energy Coordinative Optimization of Wind-Storage-Load Microgrids Based on Short-Term Prediction
Abstract
:1. Introduction
2. Topological Structure of Microgrid System and Model Description
2.1. Topological Structure of the Microgrid System
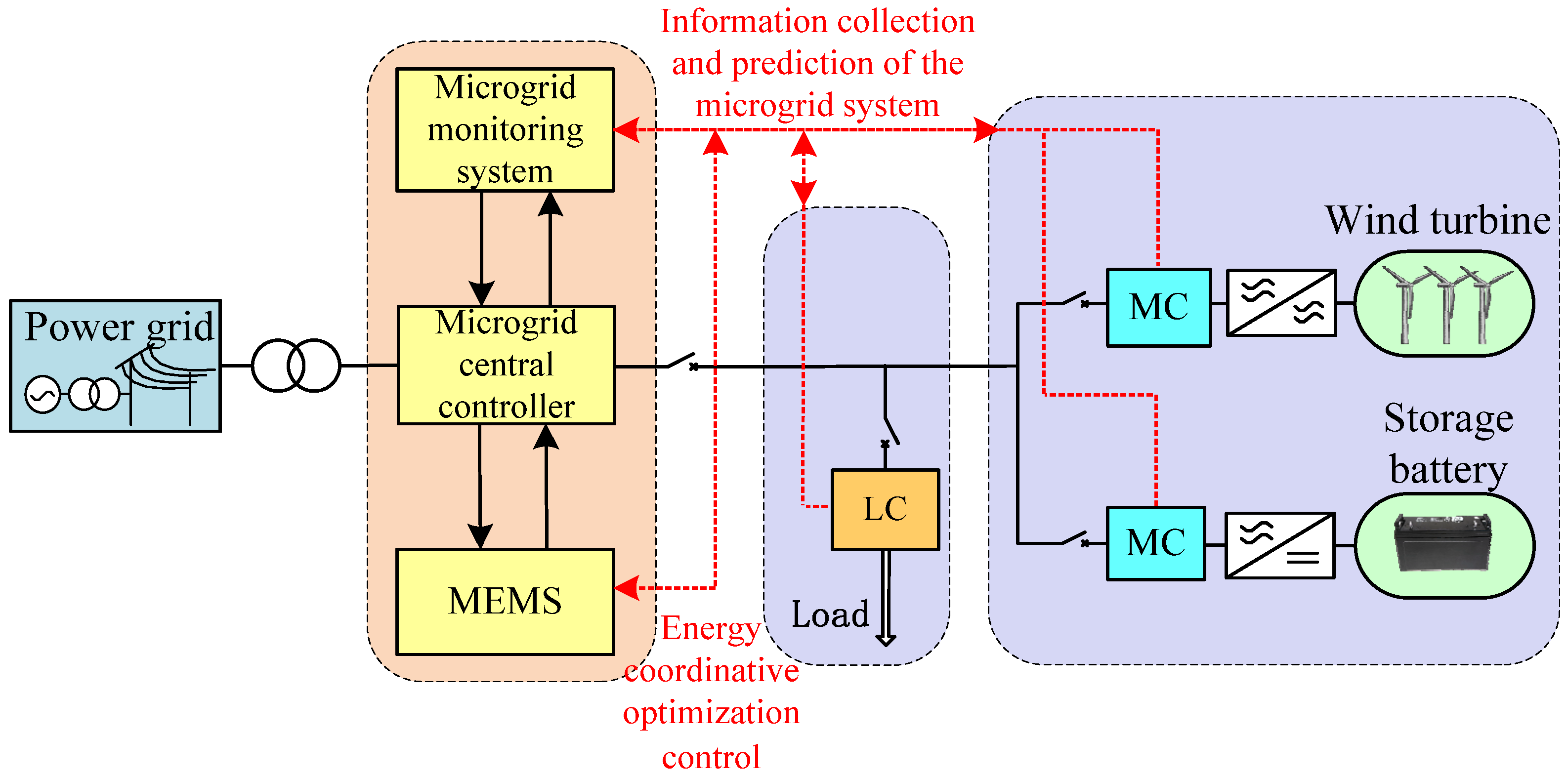
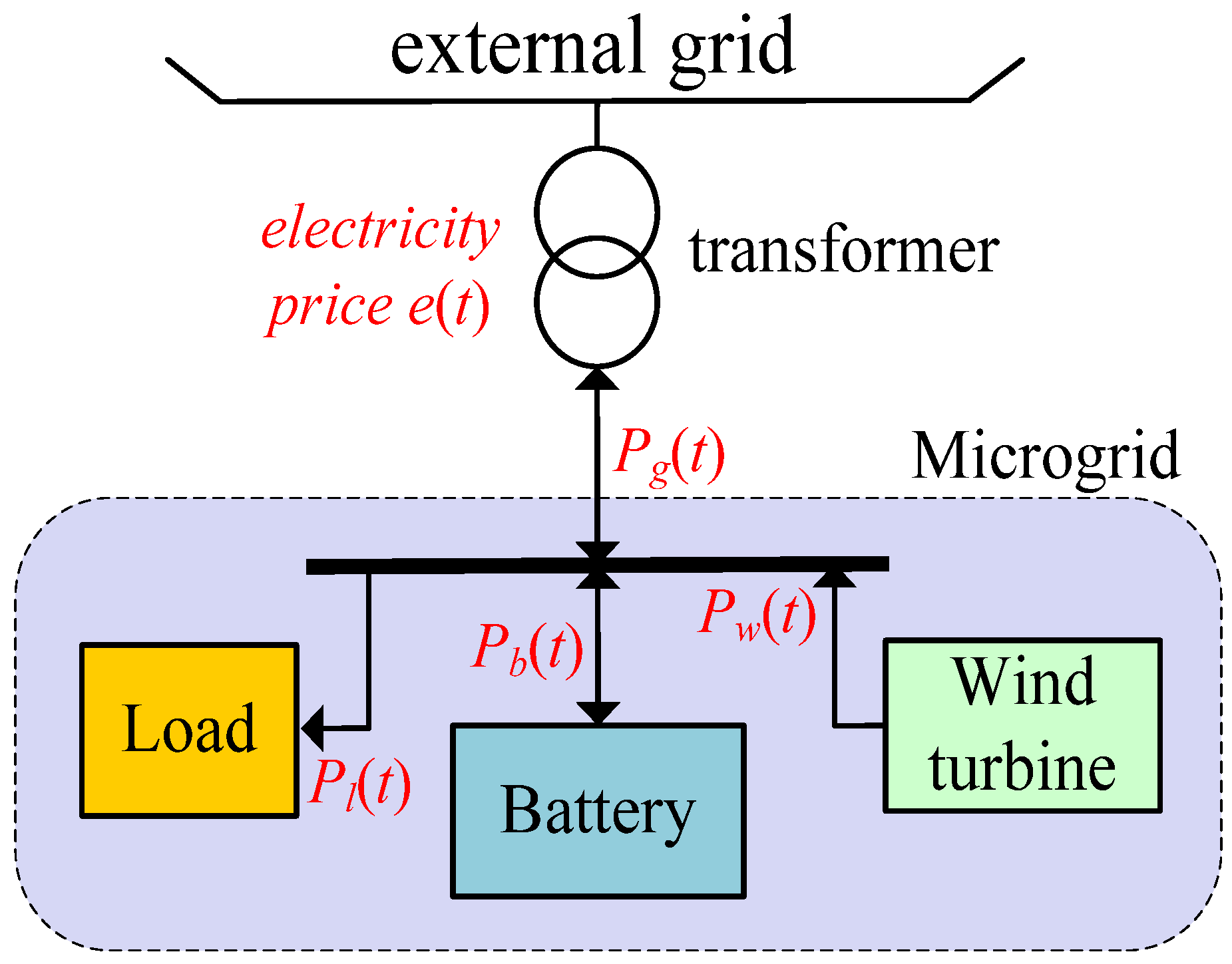
2.2. External Characteristic Model of DGs
2.2.1. The External Characteristics of Wind Turbine
2.2.2. Mathematical Model of a Storage Battery
| Parameter | Characterization | Numerical Value |
|---|---|---|
| τ | hourly self-discharge decay | 0.0001 |
| ηC | charge efficiency | 0.9 |
| ηD | discharge efficiency | 1.0 |
| KC | hourly maximum charge ratio | 0.1 |
| KD | hourly maximum discharge ratio | 0.1 |
2.3. Inverter Model
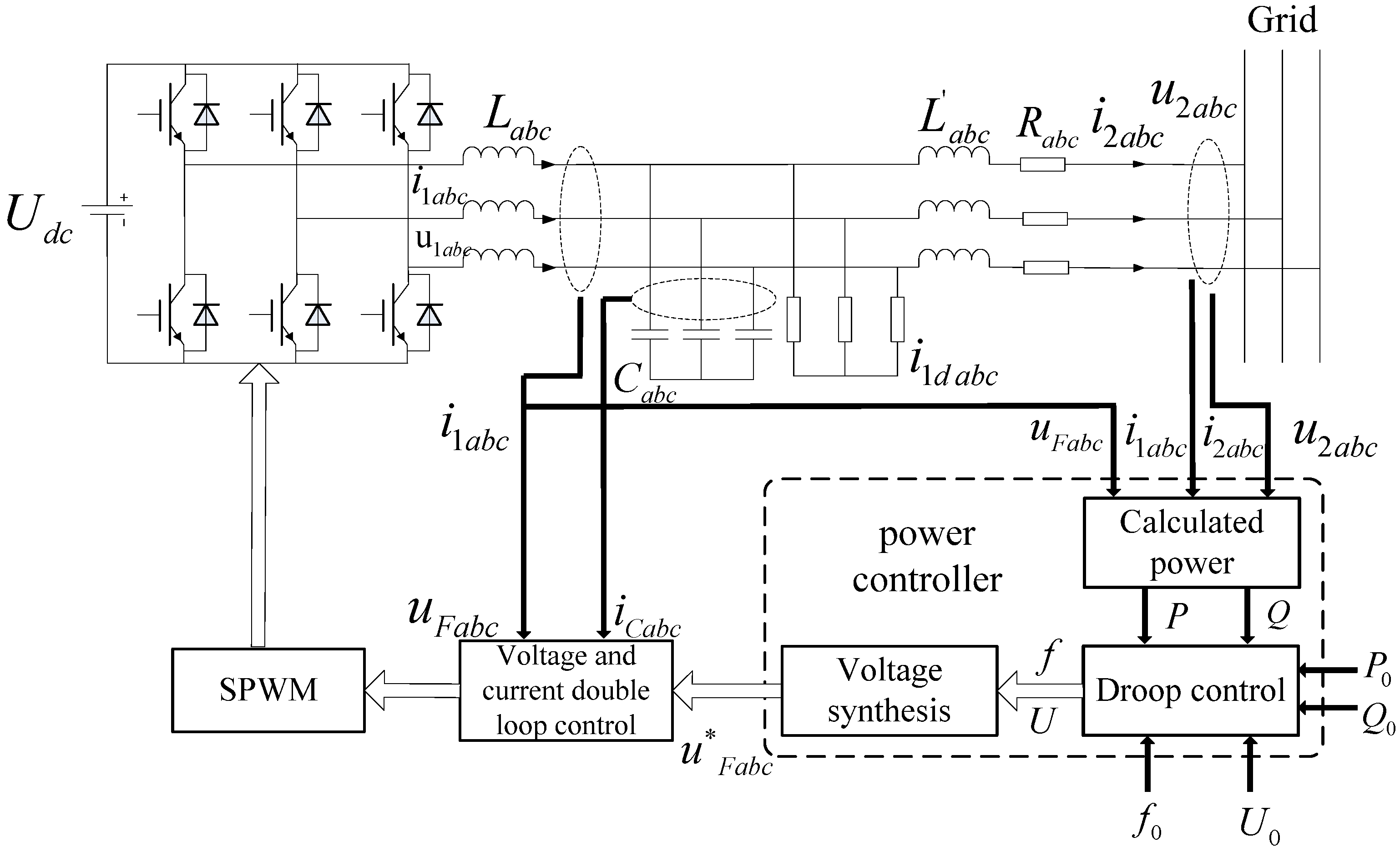
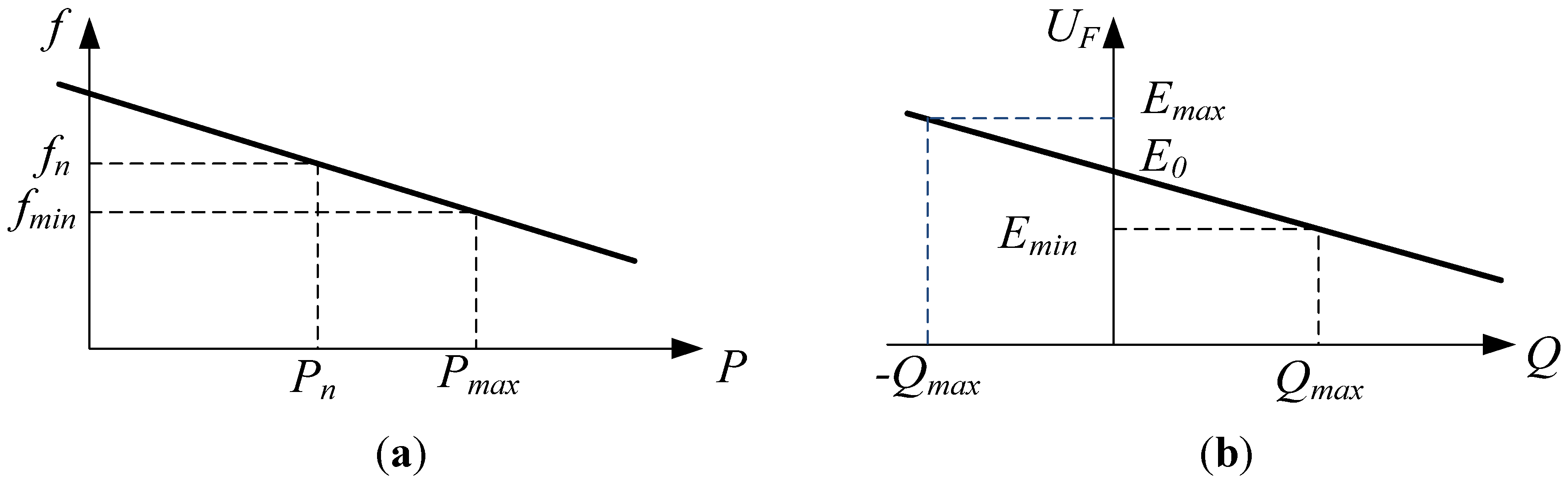
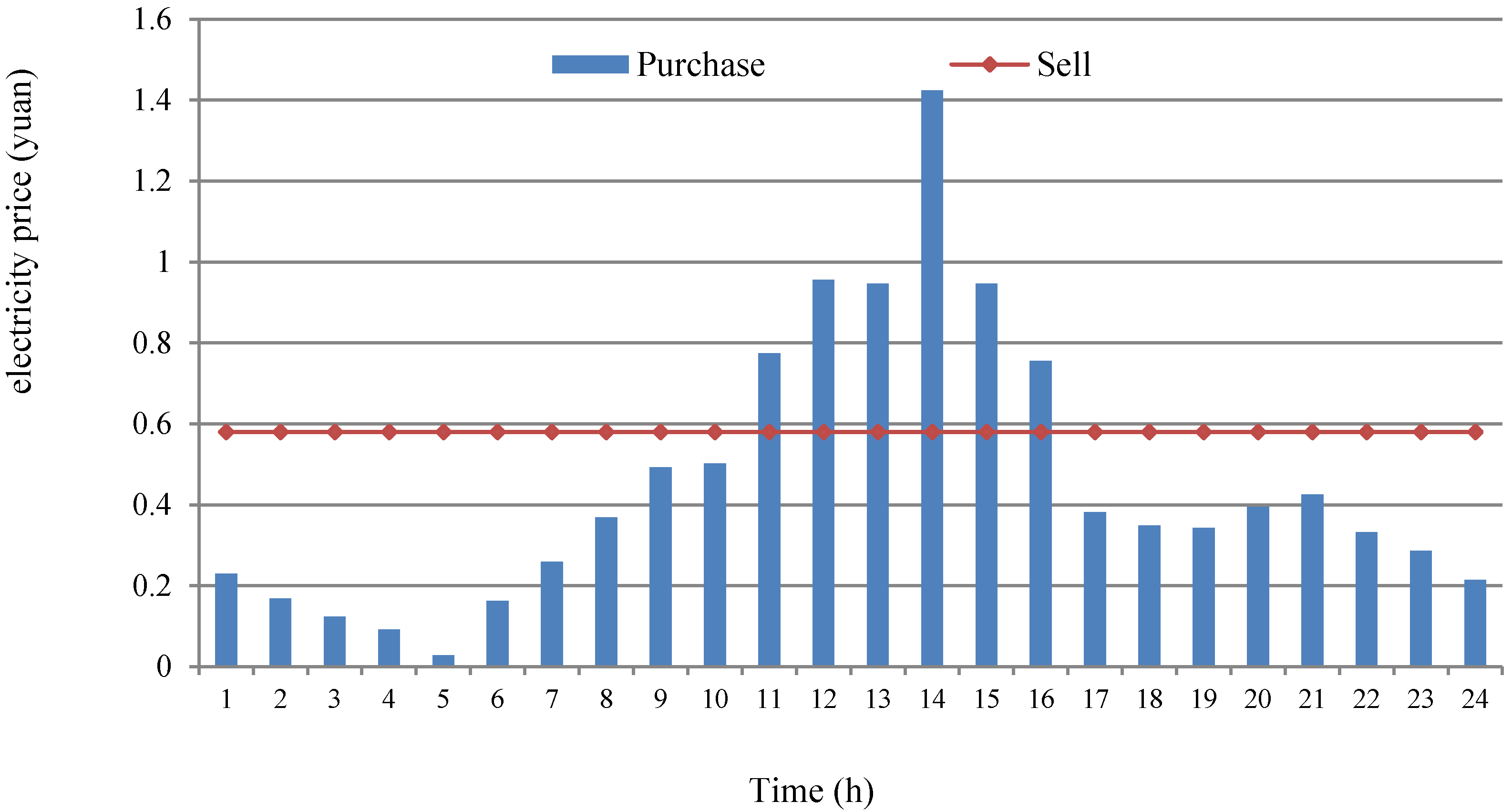
2.4. Spot Power Price Model
| Hours (h) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Price | 0.2294 | 0.1692 | 0.1243 | 0.0926 | 0.0287 | 0.1626 | 0.259 | 0.3693 |
| Hours (h) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Price | 0.4932 | 0.5028 | 0.7742 | 0.9558 | 0.9462 | 1.4241 | 0.9462 | 0.7551 |
| Hours (h) | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Price | 0.3823 | 0.3486 | 0.3427 | 0.3948 | 0.4251 | 0.3326 | 0.2867 | 0.2125 |
3. Energy Coordinative Optimization of a Microgrid System Based on Short-Term Prediction
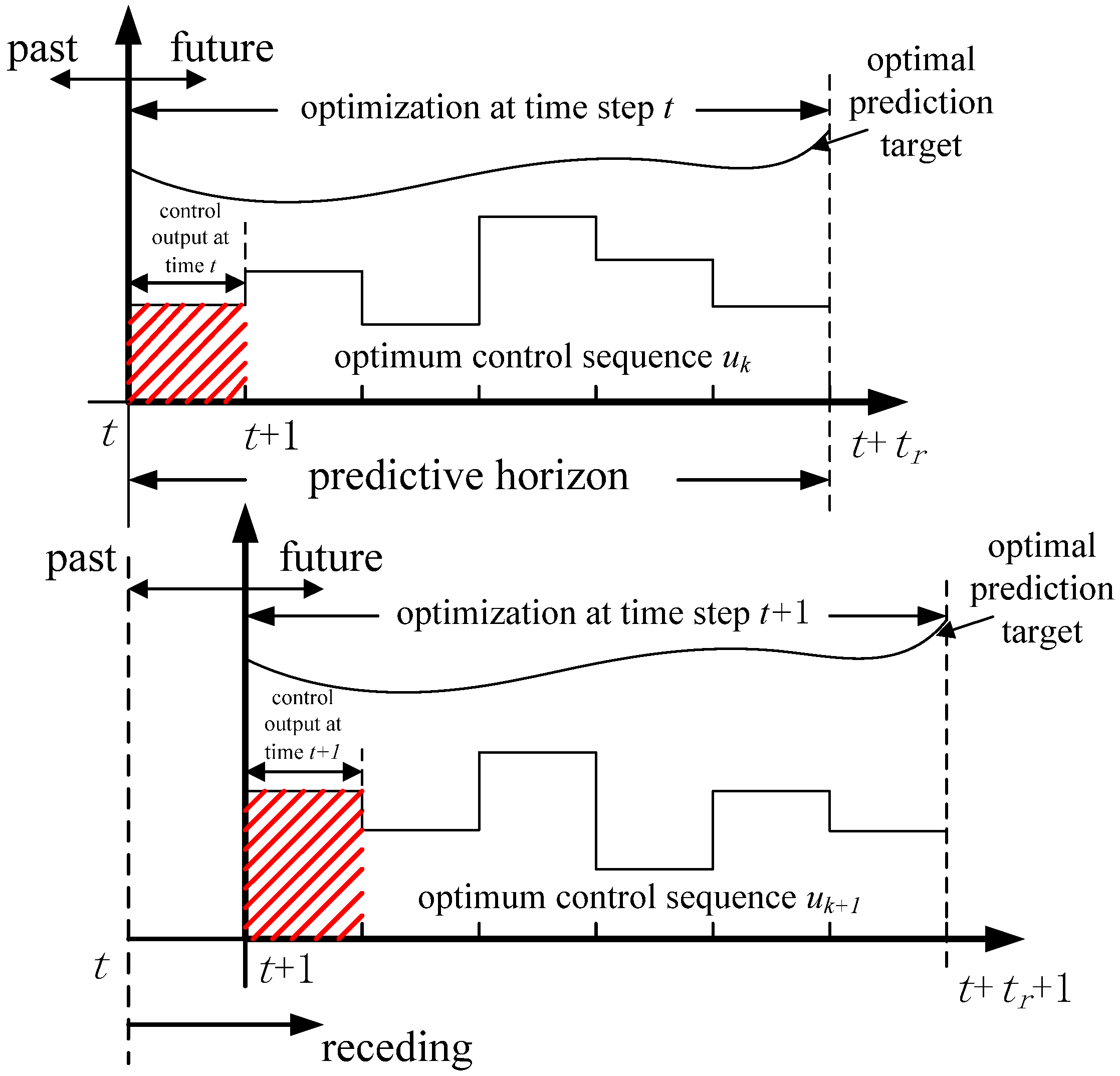
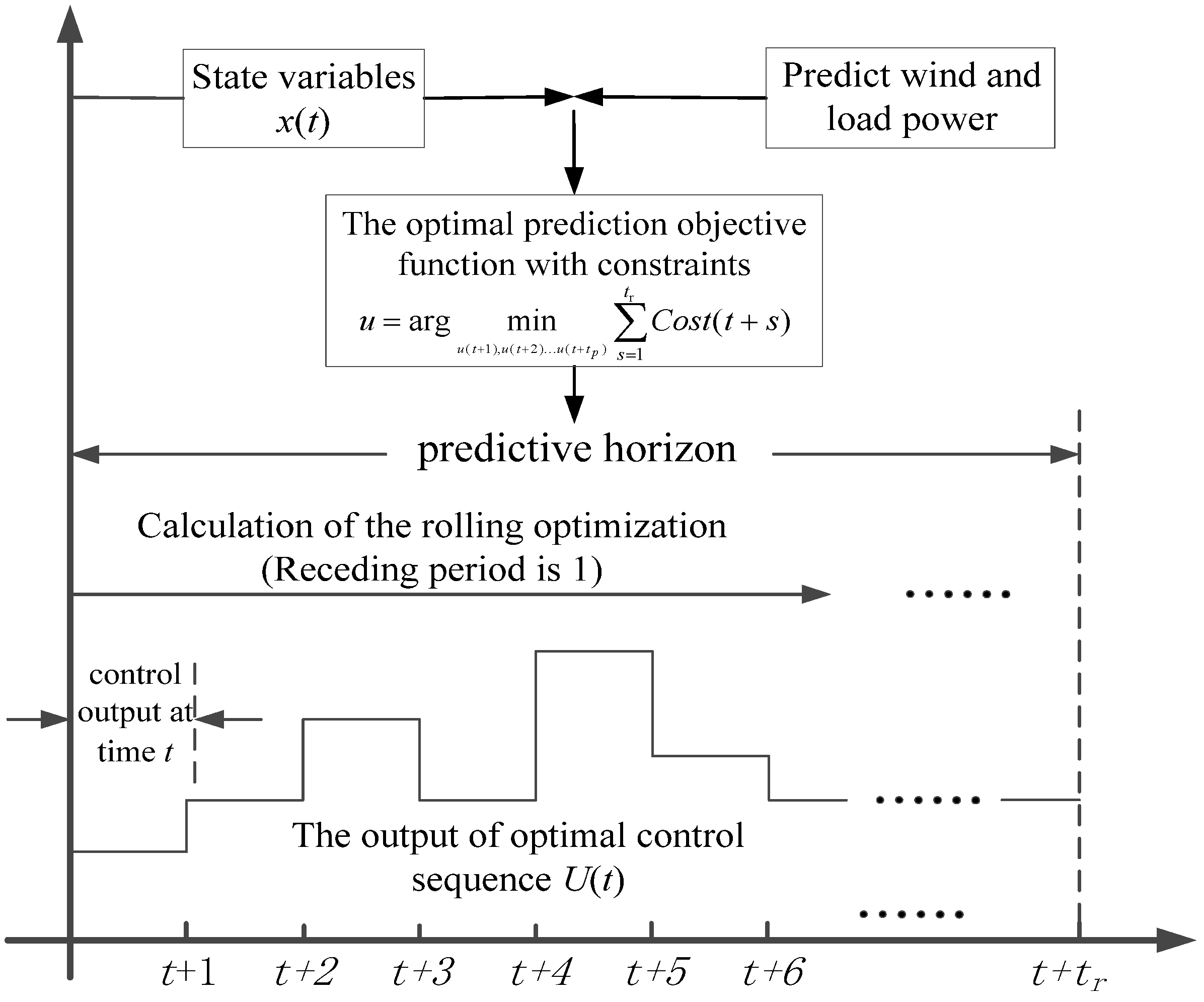
3.1. The Optimization Control in Receding Horizon
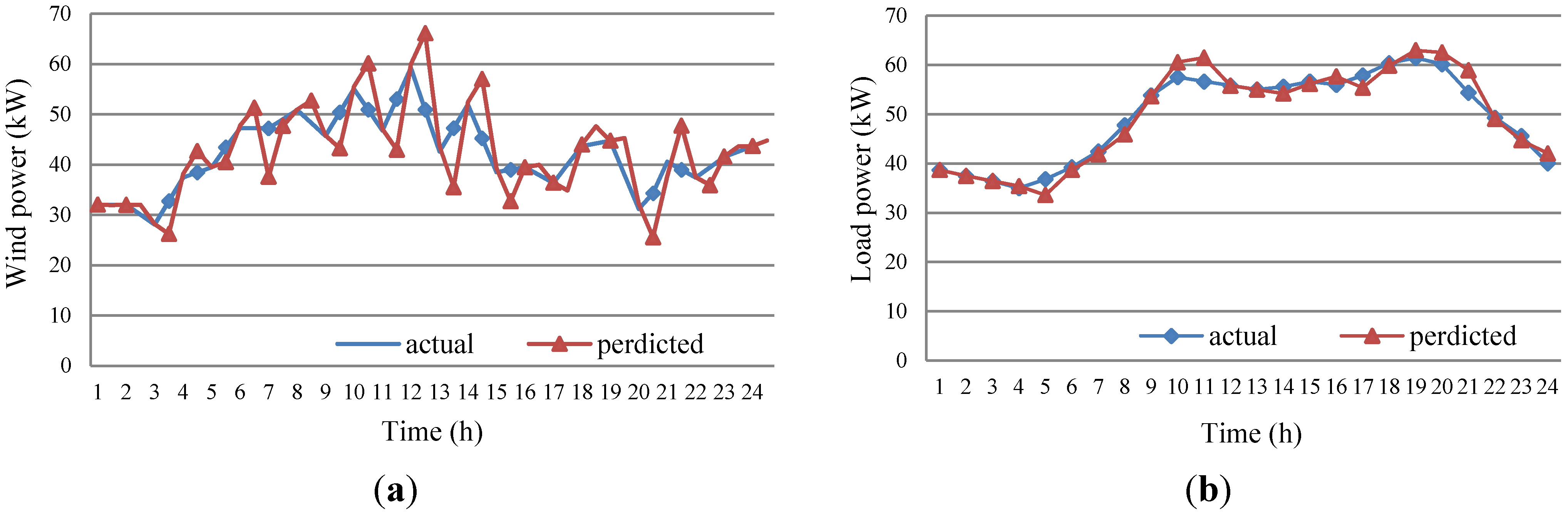
3.2. The Grey Prediction Model of Wind Power and Load with Residual Modification
| Grade of Prediction Precision | P | C |
|---|---|---|
| Good | >0.95 | <0.35 |
| Qualified | >0.8 | <0.5 |
| Barely qualified | >0.7 | <0.45 |
| Unqualified | ≤0.7 | ≥0.65 |
3.3. Energy Coordinative Optimization Management Model of Microgrid System
3.3.1. Objective Function
3.3.2. Constraints
3.4. Energy Coordinative Optimization of Microgrid System Based on GA
3.4.1. The Objective Function of the Energy Coordinative Optimization of a Microgrid System
3.4.2. The RHC Optimization Based on a Genetic Algorithm
3.5. Linearization of the Non-Linear Model in Energy Coordinative Optimization of Microgrid System
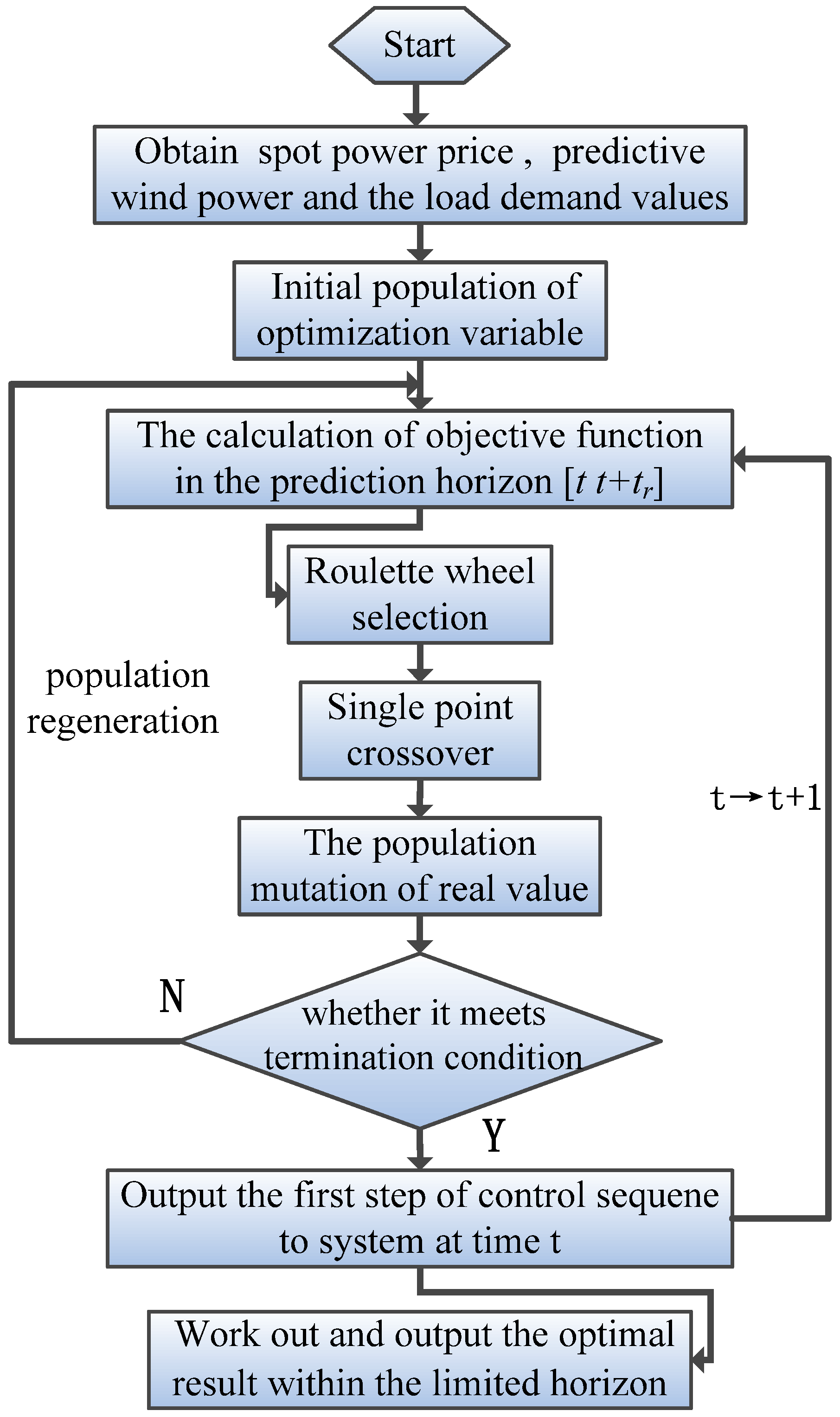
3.6. The Specific Steps of a Microgrid System’s Energy Coordinative Optimization
- Step 1
- Establish the microgrid model, including wind turbine model, storage battery model, spot power price model; initialization of the parameters involving the predictive wind power and the load demand values obtained in the predictive range and state variables Pw(t), Pg(t), Pb(t) and Pl(t).
- Step 2
- Establish the constrained objective function of economical optimization according to the actual demand by the microgrid’s energy coordinative optimization.
- Step 3
- Find a solution for the minimization problem within a limited horizon in the optimization range of [t t + tr]; in this step, every receding optimization will bring into existence a control sequence U(t) = {u(t|t),…,u(t + tr|t)}, whereby the solution for the control variable u(t|t) can be found at the first step in current moment; that is, Pg(t|t) at the first step constitutes the variables for the energy exchange between the external grid and microgrid and Pb(t|t) is the variable for the charge and discharge energy of the storage battery.
- Step 4
- The optimization horizon keeps receding: t = t + 1, return to Step 3.
- Step 5
- Output the optimal result within the limited horizon [t, t + tn] after the receding optimization stops.
4. Experimental Results and Analysis
4.1. Main Parameters
| Number | Parameter | Power Upper Limit (kW) | Power Lower Limit (kW) |
|---|---|---|---|
| 1 | Pg | 25 | −20 |
| 2 | Pb | 20 | −20 |
| 3 | E | 60 | 20 |
| 4 | △E | 30 | −30 |
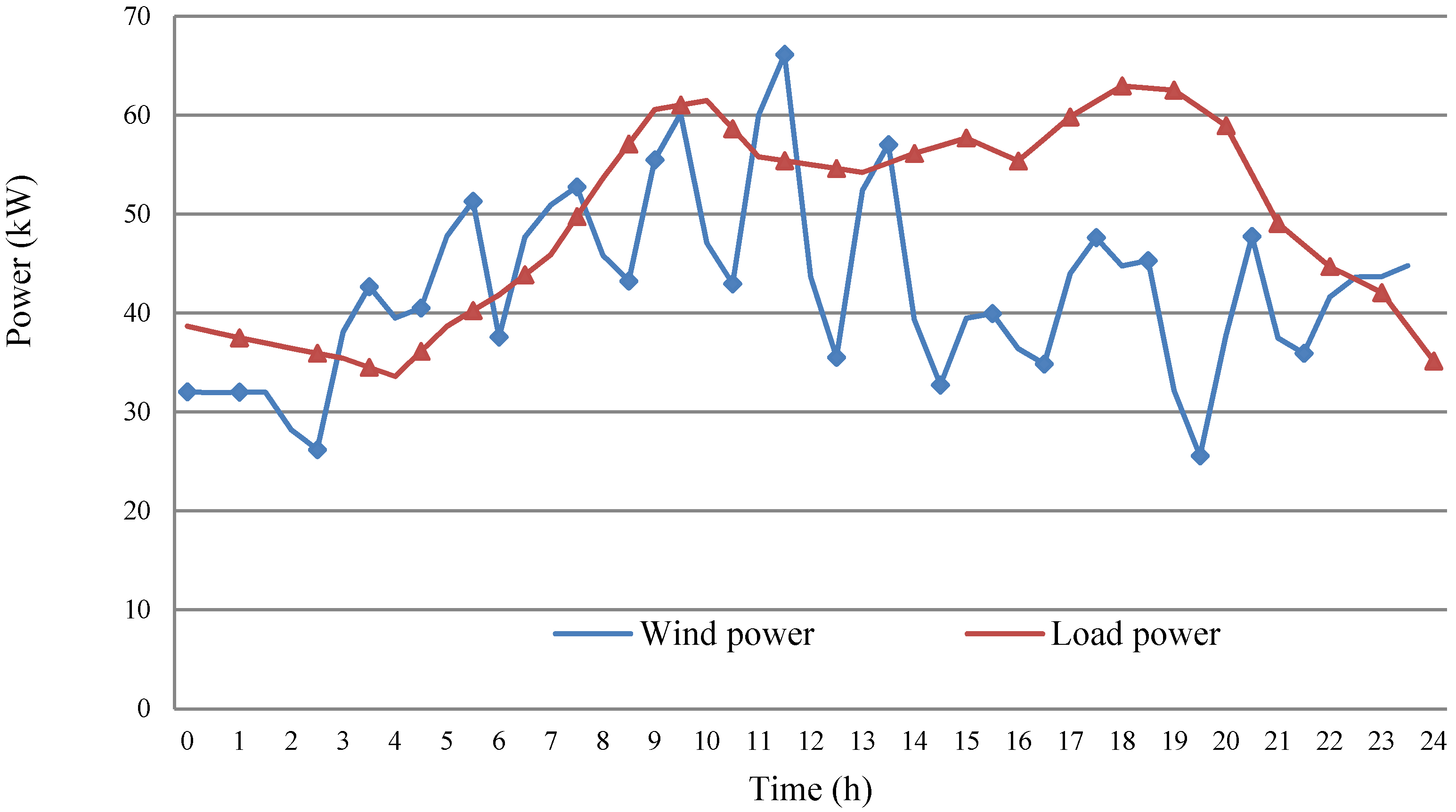
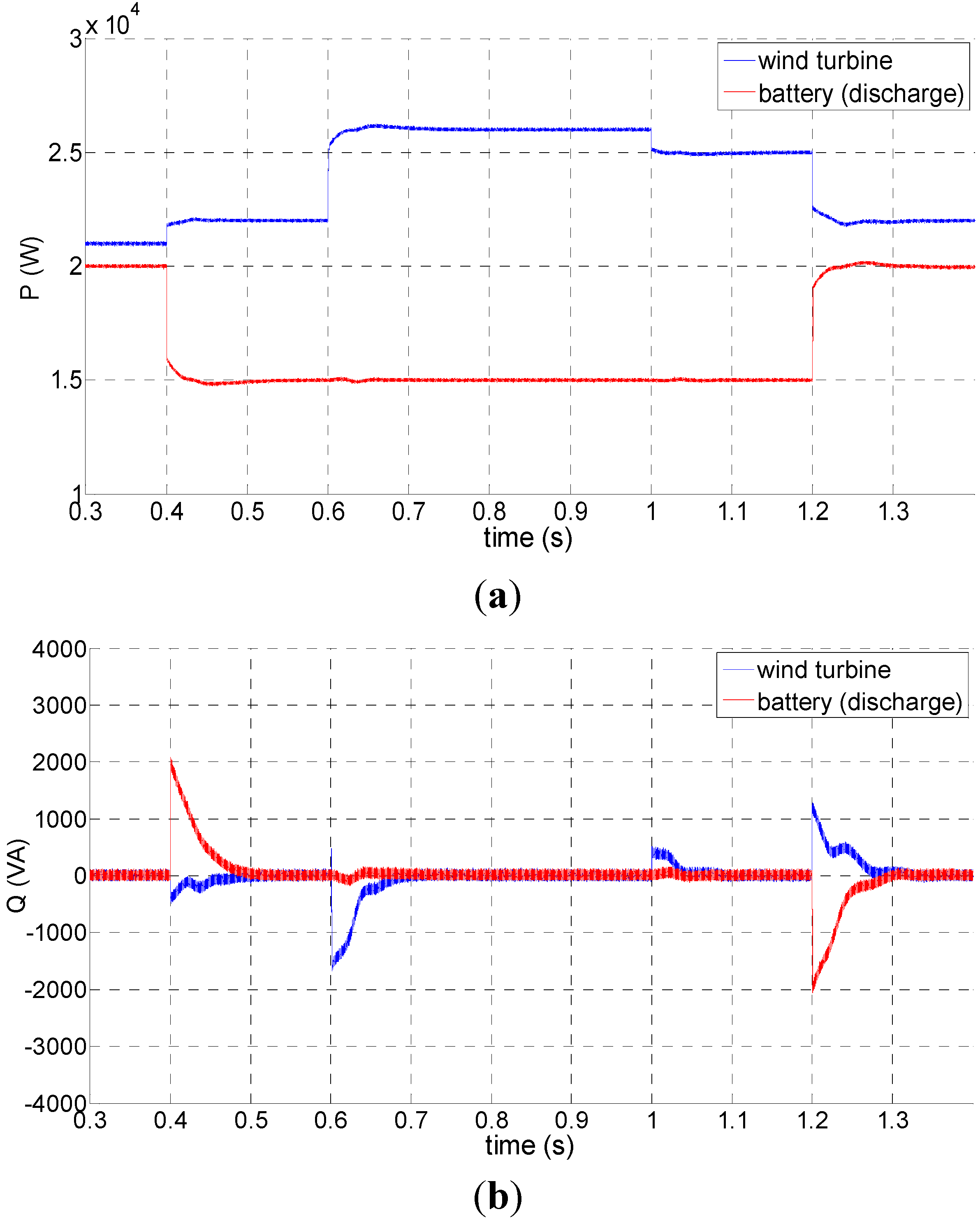
4.2. The Inverter Control Optimization Result
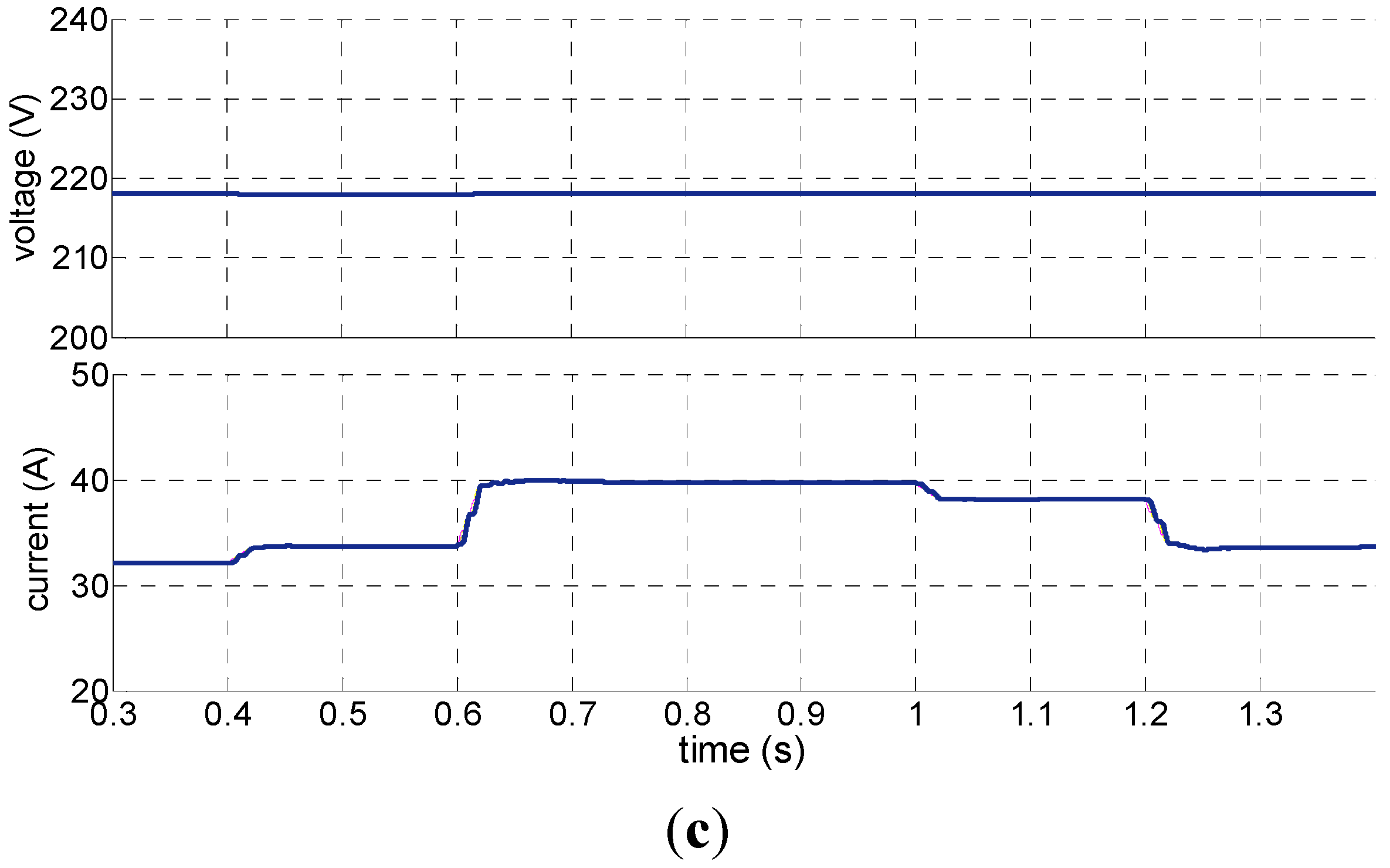
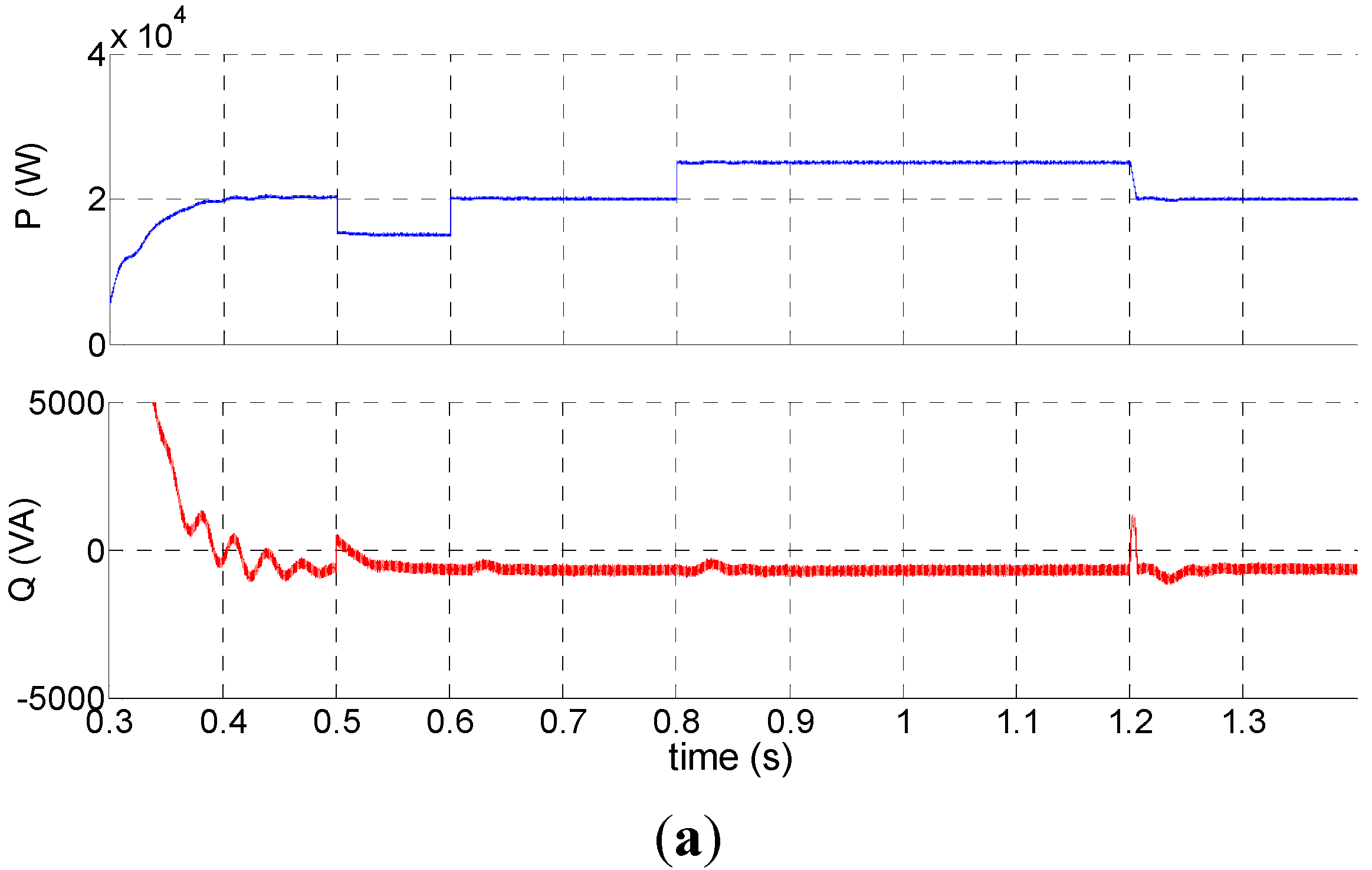
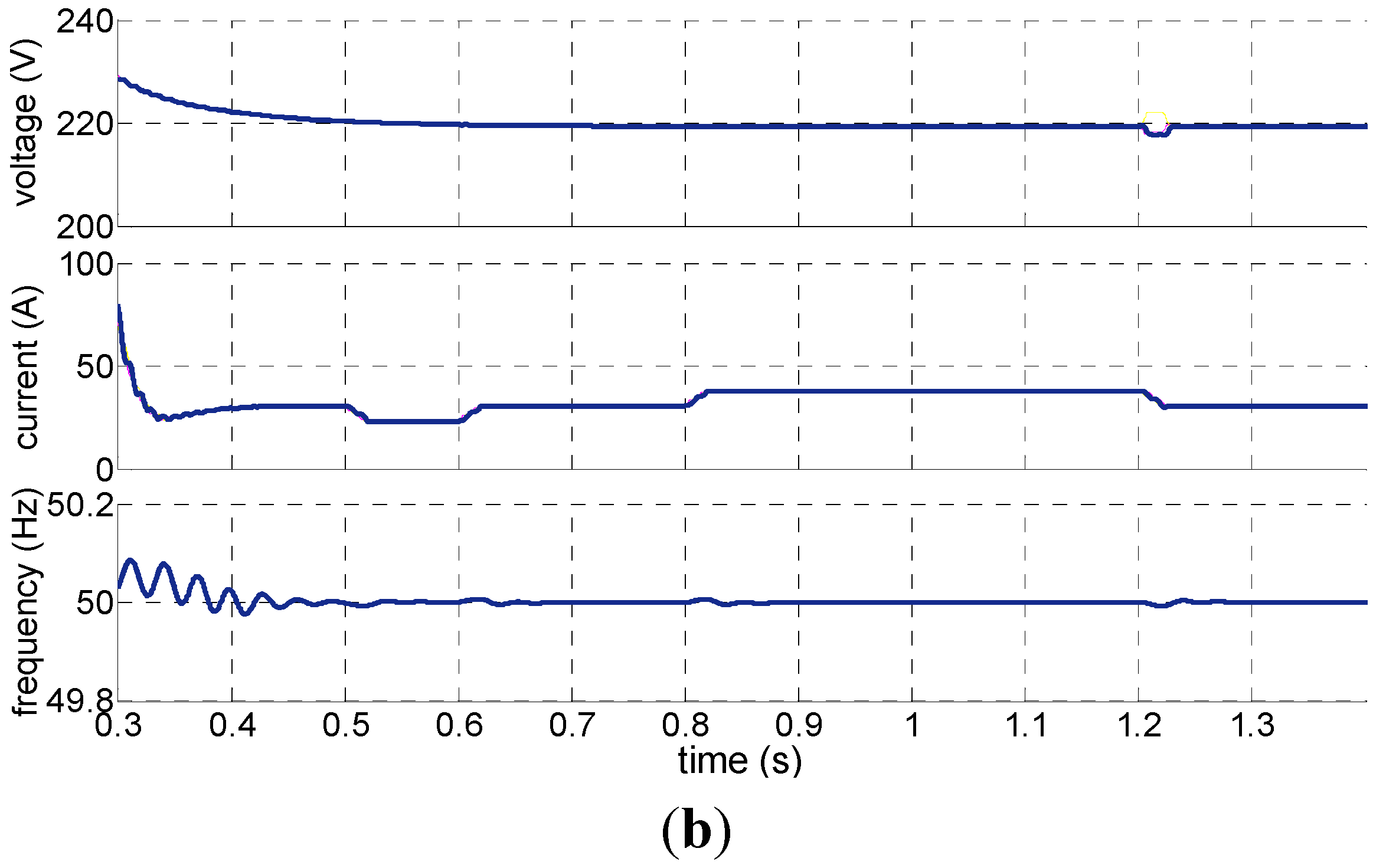
4.3. The Result Analysis of RHC Based on Prediction
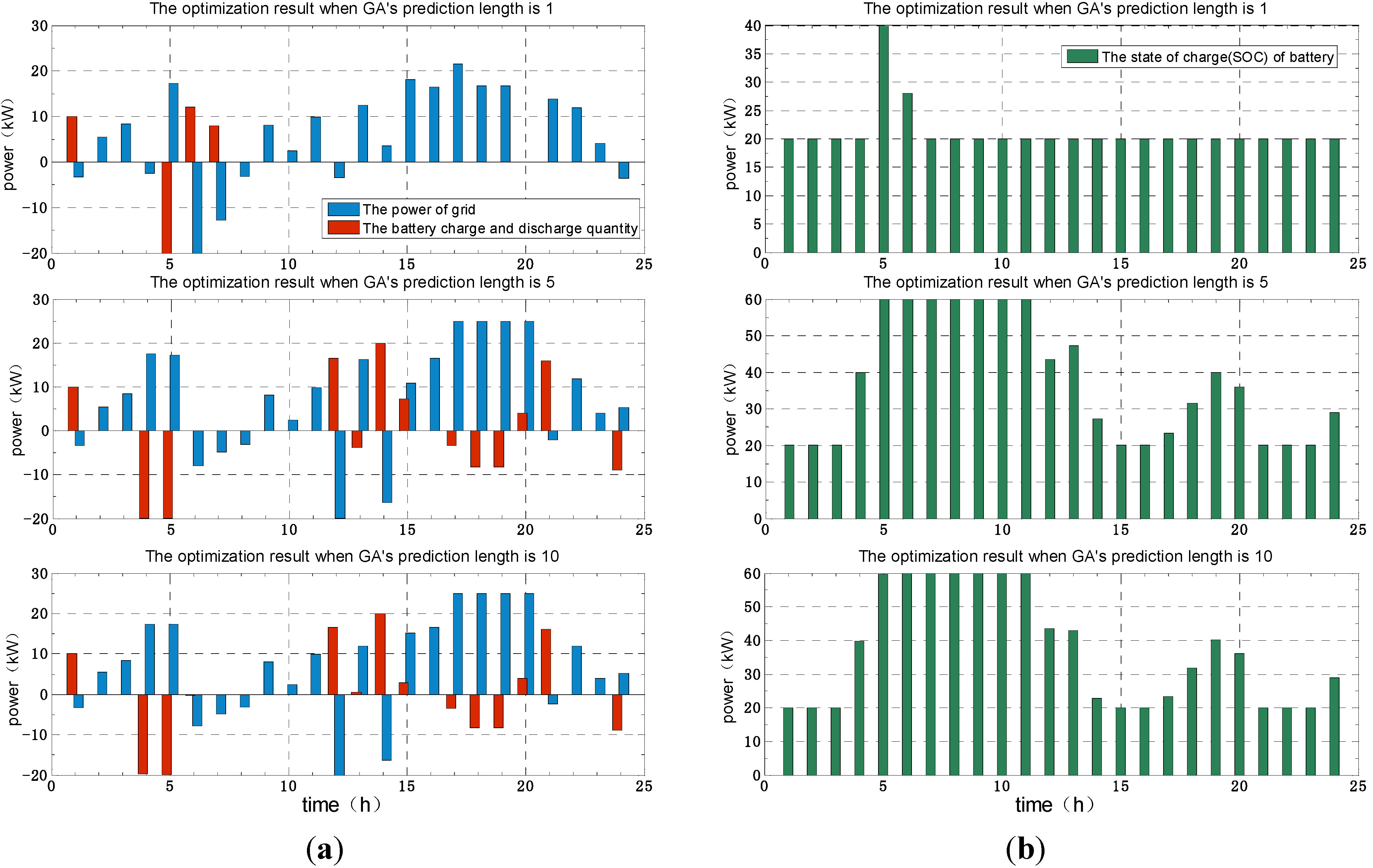
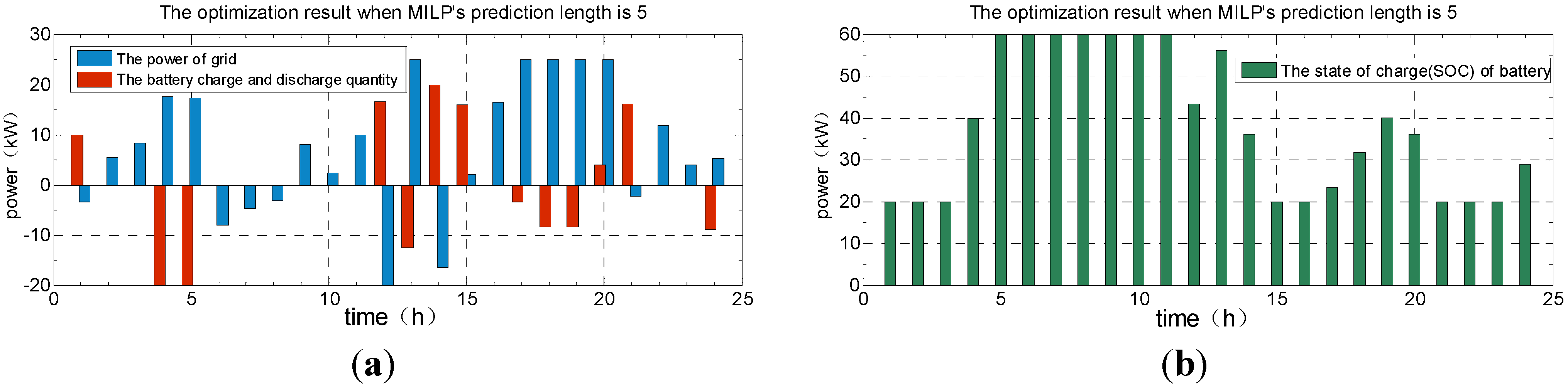
4.4. The Comparison about Optimization Results of GA and MILP
| Number | Method | Optimization Result |
|---|---|---|
| 1 | GA | 45.6 |
| 2 | MILP | 48.49 |
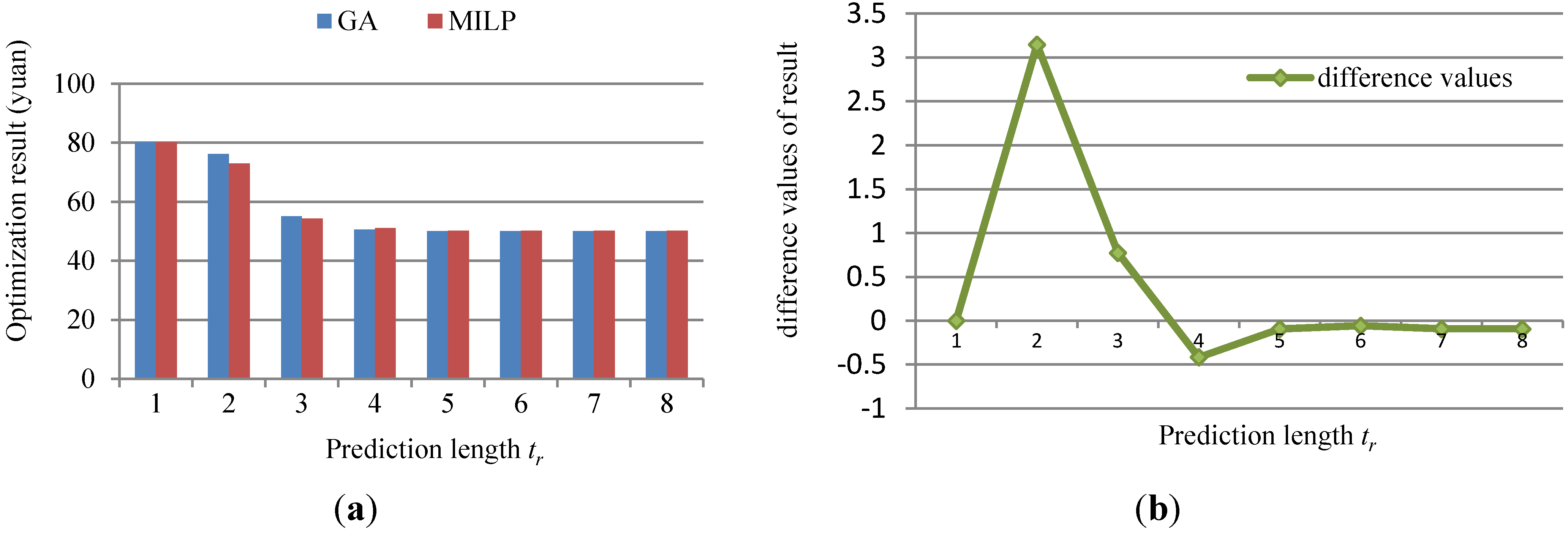
| Number | Method | Prediction Length tr | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | GA | 80.093 | 76.095 | 55.107 | 50.628 | 50.053 | 50.089 | 50.055 | 50.054 |
| 2 | MILP | 80.093 | 72.949 | 54.334 | 51.044 | 50.147 | 50.147 | 50.147 | 50.147 |
| 3 | Difference values | 0 | 3.146 | 0.773 | −0.416 | −0.094 | −0.058 | −0.092 | −0.093 |
5. Conclusions
- (1)
- Based on the characteristics of microgrids, this paper proposes a method for energy coordinative optimization which focuses on the improvement of the economic benefits of microgrids in the prediction framework.
- (2)
- The generation power of wind turbines and load power are predicted through building a grey prediction model with residual modification, which has eliminated the unstable influence of wind power on energy optimization. Meanwhile, the data such as spot power price, wind power and predicted load power are applied in the optimization algorithm.
- (3)
- Comparing GA with MILP in finding the optimal solutions, MILP has higher computing speed, but non-linear computing become difficult after model becomes more complex. A GA can efficiently figure out the optimum solution in predictive horizon for the complex non-linear coordination control model of microgrids. The effectiveness and feasibility of the proposed method which integrates RHC and GA is verified by example.
- (4)
- As for future work, we think that energy coordinative optimization model of microgrids and various constraints such as economy, environment and maintenance cost need to be improved. Furthermore, the charge and discharge frequency of the storage battery and centralized, distributed and decentralized optimization algorithms need to be discussed.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lassetter, R.H.; Akhil, A.; Marnay, C. White Paper on Integration of Distributed Energy Resources. The CERTS Microgrid Concept; LBNL: Berkeley, CA, USA.
- Wang, R.; Li, K.; Zhang, C. Optimization allocation of microgrid capacity based on chaotic multi-objective genetic algorithm. Power Syst. Prot. Control 2011, 39, 16–22. [Google Scholar]
- Venkataramanan, G.; Marnay, C. A larger role for micro grids. IEEE Power Energy Mag. 2008, 6, 78–82. [Google Scholar] [CrossRef]
- Majumder, R.G.; Ledwich, A.G. Power management and power flow control with back-to-back converters in a utility connected microgrid. IEEE Trans. Power Syst. 2010, 25, 821–834. [Google Scholar] [CrossRef]
- Ai, X.; Cui, M.; Lei, Z. Environmental and economic dispatch of microgrid using chaotic ant swarm algorithms. J. North. China Electr. Power Univ. 2009, 36, 1–5. [Google Scholar]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Smart microgrid energy and reserve scheduling with demand response using stochastic optimization. Int. J. Electr. Power Energy Syst. 2014, 63, 523–533. [Google Scholar] [CrossRef]
- Paiva, J.E.; Carvalho, A.S. Controllable hybrid power system based on renewable energy sources for modern electrical grids. Renew. Energy 2013, 53, 271–279. [Google Scholar] [CrossRef]
- Khalid, M.; Savkin, A.V. Minimization and control of battery energy storage for wind power smoothing: Aggregated, distributed and semi-distributed storage. Renew. Energy 2014, 64, 105–112. [Google Scholar] [CrossRef]
- Yucheng, H.; Xiaobo, D.; Zaijun, W. Hierarchical and distributed optimization of energy management for microgrid. Electr. Power Autom. Equip. 2014, 34, 154–161. [Google Scholar]
- Jun, X. Model Predictive Control for Energy Management of Microgrid. Master’s Thesis, East China University of Science and Technology, Shanghai, China, 2014. [Google Scholar]
- Ionela, P.; Enrico, Z. A model predictive control framework for reliable microgrid energy management. Electr. Power Energy Syst. 2014, 61, 399–409. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T. Microgrid energy management model based on improved genetic arithmetic. Trans. China Electr. Technol. Soc. 2013, 28, 196–201. [Google Scholar]
- Koyanagik, J.F.; Fujita, G.; Koyanagi, K.; Yokoyama, R. Field tests of a microgrid control system. In Proceedings of the 41st International Universities Power Engineering Conference, Newcastle, UK, 6–8 September 2006; pp. 232–236.
- Li, P.; Liu, Z.; Li, X.; Pan, Y. Modeling and simulation of microgrid based on synthesis control. High. Volt. Eng. 2011, 37, 2356–2362. [Google Scholar]
- Renhua, Y.; Wei, H.; Li, G. Structure and operation control of micro-grid. Adv. Power Syst. Hydroelectr. Eng. 2010, 26, 48–55. [Google Scholar]
- Zhang, Y. Study of Operation Optimization and Energy Management for Microgrid. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2011. [Google Scholar]
- Zhang, G.; Zhang, B. Wind speed and wind turbine output forecast based on combination method. Autom. Electr. Power Syst. 2009, 22, 109. [Google Scholar]
- Wang, L.; Singh, C. PSO-based multidisciplinary design of a hybrid power generation system with statistical models of wind speed and solar insolation. In Proceedings of the 2006 PEDES’06. International Conference on Power Electronics, Drives and Energy Systems, New Delhi, India, 12–15 December 2006; pp. 1–6.
- Wang, C. Analysis and Simulation Theory of Microgrid, 1st ed.; Science Press: Beijing, China, 2013; pp. 142–145. (In Chinese) [Google Scholar]
- Xie, K.; Song, Y. Optimal power flow based spot pricing algorithm via interior point methods—On the economic meanings of λp and λq. Autom. Electr. Power Syst. 1999, 2, 1000–1026. [Google Scholar]
- Muyeen, S.M. Wind Energy Conversion Systems, 1st ed.; Science Press: London, UK, 2012; pp. 197–226. [Google Scholar]
- Gabriel, L.; Enrique, A. Parallel Genetic Algorithms: Theory and Real World Applications,, 2nd ed.; Springer: Berlin, Germany, 2013; pp. 154–196. [Google Scholar]
- Renders, J.M.; Flasse, S.P. Hybrid method using genetic algorithms for global optimization. IEEE Trans. Syst. Man. Cybern. B Cybern. 1996, 26, 243–258. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Luo, S.; Li, Z.; Wang, X.; Sun, L. Energy Coordinative Optimization of Wind-Storage-Load Microgrids Based on Short-Term Prediction. Energies 2015, 8, 1505-1528. https://doi.org/10.3390/en8021505
Hu C, Luo S, Li Z, Wang X, Sun L. Energy Coordinative Optimization of Wind-Storage-Load Microgrids Based on Short-Term Prediction. Energies. 2015; 8(2):1505-1528. https://doi.org/10.3390/en8021505
Chicago/Turabian StyleHu, Changbin, Shanna Luo, Zhengxi Li, Xin Wang, and Li Sun. 2015. "Energy Coordinative Optimization of Wind-Storage-Load Microgrids Based on Short-Term Prediction" Energies 8, no. 2: 1505-1528. https://doi.org/10.3390/en8021505
APA StyleHu, C., Luo, S., Li, Z., Wang, X., & Sun, L. (2015). Energy Coordinative Optimization of Wind-Storage-Load Microgrids Based on Short-Term Prediction. Energies, 8(2), 1505-1528. https://doi.org/10.3390/en8021505





