Overview of Modelling and Advanced Control Strategies for Wind Turbine Systems
Abstract
:1. Introduction
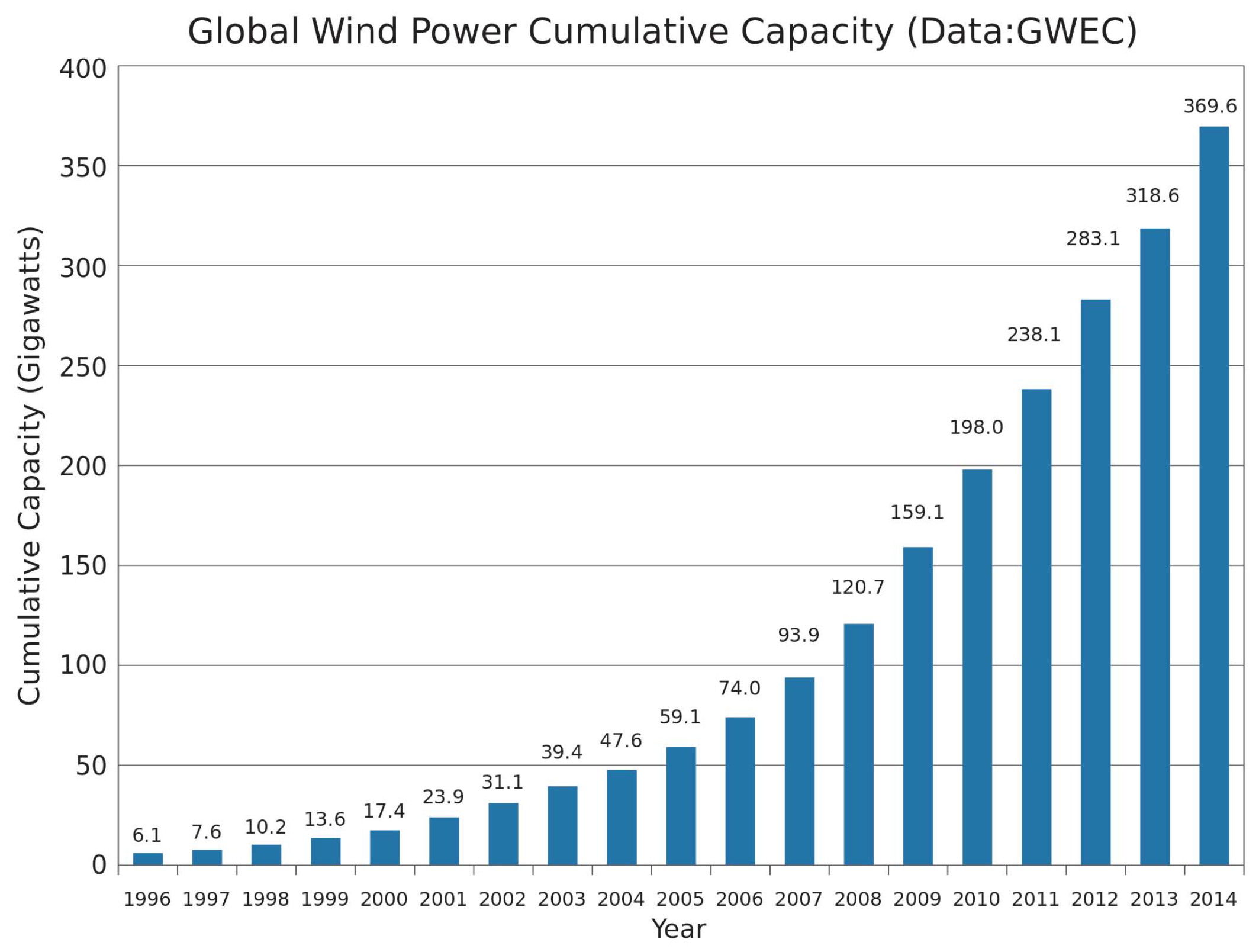
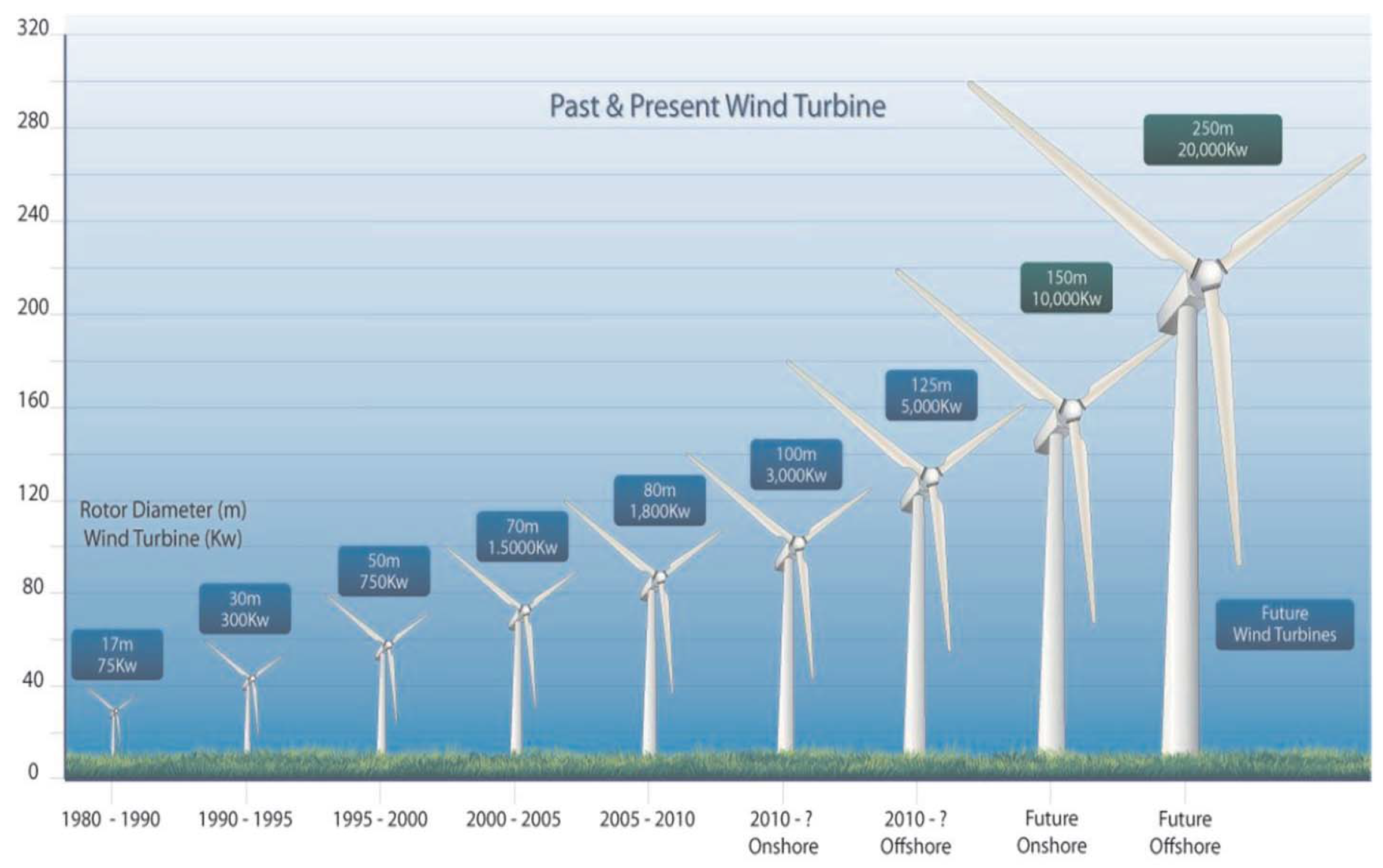
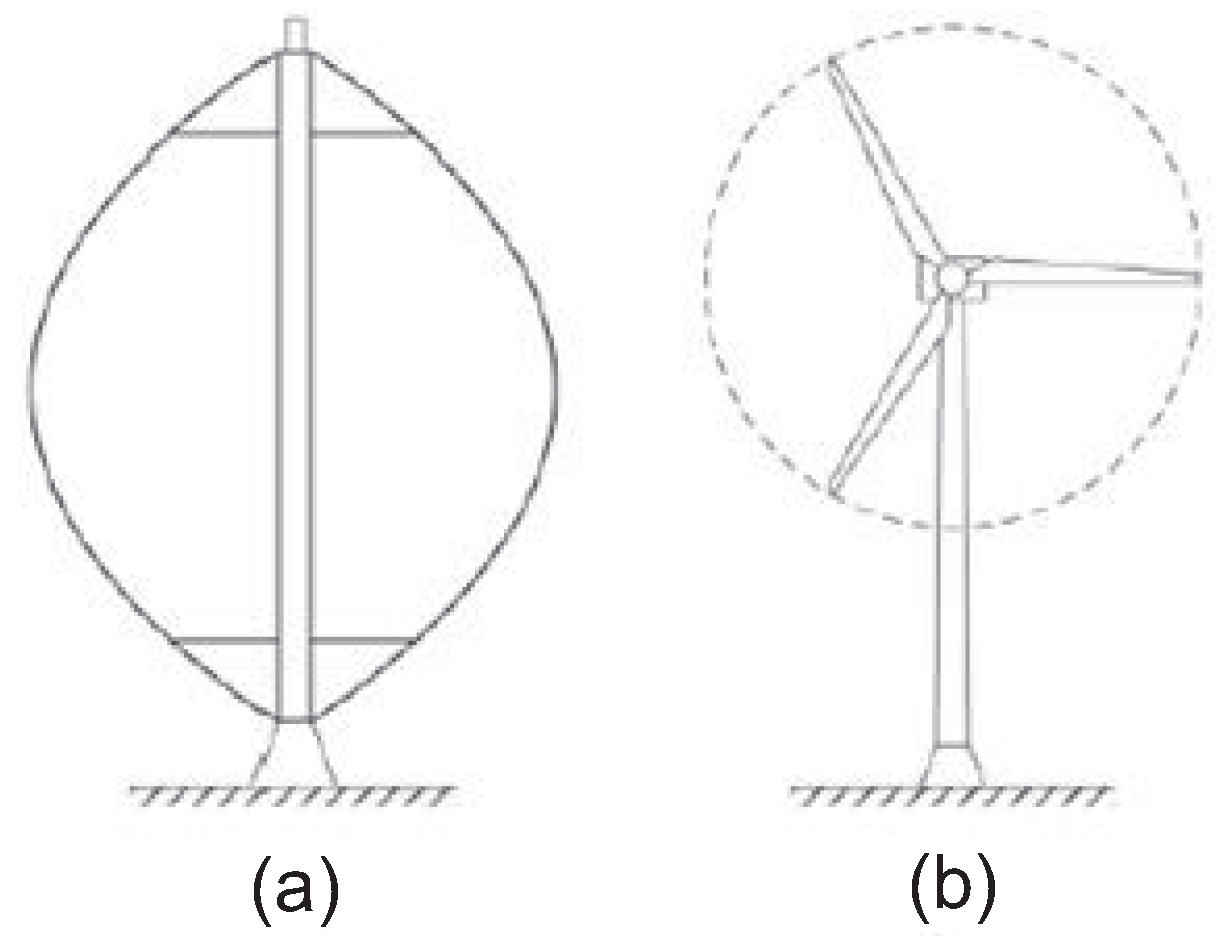
2. Wind Turbine Modelling Issues
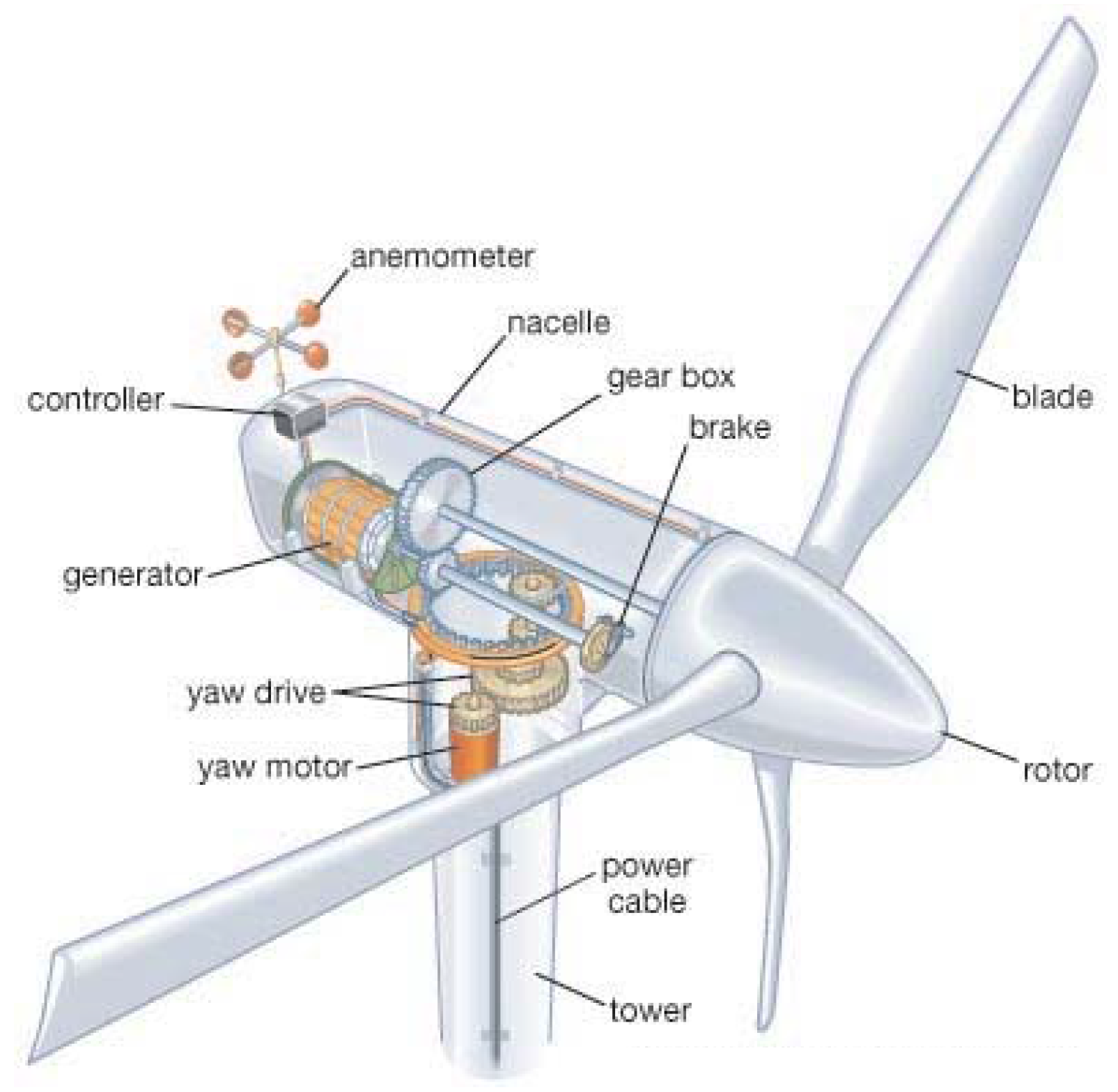

2.1. Wind Turbine Tower and Blade Models

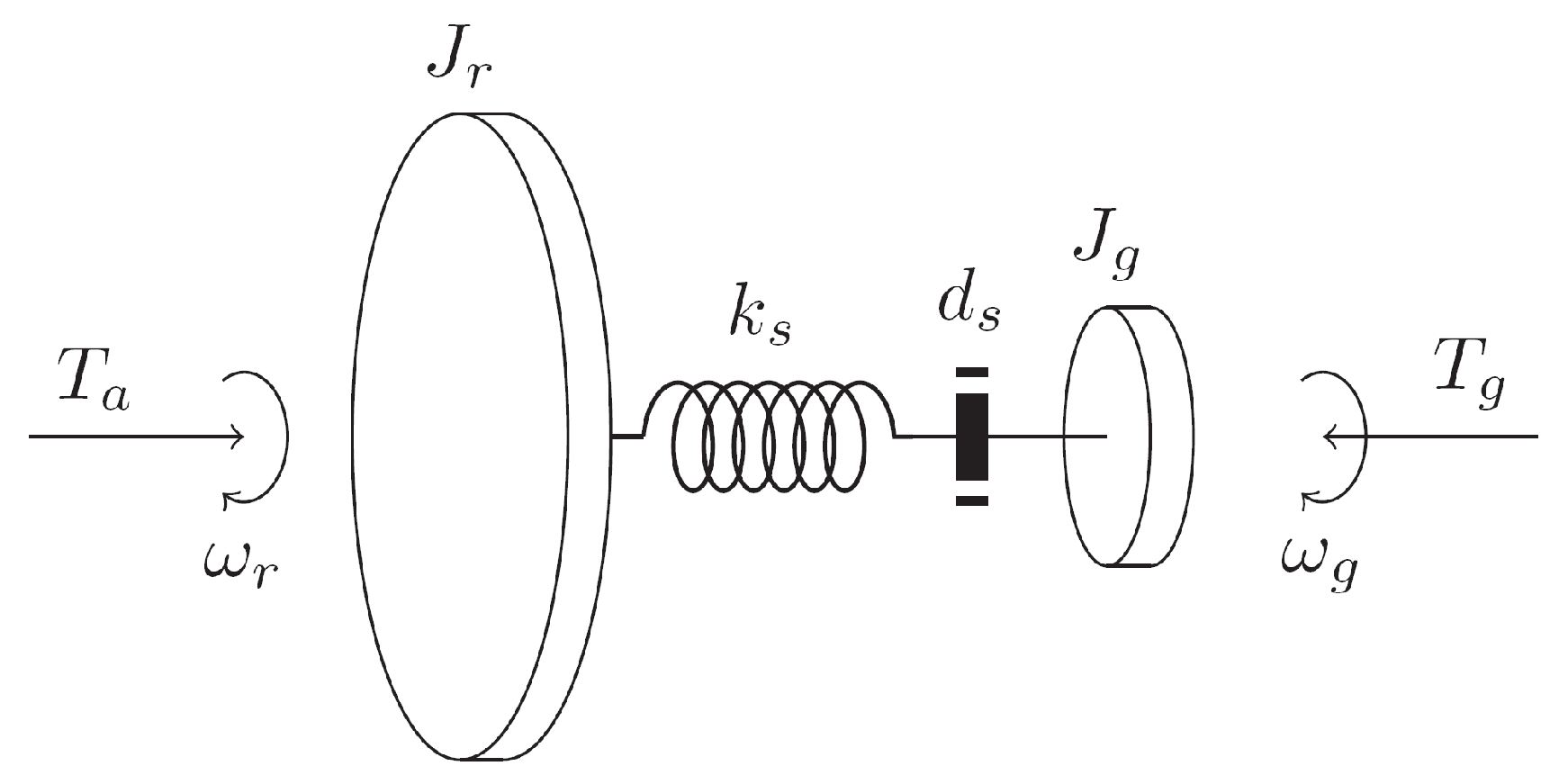
2.2. Pitch Model
2.3. Generator/Converter Dynamic Model
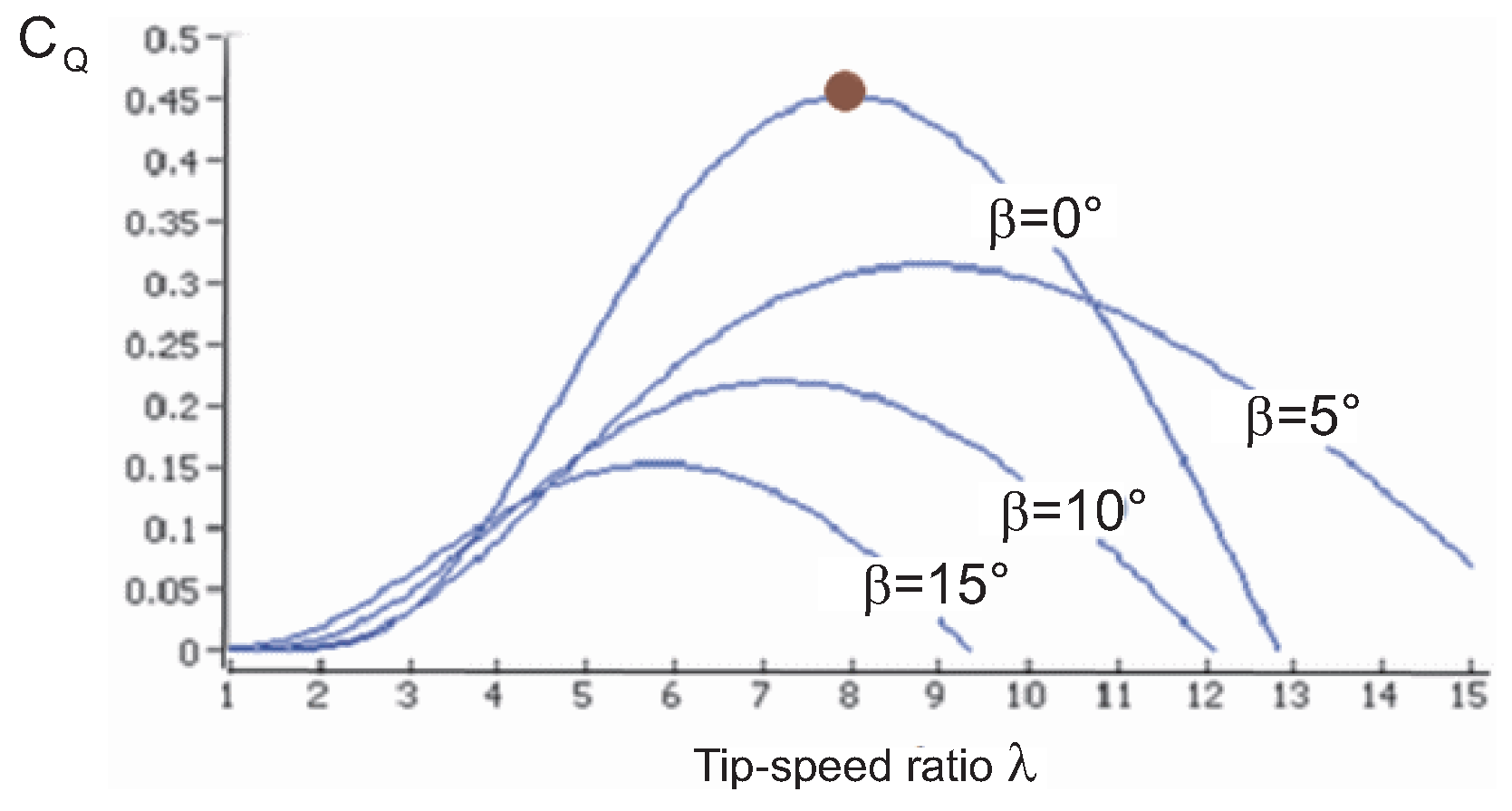
2.4. Aerodynamic Model
2.5. Wind Turbine Overall Model
2.6. Measurement Errors
3. Basic Wind Turbine Control Issues
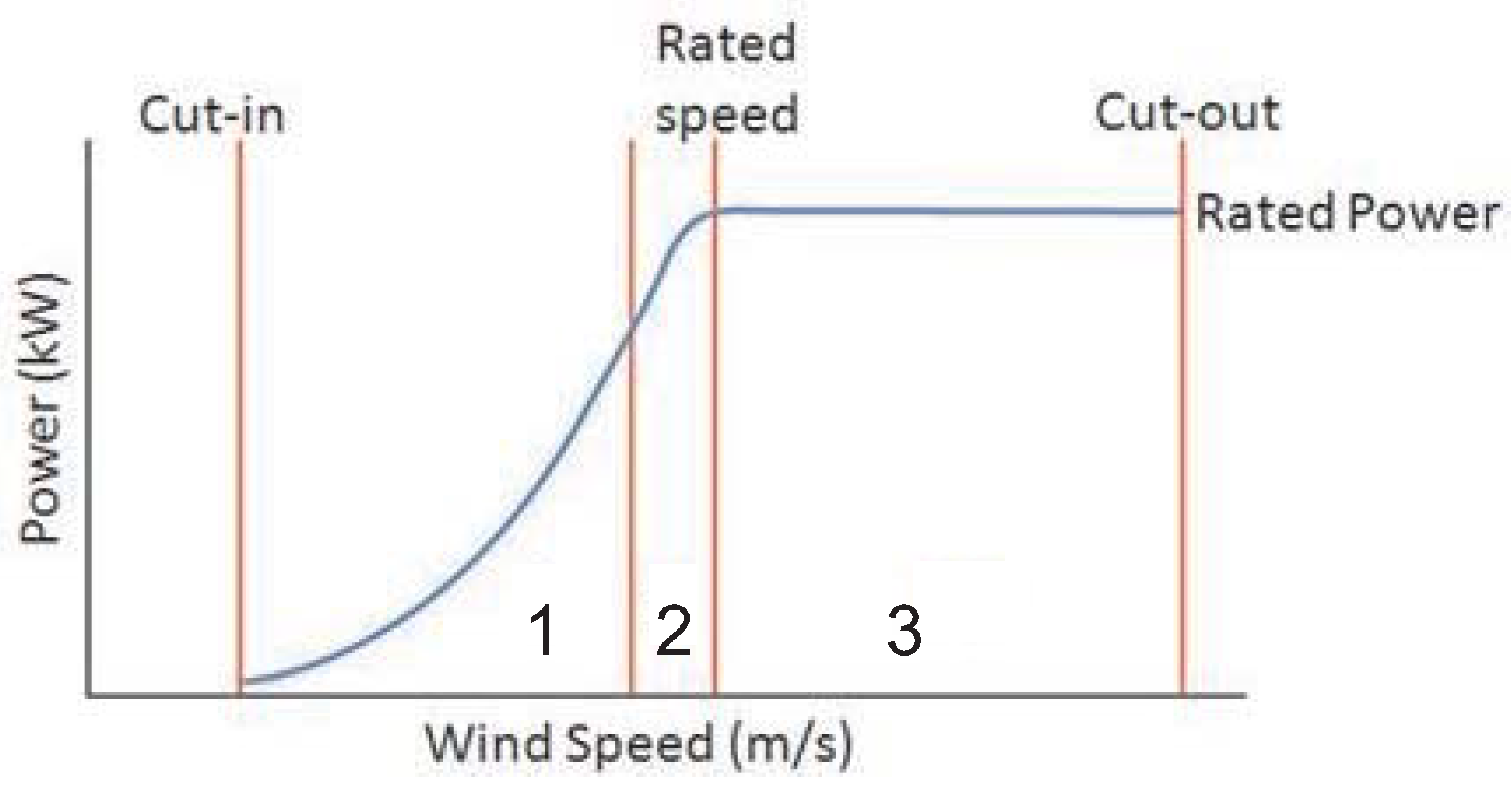
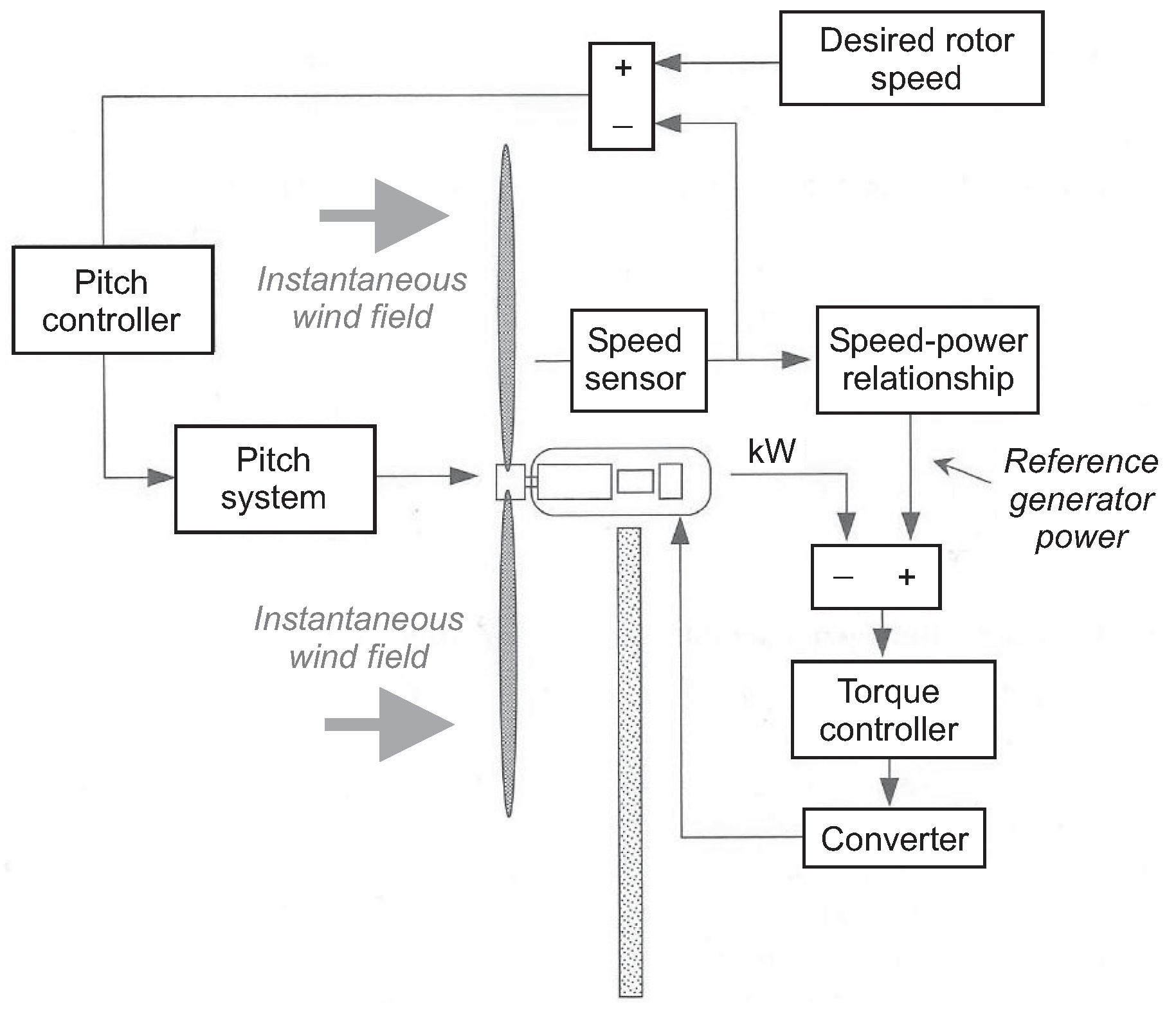
3.1. Main Control Objectives
4. Basic Feedback Control Solutions for Wind Turbines
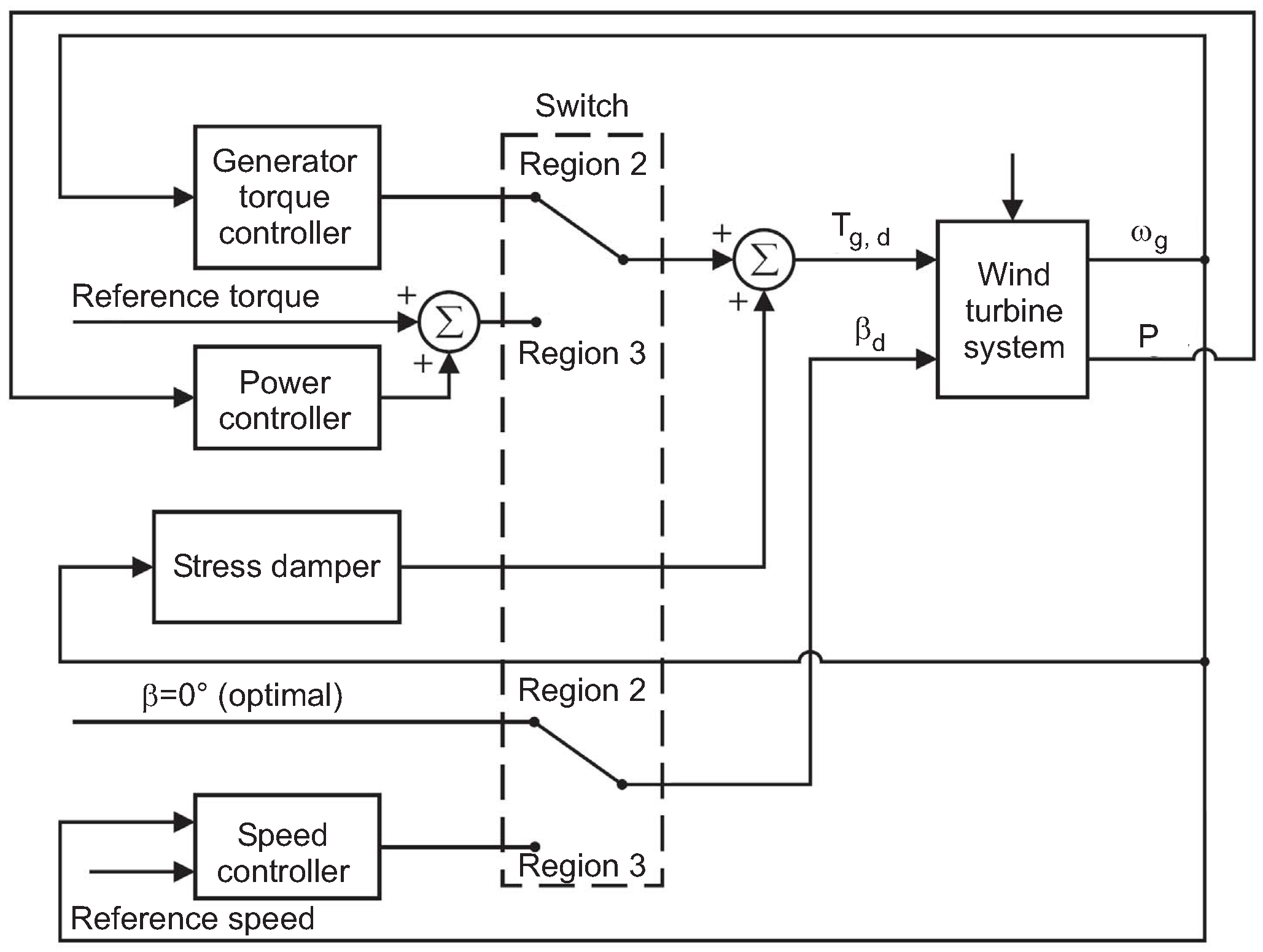
- Controller operating in partial load condition: it refers to the design of the generator torque controller. This controller operates in the partial load (Region 2), and should maximise the energy production while minimising mechanical stress and actuator usage;
- Controller operating in full load condition: it concerns the speed controller and power controller. These controllers operate in the full load (Region 3), and should track the rated generator speed and limiting the output power;
- Bumpless transfer: it describe the design of the mechanism that eliminates bumps on the control signals, when switching between the controllers in the partial load and full load regions;
- Structural stress damper: it regards the design of structure and drivetrain stress damper. The purpose of the module is to dampen drivetrain oscillations and reduce structural stress that could affect the wind turbine tower.
4.1. Partial Load Controller
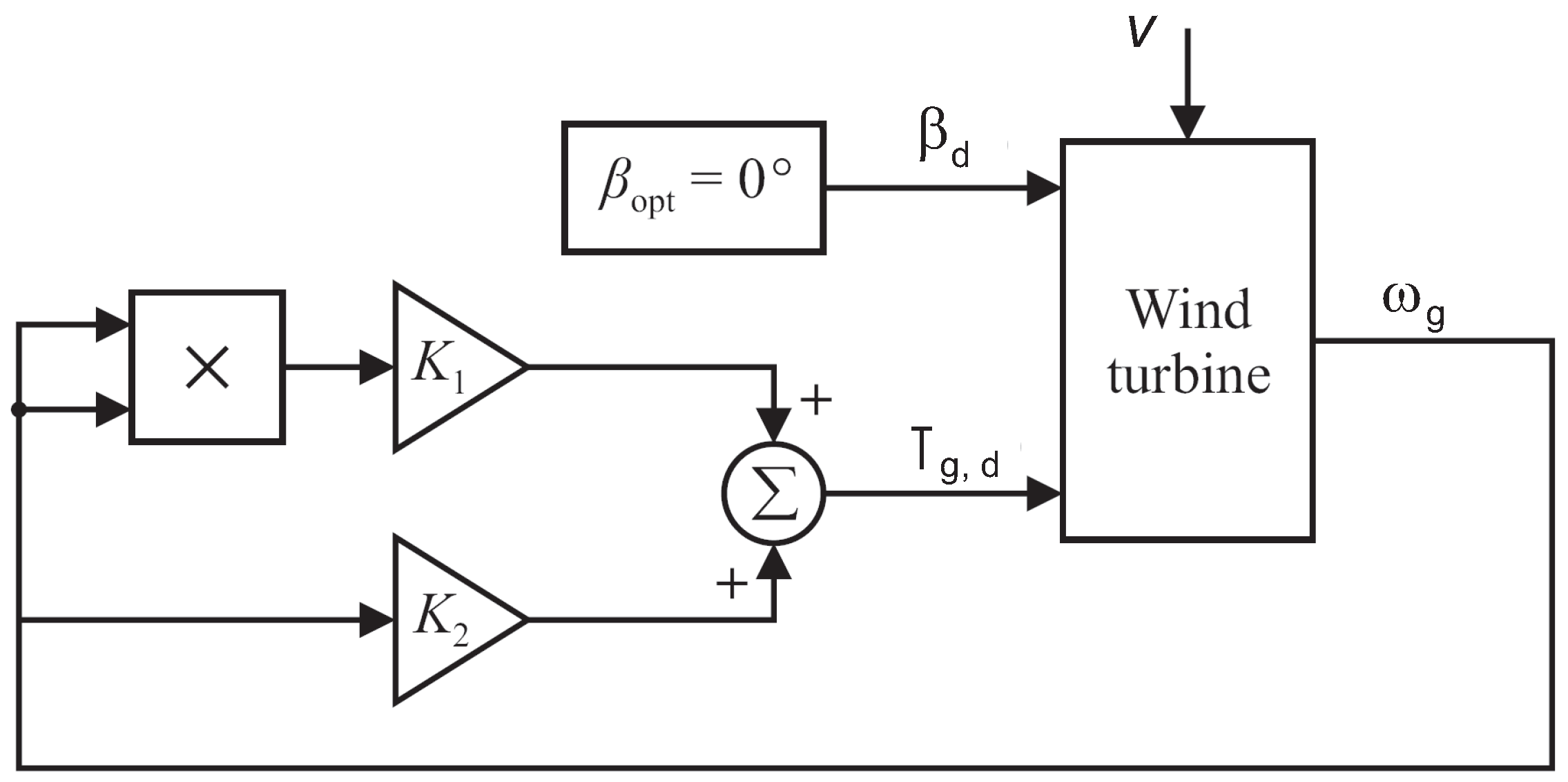
4.2. Full Load Operation Controller
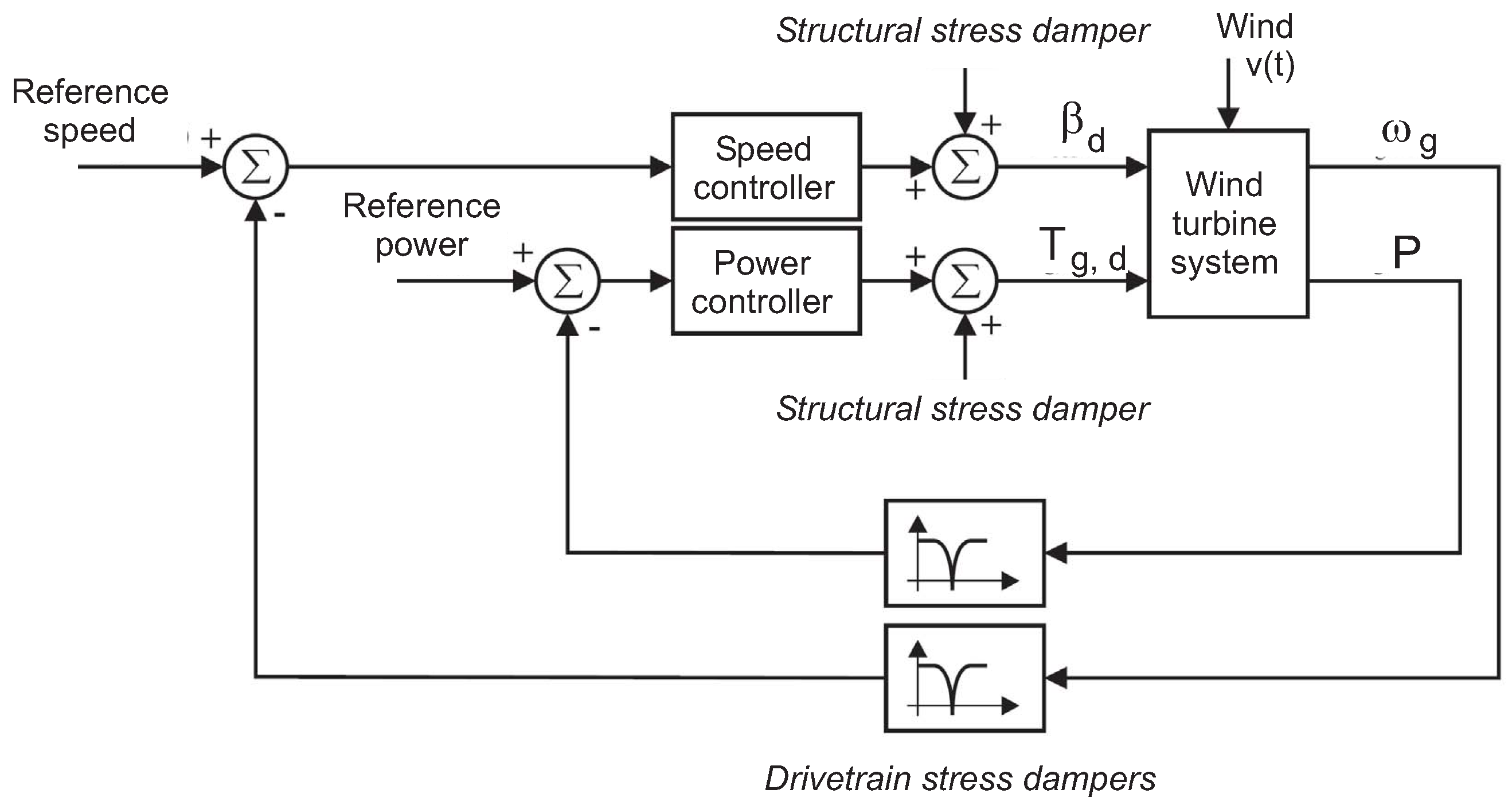
4.3. Structural and Drivetrain Stress Damper
4.4. Bumpless Transfer
5. Advanced Control of Wind Turbines
5.1. Sustainable Control Issues
5.2. Active and Passive Fault-Tolerant Control Systems
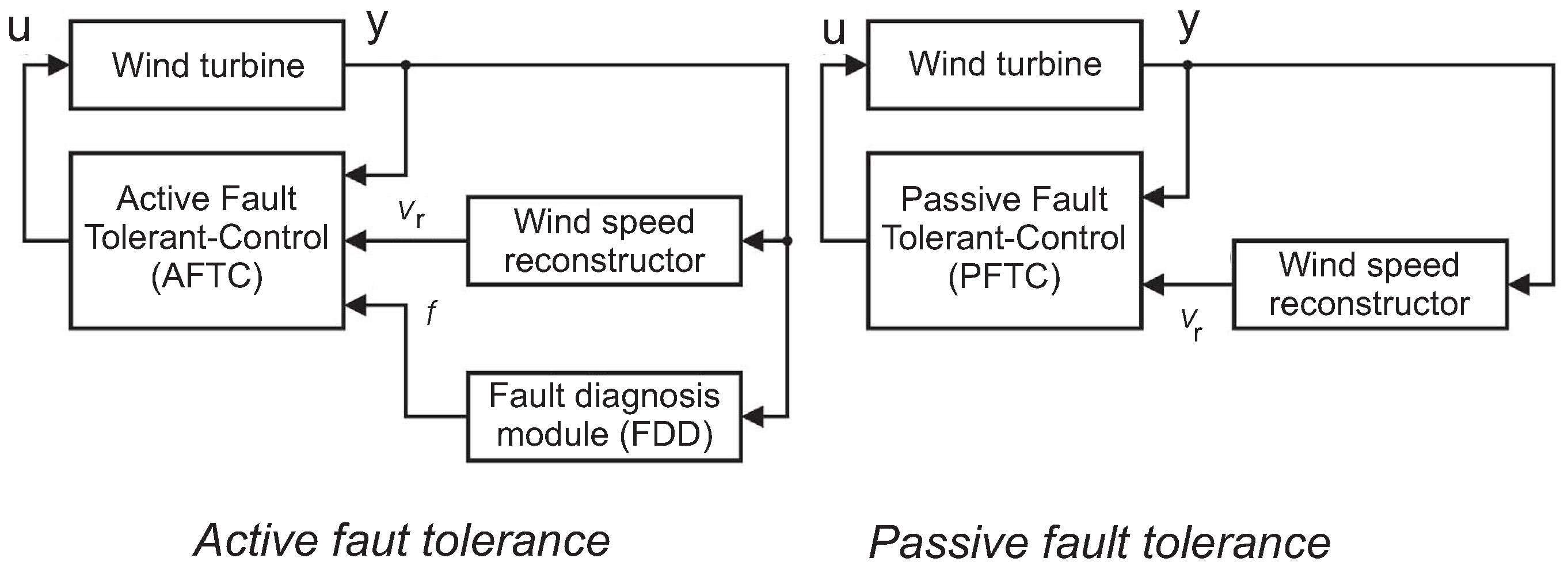
6. Conclusions
Conflicts of Interest
References
- Johnson, K.E.; Fleming, P.A. Development, implementation, and testing of fault detection strategies on the National Wind Technology Center’s controls advanced research turbines. Mechatronics 2011, 21, 728–736. [Google Scholar] [CrossRef]
- Global Wind Energy Council. Wind Energy Statistics 2014; Global Wind Energy Council: Brussels, Belgium, 10 February 2015. [Google Scholar]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault-tolerant control of wind turbines: A benchmark model. IEEE Trans. Control Syst. Technol. 2013, 21, 1168–1182. [Google Scholar] [CrossRef]
- David Rivkin, D.; Anderson, L.D.; Silk, L. Wind Turbine Control Systems, 1st ed.; Jones & Bartlett Learning: Burlington, MA, USA, 2012. [Google Scholar]
- Bianchi, F.D.; Battista, H.D.; Mantz, R.J. Advances in industrial control. In Wind Turbine Control Systems: Principles, Modelling and Gain Scheduling Design, 1st ed.; Springer-Verlag: Berlin, Germany, 2007. [Google Scholar]
- Garcia-Sanz, M.; Houpis, C.H. Wind Energy Systems: Control Engineering Design; CRC (Chemical Rubber Company) Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Ningsu, L.; Vidal, Y.; Acho, L. Advances in industrial control. In Wind Turbine Control and Monitoring; Springer-Verlag: Berlin Heidelberg, Germany, 2014. [Google Scholar]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control; Springer-Verlag: Berlin Heidelberg, Germany, 2006. [Google Scholar]
- Ding, S.X. Model-based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools, 1st ed.; Springer-Verlag: Berlin Heidelberg, Germany, 2008. [Google Scholar]
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance, 1st ed.; Springer-Verlag: Berlin Heidelberg, Germany, 2005. [Google Scholar]
- Pao, L.Y.; Johnson, K.E. Control of wind turbines. IEEE Control Syst. Mag. 2011, 31, 44–62. [Google Scholar] [CrossRef]
- Schulte, H.; Gauterin, E. Fault-tolerant control of wind turbines with hydrostatic transmission using takagi-sugeno and sliding mode techniques. Annu. Rev. Control 2015, 12. [Google Scholar] [CrossRef]
- Shi, F.; Patton, R.J. An active fault tolerant control approach to an offshore wind turbine Model. Renew. Energy 2015, 75, 788–798. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J. A benchmark evaluation of fault tolerant wind turbine control concepts. IEEE Trans. Control Syst. Technol. 2015, 23, 1221–1228. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; Technical Report NREL/EL-500-38230; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Gasch, R.; Twele, J. Wind Power Plants: Fundamentals, Design, Construction and Operation, 2nd ed.; Springer-Verlag: Berlin Heidelberg, Germany, 2012. [Google Scholar]
- Georg, S.; Schulte, H.; Aschemann, H. Control-oriented modelling of wind turbines using a Takagi-Sugeno model structure. In Proceedings of the IEEE International Conference on Fuzzy Systems, Brisbane, Australia, 10–15 June 2012; pp. 1737–1744.
- Landau, L.D.; Lifshitz, E.M. Course of theoretical physics S. In Mechanics, 3rd ed.; Butterworth-Heinemann: Waltham, MA, USA, 1976; Volume 1. [Google Scholar]
- Laino, D.J.; Hansen, A.C. Windward engineering, LC. In User’s Guide to the Wind Turbine Aerodynamics Computer Software AeroDyn; Technical Report TCX-9-29209-01; Windward Engineering: Salt Lake City, UT, USA, 2002. [Google Scholar]
- Heier, S. Grid Integration of Wind Energy: Onshore and Offshore Conversion Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Simani, S.; Castaldi, P. Estimation of the power coefficient map for a wind turbine system. In Proceedings of the 9th European Workshop on Advanced Control and Diagnosis—ACD 2011, Budapest, Hungary, 17–18 November 2011.
- Simani, S.; Castaldi, P. Active actuator fault tolerant control of a wind turbine benchmark model. Int. J. Robust Nonlinear Control 2014, 24, 1283–1303. [Google Scholar]
- Odgaard, P.F.; Stoustrup, J. Fault tolerant wind farm control—A benchmark model. In Proceedings of the IEEE Multiconference on Systems and Control—MSC2013, Florence, Italy, 10–13 December 2013; pp. 1–6.
- Odgaard, P.F.; Johnson, K. Wind turbine fault diagnosis and fault tolerant control—An enhanced benchmark challenge. In Proceedings of the 2013 American Control Conference—ACC, IEEE Control Systems Society & American Automatic Control Council, Chicago, IL, USA, 1–3 July 2013; pp. 4447–4452.
- Simani, S.; Farsoni, S.; Castaldi, P. Fault diagnosis of a wind turbine benchmark via identified fuzzy models. IEEE Trans. Ind. Electr. 2014, 62, 3775–3782. [Google Scholar] [CrossRef]
- Simani, S.; Farsoni, S.; Castaldi, P. Wind turbine simulator fault diagnosis via fuzzy modelling and identification techniques. Sustain. Energy Grids Netw. 2015, 1, 45–52. [Google Scholar] [CrossRef]
- Bossanyi, E.A.; Hassan, G. The design of closed loop controllers for wind turbines. Wind Energy 2000, 3, 149–164. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Wind turbine control for load reduction. Wind Energy 2003, 6, 229–244. [Google Scholar] [CrossRef]
- Betz, A.; Randall, D.G. Introduction to the Theory of Flow Machines; Permagon Press: Oxford, UK, 1966. [Google Scholar]
- Chatzopoulos, A.P.; Leithead, W.E. Reducing tower fatigue loads by a co-ordinated control of the Supergen 2 MW exemplar wind turbine. In Proceedings of the 3rd Torque 2010 Conference, Crete, Greece, 28–30 June 2010; pp. 667–674.
- Odgaard, P.F. FDI/FTC wind turbine benchmark modelling. In Workshop on Sustainable Control of Offshore Wind Turbines; Patton, R.J., Ed.; Centre for Adaptive Science & Sustainability, University of Hull: Hull, UK, 2012; Volume 1. [Google Scholar]
- Simani, S.; Castaldi, P. Data-driven and adaptive control applications to a wind turbine benchmark model. Control Eng. Pract. 2013, 21, 1678–1693. [Google Scholar] [CrossRef]
- Simani, S.; Castaldi, P. Identification-oriented control designs with application to a wind turbine benchmark. Int. J. Adv. Comput. Sci. Appl. 2013, 4, 184–191. [Google Scholar] [CrossRef]
- Johnson, K.E.; Pao, L.Y.; Balas, M.J.; Fingersh, L.J. Control of variable-speed wind turbines: Standard and adaptive techniques for maximizing energy capture. IEEE Control Syst. Mag. 2006, 26, 70–81. [Google Scholar] [CrossRef]
- Munteanu, I.; Bratcu, A.I. Advances in industrial control. In Optimal Control of Wind Energy Systems: Towards a Global Approach; Springer-Verlag: Berlin Heidelberg, Germany, 2008. [Google Scholar]
- Amit Dixit, A.; Suryanarayanan, S. Towards pitch-scheduled drivetrain damping in variable-speed, horizontal-axis large wind turbines. In Proceedings of 44th IEEE Conference on Decision and Control, Plaza de Espana Seville, Spain, 12–15 December 2005; pp. 1295–1300.
- Wright, A.; Fingersh, L.; Balas, M. Testing state-space controls for the controls of advanced research turbine. ASME J. Sol. Energy Eng. 2006, 128, 506–515. [Google Scholar] [CrossRef]
- Laks, J.H.; Pao, L.Y.; Wright, A.D. Control of wind turbines: Past, present, and future. In Proceedings of the American Control Conference, 2009—ACC’09, St. Louis, MO, USA, 10–12 June 2009; pp. 2096–2103.
- Kumar, A.; Stol, K. Scheduled model predictive control of a wind turbine. In Proceedings of the 47th AIAA (American Institute of Aeronautics and Astronautics) Wind Energy Symposium, Orlando, FL, USA, 7–10 January 2009; pp. 1–18.
- Laks, J.; Pao, L.Y.; Simley, E.; Wright, A.; Kelley, N.; Jonkman, B. Model predictive control using preview measurements from LIDAR. In Proceedings of the 49th AIAA (American Institute of Aeronautics and Astronautics) Wind Energy Symposium, Orlando, FL, USA, 4–7 January 2011; pp. 1–20.
- Kumar, A.; Stol, K. Simulating feedback linearization control of wind turbines using high-order models. Wind Energy 2010, 13, 419–432. [Google Scholar] [CrossRef]
- Burkart, R.; Margellos, K.; Lygeros, J. Nonlinear control of wind turbines: An approach based on switched linear systems and feedback linearization. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), Orlando, FL, USA, 12–15 December 2011; pp. 5485–5490.
- Boukhezzar, B.; Lupu, L.; Siguerdidjane, H.; Hand, M. Multivariable control strategy for variable speed, variable pitch wind turbines. Renew. Energy 2007, 32, 1273–1287. [Google Scholar] [CrossRef]
- Thomsen, S.C.; Niemann, H.; Poulsen, N.K. Individual pitch control of wind turbines using local inflow measurements. In Proceedings of the 17th IFAC (The International Federation of Automatic Control) World Congress, Seoul, Korea, 6–11 July 2008; pp. 5587–5592.
- Friis, J.; Nielsen, E.; Bonding, J.; Adegas, F.D.; Stoustrup, J.; Odgaard, P.F. Repetitive model predictive approach to individual pitch control of wind turbines. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference (CDC & ECC), Orlando, FL, USA, 12–15 December 2011; pp. 3664–3670.
- McCoy, T.J.; Griffin, D.A. Control of rotor geometry and aerodynamics: Retractable blades and advanced concepts. Wind Eng. 2009, 32, 13–26. [Google Scholar] [CrossRef]
- Gong, X.; Qiao, W. Bearing fault diagnosis for direct-drive wind turbines via current–demodulated signals. IEEE Trans. Ind. Electr. 2013, 60, 3419–3428. [Google Scholar] [CrossRef]
- Freire, N.M.A.; Estima, J.O.; Marques Cardoso, A.J. Open-circuit fault diagnosis in PMSG drives for wind turbine applications. IEEE Trans. Ind. Electr. 2013, 60, 3957–3967. [Google Scholar] [CrossRef]
- Mahmoud, M.; Jiang, J.; Zhang, Y. Lecture notes in control and information sciences. In Active Fault Tolerant Control Systems: Stochastic Analysis and Synthesis; Springer-Verlag: Berlin, Germany, 2003. [Google Scholar]
- Rodrigues, M.; Theilliol, D.; Aberkane, S.; Sauter, D. Fault tolerant control design for polytopic LPV systems. Int. J. Appl. Math. Comput. Sci. 2007, 17, 27–37. [Google Scholar] [CrossRef]
- Puig, V. Fault diagnosis and fault tolerant control using set-membership approaches: application to real case studies. Int. J. Appl. Math. Comput. Sci. 2010, 20, 619–635. [Google Scholar] [CrossRef]
- Niemann, H.; Stoustrup, J. An architecture for fault tolerant controllers. Int. J. Control 2005, 78, 1091–1110. [Google Scholar] [CrossRef]
- Chen, Z.; Patton, R.J.; Chen, J. Robust fault-tolerant system synthesis via LMI. In Proceedings of the IFAC Symposium on Fault Detection, Supervision and Safety for Technical Processes: SAFEPROCESS’97, Hull, UK, 26–28 August 1997; Volume 1, pp. 347–352.
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simani, S. Overview of Modelling and Advanced Control Strategies for Wind Turbine Systems. Energies 2015, 8, 13395-13418. https://doi.org/10.3390/en81212374
Simani S. Overview of Modelling and Advanced Control Strategies for Wind Turbine Systems. Energies. 2015; 8(12):13395-13418. https://doi.org/10.3390/en81212374
Chicago/Turabian StyleSimani, Silvio. 2015. "Overview of Modelling and Advanced Control Strategies for Wind Turbine Systems" Energies 8, no. 12: 13395-13418. https://doi.org/10.3390/en81212374
APA StyleSimani, S. (2015). Overview of Modelling and Advanced Control Strategies for Wind Turbine Systems. Energies, 8(12), 13395-13418. https://doi.org/10.3390/en81212374





