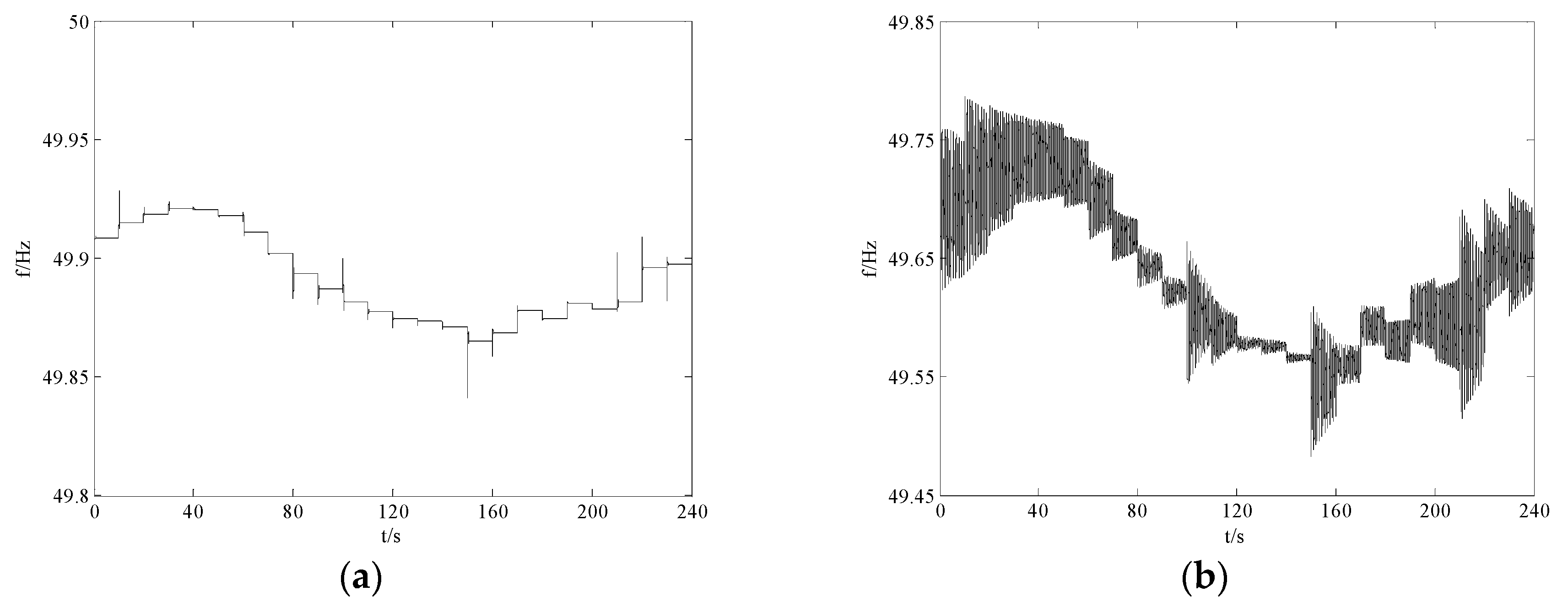
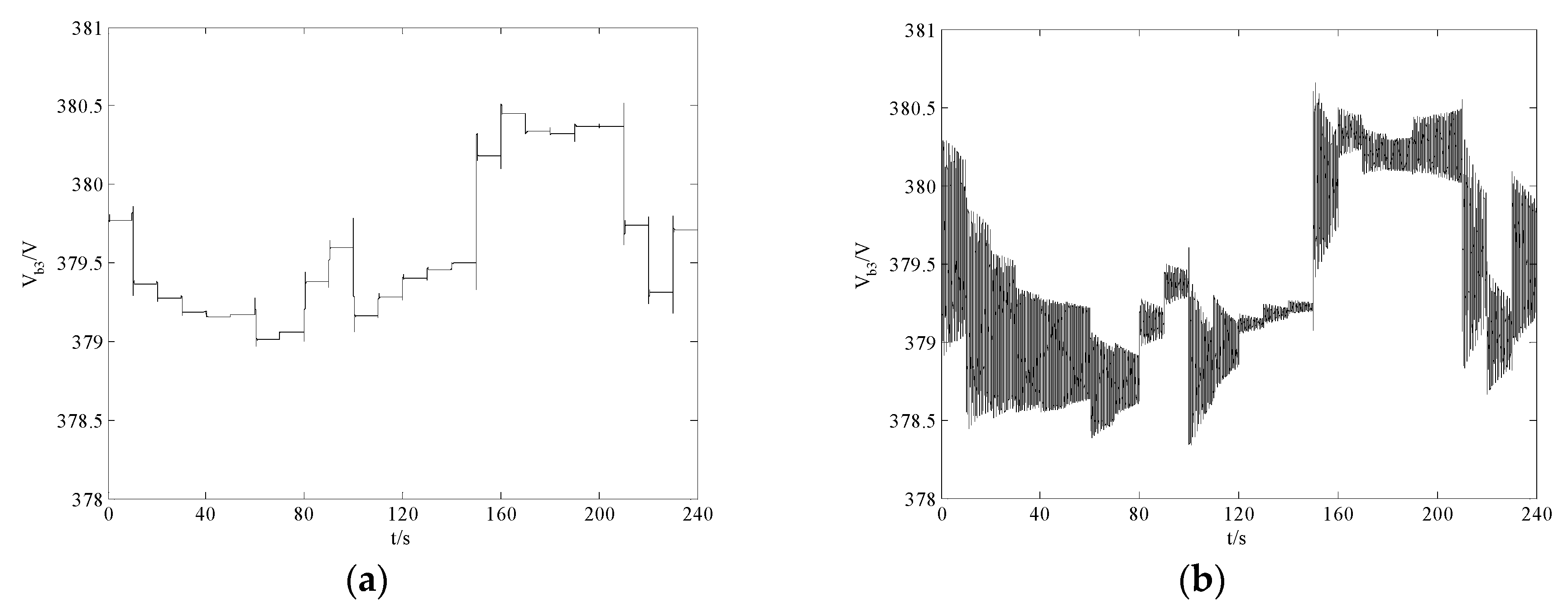
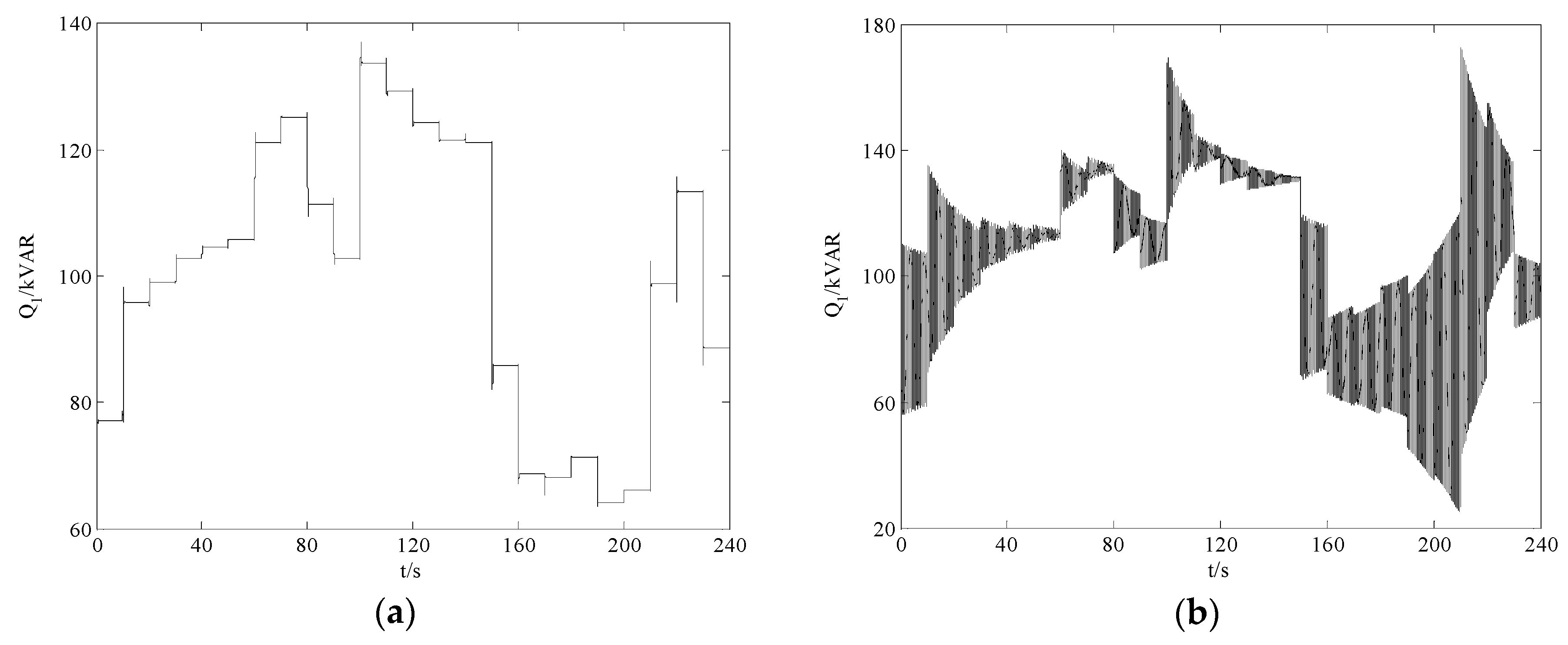
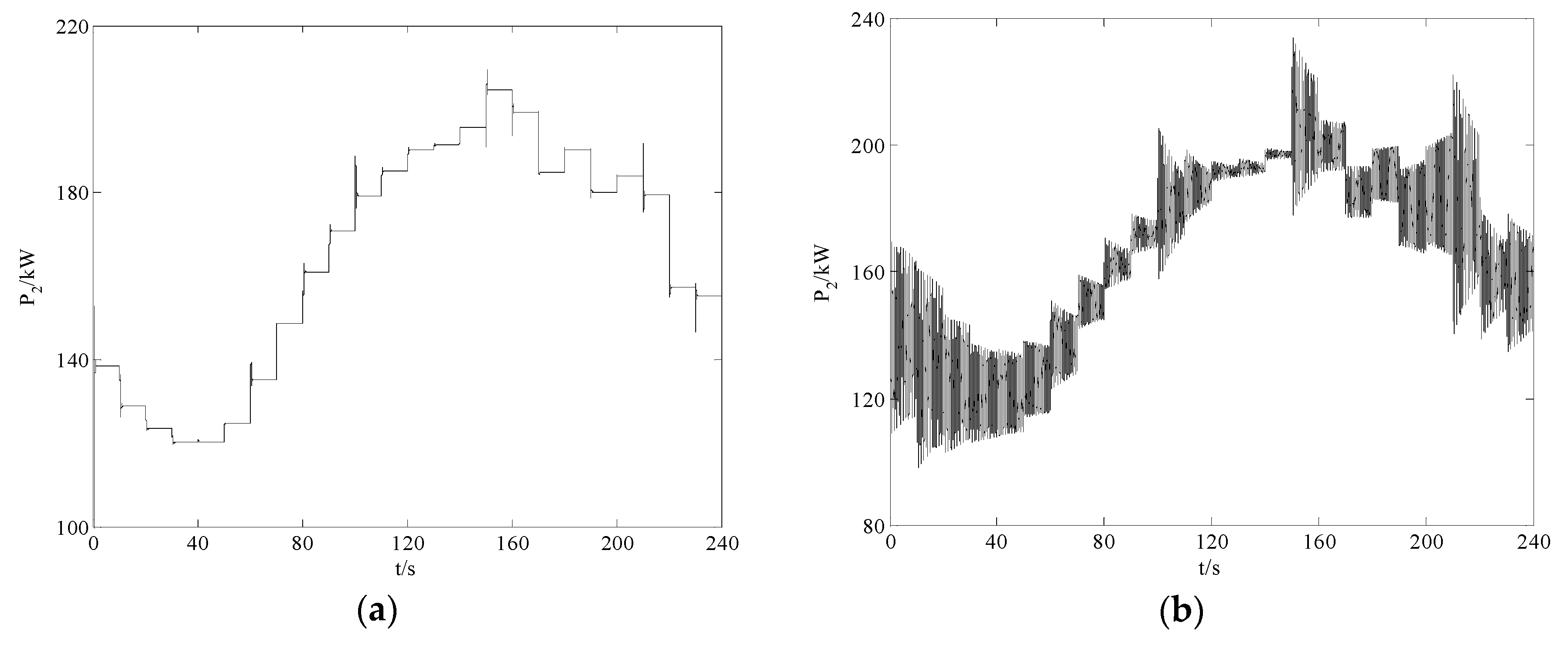A. The Detailed Configuration of the Microgrid
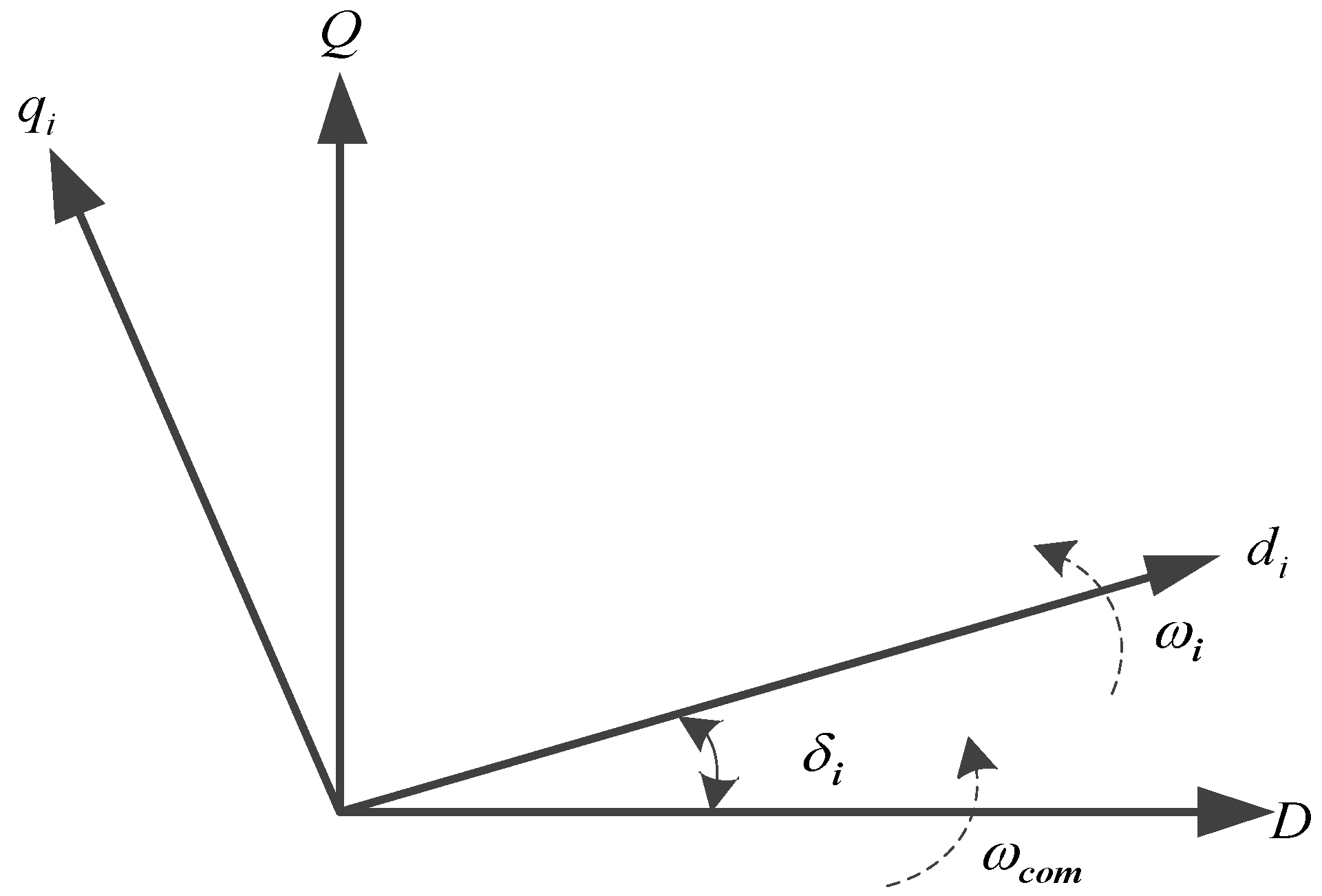
The model of each inverter is built on the individual reference frame
di-
qi rotating synchronously with the inverter output voltage angular speed
ωi. To build the whole model of the system, the reference frame of one of the DDER interfaced inverters is chosen as the common reference frame
D-
Q rotating at the frequency
ωcom, and all the other inverters are translated to this common reference frame using angle
δi, which is defined as the angle between an individual reference frame and the common reference frame, as shown in
Figure A1.
δi is given as:
where θ
i and θ
com are the rotating angle of individual reference frame and common reference frame, respectively.
Noted that in the following sections the three phase voltages and currents of each inverter model are represented as vectors in its individual di-qi frame and the network and loads are represented as vectors in the common D-Q frame.
Figure A1.
Reference frame transformation.
Figure A1.
Reference frame transformation.
(1) DDER Interfaced Inverter
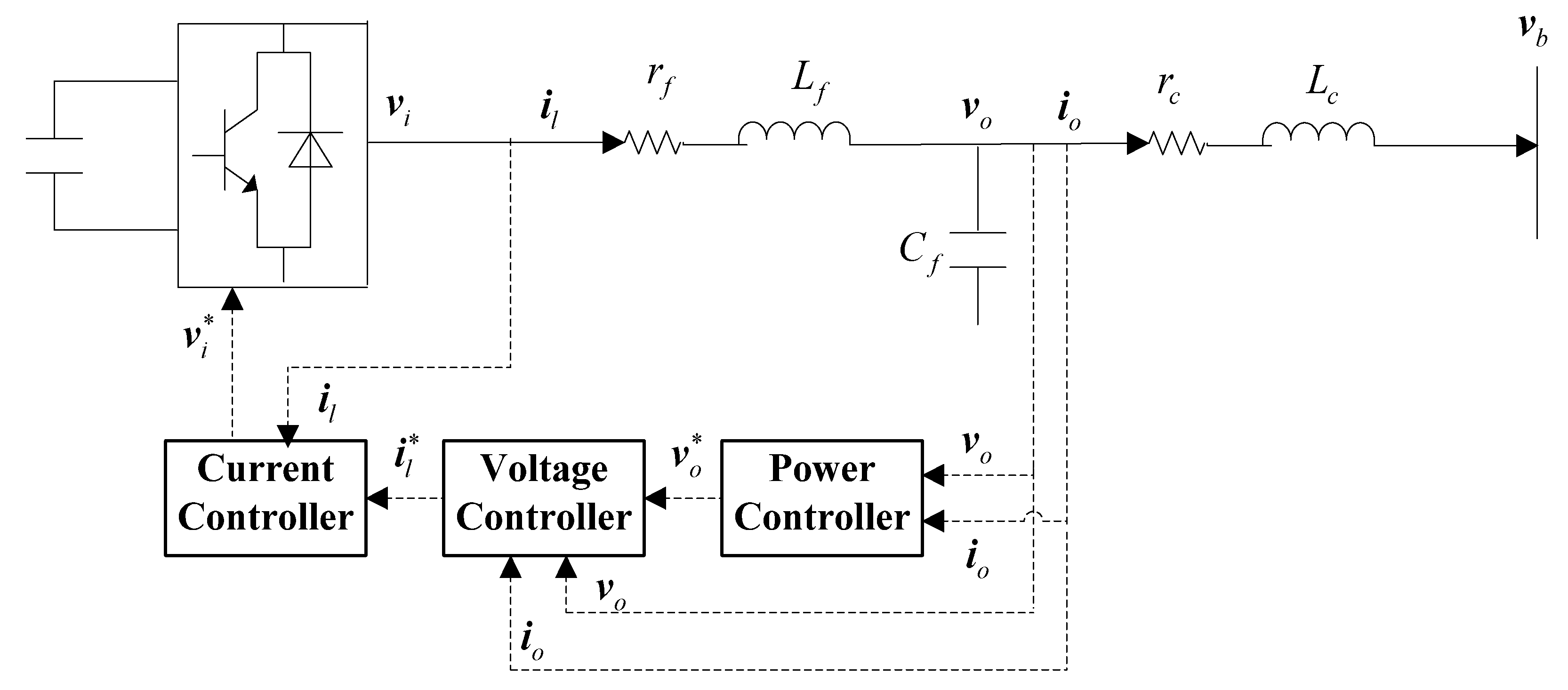
Figure A2 shows the power circuit and control block diagram of the DDER interfaced inverter. The inverter model includes power controller, voltage and current controller, LC filter and coupling inductor.
Figure A2.
Power circuit and control block diagram of DDER interfaced inverter.
Figure A2.
Power circuit and control block diagram of DDER interfaced inverter.
(a) Power Controller
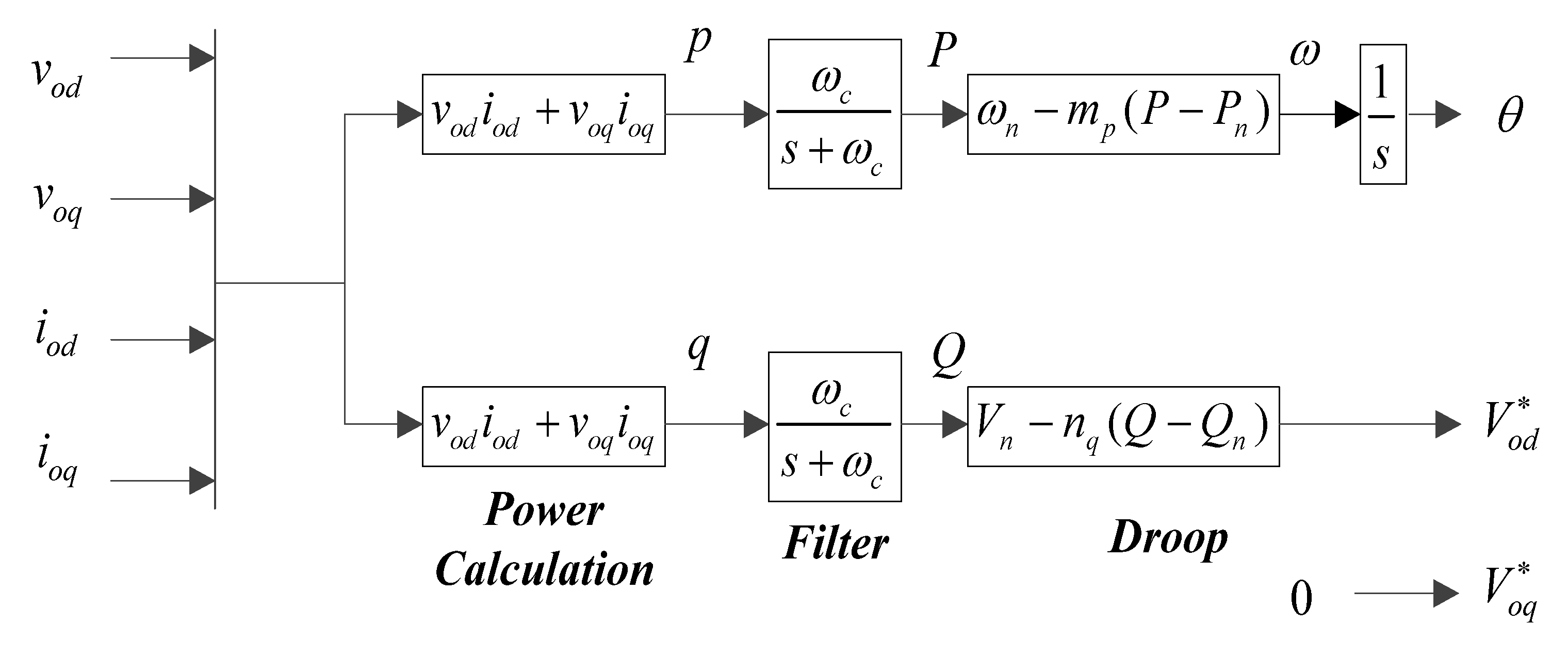
The power controller is used to generate the frequency and magnitude of the fundamental output voltage according to the droop characteristics set for the real and reactive powers. The block diagram of power controller is shown in
Figure A3.
Figure A3.
Block diagram of power controller.
Figure A3.
Block diagram of power controller.
First, the instantaneous active and reactive power components
p and
q are calculated from the measured output voltage and current as:
Second, the average active and reactive powers corresponding to the fundamental components are subjected to control actions, and they are obtained by means of a low-pass filter as:
where
ωc represents the cut-off frequency of the filter.
Finally, the fundamental voltage frequency
ω and
d-axis voltage magnitude reference
are set according to the droop characteristics and
q-axis voltage magnitude reference
is set to zero, as:
where
,
,
and
are the nominal frequency, voltage, active and reactive powers, respectively,
and
are the droop coefficients.
(b) Voltage Controller
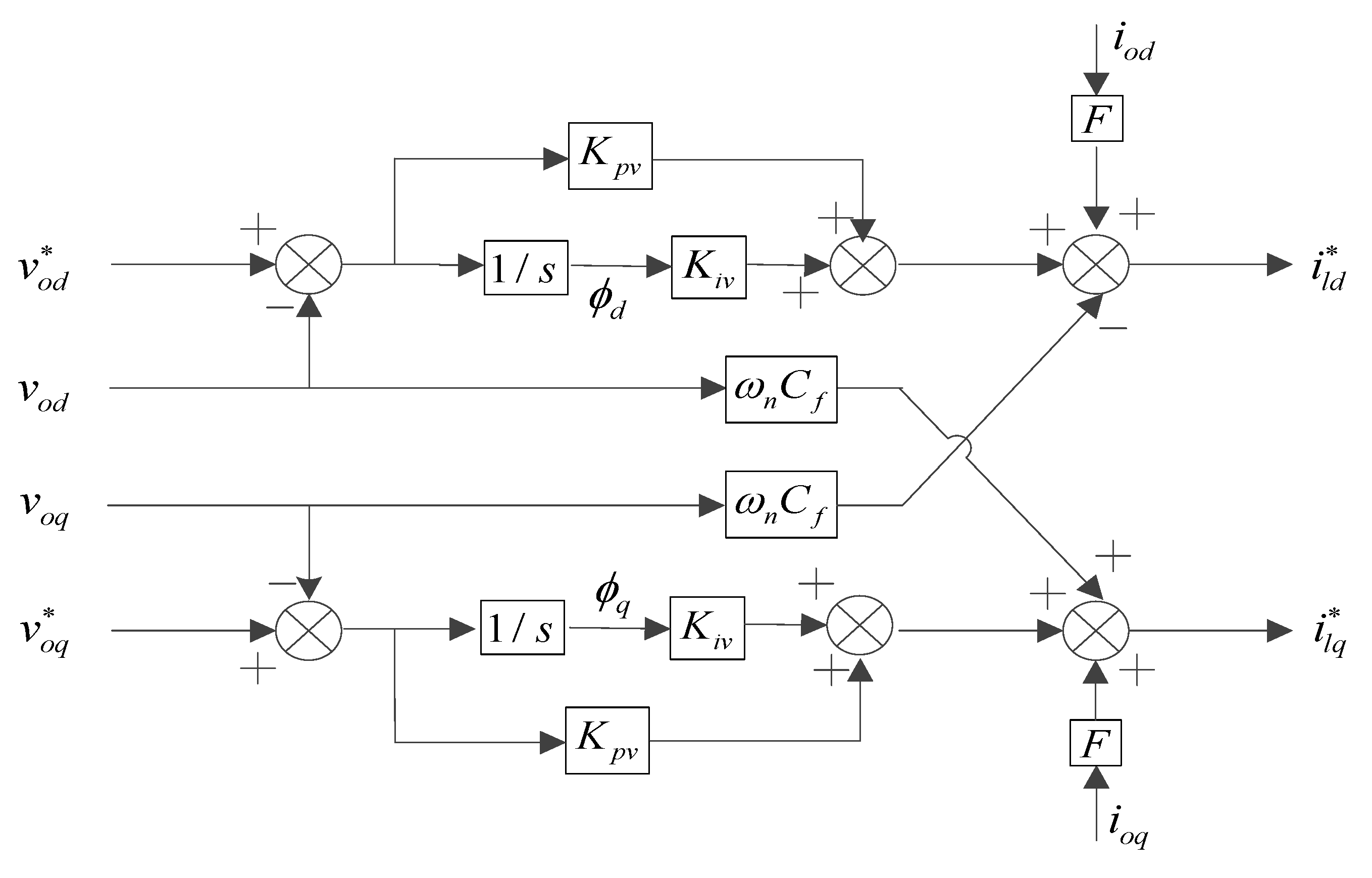
The voltage controller is used to synthesize the reference filter-inductor current vector by employing standard proportional-integral (PI) regulators with feedback and forward terms.
Figure A4 shows the block diagram of voltage controller. The corresponding state equations are given as:
Along with the algebraic equations:
where
,
are the proportional and integral gains, respectively, and
F is the feed forward gain.
Figure A4.
Block diagram of voltage controller.
Figure A4.
Block diagram of voltage controller.
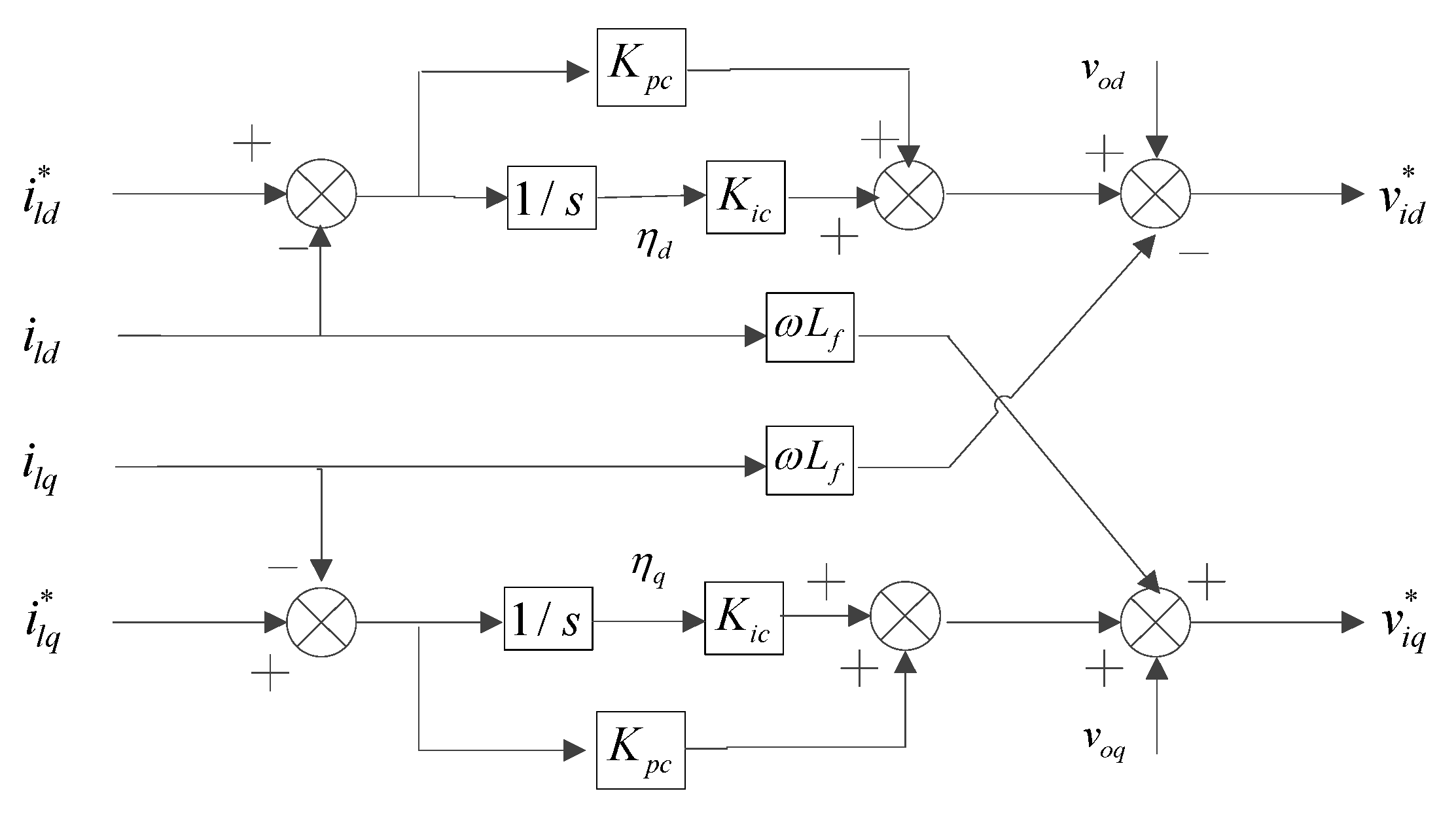
(c) Current Controller
The current controller is used to generate the command voltage vector which will be synthesized by a pulse-width-modulation (PWM) module of inverter. The structure of the PI current controller with feedback and forward control loops is shown in
Figure A5. The corresponding state equations are given as:
Along with the algebraic equations:
where
,
are the current controller parameters.
Both the voltage and current controllers are designed to reject high frequency disturbance and damp the output of the LC filter to avoid any resonance with the external network.
Figure A5.
Block diagram of current controller.
Figure A5.
Block diagram of current controller.
(d) LC Filter and Coupling Inductance
The LC filter and coupling inductance dynamics can be represented by the following equations, assuming that the inverter produces the demand voltage
.
where
,
and
are the resistance, inductance, and capacitance of the LC filter,
and
are the coupling resistance and inductance.
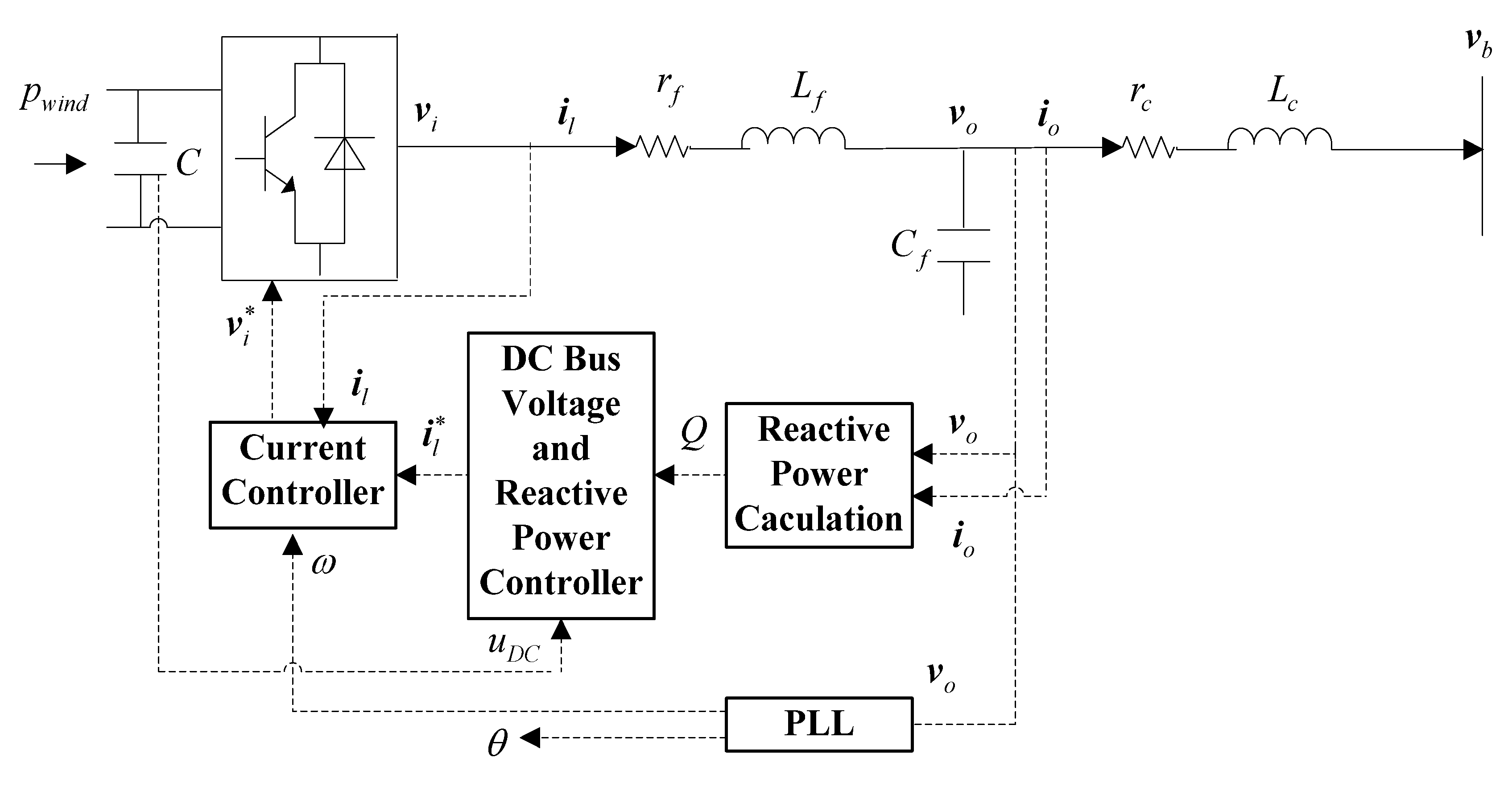
(2) WTG Interfaced Inverter
Figure A6 shows the power circuit and control block diagram of the wind turbine generator interfaced inverter. The inverter model includes phase-locked loop (PLL), DC bus capacitor, reactive power calculation, DC bus voltage and reactive power controller, current controller, LC filter and coupling inductor.
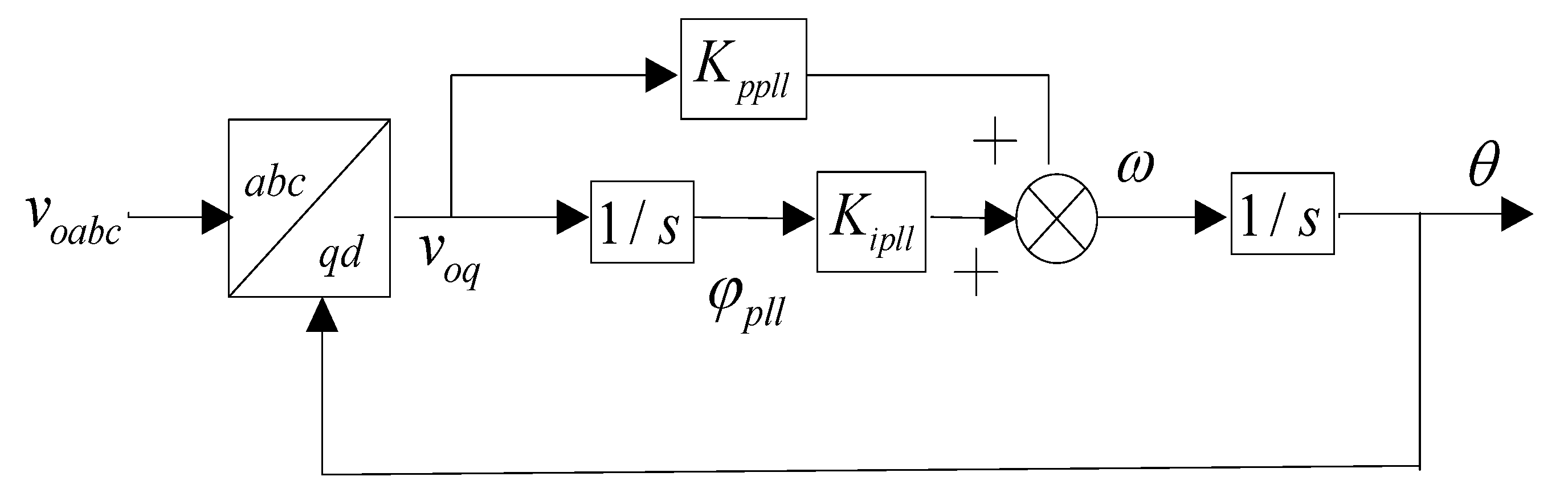
(a) PLL
The PLL form, shown in
Figure A7, is adopted to provide the rotation frequency
and reference angle
for the rotating frame of inverter output voltage.
is used to transfer the voltage and currents from
abc to
dq and vice versa. The PLL model can be written as:
Figure A6.
Power circuit and control block diagram of wind turbine generator interfaced inverter.
Figure A6.
Power circuit and control block diagram of wind turbine generator interfaced inverter.
Figure A7.
Block diagram of PLL.
Figure A7.
Block diagram of PLL.
(b) DC Bus Capacitor
The DC power
coming from the rectifier will be instantaneously transferred to the inverter DC terminal through a capacitor, and then to the grid through inverter. Assuming the inverter is lossless, the voltage of DC bus capacitor can be expressed as:
where
C is the DC bus capacitance.
(c) Reactive Power Calculation
The average reactive power
Q can be calculated as:
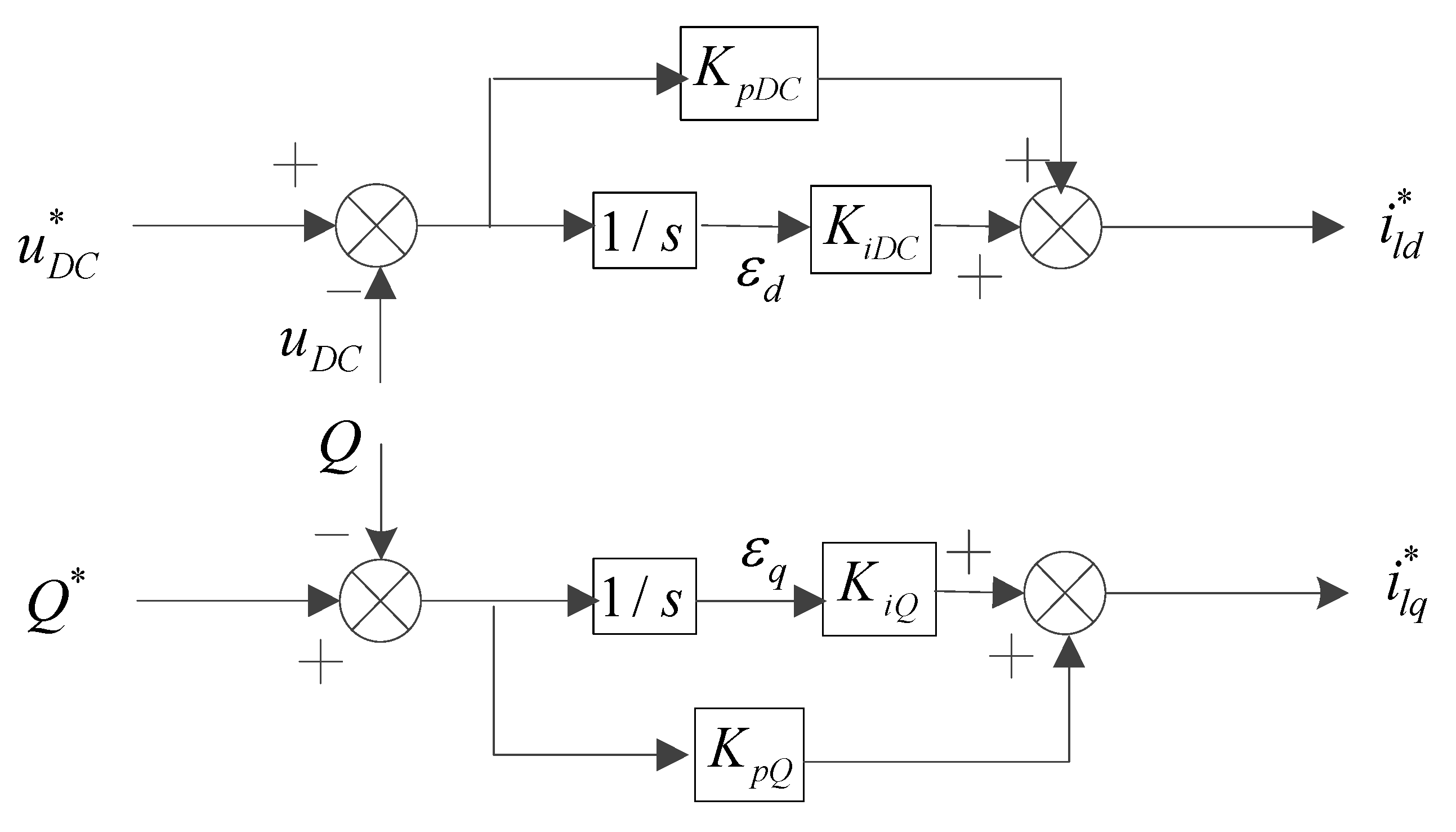
(d) DC Bus Voltage and Reactive Power Controller
The DC bus voltage and reactive power controllers are used to set the
d- and
q-axis current reference to the inner current control loops, respectively.
Figure A8 shows the block diagram of this controller. The corresponding state equations are given as:
Along with the algebraic equations:
where
,
,
and
are the proportional and integral gains of DC bus voltage and reactive power controller,
and
are the references of DC bus voltage and output reactive power of inverter (
is usually set to zero).
Figure A8.
Block diagram of DC bus voltage and reactive power controller.
Figure A8.
Block diagram of DC bus voltage and reactive power controller.
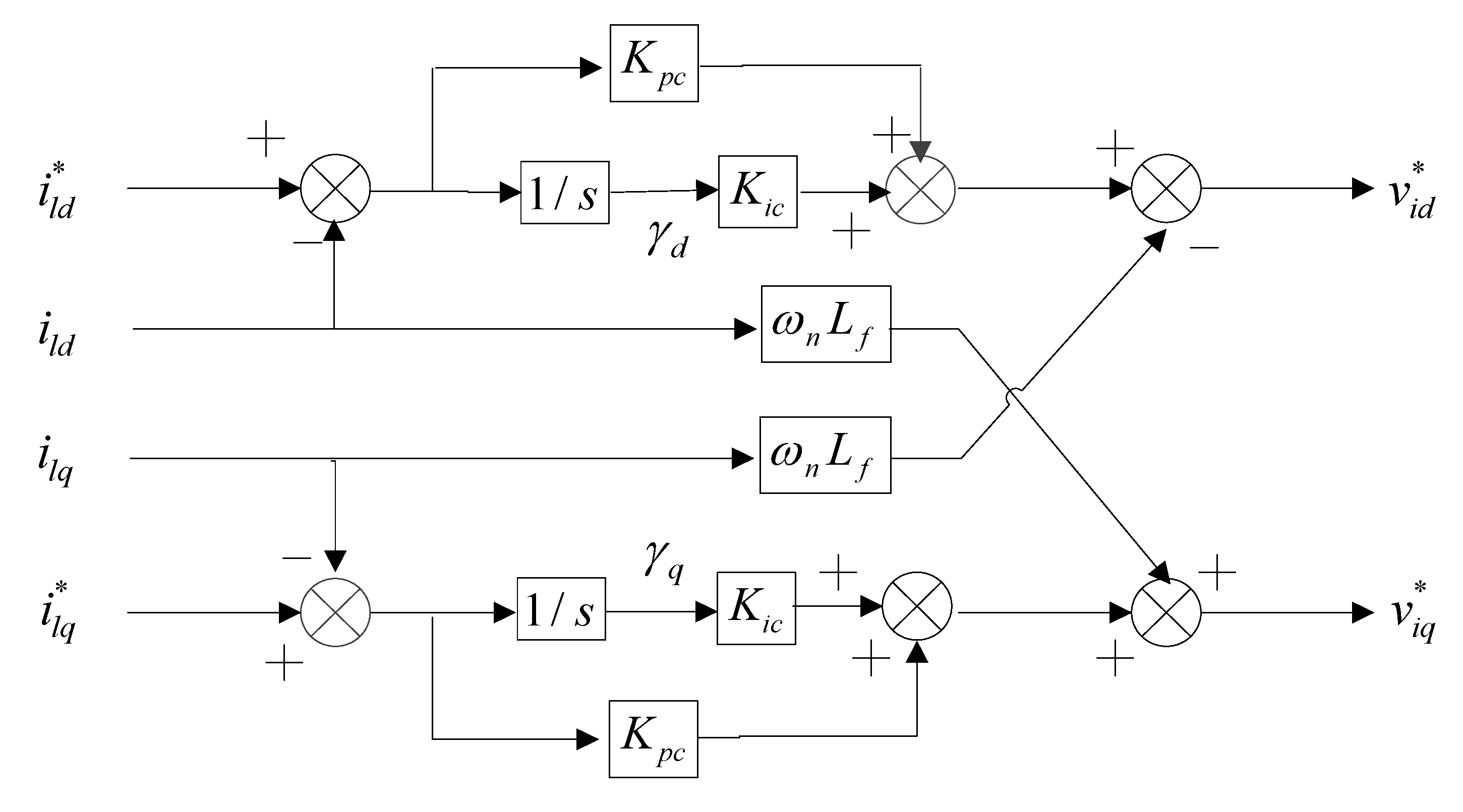
(e) Current Controller
The current controller which is essential for power quality improvement is utilized to provide the voltage reference of the inverter. The structure of the PI current controller with feedback and forward control loops is shown in
Figure A9. The corresponding state equations are given as:
Figure A9.
Block diagram of current controller.
Figure A9.
Block diagram of current controller.
Along with the algebraic equations:
where
,
are the current controller parameters.
(f) LC Filter and Coupling Inductance
The differential equations describing the LC filter and coupling inductance are unanimous to Equation (A9) and will not be repeated here.
(3) PV and ESS Interfaced Inverters
The configuration of PV and ESS interfaced inverters are analogous to WTG and will not be repeated here.
(4) Coordinate Transformation
To link the inverters with the network, the output current
and
of each inverter expressed on the individual reference frame should be transformed to the common reference frame using the following transformation:
Similarly, the input voltage
and
of each inverter expressed on the common reference frame should be conversely transformed to individual reference frame using the following transformation:
(5) Network Model
On the common reference frame, the state equations of line current of line
i connected between node
j and
k can be expressed as:
where
and
are the resistance and inductance of line
i.
(6) Load Model
The state equations of a RL load connected at node
i can be expressed as:
where
and
are the resistance and inductance of load
i.