1. Introduction
The interest in vertical axis wind turbines (VAWTs) as an alternative to the conventional horizontal axis wind turbines (HAWTs) has been growing in recent years [
1]. This is due to the potential of VAWTs to decrease the cost of wind energy [
2,
3]. VAWTs have several advantages over HAWTs: the generator of a VAWT can be located at the ground level, therefore excluding the concerns over the mass and size of the generator. The advantage of the lower center of mass (compared to HAWTs) is very important for floating platforms [
4]. Additionally, the yawing mechanism is excluded for VAWTs, since they are omni-directional. Thus, the simplicity of the concept with only a few moving parts is one of the main advantages of VAWTs over HAWTs.
The complex aerodynamics of VAWTs imposes significant challenges on the simulation models. The flow velocity at the blades of the VAWT changes constantly during the turbine rotation, which causes the angle of attack to change during every revolution. The magnitude of the variation of the angle of attack increases with the decreased turbine tip speed ratio (TSR). At low TSRs, the blades of the VAWT experience the event of dynamic stall, which is associated with the rapid decrease in the lift and the increase in the drag force, reducing the torque on the turbine. At high TSRs, the flow velocity when passing through the turbine is decreased more than at low TSRs, and therefore, the flow expansion is prevailing at high TSRs.
The simulation models for VAWTs can be divided into three groups. The first group includes the finite element method (FEM) or the finite volume method (FVM), which are used to solve the Navier–Stokes equations within the commonly-available software for computational fluid dynamics (CFD). The second method is based on the vorticity equation, and the models are usually referred to as vortex models. The third method is based on the momentum conservation principle, and one of the most common and advanced momentum models is the double multiple streamtube model. The overview of the aerodynamic models for VAWTs can be found in [
5,
6,
7]. A two-dimensional (2D) vortex model combined with the Leishman–Beddoes-type dynamic stall model is used in this study. The model combines the vorticity equation with experimental data, which results in the high computational speed of the model. This model gives the flow velocity field and is time dependent.
There is a lack of experimental data on the blade forces during one revolution for VAWTs. A series of the experiments were conducted by the Sandia National Laboratories in the 1980s, where VAWTs with curved blades (Darrieus turbines) were operated at open sites [
8,
9,
10]. Other measured data concern small vertical axis turbines operating in wind tunnels or towing tanks with low operational Reynolds numbers [
11,
12]. Since the force coefficients are dependent on the Reynolds number, the aerodynamics of large turbines are different from the aerodynamics of turbines operated in wind tunnels or towing tanks. Thus, due to high Reynolds numbers, the measured data from the Sandia National Laboratories are still used for the validation of simulation models [
13,
14,
15,
16].
This study assesses measurements from 2014 on a straight-bladed VAWT, which operates at an open site with the average Reynolds number of
[
17,
18]. A study on the power coefficient (
) of this VAWT from 2011 has shown that the turbine reaches its maximum
of 0.29 at the TSR of 3.3 [
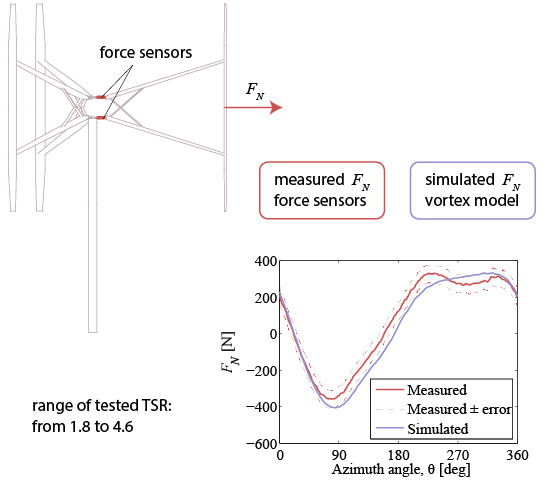
19]. However, the turbine diameter has increased from 6 to 6.5 m after mounting the load cell assembly, and the power coefficient is expected to be slightly different for the modified turbine as the turbine solidity has decreased. New experimental data on the normal forces on this VAWT are presented. The goal of the study is to describe the simulation model and to validate it against the experimental data. The normal forces are compared for the range of TSRs from 1.8 to 4.6, covering the dynamic stall region and the region of high flow expansion. The results and the capability of the model are analyzed.
2. Experimental Data
The measurement data used in this study are obtained from the 12-kW VAWT located outside Uppsala, Sweden. The experimental method and the obtained force data are described in detail in [
17,
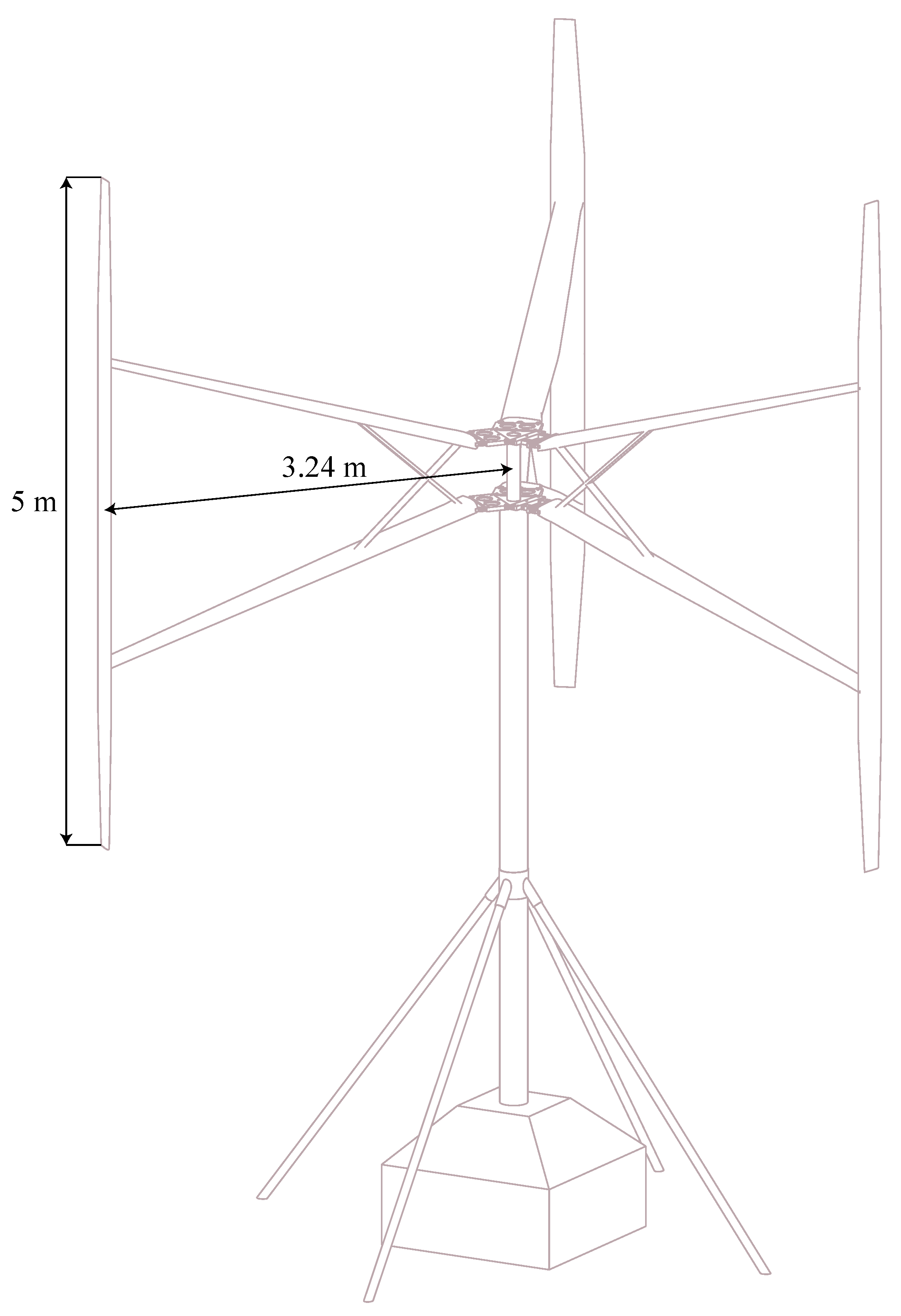
18]. It follows that the measured normal force was periodic and consistent, while the tangential force response was highly disturbed by the turbine dynamics. Hence, only the normal force measurements can be considered suitable for usage in this validation. The studied VAWT is a 3-bladed H-rotor turbine with a radius of 3.24 m and a blade length of 5 m;
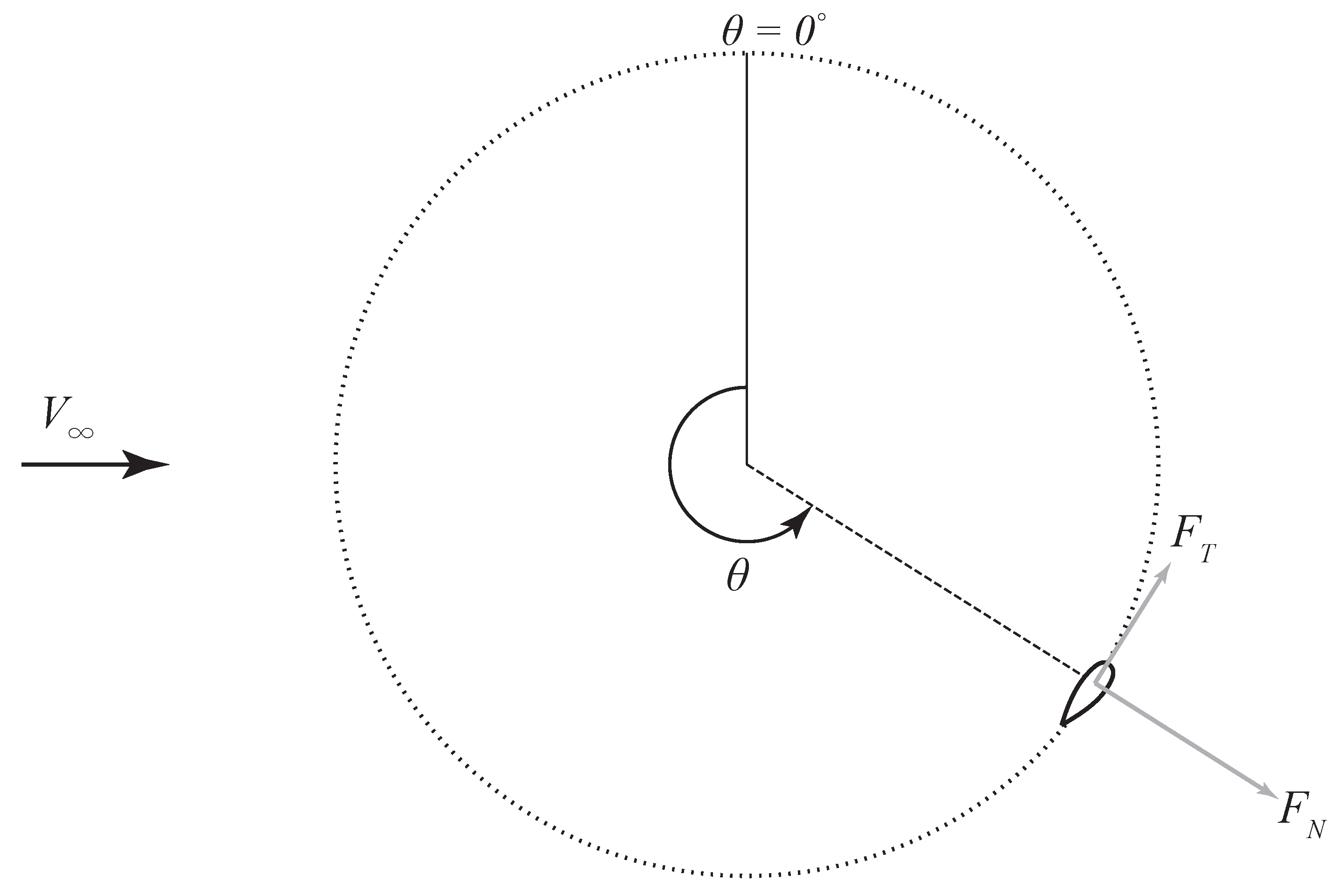
Figure 1. The blades are pitched outwards 2 degand have the NACA0021profile with a chord length of 0.25 m at the middle of the blade. The turbine with assembled force sensors is shown in
Figure 2 and
Figure 3. The sensors are single-axis load cells, which measure tension and compression at a point load. The rotational speed of this turbine can be kept at a constant level [
17,
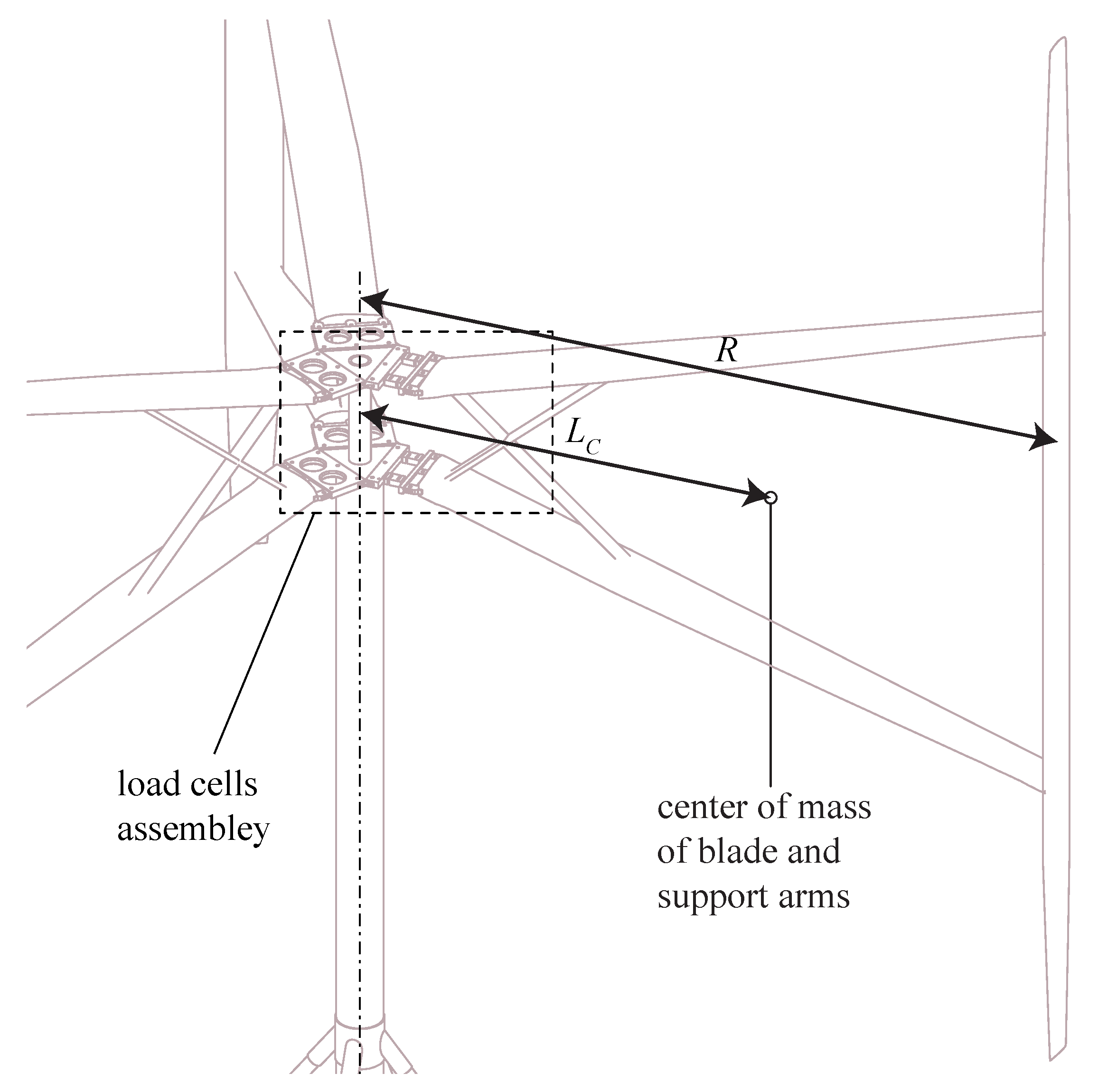
19], and the normal force is estimated using the notations from
Figure 2 and
Figure 3 as the following:
where
is the centrifugal force:
Figure 1.
The vertical axis wind turbine (VAWT) used for the experiment.
Figure 1.
The vertical axis wind turbine (VAWT) used for the experiment.
Figure 2.
Load cells installed on the VAWT.
Figure 2.
Load cells installed on the VAWT.
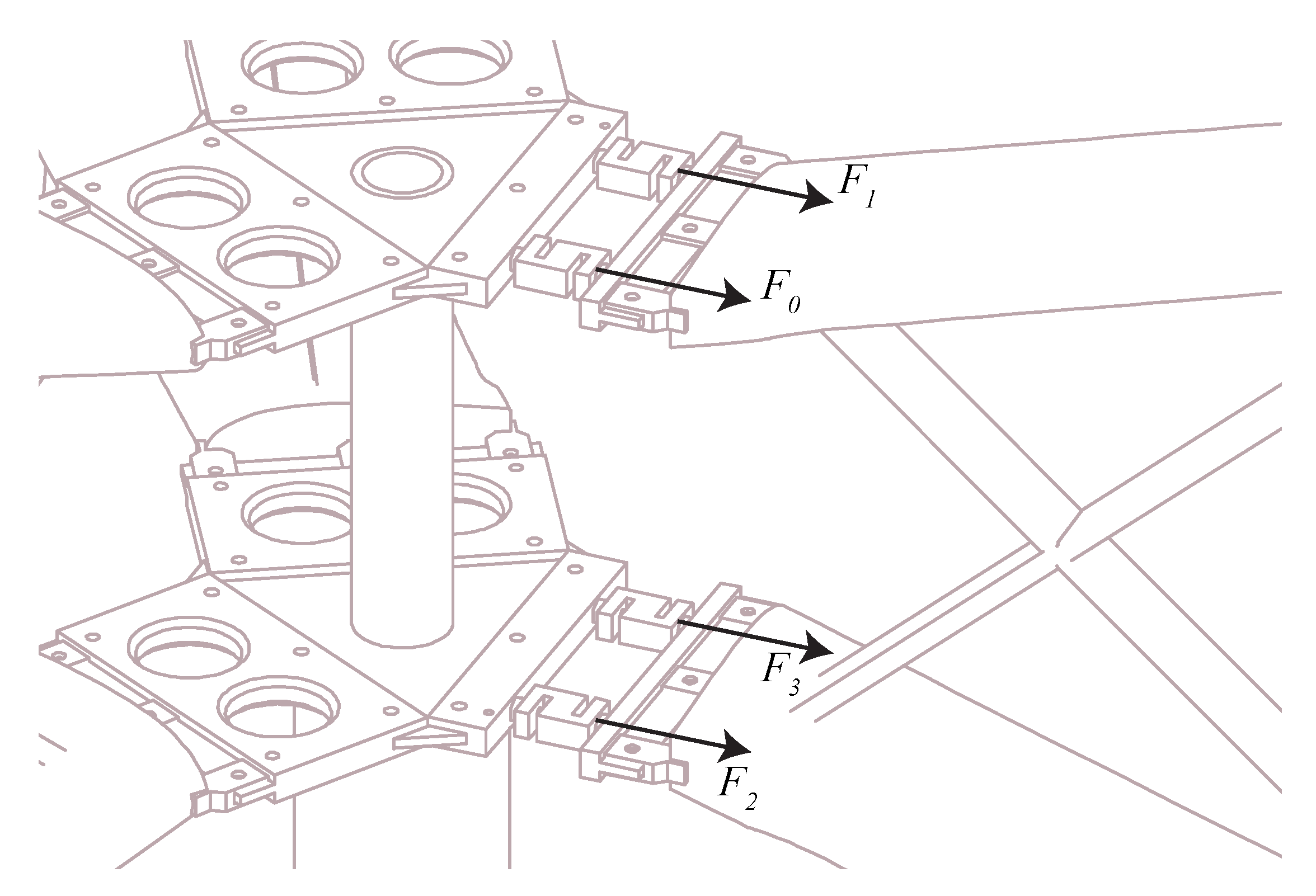
Figure 3.
The assembly of the load cells. The notation of the measured forces.
Figure 3.
The assembly of the load cells. The notation of the measured forces.
Here, is the mass of the blade and support arms, Ω is the turbine rotational speed and is the distance from the axis of rotation to the center of mass of the blade assembled with the support arms. , , and are the measured forces.
Due to varying weather conditions, the force measurements were analyzed only for times with steady wind flow conditions. The relative standard deviation (RSD) was used to quantify wind flow variations:
where
denotes the average value of variable
x.
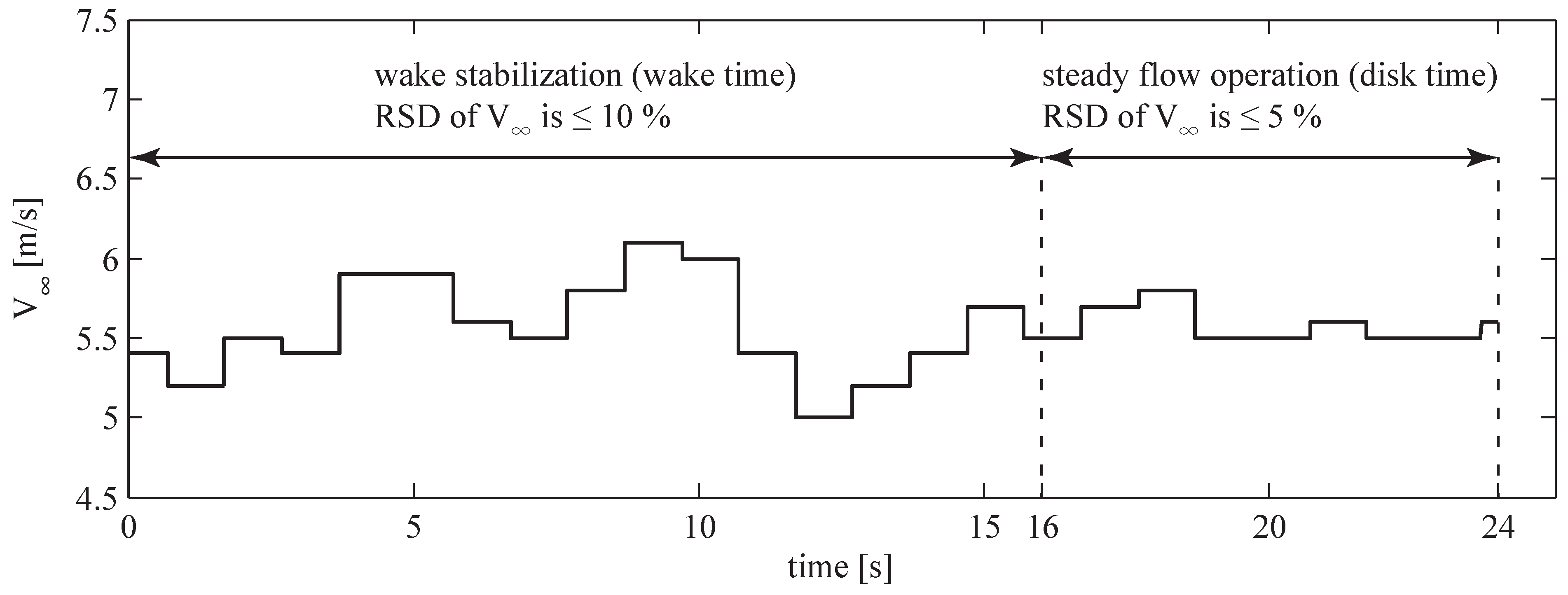
The measured data were divided into 24 s-long bins: 16 s to stabilize the turbine wake (“wake time”, corresponding to 10 revolutions at 40 rpm) followed by 8 s of steady flow operation (“disk time”, 5 revolutions at 40 rpm). Wind flow was considered as steady for bins with the RSD of the asymptotic wind velocity
of
,
and the RSD of wind direction
of
. This definition of the steady wind flow conditions is documented in [
18]. Variations of the wind speed during the steady conditions are illustrated in
Figure 4.
Figure 4.
Allowed variations of the asymptotic wind velocity inside a bin with the steady wind flow conditions.
Figure 4.
Allowed variations of the asymptotic wind velocity inside a bin with the steady wind flow conditions.
The normal force during one revolution is obtained as the average response over 5 revolutions with steady wind flow. The operational TSR is estimated as:
where Ω is the turbine rotational speed. The average values of Ω and
are taken taken over time with steady wind flow.
The analysis of the measurement accuracy has shown that the maximum error of the measured normal force is a function of the turbine rotational speed:
where
is the rotational speed in
. For the details regarding the measurement accuracy, the reader is referred to [
17,
18]. The air density ρ is calculated for the measured air temperature, pressure and humidity according to [
17]. The kinematic viscosity
ν is estimated as the function of the measured air temperature [
20].
4. Results and Discussion
This section presents the comparison of the simulation results against the measured data at different operational conditions. The discussions regarding the performance of the model are found at the end of this section.
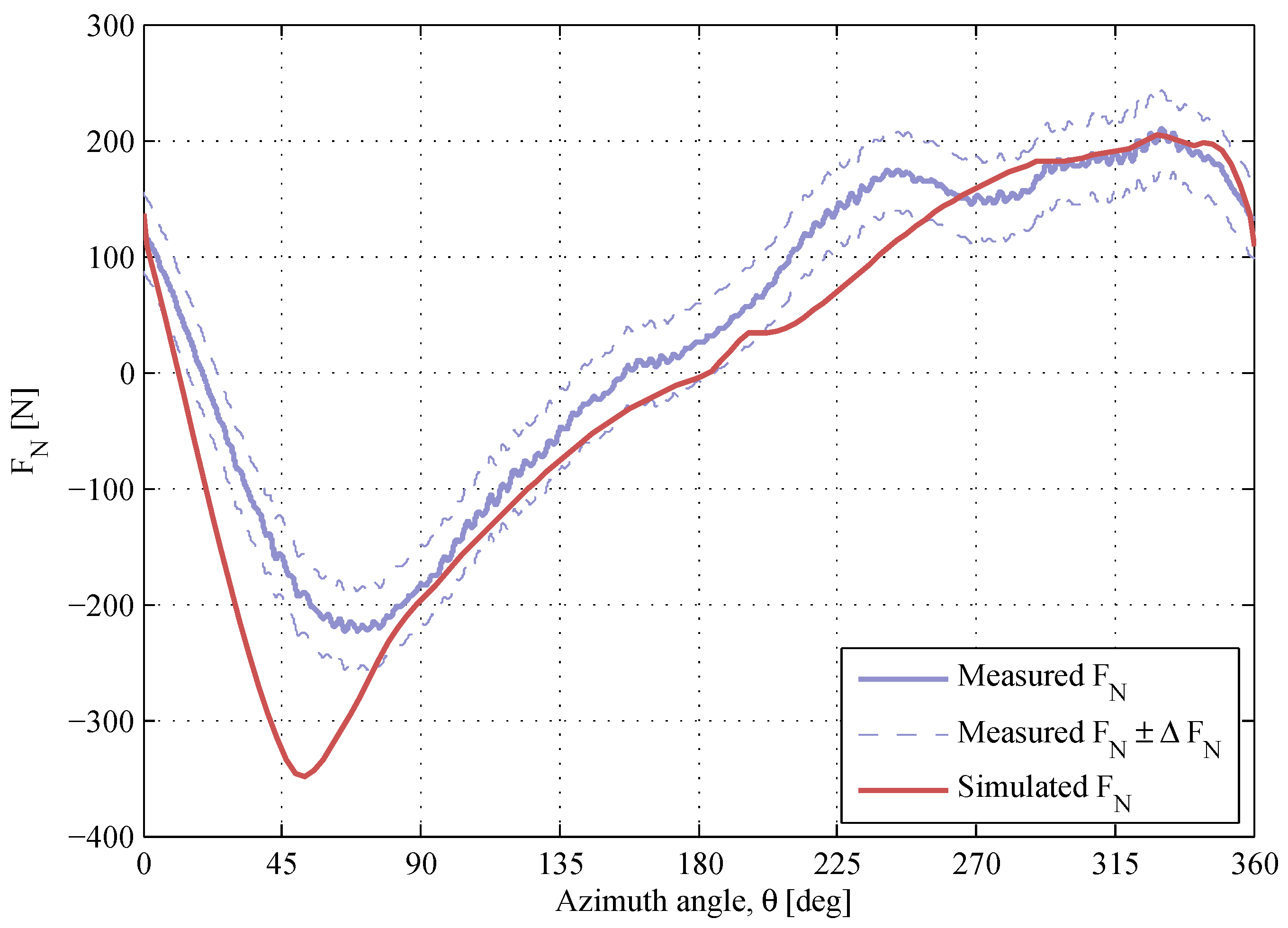
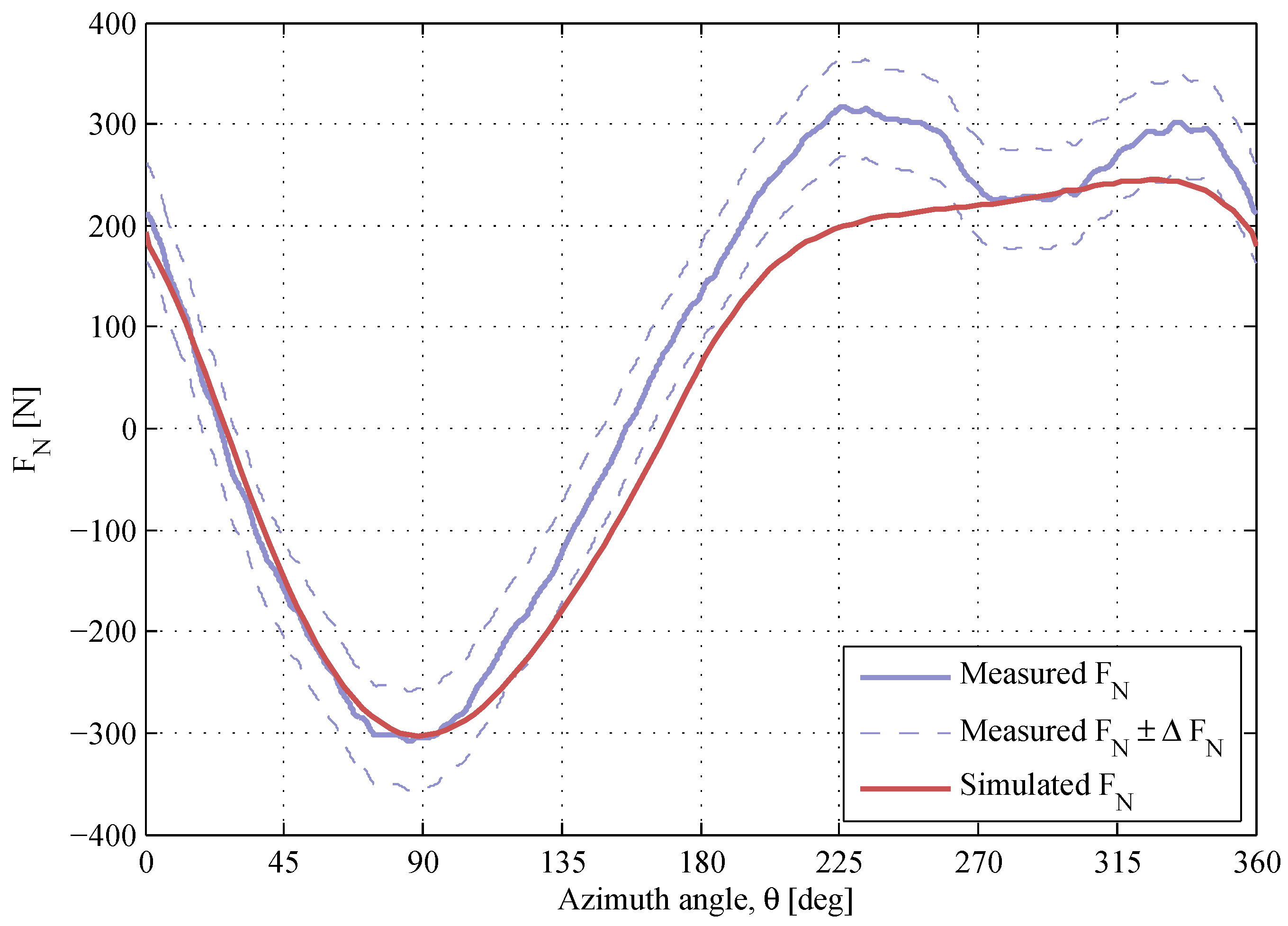
The normal force response at low TSRs is presented in
Figure 9,
Figure 10 and
Figure 11. The maximum magnitude of the
-response at the upwind is overestimated at
and
, and the shape of the modeled
-curve at the downwind deviates from the measurements. The authors presume that the difference between the simulated and the measured values at these low TSRs is due to high magnitudes of the angle of attack. The accuracy of the dynamic stall model decreases with increased angle of attack, which is shown in [
25,
29], where the dynamic stall model was tested against wind tunnel data for a single blade. As the angle of attack increases with decreased TSR, it is expected that the accuracy of the dynamic stall model should be limited at low TSRs. There is a positive offset of
at
, which is mainly due to the blade pitch angle, which was chosen to even out the magnitude of α between the upwind and the downwind regions [
18]. The value of the simulated
-offset is close to the measured one.
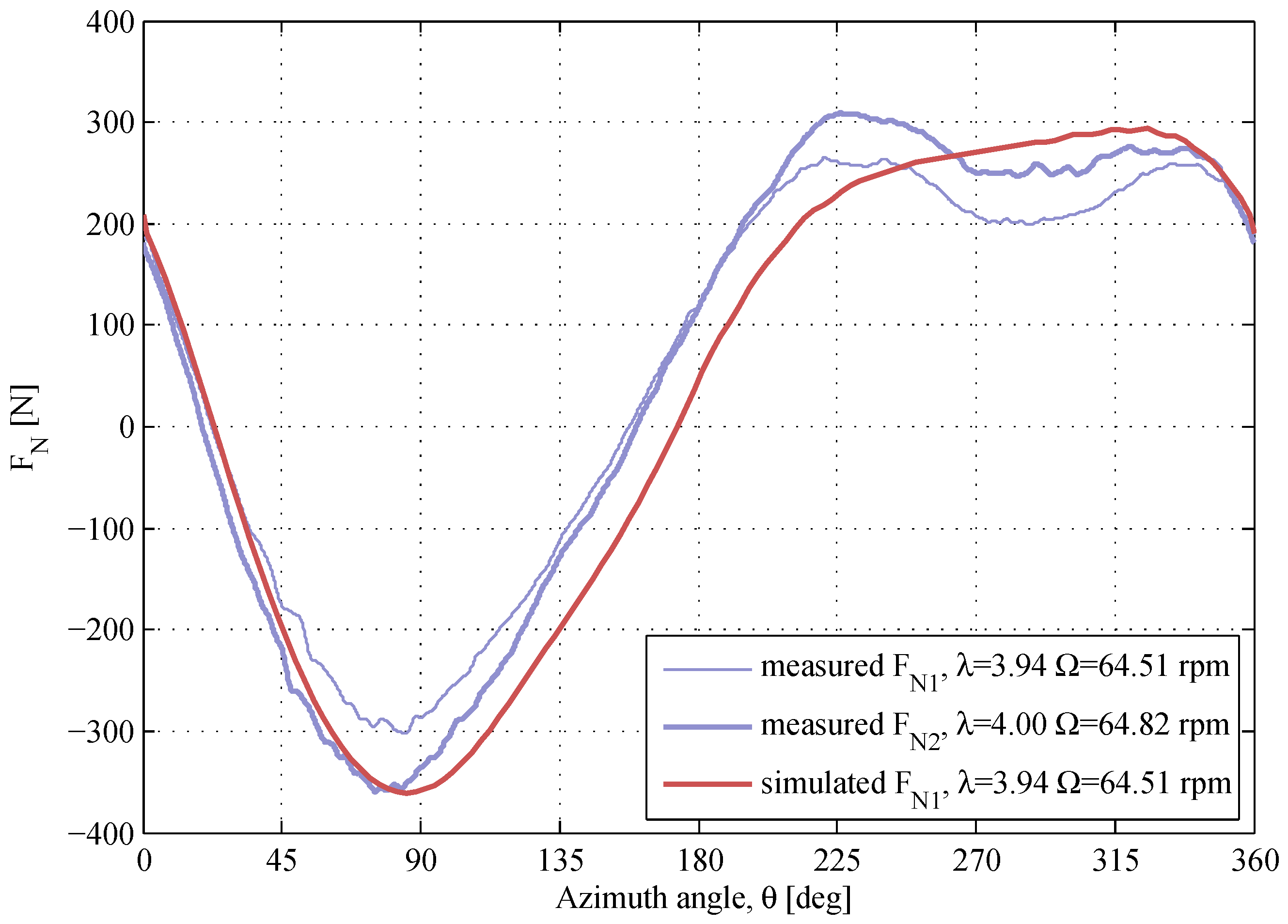
Figure 12 shows the
-response at
for two different rotational speeds. The maximum magnitude of the
-curve is overestimated for
, similarly to the overestimation in
Figure 9 and
Figure 10. The
-response at
for
and
is presented in
Figure 13. The results at these conditions are very similar to the results at
, although the model agrees better with experimental data at
. The measured
-response at
at
has a drop in the downwind region at
, which is not predicted by the model. The discussions regarding the
-drop are found further in this section.
Figure 9.
The normal force at , . The air density and the kinematic viscosity are and .
Figure 9.
The normal force at , . The air density and the kinematic viscosity are and .
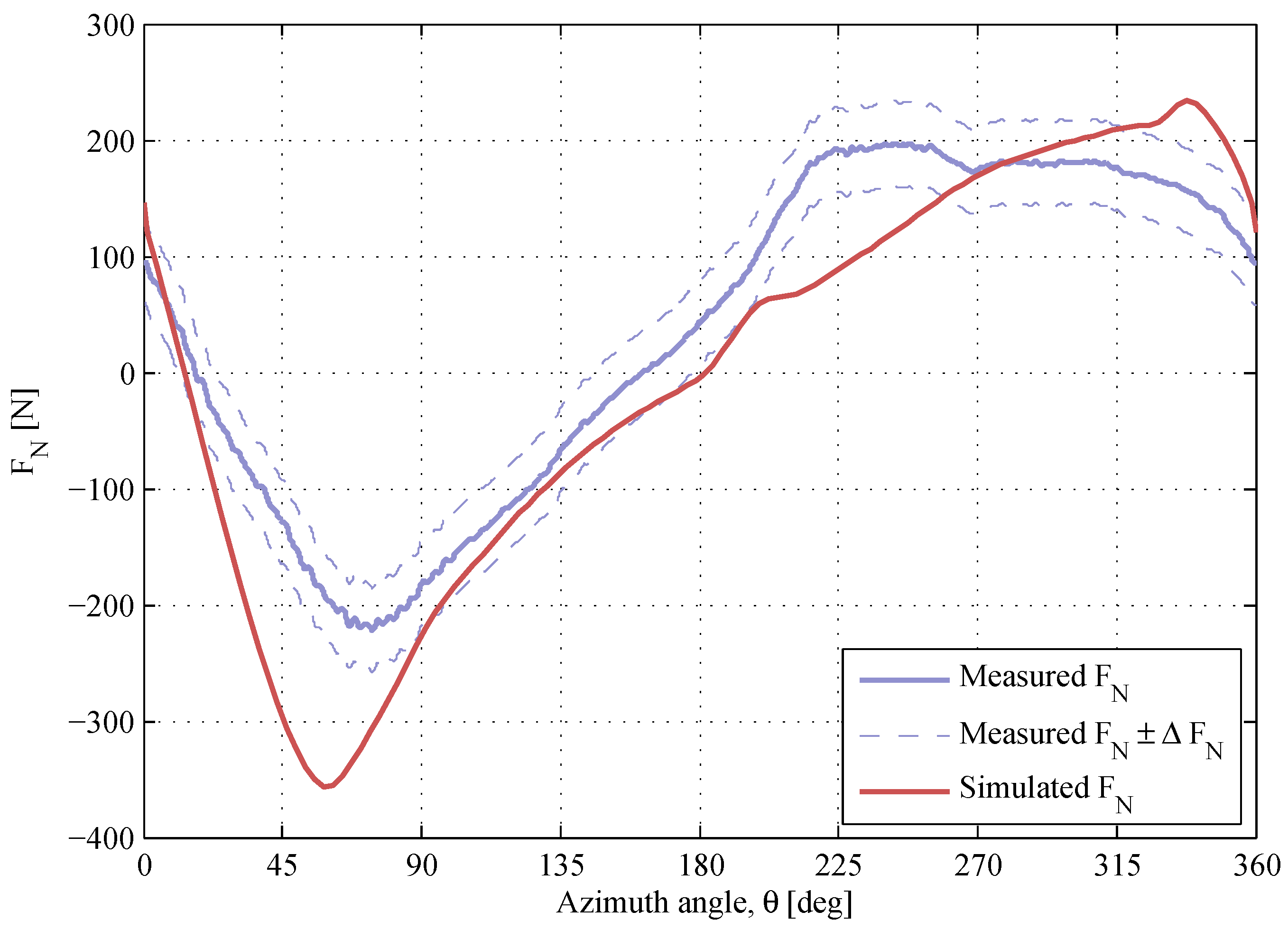
Figure 10.
The normal force at , . The air density and the kinematic viscosity are and .
Figure 10.
The normal force at , . The air density and the kinematic viscosity are and .
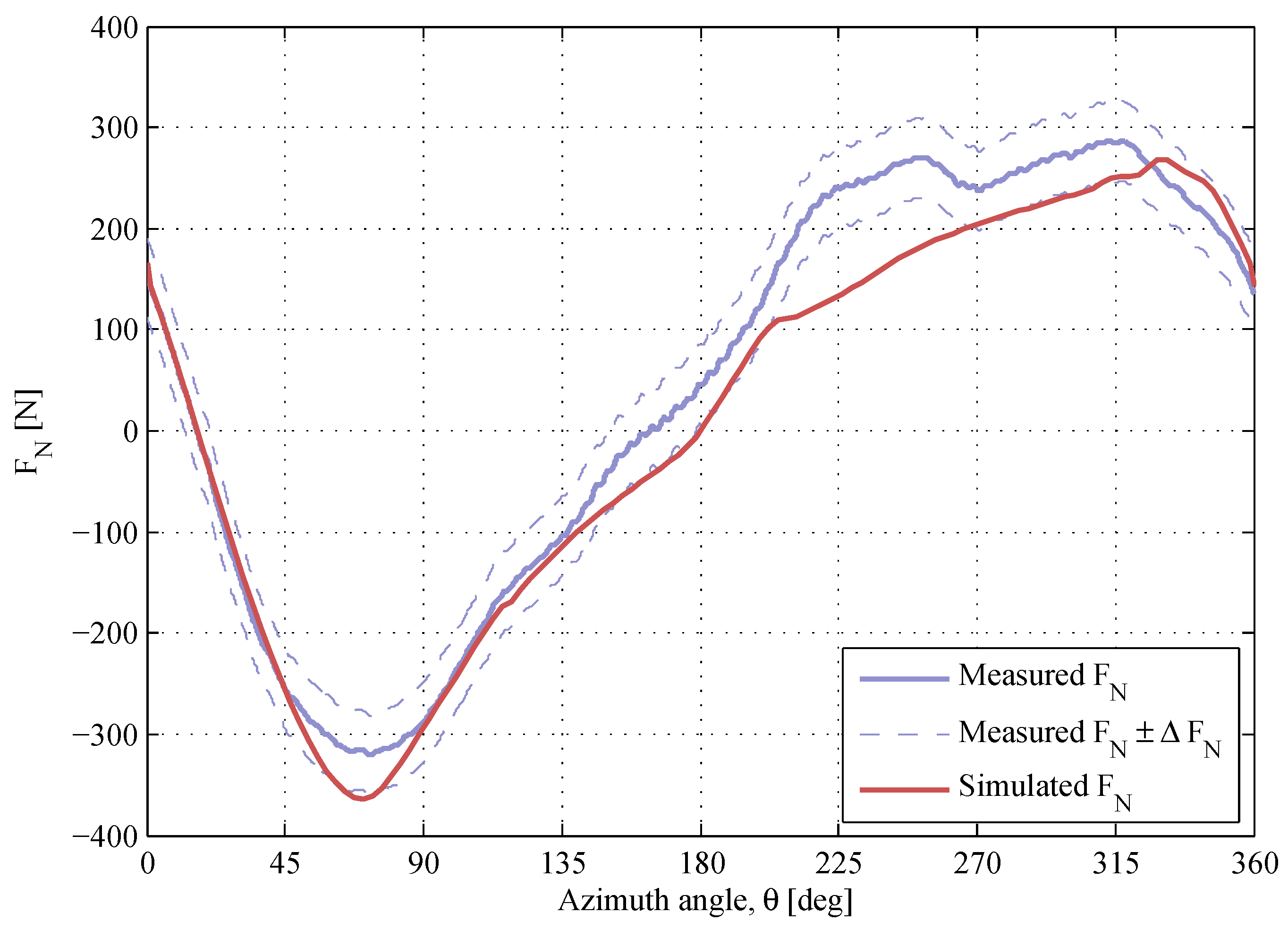
Figure 11.
The normal force at , . The air density and the kinematic viscosity are and .
Figure 11.
The normal force at , . The air density and the kinematic viscosity are and .
Figure 12.
The normal forces at similar λ and different Ω. The air densities and the kinematic viscosities are , and , .
Figure 12.
The normal forces at similar λ and different Ω. The air densities and the kinematic viscosities are , and , .
Figure 13.
The normal forces at the similar λ and different Ω. The air densities and the kinematic viscosities are , and , .
Figure 13.
The normal forces at the similar λ and different Ω. The air densities and the kinematic viscosities are , and , .
As the TSR increases, the maximum magnitude of the angle of attack decreases and the prediction of the blade forces becomes more accurate. The
-response at
is shown in
Figure 14. The simulated data are in a good agreement with the measured data except the
-drop at
, which is missed by the model. The
-response at
for two different rotational speeds is shown in
Figure 15. For both
-curves, the
-drop in the downwind is not predicted.
Figure 14.
The normal force at , . The air density and the kinematic viscosity are and .
Figure 14.
The normal force at , . The air density and the kinematic viscosity are and .
Figure 15.
The normal forces at the similar λ and different Ω. The air densities and the kinematic viscosities are , and , .
Figure 15.
The normal forces at the similar λ and different Ω. The air densities and the kinematic viscosities are , and , .
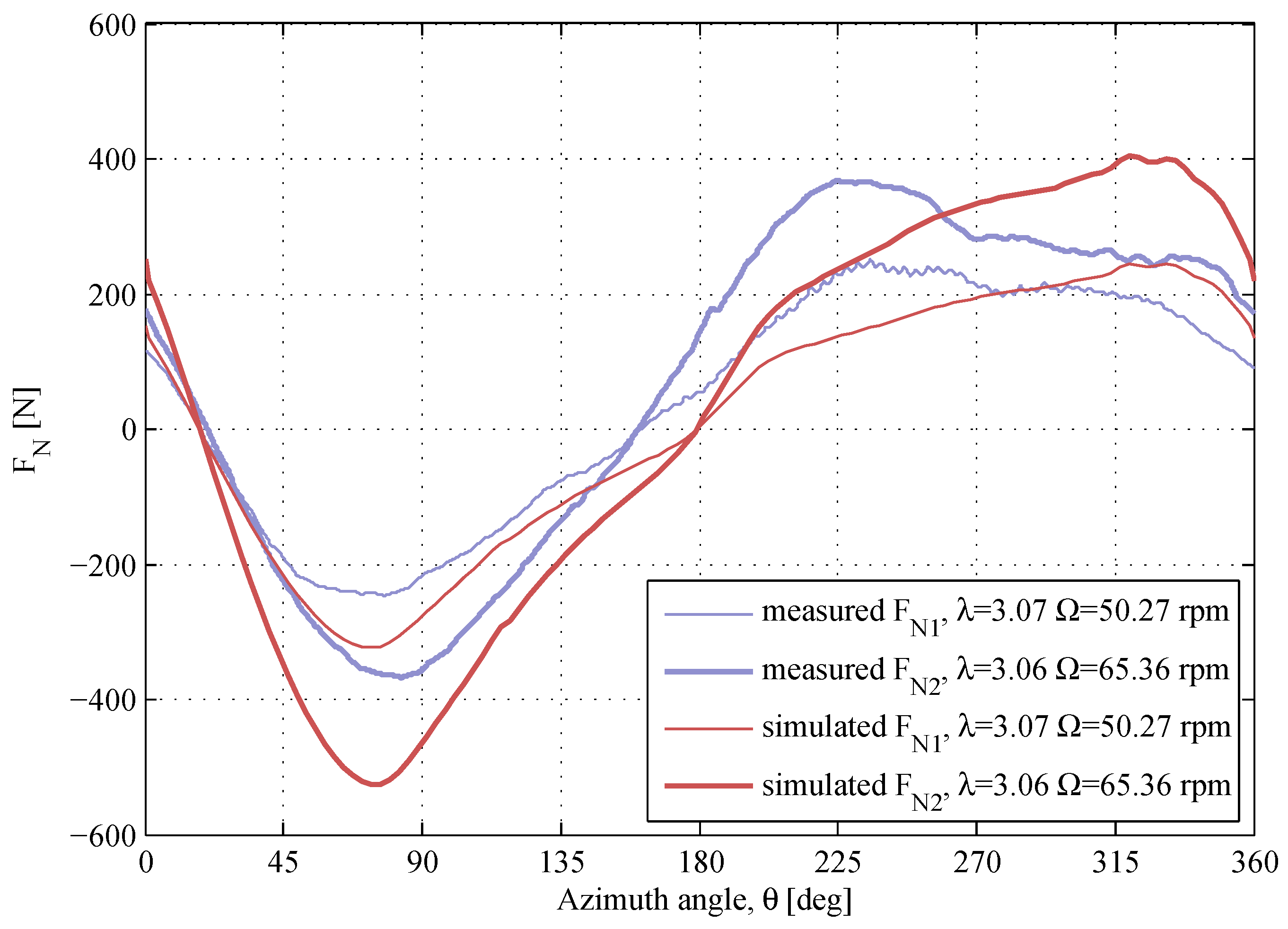
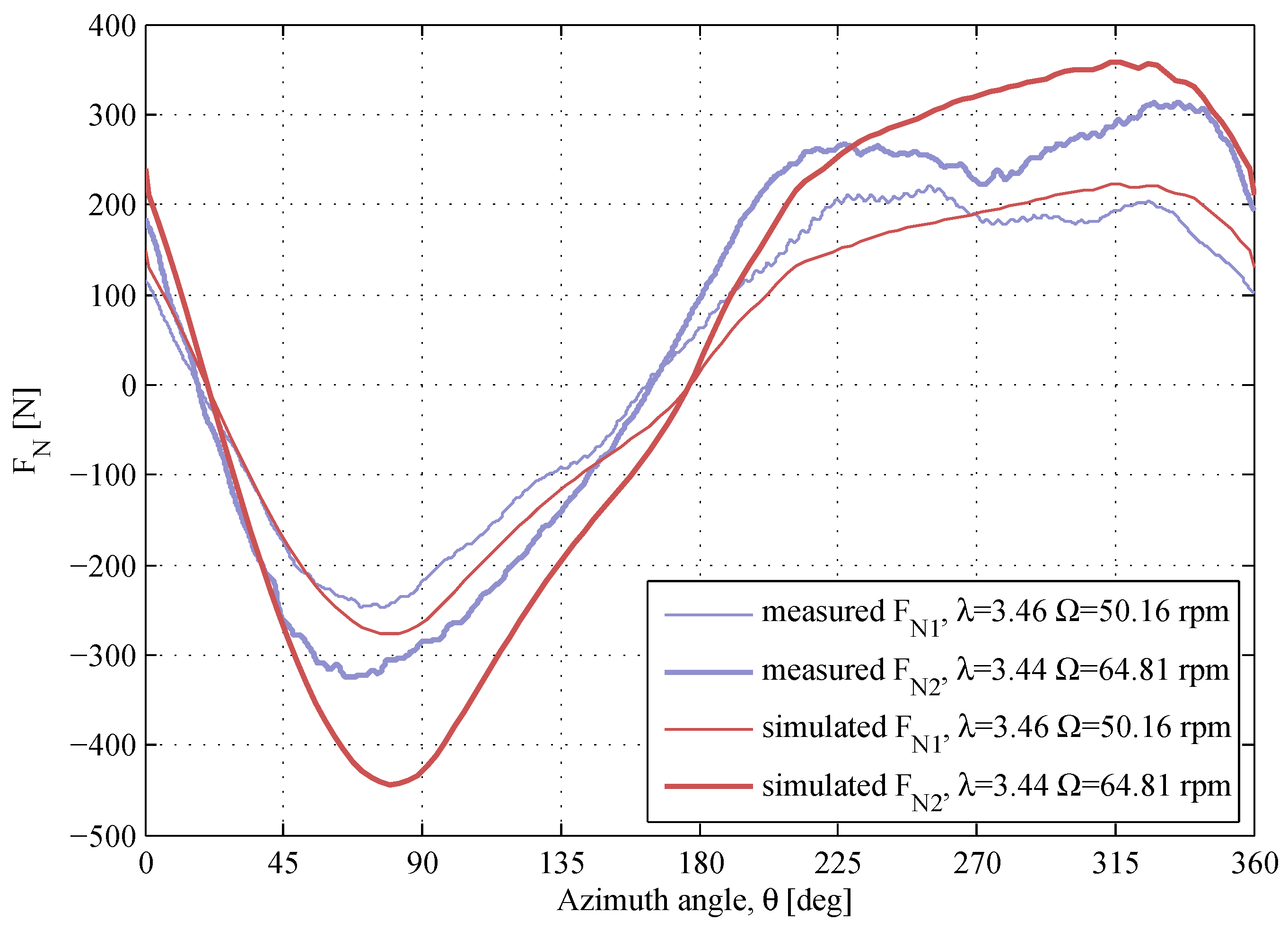
Two sets of the experimental data with almost identical operational conditions are compared against the simulated results in
Figure 16. The shape of the measured
-curves is matching, but the magnitudes are slightly different. The maximum difference in the measured
magnitudes is
, though the TSR is almost identical (
and
), and the difference in the air density is minor (see the notation to
Figure 16). The model shows a close agreement, except that the
-drop at the downwind is not present.
Figure 16.
The normal forces for two different sets of data with almost identical λ and Ω. The air densities and the kinematic viscosities are , and , .
Figure 16.
The normal forces for two different sets of data with almost identical λ and Ω. The air densities and the kinematic viscosities are , and , .
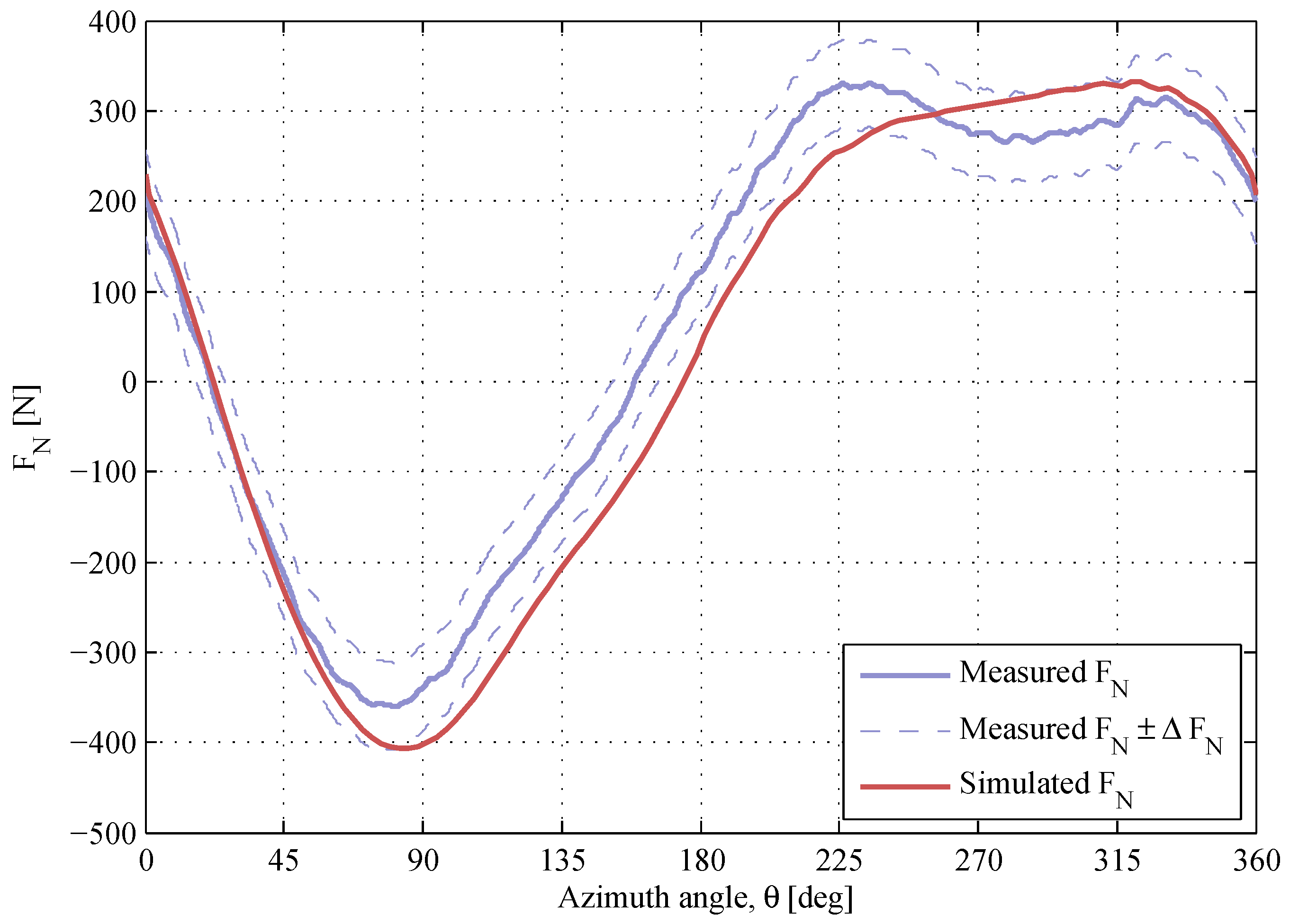
The results at the TSR of 4.6 are presented in
Figure 17. At this high TSR, the flow expansion strongly affects the turbine aerodynamics. The model underestimates the maximum magnitude of the
-response in the downwind region. The aforementioned
-drop at the downwind is clearly observed at
, and the model misses it.
Figure 17.
The normal force at , . The air density and the kinematic viscosity are and .
Figure 17.
The normal force at , . The air density and the kinematic viscosity are and .
General Discussion
The presented simulations are in 2D, while the measured data are in 3D, and the contribution of the support arms is included in the measured forces. Therefore, it is expected that the presented model cannot reproduce the experimental results in great detail, especially where 3D effects are strong. The flow expansion in the simulation model is limited to the horizontal plane only, and the vertical expansion is omitted. This error should be most prominent at high TSRs, where the flow expansion is largest. Additionally, the current 2D model will not capture wind shear, which would cause a variation of the flow velocity, and hence, the TSR over the turbine height.
Over the whole range of the presented data, the model performs better in the upwind side. This is expected, since the dynamic stall vortex is not implemented in the flow field and the wake effects should be smaller in the upwind side. Furthermore, since the support arms are not included in the model, collision of the blade with vortices from the support arms cannot be reproduced. This is a possible contributing factor to the -drop at , as the support arms can have a notable contribution to the wake. The -drop is not expected to be due to the tower wake, since the tower diameter is considerably smaller than the region of the -drop. This drop can also be caused by other three-dimensional effects, such as tip vortices, which are not included in the current model.
There are limitations of the dynamic stall model itself: it is assumed that the blade is a flat plate, and the flow velocity is constant during the change of the angle of attack [
29]. Additionally, flow curvature is represented only through a correction in the angle of attack, while it can also influence the empirical constants of the dynamic stall model. These limitations should be considered when evaluating the performance of the model.
The maximum measurement error is estimated for every
-curve using Equation (
5). Due to the high repeatability of the measured normal force, the shape of the
-curve is likely to remain, though the measurement error can change the scale of the
-response. This is observed when comparing two sets of data at almost identical operational conditions;
Figure 16. Therefore, the measurement error has to be considered throughout the assessment of the simulation model.
The major advantage of the presented model is its computational speed: one simulation with 100 revolutions is in the order of minutes on a single core machine, which is much faster than simulations with 2D CFD models. A 3D vortex model does not have the previously-mentioned constraints with the flow expansion modeling and with the implementation of the support arms. However, the computational time of the existing 3D vortex models is still high, and the computational time of 3D CFD models can be a few months [
1]. In this light, the presented simulation model can be used for the fast dimensioning of the turbine loads.