Optimal Tilt Angle of Photovoltaic Arrays and Economic Allocation of Energy Storage System on Large Oil Tanker Ship
Abstract
:1. Introduction
2. Hybrid Ship Power System and Components
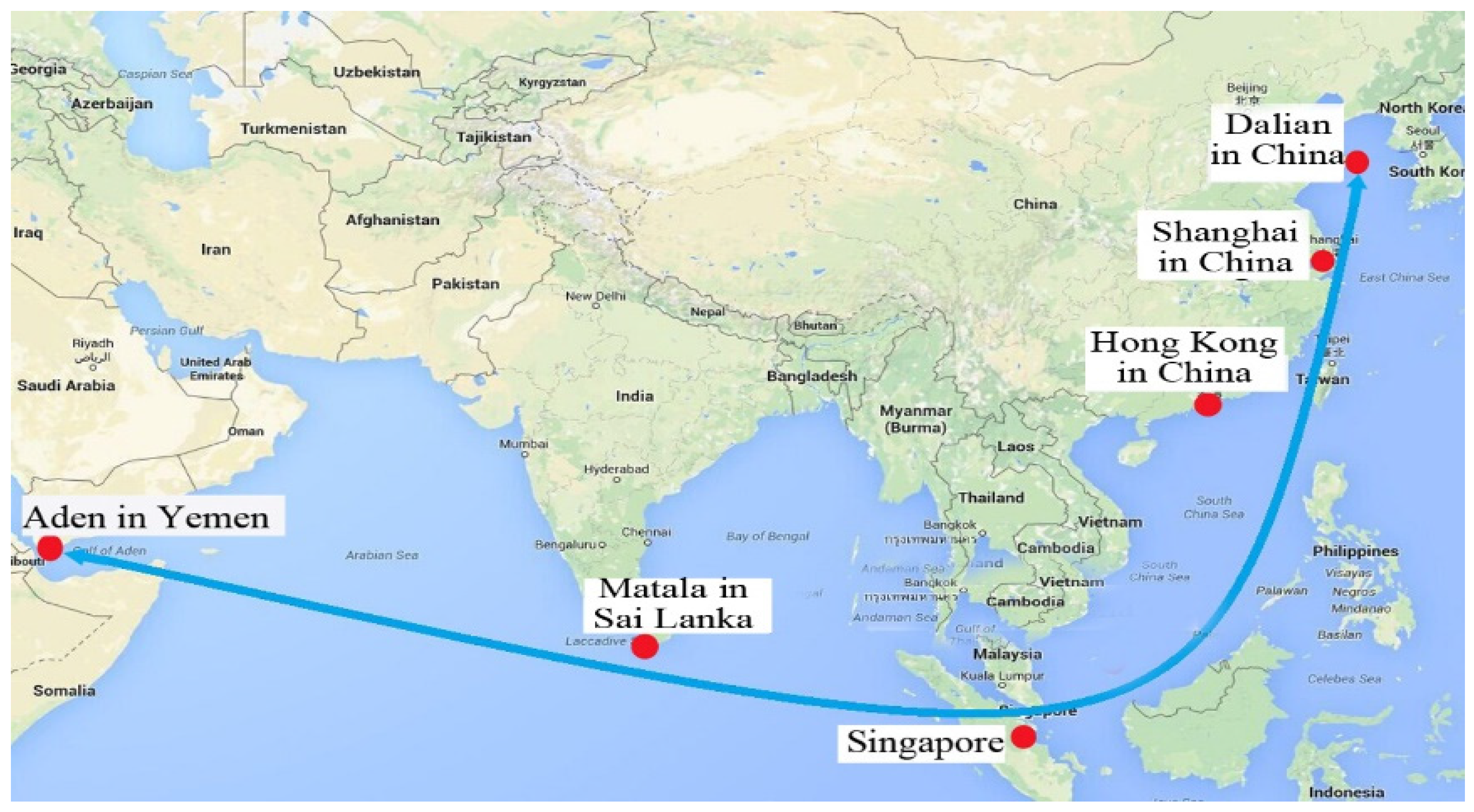
2.1. Problem Description

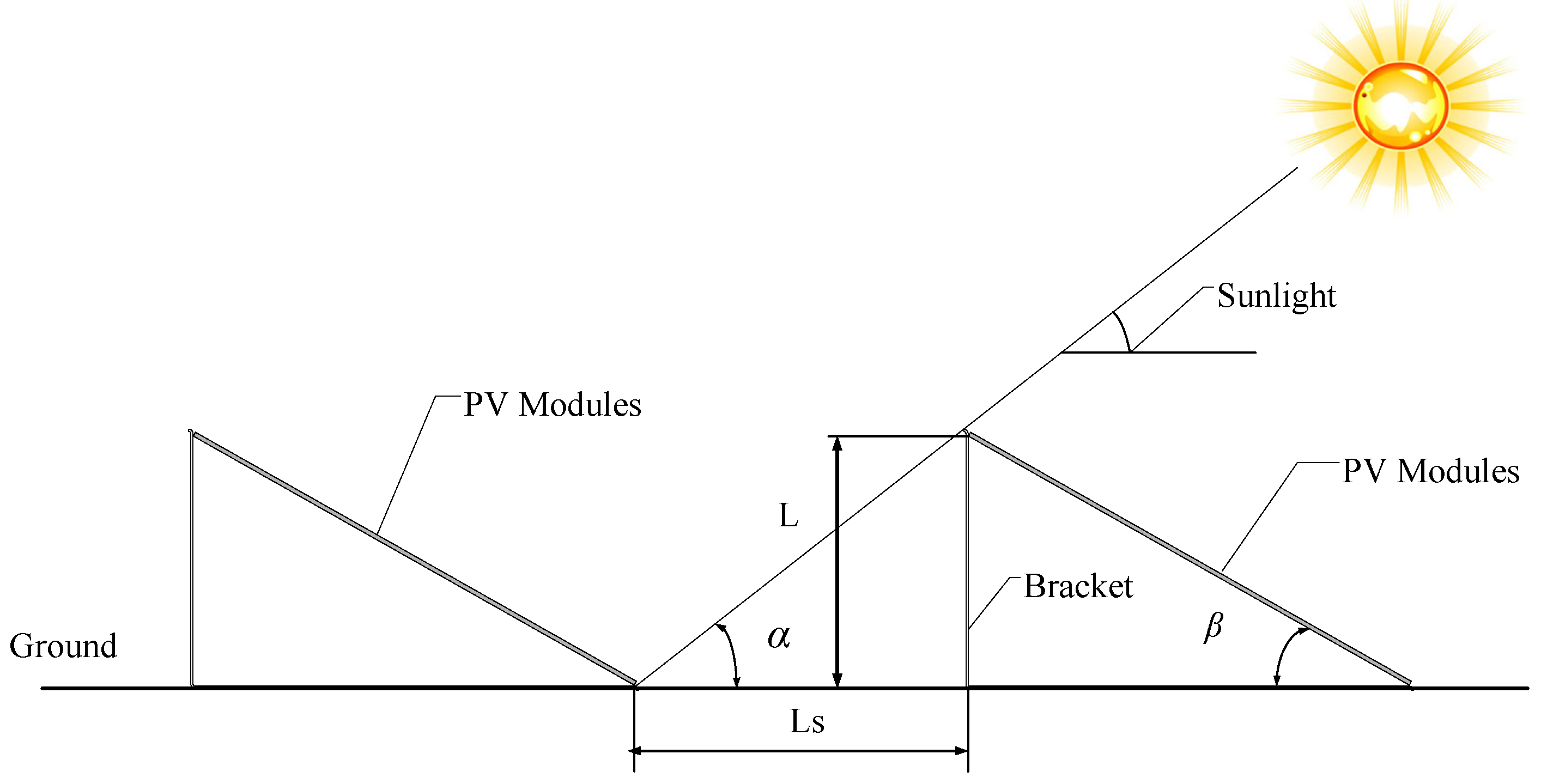
2.2. Models of System Components
2.2.1. PV System
| Items | Parameters | Items | Parameters |
|---|---|---|---|
| Life Time | 25 years | Efficiency | 14.5% |
| Cost of Investment | $1800/kW | Length of PV Panel | 1.47 m |
| Cost of Replacement | $1800/kW | Width of PV Panel | 0.68 m |
| Cost of Brackets | $1100/kW | Cost of Inverter | $655/kW |
2.2.2. Battery
| Item | Parameters |
|---|---|
| Life Time | 8 years |
| Charge Efficiency | 75% |
| Discharge Efficiency | 100% |
| Cost of Investment | $100/kWh |
| Cost of Replacement | $100/kWh |
2.2.3. Diesel Generator
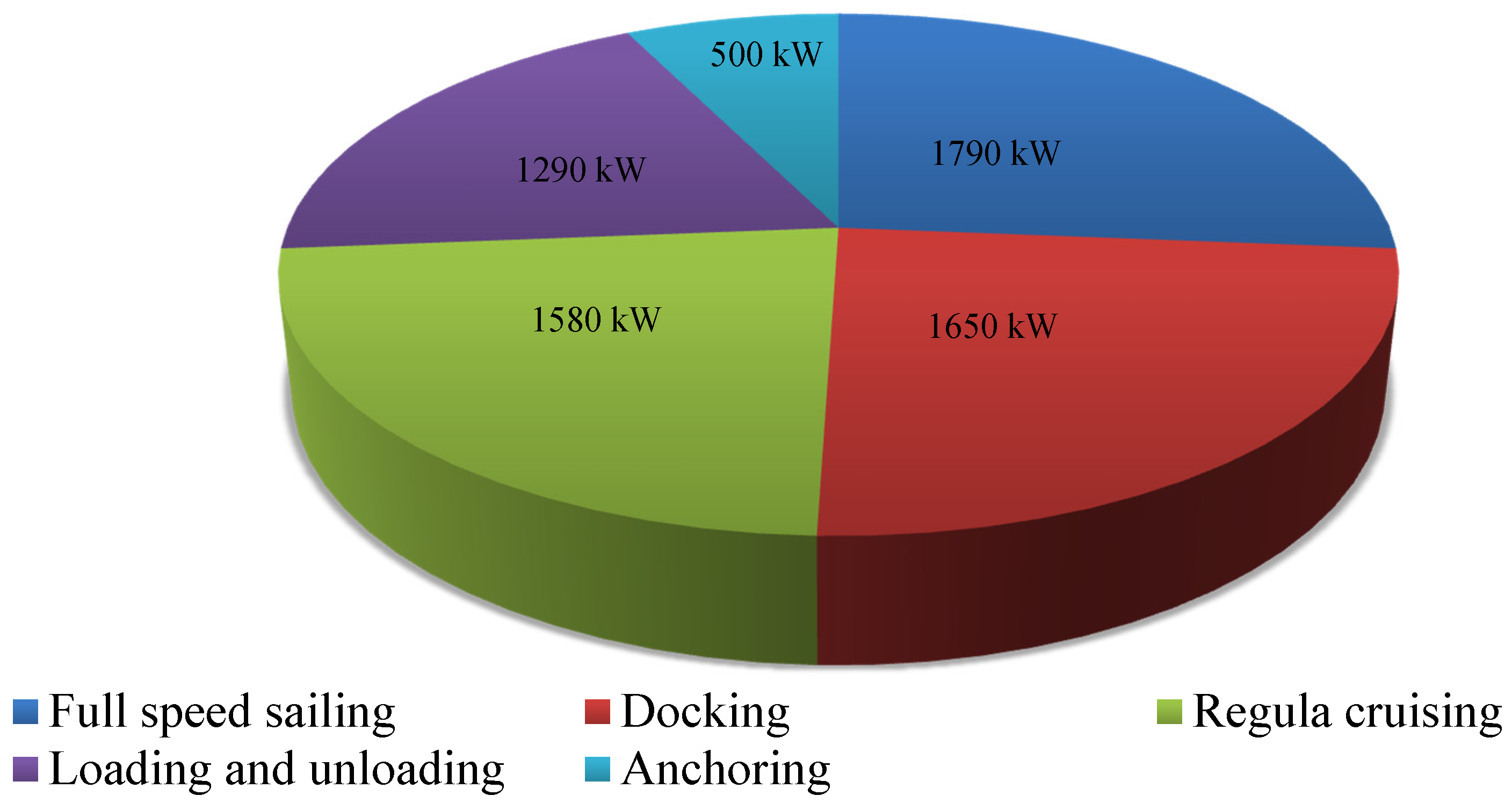
2.2.4. Load
| Operating Mode | Dalian in China | Shanghai in China | Hong Kong in China | Singapore | Matara in Sri Lanka | Aden in Yemen |
|---|---|---|---|---|---|---|
| Docking | 2 h | 2 h | 2 h | 2 h | 2 h | 2 h |
| Loading and unloading | 6 h | 8 h | 14 h | 12 h | 7 h | 6 h |
| Anchoring | 4 h | 0 h | 4 h | 5 h | 6 h | 4 h |
3. Problem Formulation
3.1. Objective Function
3.2. Constraints
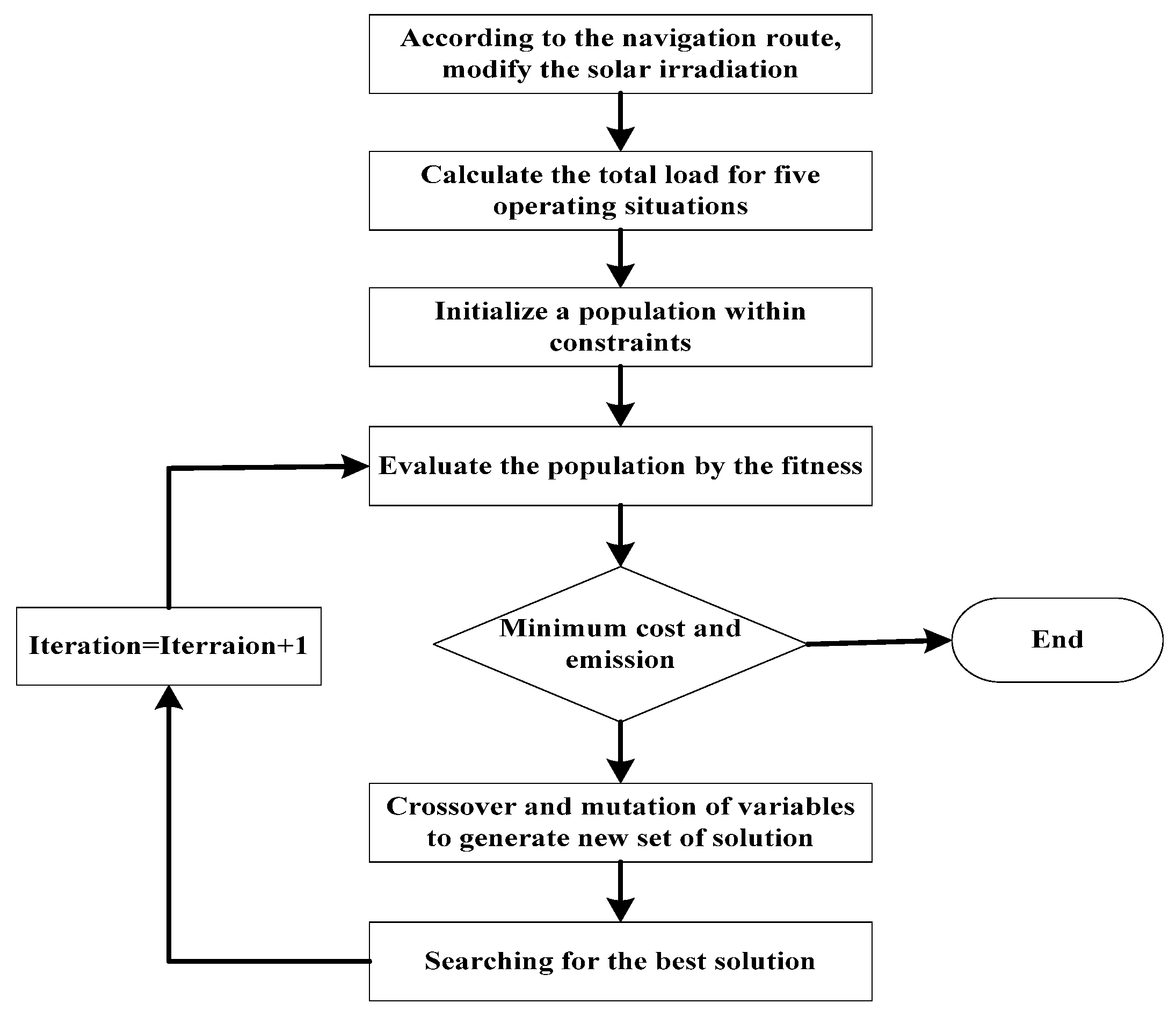
4. Solution Method
5. Simulation Result and Discussion
5.1. Optimal Tilt Angle of PV Arrays

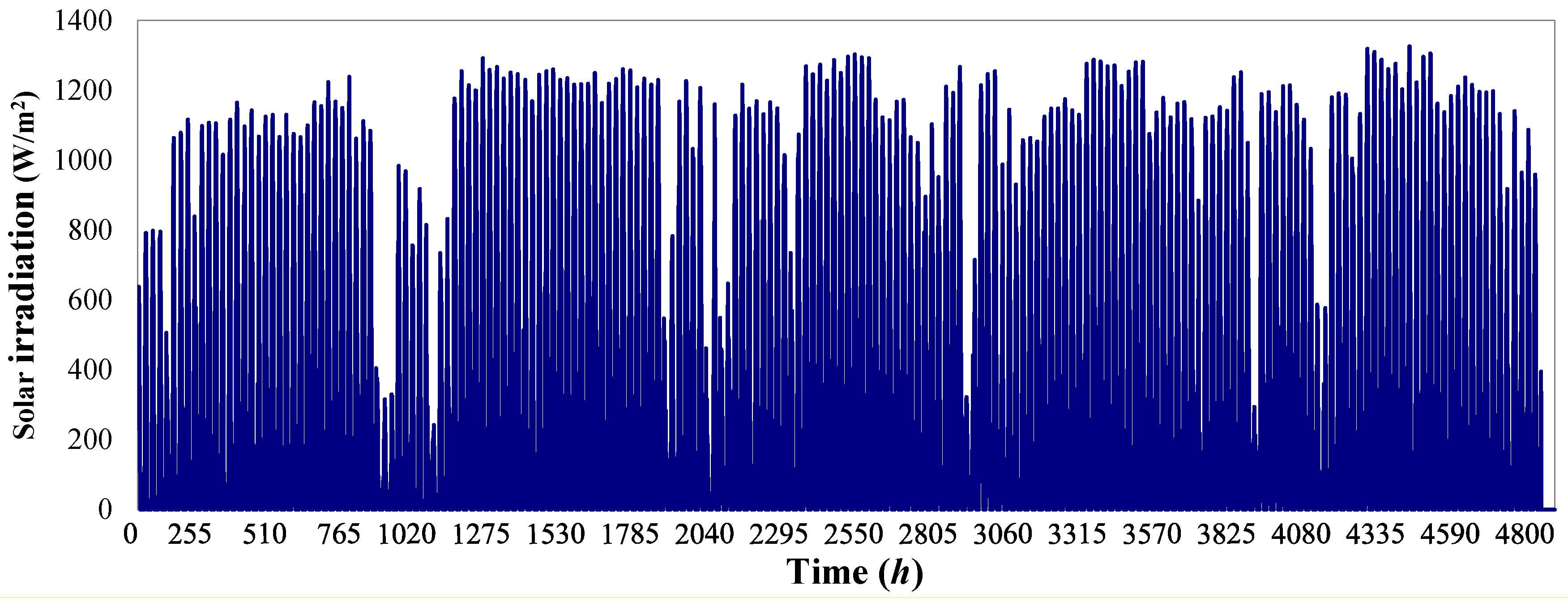
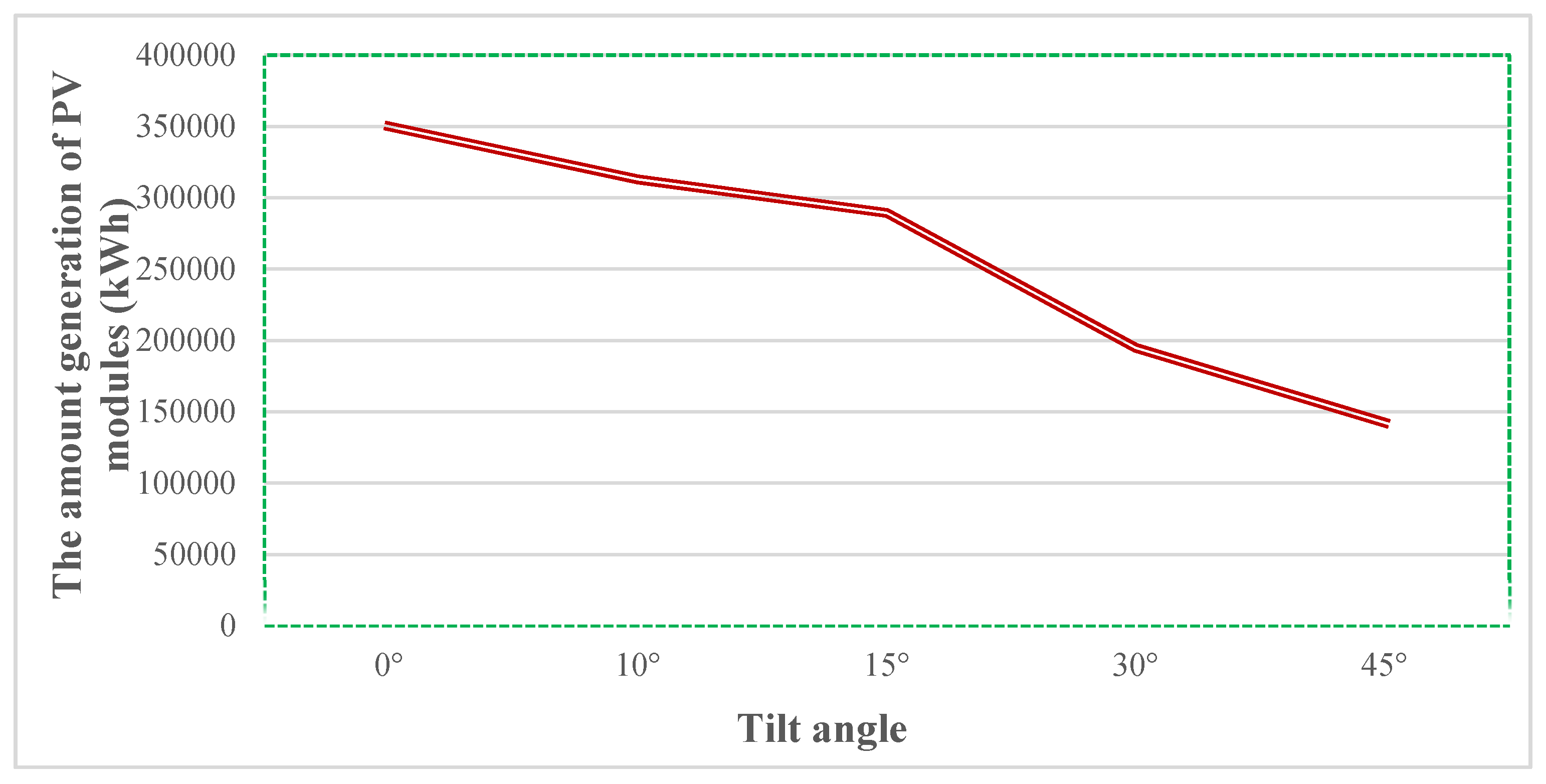

5.2. Economic Analysis

| Item | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| PV size (kW) | 0 | 292 | 292 |
| ESS size (kW) | 0 | 0 | 140 |
| ESS capacity (kWh) | 0 | 0 | 110 |
| PV installation cost ($) | 0 | 522,000 | 522,000 |
| PV replacement cost ($) | 0 | 522,000 | 522,000 |
| ESS installation cost ($) | 0 | 0 | 583,975 |
| ESS replacement cost ($) | 0 | 0 | 583,975 |
| Total NPC ($) | 2,320,645 | 1,258,245 | 1,105,975 |
| Emission (kg) | 55,314,000 | 49,557,769 | 29,853,731 |
| Total diesel output (kWh) | 8,720,000 | 2,766,500 | 2,070,326 |

6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- The International Convention for the Prevention of Pollution from Ships. Available online: http://www.eisil.org/index.php?t=link_details&id=609&cat=424 (accessed on 19 May 2005).
- Zahedi, B.; Norum, L.E.; Ludvigsen, K.B. Optimized efficiency of all-electric ships by dc hybrid power systems. J. Power Source 2014, 255, 341–354. [Google Scholar] [CrossRef]
- Bocca, A.; Chiavazzo, E.; Macii, A.; Asinari, P. Solar energy potential assessment: An overview and a fast modeling approach with application to Italy. Renew. Sustain. Energy Rev. 2015, 49, 291–296. [Google Scholar] [CrossRef]
- Najafi, G.; Ghobadian, B.; Mamat, R.; Yusaf, T.; Azmi, W.H. Solar energy in Iran: Current state and outlook. Renew. Sustain. Energy Rev. 2015, 49, 931–942. [Google Scholar] [CrossRef]
- Balcombe, P.; Rigby, D.; Azapagic, A. Environmental impacts of microgeneration: Integrating solar PV, Stirling engine CHP and battery storage. Appl. Energy 2015, 139, 245–259. [Google Scholar] [CrossRef]
- Curry, N.; Pillay, P. Integrating solar energy into an urban small-scale anaerobic digester for improved performance. Renew. Energy 2015, 83, 280–293. [Google Scholar] [CrossRef]
- Freitas, S.; Serra, F.; Brito, M.C. PV layout optimization: String tiling using a multi-objective genetic algorithm. Sol. Energy 2015, 118, 562–574. [Google Scholar] [CrossRef]
- Martinez-Rubio, A.; Sanz-Adan, F.; Santamaria, J. Optimal design of photovoltaic energy collectors with mutual shading for pre-existing building roofs. Renew. Energy 2015, 78, 666–678. [Google Scholar] [CrossRef]
- Mohammadi, S.; de Vries, B.; Schaefer, W. Modeling the allocation and economic evaluation of PV panels and wind turbines in urban areas. Procedia Environ. Sci. 2014, 22, 333–351. [Google Scholar] [CrossRef]
- Dolara, A.; Lazaroiu, G.C.; Leva, S.; Manzolini, G. Experimental investigation of partial shading scenarios on PV (photovoltaic) modules. Energy 2013, 55, 466–475. [Google Scholar] [CrossRef]
- Sarmah, N.; Mallick, T.K. Design, fabrication and outdoor performance analysis of a low concentrating photovoltaic system. Sol. Energy 2015, 112, 361–372. [Google Scholar] [CrossRef]
- Richardson, D.B.; Harvey, L.D.D. Strategies for correlating solar PV array production with electricity demand. Renew. Energy 2015, 76, 432–440. [Google Scholar] [CrossRef]
- Karakose, M.; Baygin, M. An Analysis Approach for optimization based reconfiguration in photovoltaic arrays. In Proceedings of the IEEE 23th International Symposium on Industrial Electronics, Istanbul, Turkey, 1–4 June 2014; pp. 954–959.
- Sharma, P.; Duttagupta, S.P.; Agarwal, V. A novel and universal model for accurate prediction of PV module characteristics for power optimization under various design layouts and dynamic environmental conditions. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems, Bengaluru, India, 16–19 December 2012; pp. 1–6.
- Midtgard, O.-M.; Sætre, T.O.; Yordanov, G.; Imenes, A.G.; Nge, C.L. A qualitative examination of performance and energy yield of photovoltaic modules in southern Norway. Renew. Energy 2010, 35, 1266–1274. [Google Scholar] [CrossRef]
- Shirzadi, S.; Hizam, H.; Wahab, N.I.A. Mismatch losses minimization in photovoltaic arrays by arranging modules applying a genetic algorithm. Sol. Energy 2014, 108, 467–478. [Google Scholar] [CrossRef]
- Díaz-Dorado, E.; Suárez-García, A.; Carrillo, C.J.; Cidrás, J. Optimal distribution for photovoltaic solar trackers to minimize power losses caused by shadows. Renew. Energy 2011, 36, 1826–1835. [Google Scholar] [CrossRef]
- Rani, B.I.; Ilango, G.S.; Nagamani, C. Enhanced power generation from PV array under partial shading conditions by shade dispersion using Su Do Ku configuration. IEEE Trans. Sustain. Energy 2013, 4, 594–601. [Google Scholar] [CrossRef]
- Paraskevadaki, E.V.; Papathanassiou, S.A. Evaluation of MPP voltage and power of mc-Si PV modules in partial shading conditions. IEEE Trans. Energy Convers. 2011, 26, 923–932. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, J.; Dai, Y. Capacity allocation of a hybrid energy storage system for power system peak shaving at high wind power penetration level. Renew. Energy 2015, 75, 541–549. [Google Scholar] [CrossRef]
- Bianchi, M.; Branchini, L.; Ferrari, C.; Melino, F. Optimal sizing of grid-independent hybrid photovoltaic-battery power systems for household sector. Appl. Energy 2013, 136, 805–816. [Google Scholar] [CrossRef]
- Maleki, A.; Pourfayaz, F. Optimal sizing of autonomous hybrid photovoltaic/wind/battery power system with LPSP technology by using evolutionary algorithms. Sol. Energy 2015, 115, 471–483. [Google Scholar] [CrossRef]
- Aghamohammadi, M.R.; Abdolahinia, H. A new approach for optimal sizing of battery energy storage system for primary frequency control of islanded microgrid. Int. J. Electr. Power Energy Syst. 2014, 54, 325–333. [Google Scholar] [CrossRef]
- Bahmani-Firouzi, B.; Azizipanah-Abarghooee, R. Optimal sizing of battery energy storage for micro-grid operation management using a new improved bat algorithm. Int. J. Electr. Power Energy Syst. 2014, 56, 42–54. [Google Scholar] [CrossRef]
- Fossati, J.P.; Galarza, A.; Martín-villate, A.; Font, L. A method for optimal sizing energy storage systems for microgrids. Renew. Energy. 2015, 77, 539–549. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B.; Hu, G. Optimal allocation and economic analysis of energy storage system in microgrids. IEEE Trans. Power Electron. 2011, 26, 2762–2773. [Google Scholar] [CrossRef]
- Ovrum, E.; Bergh, T.F. Modelling lithium-ion battery hybrid ship crane operation. Appl. Energy 2015, 152, 162–172. [Google Scholar] [CrossRef]
- Dedes, E.K.; Hudson, D.A.; Turnock, S.R. Assessing the potential of hybrid energy technology to reduce exhaust emissions from global shipping. Energy Policy 2012, 40, 204–218. [Google Scholar] [CrossRef]
- Andrews, R.W.; Pearce, J.M. The effect of spectral albedo on amorphous silicon and crystalline silicon solar photovoltaic device performance. Sol. Energy 2013, 91, 233–241. [Google Scholar] [CrossRef]
- Da-Rosa, A.V. Fundamentals of Renewable Energy Processes, 2nd ed.; Elsevier Academic Press: Waltham, MA, USA, 2009. [Google Scholar]
- Melo, E.G.; Almeida, M.P.; Zilles, R.; Grimoni, J.A.B. Using a shading matrix to estimate the shading factor and the irradiation in a three-dimensional model of a receiving surface in an urban environment. Sol. Energy 2013, 92, 15–25. [Google Scholar] [CrossRef]
- Feldman, D.; Barbose, G.; Margolis, R.; Darghouth, N.; James, T.; Weaver, S.; Goodrich, A.; Wiser, R. Photovoltaic System Pricing Trends: Historical, Recent, and Near-Term Projections 2014 Edition. Available online: http://eetd.lbl.gov/sites/all/files/presentation1.pdf (accessed on 22 September 2014).
- El Fathi, A.; Nkhaili, L.; Bennouna, A.; Outzourhit, A. Performance parameters of a standalone PV plant. Energy Convers. Manag. 2014, 86, 490–495. [Google Scholar] [CrossRef]
- Dufo-López, R.; Lujano-Rojas, J.M.; Bernal-Agustín, J.L. Comparison of different lead-acid battery lifetime prediction models for use in simulation of stand-alone photovoltaic systems. Appl. Energy 2014, 115, 242–253. [Google Scholar] [CrossRef]
- Maleki, A.; Pourfayaz, F. Sizing of stand-alone photovoltaic/wind/diesel system with battery and fuel cell storage devices by harmony search algorithm. J. Energy Storage 2015, 2, 30–42. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, W.; Lu, L.; Fang, Z. Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology by using genetic algorithm. Sol. Energy 2008, 82, 354–367. [Google Scholar] [CrossRef]
- Geomodel Solar Company. Solar and PV Data. Available online: http://solargis.info/doc/solar-and-pv-data (accessed on 20 March 2014).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, H.; Dai, J.; Wen, S.; Hong, Y.-Y.; Yu, D.C.; Bai, Y. Optimal Tilt Angle of Photovoltaic Arrays and Economic Allocation of Energy Storage System on Large Oil Tanker Ship. Energies 2015, 8, 11515-11530. https://doi.org/10.3390/en81011515
Lan H, Dai J, Wen S, Hong Y-Y, Yu DC, Bai Y. Optimal Tilt Angle of Photovoltaic Arrays and Economic Allocation of Energy Storage System on Large Oil Tanker Ship. Energies. 2015; 8(10):11515-11530. https://doi.org/10.3390/en81011515
Chicago/Turabian StyleLan, Hai, Jinfeng Dai, Shuli Wen, Ying-Yi Hong, David C. Yu, and Yifei Bai. 2015. "Optimal Tilt Angle of Photovoltaic Arrays and Economic Allocation of Energy Storage System on Large Oil Tanker Ship" Energies 8, no. 10: 11515-11530. https://doi.org/10.3390/en81011515
APA StyleLan, H., Dai, J., Wen, S., Hong, Y.-Y., Yu, D. C., & Bai, Y. (2015). Optimal Tilt Angle of Photovoltaic Arrays and Economic Allocation of Energy Storage System on Large Oil Tanker Ship. Energies, 8(10), 11515-11530. https://doi.org/10.3390/en81011515






