Rotor Design for Diffuser Augmented Wind Turbines
Abstract
:1. Introduction
- Infinite tip-speed ratio, λ.
- Infinite rotor blade lift-over-drag ratio, L/D.
- No centerbody (nacelle).
- Finite realistic tip-speed ratio, λ.
- Finite realistic rotor blade lift-over-drag ratio, L/D.
- A centerbody (nacelle).
2. A Simple BEM Formulation for HAWTs with Full Inclusion of Swirl Effects
2.1. BEM Derivation
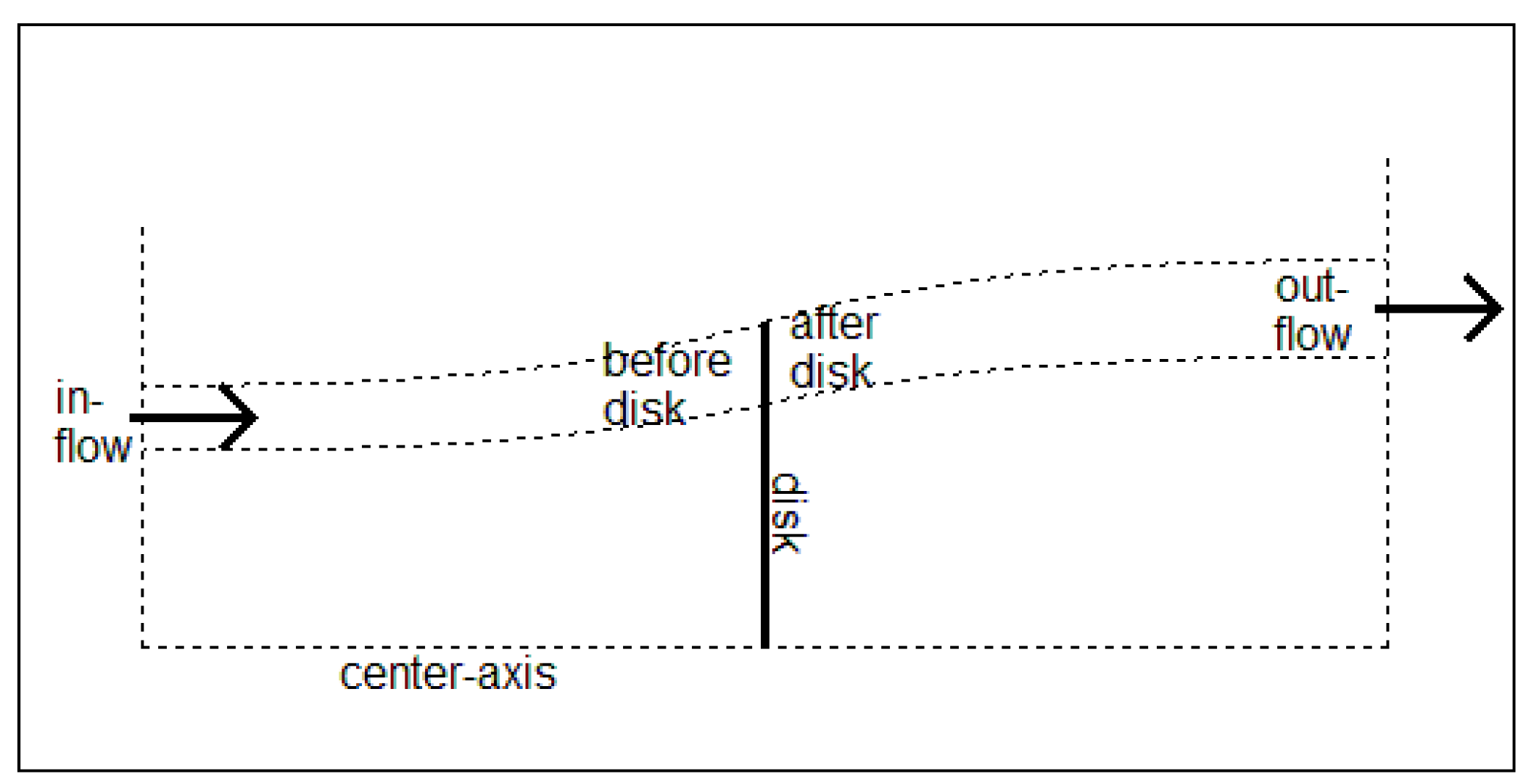
| State | Stream Tube Area | Static Pressure | Axial Velocity | Azimuthal Velocity |
|---|---|---|---|---|
| inflow | ||||
| before disk | ||||
| after disk | ||||
| outflow |
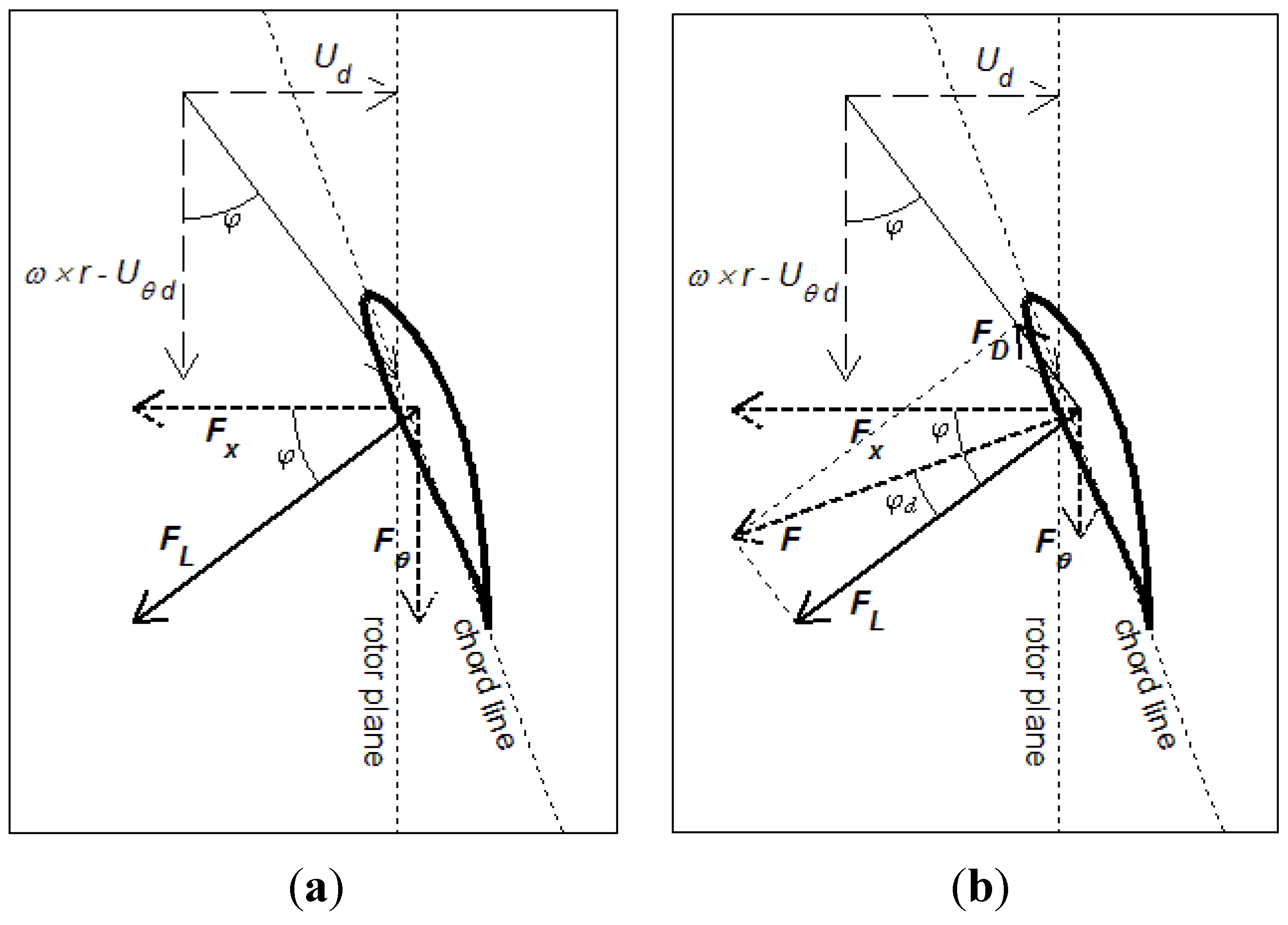
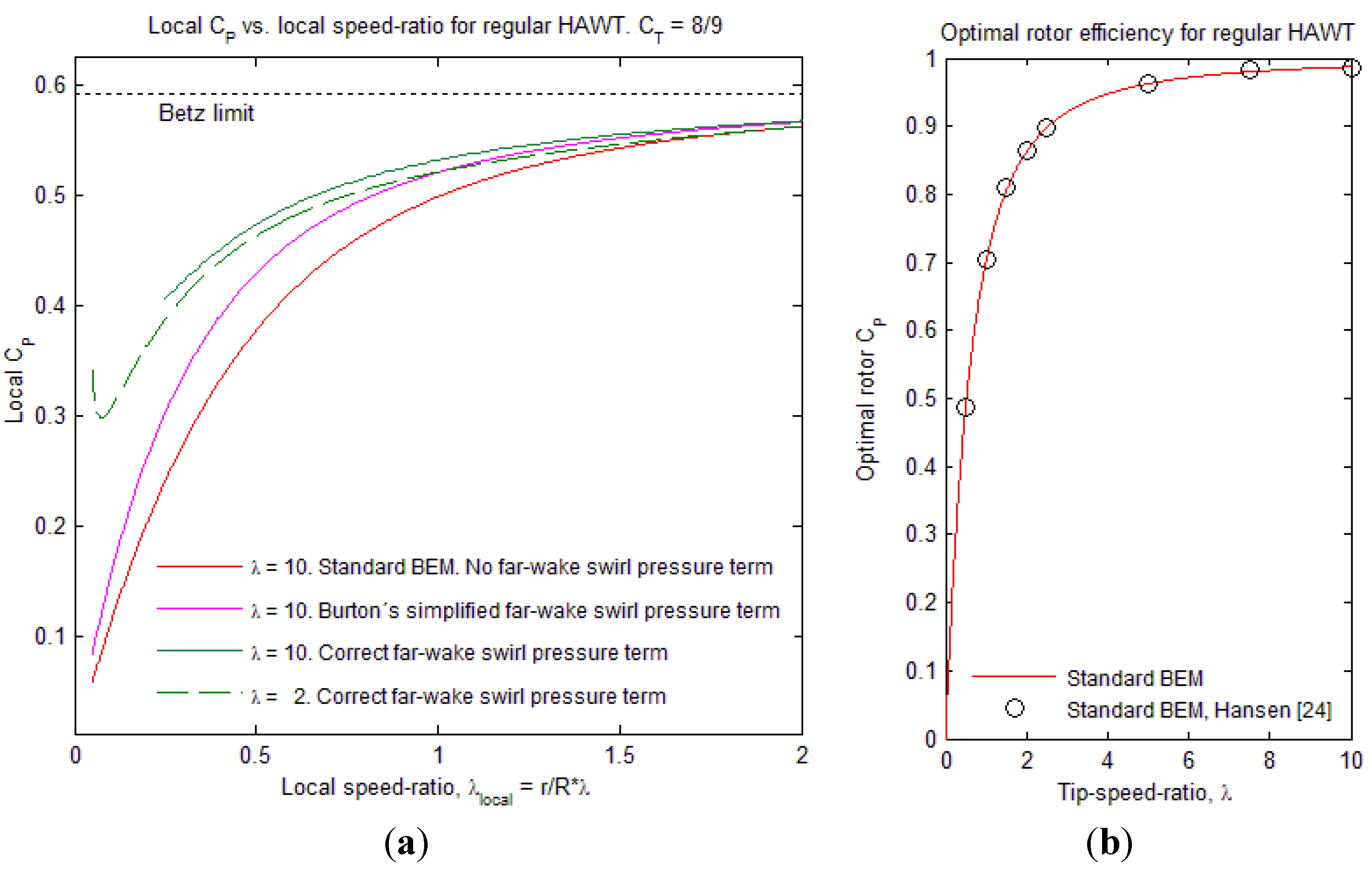
2.2. BEM Results

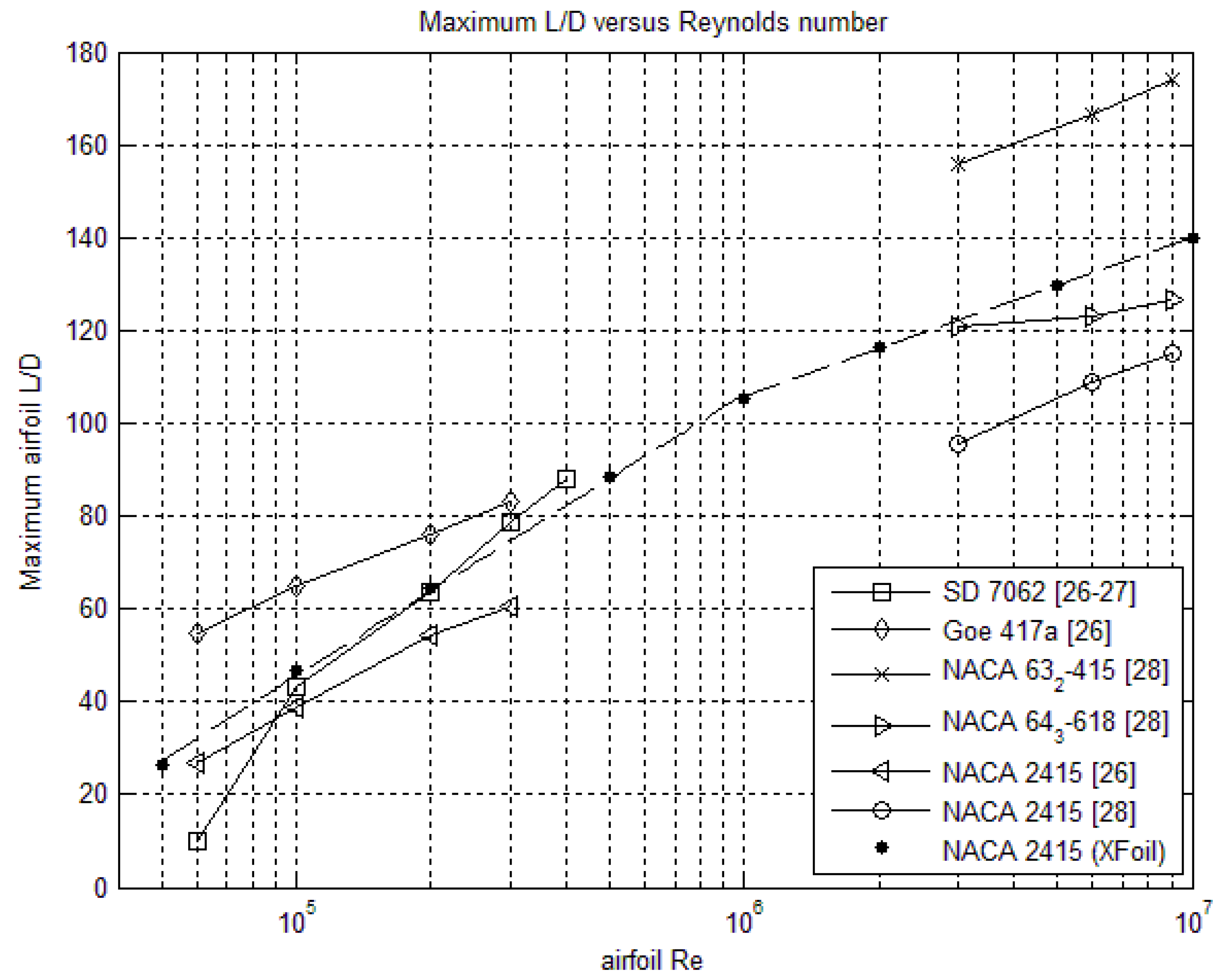
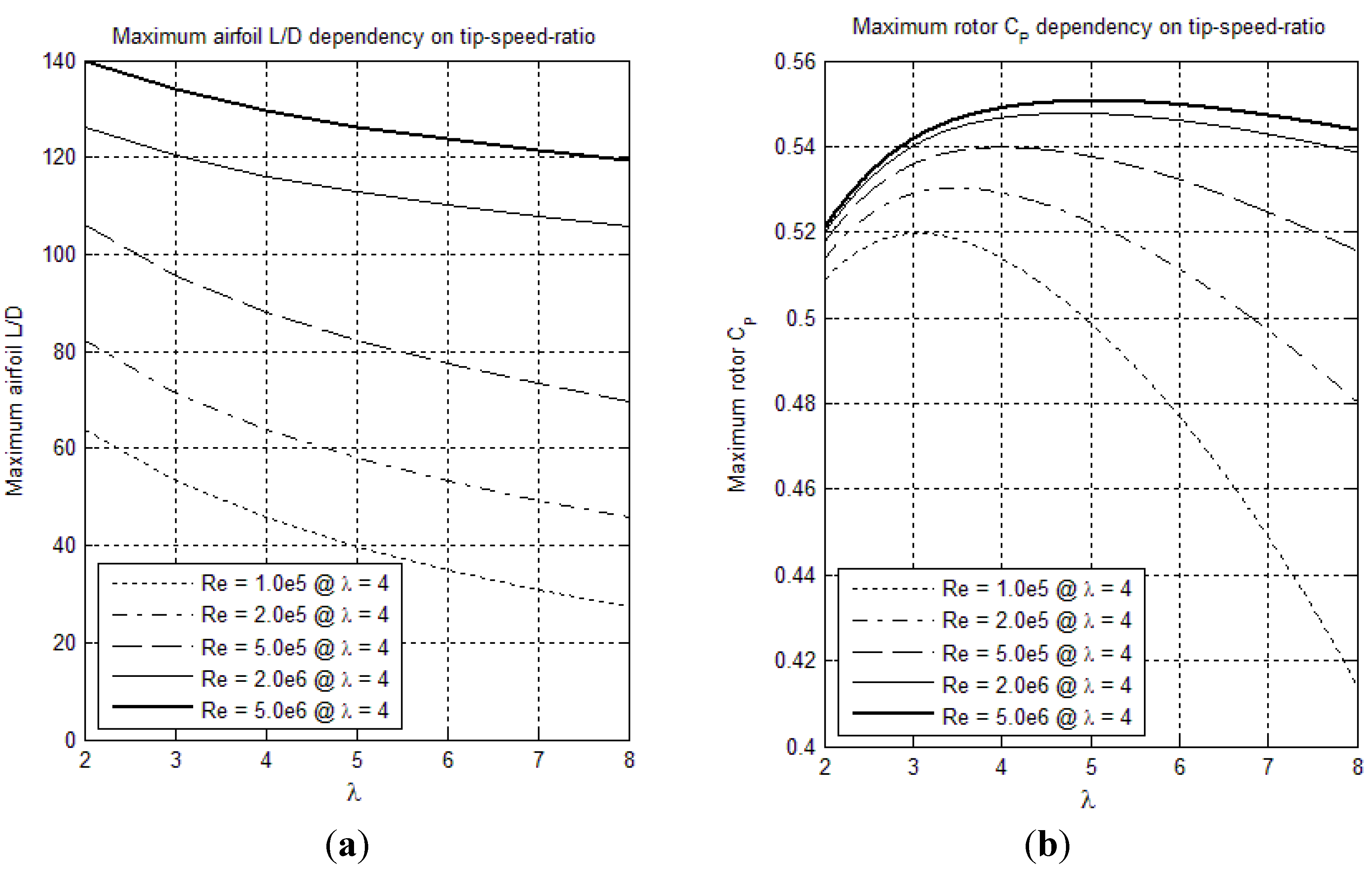
3. Validation of the Swirled AD Code
3.1. AD Model
| Configuration | Poly. Basis | [–] | [–] | [mm] | [–] | Avg() [–] | Max() [–] | Sep.loc. [%] |
|---|---|---|---|---|---|---|---|---|
| Hansen DAWT, case1 | P1P1 | 0.77 | 10 | 0.01 | 0.9054 | 4.05 | 10.2 | 100 |
| Test: Increasing polynomial | P2P1 | 0.77 | 10 | 0.01 | 0.9021 | 4.11 | 11.3 | 100 |
| basis order. | P3P2 | 0.77 | 10 | 0.01 | 0.9018 | 4.12 | 12.7 | 100 |
| Hansen DAWT, case1 | P1P1 | 0.77 | 10 | 1 | 0.9195 | 347 | 856 | 100 |
| Test: Decreasing 1st elm. | P1P1 | 0.77 | 10 | 0.1 | 0.9043 | 40.5 | 64.7 | 100 |
| height in boundary layer, | P1P1 | 0.77 | 10 | 0.01 | 0.9054 | 4.05 | 10.2 | 100 |
| P1P1 | 0.77 | 10 | 0.001 | 0.9061 | 0.40 | 1.12 | 100 | |
| Multi-element DAWT, case1 | P1P1 | 1.07 | 2 | 0.5 | 1.6431 | 358 | 620 | 54 |
| Test: Decreasing 1st elm. | P1P1 | 1.07 | 2 | 0.05 | 1.6491 | 36.5 | 55.9 | 80 |
| height in boundary layer, | P1P1 | 1.07 | 2 | 0.005 | 1.6372 | 2.23 | 8.79 | 81 |
| P1P1 | 1.07 | 2 | 0.0005 | 1.6259 | 0.40 | 0.97 | 77 |
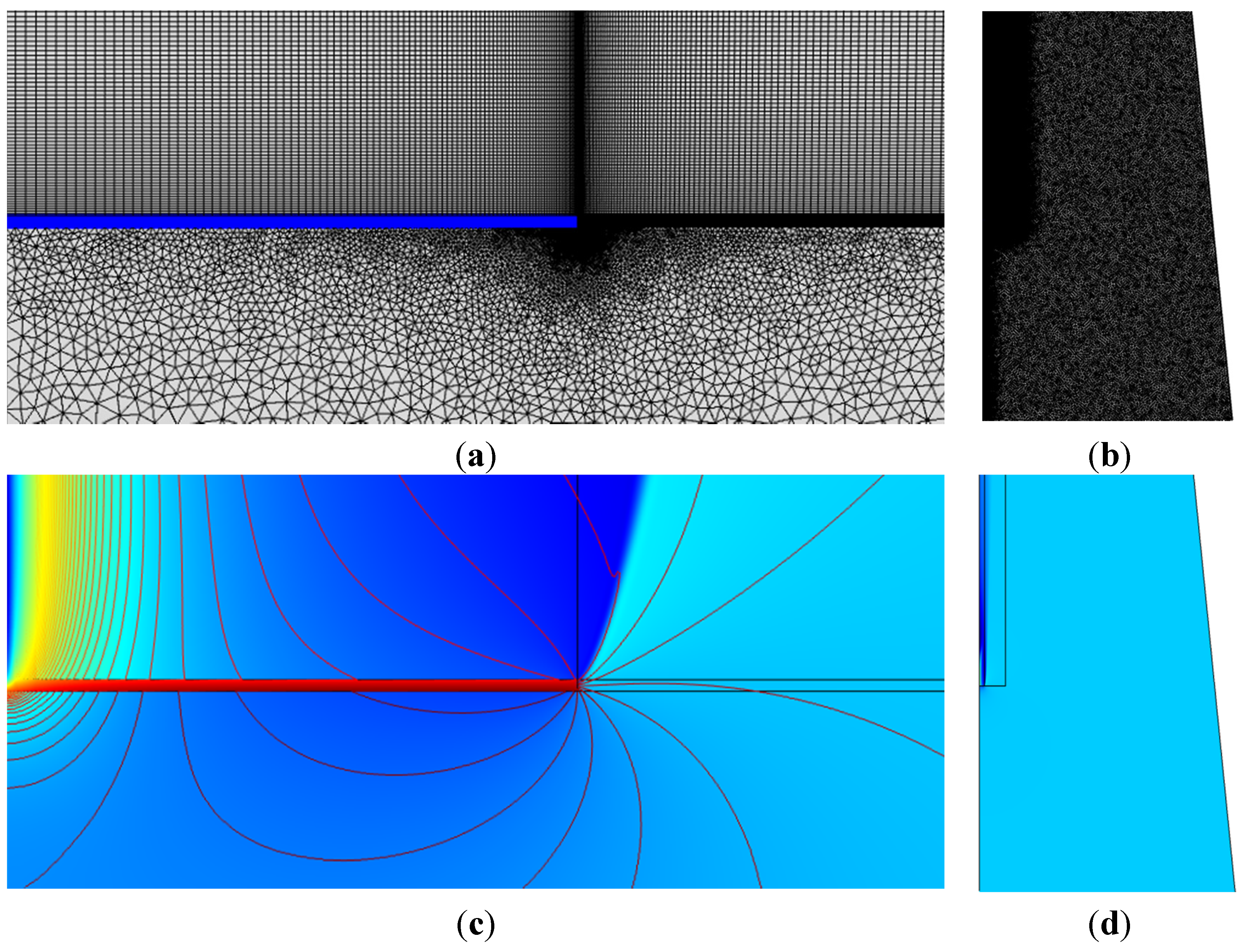
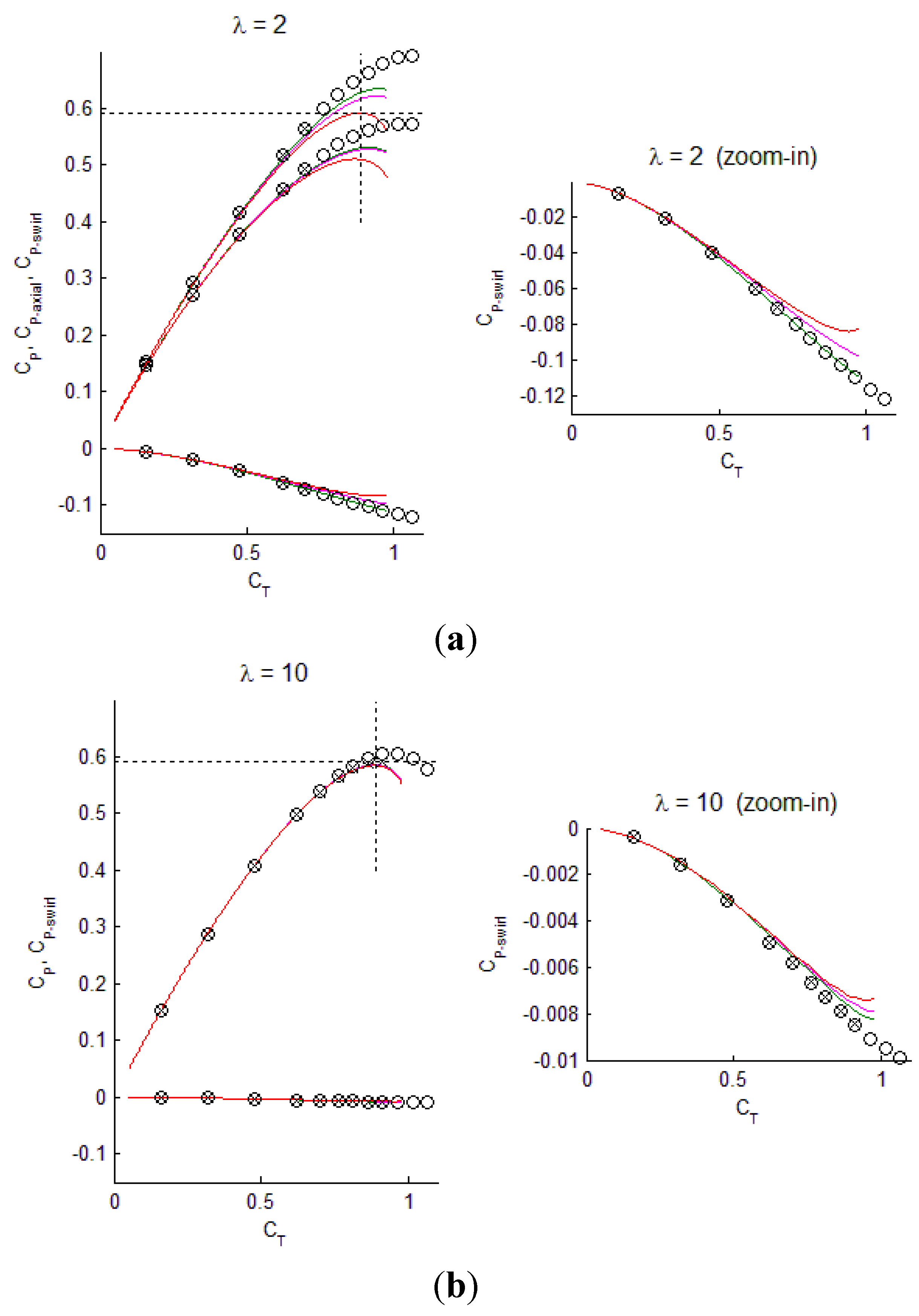
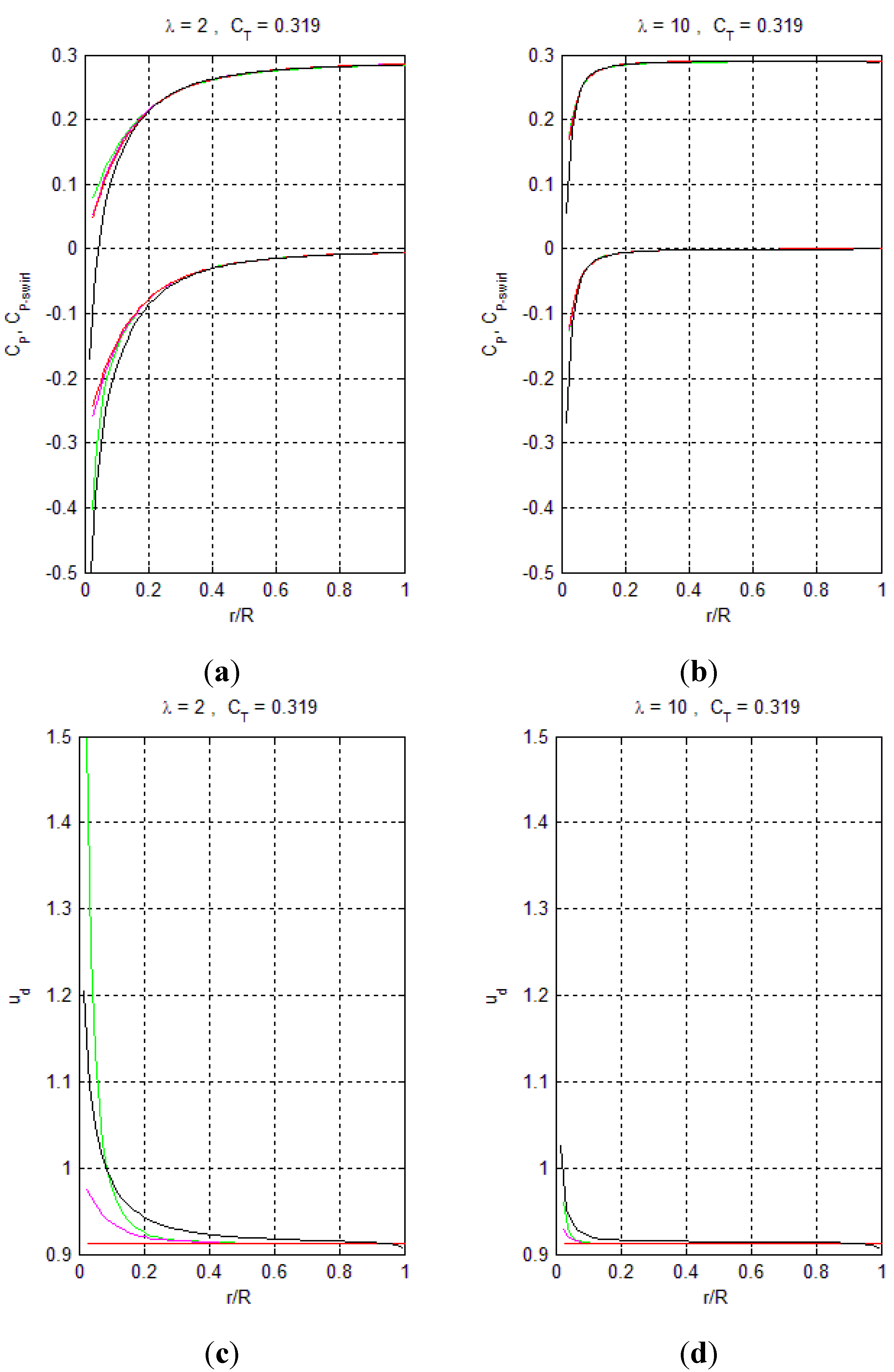
3.2. AD Results
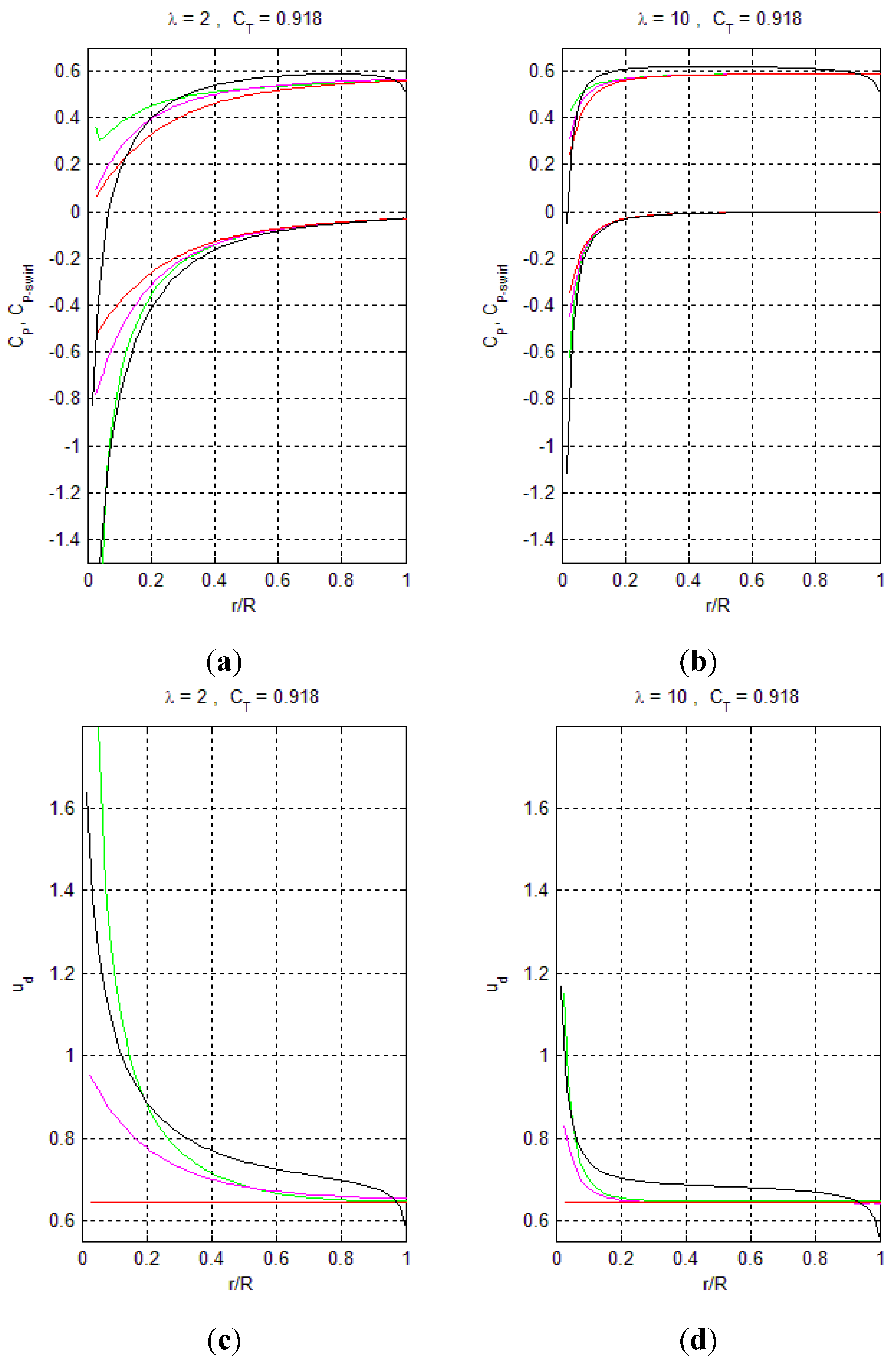
4. DAWT Rotor Design
4.1. Configurations
- Case 1: Full disk, uniform loading.
- Case 2: Disk with centerhole, uniform loading.
- Case 3: Disk with centerbody, uniform loading.
- Case 4: Disk with centerbody, uniform loading with inner ramp-down.


- High swirl: TSR = 2
- Low swirl: TSR = 10

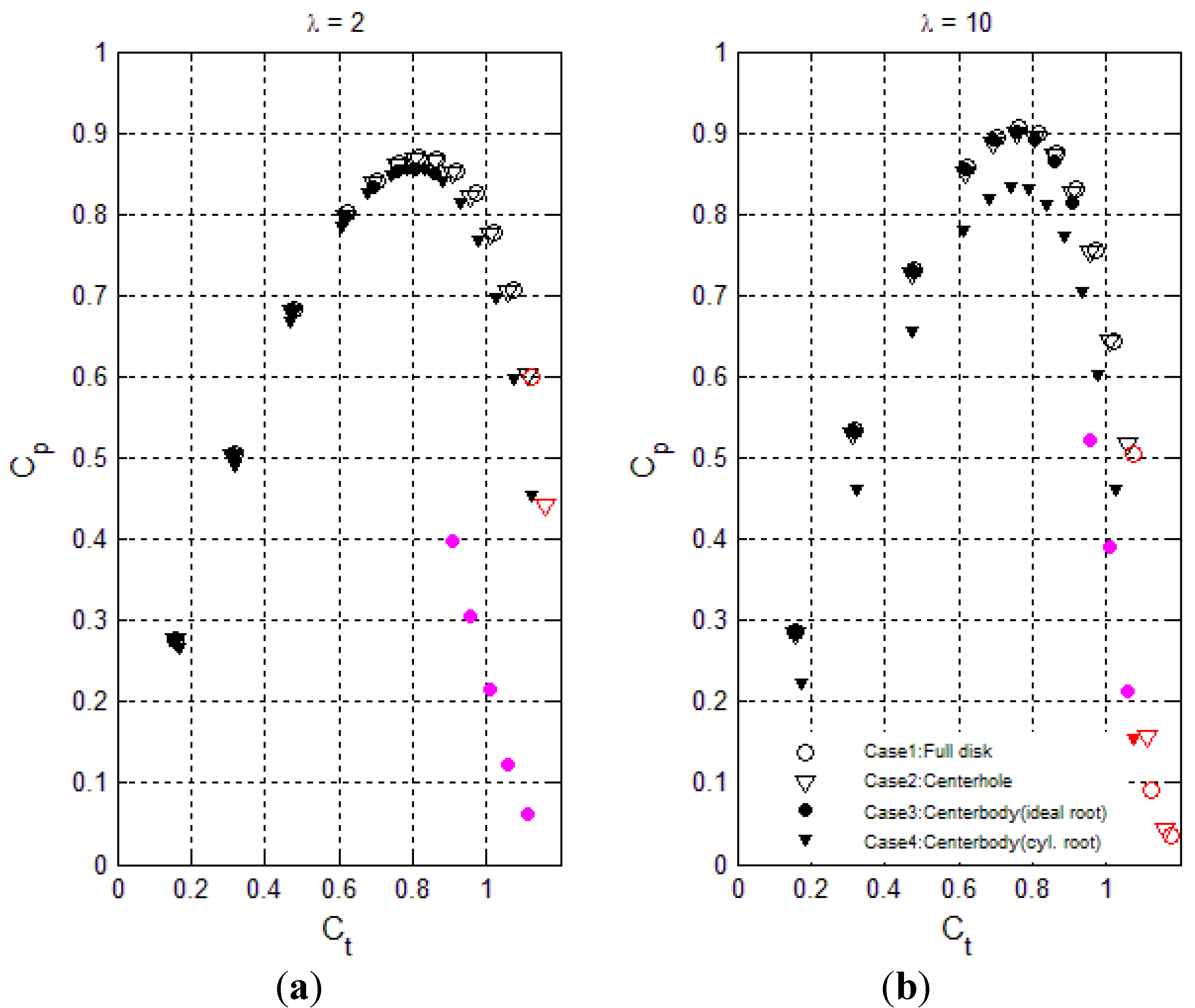
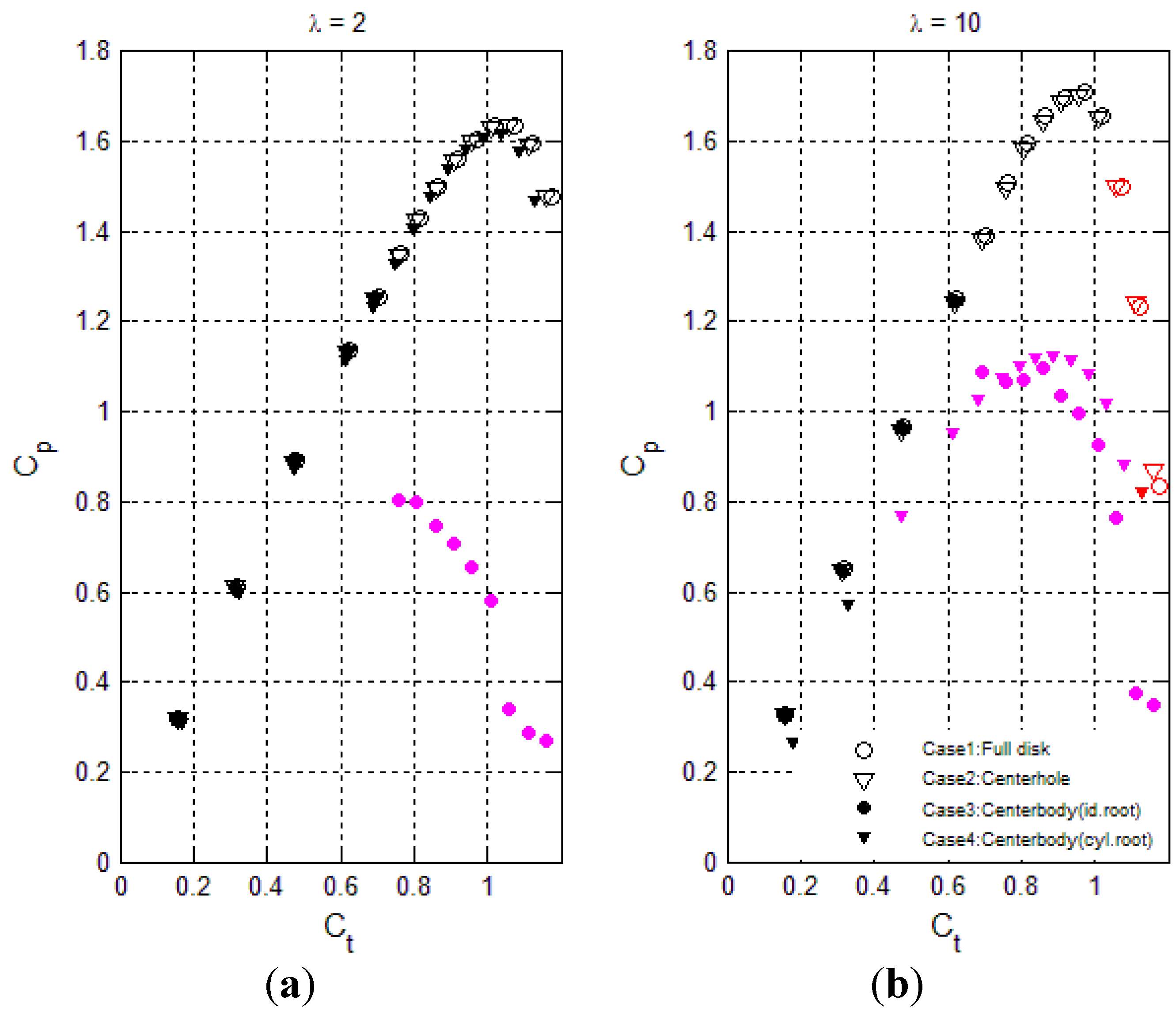
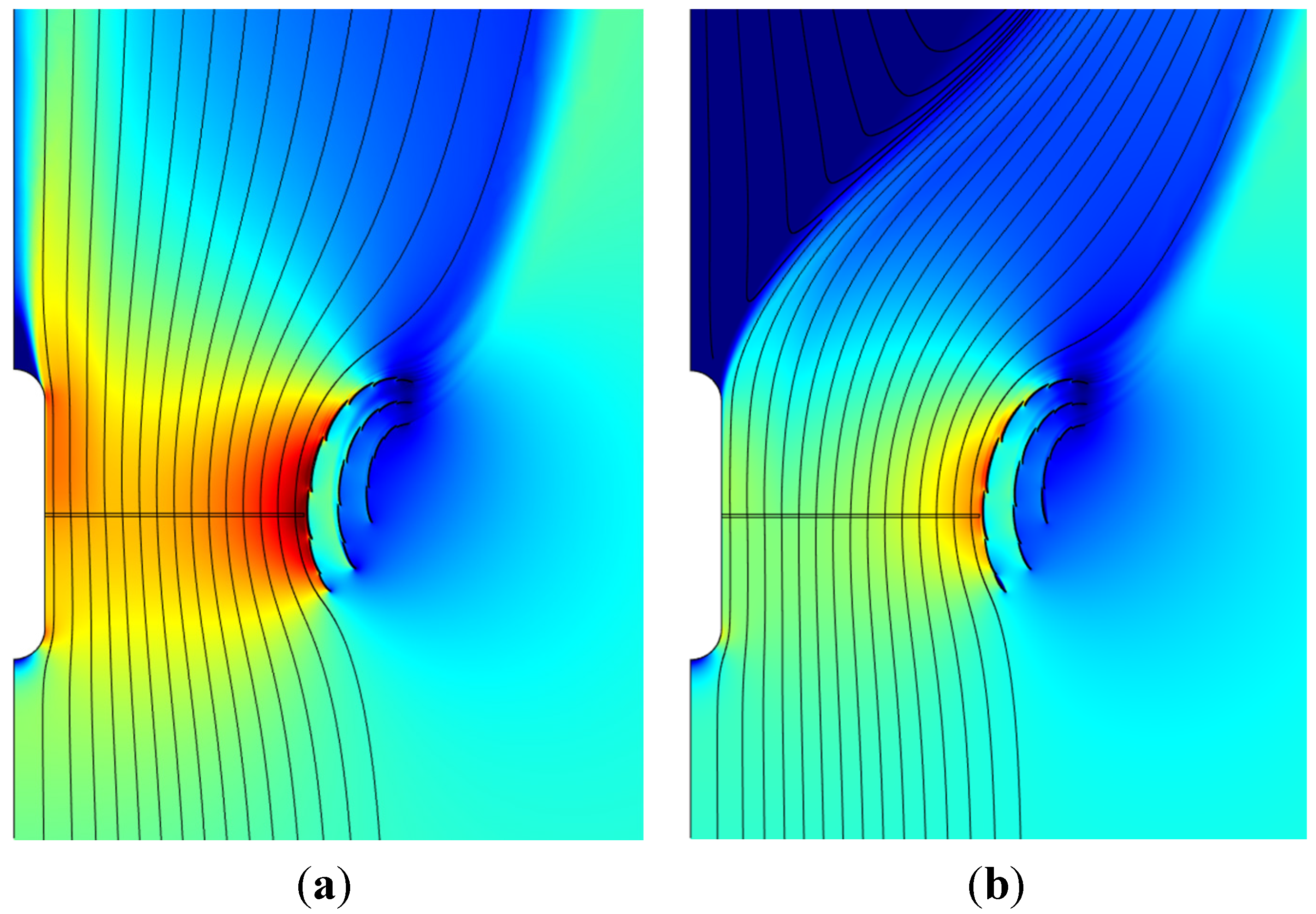
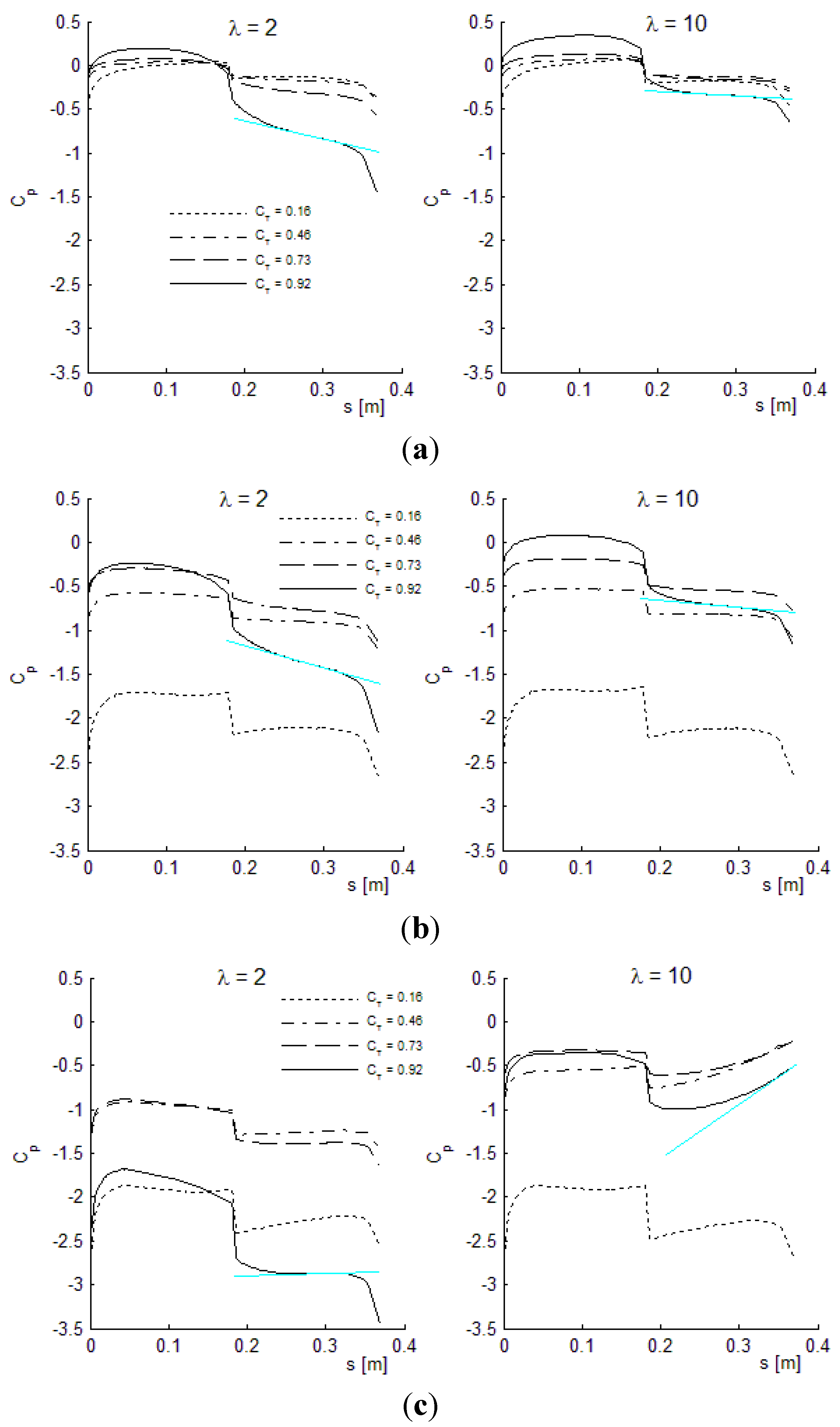
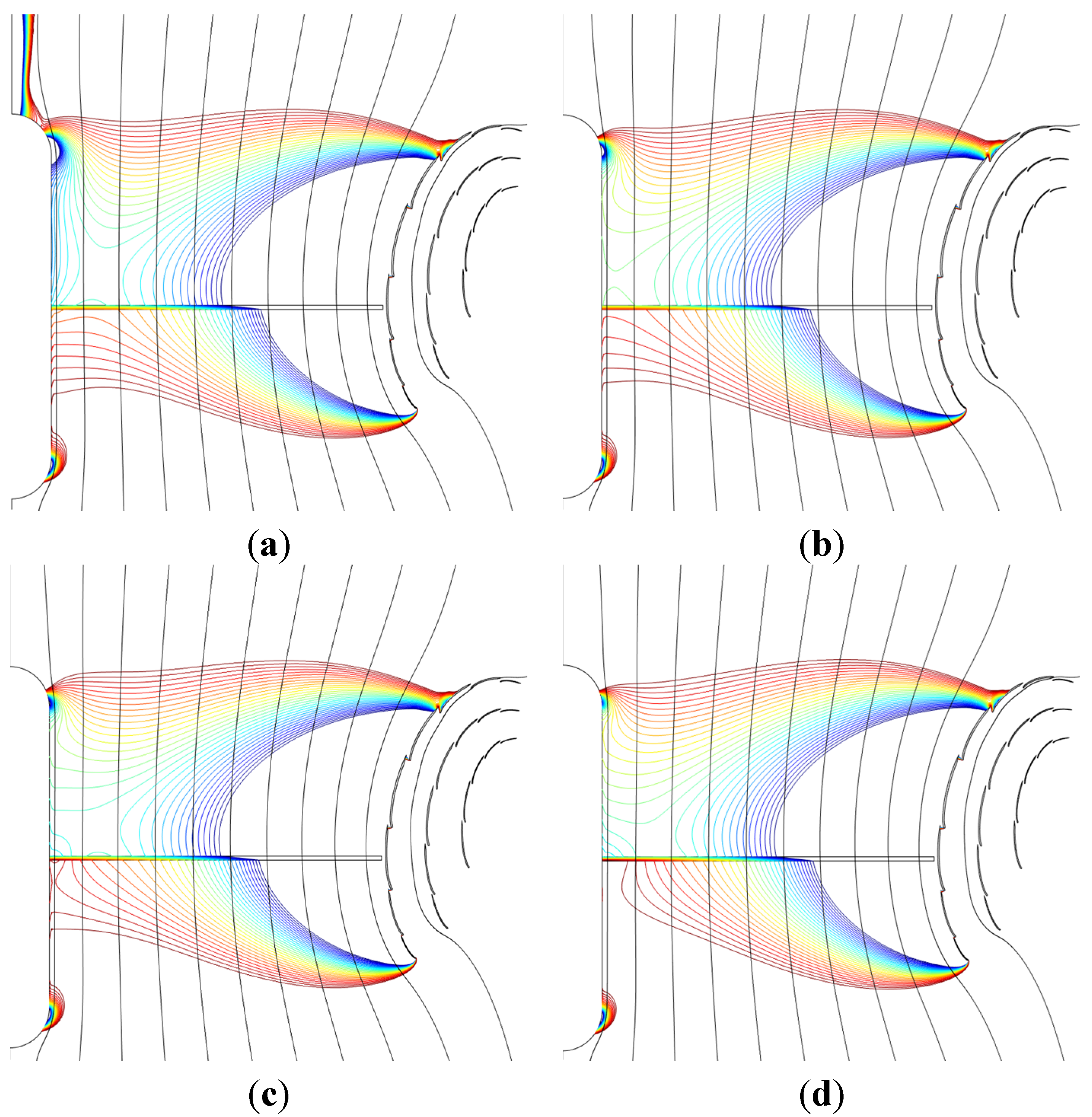
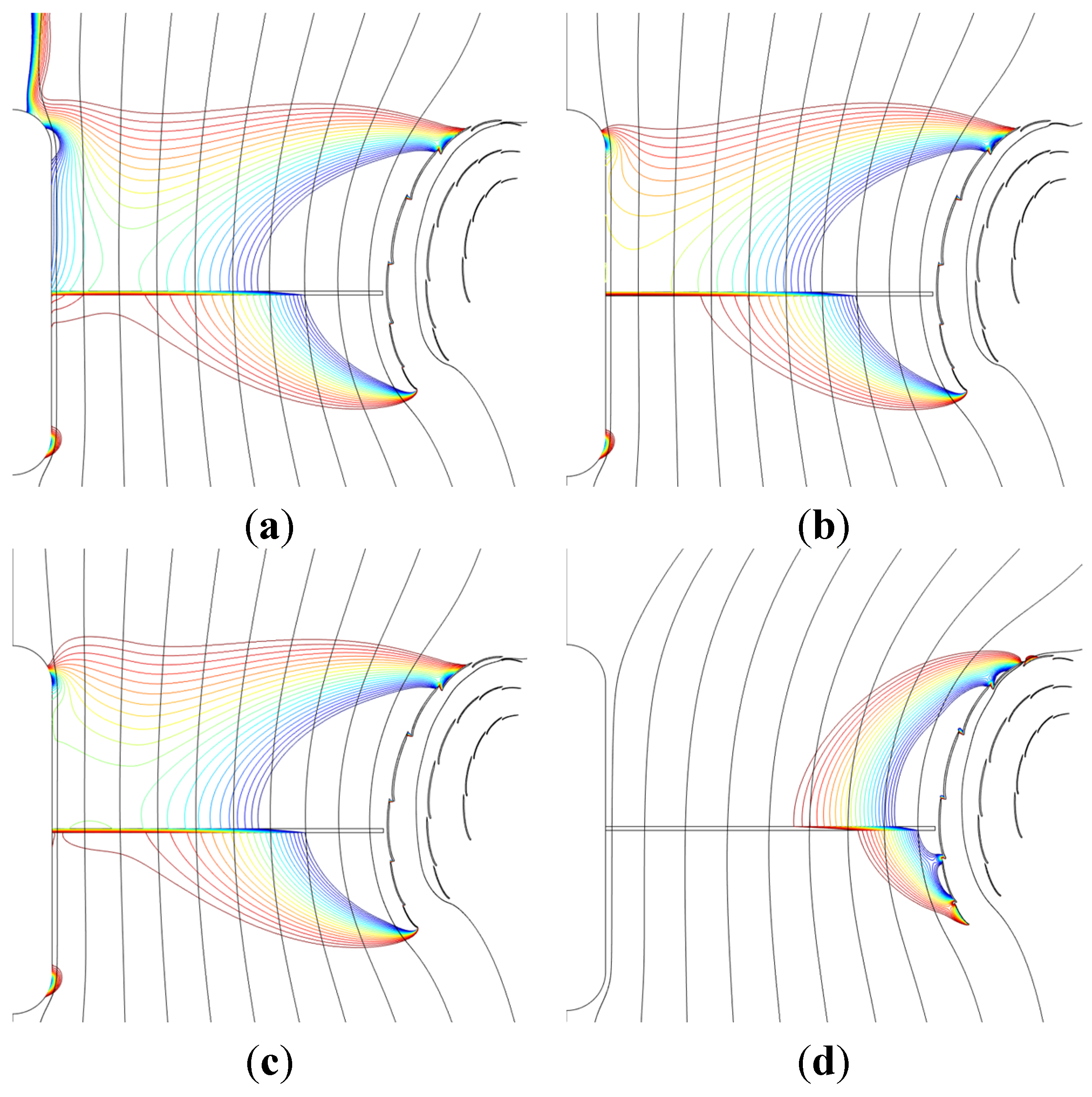
4.2. DAWT Results
- Black: No stall
- Red: Inner wake stall (vortex breakdown)
- Purple: Centerbody surface stall

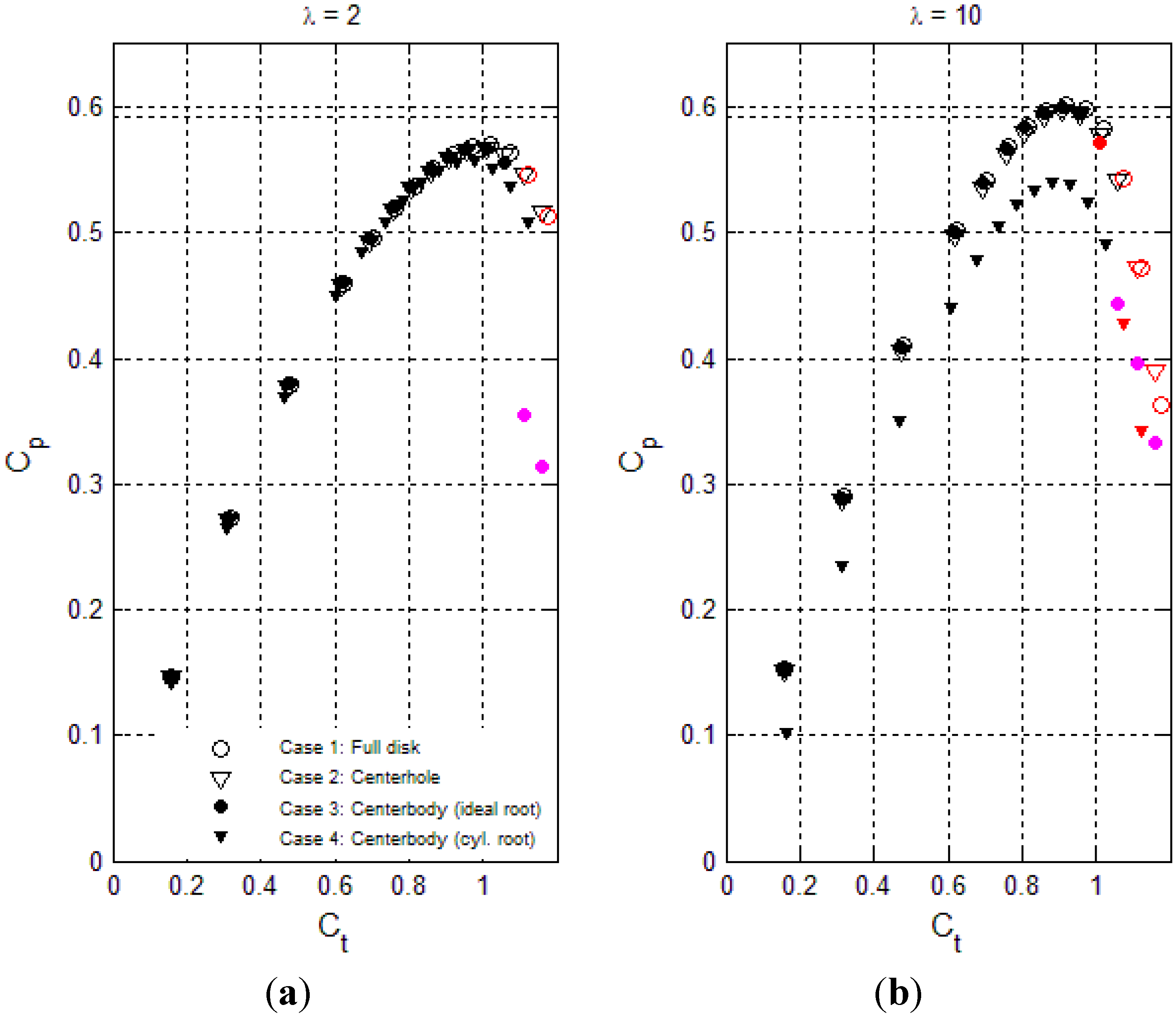

- As long as stall is avoided, the power performance is not sensitive to the type of nacelle/rotor, only exception being case 4 (centerbody with ramped-down inner loading) which performs about 0.08 lower in CP for TSR = 10 due to inner-blade cylinder drag.
- For the nacelle/rotor cases 1–2 without centerbody, the onset of inner wake stall comes at post-power-peak loading, and at lower loading for the low swirl TSR of 10 than for the high swirl TSR of 2.
- Centerbody surface stall for case 3 (centerbody, uniform disk loading) occurs at pre-power-peak thrust loading, both for high and low swirl, and most pronounced for high swirl TSR of 2.
- Very stall-resistant power performance of case 4 centerbody with ramped-down center loading and low TSR of 2.
| Configuration | |||||
|---|---|---|---|---|---|
| Bare HAWT, ideal root | 2 | 0.57 | 0.57 | 0.96 | 0.96 |
| 10 | 0.60 | 0.60 | 1.01 | 1.01 | |
| Bare HAWT, cyl. root | 2 | 0.56 | 0.56 | 0.94 | 0.94 |
| 10 | 0.54 | 0.54 | 0.91 | 0.91 | |
| Hansen DAWT, ideal root | 2 | 0.86 | 0.46 | 1.45 | 0.78 |
| 10 | 0.90 | 0.49 | 1.52 | 0.82 | |
| Hansen DAWT, cyl. root | 2 | 0.86 | 0.48 | 1.44 | 0.78 |
| 10 | 0.83 | 0.47 | 1.41 | 0.76 | |
| Multi-element DAWT, ideal root | 2 | 1.26 | 0.67 | 2.12 | 1.12 |
| 10 | 1.25 | 0.66 | 2.10 | 1.11 | |
| Multi-element DAWT, cyl. root | 2 | 1.62 | 0.86 | 2.73 | 1.45 |
| 10 | 1.13 | 0.60 | 1.90 | 1.01 |
| Configuration | |||||
|---|---|---|---|---|---|
| Bare HAWT, ideal root | 2 | 0.53 | 0.53 | 0.89 | 0.89 |
| 10 | 0.45 | 0.45 | 0.75 | 0.75 | |
| Bare HAWT, cyl. root | 2 | 0.52 | 0.52 | 0.87 | 0.87 |
| 10 | 0.39 | 0.39 | 0.65 | 0.65 | |
| Hansen DAWT, ideal root | 2 | 0.81 | 0.44 | 1.37 | 0.74 |
| 10 | 0.77 | 0.42 | 1.30 | 0.70 | |
| Hansen DAWT, cyl. root | 2 | 0.81 | 0.44 | 1.37 | 0.74 |
| 10 | 0.70 | 0.38 | 1.19 | 0.64 | |
| Multi-element DAWT, ideal root | 2 | 1.19 | 0.63 | 2.01 | 1.07 |
| 10 | 1.13 | 0.60 | 1.91 | 1.01 | |
| Multi-element DAWT, cyl. root | 2 | 1.53 | 0.81 | 2.58 | 1.37 |
| 10 | 0.97 | 0.51 | 1.64 | 0.87 |
5. Discussion, Conclusions, and Perspectives
5.1. Conclusions regarding BEM Models:
- The standard BEM model with no inclusion of the far-wake pressure drop term fails to predict any inner wake mass-flow increase due to finite TSR.
- The BEM with correct inclusion of the far-wake pressure drop predicts the swirl-induced core flow augmentation and compares well with AD results.
- The simplified inclusion of the far-wake pressure drop term (Burton, [23]) leads to a reasonable prediction of the inner wake mass-flow increase. While this BEM method is slightly less accurate than with the full wake pressure drop inclusion, the benefit of maintaining tube-element independency makes it recommendable for most engineering use.
5.2. Conclusions regarding DAWT Rotor Design
- Rotors for diffusers with high capacity for flow augmentation must be designed with low operating TSR in order to avoid premature stall-induced power drops.
- The blade loading distribution for a rotor operating inside a high capacity diffuser, such as the multi-element diffuser, must be uneven, with very little or no loading on the most inboard part.
- Power efficiency of the multi-element DAWT with a TSR of 2, uneven loading, and small wind , will exceed HAWT CP and by more than 180% and 50% respectively.
5.3. Perspectives
- Small Wind: The need for a wake core mass-flow increase makes a low rotor TSR imperative. A low TSR of, e.g., 2 will make the turbine aero-acoustically inaudible. This no-noise property is a significant upside for household DAWTs, and could enable the penetration of such WTGs into suburban areas. The partial shielding of the rotor is also visually attractive. The combination of high rotor solidity and a very short multi-element diffuser renders sideways furling to be considered for turbine control, as it will protect the rotor by facing the extreme winds with the “slim” side of the diffuser.
- High wind: The need of high-capacity DAWTs to operate at low TSRs leads to broader blades and heavier loads. While the need for structural stiffness is easily and affordably dealt with for small house-hold turbines, it is different for large wind, where turbine cost scales almost linearly with material usage and principal load levels. This will affect CoE negatively. Therefore, the high-capacity DAWT does not seem attractive for large wind applications.
Author Contributions
Conflicts of Interest
Nomenclature
Latin Symbols
| Area of stream-tube through disk at disk | [m2] | |
| Far-wake area of stream-tube through disk | [m2] | |
| Far upstream area of stream-tube through disk | [m2] | |
| Airfoil chord length | [m] | |
| Circular cylinder chord length | [m] | |
| Drag coefficient of circular cylinder section | ||
| Lift coefficient of airfoil section | ||
| Rotor (disk) axial thrust coefficient | ||
| Rotor (disk) power coefficient, all forces | ||
| Pressure coefficient on centerbody straight surface | ||
| Rotor (disk) power coefficient, axial forces only | ||
| Rotor (disk) power coefficient based on diffuser exit area | ||
| Rotor (disk) power coefficient, tangential forces only | [v] | |
| Airfoil drag force | [N] | |
| Airfoil drag force from disk on fluid | [N] | |
| Airfoil lift force from disk on fluid | [N] | |
| Thrust force from disk on fluid | [N] | |
| Thrust force from circular cylinder part | [N] | |
| Radial force from disk on fluid | [N] | |
| Force per disk volume | [N/m3] | |
| Tangential force from disk on fluid | [N] | |
| Airfoil lift force | [N] | |
| Axial length of diffuser | [m] | |
| based on rotor area normalized with Betz number | ||
| based on diffuser exit area norm. with Betz num. | ||
| Number of blades in rotor disk | ||
| Fluid static pressure | [Pa] | |
| Fluid static pressure in front of disk | [Pa] | |
| Fluid static pressure just behind disk | [Pa] | |
| Fluid static pressure at far-wake | [Pa] | |
| Fluid static ambient pressure at far-field | [Pa] | |
| Radial dimension measured from center-axis | [m] | |
| Rotor tip radius measured from center-axis | [m] | |
| Diffuser maximum radius measured from center-axis | [m] | |
| Reynolds number | ||
| Far-wake radius | [m] | |
| Centerbody straight surface length | [m] | |
| Axial velocity of flow through disk (AD) | [m/s] | |
| Normalized axial velocity of flow through disk (BEM) | ||
| Axial velocity of flow through disk (BEM) | [m/s] | |
| Axial velocity at far-wake (BEM) | [m/s] | |
| Tangential velocity of flow through disk (BEM) | [m/s] | |
| Normalized tangential velocity at far-wake (BEM) | ||
| Tangential velocity at far-wake (BEM) | [m/s] | |
| Free stream fluid velocity | [m/s] | |
| Volume | [m3] | |
| Tangential velocity of flow at disk (AD) | [m/s] | |
| Inflow velocity magnitude in rotating blade’s reference | [m/s] | |
| Weight factor for blade with lift forcing | ||
| Weight factor for cylinder root with drag forcing | ||
| Non-dimensional wall distance |
Greek Symbols
| Boundary mesh 1st row quad element height above wall | [m] | |
| Rotating reference disk angle with incoming flow | [rad] | |
| Fluid density | [kg/m3] | |
| Blade solidity at given radius | ||
| Rotor (disk) tip-speed-ratio | ||
| Disk rotational velocity | [rad/s] |
Abbreviations
| AD | Actuator Disk |
| BEM | Blade-Element Momentum |
| CFD | Computational Fluid Dynamics |
| CoE | Cost of Energy |
| DAWT | Diffuser-Augmented Wind Turbine |
| HAWT | Horizontal-Axis Wind Turbine |
| LHS | Left-Hand Side |
| NS | Navier-Stokes |
| RANS | Reynolds-Averaged Navier-Stokes |
| RHS | Right-Hand Side |
| WTG | Wind Turbine Generator |
Appendix 1
A1.1. Reduction of Variables for the Swirled-Flow BEM Formulation
A1.2. Iterative Solution Scheme for the Swirled-Flow BEM Formulation
- Initialization: Set , , and . Remaining unknowns are zero. A priori known parameters are , λ, ρ, R, plus the forcing, e.g., by specifying the axial thrust coefficient distribution, , across the radial range.
- Update rw for the far-wake stream tube corresponding to each element including Rw for the outermost stream tube, using the mass conservation property along with current values for Ud and Uw.
- Loop over all tube elements starting at the outermost element
- a
- Update Δpw using Equation (2).
- b
- Compute a range of corresponding values for Uθw, Uw, and CT using Equations (11) and (12).
- c
- Compute values for Uθw and Uw at the target CT value (specified forcing) by interpolation.
- d
- Compute Ud using Equation (A6).
- Check for convergence of the flow variables, Uw, Uθw, and Ud on all tube elements. If no convergence, goto 2).
- Solution successfully completed. Post-process by calculating all local thrust and power coefficients using Equations (12)–(15). Also calculate the area-integrated average values for thrust and power coefficients.
A1.3. Addition of Drag Forces in the Swirled-Flow BEM Formulation
Appendix 2
References
- Lilley, G.M.; Rainbird, W.J. A Preliminary Report on the Design and Performance of Ducted Windmills; Cranfield College of Aeronautics: Bedford, UK, 1956. [Google Scholar]
- Iwasaki, M. The Experimental and Theoretical Investigation of Windmills; Research Institute for Applied Mechanics, Kyushu University: Kyushu, Japan, 1953; Volume 2. [Google Scholar]
- Sanuki, M. Studies on biplane wind planes ventilation tubes and cup anemometers. Meteorol. Geophys. Jpn. 1950, 1, 279–290. [Google Scholar]
- Igra, O. Shrouds for aerogenerators. AIAA J. 1976, 14, 1481–1483. [Google Scholar] [CrossRef]
- Igra, O. Design and performance of a turbine suitable for an aerogenerator. Energy Convert. 1976, 15, 143–151. [Google Scholar] [CrossRef]
- Igra, O. Compact shrouds for wind turbines. Energy Convert. 1977, 16, 149–157. [Google Scholar] [CrossRef]
- Igra, O. The shrouded aerogenerator. Energy 1977, 2, 429–439. [Google Scholar] [CrossRef]
- Igra, O. Research and development for shrouded wind turbines. In Proceedings of the European Wind Energy Conference, Hamburg, Germany, 22–26 October 1984.
- Lewis, R.I.; Williams, J.E.; Abdelghaffar, M.A. A theory and experimental investigation of ducted wind turbines. Wind Eng. 1977, 1, 104–125. [Google Scholar]
- Oman, R.A.; Foreman, K.M.; Gilbert, B.L. Investigation of Diffuser Augmented Wind Turbines, Parts I and II; Grumman Research Department Report RE-534, ERDA Report C00–2616–2; Grumman Aerospace: New York, NY, USA, 1977. [Google Scholar]
- Gilbert, B.L.; Oman, R.A.; Foreman, K.M. Fluid dynamics of diffuser-augmented wind turbines. Energy 1978, 2, 368–374. [Google Scholar] [CrossRef]
- Phillips, D.G. An Investigation of Diffuser Augmented Wind Turbine Design. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2003. [Google Scholar]
- Betz, A. Schraubenpropeller mit geringstem Energieverlust. Mit einem Zusatz von l. Prandtl. Nachr. Ges. Wiss. zu Göttingen Math.-Phys. Kl. 1919, 193–217. (In German) [Google Scholar]
- Glauert, H. The Elements of Aerofoil and Airscrew Theory; Cambridge University Press: Cambridge, UK, 1926. [Google Scholar]
- Wilson, R.E.; Lissaman, P.B.S. Applied Aerodynamics of Wind Power Machines; Oregon State University Report; Oregon State University: Corvallis, OR, USA, 1974. [Google Scholar]
- Van Bussel, G.J.W. An assessment of the performance of diffuser augmented wind turbines. In Proceedings of the 3rd ASME Joint Fluids Engineering Conference, San Francisco, CA, USA, 18–23 July 1999.
- Van Bussel, G.J.W. The science of making more torque from wind: Diffuser experiments and theory revisited. J. Phys. Conf. Ser. 2007, 75, 1–12. [Google Scholar] [CrossRef]
- Jamieson, P. Generalized limits for energy extraction in a linear constant velocity flow field. J. Wind Energy 2007, 11, 445–457. [Google Scholar] [CrossRef]
- Werle, M.; Presz, W. Ducted wind/water turbines and propellers revisited. Propuls. Power 2008, 24, 1146–1150. [Google Scholar] [CrossRef]
- Hjort, S.; Larsen, H. A multi-element diffuser augmented wind turbine. Energies 2014, 7, 3256–3281. [Google Scholar] [CrossRef]
- Hansen, M.O.L. Effect of placing a diffuser around a wind turbine. Wind Energy 2000, 3, 207–213. [Google Scholar] [CrossRef]
- Madsen, H.A.; Mikkelsen, R.; Øye, S.; Bak, C.; Johansen, J. A detailed investigation of the blade element momentum (BEM) model based on analytical and numerical results and proposal for modifications of the BEM model. J. Phys. Conf. Ser. 2007, 75. [Google Scholar] [CrossRef]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley and Sons Ltd.: Chichester, UK, 2001. [Google Scholar]
- Hansen, M.O.L. Aerodynamics of Wind Turbines, 3rd ed.; Routledge: New York, NY, USA, 2015. [Google Scholar]
- Ohya, Y.; Karasudani, T. A shrouded wind turbine generating high output power with wind-lens technology. Energies 2010, 3, 634–649. [Google Scholar] [CrossRef]
- Lyon, C.A.; Broeren, A.P.; Giguère, P.; Gopalarathnam, A.; Selig, M.S. Summary of Low-Speed Airfoil Data; SoarTech Publications; University of Illinois: Champaign, IL, USA, 1998; Volume 3. [Google Scholar]
- Wood, D. Small Wind Turbines: Analysis, Design, and Application; Springer: Berlin, Germany, 2011. [Google Scholar]
- Abbott, I.H.; von Doenhoff, A.E. Theory of Wing Sections; Dover: New York, NY, USA, 1959. [Google Scholar]
- Drela, M. XFOIL: An analysis and design system for low reynolds number airfoils. In Low Reynolds Number Aerodynamics; Springer-Verlag: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Branlard, E. Analysis of Wind Turbine Aerodynamics and Aeroelasticity Using Vortex-based Methods. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2015. [Google Scholar]
- Mikkelsen, R. Actuator Disc Methods Applied to Wind Turbines. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2004. [Google Scholar]
- CFD Module User’s Guide, version 4.4; Comsol Inc.: Burlington, MA, USA, 2013.
- Guermond, J.L.; Minev, P.; Shen, J. An overview of projection methods for incompressible flows. Comp. Meth. Appl. Mech. Eng. 2006, 195, 6011–6045. [Google Scholar] [CrossRef]
- Glauert, H. The Analysis of Experimental Results in the Windmill Brake and Vortex Ring States of an Airscrew; HM Stationary Office: London, UK, 1926. [Google Scholar]
- Clausen, P.D.; Wood, D.H. A possible recirculation limit for expanding swirling flows. In Proceedings of the 10th Australasian Fluid Mechanics Conference, Melbourne, Australia, 11–15 December 1989.
- Clausen, P.D.; Koh, S.G.; Wood, D.H. Measurements of a swirling turbulent boundary layer developing in a conical diffuser. Exp. Therm. Fluid Sci. 1993, 6, 39–48. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hjort, S.; Larsen, H. Rotor Design for Diffuser Augmented Wind Turbines. Energies 2015, 8, 10736-10774. https://doi.org/10.3390/en81010736
Hjort S, Larsen H. Rotor Design for Diffuser Augmented Wind Turbines. Energies. 2015; 8(10):10736-10774. https://doi.org/10.3390/en81010736
Chicago/Turabian StyleHjort, Søren, and Helgi Larsen. 2015. "Rotor Design for Diffuser Augmented Wind Turbines" Energies 8, no. 10: 10736-10774. https://doi.org/10.3390/en81010736
APA StyleHjort, S., & Larsen, H. (2015). Rotor Design for Diffuser Augmented Wind Turbines. Energies, 8(10), 10736-10774. https://doi.org/10.3390/en81010736





