Optimization of Design Pressure Ratio of Positive Displacement Expander for Vehicle Engine Waste Heat Recovery †
Abstract
:1. Introduction
2. Dual-Loop Mode Engine Waste Heat Recovery System
2.1. System Configuration and Cycle Operating Conditions
2.2. Target Cycle Operating Conditions and Volume of Positive Displacement Expander
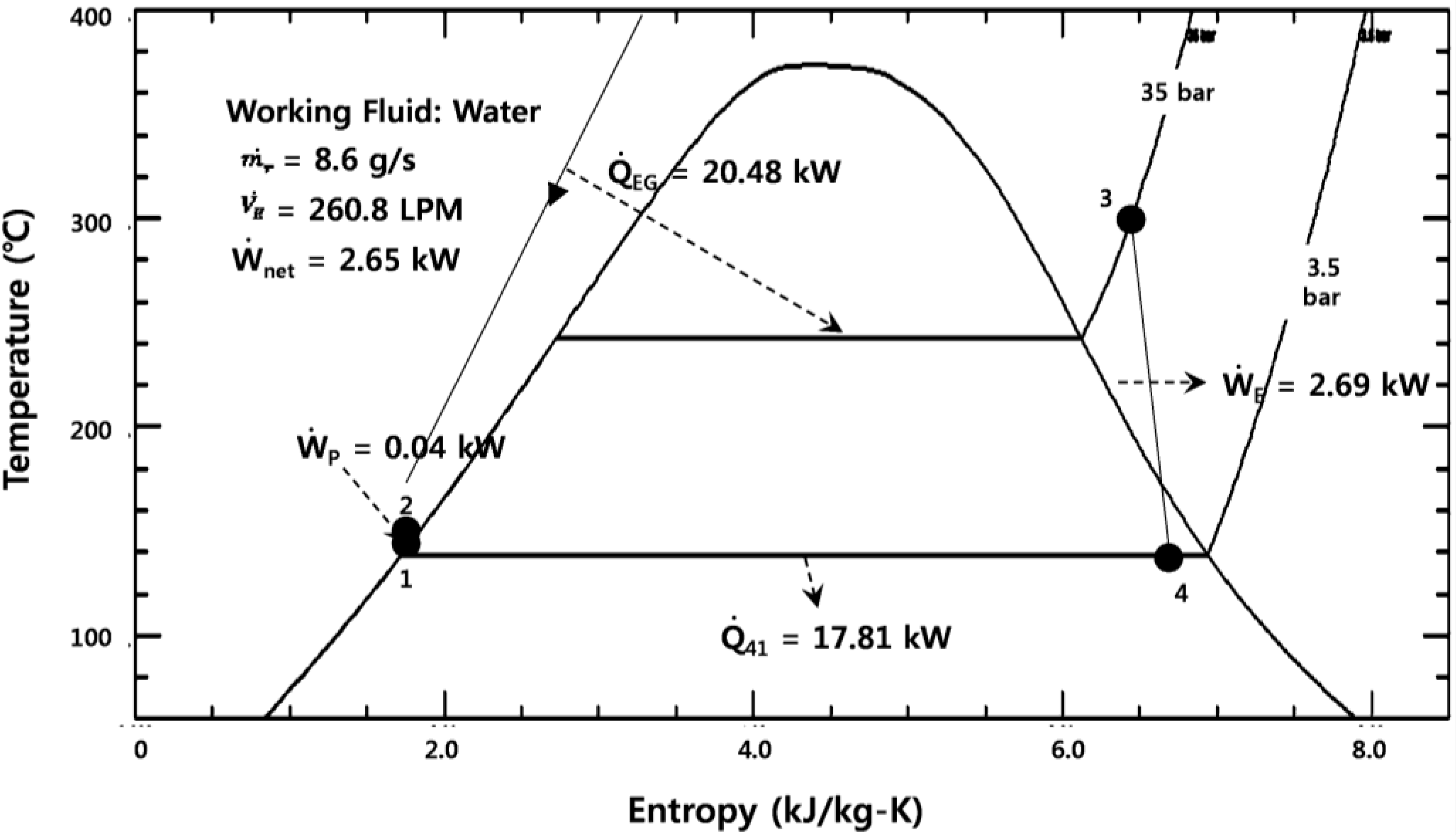
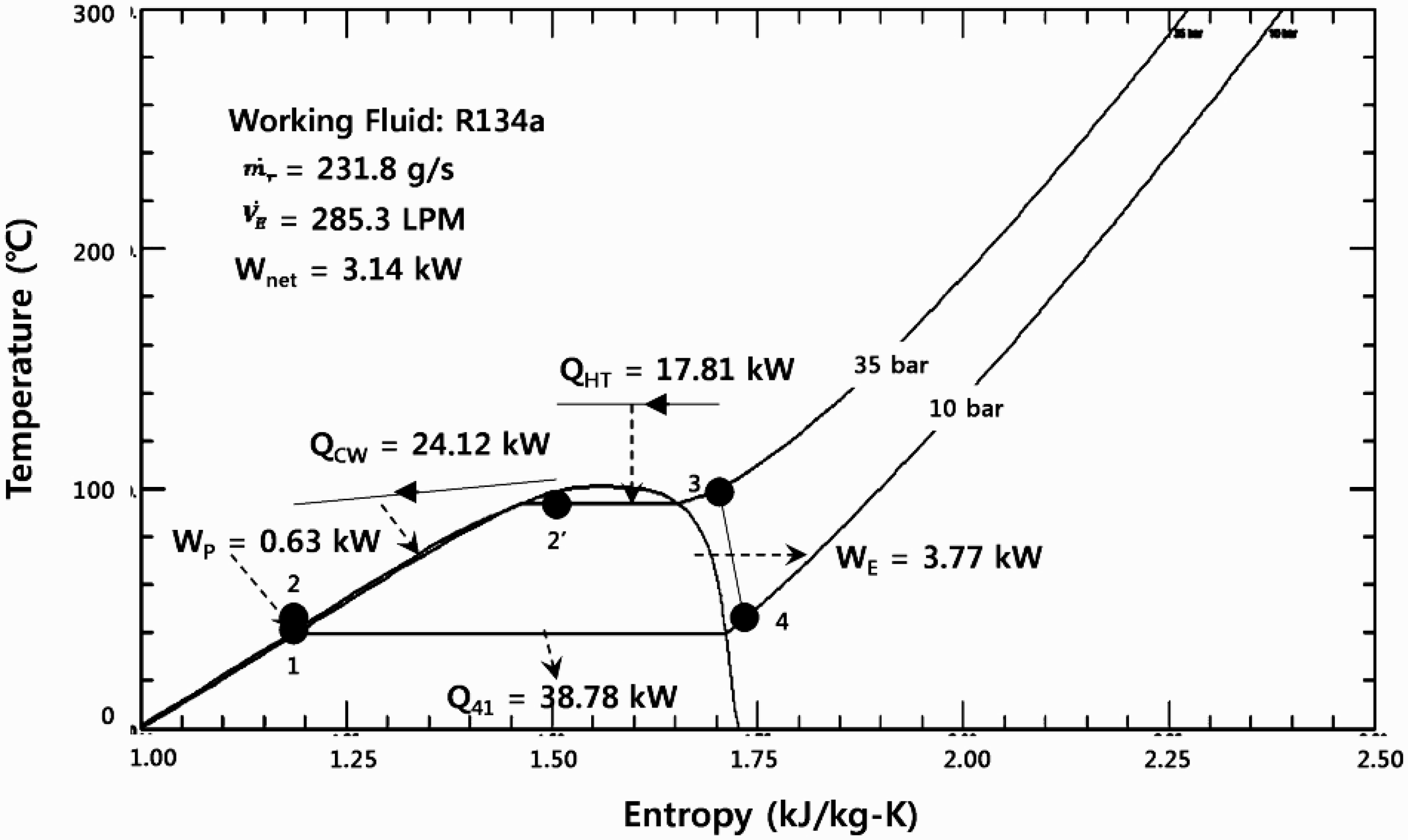
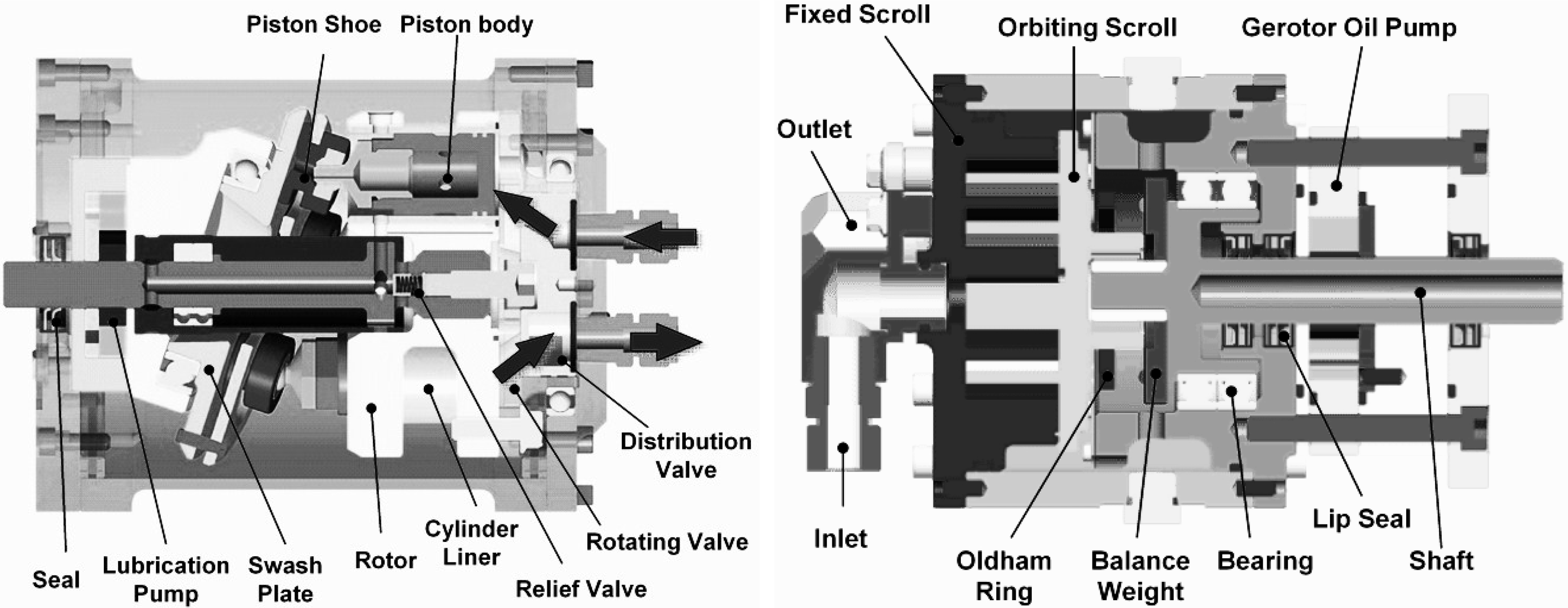
3. Expansion Characteristics of Positive Displacement Expander under Off-Design Operating Conditions
3.1. Under-Expansion and Over-Expansion
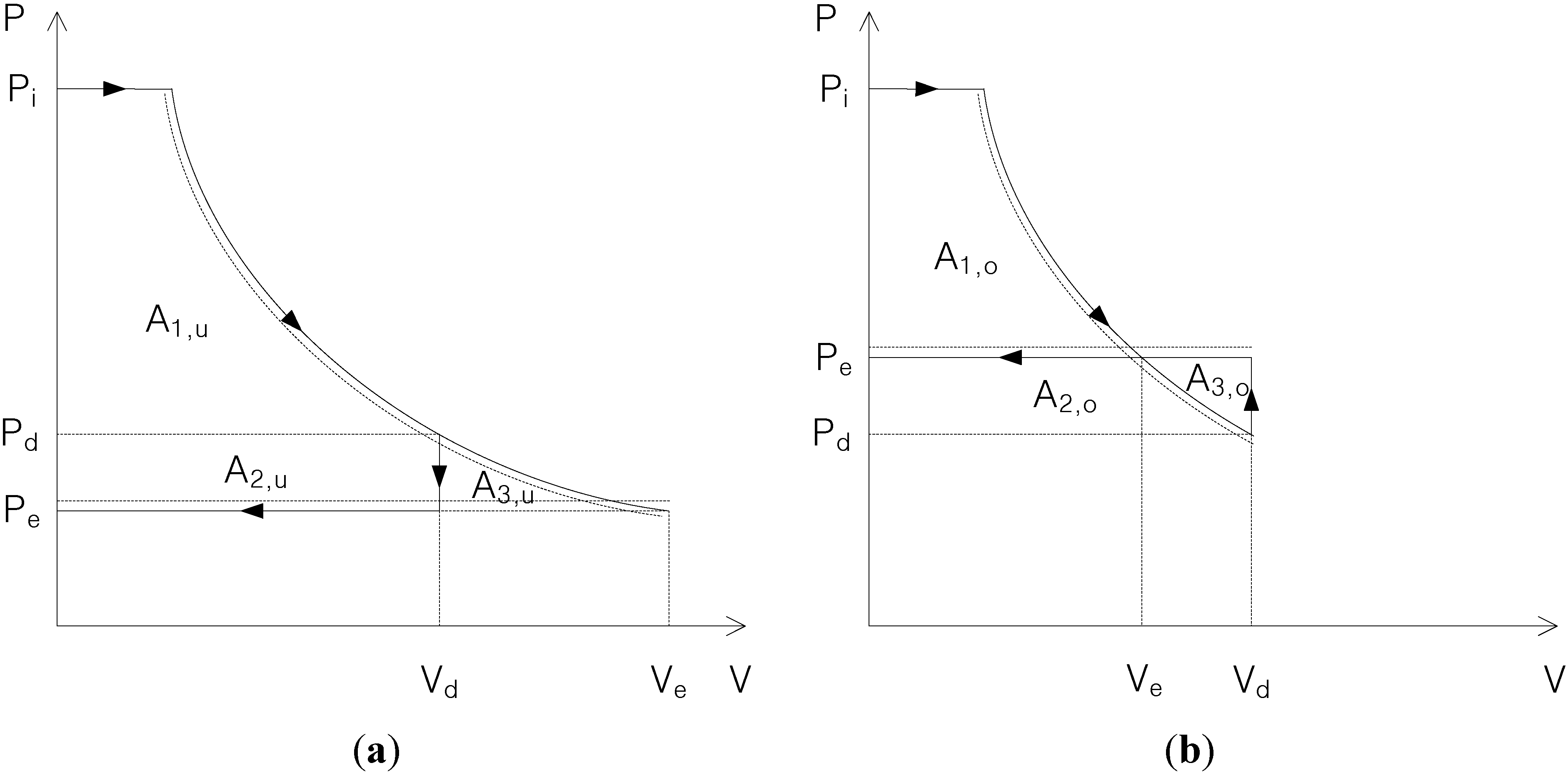
3.2. Characteristics of Expansion Efficiency during Under-Expansion and Over-Expansion
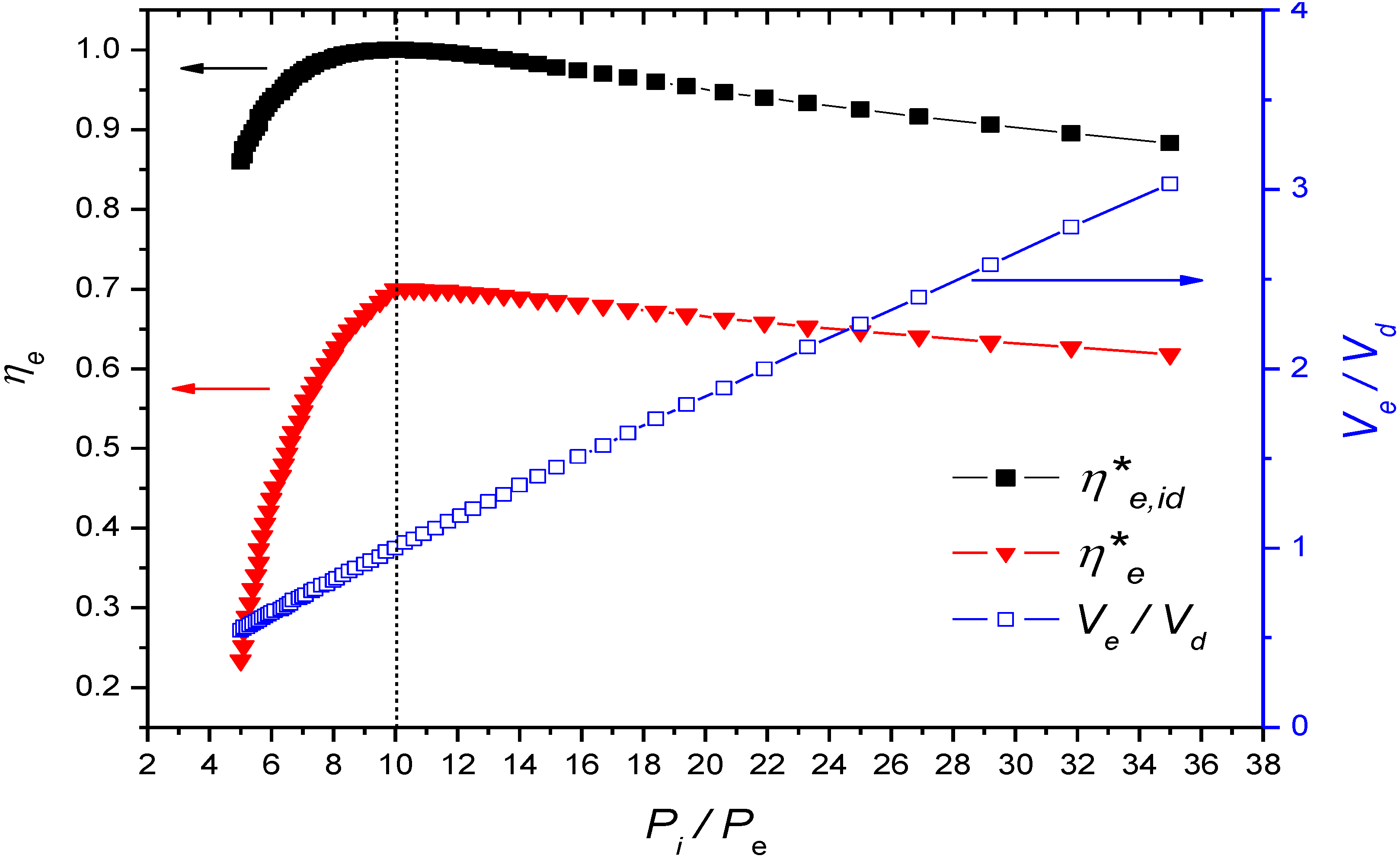
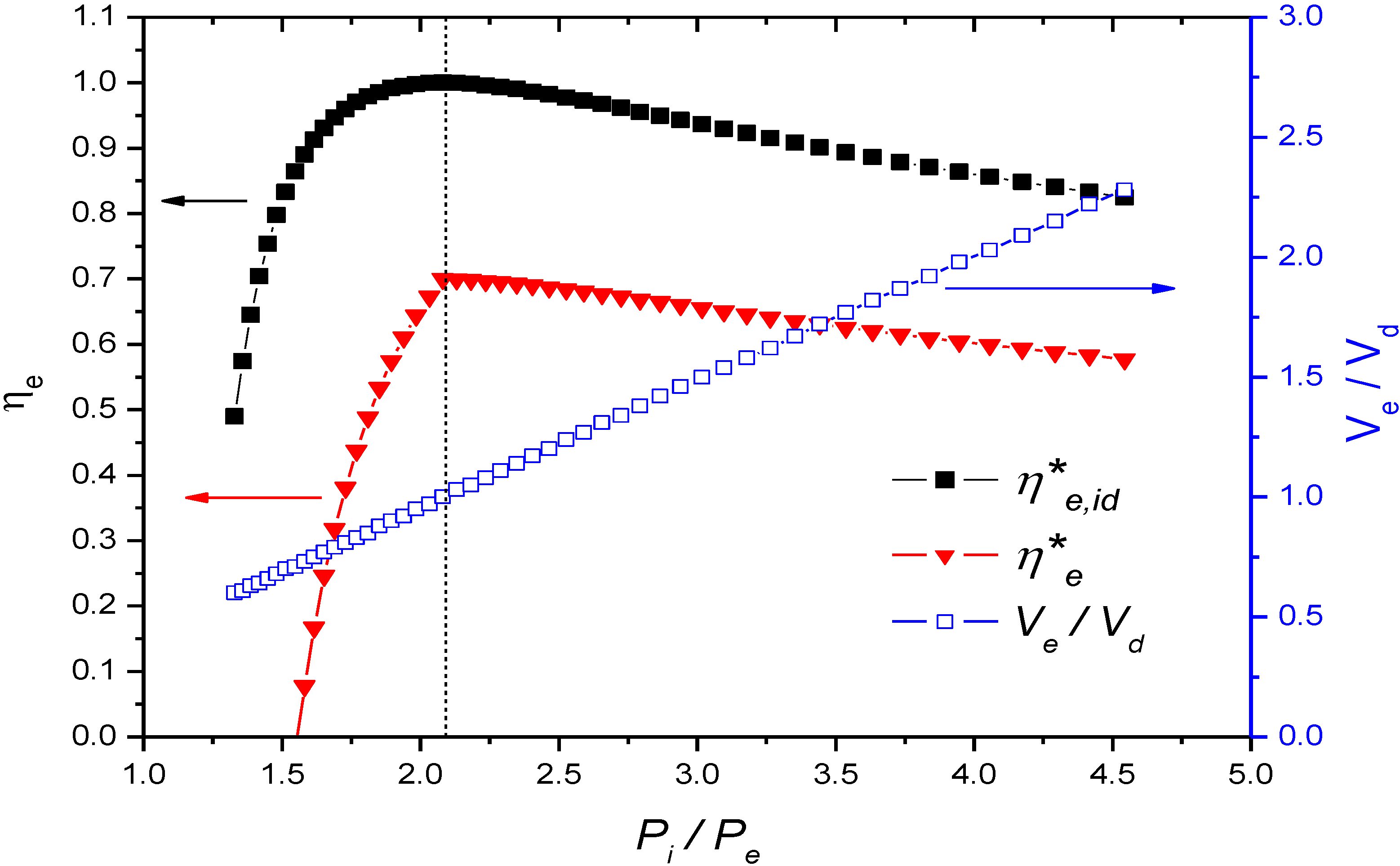
4. Performance Model of Engine Waste Heat Recovery System According to Operating Conditions
4.1. Effect of HT Cycle Condensation Temperature
| Case | (bar) | (°C) | (g/s) | (kW) | (kW) | (kW) | (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 2.0 | 138.9 | 10(7.4) | 10 | 1.00 | 0.7 | 8.6 | 0.04 | 2.69 | 2.65 | 13.0 |
| 1.2 | 120.2 | 17.5(12.3) | 17.5 | 1.00 | 0.7 | 8.6 | 0.04 | 3.25 | 3.21 | 15.1 | |
| 3.5 | 104.8 | 29.2(19.6) | 29.2 | 1.00 | 0.7 | 8.6 | 0.04 | 3.71 | 3.67 | 16.8 | |
| B | 2.0 | 138.9 | 10(7.4) | 10 | 1.00 | 0.7 | 8.6 | 0.04 | 2.69 | 2.65 | 13.0 |
| 1.2 | 120.2 | 10(7.4) | 17.5 | 1.64 | 0.675 | 8.6 | 0.04 | 3.14 | 3.10 | 14.6 | |
| 3.5 | 104.8 | 10(7.4) | 29.2 | 2.58 | 0.634 | 8.6 | 0.04 | 3.36 | 3.32 | 15.2 |
4.2. Effect of LT Cycle Condensation Temperature
| Case | (bar) | (°C) | (g/s) | (kW) | (kW) | (kW) | (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 16.8 | 60.0 | 2.1(2.4) | 2.1 | 1.00 | 0.7 | 271.1 | 0.54 | 2.49 | 1.95 | 4.7 |
| 13.2 | 50.0 | 2.7(3.2) | 2.7 | 1.00 | 0.7 | 252.8 | 0.63 | 3.20 | 2.57 | 6.1 | |
| 10.2 | 40.0 | 3.4(4.2) | 3.4 | 1.00 | 0.7 | 231.8 | 0.62 | 3.75 | 3.14 | 7.5 | |
| 7.7 | 30.0 | 4.5(5.7) | 4.5 | 1.00 | 0.7 | 214.6 | 0.61 | 4.32 | 3.71 | 8.8 | |
| B | 16.8 | 60.0 | 2.1(2.4) | 2.1 | 1.00 | 0.7 | 271.1 | 0.54 | 2.49 | 1.95 | 4.7 |
| 13.2 | 50.0 | 2.1(2.4) | 2.7 | 1.19 | 0.677 | 252.8 | 0.63 | 3.09 | 2.46 | 5.9 | |
| 10.2 | 40.0 | 2.1(2.4) | 3.4 | 1.49 | 0.631 | 231.8 | 0.62 | 3.38 | 2.76 | 6.6 | |
| 7.7 | 30.0 | 2.1(2.4) | 4.5 | 1.79 | 0.577 | 214.6 | 0.61 | 3.56 | 2.95 | 7.0 |
5. Conclusions
Author Contributions
Nomenclature
| h | specific enthalpy (kJ/kg) |
mass flow rate (kg/s) | |
| P | pressure (kPa) |
| Pr | pressure ratio |
| Vr | volume ratio |
| Q | volume ratio |
rate of heat transfer (kW) | |
| T | temperature (K) |
| V | volume (m3) |
| v | specific volume (m3/kg) |
rate of work (kW) |
Greek symbols
| ηc | compression efficiency |
| ηe, ηe* | expansion efficiency, effective expansion efficiency |
| ηth | thermal efficiency |
Subscripts
| C | condensing |
| CW | cooling water |
| d | design |
| E, e | expansion |
| HT | high temperature cycle |
| i, e | inlet, exit |
| id | ideal process |
| LT | low temperature cycle |
| net | net work |
| P | pump |
| r | refrigerant |
| s | isentropic process |
| u, o | under-expansion, over-expansion |
Conflicts of Interest
References
- Dolz, V.; Novella, R.; Garcia, A.; Sanchez, J. HD Diesel engine equipped with a bottoming Rankine cycle as a waste heat recovery system. Part 1: Study and analysis of the waste heat recovery. Appl. Therm. Eng. 2012, 36, 269–278. [Google Scholar]
- Wang, E.H.; Zhang, H.G.; Zhao, Y.; Fan, B.Y.; Wu, Y.T.; Mu, Q.H. Performance analysis of a novel system combining a dual loop organic Rankine cycle (ORC) with a gasoline engine. Energy 2012, 43, 385–395. [Google Scholar] [CrossRef]
- Vaja, I.; Gambarotta, A. Internal combustion engine (ICE) bottoming with organic Rankine cycles (ORCs). Energy 2010, 35, 1084–1093. [Google Scholar] [CrossRef]
- Heo, H.S.; Bae, S.J. Technology trends of Rankine steam cycle for engine waste heat recovery. Auto J. KSAE 2010, 32, 23–32. [Google Scholar]
- Kim, H.J.; Kim, H.J. Design of a swash plate–type of steam expander for waste heat recovery. Korean J. Air-Cond. Refrig. Eng. 2011, 23, 313–320. [Google Scholar]
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an organic Rankine cycle. Appl. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar] [CrossRef]
- Bae, S.; Heo, H.; Lee, H.; Lee, D.; Kim, T.; Park, J.; Kim, C. Performance characteristics of a steam cycle and boiler for engine waste heat recovery. SAE Tech. Pap. 2011, 2011. [Google Scholar] [CrossRef]
- Ringler, J.; Seifert, M.; Guyotot, V.; Hübner, W. Rankine cycle for waste heat recovery of IC engines. SAE Tech. Pap. 2009, 2009. [Google Scholar] [CrossRef]
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Low-grade heat conversion into power using organic Rankine cycles—A review of various applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979. [Google Scholar] [CrossRef]
- Zanelli, R.; Favrat, D. Experimental Investigation of a Hermetic Scroll Expander-Generator. In Proceedings of the International Compressor Engineering Conference, Purdue University, West Lafayette, IN, USA, 19–22 July 1994; p. 1021.
- Kim, Y.M.; Shin, D.G.; Kim, C.G.; Woo, S.J.; Choi, B.C. Performance analysis of two-loop Rankine cycle for engine waste heat recovery. J. Energy Eng. 2012, 21, 398–406. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kim, Y.M.; Shin, D.G.; Kim, C.G. Optimization of Design Pressure Ratio of Positive Displacement Expander for Vehicle Engine Waste Heat Recovery. Energies 2014, 7, 6105-6117. https://doi.org/10.3390/en7096105
Kim YM, Shin DG, Kim CG. Optimization of Design Pressure Ratio of Positive Displacement Expander for Vehicle Engine Waste Heat Recovery. Energies. 2014; 7(9):6105-6117. https://doi.org/10.3390/en7096105
Chicago/Turabian StyleKim, Young Min, Dong Gil Shin, and Chang Gi Kim. 2014. "Optimization of Design Pressure Ratio of Positive Displacement Expander for Vehicle Engine Waste Heat Recovery" Energies 7, no. 9: 6105-6117. https://doi.org/10.3390/en7096105
APA StyleKim, Y. M., Shin, D. G., & Kim, C. G. (2014). Optimization of Design Pressure Ratio of Positive Displacement Expander for Vehicle Engine Waste Heat Recovery. Energies, 7(9), 6105-6117. https://doi.org/10.3390/en7096105





