Challenges in Bioenergy Production from Sugarcane Mills in Developing Countries: A Case Study
Abstract
:1. Introduction
| Country | Power mode | Configuration | Use of trash | Surplus electricity (kWh/ton of cane) |
|---|---|---|---|---|
| Brazil | BPST | 22 bar, 300 °C | No | 0–10 |
| Brazil | BPST | 42 bar, 440 °C | No | 20 |
| Brazil | BPST | 67 bar, 480 °C | No | 40–60 |
| Brazil | CEST | 65 bar, 480 °C | Yes (50%) | 139.7 |
| Brazil | CEST | 105 bar, 525 °C | Yes (50%) | 158 |
| India | CEST | 67 bar, 495 °C | No | 90–120 |
| India | CEST | 87 bar, 515 °C | No | 130–140 |
2. Methods
2.1. Case Study: A Colombian Sugarcane Milling Plant
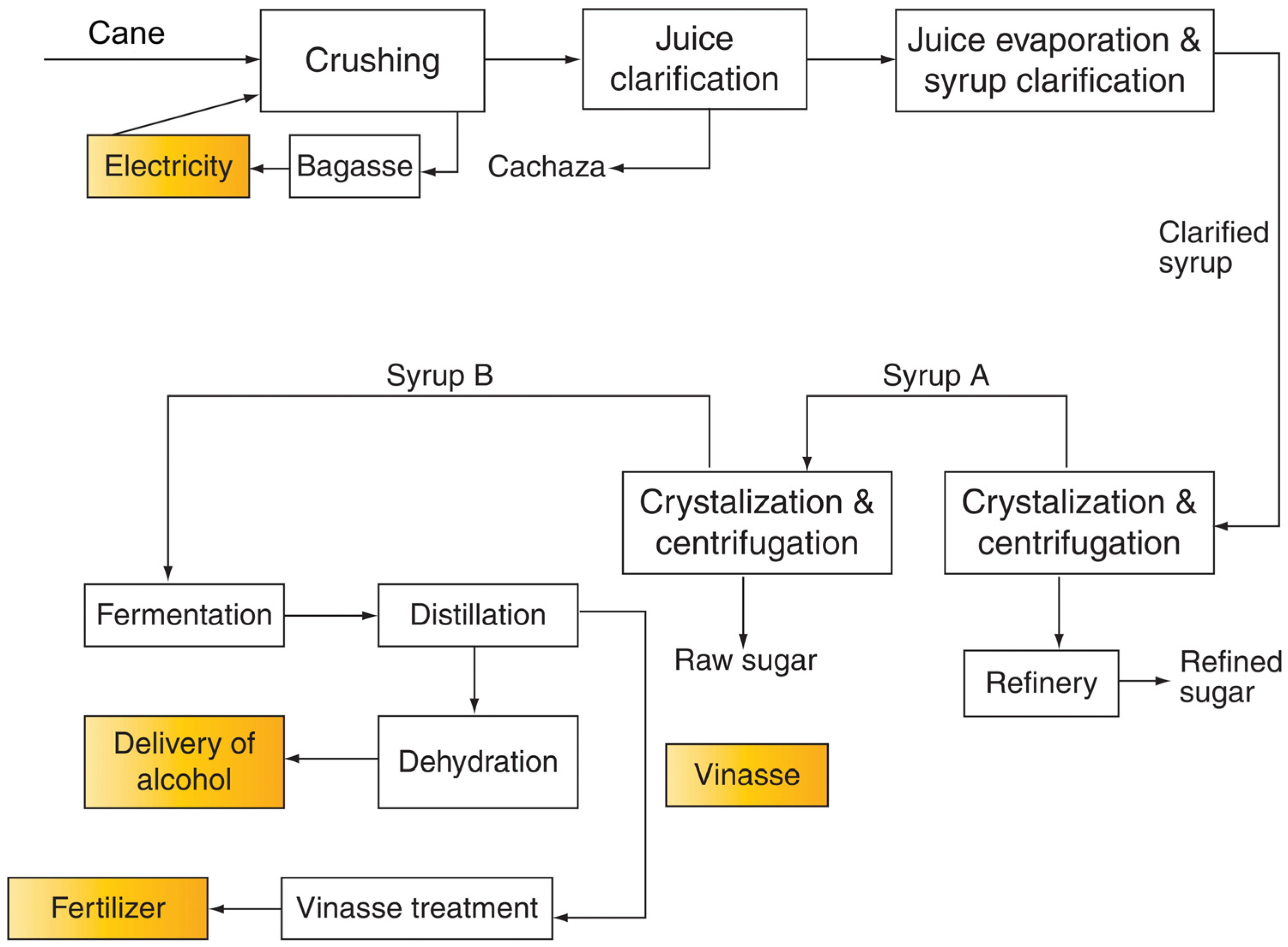
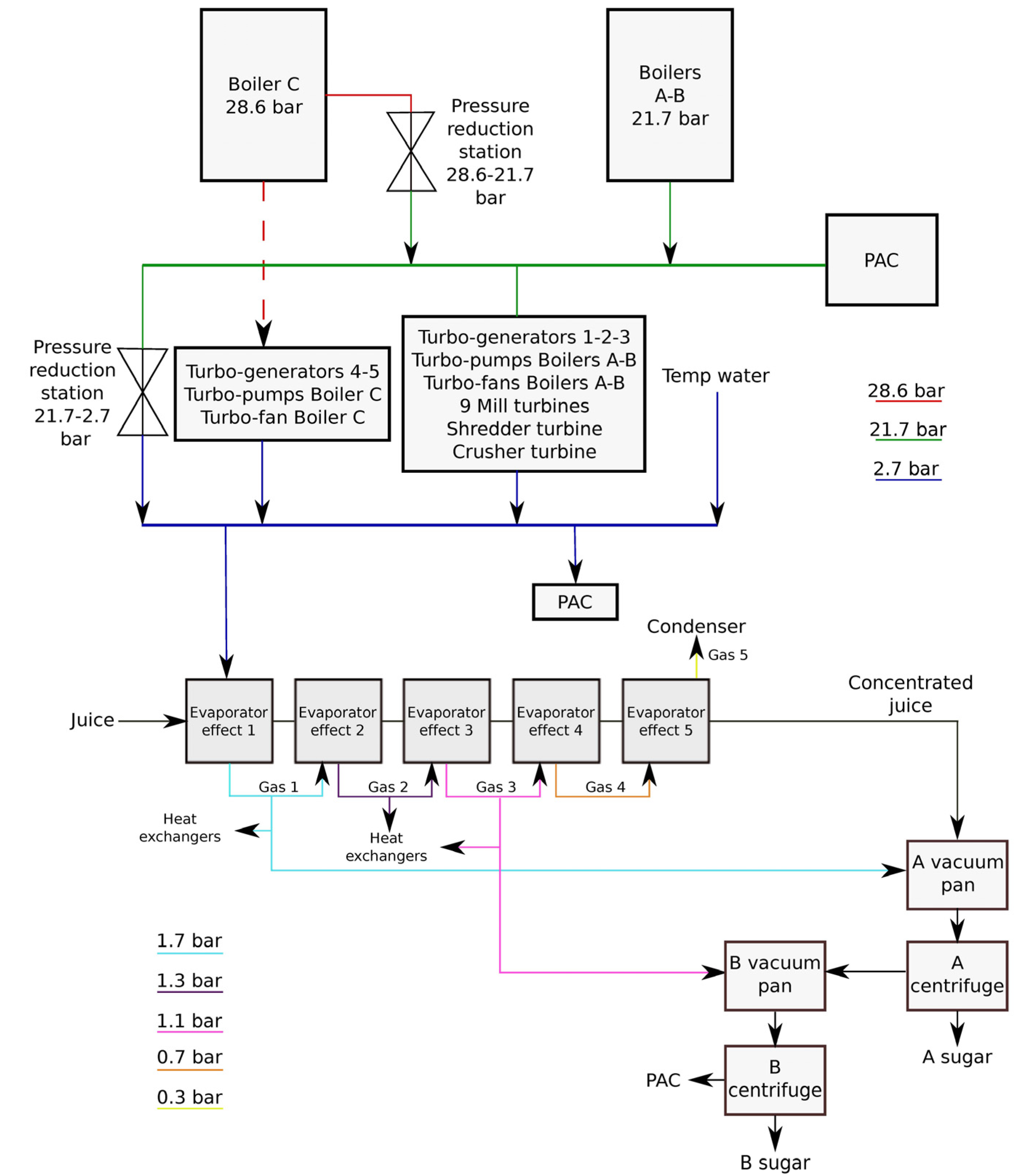
2.2. Electrical Energy and Steam Requirements in the Sugar and Bioethanol Plant Production

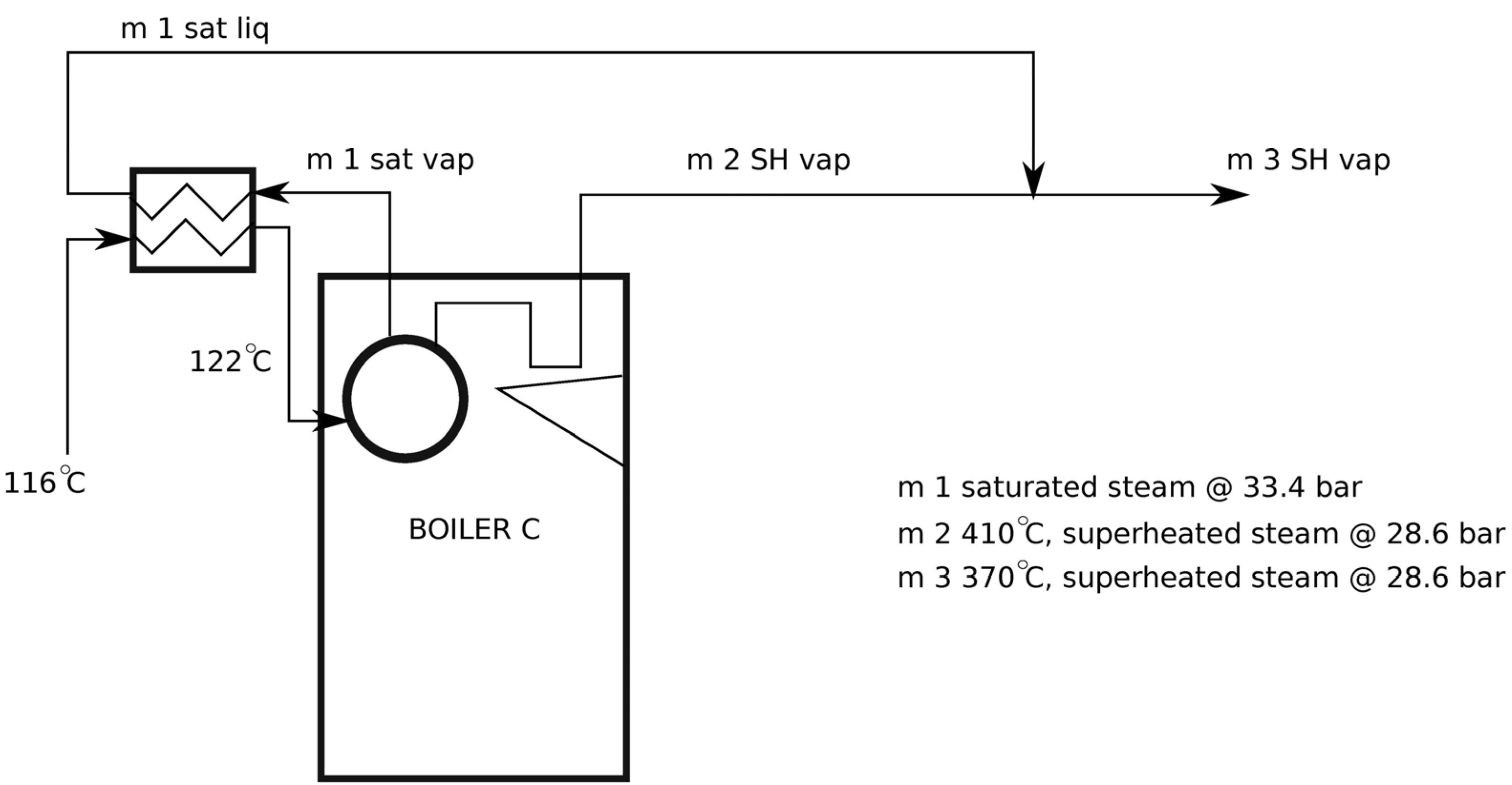
2.3. Cogeneration
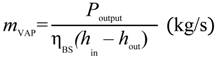
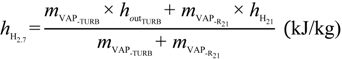
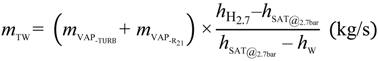
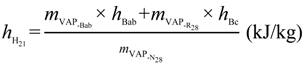
- Temperature and pressure of Boiler C: TBc = 410 °C; pBc-SH = 28.6 bar;
- Pressure of Boiler C saturated steam: pBc-sat = 33.6 bar;
- Temperature and pressure of Boilers A and B: TBab = 330 °C; pBab = 21.7 bar;
- Boilers efficiency: ηBab = 0.58; ηBc = 0.64;
- Temperature after Boiler C tempering water addition: TBc-TEMP = 370 °C;
- Temperature loss from boilers A and B to 21.7 bar turbines: ∆TBab-turb = 10 °C;
- Isentropic efficiency of the turbines: ηIS-turb = 0.60;
- Isentropic efficiency of turbines for electrical power generation 4 and 5: ηIS-TG45 = 0.68;
- Mechanical efficiency of the turbines (blades-shaft): ηB-S = 0.98;
- Electrical efficiency of the generators: ηel = 0.95;
- Turbine discharge pressure: pVE = 2.7 bar;
- Nominal power of Turbo-fan of boilers: PVTIa = 253 kW; PVTIb = 201 kW; PVTIc = 615 kW;
- Nominal power of Turbo-generators: PTG1 = PTG2 = 1250 kW; PTG3 = 2500 kW; PTG4 = 3760 kW; PTG5 = 8510 kW.
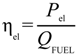
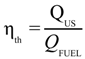
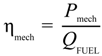
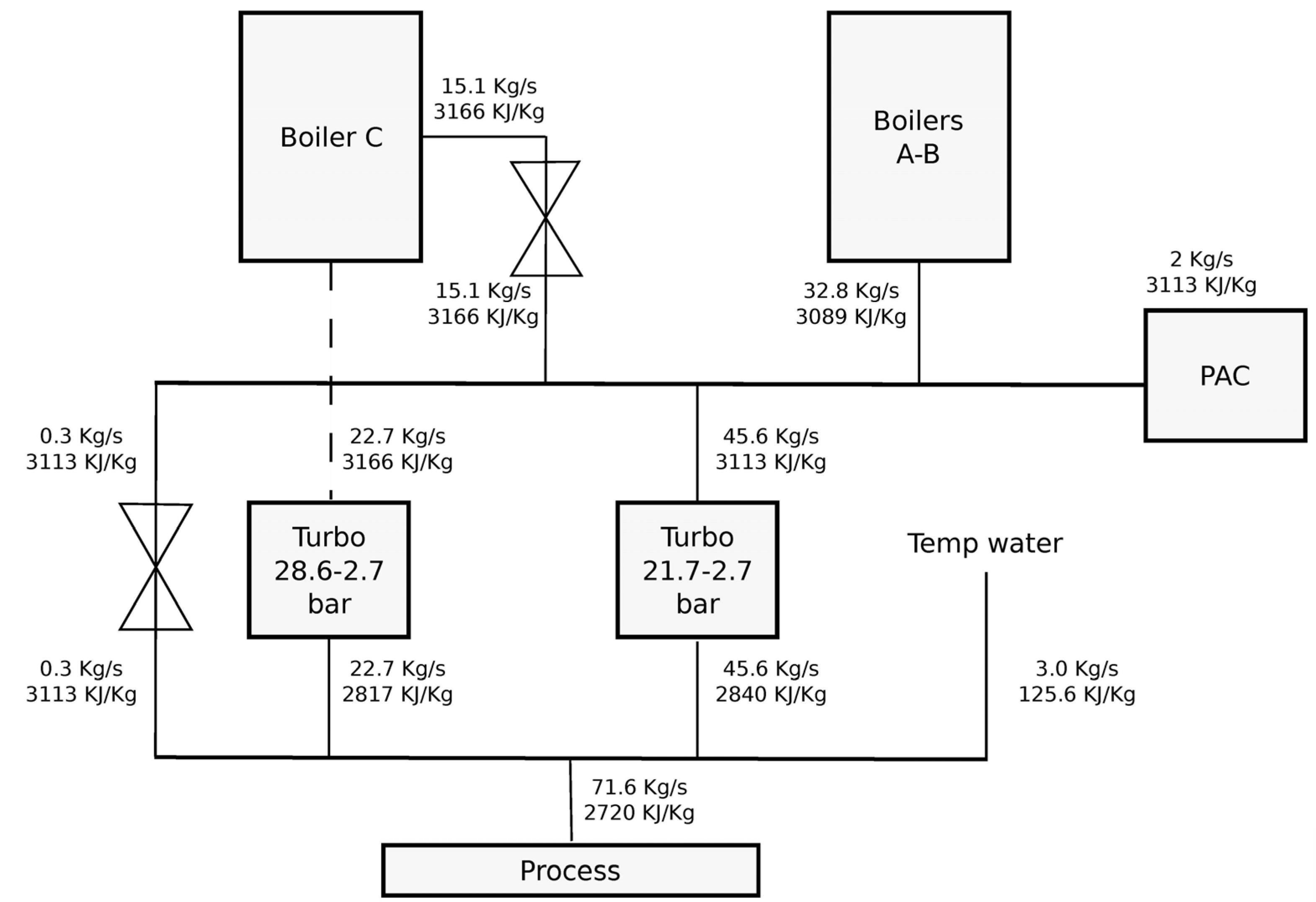
3. Results and Discussion
3.1. Milling Rate Dependence
3.2. Exergy Losses
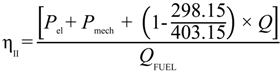
3.3. Renewable Efficiency
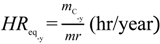
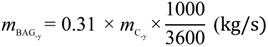
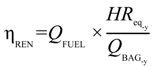
| Process | Energy loss [%] |
|---|---|
| Boiler C tempering | 3.6 |
| 28.6 to 21.7 bar reduction | 3.2 |
| 21.7 to 2.7 bar reduction | 26.4 |
| 2.7 bar head tempering | 1.2 |
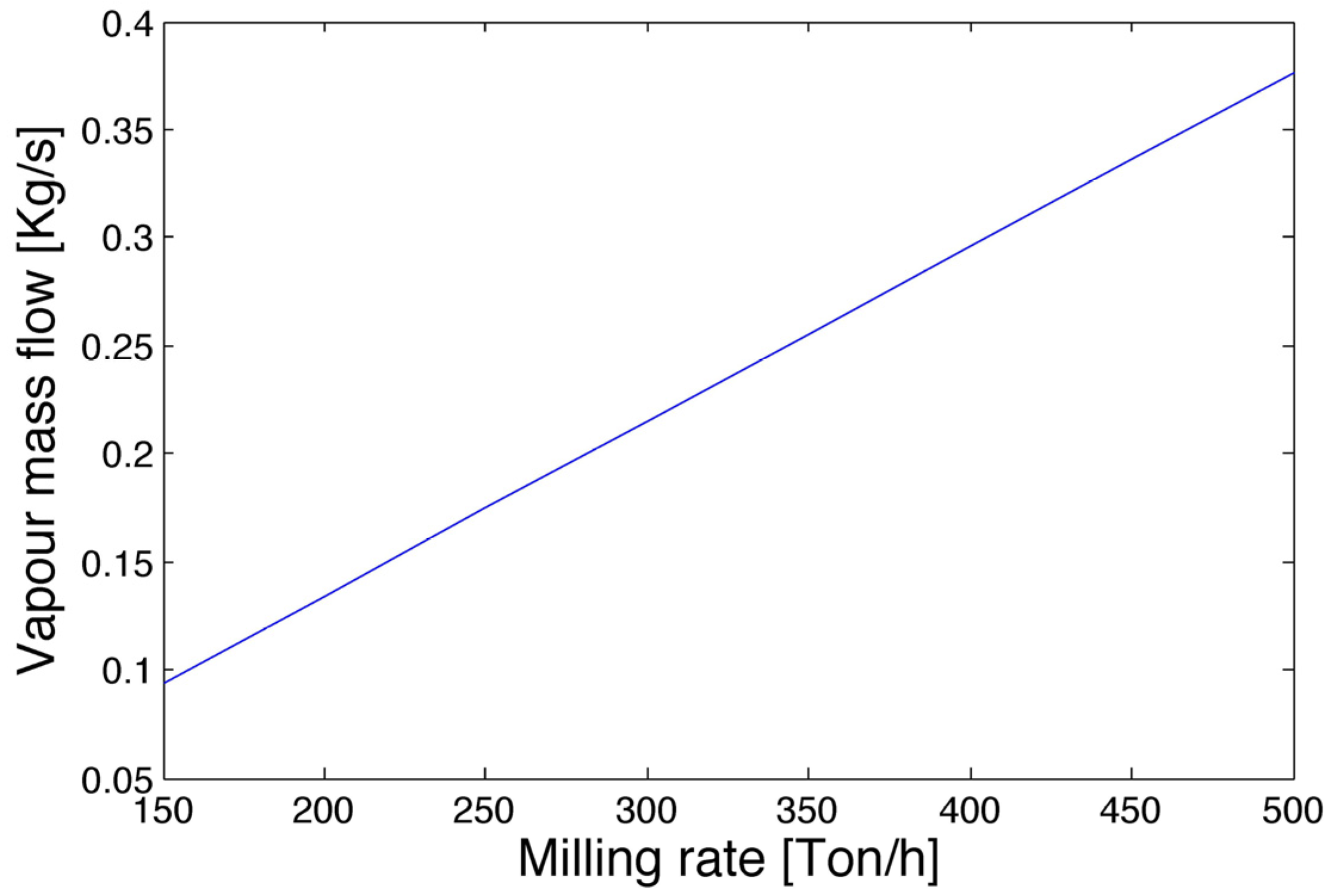
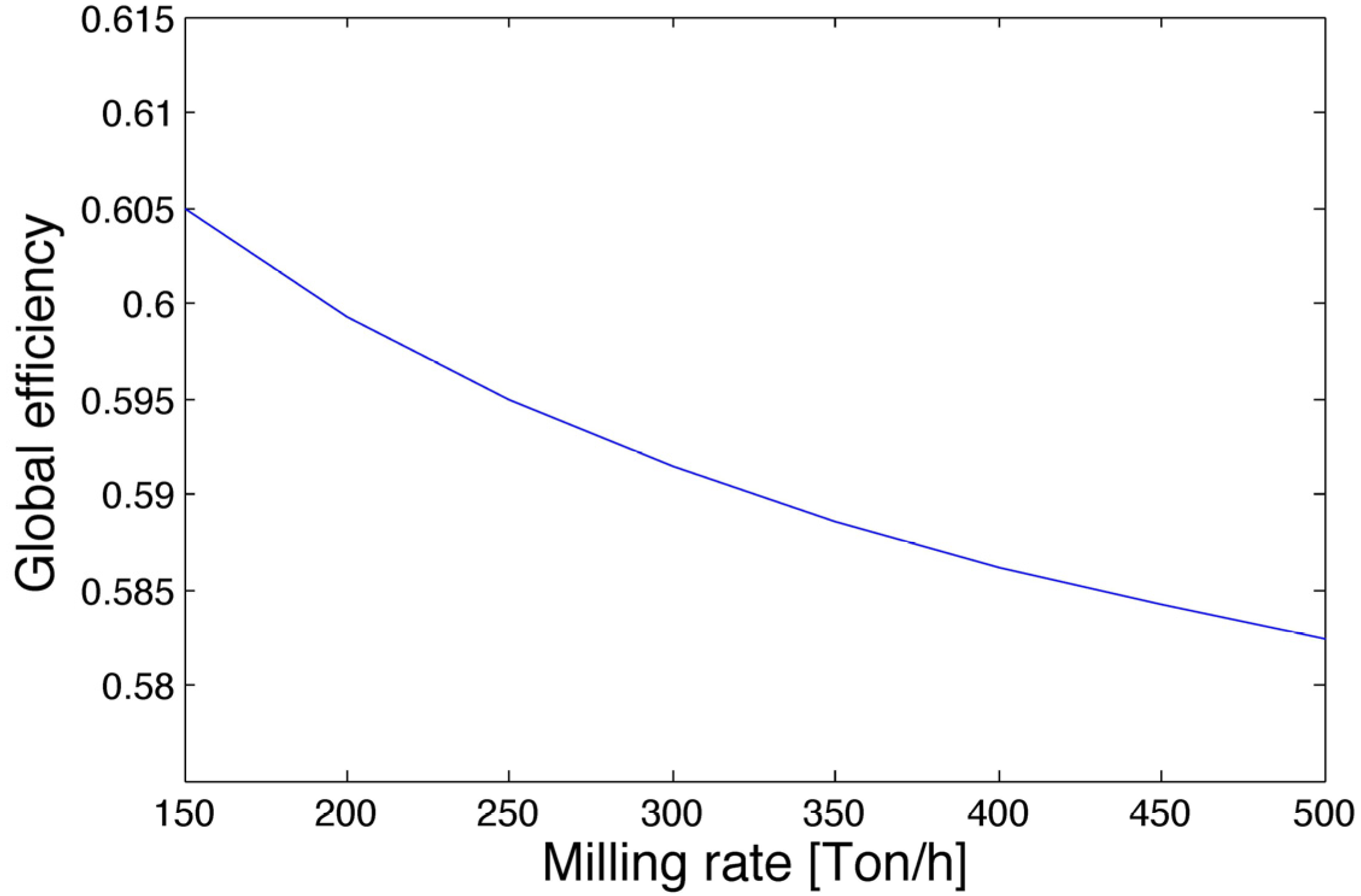
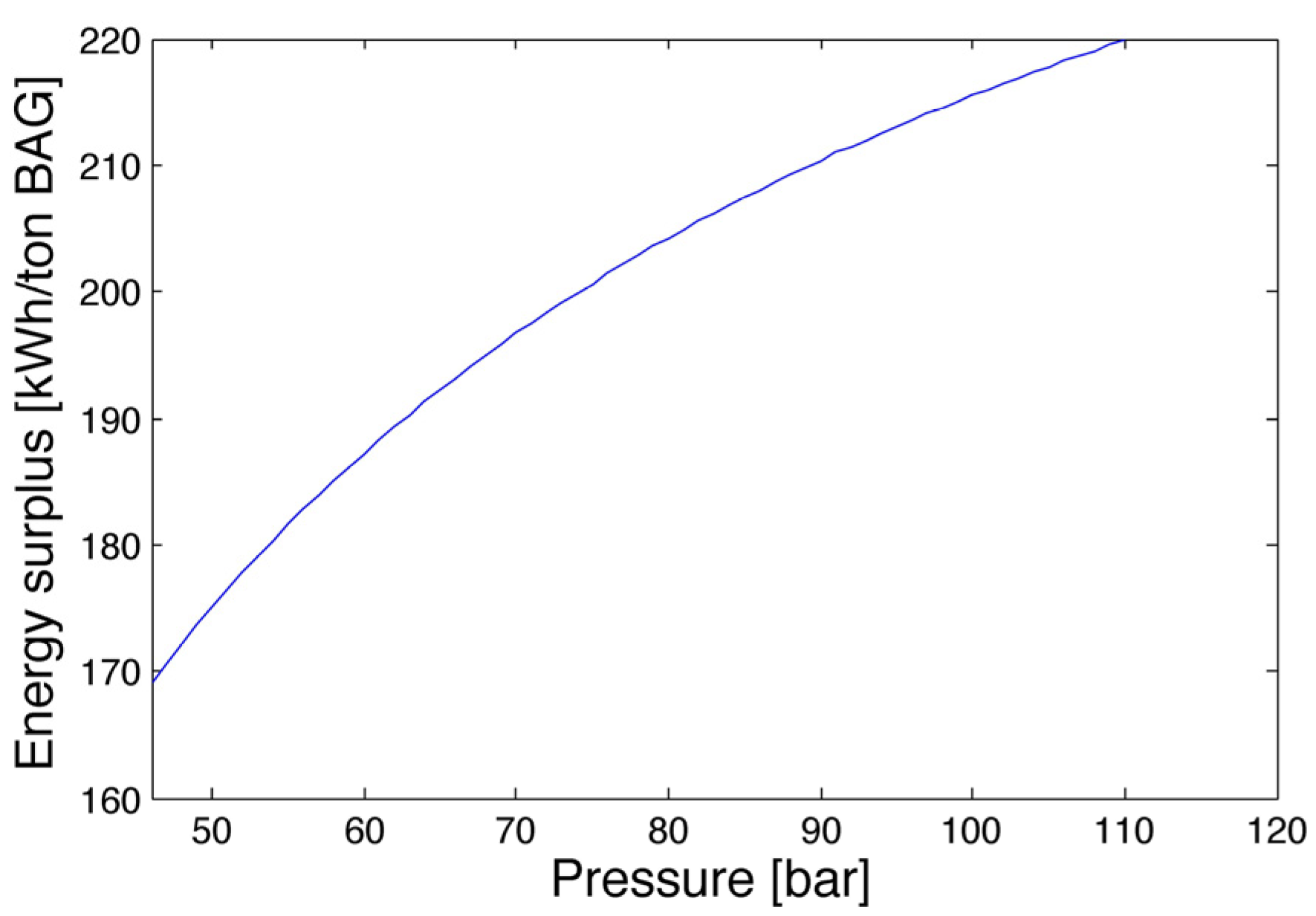
3.4. Sensitivity Analysis
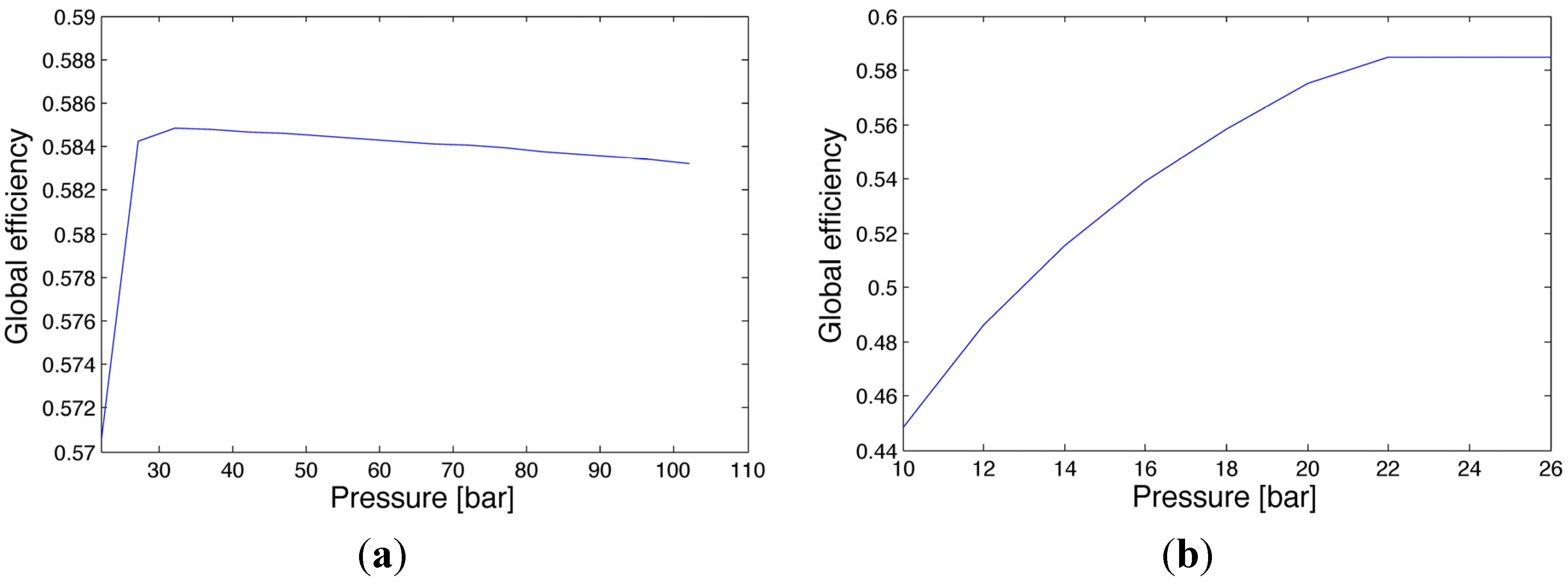
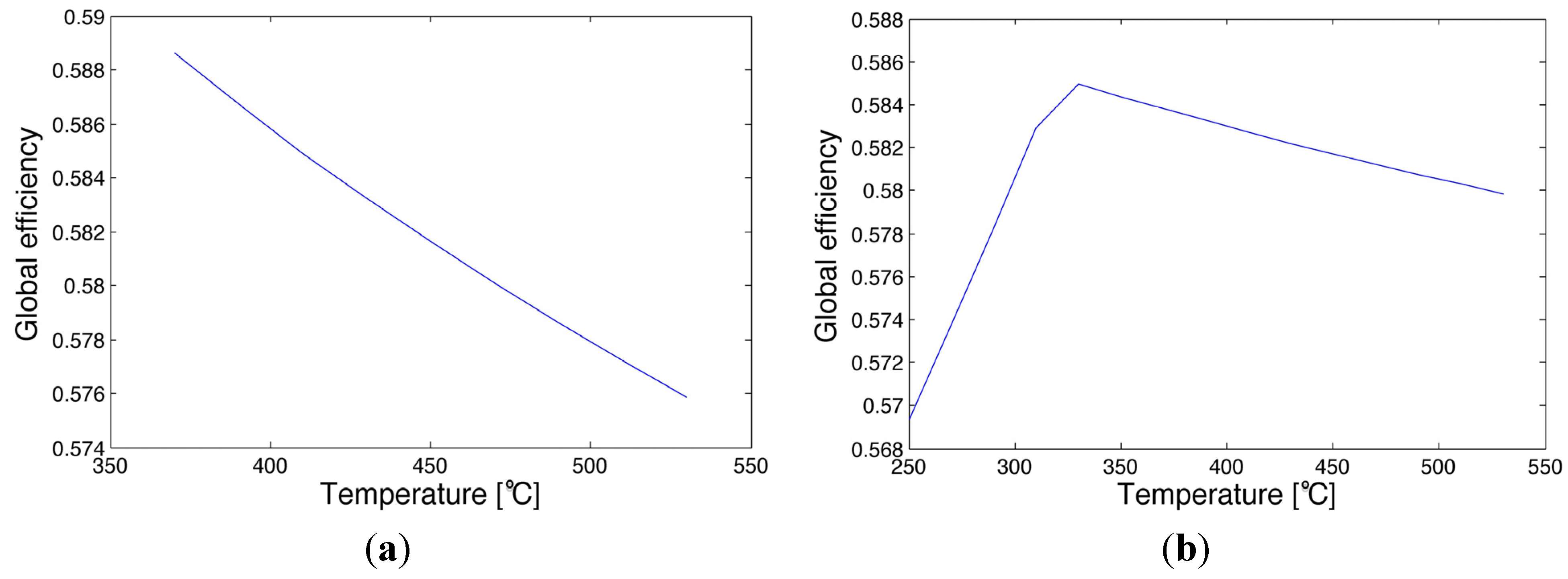
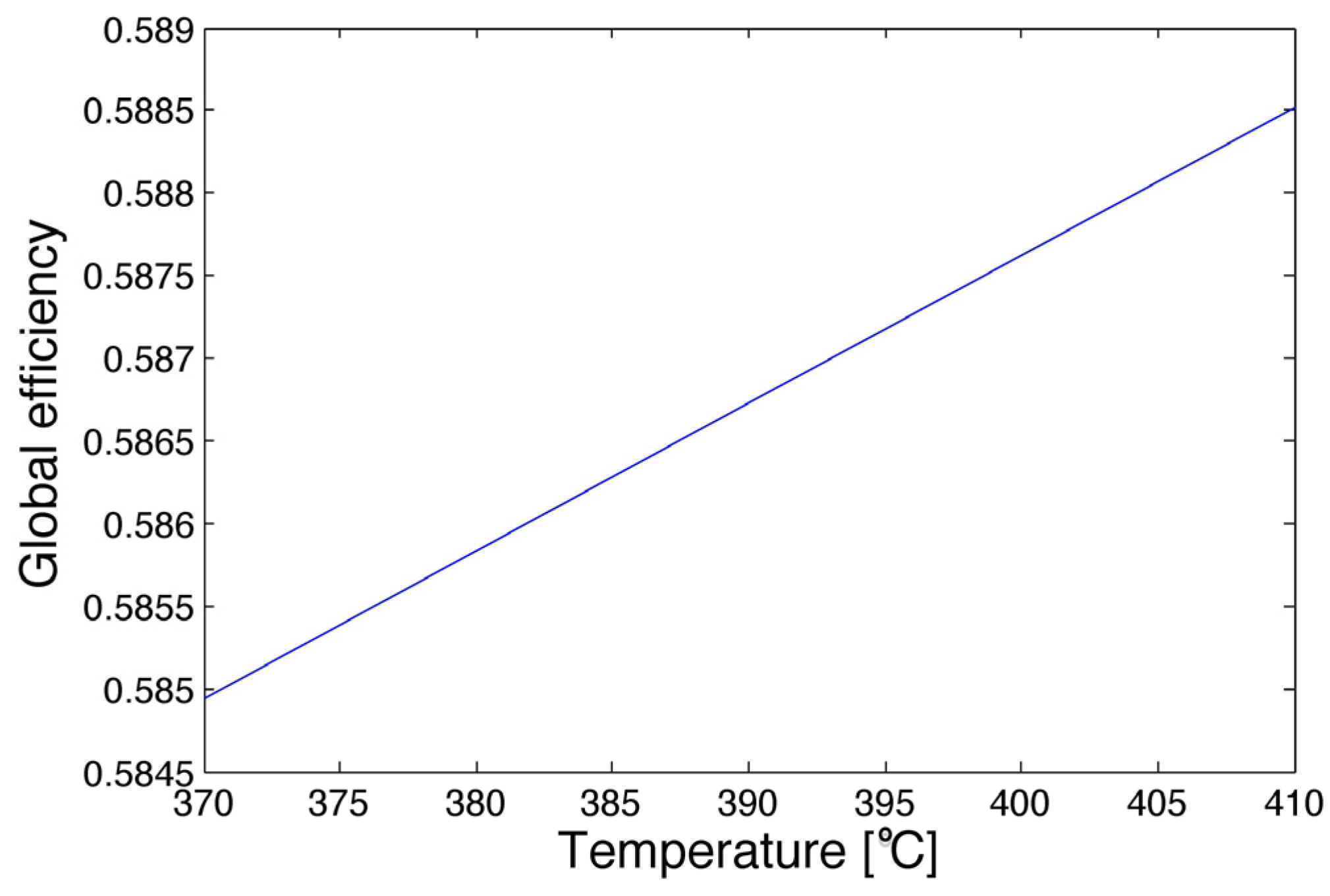
3.5. Numerical Optimization
| Temperature | Minimum value (°C) | Maximum value (°C) |
|---|---|---|
| Boiler C | 365 | 540 |
| Boilers A and B | 320 | 340 |
| Boiler C tempering output | 365 | 375 |
4. Scenarios to Improve the Global Efficiency
| Milling rate: 430 Ton/h | p boiler C (bar) | T boiler C (°C) | p boilers A, B (bar) | T boilers A, B (°C) | Toutlet tempering boiler C (°C) | Global efficiency |
|---|---|---|---|---|---|---|
| Current case | 28.6 | 410 | 21.7 | 330 | 370 | 0.5849 |
| Optimal case | 28.6 | 380 | 21.7 | 320 | 370 | 0.5880 |
4.1. Option 1 Repowering
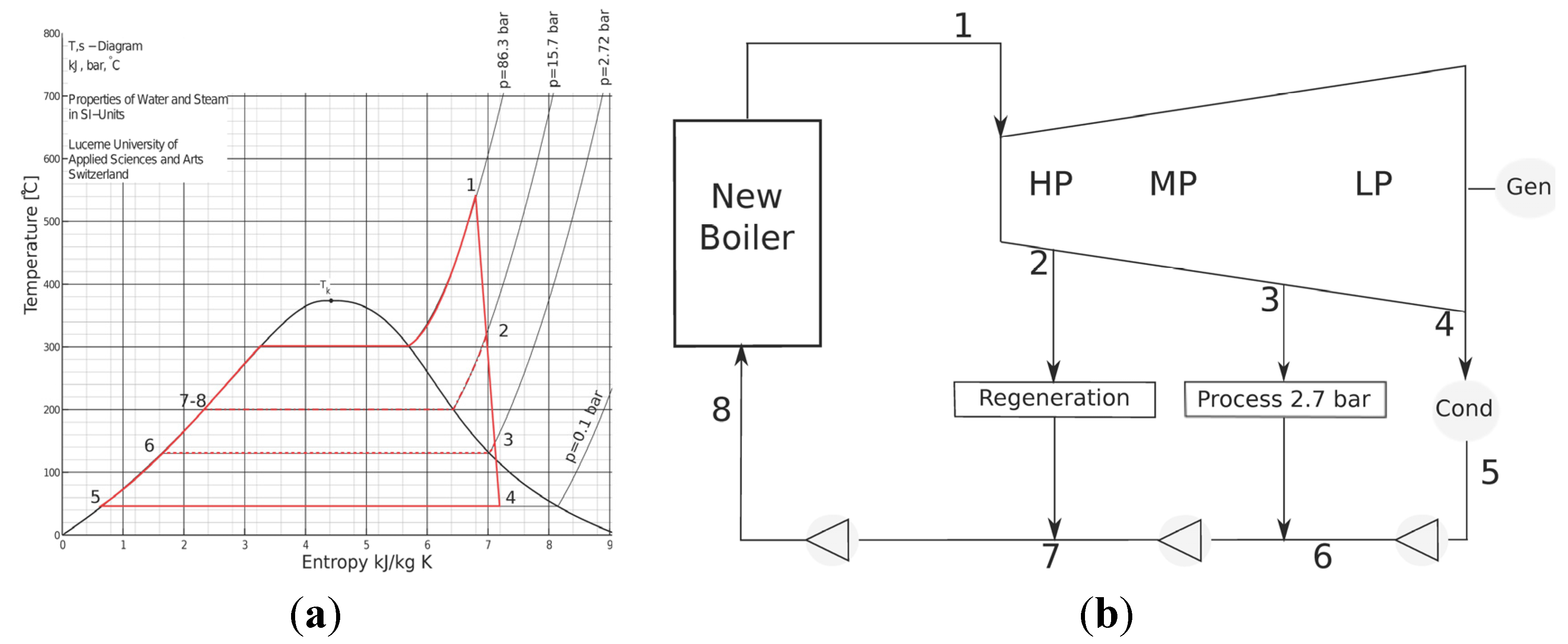
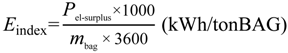
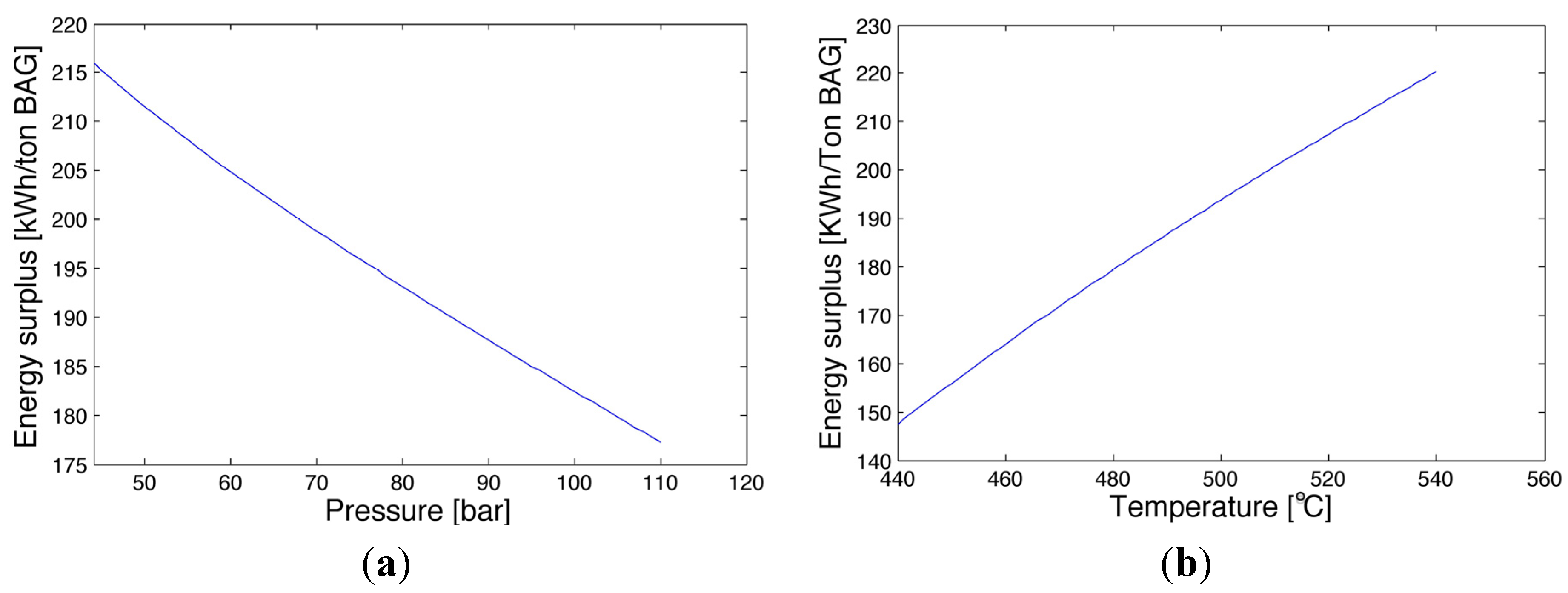
| Boiler P (bar) | Boiler T (°C) | Boiler capacity (kg/s) | Boiler Inlet T (°C) | p reg (bar) | mvap reg (kg/s) | P turbine top (MW) | ηis | Psurplus (MW) | ηII plant | Surplus (kWh/tonBAG) |
|---|---|---|---|---|---|---|---|---|---|---|
| 45.1 | 440 | 57.4 | 176 | 9.8 | 7.9 | 37.2 | 0.871 | 23.9 | 0.2371 | 179.2 |
| 64.7 | 485 | 56.7 | 187 | 12.5 | 8.6 | 39.9 | 0.863 | 26.5 | 0.2459 | 198.7 |
| 66.7 | 510 | 55.9 | 192 | 13.7 | 8.7 | 42.2 | 0.9000 | 28.7 | 0.2534 | 215.4 |
| 85.3 | 515 | 56.5 | 196 | 14.8 | 9.2 | 41.5 | 0.8468 | 27.9 | 0.2507 | 209.4 |
| 86.3 | 515 | 56.8 | 199 | 15.8 | 9.5 | 41.5 | 0.8440 | 27.8 | 0.2505 | 208.9 |
| 86.3 | 540 | 55.5 | 199 | 15.7 | 9.1 | 43.8 | 0.8858 | 30.2 | 0.2584 | 226.4 |
| 87.3 | 515 | 57.1 | 202 | 16.7 | 9.8 | 41.4 | 0.8411 | 27.8 | 0.2503 | 208.5 |
| 104 | 540 | 56.8 | 208 | 19.0 | 10.2 | 42.9 | 0.8415 | 29.2 | 0.2551 | 219.0 |
| 106.9 | 540 | 57.1 | 210 | 19.7 | 10.4 | 42.8 | 0.8350 | 29.0 | 0.2545 | 217.8 |
| 108.9 | 540 | 56.9 | 208 | 18.8 | 10.2 | 42.7 | 0.8306 | 28.9 | 0.2542 | 217.0 |
4.2. Option 2 Repowering
4.3. Economic Analysis of Repowering Options
| Boiler P (bar) | Boiler T (°C) | Boiler capacity (kg/s) | Boiler Inlet T (°C) | p reheat (bar) | p reg (bar) | mvap reg (kg/s) | P turbine top (MW) | ηis | P surplus (MW) | ηII plant | Surplus (kWh/tonBAG) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 45.1 | 440 | 51.9 | 163 | 22.2 | 6.3 | 5.7 | 39.2 | 0.9 | 25.9 | 0.2439 | 194.3 |
| 64.7 | 485 | 52.1 | 181 | 35.2 | 11.5 | 6.9 | 42.3 | 0.9 | 28.9 | 0.2540 | 216.8 |
| 66.7 | 510 | 49.8 | 176 | 30.9 | 8.4 | 6.1 | 43.3 | 0.9 | 29.9 | 0.2574 | 224.3 |
| 85.3 | 515 | 49.0 | 179 | 32.1 | 10.2 | 6.1 | 44.9 | 0.9 | 31.4 | 0.2625 | 235.6 |
| 86.3 | 515 | 50.9 | 190 | 40.5 | 11.8 | 7.3 | 45.1 | 0.9 | 31.6 | 0.2631 | 236.9 |
| 86.3 | 540 | 47.5 | 177 | 30.6 | 12.0 | 5.5 | 45.3 | 0.9 | 31.7 | 0.2637 | 238.1 |
| 87.3 | 515 | 52.3 | 221 | 32.9 | 22.1 | 9.3 | 45.0 | 0.9 | 31.5 | 0.2627 | 236.1 |
| 104.0 | 540 | 51.3 | 218 | 41.7 | 21.5 | 8.9 | 46.8 | 0.9 | 33.1 | 0.2683 | 248.5 |
| 106.9 | 540 | 52.6 | 226 | 47.8 | 24.3 | 9.8 | 46.9 | 0.9 | 33.2 | 0.2687 | 249.5 |
| 108.9 | 540 | 50.3 | 204 | 43.8 | 15.3 | 8.0 | 47.3 | 0.9 | 33.6 | 0.2699 | 251.9 |

| Variable | Option 1 | Option 2 |
|---|---|---|
| Investment (€) | 18,914,782 | 18,940,182 |
| Plant surplus energy index (kWh/tonBAG) | 226.4 | 251.9 |
| Electrical energy sell revenue (€/year) | 8,665,500 | 9,639,600 |
| 20 years NPV (€) | 54,376,553 | 68,128,494 |
| PBT (year) | 10 | 9 |
| IRR (%) | 11.0 | 12.7 |
5. Conclusion
Nomenclature
Symbols and acronyms:
| BIGCC | Biomass Integrated Gasification Combined Cycle |
| BPST | Backpressure Steam Turbine |
| CEST | Condensing Extraction Steam Turbine |
| Eindex | Surplus energy index (kWh/tonBA) |
| HR | Hours |
| HRSG | Heat Recovery Steam Generator |
| IRR | Internal Rate of Return (%) |
| LHV | Low Heating Value (kJ/kg) |
| LMTD | Log Mean Temperature Difference |
| MR | Milling Rate (ton/day) |
| NPV | Net Present Value (€) |
| P | Power (kW) |
| PAC | alcohol plant |
| PBT | Payback time (years) |
| PV | Present Value (€) |
| Q | Heat power (kW) |
| T | Temperature (°C) |
| U | Global heat exchange coefficient (W/m2·K) |
| Y | Electrical energy requirement (kWh/day) |
| c | Cost of bagasse unit (€/ton) |
| cap | Production capacity of the boiler (kg/s) |
| h | Specific enthalpy (kJ/kg) |
| i | Interest |
| m | Mass rate (kg/s) |
| mr | Milling rate (kg/s) |
| p | Pressure (bar) |
| q | Share of process heat |
| s | Specific entropy (kJ/kg·K) |
| saving | Money saving (€) |
| tc | Tons of cane |
| tfh | Tons of fiber per hour |
| εLOSS | Loss specific exergy (kJ/kg) |
| ∆T | Temperature difference (°C) |
| ∆h | Enthalpy difference (kJ/kg) |
| η | Efficiency |
Subscripts:
| Bab | Boilers A and B |
| Bc | Boiler C |
| Bc-sat | Boiler C saturated steam |
| Bc-temp | Boiler C tempering water |
| Bc-SH | Boiler C superheated steam |
| Bab | Boiler A and B |
| BAG | Bagasse |
| BAG-y | Yearly bagasse production |
| BLD | Blades |
| B-S | Blade to shaft |
| BOT | Lower pressure cycle |
| C-y | Yearly milled cane |
| D | Sugar drier |
| EFF | Effect of the evaporator |
| EVAP | Evaporation |
| FUEL | Fuel input |
| FUEL-Bc | Fuel input in Boiler C |
| FUEL-Bab | Fuel input in Boiler A and B |
| H2.7 | Head of 2.7 bar |
| H21 | Head of 21.7 bar |
| HP | High pressure |
| II | Second law |
| IS | Isentropic |
| J | Juice heating |
| LOSS | Loss |
| LP | Low pressure |
| MILL | Milling |
| MP | Medium pressure |
| OPT | Optimal |
| PAC | Alcohol plant |
| REF | Reference |
| REN | Renewable |
| SAT | Saturation |
| SV | Saving of the variable to which it is referred |
| TEMP | Tempering |
| TG | Turbo-generator |
| TOP | High pressure cycle |
| TURB | Turbine |
| TURB21 | Turbines 21.7–2.7 bar |
| TW | Tempering water |
| US | Useful |
| VAP | Steam |
| VAP-Bc | Produced by Boiler C |
| VAP-Bab | Steam produced by Boiler A and B |
| VAP-PAC | Steam demand of the alcohol plant |
| VAP-N2.7 | Steam need at 2.7 bar |
| VAP-N21 | Steam need at 21.7 bar |
| VAP-N28 | Steam need at 28.6 bar |
| VAP-R21 | Steam reduced from 21.7 to 2.7 bar |
| VAP-R28 | Steam reduced from 28.6 to 21.7 bar |
| VAP-reg | Steam for the regeneration |
| VAP-TURB | Steam of turbines |
| VAP-reg | Steam for the regeneration |
| VAP-TURB | Steam of turbines |
| VE | Turbine exhaust steam |
| VTI | Turbo-fan |
| W | Water |
| el | Electrical |
| eq-y | Year equivalent |
| g | Global |
| in | Inlet |
| is | Isentropic |
| mech | Mechanical |
| mill | Mills |
| need | requirement of the variable to which is referre |
| out | Outlet |
| reg | Regeneration |
| shred | Shredder |
| surplus | Surplus |
| th | Thermal |
| turb | Turbine |
| vap | Steam |
| vap-boiler | Capacity of the new boiler |
| vapHP | High pressure steam |
| vapMP | Middle pressure steam |
| vapLP | Low pressure steam |
| vapTOPprocess | Steam from high pressure cycle to the process |
Author Contributions
Conflicts of Interest
References
- O’Sullivan, A.; Sheffrin, S. Economics: Principle and Tools, 2nd ed.; Prentice Hall: New Saddle River, NJ, USA, 2003. [Google Scholar]
- International Energy Agency. World Energy Outlook 2011. Available online: http://www.iea.org/ (accessed on 28 August 2013).
- Committee on Biobased Industrial Products, National Research Council. Biobased Industrial Products: Research and Commercialization Priorities; National Academic Press: Washington, DC, USA, 2000; p. 74. [Google Scholar]
- Khatiwada, D.; Seabra, J.; Silveira, S.; Walter, A. Power generation from sugarcane biomass—A complementary option to hydroelectricity in Nepal and Brazil. Energy 2012, 48, 241–254. [Google Scholar] [CrossRef]
- Purohit, P.; Michaelowa, A. CDM potential of bagasse cogeneration in India. Energy Policy 2007, 35, 4779–4798. [Google Scholar]
- Coordination BNDES and CGEE. Sugarcane-based bioethanol, Energy for sustainable development. Available online: http://www.sugarcanebioethanol.org/ (accessed on 2 September 2013).
- Deshmukh, R.; Jacobson, A.; Chamberlin, C.; Kammen, D. Thermal gasification or direct combustion? Comparison of advanced cogeneration systems in the sugarcane industry. Biomass Bioenergy 2013, 55, 163–174. [Google Scholar] [CrossRef]
- Pellegrini, L.F.; de Oliveira Jùnior, S.; Burbano, J.C. Supercritical steam cycles and biomass integrated gasification combined cycles for sugarcane mills. Energy 2013, 35, 1172–1180. [Google Scholar]
- Dias, M.O.S.; Junqueira, T.L.; Cavalett, O.; Cunha, M.P.; Jesus, C.D.F.; Mantelatto, P.E.; Rossell, C.E.V.; Filho, R.M.; Bonomi, A. Cogeneration in integrated first and second generation ethanol from sugarcane. Chem. Eng. Res. Des. 2013, 91, 1411–1417. [Google Scholar] [CrossRef]
- Toasa, J. Colombia: A New Ethanol Producer on the Rise? United States Department of Agriculture Economic Research Service: Washington, DC, USA, 2009. [Google Scholar]
- Rein, P. Cane Sugar Engineering, 1st ed.; Verlag Dr. Albert Bartens KG: Berlin, Germany, 2007. [Google Scholar]
- Hugot, E. Handbook of Cane Sugar Engineering, 3rd ed.; Elsevier: New York, NY, USA, 1986. [Google Scholar]
- International Organization for Standardization. Energy Management Systems–Requirements with Guidance for Use; ISO 50001:2011; BSI Group: London, UK, 2011. [Google Scholar]
- Rinaldi, F.; Najafi, B. Temperature measurement in WTE boilers using suction pyrometers. Sensors 2013, 13, 15633–15655. [Google Scholar] [CrossRef]
- Paz, D.; Cardenas, C.J. Evaluación exergética de propuestas de disminución de consumo de vapor en usinas azucareras. Rev. Ind. Agríc. Tucumán 2005, 82, 1–8. (In Spanish) [Google Scholar]
- Dincer, I.; Al-Muslim, H. Thermodynamic analysis of reheat cycle steam power plants. Int. J. Energy Res. 2001, 25, 727–739. [Google Scholar] [CrossRef]
- El-Emam, R.S.; Dincer, I. Energy and exergoeconomic analyses optimization of geothermal organic Rankine cycle. Appl. Therm. Eng. 2013, 59, 435–444. [Google Scholar] [CrossRef]
- Dias, M.O.S.; Junqueira, T.L.; Jesus, C.D.F.; Rossell, C.E.V.; Filho, R.M.; Bonomi, A. Improving second generation ethanol production though optimization of first generation production process from sugarcane. Energy 2012, 43, 246–252. [Google Scholar] [CrossRef]
- Furlan, F.F.; Borba Costa, C.B.; de Castro Fonseca, G.; de Pelegrini Soares, R.; Resende Secchi, A.; Goncales da Cruz, A.J.; de Campos Giordano, R. Assessing the production of first and second generation bioethanol from sugarcane through the integration of global optimization and process detailed modeling. Comput. Chem. Eng. 2012, 43, 1–9. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. Direct search solution of numerical and statistical problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- The Mathworks Inc. Genetic Algorithm and Direct Search Toolbox for Use with Matlab User’s Guide. Available online: http://www.mathworks.com (accessed on 13 February 2014).
- Dysert, L.R. Sharpen your cost estimating skills. Cost Eng. 2003, 45, 22–30. [Google Scholar]
- Peters, M.; Timmerhaus, K.D. Plant Design and Economics for Chemical Engineers, 3rd ed.; McGraw Hill: New York, NY, USA, 1980. [Google Scholar]
- Coker, A.K. Ludwig’s Applied Process Design for Chemical and Petrochemical Plants, 4th ed.; Elsevier: Burlington, MA, USA, 2007. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Colombo, G.; Ocampo-Duque, W.; Rinaldi, F. Challenges in Bioenergy Production from Sugarcane Mills in Developing Countries: A Case Study. Energies 2014, 7, 5874-5898. https://doi.org/10.3390/en7095874
Colombo G, Ocampo-Duque W, Rinaldi F. Challenges in Bioenergy Production from Sugarcane Mills in Developing Countries: A Case Study. Energies. 2014; 7(9):5874-5898. https://doi.org/10.3390/en7095874
Chicago/Turabian StyleColombo, Guido, William Ocampo-Duque, and Fabio Rinaldi. 2014. "Challenges in Bioenergy Production from Sugarcane Mills in Developing Countries: A Case Study" Energies 7, no. 9: 5874-5898. https://doi.org/10.3390/en7095874
APA StyleColombo, G., Ocampo-Duque, W., & Rinaldi, F. (2014). Challenges in Bioenergy Production from Sugarcane Mills in Developing Countries: A Case Study. Energies, 7(9), 5874-5898. https://doi.org/10.3390/en7095874





