Determining the Limiting Current Density of Vanadium Redox Flow Batteries
Abstract
:1. Introduction

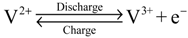
2. Theoretical
2.1. Cell Voltage of a Vanadium Redox Flow Battery
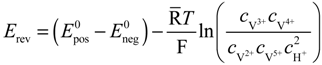
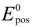 and
and 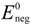 are standard reduction potentials for the reaction at the positive and negative electrodes, respectively;
are standard reduction potentials for the reaction at the positive and negative electrodes, respectively; 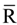 is the universal gas constant; T is the temperature; and ci is the molar concentration of species i. With measured OCV, the concentration ci can be calculated using Equation (6), and the state of charge (SOC) can be determined by:
is the universal gas constant; T is the temperature; and ci is the molar concentration of species i. With measured OCV, the concentration ci can be calculated using Equation (6), and the state of charge (SOC) can be determined by:
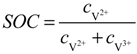
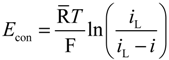
2.2. Mean Flow Velocity
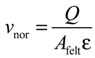
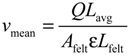
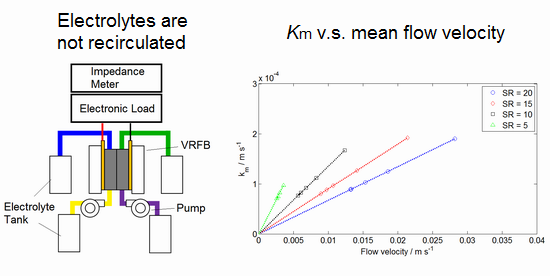
3. Experimental
3.1. Experimental Setup
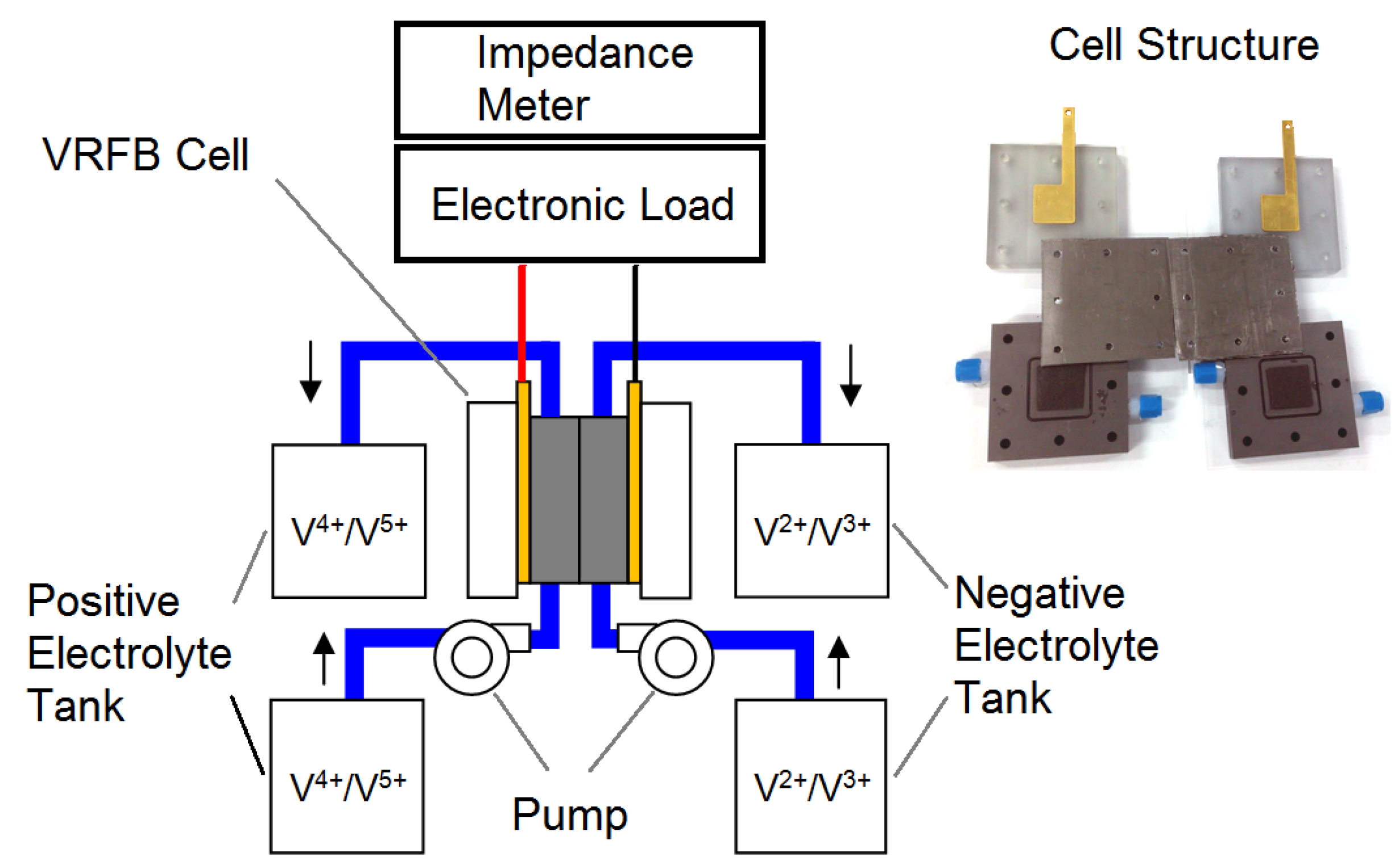
| Quantity | Value | Note |
|---|---|---|
| Active area | 3.2 × 3.2 cm2 | - |
| Electrode thickness | 0.5 cm | After compression |
| Fiber density ρfiber | 1.75 g·cm−3 | Provided by manufacturer |
| Felt density ρfelt | 0.102 g·cm−3 | Provided by manufacturer |
| Porosity ɛ | 0.93 (after compression) | Calculated |
| Tortuosity Lavg/Lfelt | 1.09 | [17] |
| Cell resistance Rcell | 45 mΩ | Measured |
3.2. Experimental Procedure
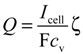
4. Results and Discussion
4.1. Effect of Operating Conditions of Polarization Curves
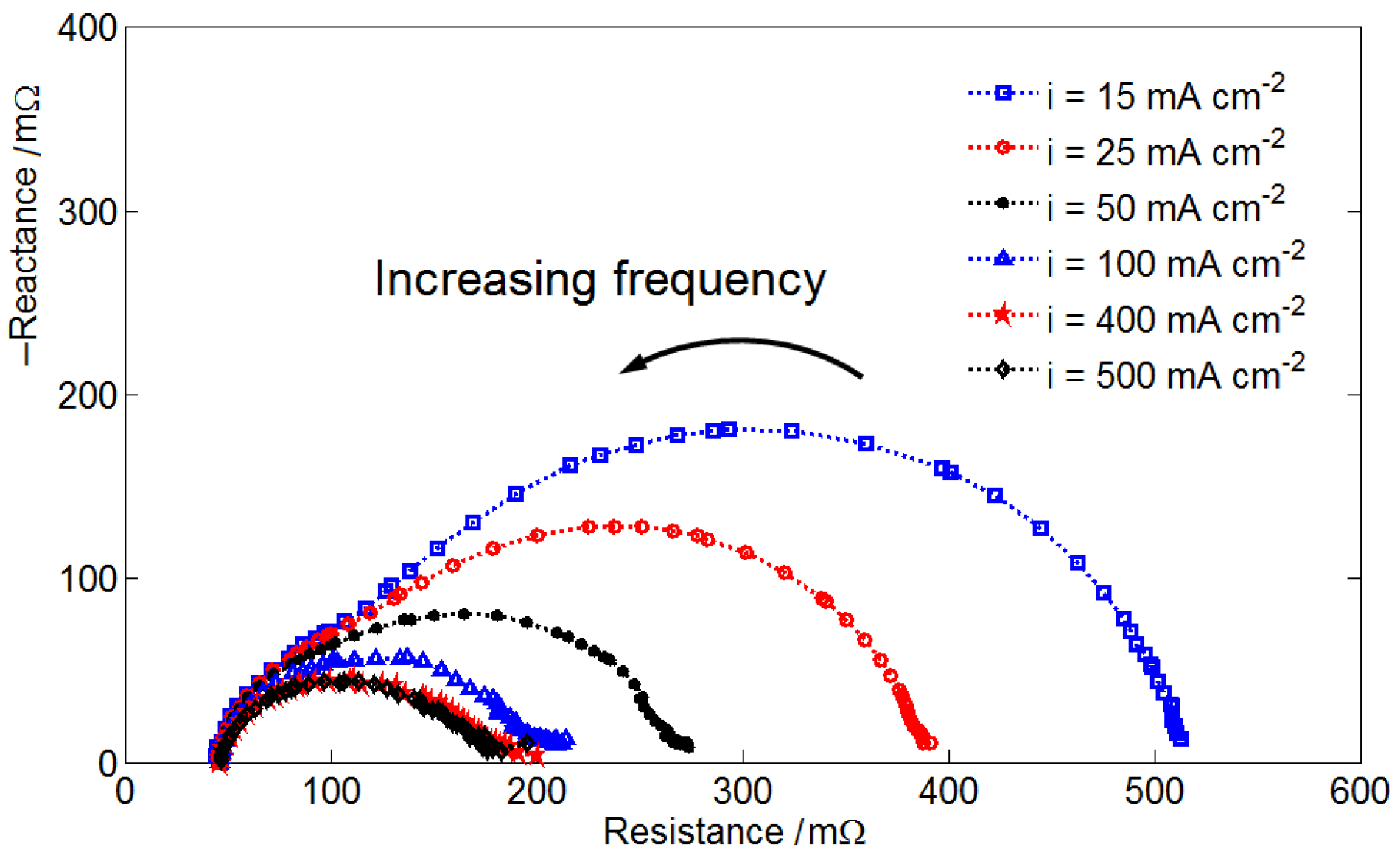
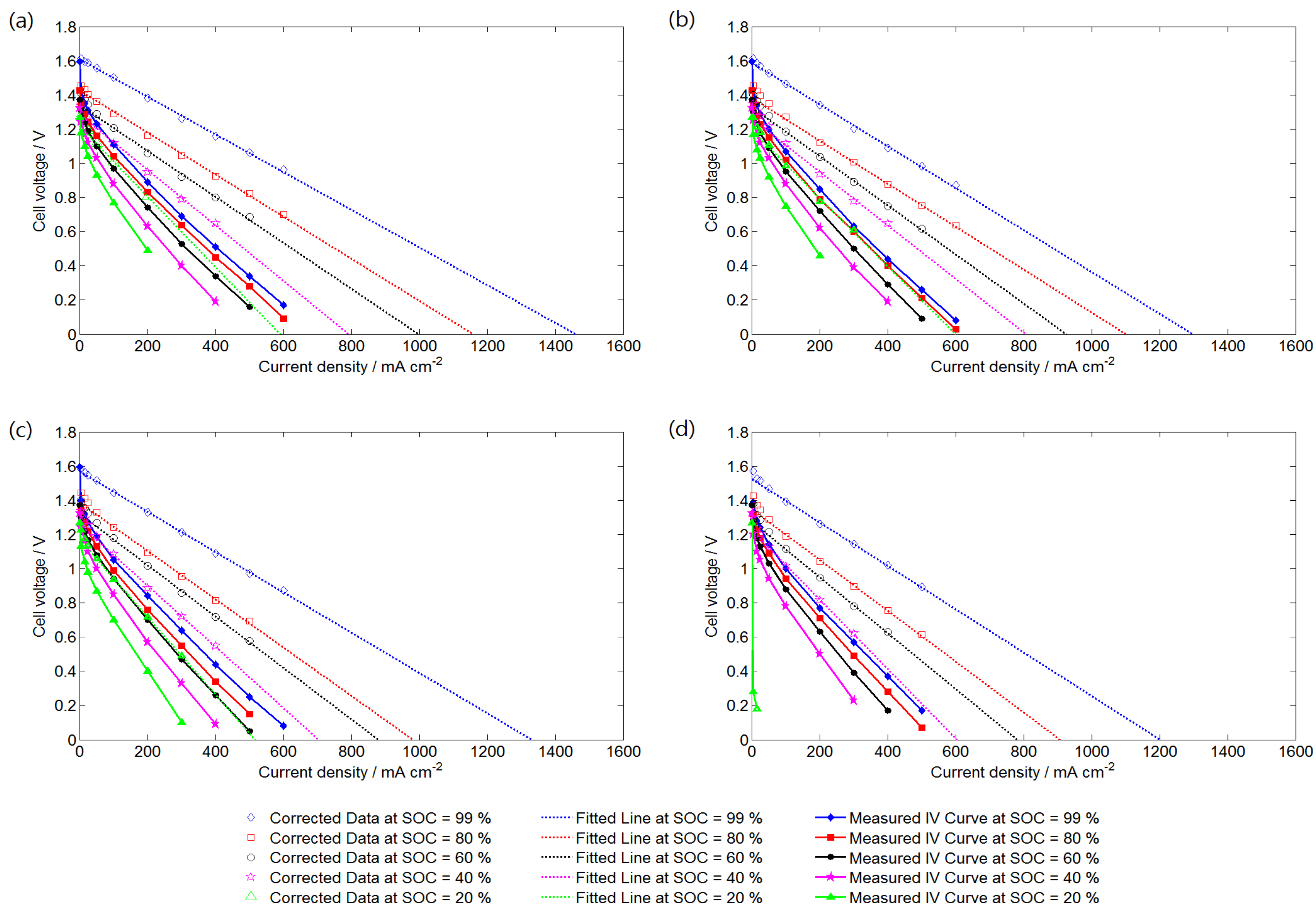
| SR | 20 | 15 | 10 | 5 |
|---|---|---|---|---|
| SOC/% | Limiting current density/mA·cm−2 (mass transfer coefficient/m·s−1) | |||
| 99 | 1463 (1.02 × 10−4) | 1300 (0.91 × 10−4) | 1332 (0.93 × 10−4) | 1203 (0.84× 10−4) |
| 80 | 1161 (1.00 × 10−4) | 1102 (0.95 × 10−4) | 982 (0.85 × 10−4) | 908 (0.78 × 10−4) |
| 60 | 1000 (1.15 × 10−4) | 927 (1.07 × 10−4) | 880 (1.01 × 10−4) | 782 (0.90 × 10−4) |
| 40 | 793 (1.37 × 10−4) | 807 (1.39 × 10−4) | 705 (1.22 × 10−4) | 605 (1.05 × 10−4) |
| 20 | 591 (2.04 × 10−4) | 600 (2.07 × 10−4) | 517 (1.79 × 10−4) | N/A |
4.2. Determination of Mass Transfer Coefficient
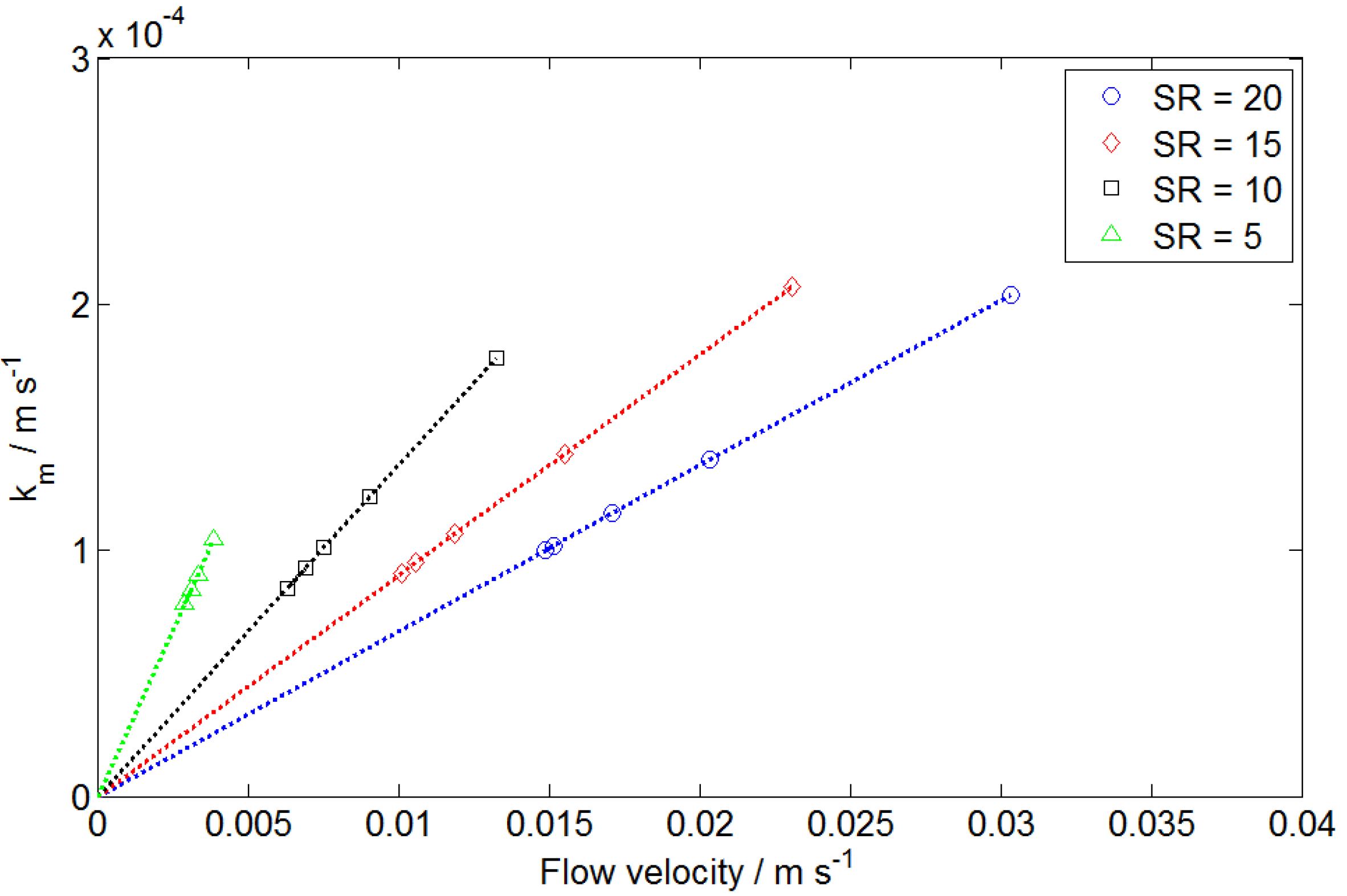
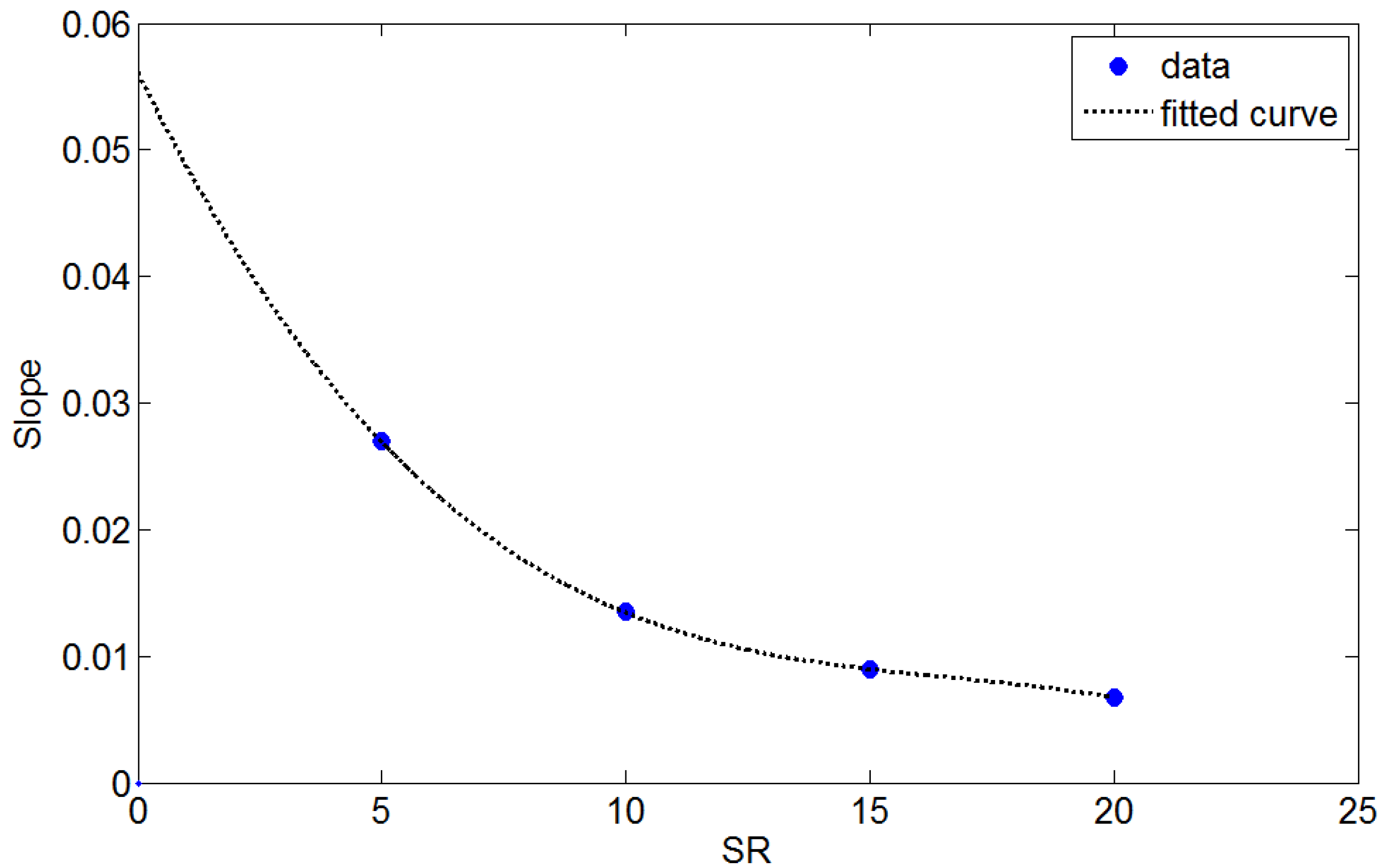
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fabjan, C.; Garche, J.; Harrer, B.; Jörissen, L.; Kolbeck, C.; Philippi, F.; Tomazic, G.; Wagner, F. The vanadium redox-battery: An efficient storage unit for photovoltaic systems. Electrochim. Acta 2001, 47, 825–831. [Google Scholar]
- Jia, Z.; Wang, B.; Song, S.; Chen, X. Effect of polyhydroxy-alcohol on the electrochemical behavior of the positive electrolyte for vanadium redox flow batteries. J. Electrochem. Soc. 2012, 159, A843–A847. [Google Scholar] [CrossRef]
- Li, L.; Kim, S.; Wang, W.; Vijayakumar, M.; Nie, Z.; Chen, B.; Zhang, J.; Xia, G.; Hu, J.; Graff, G.; et al. A stable vanadium redox-flow battery with high energy density for large-scale energy storage. Adv. Energy Mater. 2011, 1, 394–400. [Google Scholar] [CrossRef]
- Yang, H.; Hung, C.-H.; Wang, S.-P.; Chiang, I.-L. Graphite felt with vapor grown carbon fibers as electrodes for vanadium redox flow batteries. Rare Met. 2011, 30, 1–4. [Google Scholar]
- Zhu, H.Q.; Zhang, Y.M.; Yue, L.; Li, W.S.; Li, G.L.; Shu, D.; Chen, H.Y. Graphite-carbon nanotube composite electrodes for all vanadium redox flow battery. J. Power Sources 2008, 184, 637–640. [Google Scholar] [CrossRef]
- Hwang, G.-J.; Ohya, H. Preparation of cation exchange membrane as a separator for the all-vanadium redox flow battery. J. Membr. Sci. 1996, 120, 55–67. [Google Scholar] [CrossRef]
- Sukkar, T.; Skyllas-Kazacos, M. Modification of membranes using polyelectrolytes to improve water transfer properties in the vanadium redox battery. J. Membr. Sci. 2003, 222, 249–264. [Google Scholar] [CrossRef]
- Watt-Smith, M.J.; Ridley, P.; Wills, R.G.A.; Shah, A.A.; Walsh, F.C. The importance of key operational variables and electrolyte monitoring to the performance of an all vanadium redox flow battery. J. Chem. Technol. Biotechnol. 2013, 88, 126–138. [Google Scholar]
- Ma, X.; Zhang, H.; Sun, C.; Zou, Y.; Zhang, T. An optimal strategy of electrolyte flow rate for vanadium redox flow battery. J. Power Sources 2012, 203, 153–158. [Google Scholar] [CrossRef]
- Shah, A.A.; Watt-Smith, M.J.; Walsh, F.C. A dynamic performance model for redox-flow batteries involving soluble species. Electrochim. Acta 2008, 53, 8087–8100. [Google Scholar] [CrossRef]
- You, D.; Zhang, H.; Chen, J. A simple model for the vanadium redox battery. Electrochim. Acta 2009, 54, 6827–6836. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, H.; Xing, F. A three-dimensional model for negative half cell of the vanadium redox flow battery. Electrochim. Acta 2011, 58, 238–246. [Google Scholar] [CrossRef]
- Yu, V.; Dongmei, C. Dynamic model of a vanadium redox flow battery for system performance control. J. Sol. Energy Eng. 2013, 136. [Google Scholar] [CrossRef]
- Schmal, D.; Erkel, J.; Duin, P.J. Mass transfer at carbon fiber electrodes. J. Appl. Electrochem. 1986, 16, 422–430. [Google Scholar] [CrossRef]
- Shah, A.A.; Tangirala, R.; Singh, R.; Wills, R.G.A.; Walsh, F.C. A dynamic unit cell model for the all-vanadium flow battery. J. Electrochem. Soc. 2011, 158, A671–A677. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Dover: New York, NY, USA, 1972. [Google Scholar]
- Matyka, M.; Khalili, A.; Koza, Z. Tortuosity-porosity relation in porous media flow. Phys. Rev. E 2008, 78. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, J.-Y.; Hsieh, C.-L.; Hsu, N.-Y.; Chou, Y.-S.; Chen, Y.-S. Determining the Limiting Current Density of Vanadium Redox Flow Batteries. Energies 2014, 7, 5863-5873. https://doi.org/10.3390/en7095863
Chen J-Y, Hsieh C-L, Hsu N-Y, Chou Y-S, Chen Y-S. Determining the Limiting Current Density of Vanadium Redox Flow Batteries. Energies. 2014; 7(9):5863-5873. https://doi.org/10.3390/en7095863
Chicago/Turabian StyleChen, Jen-Yu, Chin-Lung Hsieh, Ning-Yih Hsu, Yi-Sin Chou, and Yong-Song Chen. 2014. "Determining the Limiting Current Density of Vanadium Redox Flow Batteries" Energies 7, no. 9: 5863-5873. https://doi.org/10.3390/en7095863
APA StyleChen, J.-Y., Hsieh, C.-L., Hsu, N.-Y., Chou, Y.-S., & Chen, Y.-S. (2014). Determining the Limiting Current Density of Vanadium Redox Flow Batteries. Energies, 7(9), 5863-5873. https://doi.org/10.3390/en7095863