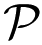Enabling Privacy in Vehicle-to-Grid Interactions for Battery Recharging
Abstract
: The diffusion of Electric Vehicles (EV) fostered by the evolution of the power system towards the new concept of Smart Grid introduces several technological challenges related to the synergy among electricity-propelled vehicle fleets and the energy grid ecosystem. EVs promise to reduce carbon emissions by exploiting Renewable Energy Sources (RESes) for battery recharge, and could potentially serve as storage bank to flatten the fluctuations of power generation caused by the intermittent nature of RESes by relying on a load aggregator, which intelligently schedules the battery charge/discharge of a fleet of vehicles according to the users' requests and grid's needs. However, the introduction of such vehicle-to-grid (V2G) infrastructure rises also privacy concerns: plugging the vehicles in the recharging infrastructures may expose private information regarding the user's locations and travelling habits. Therefore, this paper proposes a privacy-preserving V2G infrastructure which does not disclose to the aggregator the current battery charge level, the amount of refilled energy, nor the time periods in which the vehicles are actually plugged in. The communication protocol relies on the Shamir Secret Sharing threshold cryptosystem. We evaluate the security properties of our solution and compare its performance to the optimal scheduling achievable by means of an Integer Linear Program (ILP) aimed at maximizing the ratio of the amount of charged/discharged energy to/from the EV's batteries to the grid power availability/request. This way, we quantify the reduction in the effectiveness of the scheduling strategy due to the preservation of data privacy.1. Introduction
The evolution of the electric power system toward the novel Smart Grid paradigm and the progressive concurrent electrification of transportation aimed at the reduction of carbon emissions rises various issues related to the interactions between the distribution network and the Electric Vehicles (EVs). Such category of vehicles includes battery/fuel cell-powered automobiles, as well as hybrid systems combining electricity generators and conventional gasoline engines [1,2]. Several investigations on the potential market penetration of EVs and on the impacts of their possible massive introduction have been carried out by the research community [3,4]: on one hand, the additional connected load capacity required to simultaneously recharge a huge number of EVs might significantly impact the energy consumption trend; on the other hand, the EVs' batteries represent a huge storage bank that can be exploited to flatten the typically unpredictable power generation patterns of Renewable Energy Sources (RESes) by accumulating energy in case of excessive power generation and transferring it back to the grid during peak-demand periods [5,6]. To enable such synergies between EVs and the Smart Grid, which are usually referred to as Vehicle-to-Grid (V2G) interactions, the introduction of an aggregator capable of coordinating the charging/discharging process for a huge fleet of vehicles has been proposed [7,8]: the role of such agent is to operate as middleman between the vehicle owner (who could not act as stakeholder on the electricity market due to the limited power capacity of a single vehicle) and the electrical utilities or system operators. Several business models for the aggregation entity have been studied, possibly taking into account the additional costs incurred by the EVs' owners due to the frequent battery charge/discharge and the introduction of financial incentives to encourage the owners to plug their vehicle when not in use [9,10]. However, V2G assumes that detailed information about the traveling habits of the vehicle owners are available at the aggregator, which can disclose sensitive data (e.g., presence in a certain location at a given time) and thus arises privacy concerns [11,12]: according to NIST [13], once a two-way communication between the EV and the charging station is established, there is currently no technical limitation to the amount and type of data that could be obtained from the EV's microcomputers which manages specific functions such as breaking, ignition systems, lighting controls, fuel delivery, on-board diagnostics, and so on. This could lead to potentially threatening consequences: for instance, burglars could track people's movements before attempting robberies, information about vehicle maintenance could be inferred and exploited for insurance and warranties, or companies could perform targeted marketing for car-related services.
The main contributions of our paper are:
the design of a privacy preserving online framework which allows a set of Aggregators to collaboratively coordinate the charging/discharging process of the vehicles' batteries without learning the time periods in which the EVs are actually plugged-in and the current charge level of the batteries, nor the amount of refilled energy: every data is split in w parts called shares by means of the Shamir Secret Sharing (SSS) threshold cryptosystem and each share is given to a different Aggregator. The protocol ensures that a collusion of less than t ≤ w Aggregators cannot reconstruct the data.
the definition of a set of security properties which capture the requirements of V2G interactions for battery recharge and the proof that such properties are satisfied by our proposed scheduling protocol.
the formulation of a benchmark offline scheduling problem, which assumes full knowledge of the future travels of the users and of the battery-related information before the beginning of the scheduling horizon.
the comparison of the performance of our privacy-friendly mechanism to the benchmark model. This way, we quantify the reduction in the effectiveness of the scheduling strategy due to incorporating data privacy preservation in the scheduling mechanism.
The benefits introduced by our privacy-friendly protocol are twofold: on one hand, it encourages the EV owners to take part in the scheduling optimization framework by protecting their personal data. Assuming an underlying business model which rewards the users that allow for the discharge of their EV's batteries, providing privacy in V2G interactions could therefore lead to significant cost savings for the individual users. On the other hand, the wider is the EV fleet participating to the protocol, the higher is the degree of flexibility experienced by the grid in the management of the power generation/consumption balancing, thus helping in a more effective compensation of the unpredictable power generation patterns of RESes.
The remainder of the paper is structured as follows: Section 2 provides an overview of the related literature, while some background notions about the SSS scheme are recalled in Section 3. The privacy-friendly scheduling infrastructure, the collaborative scheduling procedure and the associated communication protocol are discussed in Section 4. The security analysis of the proposed scheduling mechanism are presented in Section 5, while Section 6 introduces an Integer Linear Programming formulation for the optimal scheduling to be used as evaluation benchmark. The performance assessment of our proposed solution is discussed in Section 7. Final conclusions are drawn in the last Section.
2. Related Work
The design of EVs and the characterization of their interactions with the power grid has been widely investigated in the last decade: for a comprehensive survey on the impact of the introduction of EVs in the Smart Grid ecosystem, the reader is referred to [14], while a thorough overview on the economical and technical models of aggregator agents for EV fleets can be found in [15].
A substantial body of work investigates optimal and heuristic policies for the battery recharge of a population of EVs based on various approaches, ranging from game theory [16,17] to queuing theory [18,19], possibly associated with reinforcement learning techniques [20] or stochastic/fuzzy logic-based predictors [21]. Game models are suitable for scenarios involving multiple selfish entities, each one operating with the aim of optimizing his own utility function, and allow for possible negotiations among them. Conversely, in our framework we assume that the vehicle owners fully collaborate with the aggregator in order to achieve a common optimization goal in terms of balancing of the grid's power availability, without assumption of any economical incentives. Queuing models are employed to capture constraints such as limits on the maximum number of EVs to be charged contemporaneously: our scenario assumes that the charging station is equipped with a sufficient number of plugs to serve the whole fleet without introducing additional waiting times.
However, none of the above papers addresses the privacy-related issues which are peculiar of the V2G scenario, which have been considered only by a few studies: Stegelmann and Kesdogann [22] enumerate the security requirements of a V2G infrastructure in presence of an untrusted aggregator, and formalize the model of an honest-but-curious attacker which tries to infer the traveling habits of the vehicle owners by linking the plugging/unplugging events at the charging stations in different locations. The same authors further refine such adversary model in [23] by integrating information regarding the charge level of the EV's batteries. We consider the same attacker model, and our solution ensures that the aggregators schedule the charging/discharging process without knowing the total amount of energy to be provided to the battery, nor the time periods in which the EV is actually plugged. The only information available at the aggregators is a priority tag which declares whether the EV must be necessarily charged or could also be discharged, according to the current battery charge level, which remains undisclosed.
Yang et al. [24] also assume a honest-but-curious aggregator model in a two-tiered structure including multiple local aggregators directly interacting with the vehicles and a central aggregator which interfaces the electricity market, and propose a rewarding scheme based on blind signature techniques, which ensures mutual authentication while preserving location and identity privacy, and allows for anonymous rewards. Our solution is based on Shamir Secret Sharing scheme, which is computationally less demanding, but requires the collaboration of multiple scheduling entities, thus introducing additional message exchanges among them (which would not occur in presence of a single aggregator).
Liu et al. propose in [25] a two-way anonymous payment system for EVs' battery charge/discharge providing traceability in case of car theft, while Nicanfar et al. [26] design a pseudonym-based authentication scheme, which ensures untraceability of the users' movements and assumes the presence of an external trusted entity in charge of recording the associations between pseudonyms and real identities to provide accountability for billing purposes. Though the security of the billing process is out of the scope of our contribution, similar protocols could be easily integrated in our infrastructure.
3. Background on Shamir Secret Sharing Scheme
Shamir Secret Sharing (SSS) scheme [27] is a cryptographic threshold scheme which allows multiple participants to reconstruct a secret by means of a collaborative procedure. To do so, the secret is split in w shares, which are given to the participants to the protocol: the secret can be recovered through cooperation of at least t ≤ w participants, where the threshold t is a system design parameter.
More in detail, the SSS scheme works as follows. Choose a prime number q and split the secret m ∈ Zq in w shares (xs,ys) (1 ≤ s ≤ w)by selecting t − 1 integer random numbers ρ1,ρ2, ⋯, ρt−1 with uniform distribution in [0, q − 1] and calculating the s-th share as mod q, where xs ∈ Zq is arbitrarily chosen. The secret can be reconstructed by interpolating at least t shares, using e.g., the Lagrange interpolation algorithm. The SSS scheme has homomorphic properties with respect to addition and multiplication, meaning that performing such operations on the shares and then recovering the result leads to the same result that would be obtained by computing the same operations on the secrets directly. The sum of two secrets can be independently calculated by a single participant by summing the corresponding shares, while multiplication must be performed interactively by means of a collaborative procedure, e.g., as the one described in [28]. Therefore, any function expressed in terms of additions and multiplications can be calculated directly on the shares. In particular, several collaborative methods to perform the comparison of two secrets have been proposed (see e.g., [29,30]). In this paper, we will adopt the comparison protocol presented in [30], which works as follows: each party holding the s-th shares (xs, ys), of the secrets m and m′ to be compared selects two big random numbers rs, , which can multiplicatively hide m − m′, and a random bit bs ∈ {0,1}. The collaborative protocol enables each party to obtain a share of the quantity . The result of the comparison can be computed by retrieving c, setting a bit e either to 0 in case c > 0 or to 1 otherwise (note that in a modulo n field negative numbers are represented by the upper half of the range [0, n − 1]), and calculating the result of the XOR operation ξ = e ⊕ b1 ⊕ ⋯ ⊕ bt. ξ = 0 indicates that m > m′, while ξ = 1 indicates that m < m′. The reader is referred to [30] for additional details about the collaborative procedure and the proof of the correctness of the comparison protocol.
4. The Privacy-Friendly V2G Communication Framework
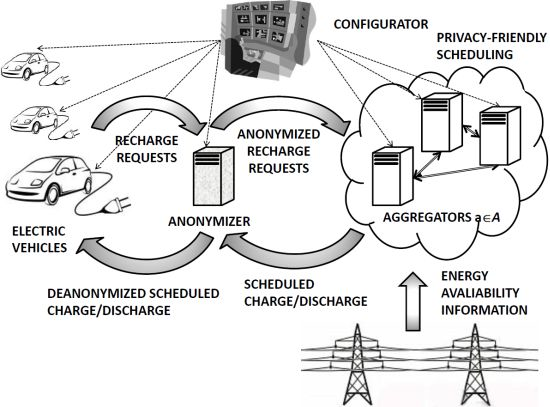
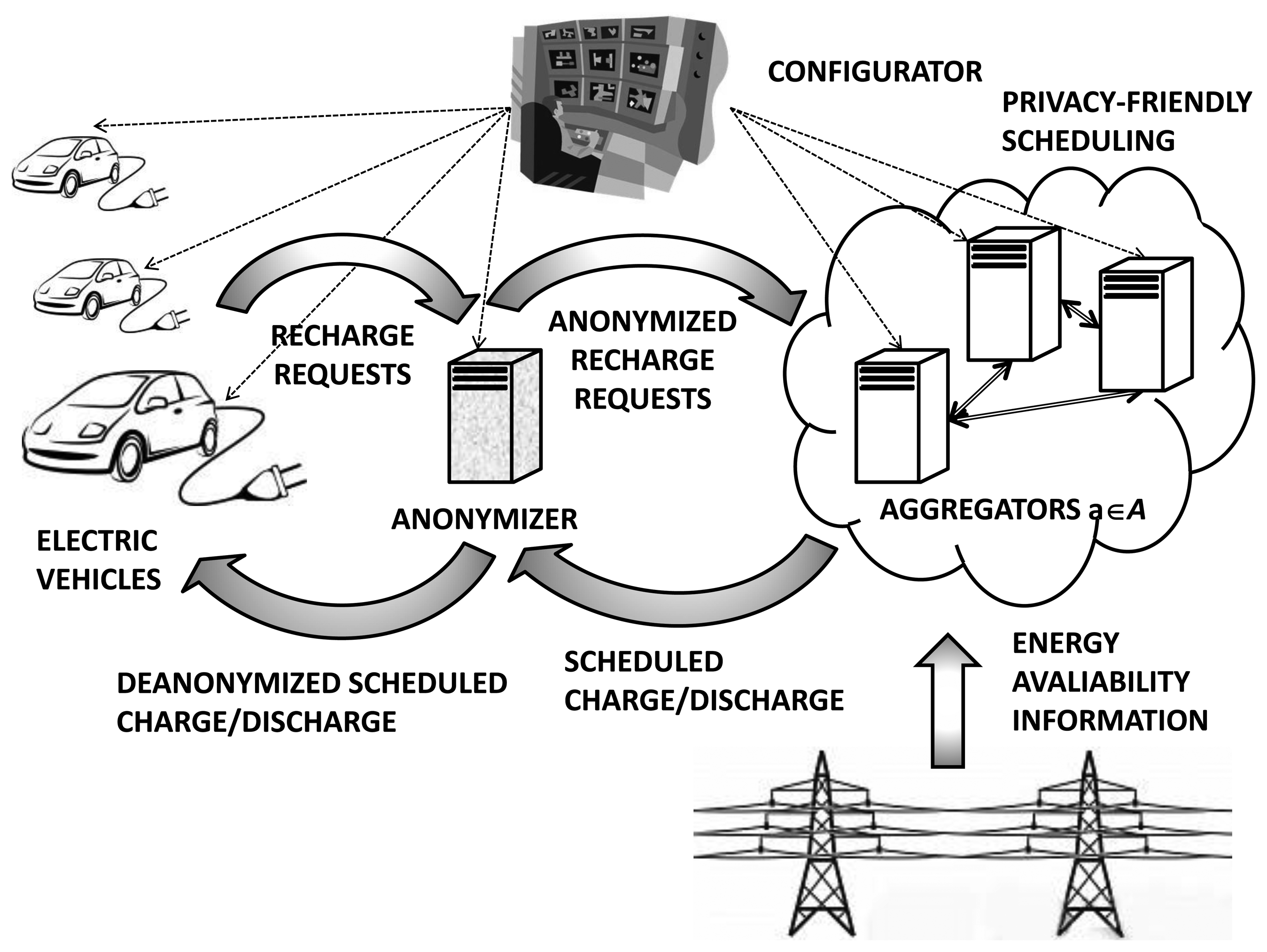
As depicted in Figure 1, our proposed architecture comprises a set of EVs,


We assume that:
- (1)
Each EV is equipped with hardware and software (e.g., as described in [31,32]) enabling Internet access at any time.
- (2)
A Configurator node is responsible for the setup of a suitable public-key infrastructure (e.g., as the one proposed in [33]).
- (3)
The parties agree on a hybrid encryption algorithm E(Ke, ·) and a corresponding decryption algorithm D(Kd, ·). The hybrid scheme is assumed to be IND-CPA secure [34] (i.e., it ensures message indistinguishability under chosen plaintext attack) and uses state-of-the art secure public key cryptography and symmetric cryptography to transmit messages of any size.
- (4)
Each Aggregator a ∈
has its own pair of public/private keys and all the EVs know the public keys of the Aggregators.
- (5)
All the communication channels between the EVs, the Anonymizer, and the Aggregators are confidential and authenticated.
We also assume that time is divided in a set of epochs


The design goal is to schedule the charge/discharge times of the EVs' batteries through a collaborative procedure in order to satisfy the customers' recharge requests while minimizing the difference between the power supplied (requested) by the grid and the power charged (discharged) to (from) the batteries, without exceeding the grid overall power availability (request).
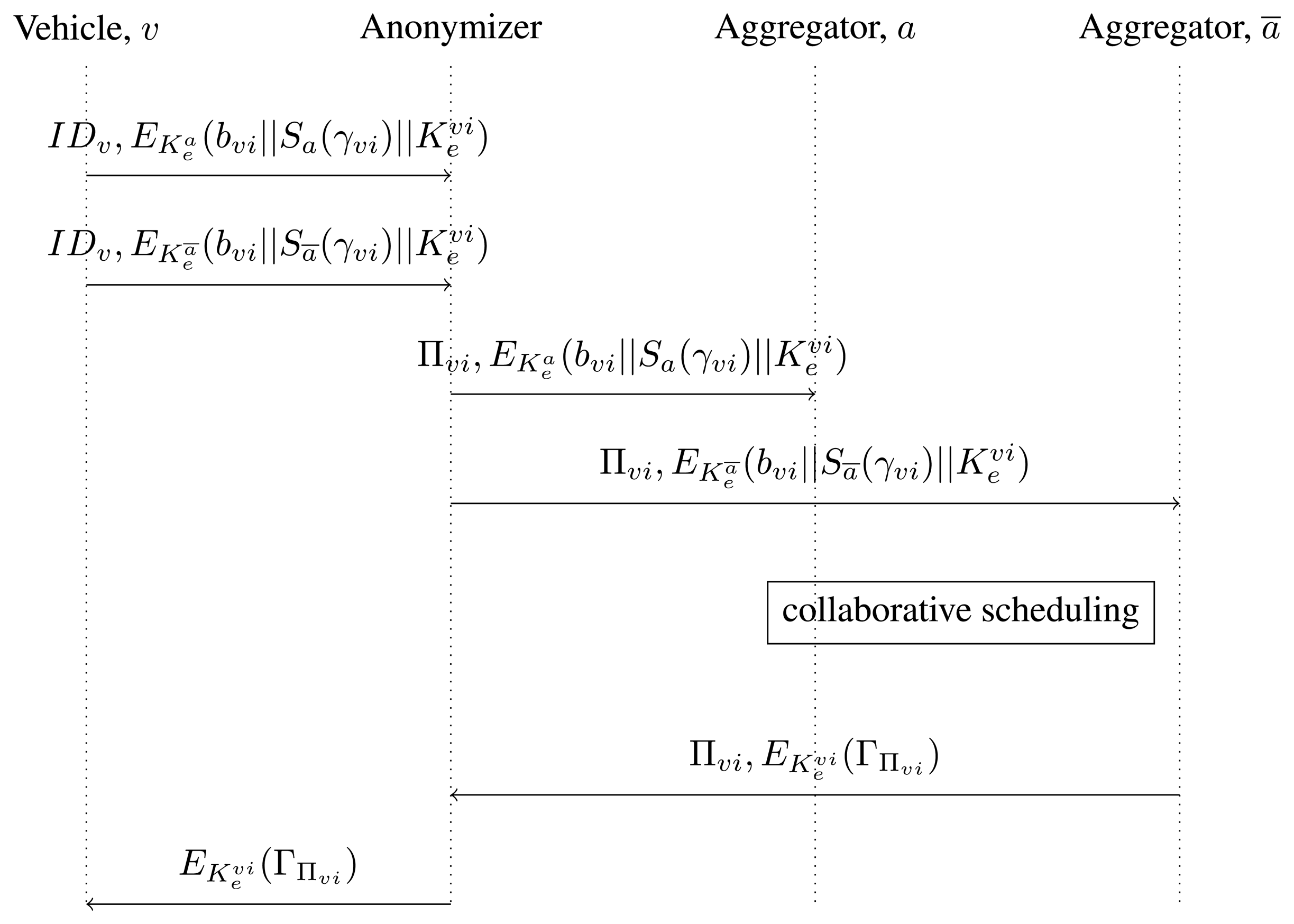
A pictorial view of the exchanged messages between Vehicles and Aggregators is presented in Figure 2, while a list of the main symbols is provided in Table 1.
Whenever a new epoch i starts, each Vehicle υ ∈





Upon reception of the |

Let ΓΠυi be the scheduling output of the Vehicle associated to the pseudonym Πυi, which can be set by the Aggregators either to 1 if the Vehicle is scheduled for recharge, to −1 if it is scheduled for discharge, or to 0 otherwise. Moreover, let Pi be a variable which records the amount of power required for the charges/discharges scheduled during the current epoch i: positive values of Pi indicate that the grid must provide power to charge the batteries, while negative values indicate that the energy collected from the batteries is injected in the grid.
| Algorithm 1 The Privacy-Friendly Scheduling Algorithm | |
| 1: | On input of the epoch number i and of Πυi, bυi, Sa(Γυi), |
| 2: | 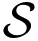 i ← {Πυi ∀υ ∈ i ← {Πυi ∀υ ∈
 }, },
 h ← {Πυi ∈ h ← {Πυi ∈
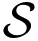 i: bυi = 1}, i: bυi = 1},
 l ← {Πυi ∈ l ← {Πυi ∈
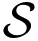 i: bυi = 0}, ΓΠυi ← bυi ∀Πυi ∈ i: bυi = 0}, ΓΠυi ← bυi ∀Πυi ∈
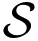 i i |
| 3: | Sa(Pi) ← Sa(Pi) + ∑ῡ:Πυī∈
 h (Γυī) h (Γυī) |
| 4: | for all Πυi ∈
 l do l do |
| 5: | if gi > 0 then |
| 6: | collaboratively compare Pi + rυ and gi |
| 7: | if Pi + rυ < gi then |
| 8: | Sa(Pi) ← Sa(Pi) + Sa (Γυi), ΓΠυi ← 1 {The grid provides enough energy to recharge υ} |
| 9: | else |
| 10: | collaboratively compare Pi and gi |
| 11: | if Pi > gi then |
| 12: | Sa(Pi) ← Sa(Pi) − Sa(Γυi), ΓΠυi ← −1 {υ is discharged to reduce the amount of energy taken from the grid} |
| 13: | end if |
| 14: | end if |
| 15: | else |
| 16: | collaboratively compare Pi − rυ and gi |
| 17: | if Pi − rυ > gi then |
| 18: | Sa(Pi) ← Sa(Pi) − Sa(Γυi), ΓΠυi ← −1 {υ is discharged to inject energy from the battery to the grid} |
| 19: | else |
| 20: | collaboratively compare Pi and gi |
| 21: | if Pi < gi then |
| 22: | Sa(Pi) ← Sa(Pi) + Sa(Γυi), ΓΠυi ← 1 {υ is charged to reduce the excessive amount of energy provided by the batteries to the grid} |
| 23: | end if |
| 24: | end if |
| 25: | end if |
| 26: | end if |
Initially, a designated Aggregator ā sets Pi to 0, divides it in shares and distributes the shares Sa(Pi) to the Aggregators. Once all the pseudonymized messages from every EV have been received by the Aggregators, each Aggregator a decrypts the incoming messages using its private key and retrieves the triple bυi, Sa(rυ), for each Vehicle υ, then it operates according to Algorithm 1 as follows:
- (1)
It groups the EVs'pseudonyms in two sets
h and
l. The former set includes all the pseudonyms associated to Vehicles with bυi = 1 which do not allow battery discharge, while all the other pseudonyms are grouped in
l. Note that the Vehicles whose pseudonyms are in
h are considered to have high charge priority, meaning that they will always be scheduled for recharge, regardless to the energy availability of the grid. Conversely, the Vehicles belonging to
l can be either charged/discharged or not, in order to meet the grid power offer/demand.
- (2)
The recharge of each Vehicle with pseudonym Πυi ∈
h is scheduled for the epoch i by setting ΓΠυi to 1 and the total power amount Pi is updated by adding the corresponding share Sa(Γυi). Note that the additions are performed directly on the shares, therefore the Aggregator operates without knowing the values Γυi. In case Γυi = 0, i.e., υ is not available for recharge/discharge, adding Sa(Γυi) to Sa(Pi) does not alter the current values of Pi.
- (3)
For each Vehicle associated to a pseudonym Πυi ∈
l, if gi > 0 (i.e., the grid has a power surplus which can be used to recharge the batteries), the Aggregators collaboratively compare Pi + Γυi and gi by means of the comparison protocol presented in [30]. Without loss of generality, we assume that the Aggregator ā is elected as responsible of defining the order of service of the vehicles in
l (which is randomly chosen at every epoch) and to communicate it to the other Aggregators. If the current power amount (including the recharge of υ) does not exceed gi, υ is scheduled for recharge, otherwise a second collaborative comparison between Pi and gi is performed: if Pi exceeds gi (meaning that the current energy used to serve the Vehicles exceeds the grid's power availability), the discharge of υ is scheduled, otherwise no charge/discharge takes place. Analogously, for gi < 0, Pi − Γυi and gi are collaboratively compared and in case Pi − rυ exceeds gi, the discharge of the battery of υ is scheduled in order to reduce the amount of energy used for recharging, otherwise the Aggregators compare again Pi to gi and if Pi < gi (i.e., the total discharged energy exceeds the grid's needs), υ is recharged. Conversely, in case Pi > gi, no action is scheduled.
Once the scheduling procedure is concluded, ā sends to the Anonymizer the scheduling output encrypted under the ephemeral encryption key of Vehicle υ and the corresponding pseudonym Πυi. The Anonymizer retrieves the identity IDυ of the Vehicle associated to Πυi, forwards to υ, which obtains ΓΠυi by decrypting the message with its private ephemeral key and schedules its battery charge/discharge accordingly.
5. Security Discussion
In this Section we discuss the adversarial model, state definitions of the privacy properties of our scheduling mechanism and provide proofs that such properties are guaranteed by our framework.
We assume that each Aggregator behave according to the honest-but-curious attacker model, meaning that it honestly executes the scheduling algorithm, but tries to obtain further information about the current battery levels of the EVs and the amount of refilled energy by performing arbitrary elaborations on the messages they receive, possibly colluding with other Aggregators (but not with the Anonymizer). The Anonymizer is also supposed to be honest-but-curious. Conversely, the EVs are assumed to by honest nodes.
We now define the property of blindness, which the proposed infrastructure satisfies.
Definition 1
The scheduling infrastructure provides blindness if during any set of epochs





More formally, we define the
Blind experiment, involving a challenger
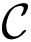
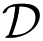
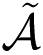
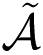

- (1)
selects four sets of Vehicles , , , the identifiers IDv, the values Γυi and the random numbers ρ1, ρ2, …, ρt−1 to be used to divide each Γυi in shares for each Vehicle in , and communicates them to
.
- (2)
selects a random bit b̄ = {0,1}, generates the pseudonyms Πυi and the shares Sa(Γυi) ∀i ∈
, a ∈
, , and communicates them to
.
- (3)
outputs a bit b̄′.
The architecture provides |

The proof that our proposed infrastructure is blind descends from the property of perfect secrecy of the SSS scheme [36] and can be constructed by straightforwardly extending the one provided in ([37], Theorem 3) for two sets of shares to a scenario with |



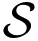
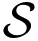
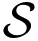
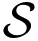
Thus, it follows that:
The proof is completed by noting that the pseudonyms Πυi are random numbers refreshed at every epoch, therefore the knowledge of Πυi does not provide any advantage to
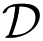
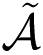
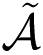

Definition 2
The scheduling architecture is oblivious if the Anonymizer has no knowledge of the priority bit bυi, the values Γυi and the scheduling outputs ΓΠυi in any epoch i.
To formalize this property, we define the
Oblivious experiment, which involves a challenger
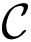
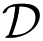
- (1)
selects two Vehicles υ0, υ1 ∈
and communicates to
the priority bits bυ0i,bυ1i, the values Γυ0i, Γυ1i, and the random numbers ρ1, ρ2, …, ρt−1 to be used to divide Γυ0i, Γυ1i, in shares.
- (2)
selects a random bit b̄ = {0,1}, generates and the encrypted scheduling output , and communicates them to
.
- (3)
outputs a bit b̄′.
The architecture provides obliviousness if:
Assuming that the cryptosystem E(Ke, ·) ensures message indistinguishability (see Section 4), the property can be proved by contradiction: let us suppose that the adversary
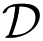
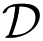
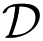
Finally, it is worth discussing the correctness of our privacy-friendly scheduling protocol: at the end of the scheduling procedure, it results Sa(Pi) = ∑Πυi∈
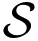
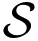
6. Benchmark ILP Model
We now introduce an Integer Linear Programming formulation which finds the optimal battery charge/discharge schedule. Such model should be considered as an ideal benchmark, since it relies on future knowledge about the periods in which EVs are plugged in, the current battery level and the amount of energy to be refilled, which would impose great limitations to its applicability to a real scenario (e.g., by requiring the users to declare in advance their traveling periods for the next day).
Sets
: set of recharge periods of the EVs (each vehicle υ ∈
has at least one recharge period within the optimization time span)
: set of discretized epochs within the optimization time span
Parameters
ep: maximum amount of power to be provided during the recharge period p (given by the difference between the battery maximum capacity and the initial battery charge level lυ of the Vehicle υ having the p-th recharge period)
ap: minimum amount of power to be provided during the recharge period p (aυ = tυ − lυ if lυ < tυ, 0 otherwise)
rp: battery charge rate (per epoch) of the vehicle υ having the p-th recharge period
kpi: it is 1 if epoch i belongs to the p-th recharge period, 0 otherwise
gi : maximum grid power supply (if gi > 0) or demand (if gi < 0) at epoch i
: boolean indicator, it is 1 if gi > 0, 0 otherwise
: boolean indicator, it is 1 if gi < 0, 0 otherwise
M: positive value, such as M ≫ maxi∈
|gi|
Variables
xpi: integer variable (−1 ≤ xpi ≤ 1), it is 1(− 1) if the battery of the vehicle associated to the p-th recharge period is recharged(discharged) at epoch i, 0 otherwise
δ: indicates the minimum ratio of the power utilized (provided) for battery recharge (discharge), to the power supplied/requested by the grid
Objective function
The objective function maximizes the minimum ratio of the power requested by the aggregator to recharge the vehicles' batteries (or obtained by the aggregator by discharging them) to the power requested/offered by the grid. Constraints 2 and 3 limit the minimum/maximum amount of energy to be charged during each recharge period, while Constraints 4 and 5 avoid recharging batteries with more energy than the grid can provide or injecting excessive energy into the grid by discharging batteries during the periods of shortages. Finally, Constraints 6 set δ to the minimum normalized amount of scheduled power absorption/supply
7. Performance Evaluation
We now evaluate our proposed scheduling mechanism in terms of computational complexity, message number and length, and compare its performance to the optimal results obtained by means of the ILP formulation presented in Section 6. Our implementation assumes a 256 bit-long modulo q for the SSS scheme and IDs/pseudonyms of 32 bits. The hybrid cryptosystem used for the share encryption is the RSA-KEM Key Transport Algorithm [38], which uses the RSA public key cryptosystem with modulo n of 1024 bits, the KDF2 key derivation function (based on SHA-1) and the AES-Wrap-128 key-wrapping scheme to communicate an ephemeral 128-bit-long key used to encrypt the samples V(i) by means of the standard AES scheme operating in Chipher Block Chaining mode (CBC). The scheduling output destined to the EVs is assumed to be encrypted with the standard RSA public key cryptosystem.
7.1. Computational Complexity
We start evaluating the asymptotic number of incoming/outgoing messages at each node. As showed in Table 2, the number of messages exchanged by the Vehicles exhibits a linear dependence on the number of shares |





Table 3 reports the operations performed by each node for the scheduling of a single battery recharge. The computational cost of each operation is detailed in Table 4 based on [28,30]. The most demanding procedure is the share collaborative comparison performed by the Aggregators in multiple rounds depending on |

Finally, it is worth discussing the message length: each service request generated by an EV and forwarded by the Anonymizer consists on a 32 bit-long ID/pseudonym and a RSA-KEM encrypted message of 2624 bits, for a total length of 2656 bits. During the share comparison procedure, each share is in turn divided in |








7.2. Numerical Results
We compare the scheduling results obtained by our proposed protocol to the ILP benchmark model. We consider a scenario of a residential area of 1000 houses with peak power consumption of 3 kW [39], a windfarm (peak production of 8 MW [40]) and 1000 EVs (battery maximum capacity between 12.75 and 17 kWh, charging rate of 0.75 or 1 kW [14], minimum recharge threshold between 1.5 and 2 kWh). The behavior of each Vehicle υ is modeled by means of a discrete random walk between 0 and 1 with state transition probability of 0.25. For each epoch, state 0 is mapped to kυi = 0, while state 1 sets kυi = rυ.
Note that, since the ILP model does not take into account the energy price, such price is assumed to be constant within the whole optimization time span and does not play any role in the scheduling strategy in both the optimal and the privacy-friendly approaches.
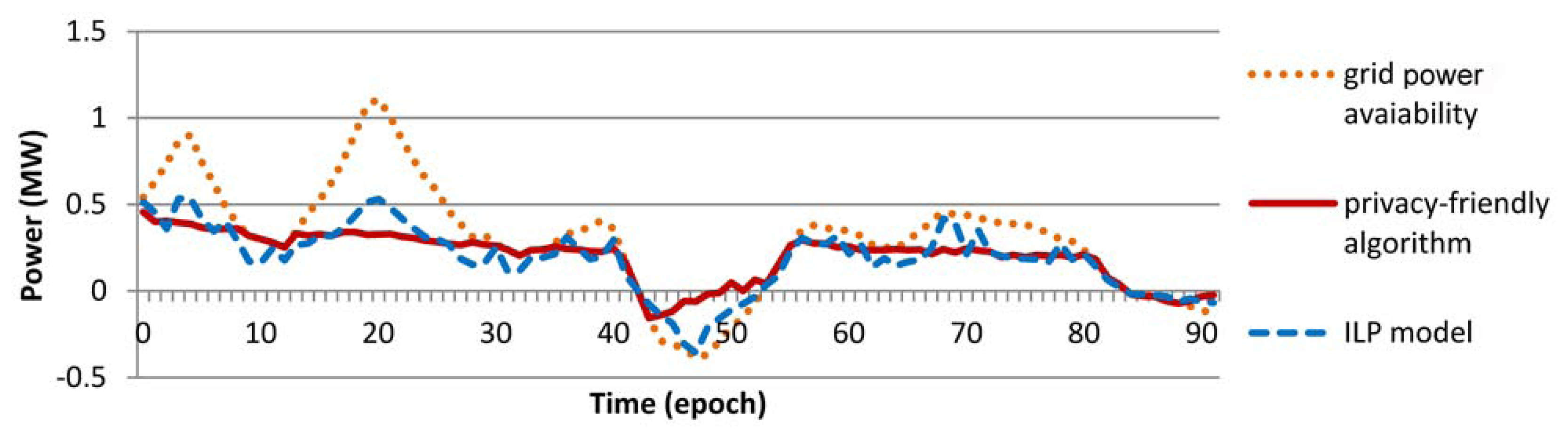
Results averaged over 365 days (each day is divided in 96 epochs of 15 min duration, see Figure 3 for an example of daily schedule) show that the running time of the privacy-friendly approach is significantly lower than the one of the ILP model (seconds vs. hours, see Table 5). The minimum power consumption-to-power availability ratio provided by our algorithm is on average lower than the optimal one, which is due to the fact that, in case gi is negative, the privacy-friendly approach always schedules the recharge of high priority EVs, while the ILP model might postpone it according to the knowledge of their future traveing behavior. However, the degree of similarity (expressed in terms of Mean Square Error) between the curve of the grid power supply/request and the curve of the scheduled energy usage is not significantly worsened w.r.t. the optimal solution provided by the ILP formulation (only 0.2% increase, as reported in Table 5).
8. Conclusions
This paper proposes a privacy-preserving Vehicle-to-Grid communication infrastructure which schedules the battery charge/discharge times of electric vehicles without exposing the users' traveling habits, the current battery level nor the amount of refilled energy. Performance in terms of computational times and gap w.r.t. the optimal schedule obtained by means of an Integer Linear Program shows the viability of the proposed privacy-friendly approach, which provides results not significantly dissimilar w.r.t. the optimal ones.
Acknowledgments
The authors thank Valeria Olivieri for her precious suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chan, C.; Bouscayrol, A.; Chen, K. Electric, hybrid, and fuel-cell vehicles: Architectures and modeling. IEEE Trans. Veh. Technol. 2010, 59, 589–598. [Google Scholar]
- Offer, G.; Howey, D.; Contestabile, M.; Clague, R.; Brandon, N. Comparative analysis of battery electric, hydrogen fuel cell and hybrid vehicles in a future sustainable road transport system. Energy Policy 2010, 38, 24–29. [Google Scholar]
- Pieltain FernaÌᾼndez, L.; RomaÌᾼn, T.; Cossent, R.; Domingo, C.; FriÌᾼas, P. Assessment of the impact of plug-in electric vehicles on distribution networks. IEEE Trans. Power Syst. 2011, 26, 206–213. [Google Scholar]
- Lopes, J.; Soares, F.; Almeida, P. Integration of electric vehicles in the electric power system. IEEE Proc. 2011, 99, 168–183. [Google Scholar]
- Markel, T.; Kuss, M.; Denholm, P. Communication and control of electric drive vehicles supporting renewables. Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC '09), Dearborn, MI, USA, 7–10 September 2009; pp. 27–34.
- Ekman, C.K. On the synergy between large electric vehicle fleet and high wind penetration—An analysis of the Danish case. Renew. Energy 2011, 36, 546–553. [Google Scholar]
- Kempton, W.; Tomic, J.; Letendre, S.; Brooks, A.; Lipman, T. Vehicle-to-Grid Power: Battery, Hybrid, and Fuel Cell Vehicles as Resources for Distributed Electric Power in California; Working Paper Series ECD-ITS-Rr-1-03; Institute of Transportation Studies, University of California, Davis: Davis, CA, USA, 2001. [Google Scholar]
- Brooks, A. Integration of electric drive vehicles with the power grid-a new application for vehicle batteries. Proceedings of the Seventeenth Annual Battery Conference on Applications and Advances, Long Beach, CA, USA, 15–18 January 2002; pp. 239–254.
- Kempton, W.; Marra, F.; Andersen, P.; Garcia-Valle, R. Business models and control and management architectures for EV electrical grid integration. In Electric Vehicle Integration into Modern Power Networks; Garcia-Valle, R., PeÃğas Lopes, J.A., Eds.; Power Electronics and Power Systems; Springer New York: New York, NY, USA, 2013; pp. 87–105. [Google Scholar]
- Brooks, A. Vehicle-to-Grid Demonstration Project: Grid Regulation Ancillary Service with a Battery Electric Vehicle; Research Report to CARB; AC Propulsion: San Dimas, CA, USA, 2002. [Google Scholar]
- Hoh, B.; Gruteser, M.; Xiong, H.; Alrabady, A. Enhancing security and privacy in traffic-monitoring systems. IEEE Pervasive Comput. 2006, 5, 38–46. [Google Scholar]
- Liao, L.; Patterson, D.J.; Fox, D.; Kautz, H. Learning and inferring transportation routines. Artif. Intell. 2007, 171, 311–331. [Google Scholar]
- National Institute of Standards and Technology, The Smart Grid Interoperability Panel, Smart Grid Cybersecurity Committee. Guidelines for Smart Grid Cybersecurity: Volume 2, Privacy and the Smart Grid. Draft NISTIR 7628 Revision 1. 2013. Available online: http://csrc.nist.gov/publications/PubsDrafts.html#NIST-IR-7628r1 (accessed on 1 January 2014). [Google Scholar]
- Liu, R.; Dow, L.; Liu, E. A survey of PEV impacts on electric utilities. Proceedings of the 2011 IEEE PES Innovative Smart Grid Technologies (ISGT), Hilton Anaheim, CA, USA, 17–19 January 2011; pp. 1–8.
- Bessa, R.J.; Matos, M.A. Economic and technical management of an aggregation agent for electric vehicles: A literature survey. Eur. Trans. Electr. Power 2012, 22, 334–350. [Google Scholar]
- Han, Y.; Chen, Y.; Han, F.; Liu, K. An optimal dynamic pricing and schedule approach in V2G. Proceedings of the 2012 Asia-Pacific Signal Information Processing Association Annual Summit and Conference (APSIPA ASC), Hollywood, CA, USA, 3–6 December 2012; pp. 1–8.
- Zou, S.; Ma, Z.; Liu, X. Distributed efficient charging coordinations for electric vehicles under progressive second price auction mechanism. Proceedings of the 52nd IEEE Conference on Decision and Control (CDC), Firenze, Italy, 10–13 December 2013; pp. 550–555.
- Li, G.; Zhang, X.P. Modeling of plug-in hybrid electric vehicle charging demand in probabilistic power flow calculations. IEEE Trans. Smart Grid 2012, 3, 492–499. [Google Scholar]
- Alizadeh, M.; Scaglione, A.; Davies, J.; Kurani, K. A scalable stochastic model for the electricity demand of electric and plug-in hybrid vehicles. IEEE Trans. Smart Grid 2013, PP, 1–13. [Google Scholar]
- Di Giorgio, A.; Liberati, F.; Pietrabissa, A. On-board stochastic control of Electric Vehicle recharging. Proceedings of the 52nd IEEE Conference on Decision and Control (CDC), Firenze, Italy, 10–13 December 2013; pp. 5710–5715.
- Khayyam, H.; Abawajy, J.; Javadi, B.; Goscinski, A.; Stojcevski, A.; Bab-Hadiashar, A. Intelligent battery energy management and control for vehicle-to-grid via cloud computing network. Appl. Energy 2013, 111, 971–981. [Google Scholar]
- Stegelmann, M.; Kesdogan, D. Design and evaluation of a privacy-preserving architecture for vehicle-to-grid interaction. In Public Key Infrastructures, Services and Applications; Petkova-Nikova, S., Pashalidis, A., Pernul, G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7163, pp. 75–90. [Google Scholar]
- Stegelmann, M.; Kesdogan, D. Location privacy for vehicle-to-grid interaction through battery management. Proceedings of the Ninth International Conference on Information Technology: New Generations (ITNG), Las Vegas, NV, USA, 16–18 April 2012; pp. 373–378.
- Yang, Z.; Yu, S.; Lou, W.; Liu, C. P2 : Privacy-preserving communication and precise reward architecture for V2G networks in smart grid. IEEE Trans. Smart Grid 2011, 2, 697–706. [Google Scholar]
- Liu, J.; Au, M.; Susilo, W.; Zhou, J. Enhancing location privacy for electric vehicles (at the right time). In Computer Security—ESORICS 2012; Foresti, S., Yung, M., Martinelli, F., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7459, pp. 397–414. [Google Scholar]
- Nicanfar, H.; Hosseininezhad, S.; TalebiFard, P.; Leung, V.C.M. Robust privacy-preserving authentication scheme for communication between electric vehicle as power energy storage and power stations. Proceedings of the IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 3429–3434.
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar]
- Bogdanov, D. Foundations and Properties of Shamir's Secret Sharing Scheme, Research Seminar in Cryptography; Institute of Computer Science, University of Tartu: Tartu, Estonia, 2007. [Google Scholar]
- Nishide, T.; Ohta, K. Multiparty computation for interval, equality, and comparison without bit-decomposition protocol. Proceedings of the 10th International Conference on Practice and Theory in Public-Key Cryptography (PKC '07), Beijing, China, 16–20 April 2007; Springer-Verlag: Berlin/Heidelberg, Germany, 2007; pp. 343–360. [Google Scholar]
- Kerschbaum, F.; Biswas, D.; de Hoogh, S. Performance comparison of secure comparison protocols. Proceedings of the 20th International Workshop on Database and Expert Systems Application (DEXA '09), Linz, Austria, 31 August– 4 September 2009; pp. 133–136.
- Bychkovsky, V.; Hull, B.; Miu, A.; Balakrishnan, H.; Madden, S. A measurement study of vehicular internet access using in situ Wi-Fi networks. Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MobiCom '06), Los Angeles, CA, USA, 24–29 September 2006; ACM: New York, NY, USA, 2006; pp. 50–61. [Google Scholar]
- Pinart, C.; Sanz, P.; Lequerica, I.; García, D.; Barona, I.; Sánchez-Aparisi, D. DRIVE: A reconfigurable testbed for advanced vehicular services and communications. Proceedings of the 4th International Conference on Testbeds and Research Infrastructures for the Development of Networks & Communities (TridentCom '08), Innsbruck, Austria, 18–20 March 2008; ICST (Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering): Brussels, Belgium, 2008; pp. 16:1–16:8. [Google Scholar]
- Bissmeyer, N.; Stubing, H.; Schoch, E.; Gotz, S.; Stotz, J.P.; Lonc, B. A generic public key infrastructure for securing Car-to-X communication. Proceedings of the 18th World Congress on Intelligent Transport Systems featuring ITS America's Annual Meeting and Exposition, Orlando, FL, USA, 16–20 October 2011.
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography (Chapman & Hall/Crc Cryptography and Network Security Series); Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Rottondi, C.; Verticale, G.; Capone, A. Privacy-preserving smart metering with multiple data Consumers. Comput. Netw 2013, 57, 1699–1713. [Google Scholar]
- Stinson, D. Cryptography Theory and Practice, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Rottondi, C.; Mauri, G.; Verticale, G. A protocol for metering data pseudonymization in smart grids. Trans. Emerg. Telecommun. Technol. 2013. [Google Scholar] [CrossRef]
- Randall, J.; Kaliski, B.; Brainard, J.; Turner, S. Use of the RSA-KEM Key Transport Algorithm in the Cryptographic Message Syntax (CMS), RFC 5990; RFC, Ed. ed; The Internet Engineering Task Force: Fremont, CA, USA, 2010. [Google Scholar]
- Barker, S.; Mishra, A.; Irwin, D.; Cecchet, E.; Shenoy, P.; Albrecht, J. Smart*: An Open Data Set and Tools for Enabling Research in Sustainable Homes. Proceedings of the 1st KDD Workshop on Data Mining Applications in Sustainability (SustKDD), Beijing, China, 12 August 2012.
- Hong, T.; Pinson, P.; Fan, S. Global energy forecasting competition 2012. Int. J. Forecast 2014, 30, 357–363. [Google Scholar]
| Notation | Description |
|---|---|
 | set of Vehicles (υ is an element of the set) |
 | set of Aggregators (a is an element of the set) |
 | set of time epochs (i is an element of the set) |
| rυ | battery charging rate of Vehicle υ |
| bυi | recharge priority indicator of Vehicle υ at epoch i |
| lυi | battery charge level of Vehicle υ at epoch i |
| Vυi | requested battery charge/discharge indicator of Vehicle υ at epoch i |
| tυ | battery threshold level below which no discharge is accepted by Vehicle υ |
| , | ephemeral encryption/decryption key-pair generated by Vehicle υ at epoch i |
| IDυ | identifier of Vehicle υ |
| Πυi | pseudonym attributed to Vehicle υ at epoch i |
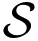 i i | set of the pseudonyms Πυi at epoch i |
| Γυi | scheduled battery charge/discharge indicator of Vehicle υ at epoch i |
| Node | Input | Output |
|---|---|---|
| Vehicle | O(1) | O(|
 |) |) |
| Anonymizer | O(|
 | · | | · |
 |) |) | O(|
 | · | | · |
 |) |) |
| Aggregator | O(|
 | 2 log2 | | 2 log2 |
 | · | | · |
 |) |) | O(|
 | 2 log2 | | 2 log2 |
 | · | | · |
 |) |) |
| Vehicle | 1 random number generation modulo |
| Anonymizer | 1 random number generation modulo 232 |
| Aggregator | (worst case) |
see Table 4 for the cost details.
| Cs(x) | cost of the generation of |
 | shares modulo x | shares modulo x | |
 |(| |(|
 | − 1) additions modulo x | − 1) additions modulo x|  |(| |(|
 | − 1) multiplications modulo x | − 1) multiplications modulo x(|  | − 1) random number generations modulo x | − 1) random number generations modulo x |
| Ca(x) | cost of a share addition modulo x | 1 addition modulo x |
| Cl(x) | cost of a share Lagrange interpolation modulo x | O(|
 |2) multiplications modulo x |2) multiplications modulo x |
| Cm(x) | cost of a share collaborative multiplication modulo x | Cs(x) + (|
 | − 1)Ca(x)+ 2 multiplications modulo x, performed in 2 rounds | − 1)Ca(x)+ 2 multiplications modulo x, performed in 2 rounds |
| Cc(x) | cost of a collaborative comparison modulo x | 2 random number generation modulo x + 1 random number generation modulo 2 2 exponentiations modulo q + 2 multiplications modulo x 2Cs(x) + (|  | + 1)Ca(x) + O(| | + 1)Ca(x) + O(|
 |)Cm(x) + Cl(x), performed in
rounds |)Cm(x) + Cl(x), performed in
rounds |
| cost of an RSA encryption modulo x | 1 exponentiation modulo x | |
| cost of an RSA decryption modulo x | 1 exponentiation modulo x | |
| cost of an RSA-KEM encryption with RSA modulo x and AES encryption of a message of l blocks | 1 random number generation modulo
1 KDF2 key derivation and AES-Wrap-128 key wrapping l AES encryptions | |
| cost of an RSA-KEM decryption with RSA modulo x and AES decryption of a message of l blocks | 1 KDF2 key derivation and AES-Wrap-128 key unwrapping l AES decryptions |
| Privacy-friendly S. | ILP | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Average | Max | Min | Aver. MSE | Time | Average | Max | Min | Aver. MSE | Time |
| −6.64 | 0.11 | −167.98 | 4.72 × 1012 | 0.6 s | 0.03 | 0.48 | −0.38 | 4.71 × 1012 | 4h |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rottondi, C.; Fontana, S.; Verticale, G. Enabling Privacy in Vehicle-to-Grid Interactions for Battery Recharging. Energies 2014, 7, 2780-2798. https://doi.org/10.3390/en7052780
Rottondi C, Fontana S, Verticale G. Enabling Privacy in Vehicle-to-Grid Interactions for Battery Recharging. Energies. 2014; 7(5):2780-2798. https://doi.org/10.3390/en7052780
Chicago/Turabian StyleRottondi, Cristina, Simone Fontana, and Giacomo Verticale. 2014. "Enabling Privacy in Vehicle-to-Grid Interactions for Battery Recharging" Energies 7, no. 5: 2780-2798. https://doi.org/10.3390/en7052780
APA StyleRottondi, C., Fontana, S., & Verticale, G. (2014). Enabling Privacy in Vehicle-to-Grid Interactions for Battery Recharging. Energies, 7(5), 2780-2798. https://doi.org/10.3390/en7052780