1. Introduction
Microgrids, containing a large number of distributed power sources, such as solar power, wind power and others, are devoted to the key technology of connecting distributed power to the grid [
1]. To increase the stability of the system, making it more immune to perturbations, such as changes in the loading conditions or changes in the electric energy production due to environmental variability, energy storage devices are configured and used, which has become an extensively and commonly employed solution. There are many possible technologies to implement an energy storage system: batteries, flywheels, superconducting magnetic energy storage SMES, ultracapacitors, and others. None of these technologies offer a clear advantage over the others. To provide the power and storage capabilities required by the microgrid, a hybrid solution is commonly adopted [
2,
3,
4,
5]. For this paper, the focus will be in ultracapacitors, but the same concepts can be applied to batteries.
In ultracapacitors (UCs), a kind of high power density type storage device, energy is stored in the form of electric charge, so it doesn’t need energy conversion in charging or discharging and therefore they have been widely used in microgrids as energy storage systems (ESSs) to absorb the perturbed power and improve microgrid stability due to their high efficiency and high power density (up to 10 kW/kg) [
4]. Power electronic converter circuits and the corresponding control algorithms are needed in the management and application of UCs, therefore different kinds of ultracapacitor application circuits and control algorithms have been extensively studied. Reference [
2] studied three kinds of UC application circuit topologies and analyzed their advantages and disadvantages.
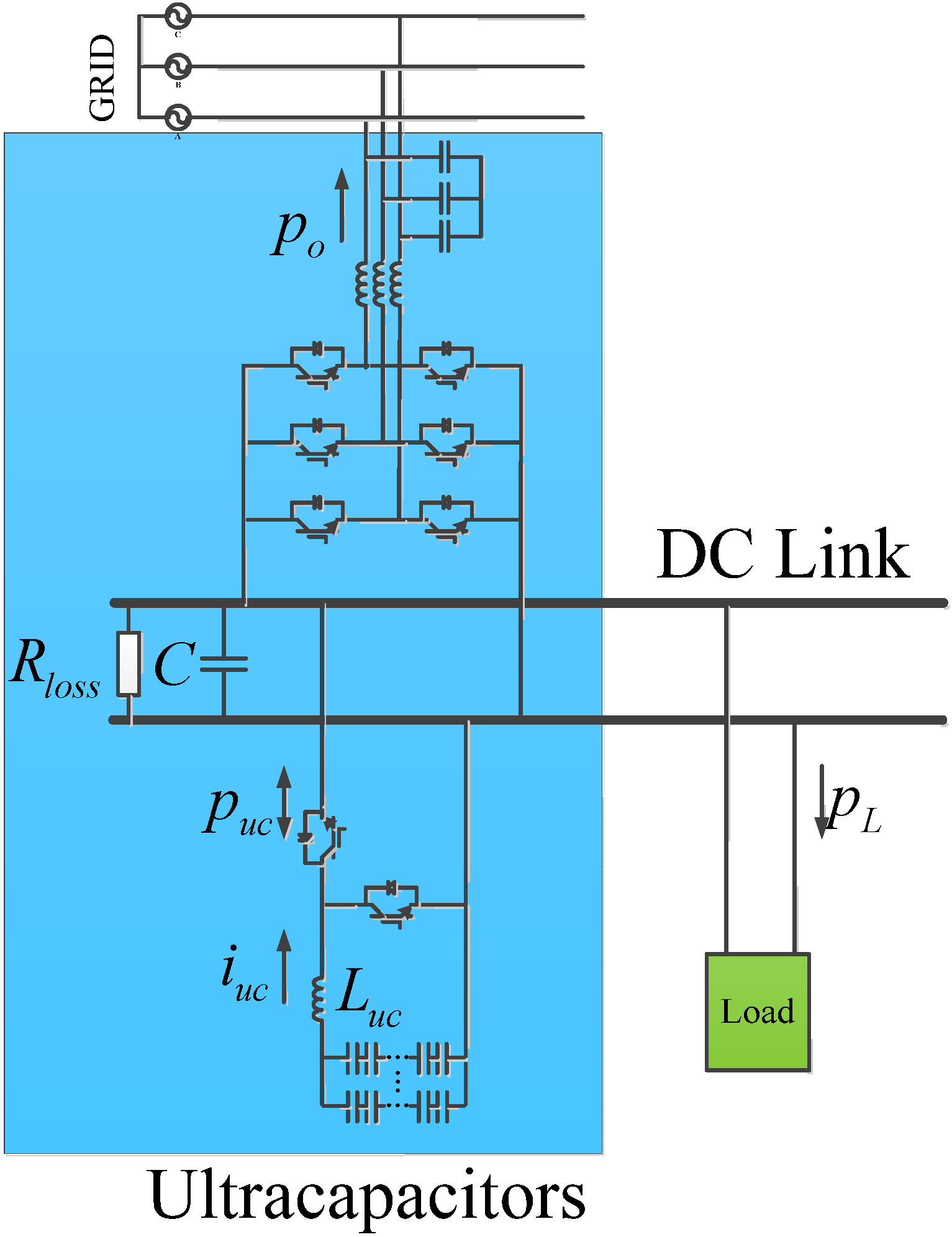
In the context of microgrids, a universal ESS based on ultracapacitors consists of an AC/DC Grid Side Converter (GSC) and a bidirectional DC/DC Energy Storage Side Converter (ESSC) with a common DC link. A typical system structure is shown in
Figure 1. The UC is connected to the DC link through an ESSC. The DC link is connected to the grid through a GSC. There is a DC load hanging on the DC link which represents the perturbed power.
The control algorithms of the ESSC and GSC are crucial for the utilization of UCs. ESSC, as the interface between the UC and DC link, is usually used to archive the charging-discharging of the UC which decides the utilization factor of the UC. GSC, as the direct interface between the DC link and the grid, is usually controlled to improve the power quality and grid-connected operational properties, such as suppression of current harmonics and grid fault support functions. How the DC link voltage is maintained constant under various operation conditions is the core of the control algorithms. Those issues have been investigated by many authors around the world. Reference [
5] proposed a sliding model control algorithm to control the power exchange between UCs and grid-connected inverters, the compensation effect of which depends on the power instructions issued by the micro-grid control center (MGCC) and the DC link voltage was controlled by the GSC and not the ESSC (UC). Reference [
6] used a nonlinear model based on instantaneous power balance to establish a nonlinear control strategy based on smoothness which can control the DC link voltage as well as the UC voltage and effectively improve the power response speed of the system.
Figure 1.
Diagram of system structure.
Figure 1.
Diagram of system structure.
As previously mentioned maintaining the DC link voltage under any unusual operation conditions is very important. When imbalance faults or single-phase loads cause three-phase imbalance, an instantaneous power exchange between the GSC and grid will produce a double frequency instantaneous power fluctuation, which will cause double frequency fluctuation of the DC link voltage of the inverter [
7,
8,
9,
10], thus adversely affecting the control of the GSC. Methods to eliminate DC link voltage fluctuations have been studied by a large number of scholars. The DC link voltage control algorithms proposed in reference [
7,
8,
9,
10] are similar. They all use grid-connected inverters to control the DC link voltage and utilize the injected negative sequence current to directly control the double frequency instantaneous active power to zero. However, the essence of the algorithm is an open-loop control algorithm, which is valid when and only when the inverter is grid-connected (P/Q control mode).
Generally the DC link voltage is controlled by the active current (current of d axis) of the GSC [
5,
6,
7,
8,
9,
10]. A PI regulator is used in conventional closed-loop DC link voltage control [
7,
8,
9,
10]. The essence of DC link voltage fluctuations caused by three-phase imbalance is the active power AC component at the double frequency, which can be fully compensated by a UC with fast power throughput capacity. Hence, this paper has designed a control strategy that includes a DC link voltage outer loop adopted proportional-integral-resonant (PIR) regulator and a UC current inner loop adopted proportional-integral (PI) regulator, which realize the UC stabilized DC link voltage as well as compensate for instantaneous active power fluctuation at the double frequency and eliminate fluctuations of DC link voltage at the double frequency.
This paper analyzes the transmission process of instantaneous power between ESSCs and GSCs and establishes an analytical dynamic mathematical model for an ESS. The established model is an improvement on the model presented in reference [
10]. Consequently it facilitates the control design for the DC link voltage of ESSs. The ESSC-side or GSC-side can be chosen flexibly for DC link voltage control on the basis of the established model.
Based on the established model the paper proposes an improved compensation control strategy for the ESS of a UC in the context of microgrid applications. The proposed strategy is composed of two parts that are the ESSC control strategy and the GSC control strategy. The first part is applied to controlling charge-discharging of the UC and maintaining the DC link voltage constant under all operating conditions such as unbalanced grid, load change and different UC voltage. Therefore, the degrees of freedom for the control of GSC, which is implemented in the second part, is increased and the advanced upper layer control commands from the MGCC will be accepted. The adoption of the proposed control strategy takes full advantage of the high power density characteristics of UCs and improves the utilization factor of UCs in microgrids.
The remainder of this paper is organized as follows: in
Section 2, the mathematical model of the system is derived through instantaneous power balancing. In
Section 3, the DC link voltage control strategy of the ESSC with PIR regulator is proposed. The control strategy of the GSC is recommended. The design of the control loop and the simulation are addressed in
Section 4. In
Section 5, the results of our experiments are presented. The paper ends with some concluding remarks.
2. Modelling of the System
The GSC control is to perform the control of power flow between the DC link and grid. When the grid voltage dips, the DC link voltage may fluctuate due to the instantaneous unbalanced power flow between the grid and the DC link. The dynamics of the capacitor in the DC-link between the grid and UCs side converters are described by:
where
is the equivalent resistance of system losses,
C is the capacitance of the DC link,
represents the perturbed power of the DC link,
is the instantaneous active power exchanged between the grid-connected inverter and the DC link [
10], and can be expressed as:
where
is the DC component of instantaneous power, while
,
are the AC components. The expressions are as follows [
10]:
The dynamic instantaneous power of the filter inductor is taken into account in Equations (3) and (4); L indicates the output filter inductor of the grid-connected inverters; superscript P indicates the positive sequence rotating component; superscript N indicates the negative sequence rotating components. It can be seen from Equation (2) to Equation (4) that when there is an unbalance (voltage or current) of the DC/AC converters, because of the product term of the positive sequence voltage and negative sequence current, an instantaneous active power fluctuation at the double frequency will be generated. The product term is also the essential reason for double frequency ripple of the DC link voltage.
If the instantaneous power of the UC in Equation (1)
contains the double frequency component and offsets the AC component of
, the DC link voltage fluctuation can be eliminated and the UC can achieve AC and DC compensation at the same time, based on which, the UC current can be assumed as follows:
Considering the value of the capacitance of UC is large enough that the voltage fluctuation of UC caused by the AC current can be ignored, then the instantaneous output power of the UC is expressed as:
where
indicates the filter inductance of the bidirectional DC/DC circuit. According to Equation (6) when the UC current contains a double frequency component, its instantaneous power includes not only the DC power and the double frequency component power, but also the power fluctuation at the quadruple frequency caused by inductance. Because
usually takes a small value, the quadruple frequency power fluctuation has little effect on the DC link voltage, which will be verified in subsequent simulations and experiments.
Rewriting the DC link voltage in the form of components:
where
stands for the DC component of the DC link voltage and
stand for the double frequency fluctuation component of the DC link voltage. Substituting Equations (2), (6), (7) into Equation (1) we obtain the component expression:
Equations (8) and (9) describe the dynamics of the DC and AC components of the DC link voltage respectively. in Equation (8) is given by Equation (3), while and in Equation (9) are given by Equation (4). indicates the effect of other possibly existing branches’ power on the DC link voltage. and represent the disturbance power.
It can be known from Equation (8) that the DC component of the UC current can be taken as the controlled variable of the DC component of the DC link voltage . In this case, the output power and other possibly existing branches’ become disturbance items. Also, when there is photovoltaic or other distributed generations connected to the DC link, the output power can be taken as disturbance power. Similarly, according to Equation (9), the AC component of the UC current can be taken as the controlled variable of the AC component of the DC link voltage.
However, the instantaneous power models in Equations (8) and (9) are nonlinear, so the equations should be linearized to design the control loop:
After linearization, Equations (10) and (11) are the steady state equations and dynamic small-signal equations, respectively.
Analyzing the small-signal equation in Equation (10), the DC component of the DC link voltage is disturbed by the AC component of the UC current, and its disturbance gain is related to the steady state amplitude and inductor value. The control object is first order, which has a moving zero point that is changed with the magnitude and direction of the DC steady state component , so that the regulator can be designed.
In Equation (11), and are the amplitude of the steady state component of the DC link voltage fluctuation, and will finally be zero according to the control target. Equation (11) is a dual-input and dual-output system, whose control variables are and and controlled variables are and . The transfer function matrix is a second order system. The main diagonal transfer function includes moving zero points changed with the magnitude and direction of the DC steady state component , and the DC component of the UC will have an impact on the DC link voltage ripple due to the coupling of the inductor. The introduction of Equation (11) is to provide a basis for the design of the resonant controller.
3. Proposed Control Strategy
3.1. The Control Scheme of the Energy Storage Side Converter
The DC link voltage reflects the instantaneous power fluctuation. When there are system load disturbances or instantaneous power imbalances, the most direct and rapid reaction is the variation of DC link voltage. Therefore, the current reference command of the UC can be obtained by feedback control of the DC link voltage. The control algorithm of the DC link voltage outer loop and UC current inner loop was designed in this paper, in which the current reference of UC can be calculated dynamically by the DC link voltage regulator, whose output includes the system instantaneous power disturbance and double frequency power fluctuation. However, a conventional PI regulator has inadequate gain at the double frequency restricted by stability, so the fluctuation information at the double frequency cannot be extracted completely. To solve the problem, a PIR regulator is designed in this paper to eliminate the double frequency ripple and realize AC and DC hybrid compensation control of the UC.
We rewrite the small signal equations as follows:
The transfer function in Equation (12) is the same as that in Equation (10), where matrices A, B and C can be obtained from Equation (11). The specific expressions can be found in the Appendix. Equations (12) and (13) are used for the DC link voltage regulator design.
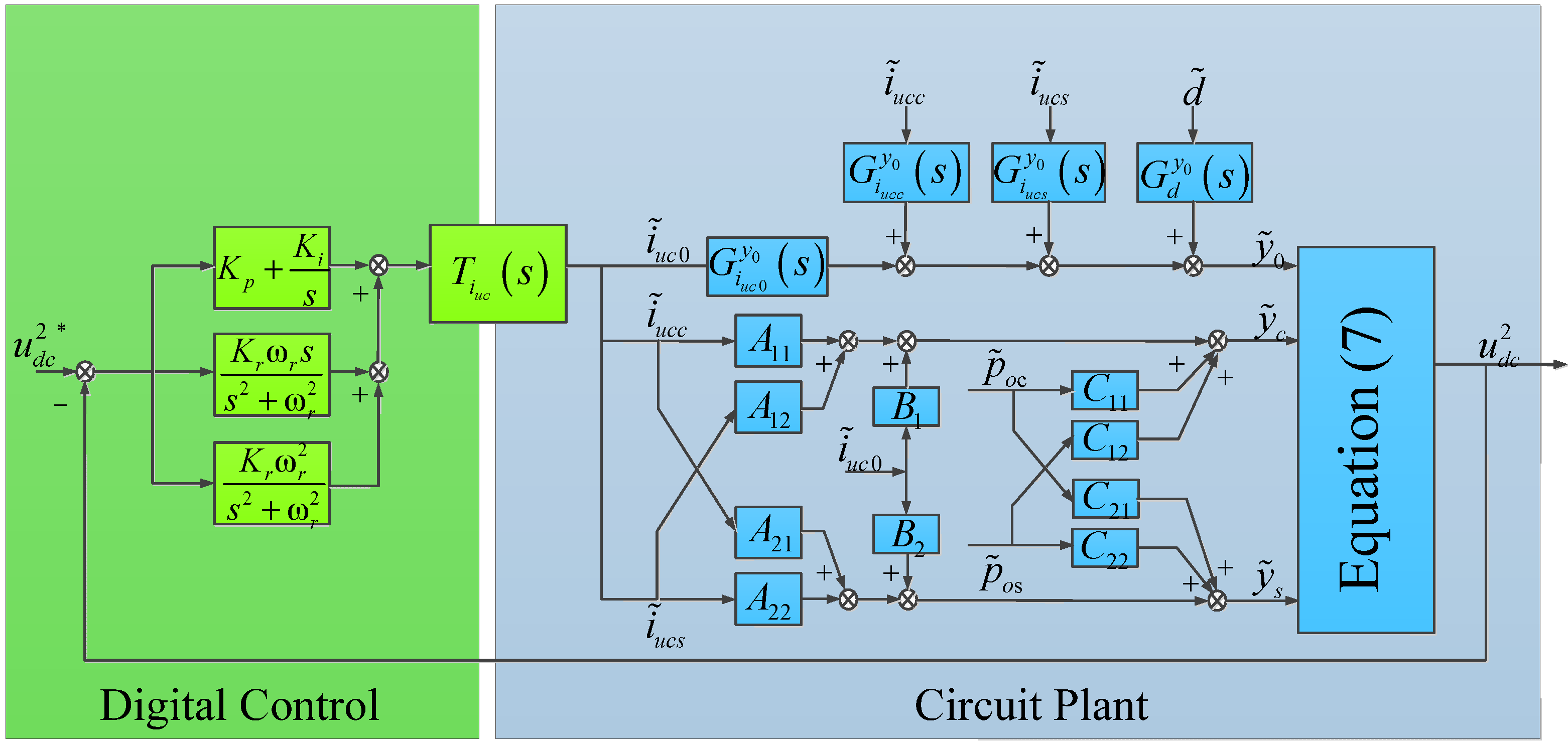
The structure of the DC link voltage control designed according to Equations (12) and (13) is shown in
Figure 2, where
represents for the closed loop transfer function of UC current which has been described in detail in the literature [11–15]. There will be special requirements for closed loop control of the UC current, which will be described later because of the special design of regulators in this paper. The DC link voltage regulator uses a proportional-integral-resonant (PIR) regulator, of which the proportional coefficient and integral coefficient are
and
, respectively. The PI regulator is designed to ensure that there is no steady-state error in the control of the DC component of the DC link voltage.
and
are the resonance regulators, where
is the coefficient and
is the central frequency of the controllers, which is twice the grid frequency (
); To ensure the AC instantaneous power is compensated completely by the UC, the resonant regulator is designed to regulate AC instantaneous power components at the double frequency. Therefore, the cooperation between the I and R regulators makes the UC realize AC and DC hybrid compensation and fully utilize the fast charging and discharging characteristics of UCs.
In a practical control system, the DC and AC components of both the UC current and voltage of the DC link are not separated, therefore the input error signals of the regulators in
Figure 2 include error signals of both the AC loop and DC control loop, causing a negative effect on the performance of the resonant regulator form PI regulator. This should be considered in the design.
In a practical system, there is coupling and interaction between AC and DC components. Equations (10) and (11) clearly show the disturbance relationship between AC and DC small signals, making it possible for regulators to decouple AC and DC, respectively, and control loops to be designed, respectively.
Figure 2.
Control scheme for the ESSC.
Figure 2.
Control scheme for the ESSC.
3.2. The Control Scheme of Grid-Side Converter
The control methods of the DC/AC converter, which include P/Q mode, V/f mode and Droop mode, are all based on current control. Current DC/AC converter control algorithms are generally divided into two control methods: one based on a rotating reference frame and another based on a stationary reference frame. The mathematical models of a DC/AC converter and its current control algorithm have been researched in numerous publications, and several control strategies with good performance have been proposed [
16,
17,
18,
19,
20], so only the current control algorithm of a grid-connected converter proposed in this paper will be described.
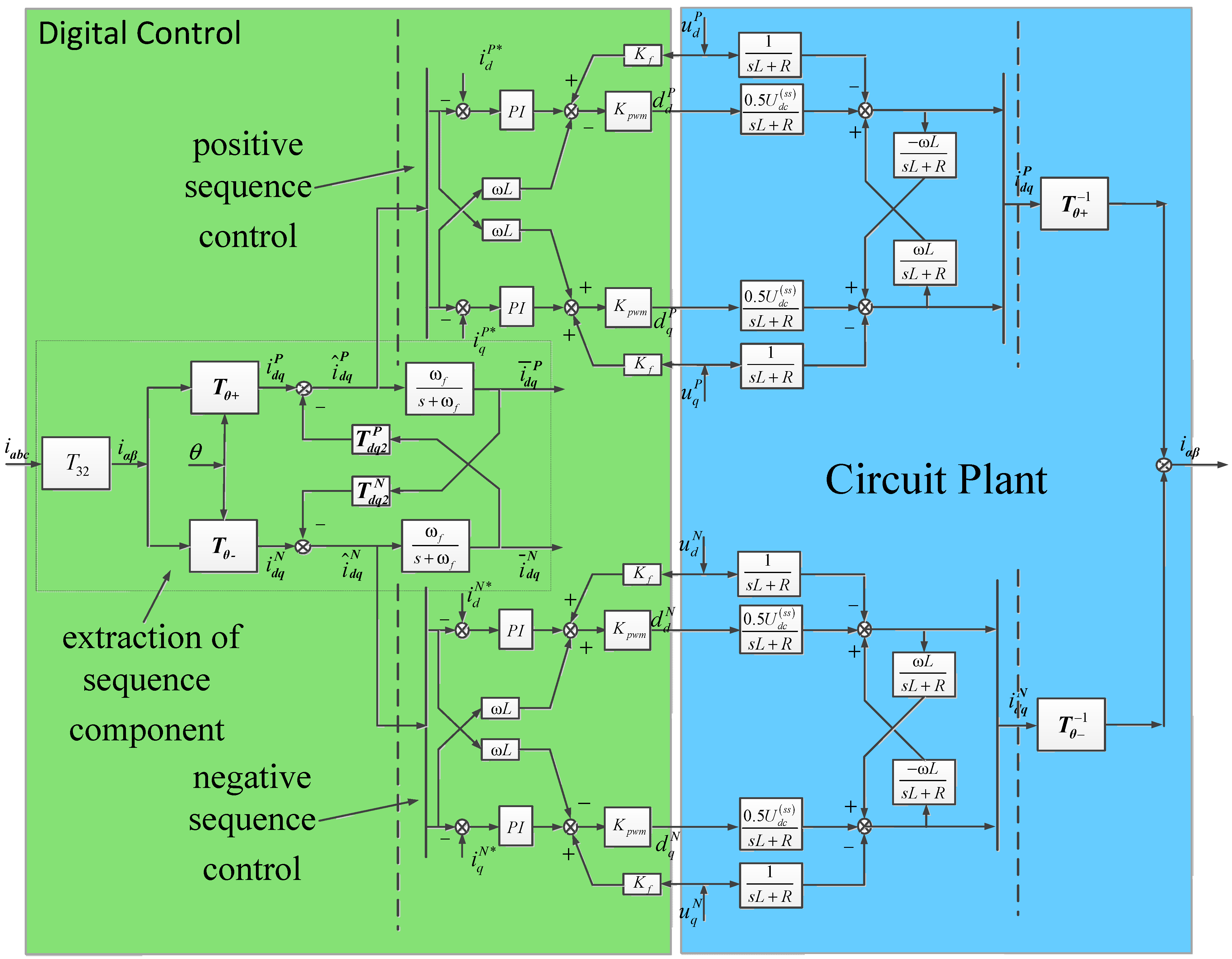
The positive and negative sequence current control structure shown in
Figure 3 was used in this paper, based on double synchronous rotating coordinate system, which is divided into three parts:
- (a)
Extraction of sequence component
The primary mission for unbalanced current control is to extract the positive-sequence and negative-sequence components from three-phase current in real-time. In [
18] the authors proposed the phase-locked technology of a decoupled double synchronous reference frame (DDSRF) and provided a time-domain analysis. This paper established a sequence component extraction system based on the above technology to extract the positive-sequence and negative-sequence components from three-phase current in real-time. As shown in
Figure 3, the current control characteristics can be influenced by the dynamic response features of sequence component extraction, and as a result the related transfer function should be obtained. Paper [
21] can be the reference for the transfer function which won’t be covered in this paper. In
Figure 3,
represents the Clark transformation matrix.
and
represent the positive and negative sequence rotation transformation matrices, respectively.
and
represent the decoupling matrices. The matrix expressions have been listed in the Appendix.
- (b)
The positive and negative sequence current control
Papers [
16,
17,
18,
19,
20] studied and put forward a large number of current control strategies, with excellent grid-connected inverter performance under unbalanced power grid conditions, including the control algorithm of a PR regulator in static frame and the control algorithm of a PI regulator in synchronous frame. This paper adopts the unbalanced current control structure in DDSRF.
Figure 3 shows the mathematical model of the grid-connected inverter in dual synchronous frame and relevant digital control algorithms. Literature [
21] can be the reference for the derivation steps of relevant mathematical models.
Figure 3.
Control scheme for the grid-side converter.
Figure 3.
Control scheme for the grid-side converter.
- (c)
The calculation of current reference
Current references are generally generated from MGCC, which can calculate current references based on different control targets. Instantaneous power exchanged between grid-connected inverter and the grid can be expressed as [
7,
8,
18]:
where
As can be seen from Equation (15), the current that needs to be injected into grid-connected inverter has four degrees of freedom, so only four out of six power amplitudes defined in Equation (15) can be controlled by current and voltage of the grid. In the case of unbalanced power grid, control targets generally conclude target 1: simple sinusoidal current; target 2: zero AC instantaneous active power and target 3: zero AC instantaneous reactive power. And the targets are contradictory. Usual control strategy is based on target 1 or 2 regardless of target 3. However, the control strategy in this paper is based on target 3 regardless of target 2.
4. Control Design and Simulation
This paper designs the control loop in
Figure 2 with MATLAB and verifies the design with simulation model established in the MATLAB/SIMULINK environment.
Equation (12) is the basis of the DC component of the DC link voltage control. The open-loop transfer function of the DC component obtained from
Figure 2 can be expressed as:
where
is closed-loop transfer function of the UC current. The UC current loop is much faster than the DC link voltage loop, so the value of
can be 1, with which the transfer function of controller and control objects can be described as:
Control parameters are selected based on classic control theory. The open-loop bode diagram of the DC component of the voltage has been designed in
Figure 4. The open-loop gain at double frequency of the control loop of the DC component has an impact on the performance of the R regulator because the unified error signal contains DC and AC components. The output of the DC regulator will definitely impact the AC regulator if the DC regulator has high gain at double frequency.
Figure 4.
Bode plot of DC open-loop of DC link voltage control.
Figure 4.
Bode plot of DC open-loop of DC link voltage control.
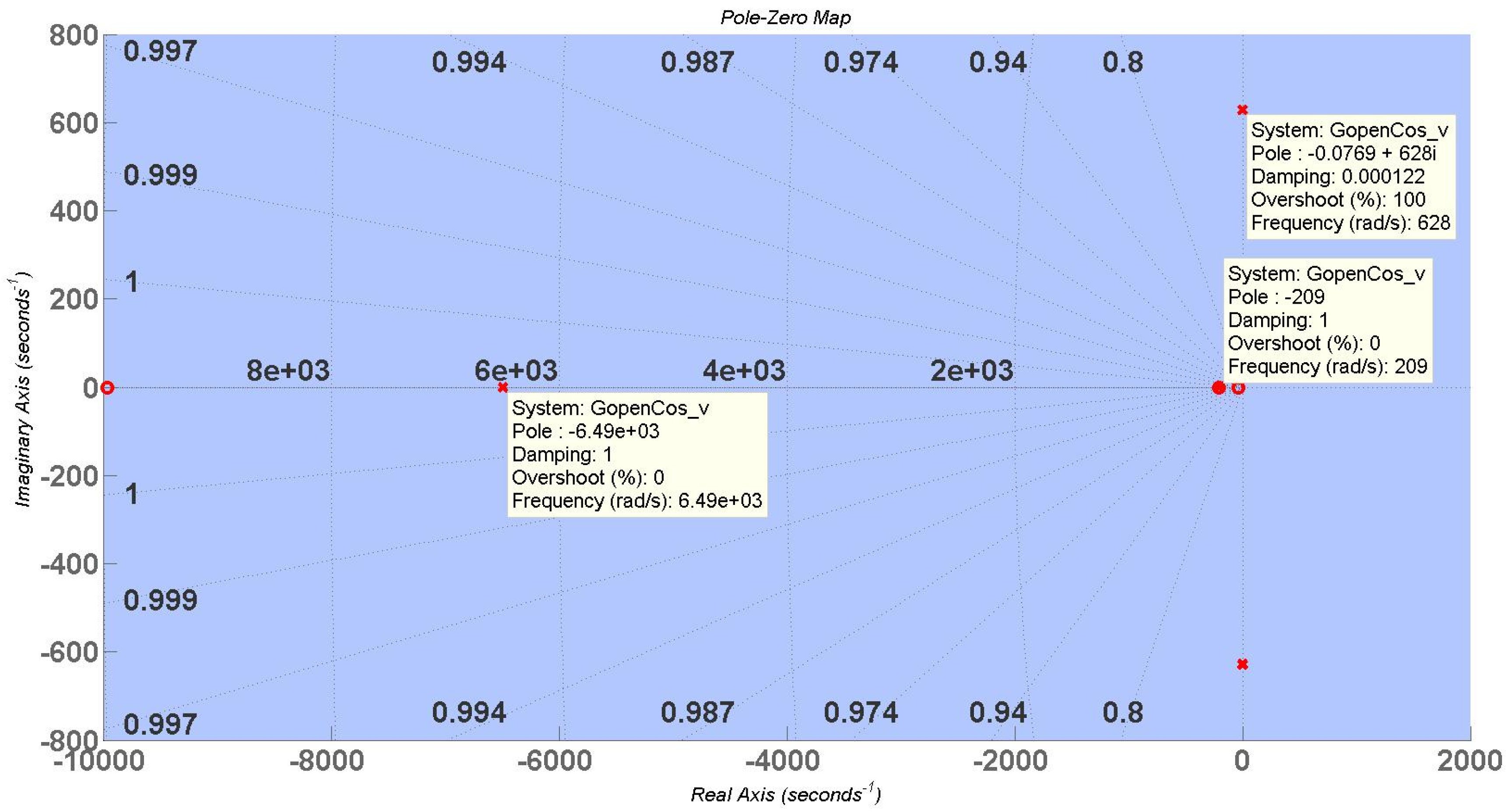
To achieve AC compensation of the UC, the R regulator of the DC link voltage has been designed by the root-locus method [
22]. As shown in
Figure 2, the open-loop transfer function matrix of the AC component of the DC link voltage is:
where
is the current closed-loop transfer function of the UC. As can be seen from Equation (18), in order to acquire the better tracking performance of the AC component of the DC link voltage,
must have a high gain in the double frequency, so the current control loop of the UC in this paper should have high gain in the double frequency to meet the tracking performance of the AC component of the UC current. Matrix A is the transfer function from AC component of DC link voltage to that of UC current, equation of which is listed in appendix. The zero-pole distributive chart of main diagonal transfer function of matrix
is shown in
Figure 5.
This paper designs four kinds of regulator solution of DC link voltage as comparisons to verify the above content: (1) PIR controller, the cutoff frequency of PI regulator of DC loop is slightly lower than twice the power frequency; (2) PIR controller, the cutoff frequency of PI regulator of DC loop is slightly higher than twice the power frequency; (3) PI controller, of which the cutoff frequency is high and control loop has gain high enough in the twice frequency; (4) PI controller, of which the cutoff frequency is low and control loop does not has gain high enough in the twice frequency.
Figure 5.
Zero-pole distributive chart of .
Figure 5.
Zero-pole distributive chart of .
The control waveforms of these four control schemes are shown in
Figure 6.
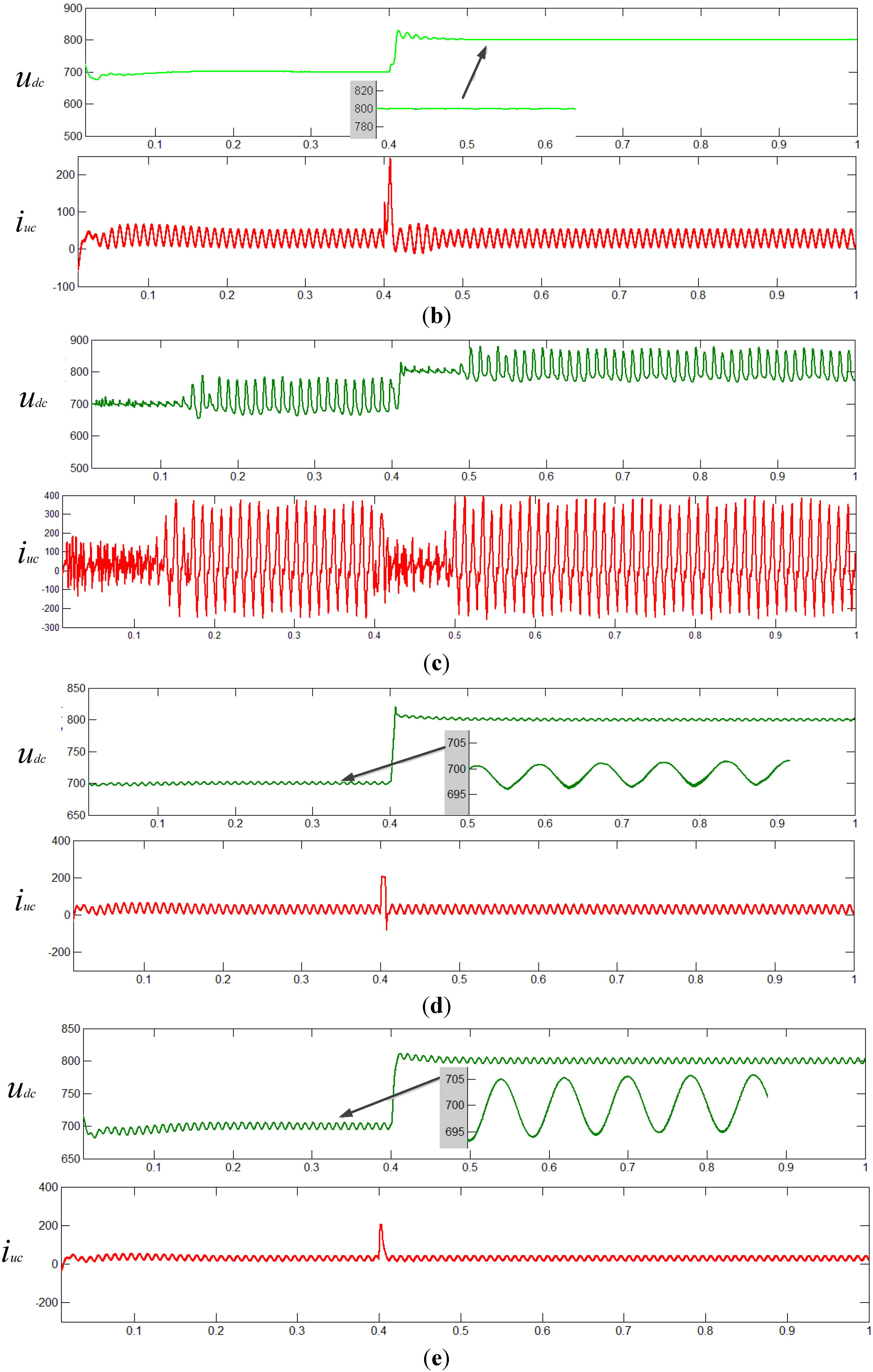
Figure 6a shows output current waveforms of these control schemes in AC side, which are unbalanced current waveforms.
Figure 6b–e show the DC link voltage and UC current waveforms of four control schemes respectively in the situation of step of DC link voltage reference. As can be seen from these figures, scheme (1) can eliminate DC link voltage ripples perfectly and UC can completely compensate the active power fluctuation in AC side, meanwhile the output current of UC is overlapped by AC and DC component. The waveforms of scheme (2) show the impact PI controller acted on resonant controller, resulting in a rather poor control effect. Through contrasting the waveform of scheme (3) with schemes (1) and (4) show when control loop has higher gain in the twice frequency without resonant controller, the DC link voltage ripple in the twice frequency can be restrained to some degrees but not eliminated.
Figure 7 shows the spectral analysis of UC output power. The output instantaneous power of UC has high DC component and the twice frequency component but few quadruple frequency component. The spectral analysis testifies correctness of the analysis in
Section 3.
Figure 6.
Diagram of simulation of the DC-link voltage control: (a) unbalance current of DC/AC circuits; (b) DC link voltage and UC current under control scheme (1); (c) DC link voltage and UC current under control scheme (2); (d) DC link voltage and UC current under control scheme (3); (e) DC link voltage and UC current under control scheme (4).
Figure 6.
Diagram of simulation of the DC-link voltage control: (a) unbalance current of DC/AC circuits; (b) DC link voltage and UC current under control scheme (1); (c) DC link voltage and UC current under control scheme (2); (d) DC link voltage and UC current under control scheme (3); (e) DC link voltage and UC current under control scheme (4).
Figure 7.
Spectrum of instantaneous power of UC.
Figure 7.
Spectrum of instantaneous power of UC.
5. Experimental Results
In order to analyze and verify the correctness of the proposed control algorithm, experiments based on normal PI regulator and proposed PIR regulator are conducted, respectively, under unbalanced conditions at first. The dynamic and steady-state characteristics of the DC link voltage and discharge current of the UC with different kinds of regulators are observed during the experiment. The following experiments display the dynamic characteristics of the proposed control strategy under the condition of load change and different UC voltages. It should be pointed out that because the AC current is produced by the UC according to the proposed control strategy that the working range of the UC voltage is set from 150 V to 250 V.
Table 1,
Table 2 and
Table 3 list the relevant parameters which are used in the experiment.
Table 1.
Parameters of system circuit in the
Figure 1.
Table 1.
Parameters of system circuit in the Figure 1.
| Parameters | Value |
|---|
| 5 µF |
| 10 mH |
| 6500 µF |
| 7.76 mH |
Table 2.
Parameters of UC.
Table 2.
Parameters of UC.
| Parameters | Value |
|---|
| Capacity | 6.4 F |
| Max voltage | 270 V |
Table 3.
Control parameters of regulator.
Table 3.
Control parameters of regulator.
| Control loop | | | |
|---|
| Control Parameters of current loop of GSC | 5.4 | 113.4 | × |
| Control Parameters of current loop of ESSC | −22.3 | −2453 | × |
| Control Parameters of DC link voltage loop | 0.00023 | 0.0046 | −0.000021 |
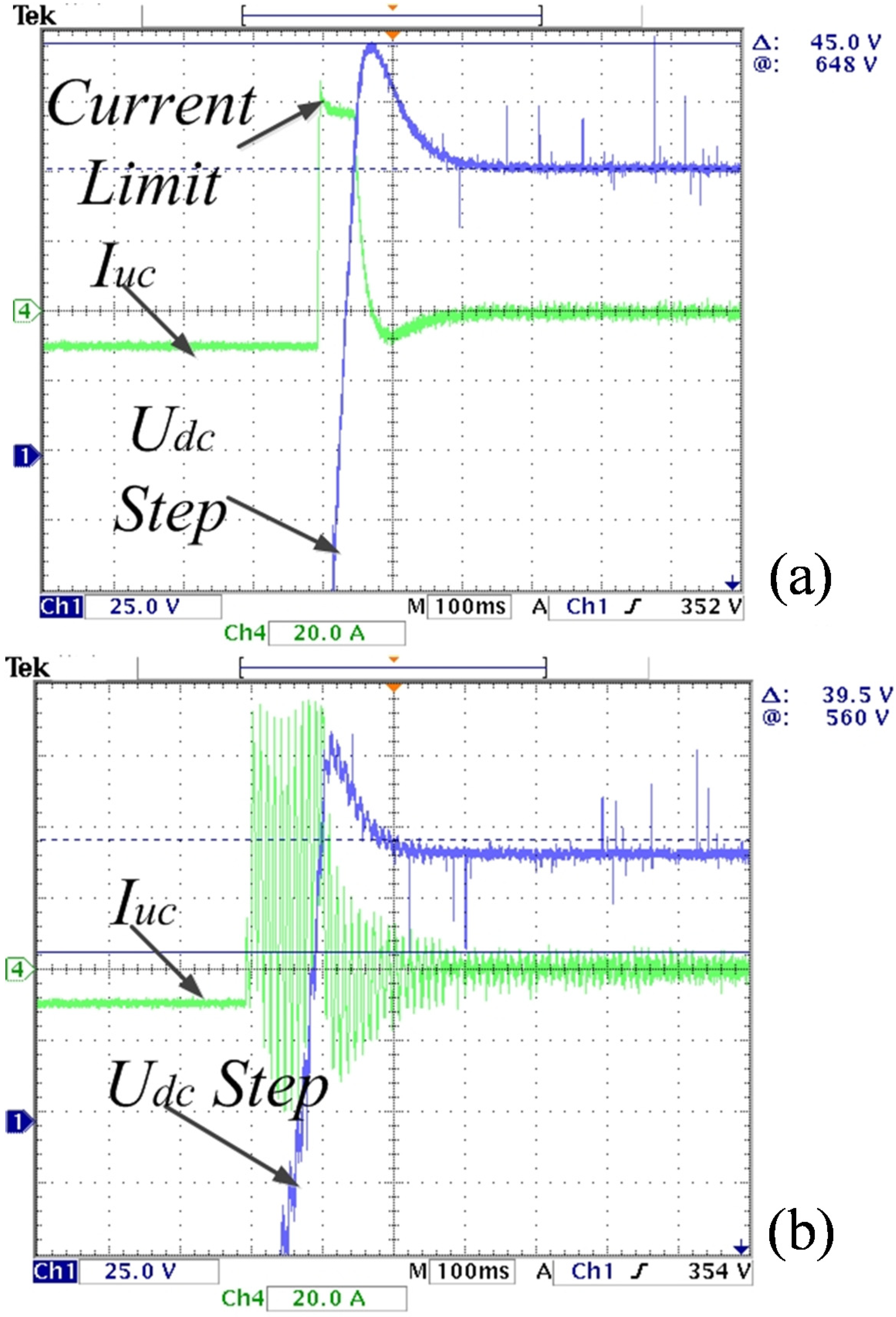
Figure 8 shows the DC link voltage and UC current dynamic response with different kinds of regulators without three-phase unbalance. As seen from
Figure 8, the R regulator has little impact on the dynamic characteristics of the DC component of the DC link voltage and no impact on the steady-state error of the DC link voltage DC component, so it is feasible to perform the decoupling control of the DC and AC components of the DC link voltage.
Figure 8.
Dynamic response figure of the control loop: (a) PI regulator adopted in the DC link voltage control; (b) PIR regulator adopted in the DC link voltage control.
Figure 8.
Dynamic response figure of the control loop: (a) PI regulator adopted in the DC link voltage control; (b) PIR regulator adopted in the DC link voltage control.
Figure 9 and
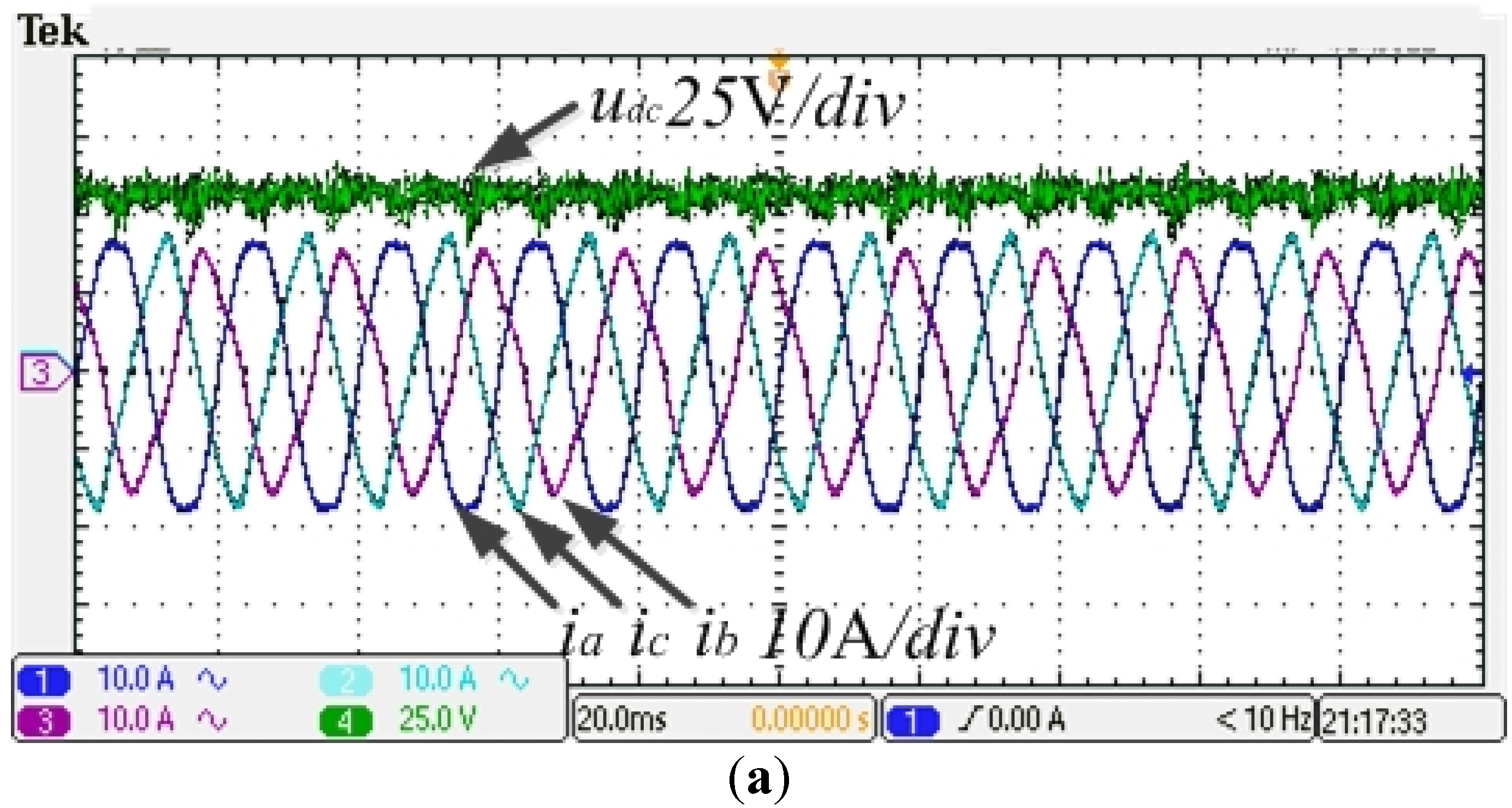
Figure 10 show waveforms of the DC link voltage and UC current when the grid-connected inverter outputs an unbalanced current with different control algorithms. From
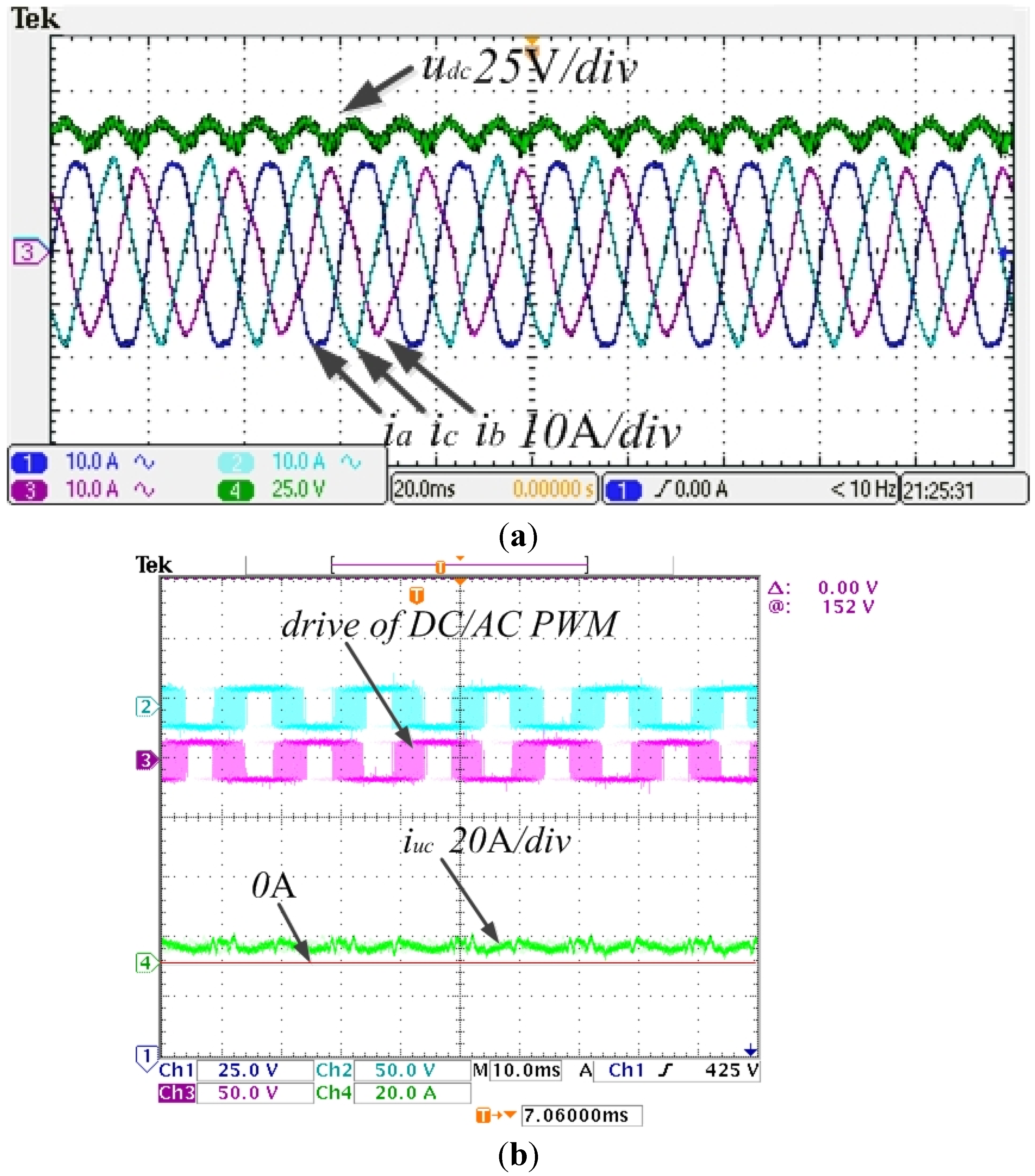
Figure 9, the DC component of the DC link voltage can be stabilized using a PI regulator, meanwhile a ripple wave in the double frequency appears in the DC link voltage and the UC outputs DC current. Comparatively,
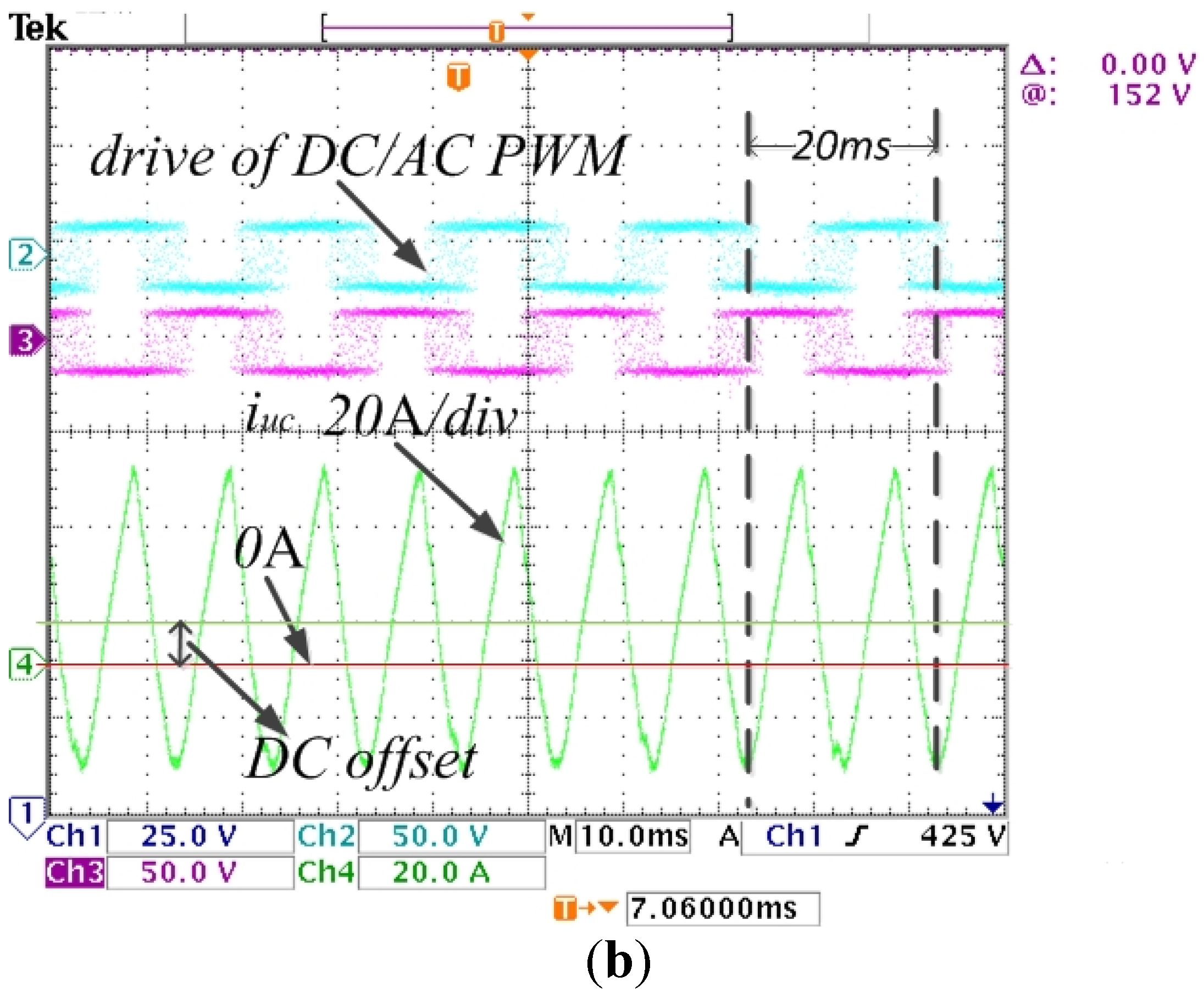
Figure 10 shows that when the DC link voltage is controlled by the PIR regulator the ripple wave of the DC voltage in the double frequency is eliminated and the UC outputs AC current in the double frequency with DC offset, which can completely compensate for any instantaneous active power fluctuations of the grid-connected inverter.
Figure 9.
Waves of PI regulator for DC link voltage: (a) waves of DC link voltage and unbalanced three-phase current; (b) waves of UC current with and PWM driver of GSC.
Figure 9.
Waves of PI regulator for DC link voltage: (a) waves of DC link voltage and unbalanced three-phase current; (b) waves of UC current with and PWM driver of GSC.
Figure 10.
Waves of PIR regulator for DC link voltage: (a) waves of DC link voltage and unbalanced three-phase current; (b) waves of UC current with and PWM driver of GSC.
Figure 10.
Waves of PIR regulator for DC link voltage: (a) waves of DC link voltage and unbalanced three-phase current; (b) waves of UC current with and PWM driver of GSC.
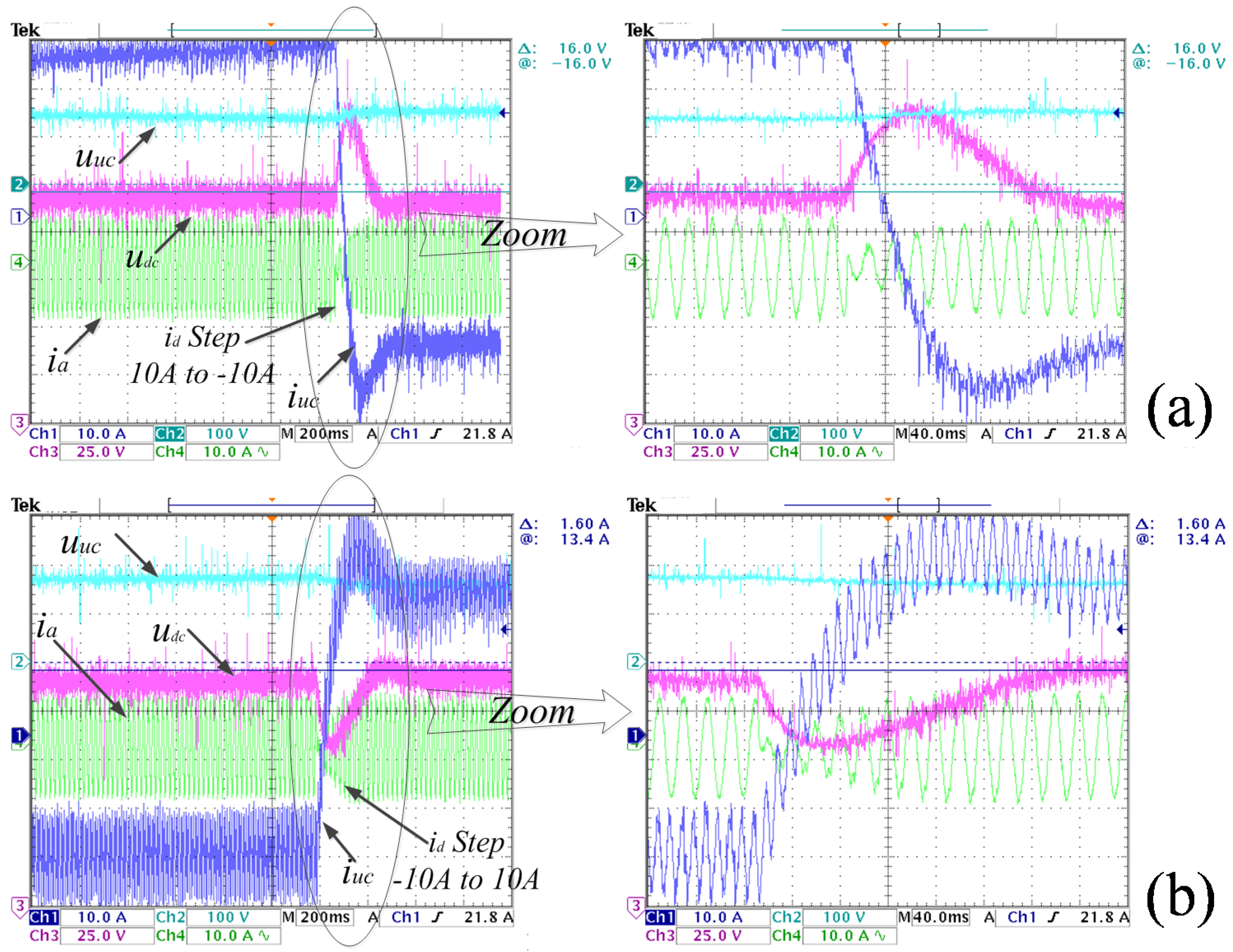
Figure 11 and
Figure 12 display waveforms of the dynamic response under conditions of AC load change with 150 V and 250 V UC voltage respectively. From
Figure 11 and
Figure 12, when
steps from 10 A to −10 A the UC can switch rapidly from discharge state to charge state automatically. On the contrary, when
steps from −10 A to 10 A the UC can switch rapidly from charge state to discharge state automatically. The difference between
Figure 11 and
Figure 12 is that the amplitude of UC current step is larger under the condition of UC voltage 150 V than that under the condition of 250 V, but the similarity is that the DC link voltage can be returned to reference rapidly.
Figure 11.
Dynamic waves under condition of AC load change with 150 V UC voltage: (a) waves of step from 10 A to −10 A; (b) waves of setp from −10 A to 10 A.
Figure 11.
Dynamic waves under condition of AC load change with 150 V UC voltage: (a) waves of step from 10 A to −10 A; (b) waves of setp from −10 A to 10 A.
Figure 12.
Dynamic waves under condition of AC load change with 250 V UC voltage: (a) waves of step from 10 A to −10 A; (b) waves of setp from −10 A to 10 A.
Figure 12.
Dynamic waves under condition of AC load change with 250 V UC voltage: (a) waves of step from 10 A to −10 A; (b) waves of setp from −10 A to 10 A.
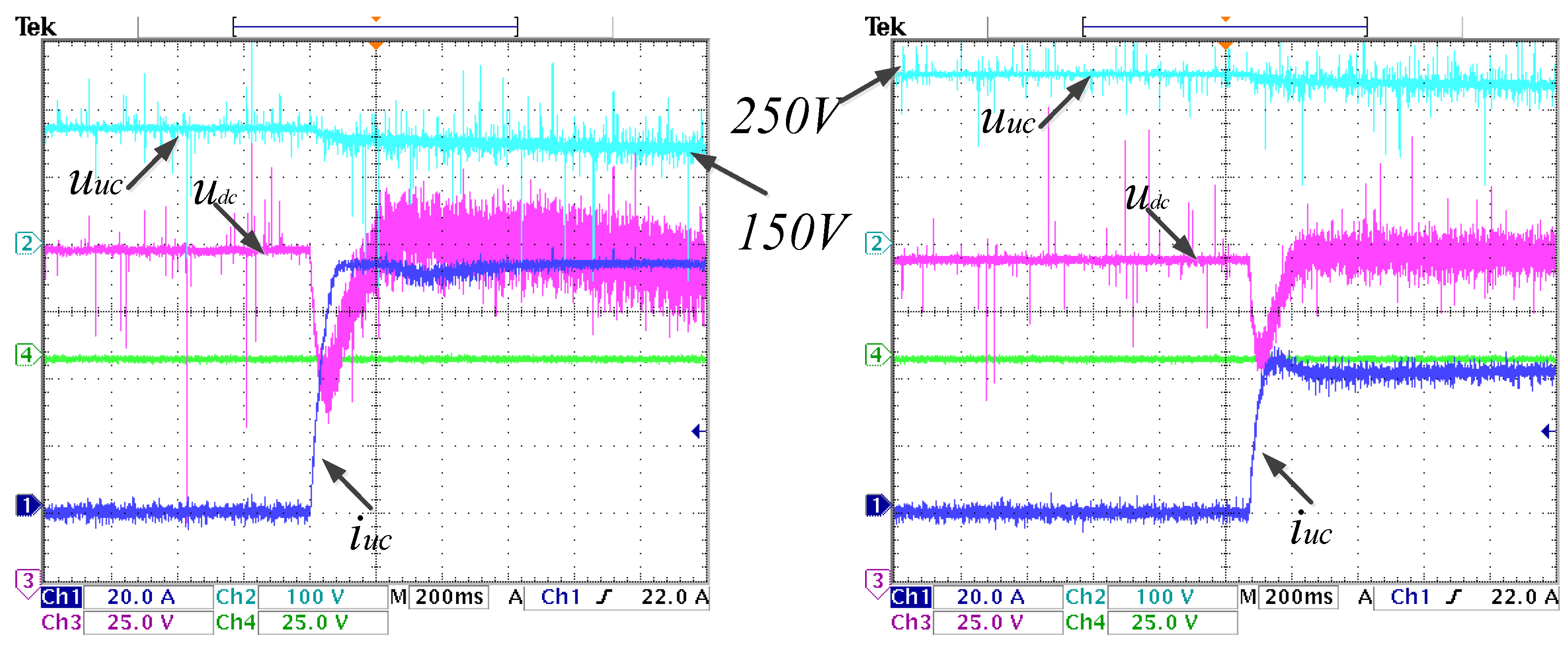
The dynamic response waves under condition of DC load change with 150 V and 250 V UC voltage can be derived from
Figure 13. During the experiment, a 10 kW DC load is directly connected to the DC link suddenly. It can be revealed from the waves that the UC immediately outputs about 40 A current when the UC voltage is 250 V while the output is about 80 A current when the UC voltage is 250 V to keep the DC link voltage constant.
Figure 13.
Dynamic waves under condition of DC load change with 150 V and 250 V UC voltage.
Figure 13.
Dynamic waves under condition of DC load change with 150 V and 250 V UC voltage.
6. Conclusions
The paper presents a dynamic model for the ESS-based AC/DC GSC and a bidirectional DC/DC ESSC with a common dc link system. The mathematical model is applicable to the dynamic analysis and control synthesis, under three-phase unbalanced as well as balanced conditions. The model is developed based on the concept of sequential subsystems and an accurate formulation of the instantaneous power balance between the ESS AC-side and DC-sides.
Based on the developed model, the UC current, which is injected a double frequency component by a R (resonant) controller, is selected to regulate the DC link voltage; With the introduction of an R regulator, the excellent charge-discharge properties of the UC are fully utilized to compensate instantaneous active power fluctuations; thereby the ripple of DC voltage at the double frequency is eliminated and the utilization factor of the UC is improved. The application of the proposed control strategy can effectively control the DC component of DC link voltage and eliminate ripples in the double frequency produced by an unbalanced grid-connected inverter. Therefore the proposed control strategy can operate perfectly under the unbalanced conditions of the microgrid. Besides that, thanks to escaping from the control of the DC link voltage, the control strategy of the GSC can be more simple and flexible. With the application of the proposed control strategy, the performance of the ESS of the UC is improved, the stability of the ESS is enhanced and the utilization of the UC becomes more facile and practical.
The proposed control strategy also can be applied to a DC microgrid where the DC link voltage is critical for the operation of the system.