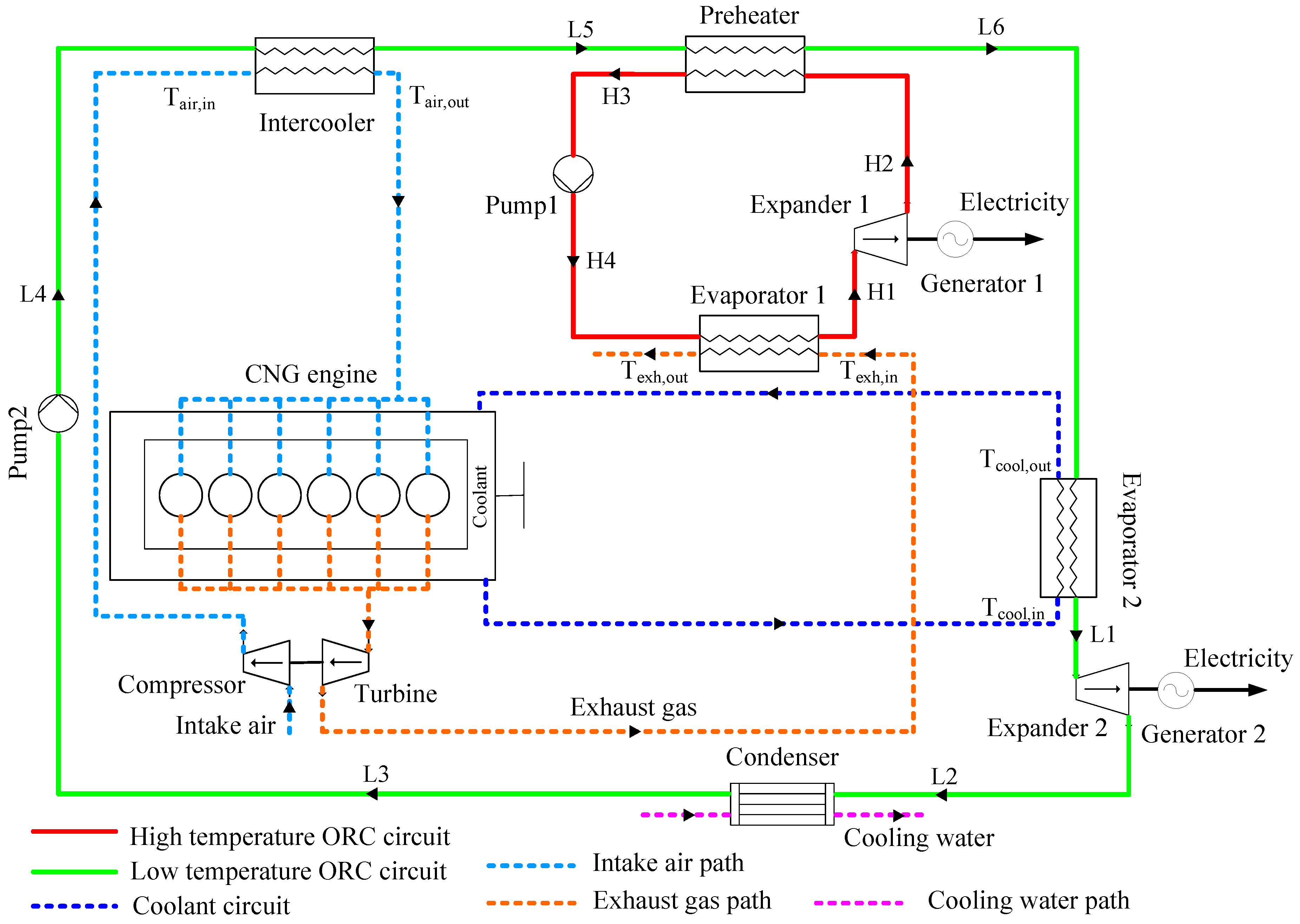
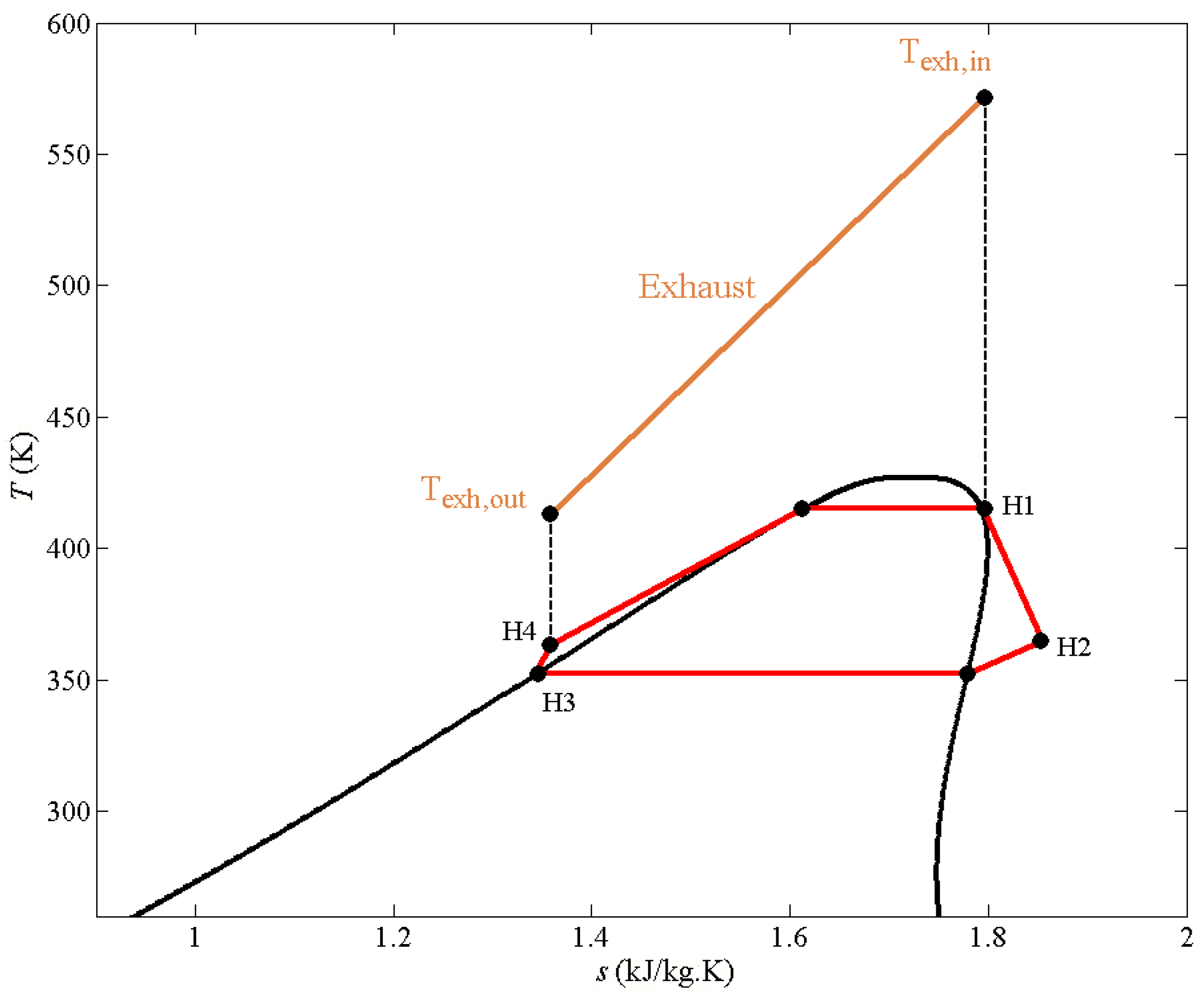
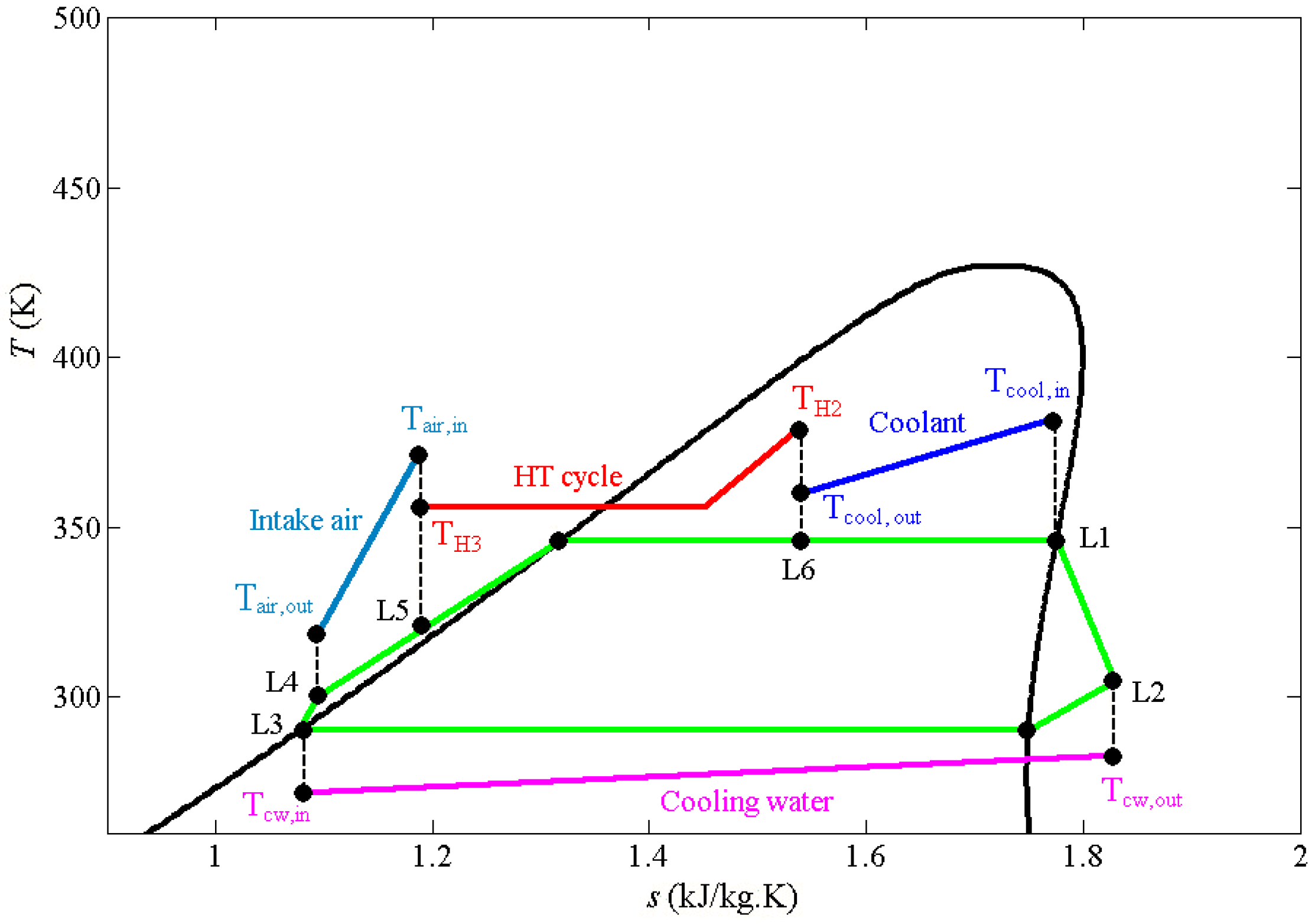
1. Introduction
At present, petroleum resources are being rapidly depleted worldwide as energy consumption demand further increases with the development of human society. A growing number of strict emission rules are also being formulated and implemented to reduce the environmental impact of petroleum consumption. Given these situations, alternative energy vehicles are promoted with the advantages of relieving stress on petroleum consumption and reducing harmful emissions. Natural gas is regarded as one of the most important alternative fuels because of its abundant reserves, low cost, and low emissions. In addition, both compressed natural gas (CNG) and liquefied natural gas (LNG) engines are widely used in commercial vehicles, power-generating systems, and construction machineries. However, compared with gasoline and diesel engines, natural gas engines experience power loss and are less thermal efficient [
1]. Thus, natural gas engines may waste high amounts of fuel combustion power via the exhaust and coolant systems. Investigating waste heat recovery (WHR) of natural gas engines is therefore valuable to improve the power output and thermal efficiency of these engines.
The organic Rankine cycle (ORC) has been implemented widely in various fields, such as in low-grade WHR, waste heat power-generating systems [
2], industrial waste heat [
3], geothermal energy [
4,
5], and solar energy [
6,
7]. Different heat resources have varying characteristics; meanwhile, numerous organic working fluids with different thermophysical and environmental properties are available in practical applications. Considerable research has been conducted to determine appropriate organic working fluids for a given heat resource. Hung
et al., indicated that wet working fluids with extremely steep saturated vapor curves in the
T-s diagram generally perform better than dry working fluids [
8]. Wang
et al., selected nine pure organic working fluids according to their physical and chemical properties; among these, R245fa and R245ca are found to be the most environment friendly for engine WHR applications [
9]. Toffolo
et al., assessed the performance of two working fluids, namely, isobutane and R134a, in temperatures ranging from 130 to 180 °C. The results showed that the maximum power output of R134a is higher than that of isobutene in all temperature ranges [
10]. Moreover, similar to the traditional Rankine cycle, the ORC has several structures, which include simple, regenerative, and reheat ORCs. The analysis and optimization of different ORC structures are found in previous research [
11,
12,
13].
Waste heat resources in internal combustion engines (ICEs) are low- or medium-grade energy. Applying the ORC system to ICEs is reasonable because it is suitable for the temperature regions of the waste heat resources of ICEs. Recently, works in this field have been conducted actively, and the results show that engine waste heat recovery through the ORC system can potentially improve the total power output and fuel consumption performance of ICEs. Srinivasan
et al., analyzed the WHR performance of a dual fuel low-temperature combustion engine through the ORC system [
14]. Boretti
et al., investigated the exhaust and coolant heat recovery performance of R245fa ORCs in a hybrid passenger car with a naturally aspirated gasoline engine [
15]. Wang
et al., evaluated the improvement in efficiency of a gasoline engine through experiments and numerical simulations based on the steam Rankine cycle. The test results indicated that the engine can save up to 34% fuel under several operating conditions [
16].
In particular, the ORC is regarded as an effective means to recover waste heat from ICEs. However, previous studies have mostly focused on gasoline [
17] and diesel engines [
18,
19,
20], and only a few of these studies have been conducted for natural gas engines. Given that the development of alternative energy is a worldwide agreement, the present work is performed on a heavy-duty CNG engine platform for commercial vehicles. A WHR system is designed based on the dual loop ORC (DORC) to recover waste heat energy from exhaust gas, intake air, and engine coolant. First, the system is schemed, described, and numerically modeled based on DORC theory and the features of the CNG engine. Second, the characteristics of waste heat from CNG engines, which function as high-temperature heat sources of the DORC WHR system, are calculated according to engine test data under various operating conditions. Subsequently, the thermal efficiency, power output increase ratio (POIR), and brake specific fuel consumption (BSFC) improvement ratio (BIR) of the DORC–CNGE combined system are calculated to evaluate its WHR performance according to the simulation results.
3. Performance and Waste Heat Characteristics of the CNG Engine
Discussing the performance and waste heat characteristics of the CNG engine is important to optimize a matching ORC system and achieve efficient WHR from these engines. In the present work, an electronically controlled, heavy-duty, and lean-burn CNG engine is selected and tested under various operating conditions. The main specifications of the CNG engine are listed in
Table 2.
Table 2.
The main specifications of the compressed natural gas (CNG) engine.
Table 2.
The main specifications of the compressed natural gas (CNG) engine.
| Items | Parameters |
|---|
| Cylinder arrangement | in-line |
| Cylinder number | 6 |
| Stroke and cylinder bore | 114 mm × 144 mm |
| Stroke number | 4 |
| Displacement | 8.8 L |
| Cooling type | Water cooling |
| Aspiration | Turbocharged and Intercooled |
| Rated power (Rated speed) | 210 kW (2200 r/min) |
| Maximum torque (speed) | 1120 N·m(1400 r/min) |
| Fuel supply | Port fuel injection |
| Ignition type | Spark ignition |
The engine speed for the test varies from 800 to 2200 r/min with an interval of 100 r/min. For each selected engine speed, 10 load conditions, which range from full load to minimum stable load condition, are chosen. Brake output power, fuel consumption parameters, intake/exhaust parameters, and coolant parameters are acquired under each operating condition with a given engine speed and torque.
The performance and waste heat characteristics of the CNG engine are expressed by the distribution of the test and calculated parameters on the operating condition map that is coordinated by engine speed and engine torque in this study.
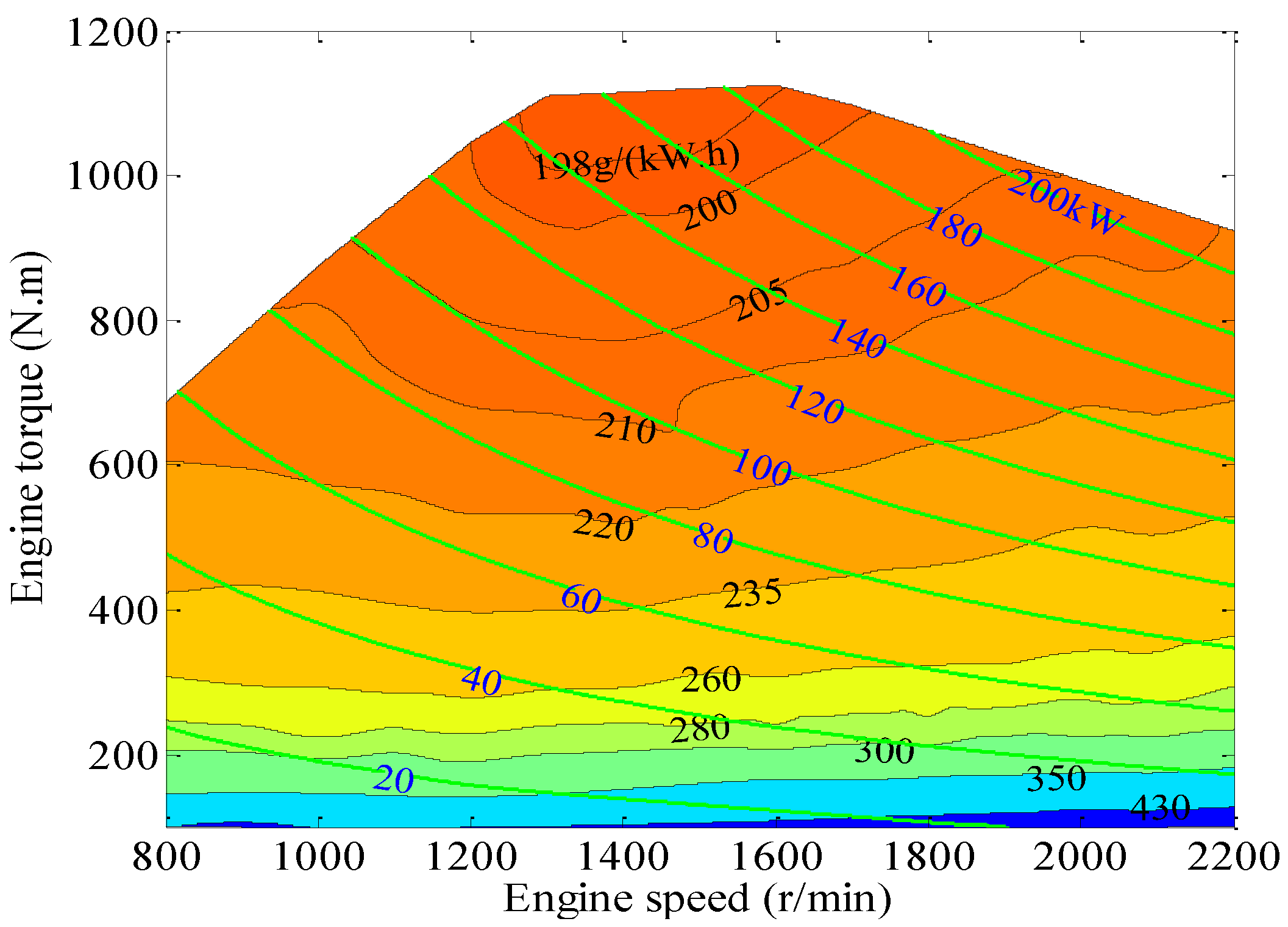
Based on engine test data, the distributions of the BSFC and the brake output power of the CNG engine under different engine speeds and torques are plotted in
Figure 4. The BSFC is expressed using colored contour bands with black contour lines, and engine performances with the same BFSC are found on the same colored contour band or black contour line. Under low load conditions, the BSFC is slightly influenced by engine speed, but under medium and high load conditions, the BSFC increases after decreasing as engine speed increases. However, the BSFC evidently and monotonously increases as engine torque increases. The zone where BSFC is lower than 200 g/(kW·h) is located in engine speed conditions ranging from 1200 to 1700 r/min and in engine torque conditions ranging from 900 N·m to the maximum value. As shown in the plot, the engine performs with the same brake output power on the same green contour line. Brake output power rises as engine speed and engine torque increase, and when the maximum value of the brake output is 212 kW under the rated power condition.
Exhaust temperature and exhaust mass flow, which are acquired after the turbine, are plotted in
Figure 5 according to engine test data.
Figure 4.
The distribution of BSFC and brake output power of the CNG engine.
Figure 4.
The distribution of BSFC and brake output power of the CNG engine.
Figure 5.
(a) The distributions of the exhaust temperature of the CNG engine; (b) The distributions of the exhaust mass flow rate of the CNG engine.
Figure 5.
(a) The distributions of the exhaust temperature of the CNG engine; (b) The distributions of the exhaust mass flow rate of the CNG engine.
As shown in
Figure 5a, exhaust temperature is relatively low under low speed–low torque conditions, and relatively high under both low speed–high torque and high speed conditions. In addition, the highest exhaust temperature is 910 K under high speed–low torque condition. Moreover, exhaust temperature rises as engine torque increases in the low-speed area, but the trend is complex in the area with medium- and high-speed conditions. The complex trend may be attributed to the control strategy of the turbocharger. As shown in
Figure 5b, exhaust mass flow rate increases in the entire engine test region when engine speed and engine torque increase because the throttle-equipped engines consume a growing amount of intake air and fuel masses.
In
Figure 6, the distributions of several engine input and output energy are plotted under various engine speed and engine torque conditions.
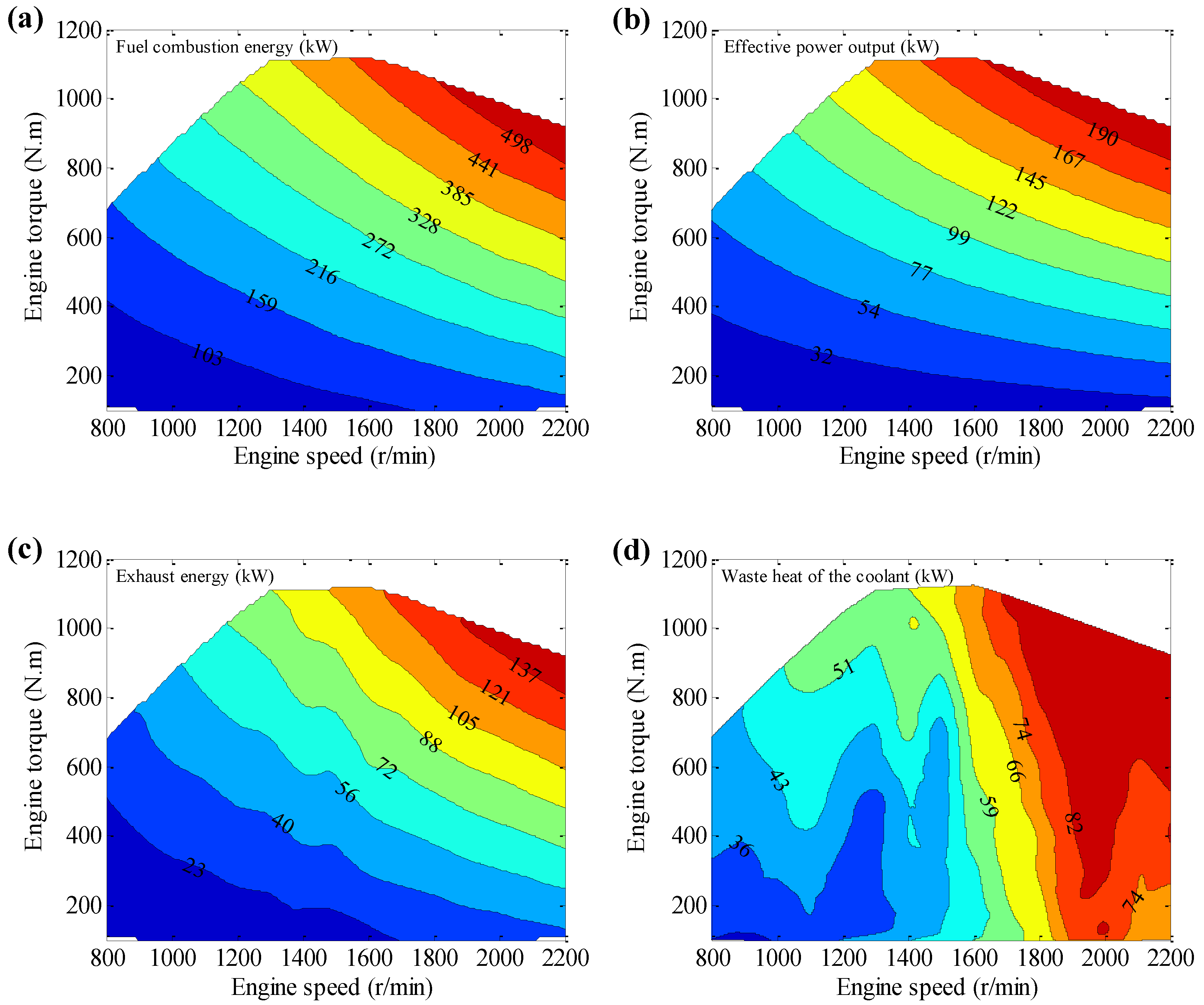
The distribution of fuel combustion power under different operating conditions is shown in
Figure 6a. As shown in the figure, the engine consumes more fuel to produce more energy as engine speed and engine torque increase. The maximum fuel combustion power is 556 kW under the rated output power condition. Similarly, in
Figure 6b,c, the effective engine power output and exhaust energy flow rate increase as engine speed and engine torque increase. In addition, the maximum exhaust energy flow rate is 154kW under the rated output power condition. The distribution of the waste heat flow rate of the engine coolant under different operating conditions is shown in
Figure 6d. The waste heat flow rate of the engine coolant has a relatively low energy under low speed–low torque condition and a relatively high energy under high speed–high torque condition. However, the trend is not as monotonous as that of fuel combustion power. The maximum waste heat flow rate of the engine coolant is 86 kW under all test conditions. Hence, recovering waste heat of heavy-duty CNG engines is reasonable because a large part of the fuel combustion power is drained by the exhaust gas and the cooling liquid.
Figure 6.
(a) The fuel combustion power of the CNG engine; (b) The effective power output of the CNG engine; (c) The exhaust energy flow rate of the CNG engine; (d) The waste heat flow rate of the engine coolant.
Figure 6.
(a) The fuel combustion power of the CNG engine; (b) The effective power output of the CNG engine; (c) The exhaust energy flow rate of the CNG engine; (d) The waste heat flow rate of the engine coolant.
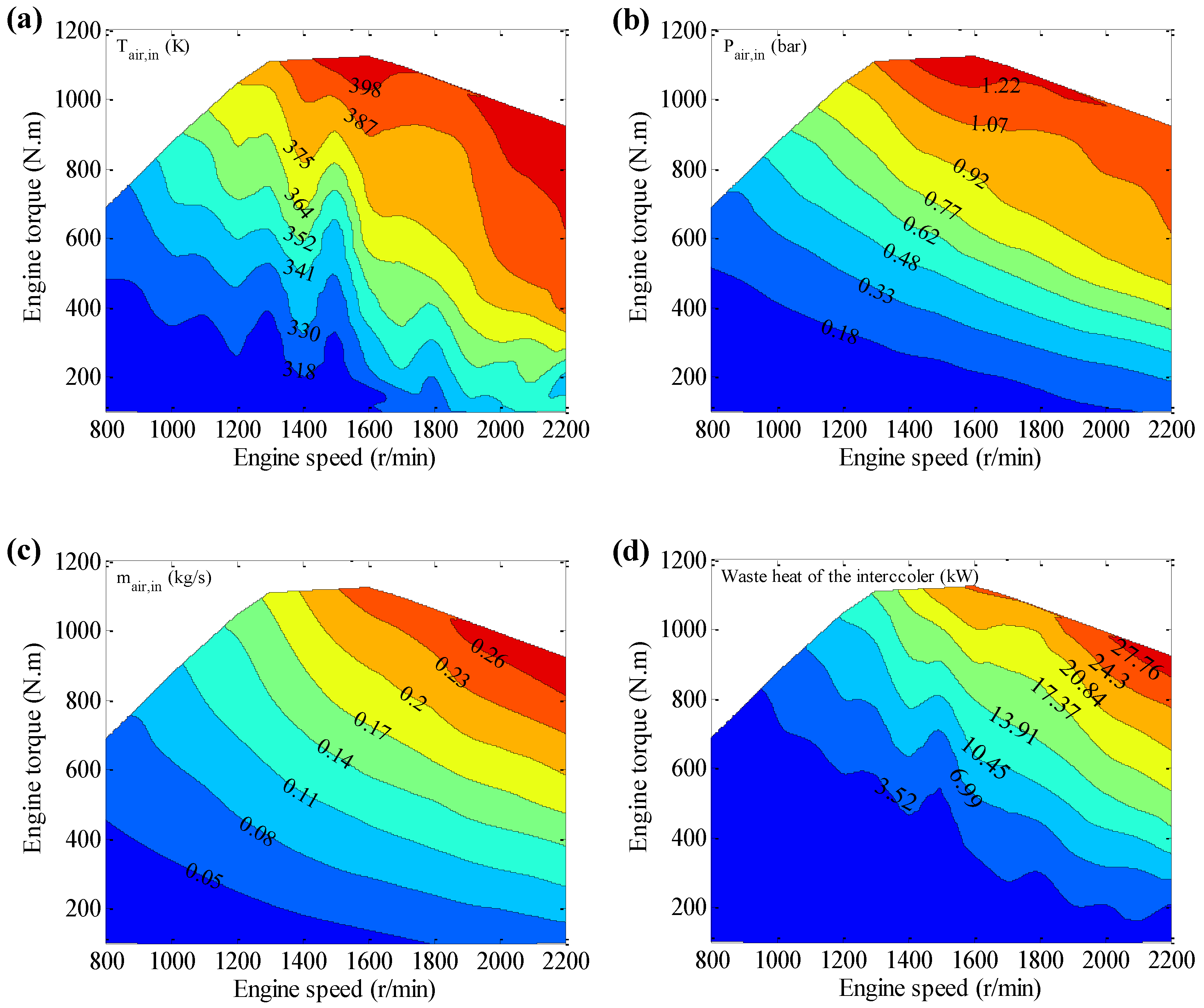
The waste heat energy flow rate of intake air is used to preheat the supercooled working fluid in the LT cycle, and the distributions of several intake air parameters are plotted in
Figure 7. As shown in
Figure 7a, intake air temperature ranges from 306 to 409 K in the entire engine test region before it goes into the intercooler. This temperature rises unsteadily as engine speed increases, and then increases stably as engine torque rises. As shown in
Figure 7b,c, intake air pressure and air mass flow rate increase monotonously as engine speed and engine torque rise. The maximum intake air mass rate is 0.29 kg/s under the rated power output condition. The trend of intake air waste heat power is similar to that of intake air temperature before it enters the intercooler in the entire engine test region, and the maximum value of intake air waste heat is 31.24 kW, which is worth recovering.
Figure 7.
(a) The intake air temperature in the preheater; (b) The intake air pressure in the preheater; (c) The intake air mass flow rate in the preheater; (d) The intake air waste heat flow rate in the preheater.
Figure 7.
(a) The intake air temperature in the preheater; (b) The intake air pressure in the preheater; (c) The intake air mass flow rate in the preheater; (d) The intake air waste heat flow rate in the preheater.
4. Optimization of the DORC System
Before the simulation of the performance of the DORC–CNGE combined system, several operating parameters of the DORC system should be settled first according to the waste heat characteristics of the CNG engine.
In the LT cycle, the condensing temperature of the working fluid is set to 293.15 K, given that the temperature of the cooling water in the condenser is 288.15 K, and an appropriate heat transfer temperature difference between the working fluid and the cooling water should be ensured. The evaporating temperature of the working fluid in the LT cycle is set to 348.15 K because engine coolant temperature is maintained at near 363.15 K, and an appropriate heat transfer temperature difference between the two fluids should also be ensured. Similarly, the condensing temperature of the working fluid in the HT cycle is set to 353.15 K according to the evaporating temperature of the working fluid in the LT cycle.
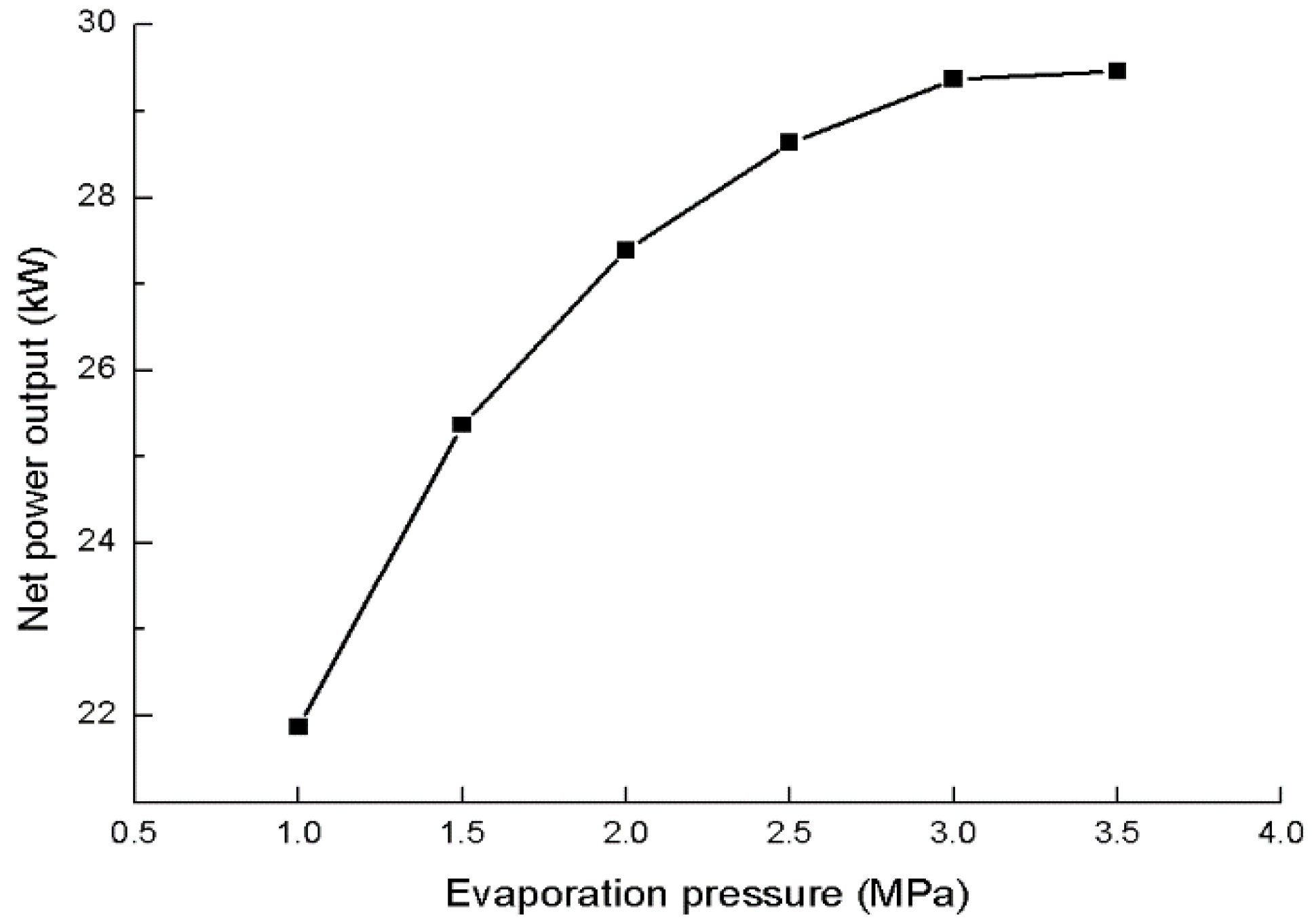
After several operating parameters are settled and the waste heat characteristics of the CNG engine are calculated through the aforementioned equations, the performance of the DORC system is simulated, and the influence of the evaporating temperature in the HT cycle is discussed as follows. Under the rated power output condition of the CNG engine, the relationship between the net power output of the DORC system and the HT cycle evaporating pressure is shown in
Figure 8. As shown in the figure, the net power output increases rapidly from 21.87 to 29.37 kW as the evaporating pressure of the HT cycle rises from 1to 3 MPa. However, the trend line flattens near the critical evaporating pressure of the HT cycle. When the evaporating pressure is 3.5 MPa, the net power output is 29.46 kW, which only slightly increases by 0.09 kW when the evaporating pressure is 3 MPa. Moreover, the working fluid easily decomposes and its characteristics are unstable near the critical pressure area. Hence, setting the evaporating pressure to 3 MPa during simulation is reasonable.
Figure 8.
Influence of the evaporating pressure of the HT cycle on the net power output of the DORC system.
Figure 8.
Influence of the evaporating pressure of the HT cycle on the net power output of the DORC system.
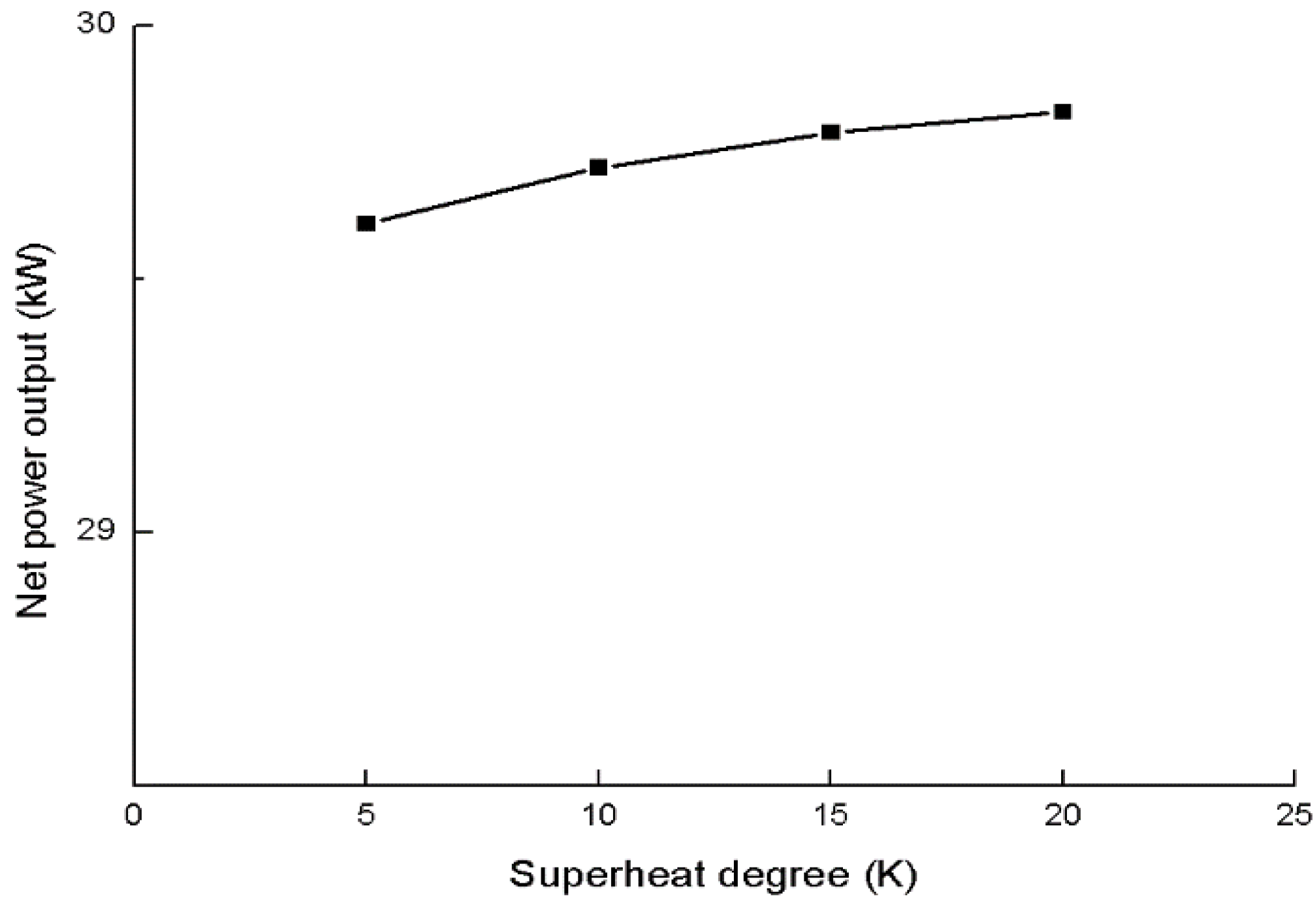
When the evaporating pressure of the working fluid is set to 3 MPa, the influence of the superheat degree of the HT cycle working fluid on the net power output of the DORC system is investigated. As shown in
Figure 9, as the superheat degree increases from 5 to 20 K, the net power output increases by 0.74%, that is, from 29.61 to 29.83 kW. In addition, the net power output only increase by less than 0.5 kW compared with the net power output in the saturated state. Moreover, the number of system assemblies and the heat loads of these assemblies increase if the working fluid is heated to the superheated state. Hence, the state of the HT cycle working fluid assumes a saturated state after passing through evaporator 1 in the present work.
Figure 9.
Influence of the superheat degree of the HT cycle working fluid on the net power output of DORC system.
Figure 9.
Influence of the superheat degree of the HT cycle working fluid on the net power output of DORC system.
5. Performance of the DORC–CNGE Combined System
The performance of the WHR system based on DORC is simulated and discussed for the entire engine test region according to the waste heat characteristics of the CNG engine and the settled parameters of the DORC system.
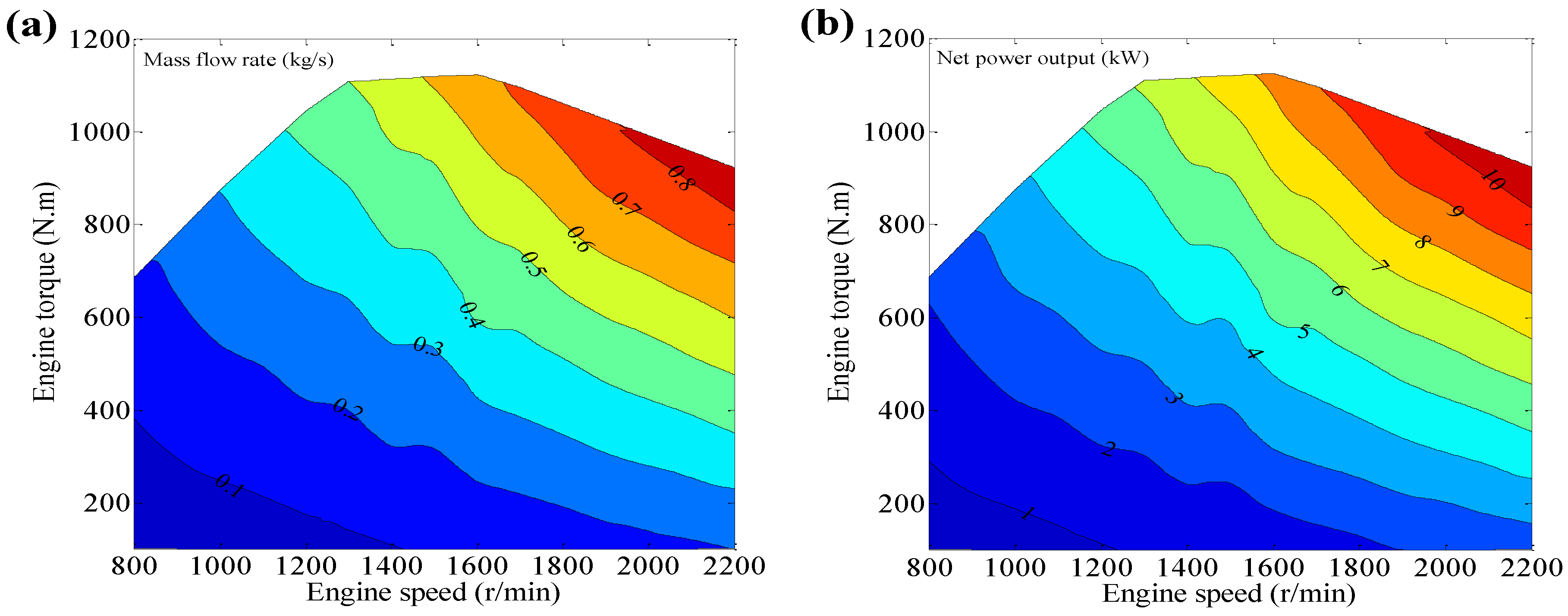
As shown in
Figure 10, the working fluid mass flow rate and the net power output of the HT cycle exhibit the same trend, which increases as engine speed and engine torque rise, because the net power output of the ORC system is determined by the working fluid mass flow rate when the other parameters of the DORC system are settled in Equations (3), (7), and (28). In the present DORC system, the HT cycle recovers waste heat energy from exhaust gas, and thus, when the amount of exhausted waste heat energy is high, a high value of working fluid flow mass is necessary, and correspondingly, a high net power output is generated. The waste heat energy in exhaust gas, working fluid mass flow rate, and net power output of the HT cycle exhibit the same trends as the engine operating conditions, which vary as shown in
Figure 6c and
Figure 10, and the maximum values of the three parameters are 154 kW, 0.88 kg/s, and 10.89 kW, respectively.
Figure 10.
(a) The working fluid mass flow rate of the HT cycle; (b) The net power output of the HT cycle.
Figure 10.
(a) The working fluid mass flow rate of the HT cycle; (b) The net power output of the HT cycle.
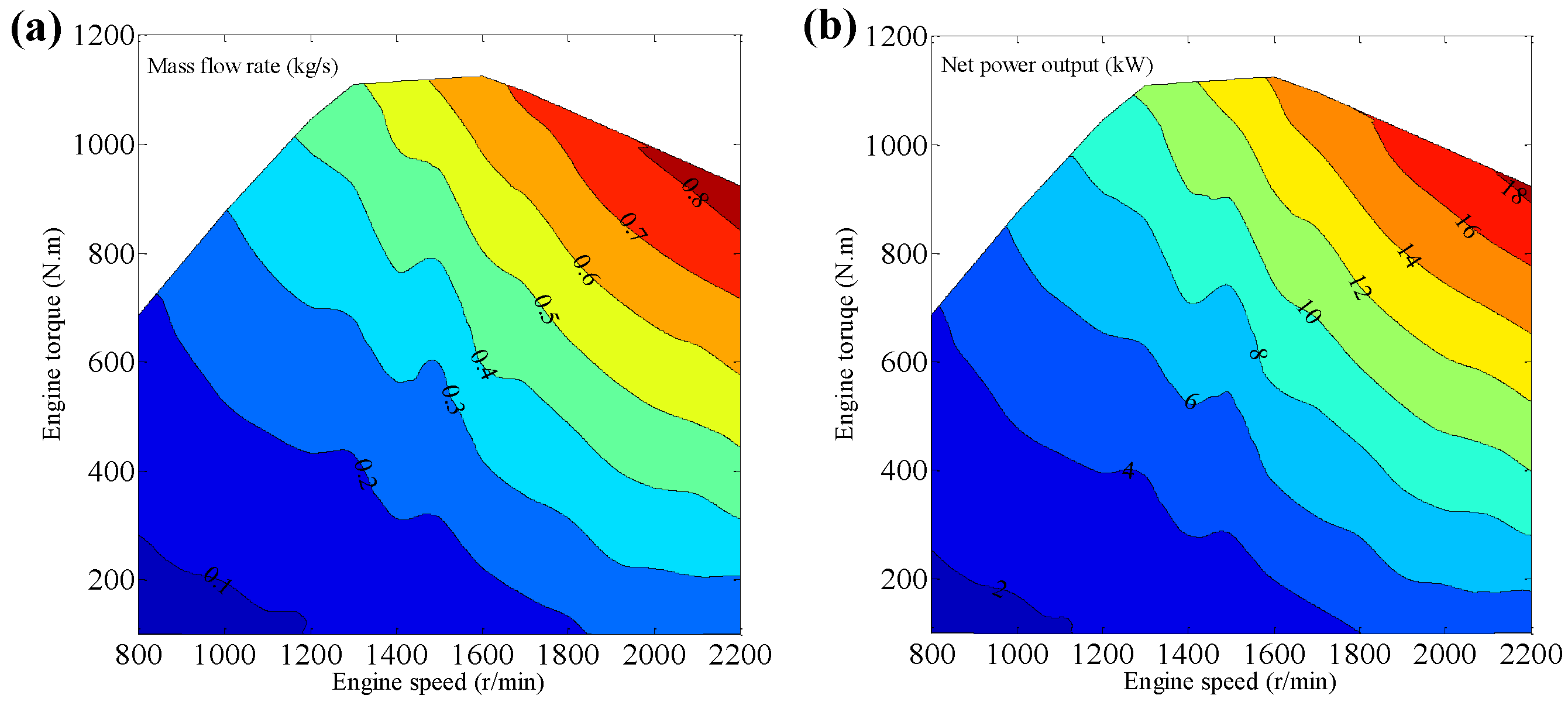
Figure 11 shows the trends of the working fluid mass flow rate and the net power output of the LT cycle
versus the engine operating conditions. The two parameters increase as engine speed and engine torque rise. Under the rated engine operating condition, the working fluid mass flow rate and the net power output of the LT cycle reach the maximum values of 0.86 kg/sand 18.48 kW, respectively. Compared with
Figure 10a and
Figure 11a, the maximum working fluid mass flow rates of the LT and HT cycles lightly differ. However, the maximum net power output of the LT cycle is obviously larger than that of the HT cycle under the same conditions. The main reason for this phenomenon is that the LT and HT cycles have similar working fluid mass rates but the enthalpy difference between the inlet and outlet of expander 2 is obviously larger than that of expander 1.
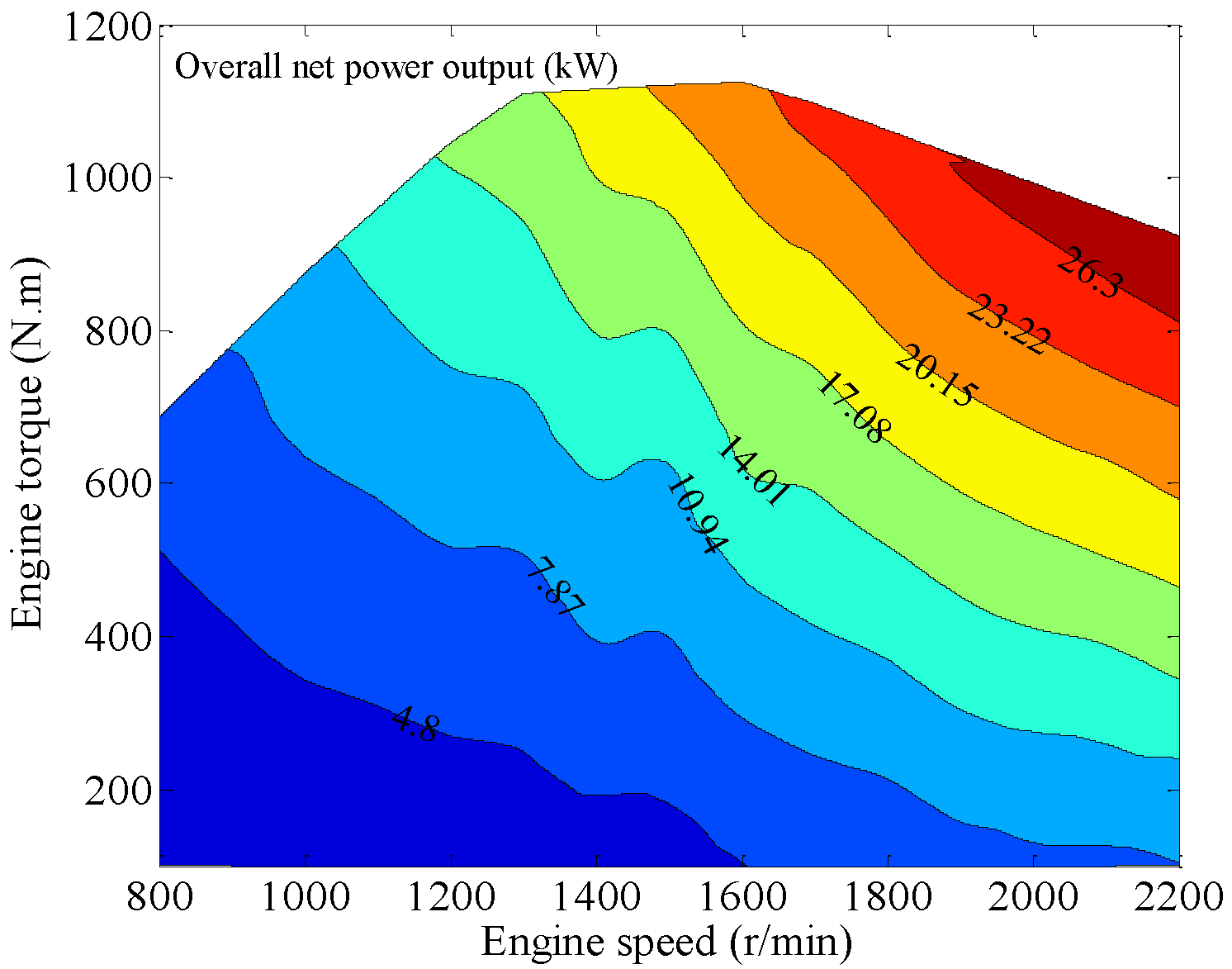
The distribution of the overall power output of the DORC system within the engine test region is plotted in
Figure 12. The overall power output reaches the maximum value of 29.37 kW under the rated power output condition of the engine, and then increases as engine speed and engine torque rises because the overall power output is the total of the net power outputs of the HT and LT cycles.
Figure 11.
(a) The working fluid mass flow rate of the LT cycle; (b) The net power output of the LT cycle.
Figure 11.
(a) The working fluid mass flow rate of the LT cycle; (b) The net power output of the LT cycle.
Figure 12.
The distribution map of the net power output of the DORC system.
Figure 12.
The distribution map of the net power output of the DORC system.
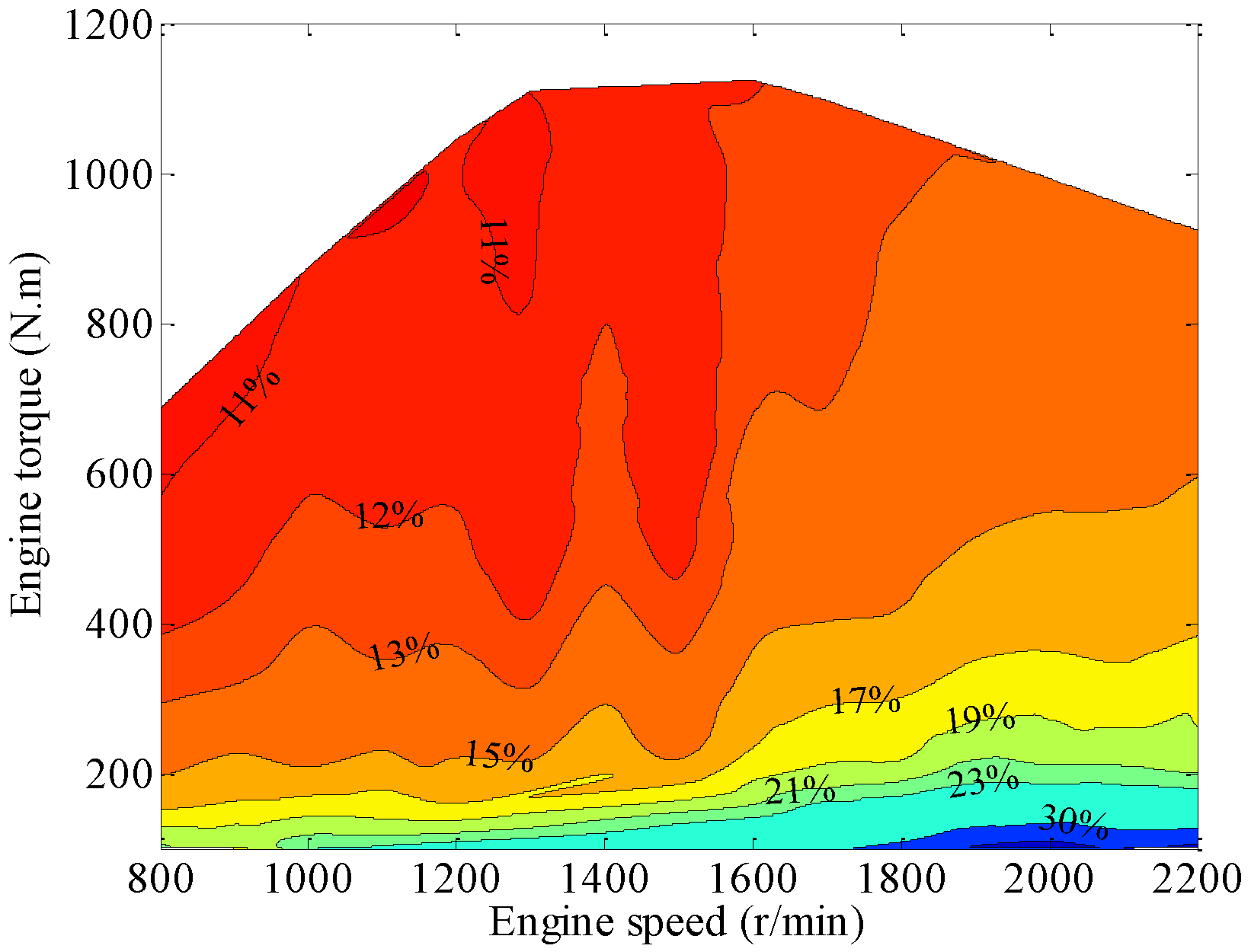
The distribution map of the thermal efficiency of the DORC system under the CNG engine test conditions is shown in
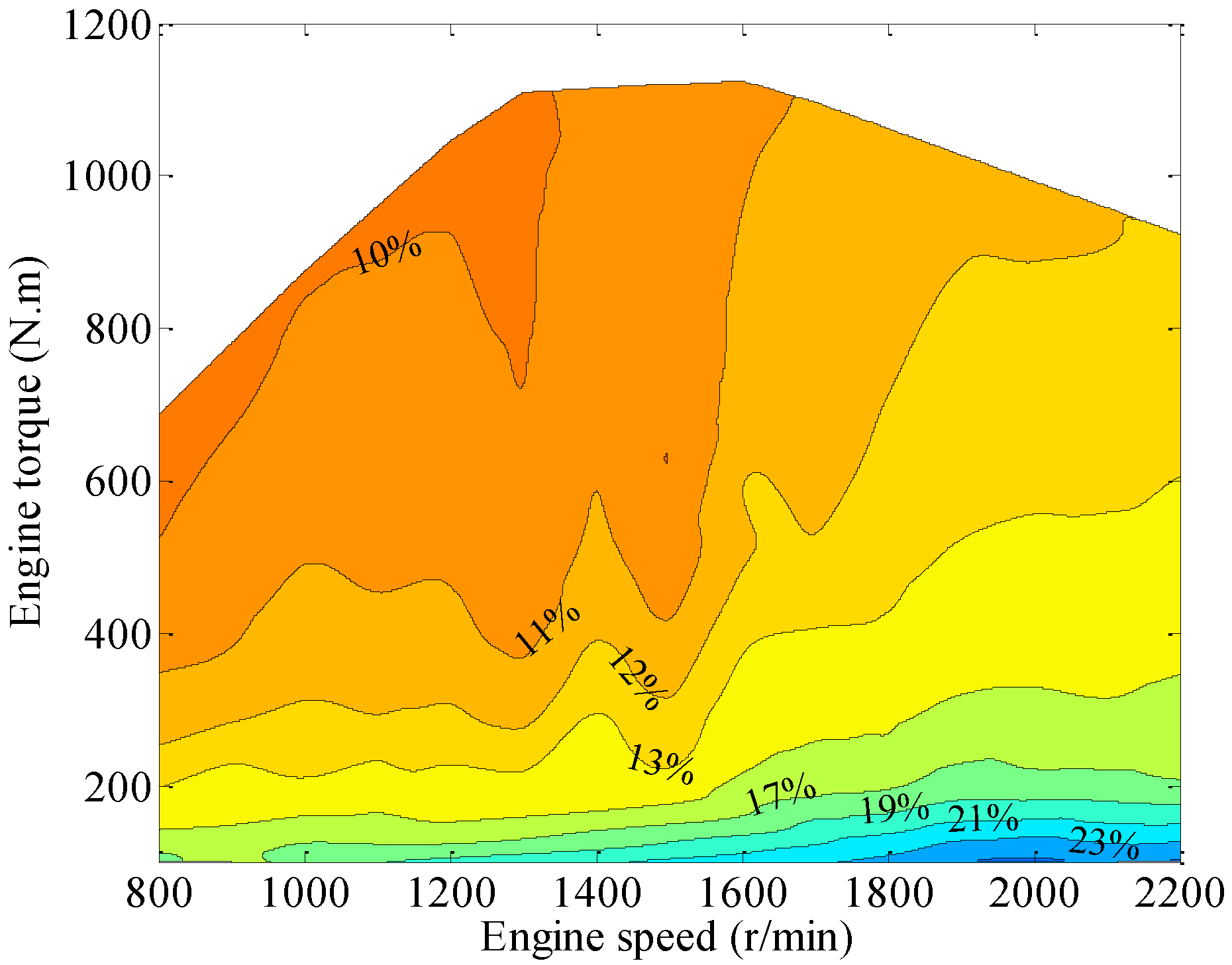
Figure 13. As shown in the figure, the thermal efficiency of the DORC system increases as engine speed and engine torque rise under a low engine speed ranging from 800 to 1200 r/min. Moreover, the maximum thermal efficiency within this range is 9.78% when the engine torque varies from 400 to 700 N·m. Under medium and high engine speed ranging from 1200 to 2200 r/min, thermal efficiency obviously increases with engine torque, while simultaneously experiencing a slow concussion with engine speed. The maximum thermal efficiency within the entire engine test region reaches up to 10.81% under the rated power output operating condition of the CNG engine.
Based on the comparison between the DORC–CNGE combined system and the original engine under the CNG engine test region, the POIR of the DORC–CNGE combined system is calculated, and the results are plotted in
Figure 14. Under low torque ranging from 0 to 200 N·m, the POIR decreases as engine torque obviously increases. However, the POIR increases slowly with engine speed. Under a medium and high torque value of over 200 N·m, the POIR also decreases as engine torque increases. However, the POIR fluctuates as engine speed reaches 800–1500 r/min, but monotonously increases as engine speed reaches 1500–2200 r/min under medium and high torque ranges. The POIR varies from 13.22% to 33.73% under a low torque range, and from 10.41% to 18.62% under medium and high torque ranges. Hence, power output is suggested to improve obviously by equipping the DORC system when a CNG-fueled heavy-duty truck runs under highway conditions.
Figure 13.
The distribution map of the thermal efficiency of the DORC system.
Figure 13.
The distribution map of the thermal efficiency of the DORC system.
Figure 14.
The distribution map of the POIR under the CNG engine test region.
Figure 14.
The distribution map of the POIR under the CNG engine test region.
Figure 15 shows the distribution map of the BIR, which is also obtained by comparing the data between the DORC-equipped CNG engine and the original CNG engine under the test region. In addition, the BIR exhibits the same trend as the POIR, given that engine operating conditions vary because the increase in power output is equivalent to the BIR, as shown in Equations (35) and (36). The BIR decreases with engine load, and its value is remarkably high (11%–25%) in low torque operating conditions.
Figure 15.
The distribution map of the BIR under the CNG engine test region.
Figure 15.
The distribution map of the BIR under the CNG engine test region.
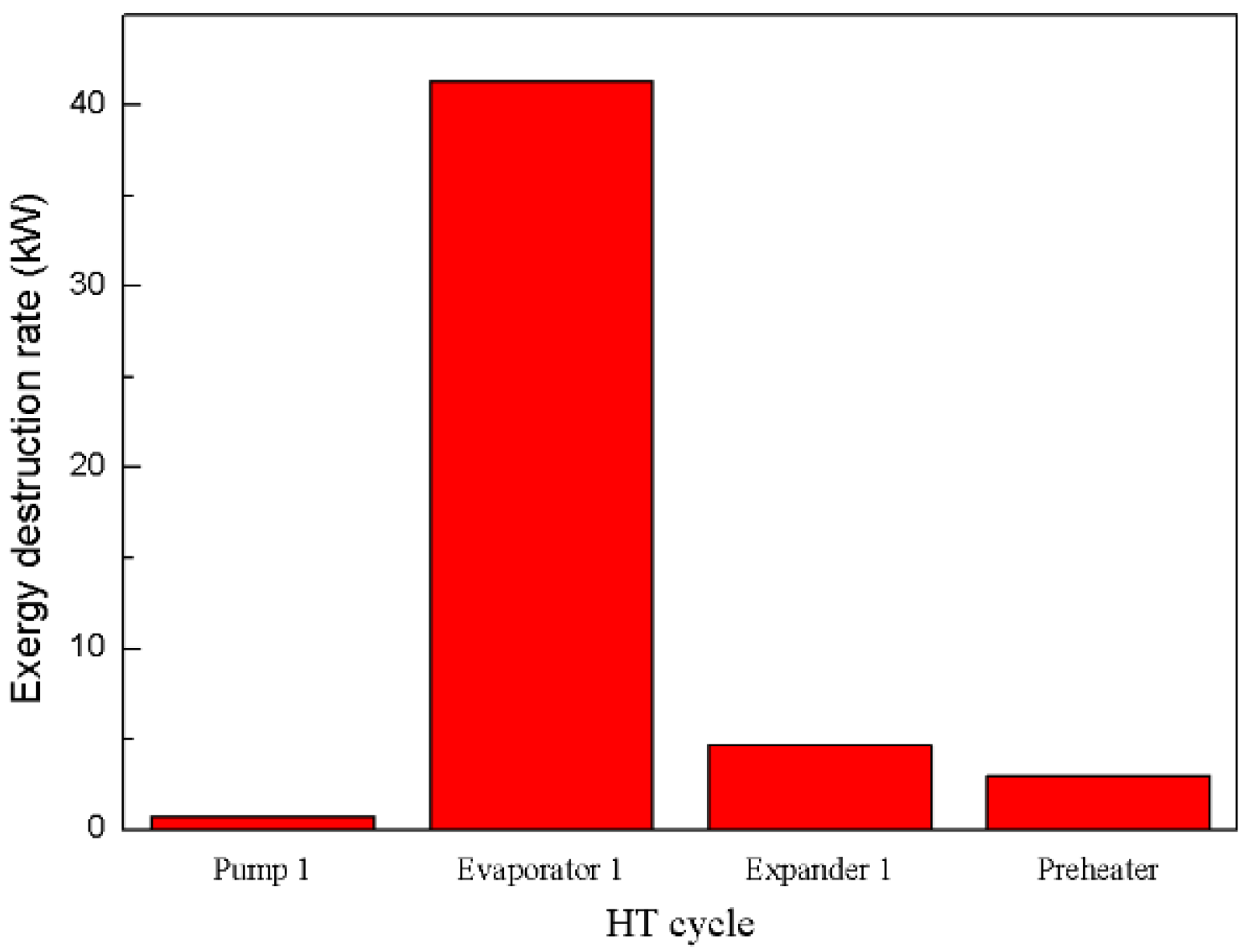
In
Figure 16, the exergy destruction rates of the HT cycle components under the rated power output condition of the CNG engine is shown. Obviously, evaporator 1 has the largest exergy destruction rate, which reaches up to 41.32 kW, because the exhaust gas temperature of the engine is significantly high (generally over 750 K), and thus, the temperature difference between the exhaust gas and the working fluid is large and causes huge irreversible losses in evaporator 1. Comparatively, the exergy destruction rates of pump 1, expander 1, and the preheater are remarkably smaller, that is, 0.73, 4.66, and 2.97 kW, respectively. Optimizing evaporator 1 is seemingly the key to lowering the total exergy destruction rate in the HT cycle.
Figure 16.
The exergy destructions rates of components in the HT cycle under the rated power output condition of the CNG engine.
Figure 16.
The exergy destructions rates of components in the HT cycle under the rated power output condition of the CNG engine.
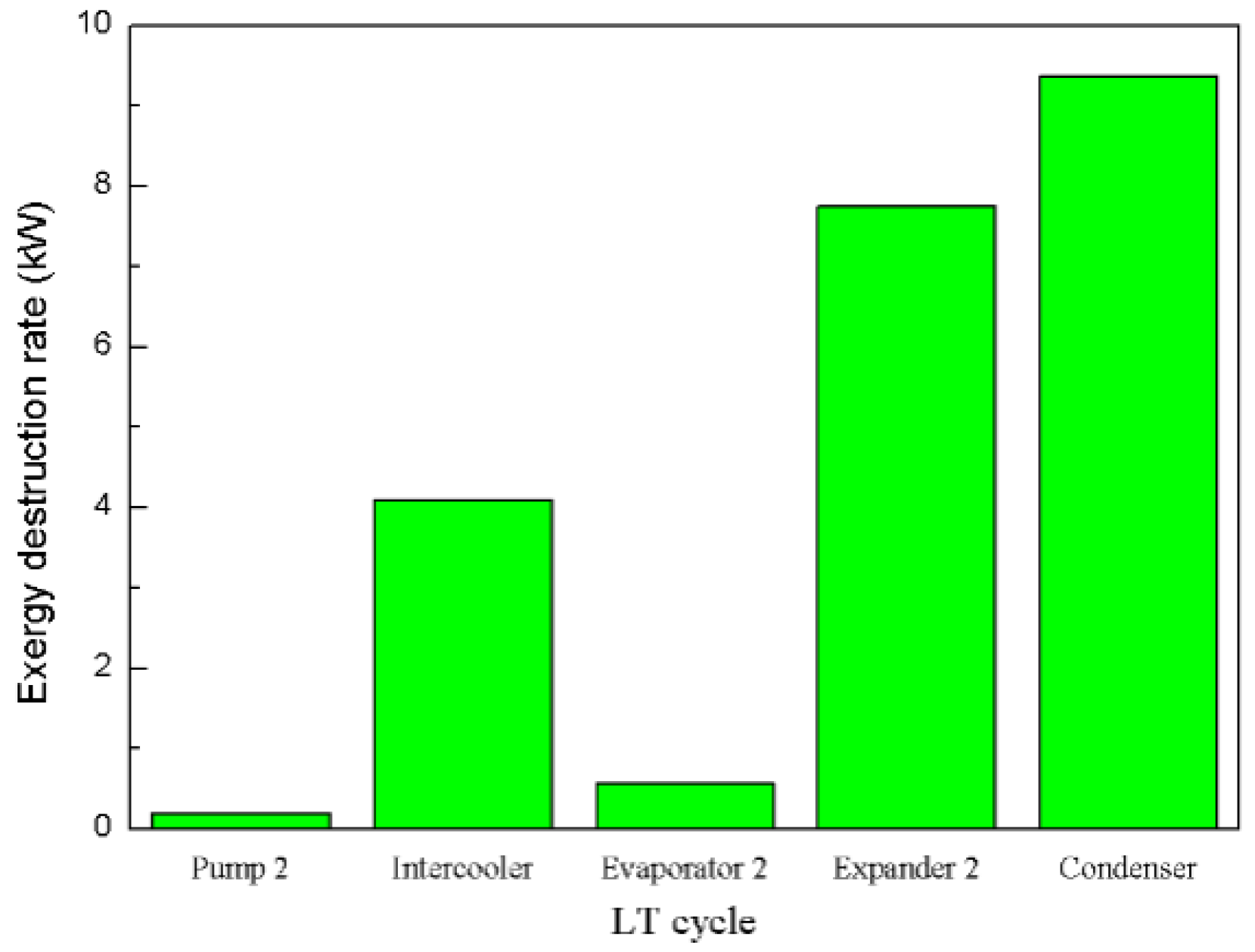
The exergy destruction rates of the LT cycle components under the rated power output condition of the CNG engine is shown in
Figure 17. In the LT cycle, the exergy destruction rates of the intercooler, expander 2, and the condenser are relatively high, namely, 4.1, 7.75, and 9.36 kW, respectively. Both the intercooler and the condenser are heat exchangers, whose irreversible loss is determined by the temperature difference between heat exchanges. Meanwhile, the irreversible loss of expander 2 is determined by its isentropic efficiency. Otherwise, the exergy destruction rate of pump 2 is as low as 0.2 kW because of the small power dissipation of pump 2. The exergy destruction rate of evaporator 2 is only 0.57 kW, given the small irreversible loss in evaporator 2 because of the slight temperature difference between the cooling water and the working fluid in the LT cycle.
Figure 17.
The exergy destruction rates of the LT cycle components under the rated power output condition of the CNG engine.
Figure 17.
The exergy destruction rates of the LT cycle components under the rated power output condition of the CNG engine.
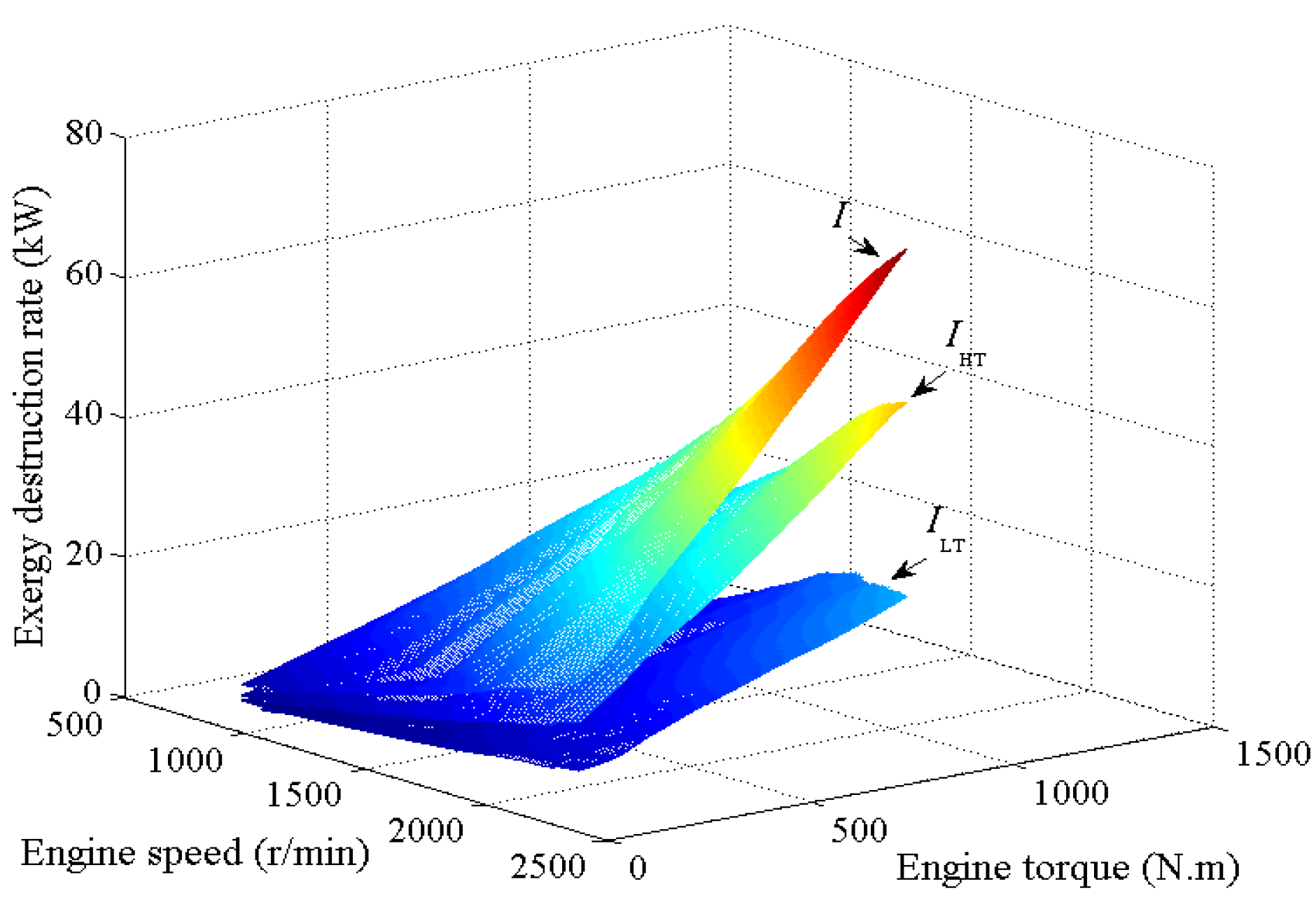
The total exergy destruction rate of the DORC system, the exergy destruction rate of the HT cycle, and the exergy destruction rate of the LT cycle under the entire engine test conditions are shown in
Figure 18.
Figure 18.
Three kinds of exergy destruction rates of the DORC system under the whole engine test region.
Figure 18.
Three kinds of exergy destruction rates of the DORC system under the whole engine test region.
The exergy destruction rates of the HT and LT cycles increase as engine speed and engine load rise. This finding may be attributed to the rise in working fluid mass flow rates of the HT and LT cycles, which is determined by the available waste heat energy. Another reason for this finding is the increase in the irreversible losses of the HT and LT cycles because of the increase in the temperature differences between the heat exchangers. The total exergy destruction rate of the WHR system exhibits the same trend given that it is the total exergy destruction rates of the HT and LT cycles. Under the rated power output of the engine, the maximum exergy destruction rate of the HT and LT cycles are 49.68 and 21.98 kW, respectively, and the maximum total exergy destruction rate is 71.66 kW. Otherwise, the exergy destruction rate of the HT cycle is larger than that of the LT cycle because the exergy destruction rate of evaporator 1 is remarkably larger than those of the other system components according to
Figure 16 and
Figure 17.