Lorenz Wind Disturbance Model Based on Grey Generated Components

Abstract

In order to meet the needs of wind speed prediction in wind farms, we consider the influence of random atmospheric disturbances on wind variations. Considering a simplified fluid convection mode, a Lorenz system can be employed as an atmospheric disturbance model. Here Lorenz disturbance is defined as the European norm of the solutions of the Lorenz equation. Grey generating and accumulated generating models are employed to explore the relationship between wind speed and its related disturbance series. We conclude that a linear or quadric polynomial generating model are optimal through the verification of short-term wind speed prediction in the Sotavento wind farm. The new proposed model not only greatly improves the precision of short-term wind speed prediction, but also has great significance for the maintenance and stability of wind power system operation.

1. Introduction

Wind energy is one of the most popular and potential renewable energies worldwide [1,2]. Rapid development of wind energy has contributed greatly to energy supply systems. The Global Wind Energy Council (GWEC) has provided the latest and comprehensive statistics about the development of wind power industries. By the end of 2013, global cumulative and new installed wind power capacities have exceeded 318 GW and 35 GW, respectively. China occupied the largest share of both parts [3]. As a result how to effectively utilize wind resources has received increasing attention [4,5]. Wind power generation in wind farms could make full use of wind energy on a large-scale [6,7], but considering the stochastic volatility nature of wind energy, integration of wind power into power systems becomes a challenge [8,9,10,11]. Necessary measures should be taken to maintain the normal operation of electric systems and decrease losses that could affect people’s daily prodivity and life. Therefore, high precision wind speed and power prediction is urgently needed. Scholars at home and abroad have done lots of studies on wind forecasting and achieved excellent results [5,12,13,14]. In this paper a novel wind disturbance model to improve the performance of conventional back propagation (BP) neural networks is proposed.

Wind formation and variation in the atmosphere are typical nonlinear processes [15]. As Lorenz said in his 2008 lecture at the University of Rome named the Butterfly Effect, the real atmospheric state of motion is actually the observed state plus a small perturbation. This random perturbation is the key consideration that affects wind speed forecasting precision. This problem could not be resolved by linear theory. Lorenz extracted a three-variable system called the Lorenz system from a fluid convection model in 1963 [16,17,18,19]. The Lorenz system is frequently used to study nonlinear science since it was first proposed due to its good performance in accomodating chaos [20,21]. Here it is used as a typical atmospheric disturbance model. Different initial conditions and values of parameters could result in different evolutions of a Lorenz system. Various types of Lorenz disturbances are used to establish wind disturbance models in this article.

This paper is organized as follows: Section 2 briefly introduces the related content on the topic of nonlinear Lorenz disturbances. Section 3 presents the modeling process and the verification on disturbance model through short-term wind speed prediction. Section 4 concludes the paper.

2. Nonlinear Lorenz Disturbance and Data Preprocessing Forms

2.1. Different Types of Lorenz Disturbance and Normalization Constants

2.1.1. Different Types of Disturbance in a Lorenz System

The Lorenz system was extracted from the seven-variable fluid convection model of Saltzman [17,18,19,22]. A Lorenz system could exhibit chaotic state in a simplest way in nonlinear systems. It has enriched people’s acknowledgement of the dynamics of nonlinear systems and played a vital role on the development of chaos theory. The fluid convection model simplified by Saltzman can be expressed as follows [17]:

$$\begin{array}{l}\frac{\partial }{\partial t}{\nabla }^2\text{ψ}+\frac{\partial \left(\text{ψ},{\nabla }^2\text{ψ}\right)}{\partial \left(x,z\right)}-g\text{ς}\frac{\partial \text{θ}}{\partial x}-\upsilon {\nabla }^4\text{ψ}=0\\ \frac{\partial \text{θ}}{\partial t}+\frac{\partial \left(\text{ψ},\text{θ}\right)}{\partial \left(x,z\right)}-\frac{\Delta T_0}{H}\frac{\partial \text{ψ}}{\partial x}-\text{κ}{\nabla }^2\text{θ}=0\end{array}$$

(1)

where ψ is a two-dimensional stream function, θ is a temperature difference from that occurring in equilibrium state, g,ς,υ,κ denote the acceleration of gravity, the coefficient of thermal expansion, the kinematic viscosity, and the thermal conductivity, respectively.

The convection Equation (1) describes the following system. The fluid moves between two fixed parallel surfaces, whose temperature difference is kept constant by external heating. The whole procedure was assumed to develop in the vertical plane. If the solution of Equation (1) was unstable, convective motion would develop. This system was similar with what Lorenz studied at that time. Then Equation (1) was further simplified into the following three-variable system called Lorenz system given by:

$$\begin{array}{l}\dot{x}=-\sigma \left(x-y\right)\\ \dot{y}=-xz+rx-y\\ \dot{z}=xy-bz\end{array}$$

(2)

where x is proportional to fluid intensity, y is proportional to the temperature difference between the ascending current and the descending current, z is proportional to the temperature difference in the vertical direction compared to the equilibrium state, σ, r and b are all positive parameters. We can obtain various Lorenz attractors by taking different values of r. Those attractors in phase space correspond to various forms of disturbance in a real atmospheric system. The values of r can be divided into four intervals as shown in Table 1 [16].

Table 1. The actual fluid motions in Lorenz system when parameters σ and b are respectively equal to 10 and 8/3.

Items to be Compared	The Values of r and its Corresponding Fluid Motions
Rayleigh Number (r)	0 < r < 1	1 < r < 13.97	13.97 < r < 24.74	r > 24.74
Actual fluid motion	Heat conduction	Regular convection	Transient chaos	Chaos

Table 1. The actual fluid motions in Lorenz system when parameters σ and b are respectively equal to 10 and 8/3.

Items to be Compared	The Values of r and its Corresponding Fluid Motions
Rayleigh Number (r)	0 < r < 1	1 < r < 13.97	13.97 < r < 24.74	r > 24.74
Actual fluid motion	Heat conduction	Regular convection	Transient chaos	Chaos

2.1.2. Normalization Constant of Lorenz Disturbance

It is convenient to discuss the solutions of Lorenz system in R³. Here we define the European norm of vectors in R³ as the atmospheric disturbance. Let P(x,y,z) be an arbitrary vector in R³. The European norm of P(x,y,z) can be expressed as:

$$L=\Vert p\Vert =\sqrt{x^2{\text{+y}}^2{\text{+z}}^2}$$

(3)

There will be a problem if taking Formula (3) as the form of the Lorenz disturbance. Let the initial condition and parameters σ, b, r be (0,1,0),10,8/3,45, respectively. The Lorenz disturbance defined by Formula (3) is demonstrated in Figure 1a. We can clearly see that the disturbance fluctuates within interval (0,90), which is larger than the range of the actual wind speed changes. Therefore, we need to define a normalization constant to reduce this range to a reasonable small interval like (0,3), which is decided by the deviations occurred in previous wind speed predictions. Let the normalization constant be 50 for the disturbance shown in Figure 1a. The normalized disturbance is shown in Figure 1b. Generally the normalization constant varies according to different size of Lorenz disturbance and wind fluctuations.

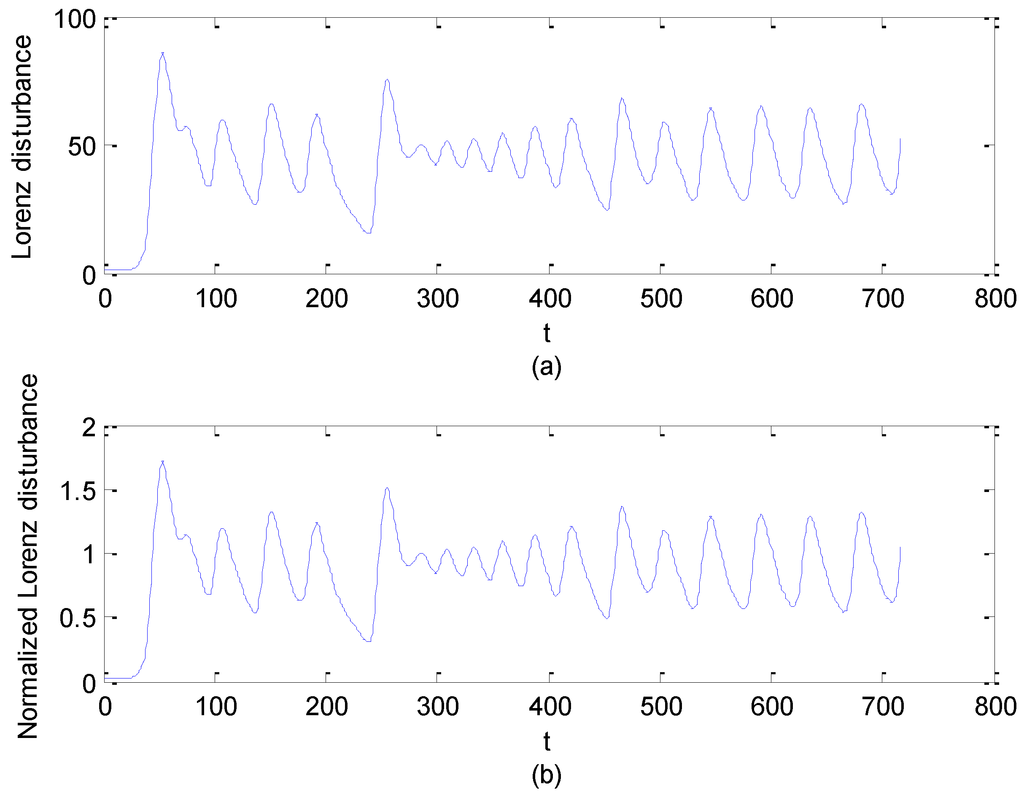
Figure 1. (a) The initial Lorenz disturbance defined by Formula (3). (b) The normalized Lorenz disturbance.

Figure 1. (a) The initial Lorenz disturbance defined by Formula (3). (b) The normalized Lorenz disturbance.

2.2. Data Preprocessing

It is necessary to preprocess the scattered sample data before building the disturbance model. Figure 2 shows the distribution of wind speed sequence and its corresponding disturbance series in a certain period. For the calculation of the two arrays we can refer to the modeling process in Section 3.3. We can see that the points are distributed extremely irregularly. A further calculation of the correlation coefficient can quantitatively describe the relationship of the two arrays. The calculated result is 0.1713, which is less than 0.3 and proves the irrelevance between the two arrays. The correlation coefficient is expressed by:

$$r=\frac{{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}}{\sqrt{{\displaystyle \sum {\left(x-\overline{x}\right)}^2{\left(y-\overline{y}\right)}^2}}}$$

(4)

where x and y denote the two arrays to be analyzed, $\overline{x}$ and $\overline{y}$ denote the average of x and y, respectively.

In this section grey generating is applied to discover the inherent relationship between variables x and y. Grey generating commonly includes Accumulated Generating Operation (AGO), Inverse AGO (IAGO), Mean (MEAN), and Effect Measure (EM), etc. AGO not only does well in establishing a grey model, but also can be used to reduce the randomness of discrete sequences [23,24]. AGO means adding original data in sequence to obtain the generating series [25,26].

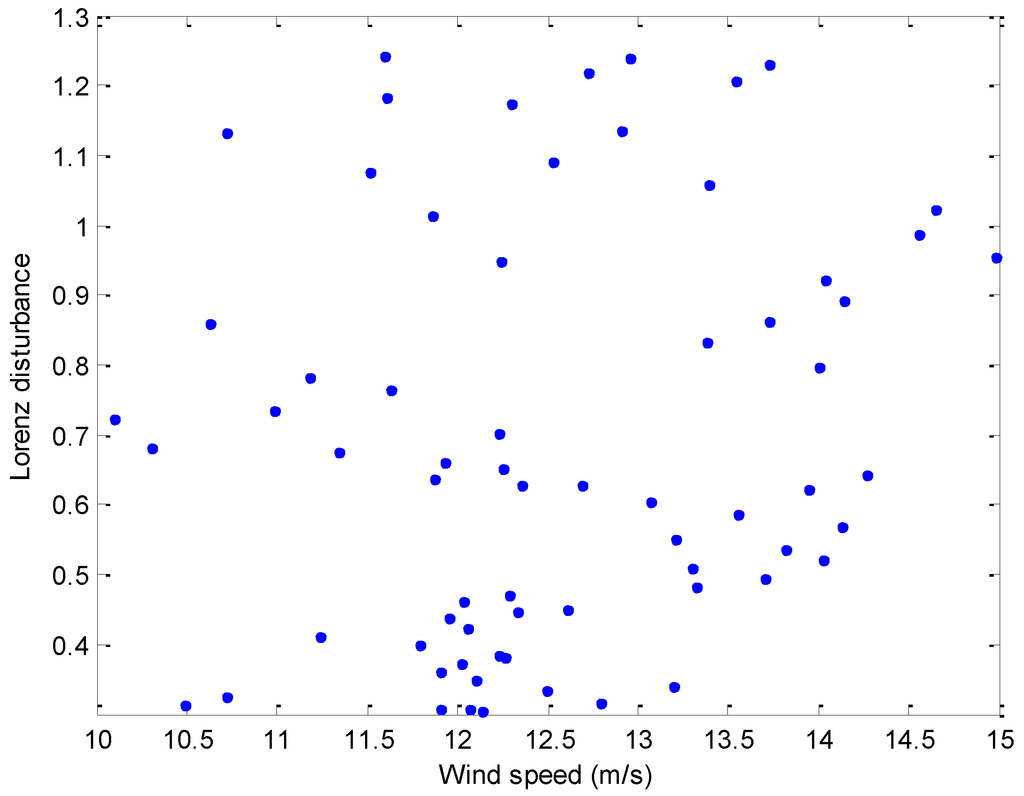
Figure 2. Wind speed versus the corresponding disturbance series for a period of time.

Figure 2. Wind speed versus the corresponding disturbance series for a period of time.

Definition 1 

Let $x^{\left(0\right)}$ be raw series:

$$x^{\left(0\right)}=\left(x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\dots ,x^{\left(0\right)}\left(n\right)\right)$$

(5)

$x^{\left(1\right)}$ is AGO series of $x^{\left(0\right)}$ , denoted as:

$$x^{\left(1\right)}=AGO{x}^{\left(0\right)}$$

(6)

Provided that:

$$x^{\left(1\right)}=\left(x^{\left(1\right)}\left(1\right),x^{\left(1\right)}\left(2\right),\cdots ,x^{\left(1\right)}\left(n\right)\right)$$

(7)

where:

$$x^{\left(1\right)}\left(k\right)={\displaystyle \sum _{m=1}^k{x}^{\left(0\right)}\left(m\right)},k=1,2,\cdots ,n$$

(8)

Definition 2 

y is IAGO series of $x^{\left(0\right)}$ , denoted as:

$$y=IAGO{x}^{\left(0\right)}$$

(9)

Provided that:

$$y=\left(y\left(1\right),y\left(2\right),\cdots ,y\left(n\right)\right)$$

(10)

where:

$$y(1)=x^{\left(0\right)}(1),y\left(k\right)=x^{\left(0\right)}\left(k\right)-x^{\left(0\right)}\left(k-1\right),k=2,3,\cdots ,n$$

(11)

Based on the ways of data processing like Formulas (5)–(8), the same treatment could be applied to the arrays in Figure 2. Figure 3 shows the generated data of Figure 2. It is clear that the irregular data in Figure 2 are converted into a monotonically increasing sequence in Figure 3. This conversion will realize a high precision curve fitting called accumulated generating model, namely the new proposed wind disturbance model in this research.

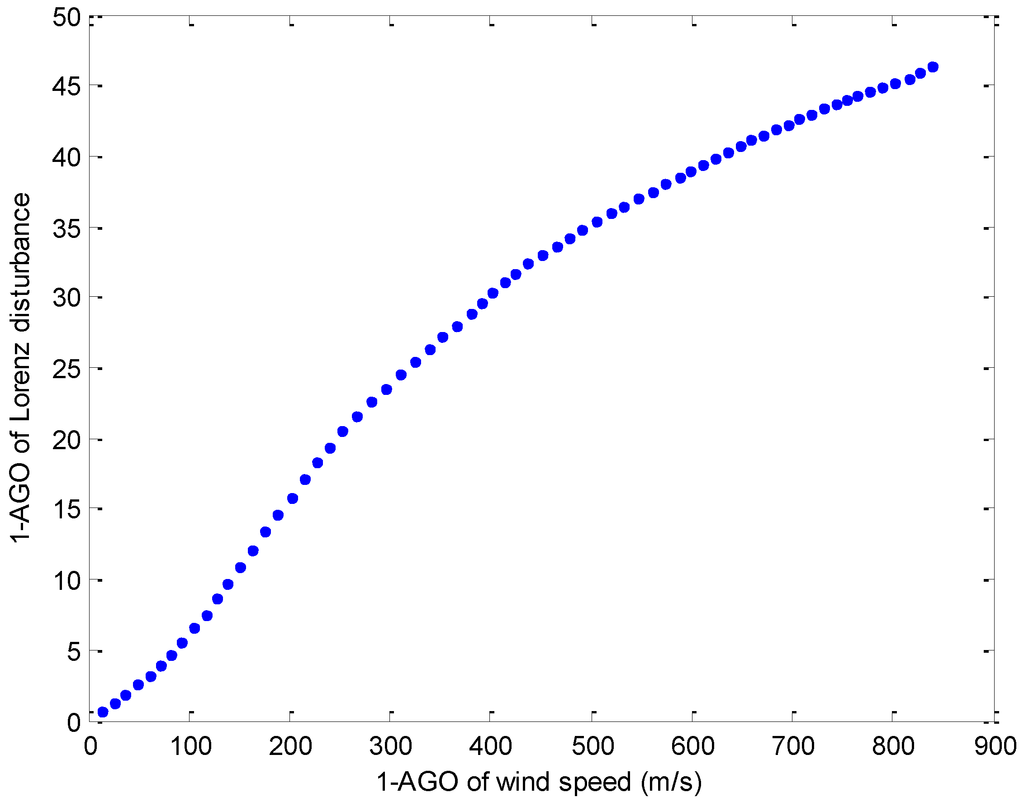
Figure 3. The points in this figure denote the AGO series of the data shown in Figure 2.

Figure 3. The points in this figure denote the AGO series of the data shown in Figure 2.

3. Wind Disturbance Model Based on Grey Generation

3.1. Data Description

The modeling data set is derived from the Sotavento wind farm from 1 January to 28 February in 2014. The observations contain 8196 groups of wind speed and wind direction. Figure 4 shows the distribution of wind speed in the above two months. The average, maximum, and minimum wind speed are 10.83 m/s, 38.67 m/s, and 2.6 m/s, respectively. We can see that the range of wind fluctuation is quite large.

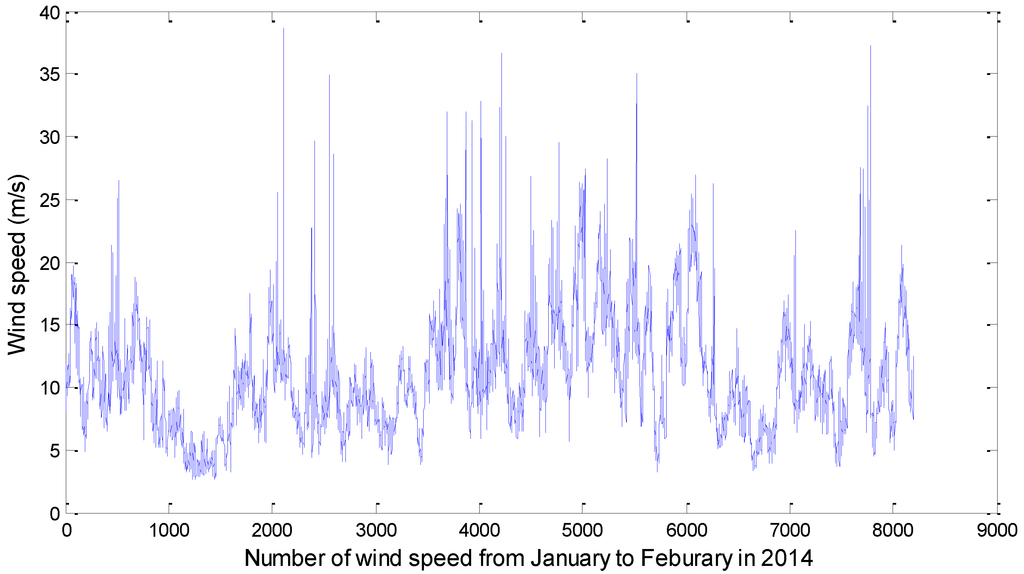
Figure 4. The distribution of wind speed recorded from January to February in 2014 in Sotavento wind farm.

Figure 4. The distribution of wind speed recorded from January to February in 2014 in Sotavento wind farm.

3.2. Error Criteria

Selecting a reasonable set of error indicators can objectively evaluate the level of wind speed predictions and the effectiveness of forecasting models. Some common error criteria include absolute error (AE), mean absolute error (MAE), mean absolute percentage error (MAPE), root mean-square error (RMSE), standard deviation of error (SDE) [8,15,27,28,29], etc. Compared to MAE, RMSE is more sensitive to large data samples and is robust when dealing with large errors [30]. Here we use MAE and RMSE, given by:

$$MAE=\frac{1}{M}{\displaystyle \sum _{k=1}^M\left|y\left(k\right)-f\left(k\right)\right|}$$

(12)

$$RMSE=\sqrt{\frac{1}{M}{\displaystyle \sum _{k=1}^M{\left(y\left(k\right)-f\left(k\right)\right)}^2}}$$

(13)

where y(k) and f(k) respectively denote the observed data and predicted value, M is sample size.

3.3. Wind Disturbance model When Rayleigh Number Equals to 45

3.3.1. BP Neural Network

BP neural network is widely used in wind forecasting and does well in dealing with nonlinear problems [31,32,33]. Thus, it is adopted as the basic forecasting model in this study. Based on a gradient descent algorithm, the BP neural network obtains the minimum mean square error between output vectors and the sample values through constantly adjust the weights and biases in networks. This particular network could perfectly learn and store the mapping relations between input and output variables.

The structure of the BP neural network used in this paper is shown in Figure 5. A BP network generally consists of three layers, i.e., input layer, hidden layer, and output layer. The three input vectors of BP network are wind speed (V(t)) and sine-cosine of wind direction ((sin D, cos D)) at time t. The hidden layer has three sigmoid neurons followed by an output layer of one linear neuron. The outputs of hidden layer and output layer are ruled by the following two formulas:

$$y_j=f_j\left({\displaystyle \sum _{i=1}^3{w}_{ij}{x}_i+b_j}\right)$$

(14)

$$y=f_0\left({\displaystyle \sum _{j=1}^3{w}_j{y}_j+b_0}\right)$$

(15)

where x_i is input vector with i = 1,2,3, y_j and y are the output vectors of hidden layer and output layer with j = 1,2,3, f_j and f₀ are transfer functions of nodes, w_ij and w_j are connection weights, b_j and b₀ are biases.

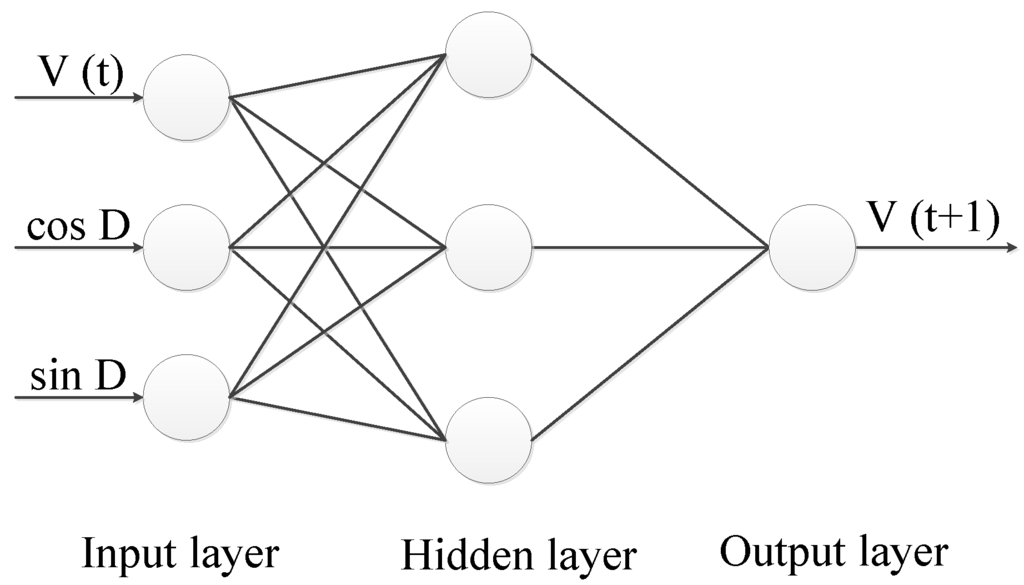
Figure 5. Three-layer BP neural network.

Figure 5. Three-layer BP neural network.

3.3.2. Modeling Process and Discussion

We attempt to establish a disturbance model that it is able to output a valid disturbance sequence according to a given wind speed series. Then we could use this relevant disturbance sequence to reduce the nonlinear components contained in the wind speed series. Polynomial functions are some of the most widely used and simplest fitting functions. Hence, we use a polynomial generating function to construct the disturbance model, which is based on the principle of least squares. The modeling procedure can be divided into the following four steps:

Step one: 

Determine the wind speed and sine-cosine of wind direction as the input variables of BP network. Train the BP network with the training data and predict the subsequent wind speed series. Denote the initial forecasting result and the real wind speed as W_I and W_R, respectively.

Step two: 

In order to seek the minimum deviation between W_I and W_R, we need to seek a certain disturbance sequence called D_L from the normalized disturbance series shown in Figure 1b. D_L is said to be the best compensation to W_I.

Step three: 

According to the data preprocessing method in Section 2.2, we apply AGO to W_I and D_L, respectively. Then we can obtain two arrays that possess a clear relationship as shown in Figure 3. No more than fifth degree polynomials are applied to analyze the generated data. Table 2 shows the detailed statistics of the disturbance models, including the polynomial expression, accumulated generating model, and the fitting error (RMSE). The polynomial expressions are used to describe the features of related disturbance models. f (x) and x denote 1-AGO of Lorenz disturbance and 1-AGO of wind speed, respectively.

Table 2. Detailed statistics of grey generating models based on various polynomials.

Polynomial Expression	Accumulated Generating Model	Fitting Error (RMSE)
f (x) = p1 · x + p2 p1 = 0.0648, p2 = 2.6455		2.218
f (x) = p1 · x2 + p2 · x + p3 p1 = −1.0713 × 10−6, p2 = 0.0657 p3 = 2.5099		2.234
f (x) = p1 · x3 + p2 · x2 + p3 · x + p4 p1 = 1.672 × 10−7, p2 = −0.0002 p3 = 0.1430, p3 = −3.2818		0.8353
f (x) = p1 · x4 + p2 · x3 + p3 · x2 + p4 · x + p5 p1 = 9.1690 × 10−11, p2 = 6.0698 × 10−9 p3 = −1.2911 × 10−4, p4 = 0.1248 p5 = −2.4246		0.8027
f (x) = p1 · x5 + p2 · x4 + p3 · x3 + p4 · x2 + p5 · x + p6 p1 = −1.1187 × 10−12, p2 = 2.5436 × 10−9 p3 = −1.9104 × 10−6, p4 = 5.0681 × 10−4 p5 = 0.0429, p6 = 0.2498		0.4496

Table 2. Detailed statistics of grey generating models based on various polynomials.

Polynomial Expression	Accumulated Generating Model	Fitting Error (RMSE)
f (x) = p1 · x + p2 p1 = 0.0648, p2 = 2.6455		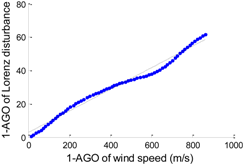2.218
f (x) = p1 · x2 + p2 · x + p3 p1 = −1.0713 × 10−6, p2 = 0.0657 p3 = 2.5099		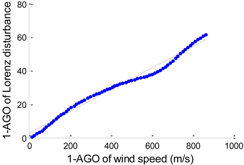2.234
f (x) = p1 · x3 + p2 · x2 + p3 · x + p4 p1 = 1.672 × 10−7, p2 = −0.0002 p3 = 0.1430, p3 = −3.2818		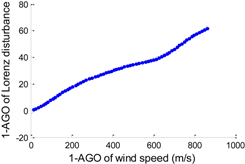0.8353
f (x) = p1 · x4 + p2 · x3 + p3 · x2 + p4 · x + p5 p1 = 9.1690 × 10−11, p2 = 6.0698 × 10−9 p3 = −1.2911 × 10−4, p4 = 0.1248 p5 = −2.4246		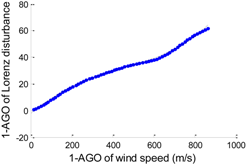0.8027
f (x) = p1 · x5 + p2 · x4 + p3 · x3 + p4 · x2 + p5 · x + p6 p1 = −1.1187 × 10−12, p2 = 2.5436 × 10−9 p3 = −1.9104 × 10−6, p4 = 5.0681 × 10−4 p5 = 0.0429, p6 = 0.2498		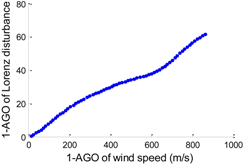0.4496

Step four: 

In this step we will use the disturbance models to predict wind speed for a period of time in the future. We retrain the BP network and make an initial prediction of the future wind speed, which is similar to Step one. We denote the initial prediction in predicted period as W_IP, and then input the $AGO{W}_{\text{IP}}$ series into the disturbance models established in step three, respectively. The generated outputs are in turn written as $D_i,i=1,2,\cdots ,5$ , which needs to be reduced by IAGO. The compensating formula is given by:

$$W_i=W_{\text{IP}}-IAGO{D}_i$$

(16)

where W_i denotes the wind prediction result corresponding to each disturbance model with $i=1,2,\cdots ,5$ . The prediction results are presented in Table 3. The indicator (I), which means initial result, is used to distinguish the result of initial predictions and disturbed predictions.

We can draw the following conclusions through a comprehensive analysis of Table 2 and Table 3. On the one hand, seen from the figures of generating models and the fitting errors in Table 2, the fitting does become much better with a higher degree of polynomial. On the other hand, coefficients of high-order terms of generating functions approximate to zero. Hence, it is not wise to use high order polynomials. Besides, the MAE and RMSE results in Table 3 suggest that the forecasting errors become apparently worse starting from the third degree polynomial model. Therefore, a good fitting cannot promise a good forecasting performance. The universality of disturbance models is seriously reduced due to over-fitting problem. It turns out that linear or quadratic polynomials could work out much better wind predictions compared to other forms of polynomials.

Table 3. MAE and RMSE results of wind speed prediction in February 2014.

Degree of Polynomial	Wind Forecasting Error
	MAE (I) (m/s)	MAE (m/s)	RMSE (I) (m/s)	RMSE (m/s)
1	0.5772	0.0729	0.5870	0.0979
2	0.5935	0.0535	0.5989	0.0789
3	0.6632	0.2230	0.6720	0.2672
4	0.6248	0.1897	0.6365	0.2267
5	0.4377	0.1643	0.4683	0.2268

Table 3. MAE and RMSE results of wind speed prediction in February 2014.

Degree of Polynomial	Wind Forecasting Error
	MAE (I) (m/s)	MAE (m/s)	RMSE (I) (m/s)	RMSE (m/s)
1	0.5772	0.0729	0.5870	0.0979
2	0.5935	0.0535	0.5989	0.0789
3	0.6632	0.2230	0.6720	0.2672
4	0.6248	0.1897	0.6365	0.2267
5	0.4377	0.1643	0.4683	0.2268

3.4. Wind Disturbance Models When Rayleigh Numbers are Equal to 0.7, 12, and 16, Respectively

A Lorenz system would present various evolutions when taking different Rayleigh numbers. Each evolution corresponds to a concrete fluid motion referred in Table 1. In order to verify the universality of Lorenz fluid motions in founding a disturbance model, we can respectively choose four values of Rayleigh number from each interval in Table 1, such as 0.7, 12, 16, and 45. We have made a detailed analysis when the Rayleigh number is equal to 45. Now we continue to verify the other three cases. According to the conclusions in Section 3.3, a linear or quadratic polynomial generating model is adopted in this section. Similar steps are applied to the modeling processes in this section. The optimal disturbance models are shown in Table 4. Persistence model (PM) is introduced as a reference with indicator (P). Table 5 presents the related wind prediction results. Figure 6, Figure 7, Figure 8 and Figure 9 are the wind speed forecast curves corresponding to each disturbance model in Table 5. The red curves, blue curves, and black curves respectively denote the initial wind predictions of BP neural network, the improved predictions of disturbance model, and the actual wind speed series.

Table 4. The optimal disturbance models when taking different Rayleigh number values.

Rayleigh Number	Polynomial Expression	Accumulated Generating Model	Error (RMSE)
0.7	f (x) = p1 · x2 + p2 · x + p3 p1 = −4.8249 × 10−5, p2 = 0.0919 p3 = 2.3845		0.7586
12	f (x) = p1 · x + p2 p1 = 0.0888, p2 = 5.1913		4.125
16	f (x) = p1 · x2 + p2 · x + p3 p1 = 2.2630 × 10−5, p2 = 0.0542 p3 = 7.8821		2.746
45	f (x) = p1 · x2 + p2 · x + p3 p1 = −1.0713 × 10−6, p2 = 0.0657 p3 = 2.5099		2.234

Table 4. The optimal disturbance models when taking different Rayleigh number values.

Rayleigh Number	Polynomial Expression	Accumulated Generating Model	Error (RMSE)
0.7	f (x) = p1 · x2 + p2 · x + p3 p1 = −4.8249 × 10−5, p2 = 0.0919 p3 = 2.3845		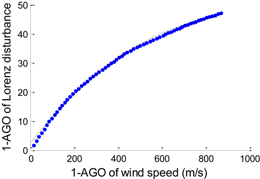0.7586
12	f (x) = p1 · x + p2 p1 = 0.0888, p2 = 5.1913		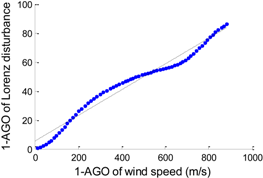4.125
16	f (x) = p1 · x2 + p2 · x + p3 p1 = 2.2630 × 10−5, p2 = 0.0542 p3 = 7.8821		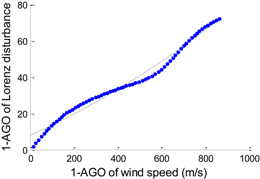2.746
45	f (x) = p1 · x2 + p2 · x + p3 p1 = −1.0713 × 10−6, p2 = 0.0657 p3 = 2.5099		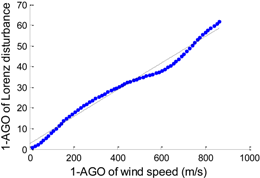2.234

Although the improvements are not exactly the same, these results have fully proved that all forms of Lorenz disturbance flow could contribute to the predicted level of a BP neural network. Table 5 presents another important discovery. The models could be easily grouped into two categories by the errors in Table 5. The forecasting accuracy tends to be high when the Rayleigh numbers equal 16 and 45. MAE and RMSE are respectively about 0.056 m/s and 0.078 m/s. The same quantities are about 0.14 m/s and 0.18 m/s when the Rayleigh numbers are equal to 0.7 and 12. Theoretically speaking, when the Rayleigh number is larger than 13.97, a Lorenz system has transient chaotic or chaotic solutions, whose disturbance forms are quite complex. This kind of complexity greatly helps to describe the real wind variations.

Table 5. MAE and RMSE results of wind speed prediction in February 2014.

Rayleigh Number	Wind Forecasting Error
	MAE (I) (m/s)	MAE (m/s)	MAE (P) (m/s)	RMSE (I) (m/s)	RMSE (m/s)	RMSE (P) (m/s)
0.7	0.5278	0.1447	0.4047	0.5429	0.1720	0.5201
12	0.7690	0.1397	0.7185	0.8035	0.1903	0.9870
16	0.6137	0.0581	0.4108	0.6139	0.0769	0.5230
45	0.5935	0.0535	0.4650	0.5989	0.0789	0.6486

Table 5. MAE and RMSE results of wind speed prediction in February 2014.

Rayleigh Number	Wind Forecasting Error
	MAE (I) (m/s)	MAE (m/s)	MAE (P) (m/s)	RMSE (I) (m/s)	RMSE (m/s)	RMSE (P) (m/s)
0.7	0.5278	0.1447	0.4047	0.5429	0.1720	0.5201
12	0.7690	0.1397	0.7185	0.8035	0.1903	0.9870
16	0.6137	0.0581	0.4108	0.6139	0.0769	0.5230
45	0.5935	0.0535	0.4650	0.5989	0.0789	0.6486

Besides, the forecasting errors of PM are used to evaluate the existing results. PM is especially suitable for short-term wind prediction [34]. In this paper, PM behaves better than the BP network on short-term wind prediction. Seen from Table 5, except for RMSE (P) when Rayleigh numbers are equal to 12 and 45, all errors of PM are smaller than the corresponding errors of a conventional BP network. Both MAE and RMSE of disturbance models greatly outperform PM and the BP neural network.

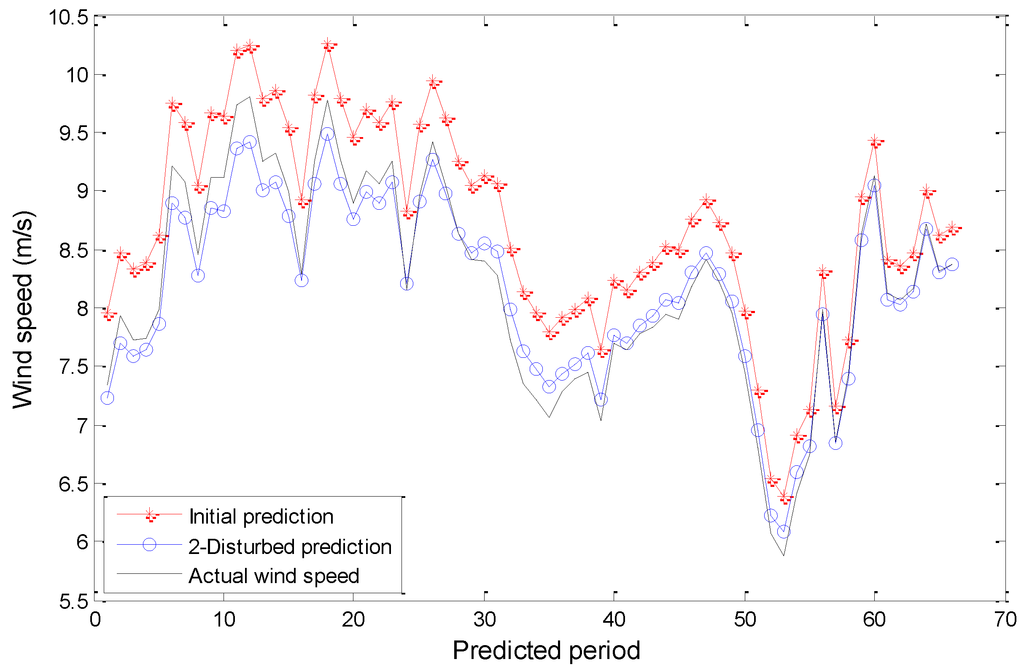
Figure 6. Wind speed forecasting results of the quadratic polynomial generating model when Rayleigh number equals 0.7.

Figure 6. Wind speed forecasting results of the quadratic polynomial generating model when Rayleigh number equals 0.7.

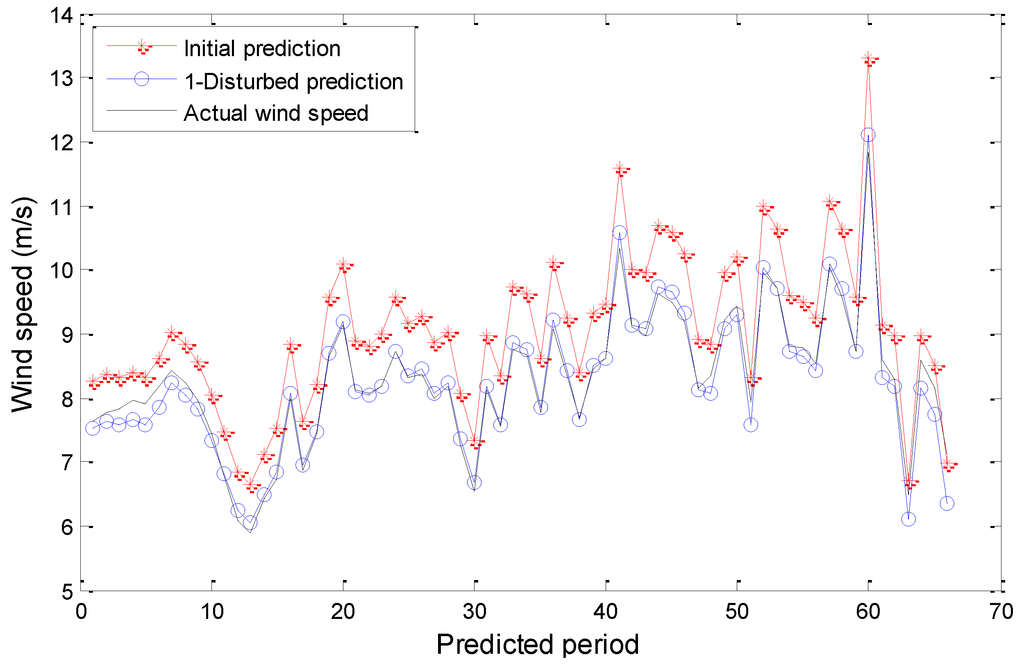
Figure 7. Wind speed forecasting results of the linear polynomial generating model when Rayleigh number equals 12.

Figure 7. Wind speed forecasting results of the linear polynomial generating model when Rayleigh number equals 12.

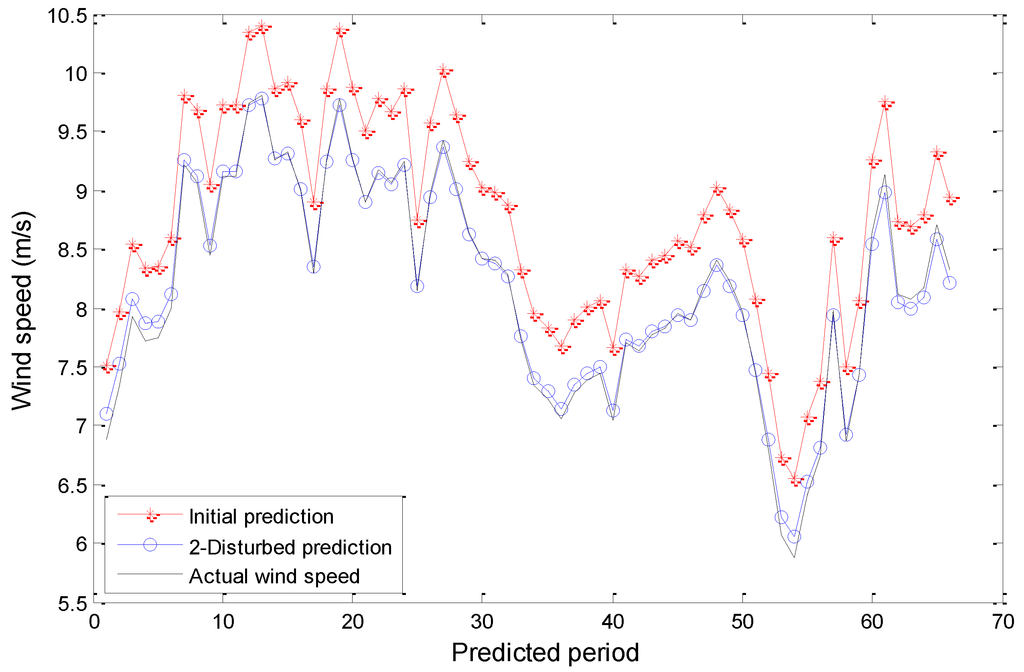
Figure 8. Wind speed forecasting results of the quadratic polynomial generating model when Rayleigh number equals 16.

Figure 8. Wind speed forecasting results of the quadratic polynomial generating model when Rayleigh number equals 16.

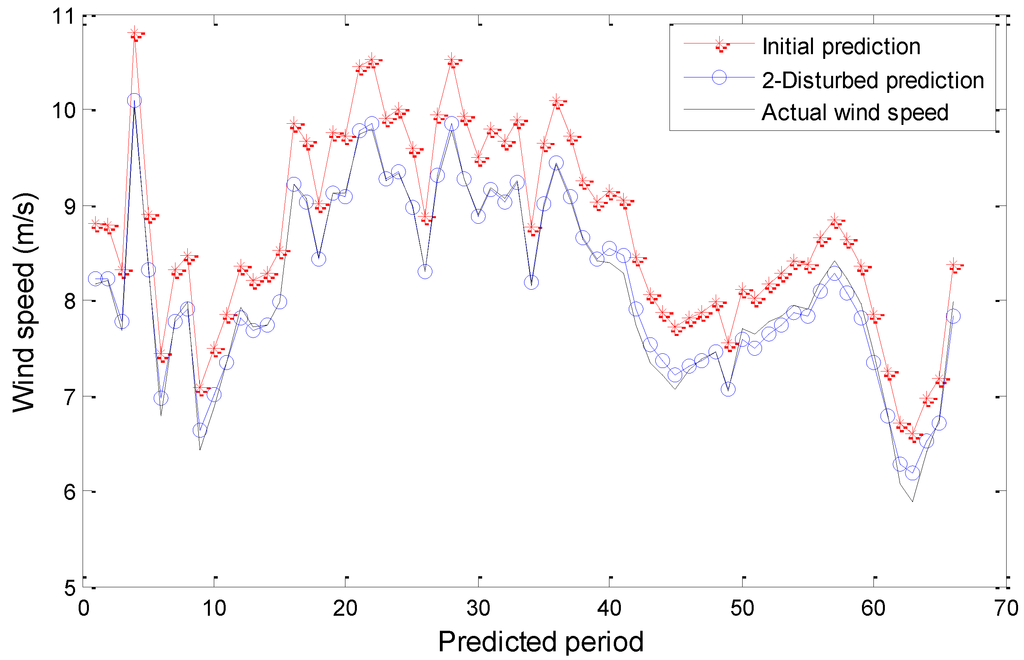
Figure 9. Wind speed forecasting results of the quadratic polynomial generating model when Rayleigh number equals 45.

Figure 9. Wind speed forecasting results of the quadratic polynomial generating model when Rayleigh number equals 45.

4. Conclusions

With the rapid development of the wind power industry, wind speed and power generation forecasting methods have become a focus of research in the fields of power systems and renewable energy. After a deeper study on the atmospheric dynamics system and wind prediction methods, in this paper we introduce the Lorenz system to reduce the negative impact of atmospheric disturbances on wind forecasting. Based on grey generating and an accumulated generating model, we propose a new wind disturbance model to improve the wind forecasting precision of a BP network. PM is also introduced for comparison. The best improvements (r = 45) in this paper are measured by the following two criteria: MAE with 0.0535 m/s and RMSE with 0.0789 m/s. In [32], the new proposed model IS-PSO-BP obtained good wind prediction performance based on different training numbers and data sources, whose MAE is 0.16 m/s and RMSE with 0.4123 m/s. In [34] its authors adopted low-quality measurements as exogenous information to refine the one-hour-ahead wind predictions. The smallest MAE of BP neural network in [34] is 0.18 m/s and RMSE with 0.2236 m/s.

All the above statistics and analysis suggest that we have proposed a valid and feasible wind disturbance model based on a BP neural network. This model fully considers the basic features of nonlinear atmospheric systems. Given an appropriate Lorenz disturbance sequence, it can be used to predict any type of wind speed series without seasonal limitations. Nevertheless there is no unified algorithm or principle at the moment for the selection of Rayleigh numbers. In addition, in view of the advantages and features of grey system theory [26,35,36], the application of the Lorenz system to the grey model is worthy of further exploration.