1. Introduction
Forecasted fossil fuel depletion and growing environmental concern have stimulated the development of vehicles with ever-higher efficiency. By combining a renewable energy storage mechanism within the conventional powertrain, hybrid vehicles achieve a significant improvement in fuel economy. The gains are expected from the increasing efficiency of component operations, the utilizing of regenerative braking energy, and the optimizing of engine operation.
In the context of longitudinal dynamics of vehicles, accelerating rate, grade-ability, and maximum vehicle velocity are typical performance criteria. With the purpose of evaluating fuel economy improvement, velocity tracking is the main performance criterion of hybrid vehicles. In conventional vehicles, velocity relates directly to engine speed through a rigid mechanical transmission system. Driving power relates to engine power in the same fashion. A typical cruising control system uses a standard Proportional-Integral/Proportional-Integral-Derivative (PI/PID) controller to estimate the desired throttle opening of the engine. Thus, cruising control of a conventional vehicle is a single-input-single-output control problem.
As a short- and mid-term solution, hybrid vehicles have aroused the attention of researchers and manufacturers all over the world. In the recent past, most commercialization efforts have focused on hybrid electric vehicles (HEVs). Several commercially available HEVs are passenger cars and light truck applications [
1]. Recent studies have indicated that hydraulic hybrid vehicles (HHVs) produce further advantages associated with the higher efficiencies of component operations and regenerative braking. Modern hydraulic pumps and motors have higher power density than their electric counterparts. Thus, a compact configuration of HHV can be achieved. In addition, hydraulic accumulators have the ability to operate at high frequencies and high rate of charging and discharging but a relatively low energy density in comparison with electro-chemical batteries. The relative low energy density of the hydraulic accumulator should be considered and required a carefully designed control strategy if the fuel economy potential is to be realized.
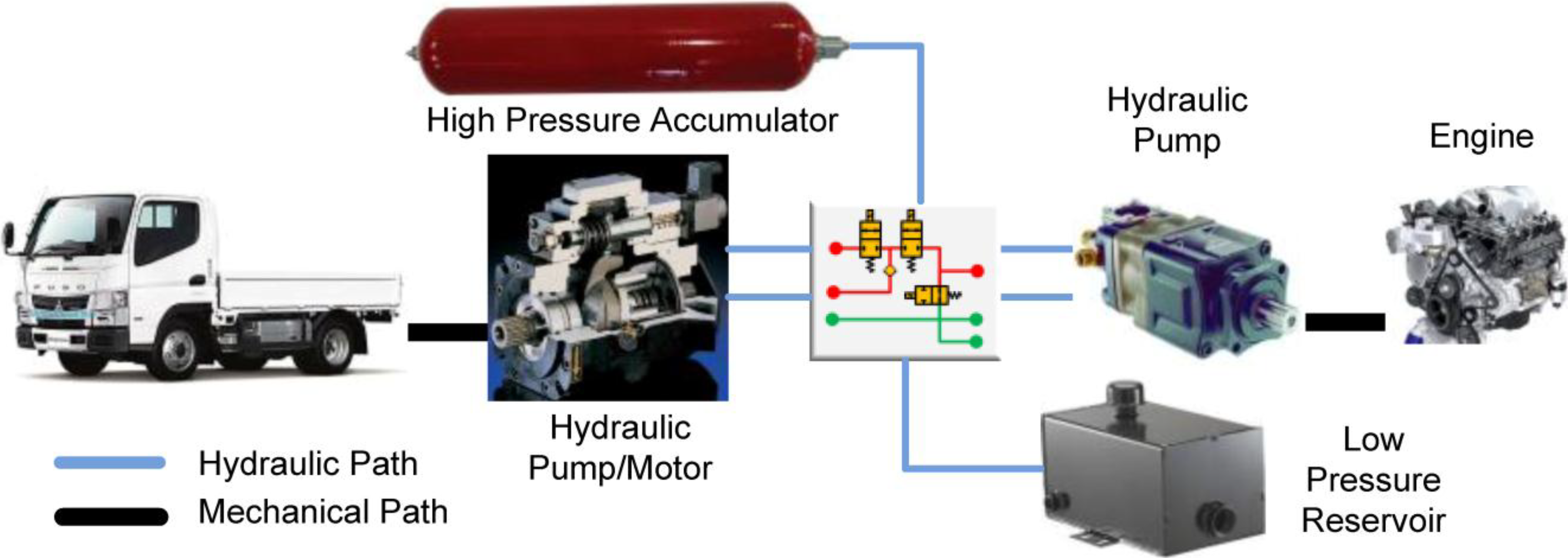
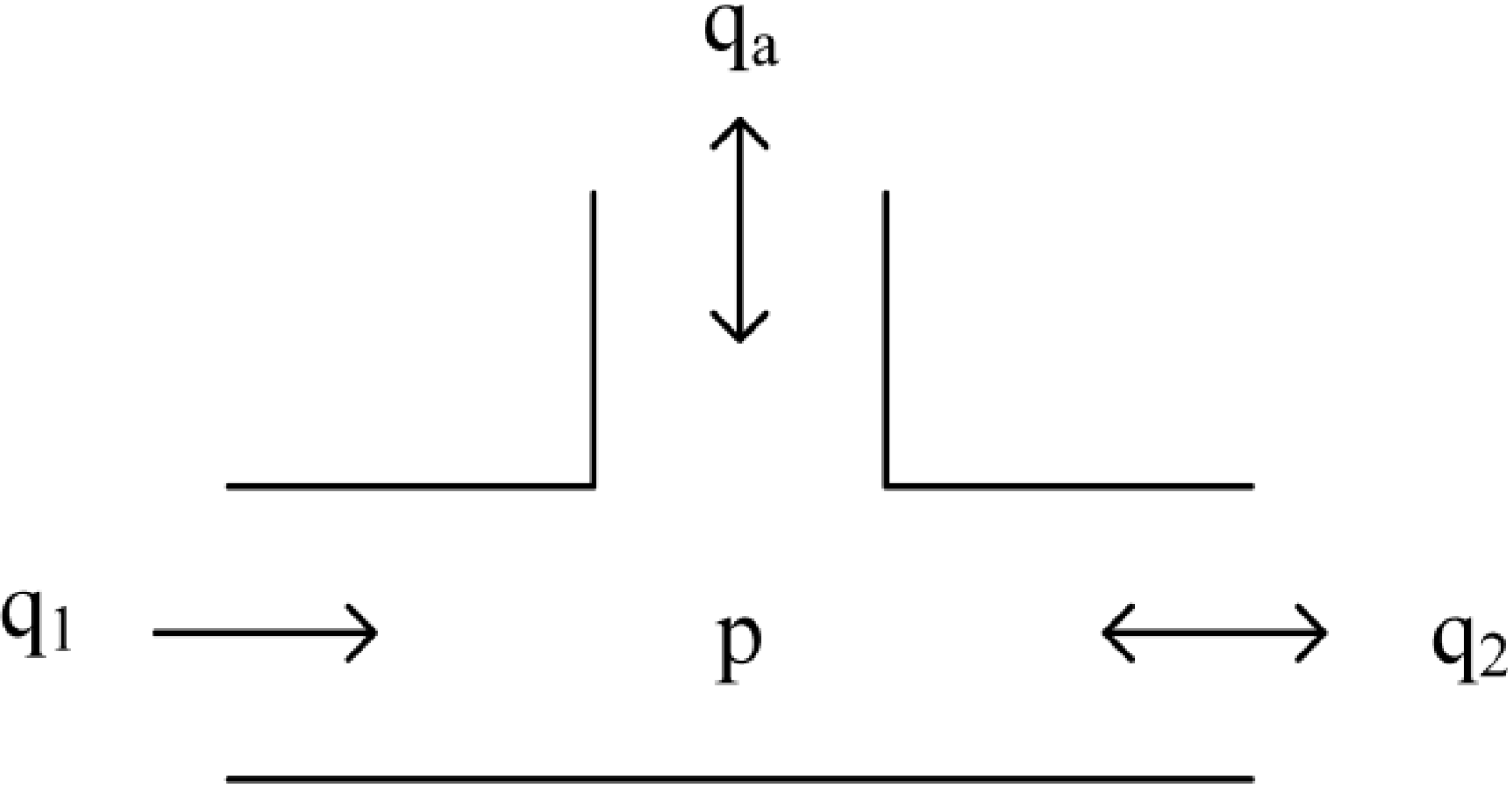
In a series hydraulic hybrid vehicle (SHHV), a hydrostatic transmission is used instead of a conventional mechanical transmission. Integrated hydraulic accumulator works as an on-board energy storage device in addition to the conventional engine. Therefore, a power demand can be satisfied by combining the two power sources in different manner. The power can be supplied by only the engine, only the accumulator, or both simultaneously. In addition, by decoupling the engine from the wheels, the series hydraulic hybrid architecture adds more degree-of-freedom to engine control. In this scenario, engine torque, engine speed, and accumulator pressure are control variables in addition to vehicle velocity. Due to physical constraints and input-output interactions, cruising control in an SHHV remains a challenge for standard PI/PID controllers.
Several approaches have been developed for cruising control in HHVs. A fuzzy logic controller (FLC) was developed by Matheson and Stecki [
2] for use in the parallel HHV. For a given power demand from drivers, the FLC determined the most suitable operating points of the engine corresponding to current states system. However, the resulting control law cannot be implemented in real-time system because ADVISOR is a backward-facing simulation.
In [
3], Wu
et al. divided the engine operating range into three zones by two constant-power lines: a low- and a high-power limit. This rule-based power management strategy improves fuel economy by forcing the engine to operate at higher efficiency. The optimal gearshift logic was achieved by applying dynamic programming (DP) technique. The DP results were extracted for use in improving the initial rule-based control strategy to achieve further improvement in fuel economy. However, how to regulate the engine to its reference power was not presented in this study. Similar problems were found in [
4,
5,
6].
In [
7], engine speed is controlled using a PI controller, which uses vehicle velocity error as the input. Engine torque is controlled by adjusting the control signal of the fuel rack. Control of vehicle velocity is not discussed explicitly in this study. In [
1], engine speed and vehicle velocity are controlled by individual PID controllers. Similarly, in [
8], three individual PID controllers are used to control engine torque, engine speed, and vehicle velocity to track to the corresponding references. Controller parameter tuning, input-output interaction and physical constraint are obstacles to this control approach.
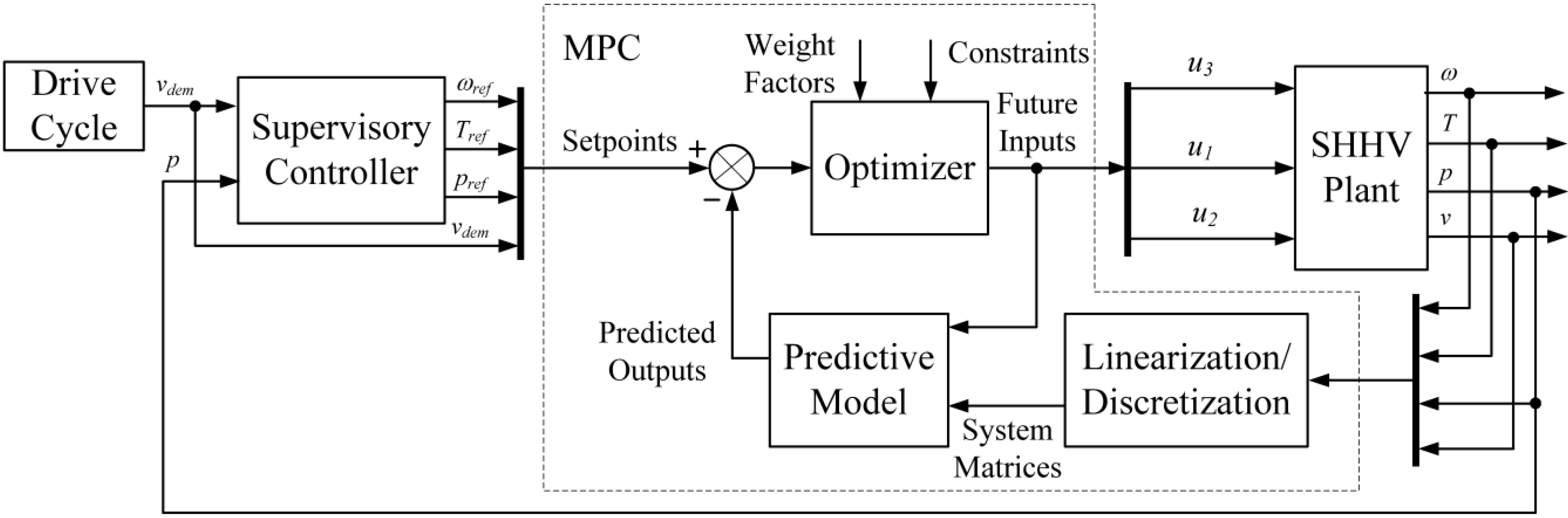
With the capability of applying constraints on both state and control inputs, model predictive control (MPC) is a widely recognized control methodology for complex systems. The controller estimates a future control trajectory that minimizes the quadratic cost function, which reflects the optimization goals, and is subject to the dynamic constraints of the system over a finite prediction horizon. Recently, MPC has been applied to solve the optimal control problem in power-split HEVs [
9,
10,
11], and in HHVs [
12,
13].
Deppen
et al. developed MPC-based energy management for a parallel HHV [
12] and a lightweight passenger SHHV [
13]. Engine throttle, pump displacement, and valve opening are the input variables. The optimal input is obtained by solving the optimal control, in which the objective function is to minimize the velocity tracking error and ensure that the actuators operate efficiently. Ignoring braking energy regeneration, limiting the engine to operate with constant torque and speed are restraints associated with these work.
This study presents a systematic illustration of a controller for the tracking problem in a hydraulic hybrid powertrain system using a linear MPC methodology. The remainder of this paper is divided into four sections.
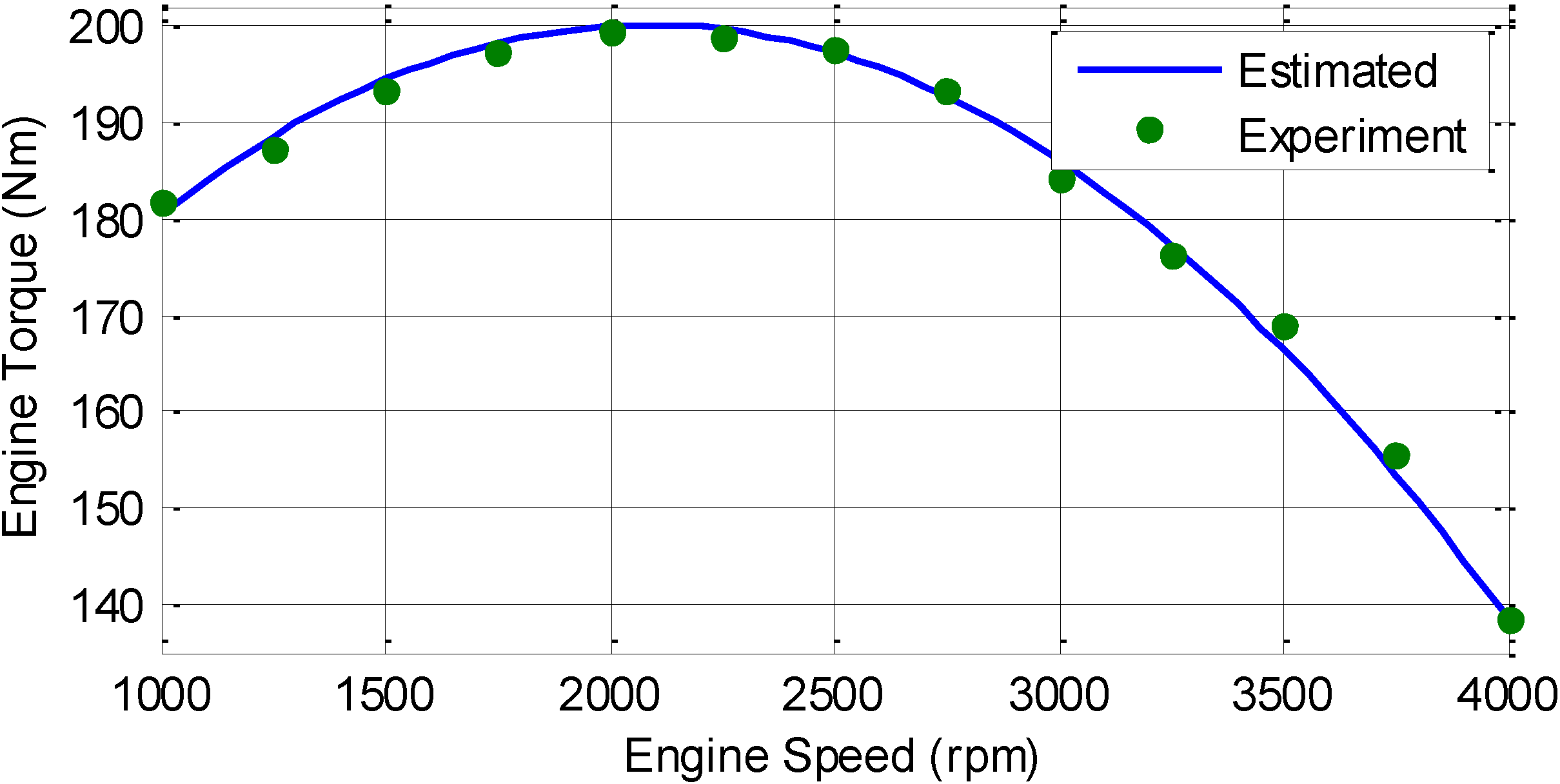
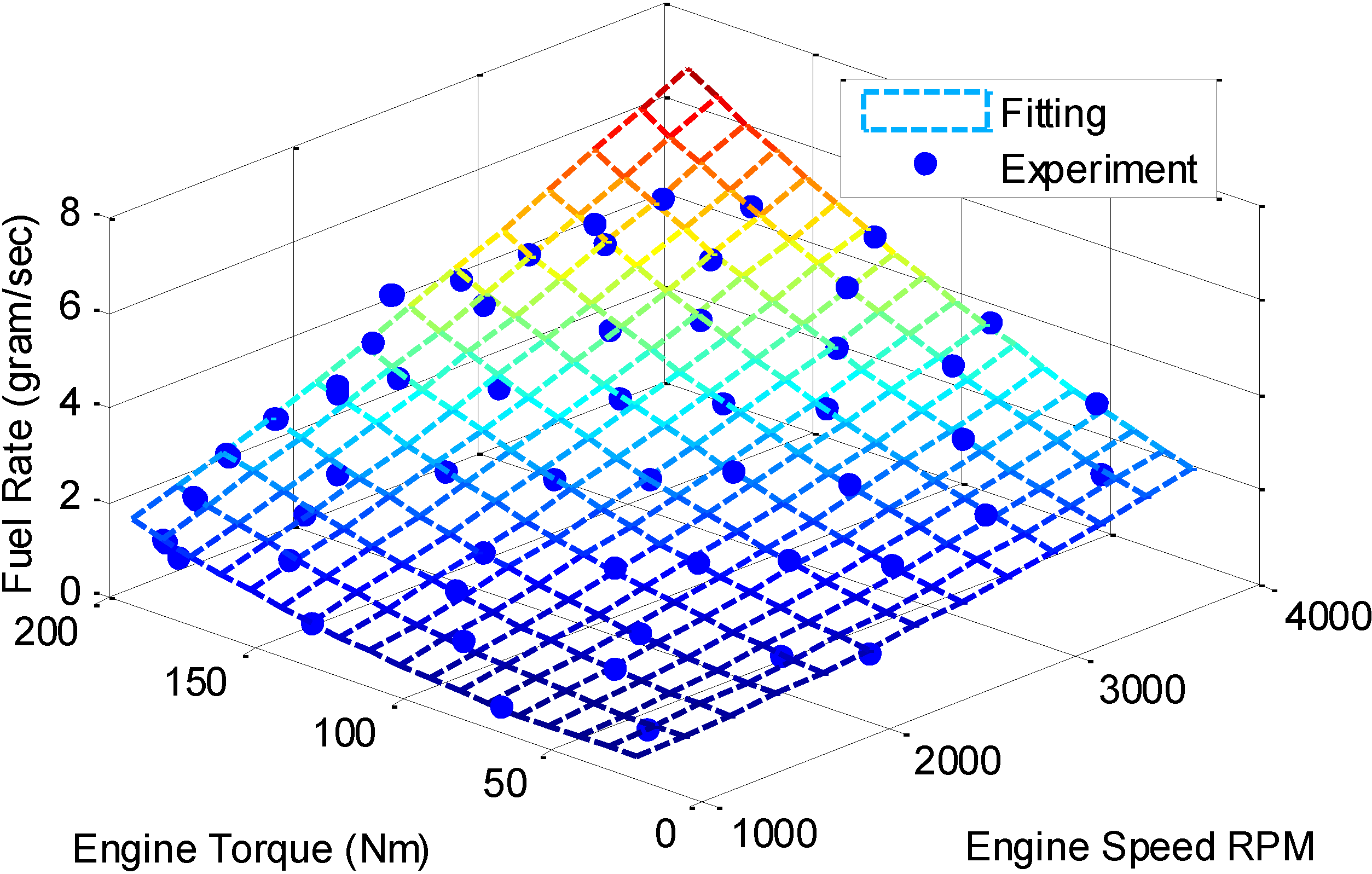
Section 2 describes the modeling configuration of the series hydraulic hybrid powertrain system. A high-fidelity nonlinear model of the SHHV was established in MATLAB/Simulink. This model is used as the plant in the simulation. In addition, a control-oriented model for the design of MPC was also derived in this section.
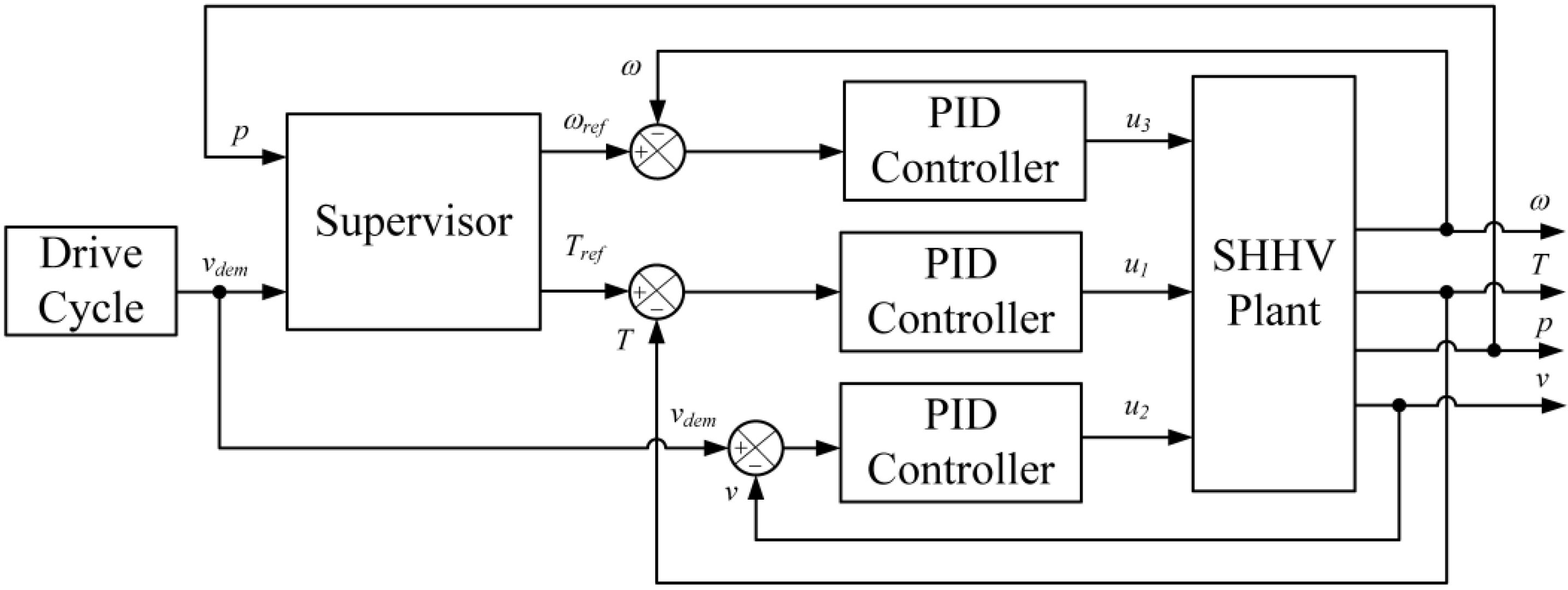
In
Section 3, the MPC-based control system is presented. The supervisory controller determines optimal reference values for engine speed, engine torque, and accumulator pressure to satisfy the demand for a given vehicle velocity. The MPC regulates the engine, the variable displacement pump, and the pump/motor to ensure that vehicle velocity, engine speed, engine torque, and accumulator pressure adhere to their corresponding reference values. At each time step, the MPC algorithm uses a linearized model to predict future output. A quadratic programming problem is then solved resulting optimal input vector, which minimizes the objective function with respect to physical and dynamic constraints. The objective function includes the penalty on the output tracking error and the rate of change of the control input. The effect of various output-weighting factors on system outputs is also investigated in this section.
Simulation and results are presented in
Section 4. The proposed MPC-based control scheme was evaluated under urban and highway driving conditions using Japan 1015 and Highway fuel economy test (HWFET) drive cycles. The proposed control scheme shows noticeable improvements over the PID-based control scheme. In
Section 5, important conclusions and further directions of study are discussed.
4. Simulation and Results
Design parameters of the standard MPC include penalty weights, prediction horizon, and control horizon. These parameters can be tuned using simulations and observations for the SHHV working under different driving conditions. In this simulation, the control interval of the MPC is set to 0.1 s, the prediction horizon is chosen twenty steps, and the control horizon is five steps. The weight factors for the control rate are γi=1,..,3 = 0.1.
To select suitable output weight factors, the system outputs are regulated to constant references. The vehicle was demanded to run at velocity of 90 kph. The engine is required to operate at 2500 rpm with 100 Nm torque output. The desired pressure in the accumulator is 250 bars. In the first case, the weigh factors are initially set at 0.1 for all outputs. In the second case, the weight factors are tuned to ensure vehicle velocity, engine torque, and engine speed are in accordance with the reference values. In the third case, the accumulator pressure is also regulated according to its reference value in addition to vehicle velocity, engine torque, and engine speed. Three sets of output weight factors and the corresponding output steady-state errors are summarized in
Table 3.
Table 3.
Weight factors and steady-state error.
Table 3.
Weight factors and steady-state error.
| Case Study | Case 1 | Case 2 | Case 3 |
|---|
| Weight Factor λ1,...,4 | 0.1, 0.1, 0.1, 0.1 | 0.1, 0.1, 0, 100 | 0.5, 1, 50, 1000 |
| Steady-State Error [rpm, Nm, bar, kph] | 5.71, 4.02, 1.43, 15.75 | 8.74, 4.06, 129.85, 0.46 | 14.30, 3.99, 0.90, 0.40 |
| Relative Steady-State Error (%) | 0.23, 4.02, 0.57, 17.50 | 0.35, 4.06, 51.94, 0.51 | 0.57, 3.4, 0.36, 0.4 |
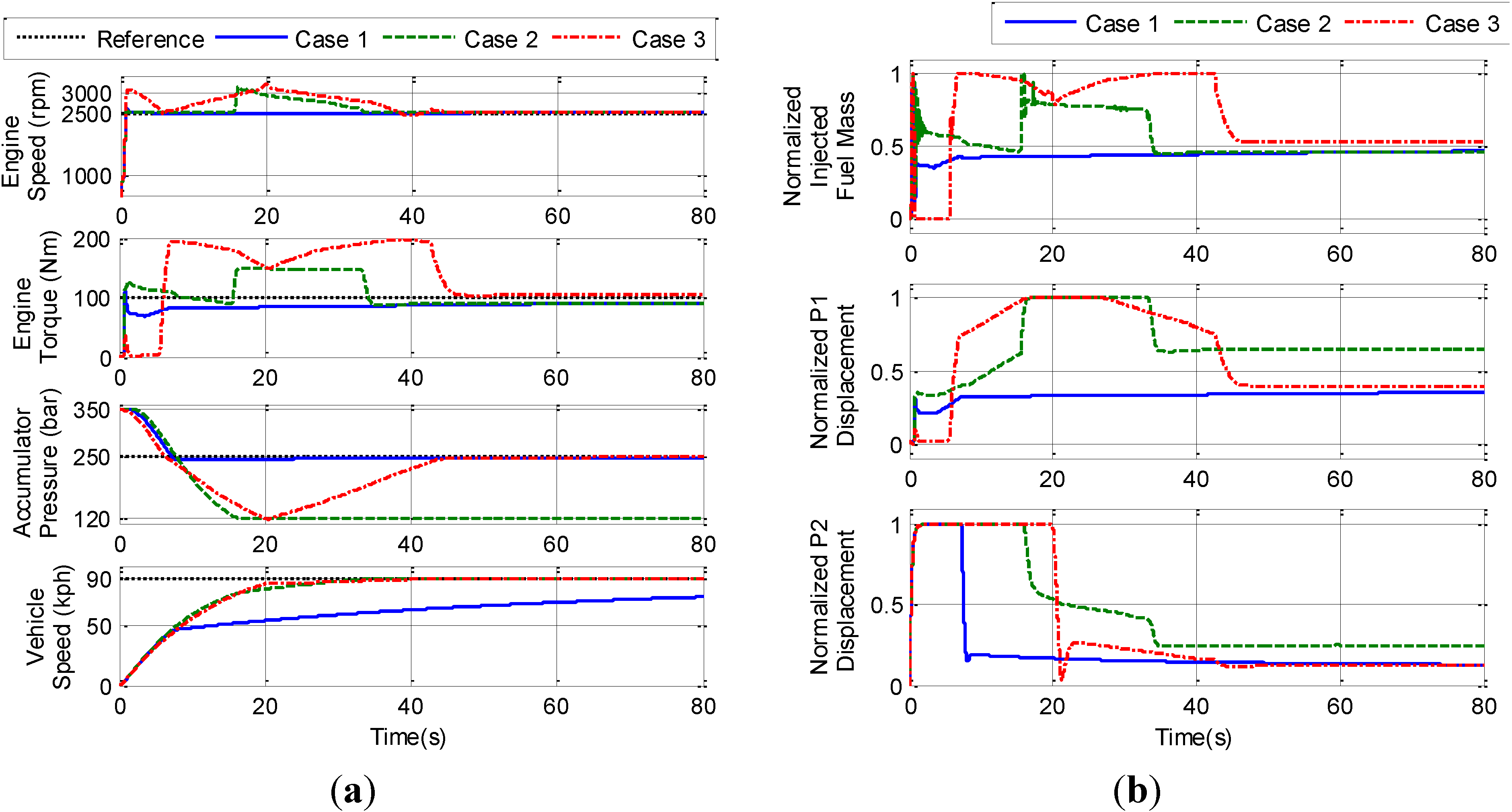
The behavior of the system under various weight factors is presented in
Figure 9. In Case 1, engine speed reaches its reference value after just a short time. Engine torque approaches its reference value with some steady-state error. Accumulator pressure also reaches its reference value after 8 s. However, vehicle velocity cannot reach its reference value during the simulation time. In Case 2, the weight factor on the vehicle velocity is increased. The penalty on accumulator pressure is released. Vehicle velocity approaches to its reference value after 20 s. At 20 s, pressure in accumulator reaches its minimum threshold. Up to that point, the engine generated more power to fulfil the power demand. Hence, by handling this constraint, the MPC-based control system prevents the depletion of pressure in the accumulator. In Case 3, the four outputs are controlled to ensure that they approach their reference values. The results indicate that selecting suitable weight factors enables the MPC-based control system to designate various outputs in accordance with their reference values.
Focusing on regulating vehicle velocity and controlling engine, the output weight factors used in Case 2 were selected for simulations. With this approach, the controller regulates the vehicle velocity in accordance to desired driving cycles and controls the engine to operate at desired operating points.
Figure 9.
Effect of weight factors on system performance: (a) Outputs; and (b) Inputs.
Figure 9.
Effect of weight factors on system performance: (a) Outputs; and (b) Inputs.
To evaluate the effectiveness of the proposed control system, two typical driving cycles, the Japan 1015 and the HWFET, were selected as reference trajectories. The Japan 1015 is used in Japan for emissions and fuel economy testing for light duty vehicles. This driving test presents typical stop-and-go patterns found in urban driving condition, which is an attractive application for HHVs. The HWFET, a chassis dynamometer-driving schedule developed by the US Environmental Protection Agency, is used to determine the fuel economy of light duty vehicles under highway condition.
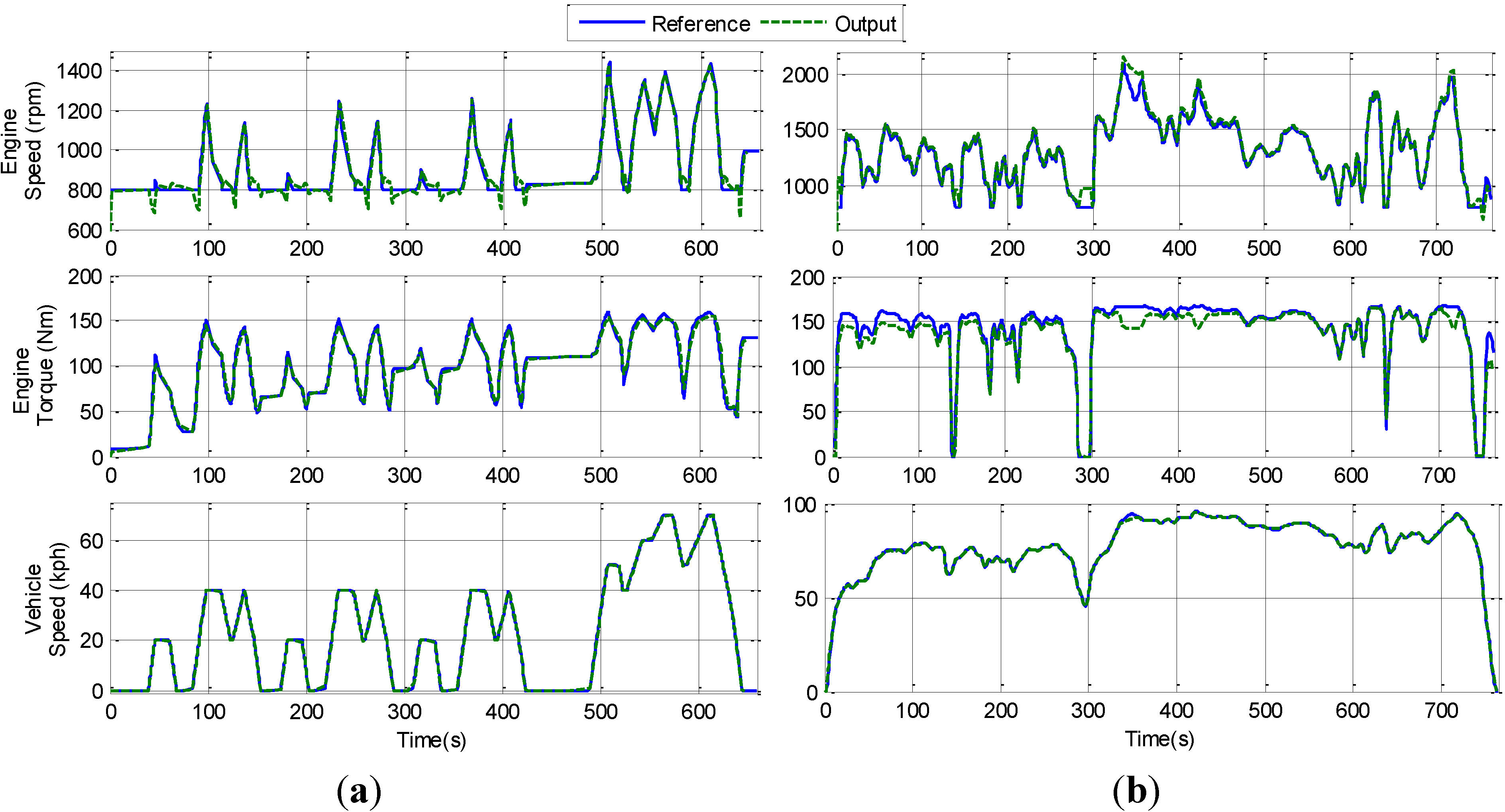
The behavior of the SHHV with the proposed control system are shown in
Figure 10. The simulation results indicate that vehicle velicoty as wel as engine torque, engine speed, and accumulator pressure approach their reference values. As shown in the figures, the constraints on system inputs and outputs are internally handled by the controller without the need for any saturated component. Since the priority of tracking vehicle velocity is higher than tracking other outputs, a certain degree of tracking errors for engine speed, engine torque, and accumulator pressure is considered acceptable.
Figure 10.
System behaviors: (a) Under Japan 1015; and (b) Under HWFET.
Figure 10.
System behaviors: (a) Under Japan 1015; and (b) Under HWFET.
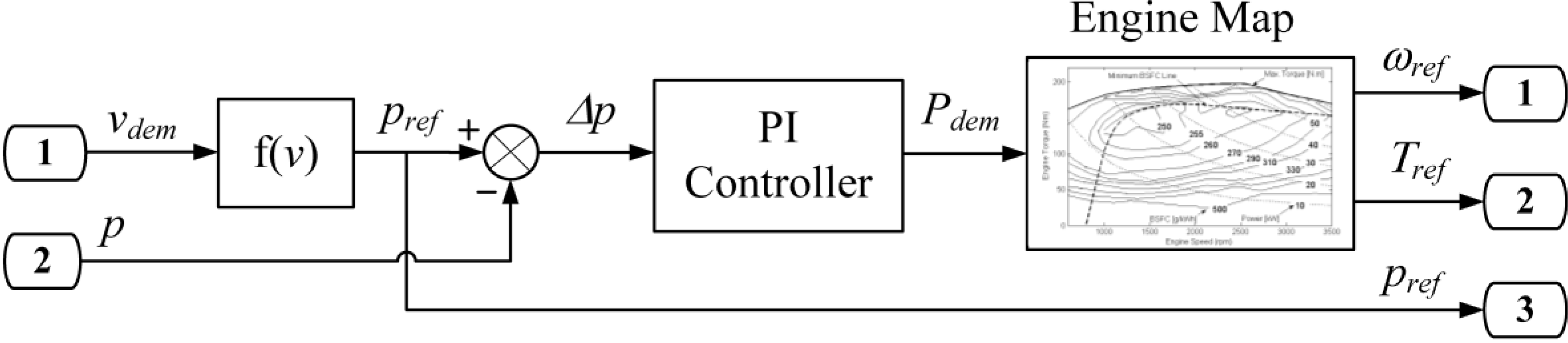
For comparison, a PID-based control system, developed in a previous work [
8], is used as a baseline. A diagram of this control scheme is shown in
Figure 11. In this approach, three individual PID controllers are used to generate control signals. The first PID uses engine speed error as the input to calculate the control signal for the injected fuel mass of the engine,
u3. The second PID adjusts the displacement of the pump,
u1, to achieve the desired engine output torque. The desired vehicle velocity is obtained by adjusting the displacement of the pump/motor,
u2. The supervisor determines the reference values for engine speed and engine torque according to the demand vehicle velocity and current pressure in the accumulator.
In an SHHV, the pressure of the accumulator must be maintained within a working range. The minimum working pressure must exceed the pre-charged pressure in order to avoid depletion. In this work, the pre-charge pressure was 100 bar, the minimum working pressure was 120 bar, and the maximum working pressure was 350 bar.
Figure 11.
Schematic of the PID-based control system.
Figure 11.
Schematic of the PID-based control system.
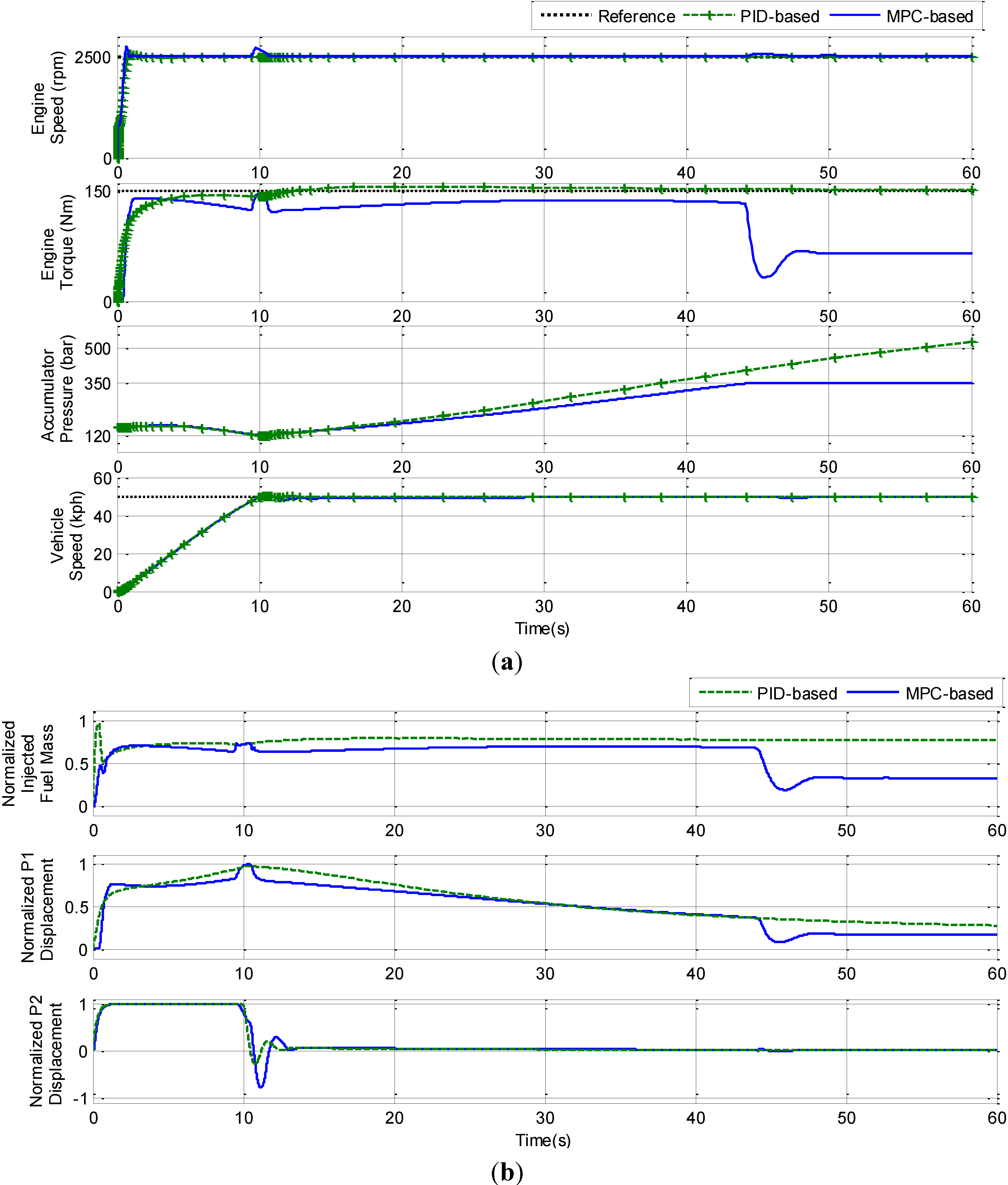
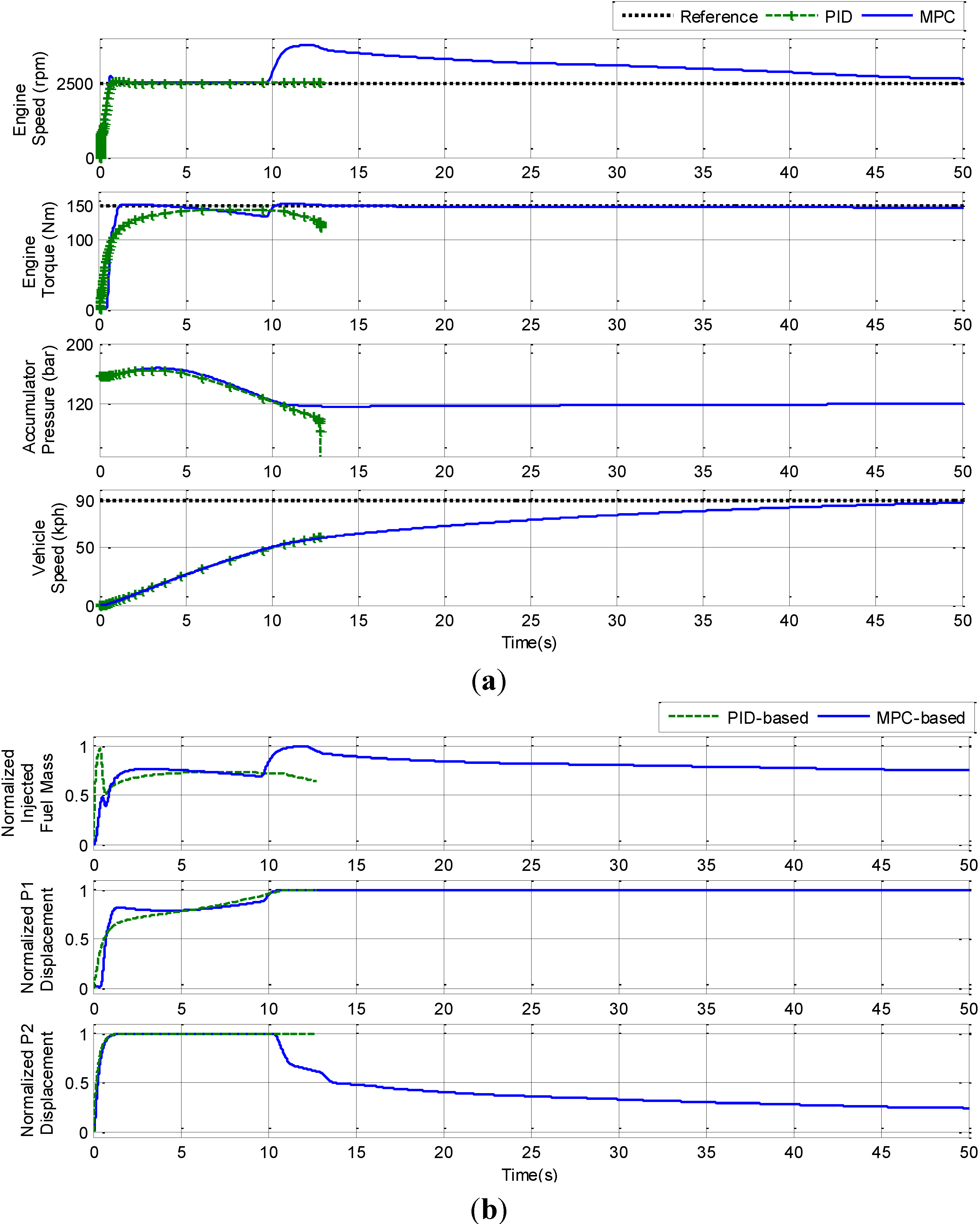
To evaluate the capability of constraint handling of the control systems, the SHHV was tested under two different sets of conditions, low and high target velocities. In both cases, the engine was demanded to operate at h the angular speed of 2500 rpm and the torque of 150 Nm. The target velocities were 50 and 90 kph, respectively. The behavior of the proposed and the baseline systems for these two cases are presented in
Figure 12 and
Figure 13, respectively.
Figure 12.
The behaviors of the SHHV with a low speed demand: (a) Outputs; and (b) Inputs.
Figure 12.
The behaviors of the SHHV with a low speed demand: (a) Outputs; and (b) Inputs.
Figure 13.
The behaviors of the SHHV with a high speed demand: (a) Outputs; and (b) Inputs.
Figure 13.
The behaviors of the SHHV with a high speed demand: (a) Outputs; and (b) Inputs.
It can be seen that the inputs and outputs of the SHHV with PID-based and MPC-based control systems are initially quite similar. Difference only becomes apparent when pressure in the accumulator reaches its threshold. As can be seen in
Figure 12, after the vehicle reaches the target velocity, the demand power becomes less than the engine power demand. The extra power is absorbed by the accumulator, which causes a gradual increase in pressure. In the PID-based control system, pressure in the accumulator continues increasing even after the maximum threshold has been reached (at 38.24 s). In contrast, the MPC-based control system reduces the engine injected fuel mass and pump displacement, such that the engine output power is reduced until it is equal to the demand. Thus, no additional power is converted for storage in the accumulator.
From
Figure 13, it can be seen that after engine speed and engine torque have reached their reference values, engine power reaches a steady state. When the power demand of the vehicle exceeds the engine output power, the accumulator must make up the deficit. With the PID-based control system, accumulator pressure continues decreasing until the system failure at 12.76 s. Meanwhile, with the MPC-based control system, after 9.75 s, the injected fuel mass of the engine and the displacement of the pump were increased, such that the engine generated additional output power to satisfy the power demand. This strategy can help to avoid the system failure caused by the depletion of pressure in the accumulator.
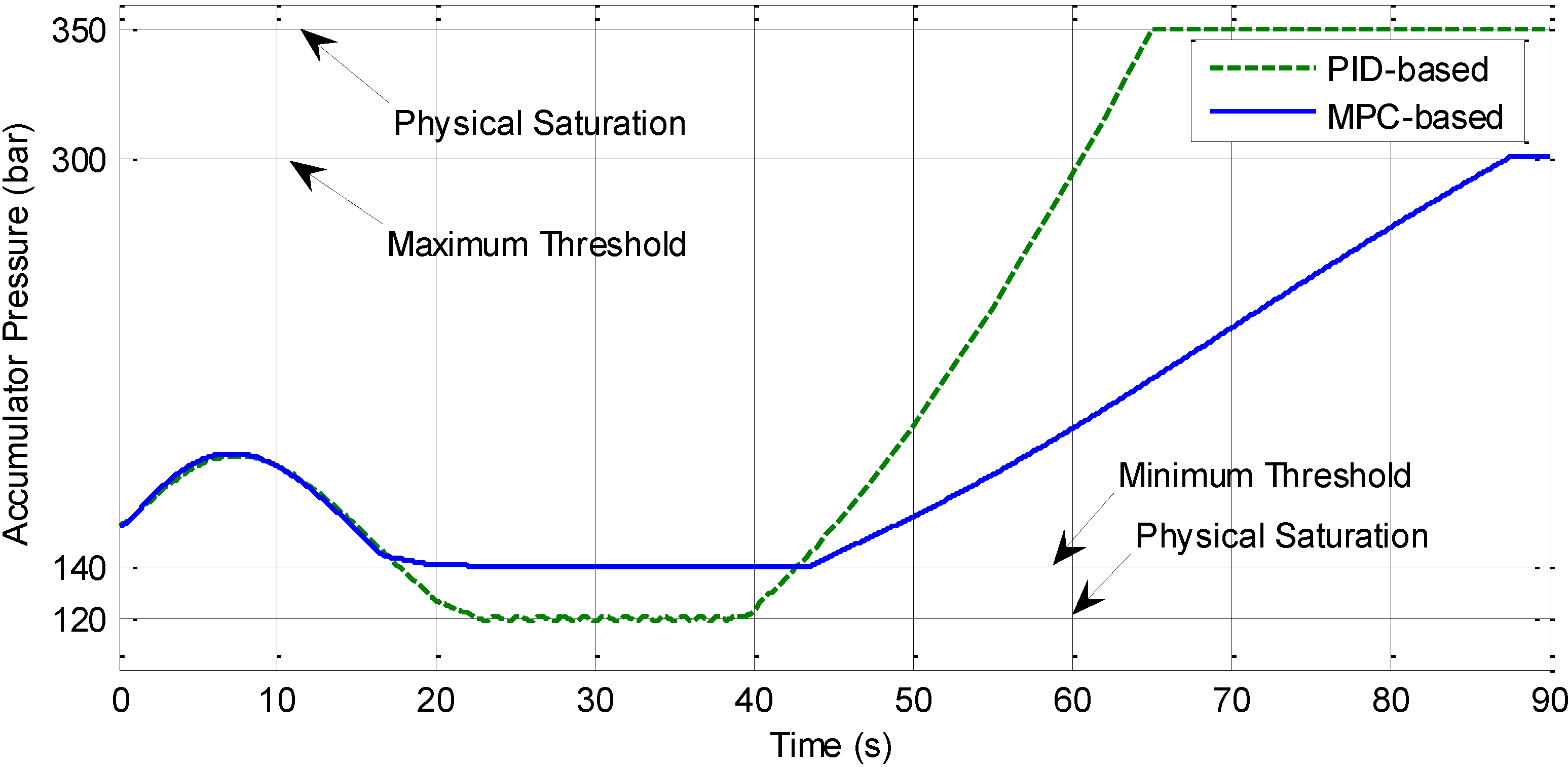
The behavior of the PID-based and MPC-based systems with physical saturation and state constraints is presented in
Figure 14. In this case, the physical limitation of the accumulator pressure are 120 and 350 bar respectively. The minimum working pressure, 120 bar, is used to avoid the depletion of the accumulator while the high-threshold, 350 bar, is the maximum working condition of the accumulator. In addition, the pressure of the accumulator was maintained greater than 140 bar to ensure that the system can support the driving torque in any condition. The maximum threshold, 300 bar, is added to make sure that the accumulator reserves enough volume for recovering braking energy. The figure shown that in the PID-based system, pressure in the accumulator is maintained within the working range. However, using additional compensated valves will reduce efficiency of hydraulic system. In addition, the engine produced unnecessary power. When using the MPC-based control system, constraints on accumulator pressure are handled by the controller itself, thereby increasing the efficiency of the components.
Figure 14.
Systems behaviors with physical saturations and state constraints.
Figure 14.
Systems behaviors with physical saturations and state constraints.
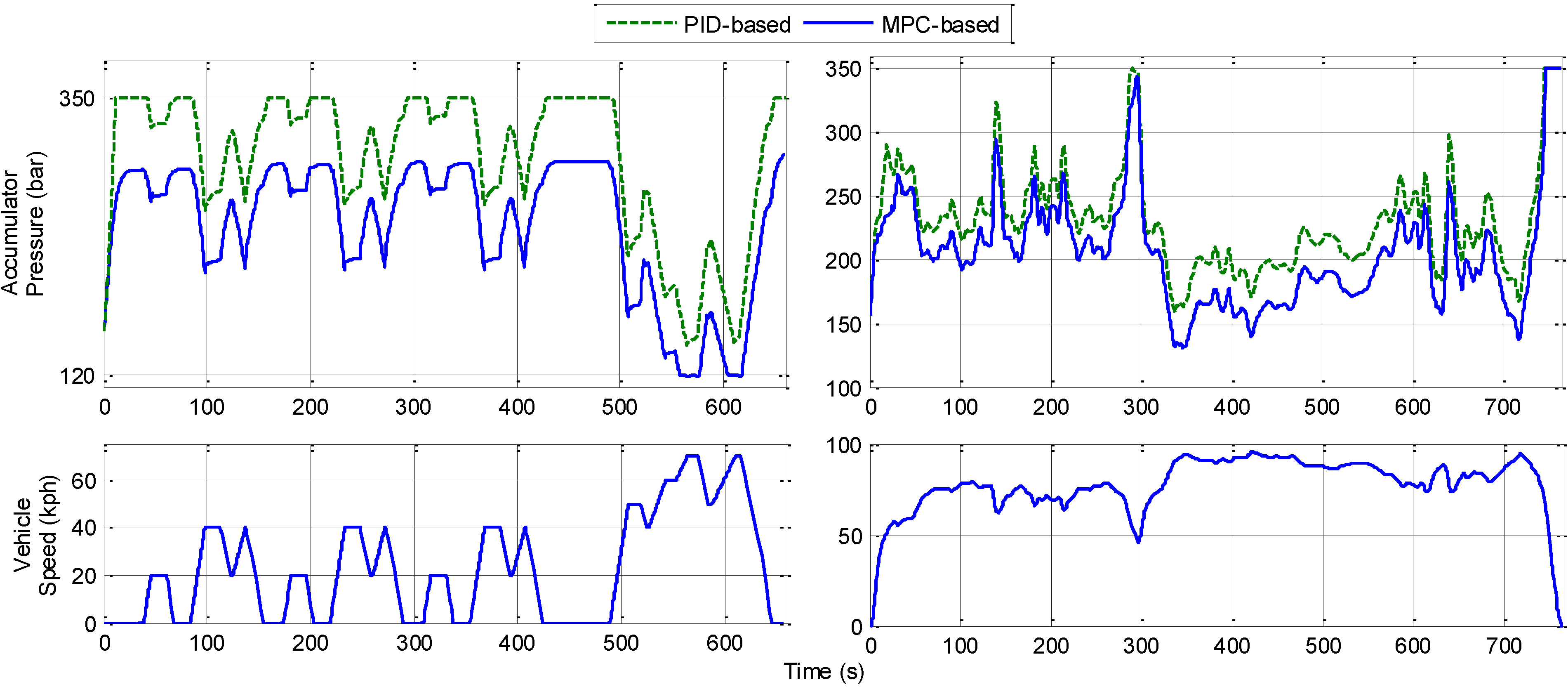
The performance of the SHHV with PID-based and MPC-based is presented in
Figure 15. The results indicate that the accumulator pressure of the SHHV with the MPC-based control system is maintained at a lower value than that of the SHHV with the PID-based control system. In this way, unnecessary energy conversion from the engine to the accumulator is avoided, Thereby increasing the volume available for the storage of energy from regenerative braking.
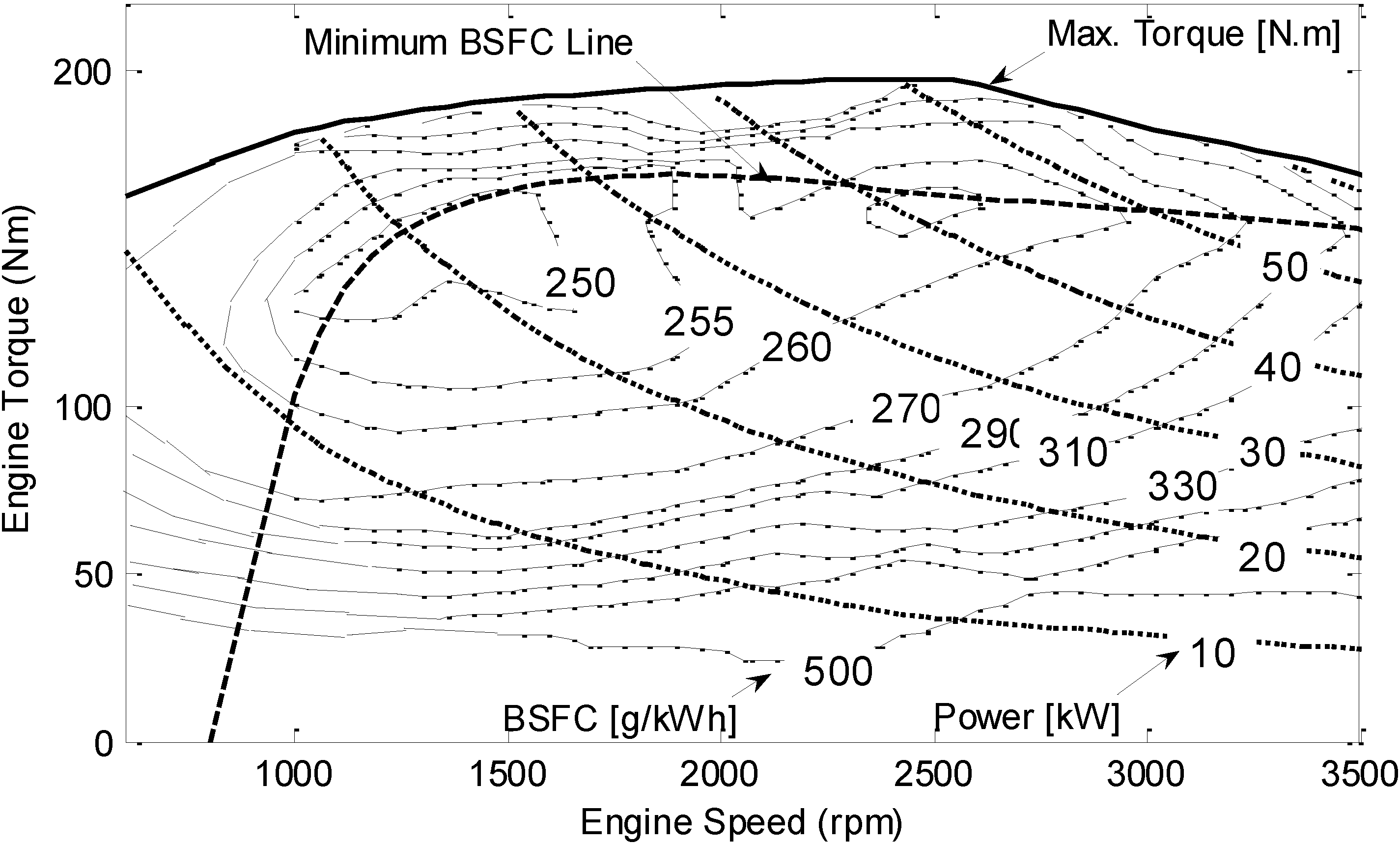
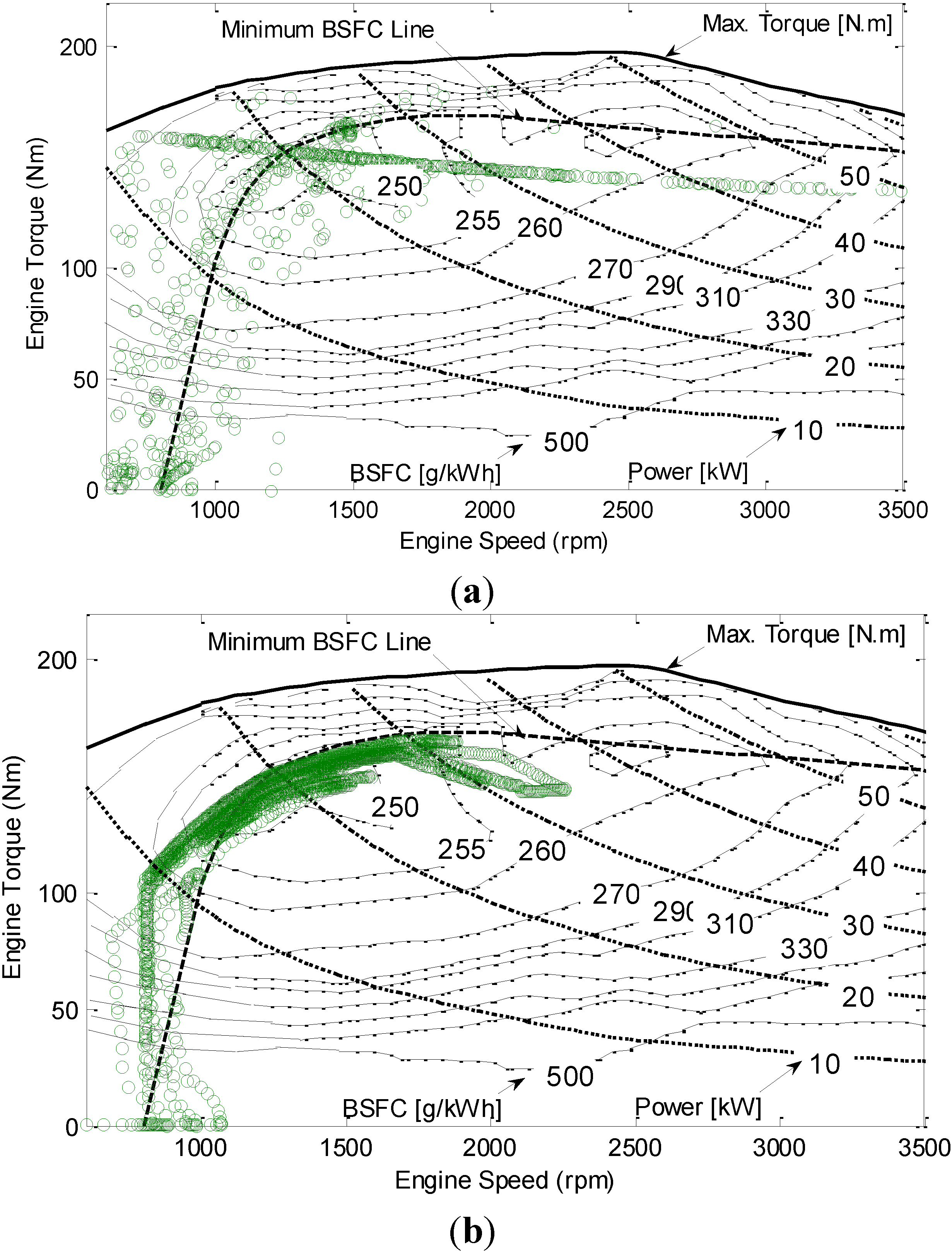
Figure 16 presents the distribution of the engine operating points under HWFET with the baseline and the proposed control schemes. It can be seen that the MPC-based control scheme keeps the engine operating in the sweet-spot region or along the minimum brake-specific-fuel-consumption (BSFC) line. In this way, the total fuel consumption of the engine is reduced and the fuel economy of the system is improved.
Figure 15.
System behaviors under Japan 1015 driving cycle with MPC-based and PID-based control scheme.
Figure 15.
System behaviors under Japan 1015 driving cycle with MPC-based and PID-based control scheme.
Figure 16.
Engine operating points visitation on the BSFC map under HWFET: (a) Using the PID-based control system; and (b) Using the MPC-based control system.
Figure 16.
Engine operating points visitation on the BSFC map under HWFET: (a) Using the PID-based control system; and (b) Using the MPC-based control system.
The fuel economy of the system using MPC-based and PID-based control system was evaluated under Japan 1015 and HWFET driving cycles. For each type of driving cycle, the simulation was conducted five times corresponding to the number of repetitions of the cycle from 1 to 5. The average fuel economy is listed in
Table 4.
Table 4.
Average fuel economy with different control schemes.
Table 4.
Average fuel economy with different control schemes.
| Control Scheme | Average Fuel Economy (km/L) |
|---|
| Japan 1015 | HWFET |
|---|
| PID-based | 11.36 | 10.64 |
| MPC-based | 15.35 | 11.75 |
The results indicate that by capturing and reusing the braking energy, the SHHV achieves higher fuel economy when working under urban than under highway conditions. The ability of the MPC-based control scheme to manage the maximum and minimum thresholds of accumulator pressure ensures that the accumulator reserves sufficient volume for regenerative braking and prevents the system failure arising from the depletion of pressure in the accumulator. In contrast, preventing depletion of pressure in the accumulator under the PID-based control scheme requires that the minimum threshold for accumulator pressure be set high. This causes the engine to shift to a higher power region and limits the volume available for regenerative braking. The effect can be considerable when the system is working under a start-stop-and-go pattern such as Japan 1015. Thus, under Japan 1015, the MPC-based system improves fuel economy by 35% over that of the PID-based system. An improvement of only 10.43% is obtained under HWFET.