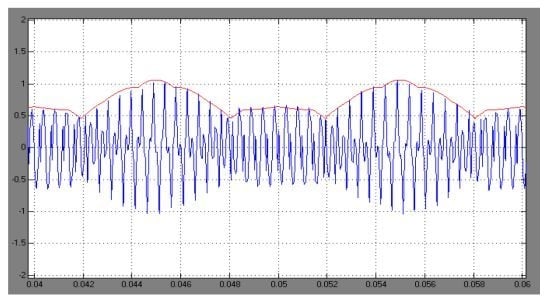
Analysis of Peak-to-Peak Current Ripple Amplitude in Seven-Phase PWM Voltage Source Inverters
Abstract
:1. Introduction
2. Evaluation of Peak-to-Peak Current Ripple Amplitude
2.1. Load Model and Current Ripple Definitions
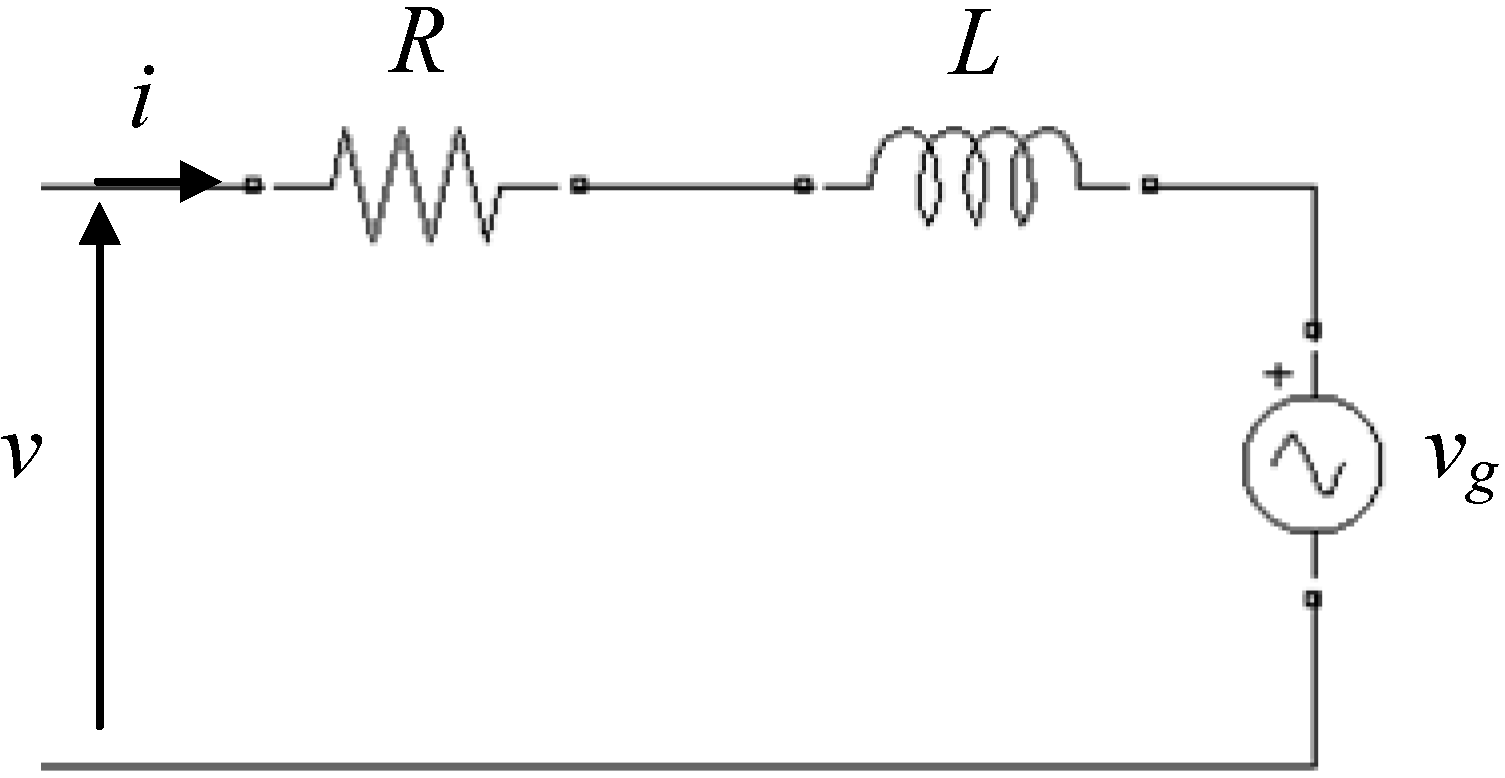
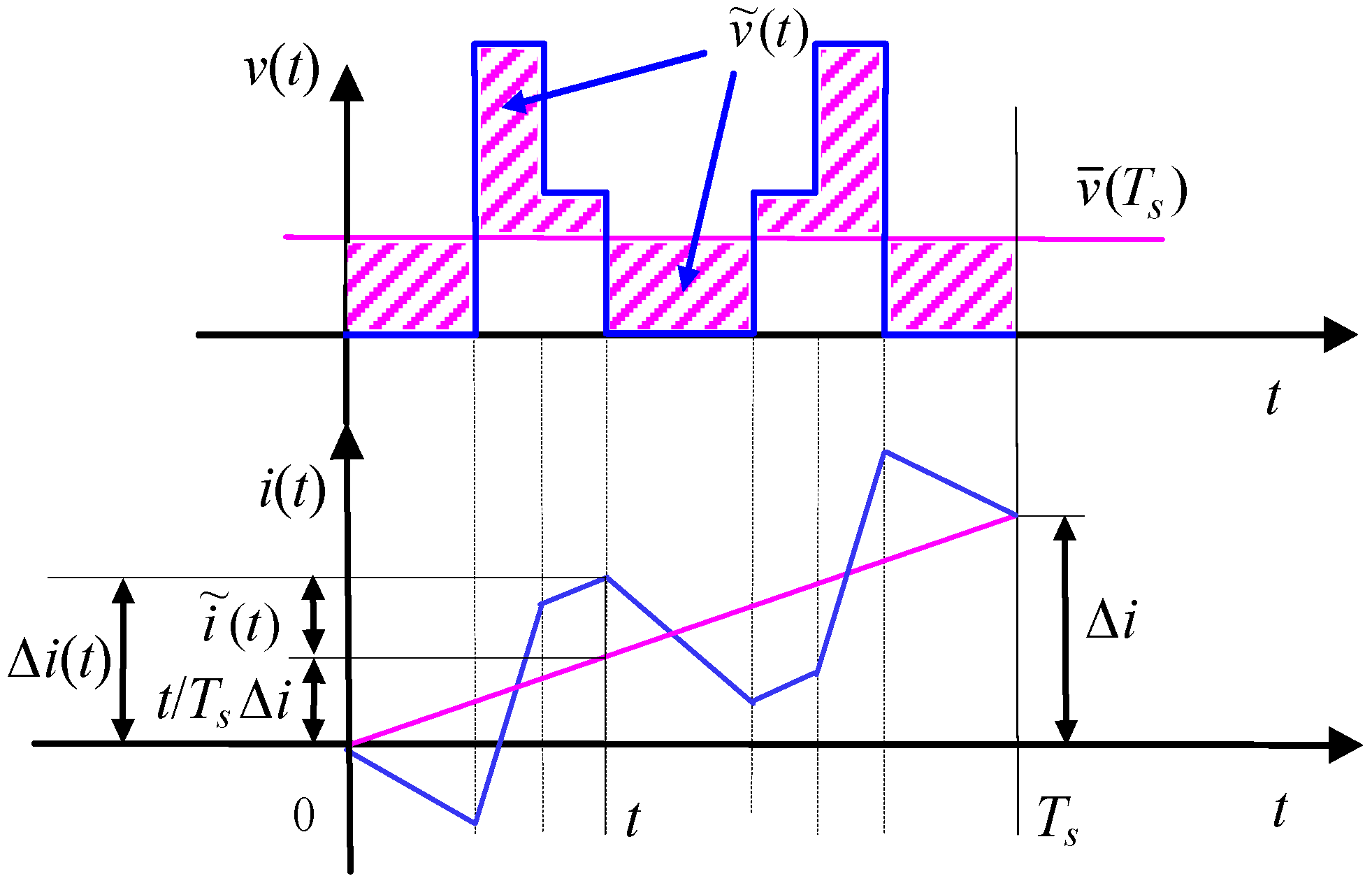
2.2. Multiple Space Vectors and PWM Equations
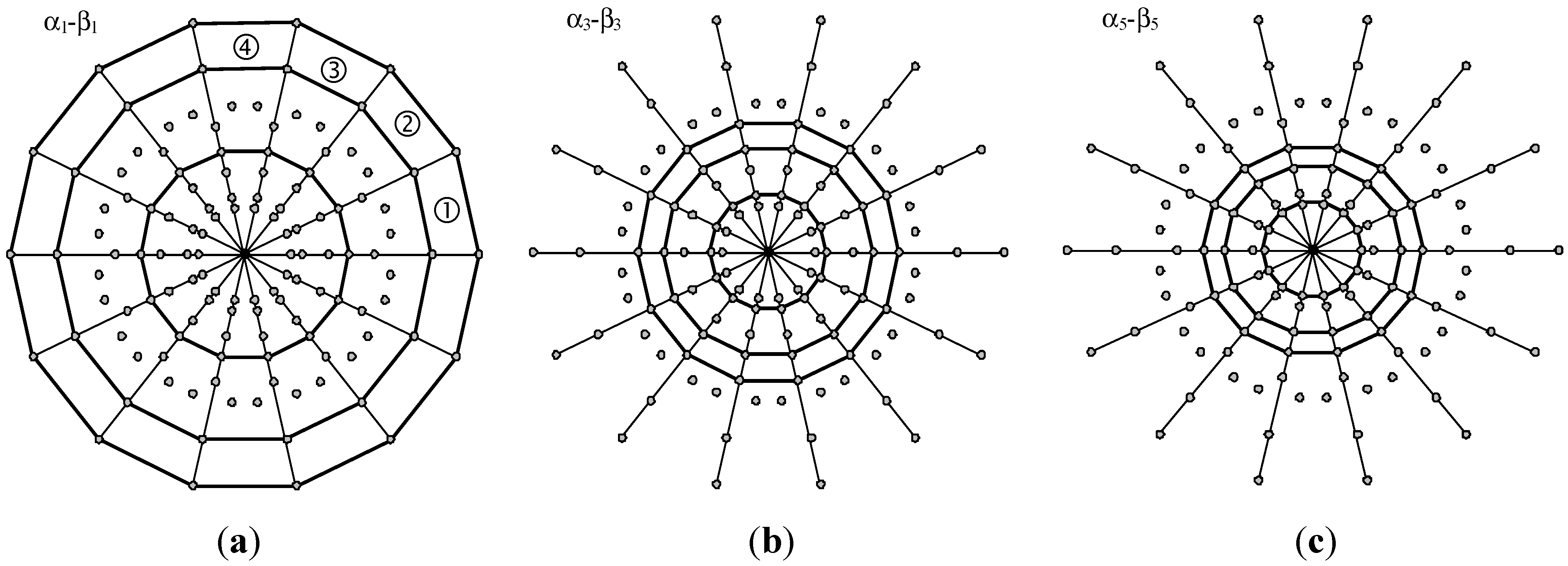

2.3. Ripple Evaluation
2.3.1. Evaluation in the First Sector

2.3.2. Evaluation in the Second Sector
- In the first situation, yellow area (solid orange line in Figure 5b), can be determined as in the previous sub-case by considering the switch configurations {00} and {20} with the corresponding application intervals t0/2 and t6, leading to Equations (33) and (34);
- In the second situation, green area (dashed orange line in Figure 5b), can be determined by considering the switch configurations {7F} and {7B} with the corresponding application intervals t0/2 and t1, leading to:
- In the first situation, yellow area (solid green line in Figure 5b), can be determined as in the previous sub-case by considering the switch configurations {00} and {20} with the corresponding application intervals t0/2 and t6, leading to Equations (33) and (34);
- In the second situation, violet area (dashed green line in Figure 5b), can be determined by considering the switch configurations {7F}, {7B}, and {79}, with the corresponding application intervals t0/2, t1, and t2, leading to:
2.3.3. Evaluation in the Third Sector

2.3.4. Evaluation in the Fourth (Half) Sector
2.4. Peak-to-Peak Current Ripple Diagrams

2.5. Maximum of the Current Ripple
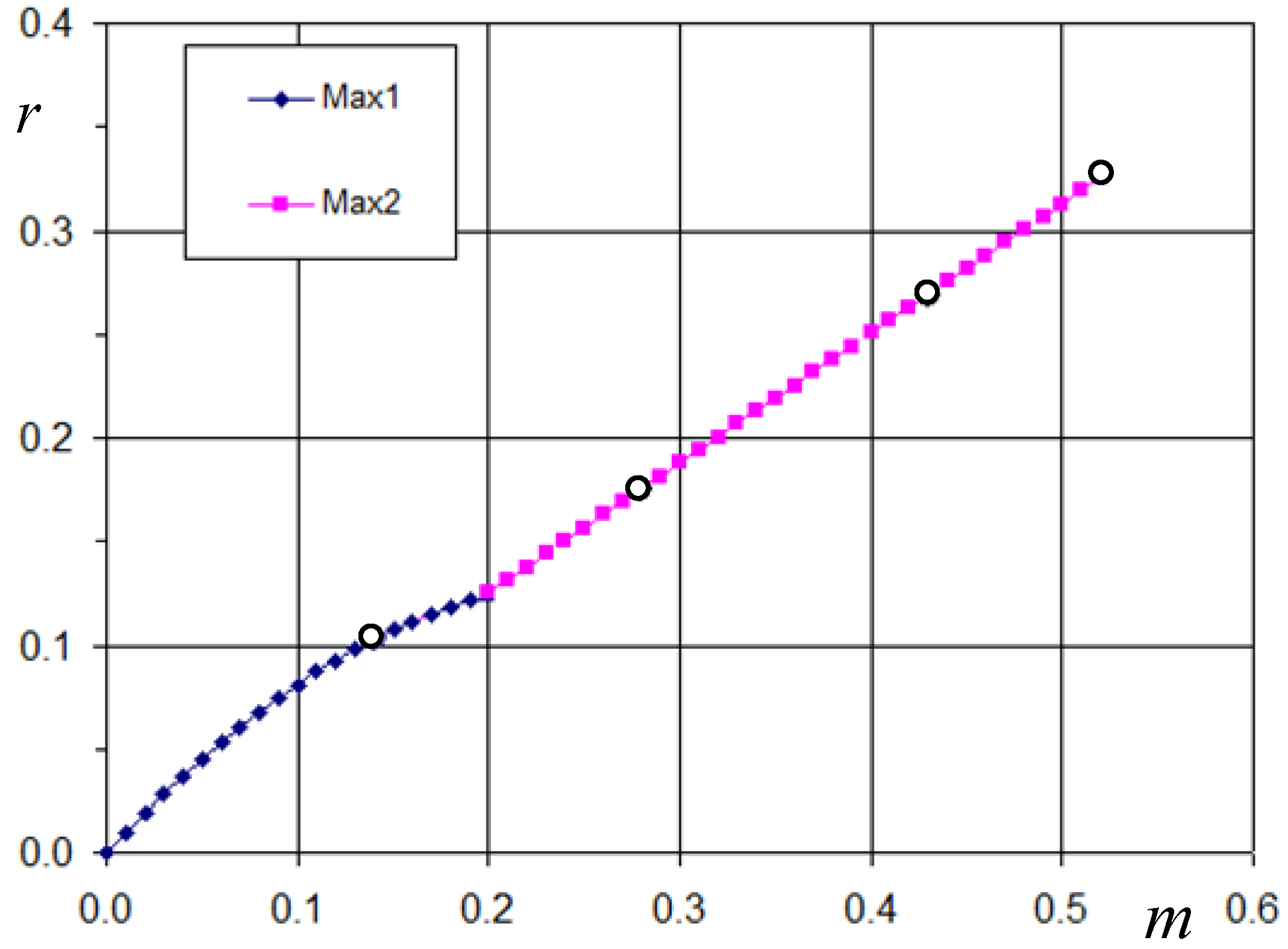
3. Numerical Results
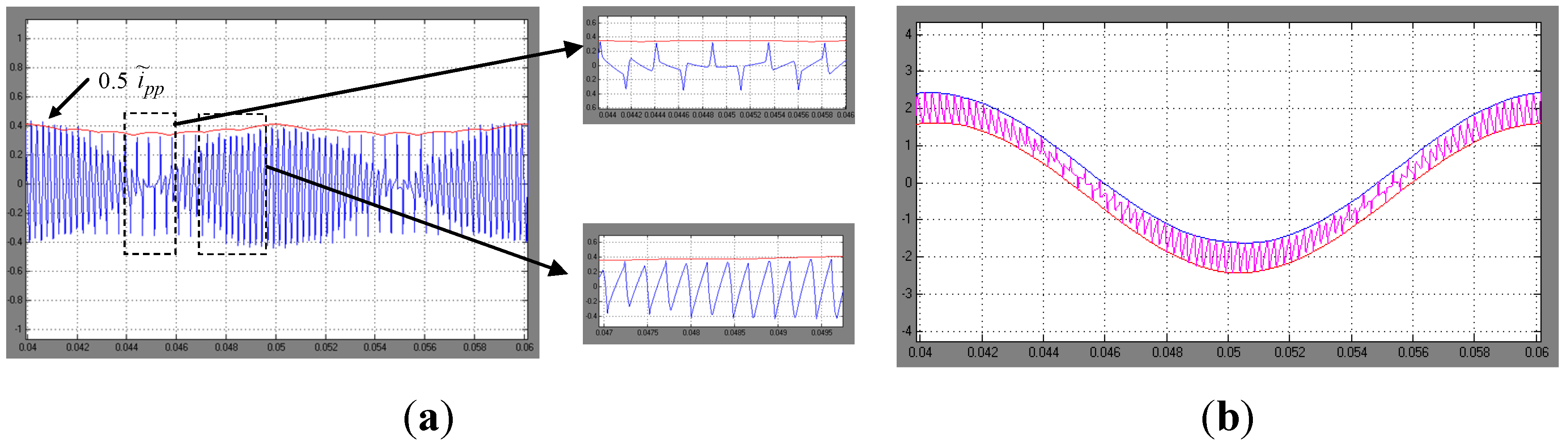
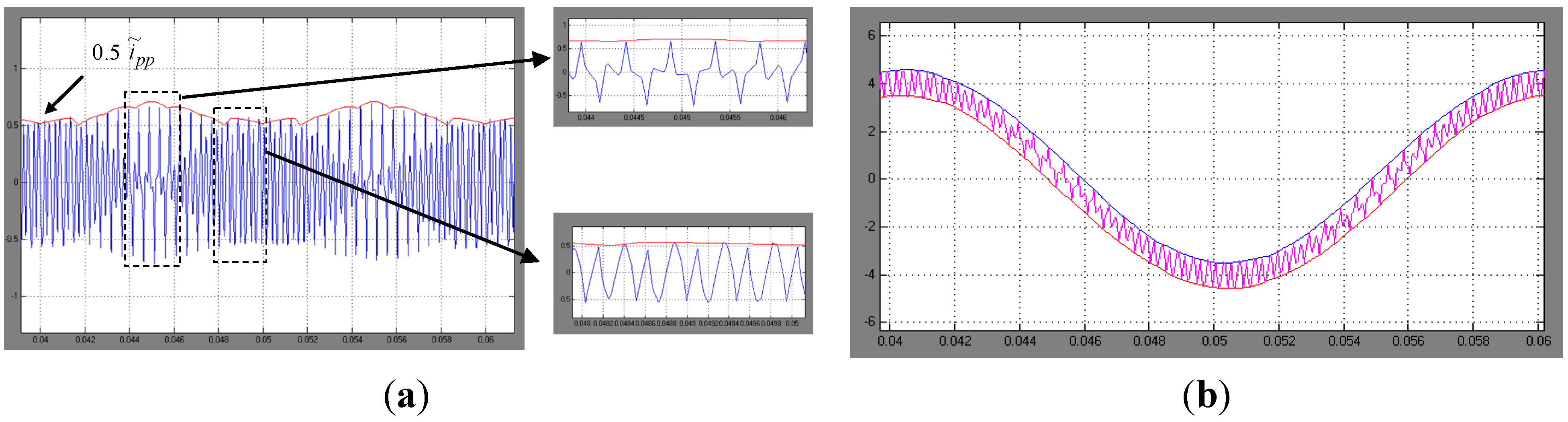


4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Toliyat, H.A.; Waikar, S.P.; Lipo, T.A. Analysis and simulation of five-phase synchronous reluctance machines including third harmonic of airgap MMF. IEEE Trans. Ind. Appl. 1998, 34, 332–339. [Google Scholar] [CrossRef]
- Xu, H.; Toliyat, H.A.; Petersen, L.J. Five-phase induction motor drives with DSP-based control system. IEEE Trans. Power Electron. 2002, 17, 524–533. [Google Scholar] [CrossRef]
- Ryu, H.M.; Kim, J.K.; Sul, S.K. Synchronous Frame Current Control of Multi-Phase Synchronous Motor: Part I. Modeling and Current Control based on Multiple d-q Spaces Concept under Balanced Condition. In Proceedings of the 39th Annual Meeting of IEEE Industry Application Society, Seattle, WA, 3–7 October 2004; pp. 56–63.
- Parsa, L.; Toliyat, H.A. Five-phase permanent-magnet motor drives. IEEE Trans. Ind. Appl. 2005, 41, 30–37. [Google Scholar] [CrossRef]
- Grandi, G.; Serra, G.; Tani, A. General Analysis of Multi-Phase Systems based on Space Vector Approach. In Proceedings of 12th Power Electronics and Motion Control Conference (EPE-PEMC), Portoroz, Slovenia, 30 August–1 September 2006; pp. 834–840.
- Ryu, H.M.; Kim, J.W.; Sul, S.K. Analysis of multi-phase space vector pulse width modulation based on multiple d-q spaces concept. IEEE Trans. Power Electron. 2005, 20, 1364–1371. [Google Scholar] [CrossRef]
- Iqbal, A.; Levi, E. Space Vector Modulation Schemes for a Five-Phase Voltage Source Inverter. In Proceedings of 11th European Conference on Power Electronics and Applications (EPE), Dresden, Germany, 11–14 September 2005; pp. 1–12.
- De Silva, P.S.N.; Fletcher, J.E.; Williams, B.W. Development of Space Vector Modulation Strategies for Five Phase Voltage Source Inverters. In Proceedings of Power Electronics, Machines and Drives Conference (PEMD), Edinburgh, UK, 31 March–2 April 2004; pp. 650–655.
- Ojo, O.; Dong, G. Generalized Discontinuous Carrier-Based PWM Modulation Scheme for Multi-Phase Converter-Machine Systems. In Proceedings of 40th Annual Meeting of IEEE Industry Applications Society, Hong Kong, China, 2–6 October 2005; pp. 1374–1381.
- Grandi, G.; Serra, G.; Tani, A. Space Vector Modulation of a Seven-Phase Voltage Source Inverter. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Taormina, Italy, 23–26 May 2006; pp. 1149–1156.
- Dujic, D.; Levi, E.; Serra, G.; Tani, A.; Zarri, L. General modulation strategy for seven-phase inverters with independent control of multiple voltage space vectors. IEEE Trans. Ind. Electron. 2008, 55, 1921–1932. [Google Scholar] [CrossRef]
- Dujic, D.; Levi, E.; Jones, M.; Grandi, G.; Serra, G.; Tani, A. Continuous PWM Techniques for Sinusoidal Voltage Generation with Seven-Phase Voltage Source Inverters. In Proceedings of the Power Electronics Specialists Conference (IEEE-PESC), Orlando, FL, USA, 17–21 June 2007; pp. 47–52.
- Hu, J.S.; Chen, K.Y.; Shen, T.Y.; Tang, C.H. Analytical solutions of multilevel space-vector PWM for multiphase voltage source inverters. IEEE Trans Power Electron. 2011, 26, 1489–1502. [Google Scholar] [CrossRef]
- Lopez, O.; Alvarze, J.; Gandoy, J.D.; Freijedo, F.D. Multiphase space vector PWM algorithm. IEEE Trans Ind. Electron. 2008, 55, 1933–1942. [Google Scholar] [CrossRef]
- Casadei, D.; Mengoni, M.; Serra, G.; Tani, A.; Zarri, L. A New Carrier-Based PWM Strategy with Minimum Output Current Ripple for Five-Phase Inverters. In Proceedings of the 14th European Conference on Power Electronics and Applications (EPE), Birmingham, UK, 30 August–1 September 2011; pp. 1–10.
- Dujic, D.; Jones, M.; Levi, E. Analysis of output current ripple rms in multiphase drives using space vector approach. IEEE Trans. Power Electron. 2009, 24, 1926–1938. [Google Scholar] [CrossRef]
- Jones, M.; Dujic, D.; Levi, E.; Prieto, J.; Barrero, F. Switching ripple characteristics of space vector PWM schemes for five-phase two-level voltage source inverters—Part 2: Current ripple. IEEE Trans. Ind. Electron. 2011, 58, 2799–2808. [Google Scholar] [CrossRef]
- Dahono, P.A.; Supriatna, E.G. Output current-ripple analysis of five-phase PWM inverters. IEEE Trans. Ind. Appl. 2009, 45, 2022–2029. [Google Scholar] [CrossRef]
- Dujic, D.; Jones, M.; Levi, E. Analysis of output current-ripple RMS in multiphase drives using polygon approach. IEEE Trans. Power Electron. 2010, 25, 1838–1849. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, F. Study of Analytical Current Ripple of Three-Phase PWM Converter. In Proceedings of the 27th IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 1568–1575.
- Grandi, G.; Loncarski, J.; Seebacher, R. Effects of Current Ripple on Dead-Time Distortion in Three-Phase Voltage Source Inverters. In Proceedings of the 2nd IEEE ENERGYCON Conference and Exhibition—Advances in Energy Conversion, Florence, Italy, 9–12 September 2012; pp. 207–212.
- Herran, M.A.; Fischer, J.R.; Gonzalez, S.A.; Judewicz, M.G.; Carrica, D.O. Adaptive dead-time compensation for grid-connected PWM inverters of single-stage PV systems. IEEE Trans. Power Electron. 2013, 28, 2816–2825. [Google Scholar] [CrossRef]
- Schellekens, J.M.; Bierbooms, R.A.M.; Duarte, J.L. Dead-Time Compensation for PWM Amplifiers Using Simple Feed-Forward Techniques. In Proceedings of the 19th International Conference on Electrical Machines (ICEM), Rome, Italy, 6–8 September 2010; pp. 1–6.
- Mao, X.; Ayyanar, R.; Krishnamurthy, H.K. Optimal variable switching frequency scheme for reducing switching loss in single-phase inverters based on time-domain ripple analysis. IEEE Trans. Power Electron. 2009, 24, 991–1001. [Google Scholar] [CrossRef]
- Ho, C.N.M.; Cheung, V.S.P.; Chung, H.S.H. Constant-frequency hysteresis current control of grid-connected VSI without bandwidth control. IEEE Trans. Power Electron. 2009, 24, 2484–2495. [Google Scholar] [CrossRef]
- Holmes, D.G.; Davoodnezhad, R.; McGrath, B.P. An improved three-phase variable-band hysteresis current regulator. IEEE Trans. Power Electron. 2013, 28, 441–450. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, F. Variable Switching Frequency PWM for Three-Phase Converter for Loss and EMI Improvement. In Proceedings of the 27th IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 1576–1583.
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. Theoretical and experimental analysis for the RMS current ripple minimization in induction motor drives controlled by SVM technique. IEEE Trans. Ind. Electron. 2004, 51, 1056–1065. [Google Scholar] [CrossRef]
- Iqbal, A.; Moinuddin, S. Comprehensive relationship between carrier-based PWM and space vector PWM in a five-phase VSI. IEEE Trans. Power Electron. 2009, 24, 2379–2390. [Google Scholar] [CrossRef]
- Levi, E.; Dujic, D.; Jones, M.; Grandi, G. Analytical determination of DC-bus utilization limits in multi-phase VSI supplied AC drives. IEEE Trans. Energy Convers. 2008, 23, 433–443. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J. Analysis of Dead-Time Effects in Multi-Phase Voltage Source Inverters. In Proceedings of the 6th IET Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, UK, 27–29 March 2012.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Grandi, G.; Loncarski, J. Analysis of Peak-to-Peak Current Ripple Amplitude in Seven-Phase PWM Voltage Source Inverters. Energies 2013, 6, 4429-4447. https://doi.org/10.3390/en6094429
Grandi G, Loncarski J. Analysis of Peak-to-Peak Current Ripple Amplitude in Seven-Phase PWM Voltage Source Inverters. Energies. 2013; 6(9):4429-4447. https://doi.org/10.3390/en6094429
Chicago/Turabian StyleGrandi, Gabriele, and Jelena Loncarski. 2013. "Analysis of Peak-to-Peak Current Ripple Amplitude in Seven-Phase PWM Voltage Source Inverters" Energies 6, no. 9: 4429-4447. https://doi.org/10.3390/en6094429
APA StyleGrandi, G., & Loncarski, J. (2013). Analysis of Peak-to-Peak Current Ripple Amplitude in Seven-Phase PWM Voltage Source Inverters. Energies, 6(9), 4429-4447. https://doi.org/10.3390/en6094429