Abstract
Battery model identification is very important for reliable battery management as well as for battery system design process. The common problem in identifying battery models is how to determine the most appropriate mathematical model structure and parameterized coefficients based on the measured terminal voltage and current. This paper proposes a novel semiparametric approach using the wavelet-based partially linear battery model (PLBM) and a recursive penalized wavelet estimator for online battery model identification. Three main contributions are presented. First, the semiparametric PLBM is proposed to simulate the battery dynamics. Compared with conventional electrical models of a battery, the proposed PLBM is equipped with a semiparametric partially linear structure, which includes a parametric part (involving the linear equivalent circuit parameters) and a nonparametric part [involving the open-circuit voltage (OCV)]. Thus, even with little prior knowledge about the OCV, the PLBM can be identified using a semiparametric identification framework. Second, we model the nonparametric part of the PLBM using the truncated wavelet multiresolution analysis (MRA) expansion, which leads to a parsimonious model structure that is highly desirable for model identification; using this model, the PLBM could be represented in a linear-in-parameter manner. Finally, to exploit the sparsity of the wavelet MRA representation and allow for online implementation, a penalized wavelet estimator that uses a modified online cyclic coordinate descent algorithm is proposed to identify the PLBM in a recursive fashion. The simulation and experimental results demonstrate that the proposed PLBM with the corresponding identification algorithm can accurately simulate the dynamic behavior of a lithium-ion battery in the Federal Urban Driving Schedule tests.
1. Introduction
Currently, lithium-ion batteries play a significant role in the energy storage devices used in electric vehicles (EVs) because of their high energy density, low self-discharge rate, lack of a memory effect, high operating voltage, and long life cycle. The primary concerns in the design of EVs are how to maintain optimum battery performance and extend the battery’s expected life. To achieve these goals, the battery must have a well-designed battery management system (BMS). The BMS must track the dynamic behaviors of the battery for reliable and efficient operation, which requires battery models that can accurately determine battery behavior under various operating conditions. Another important task for the battery model is to provide precise battery data for simulation of an EV energy system.
Due to the complex chemical and physical processes that occur in batteries, developing an accurate battery model is challenging. Researchers worldwide have developed a wide variety of battery models for different purposes. Almost all the existing battery models can be classified into the following two types: (1) parametric models, e.g., electrochemical models [,] and electrical models [,,,]; and (2) nonparametric models, e.g., artificial neural network (ANN) models [,,] and abstract mathematical models []. Parametric battery models have been developed in terms of the equivalent electric-circuit parameters (for electrical models) or electrochemical parameters (for electrochemical models). These parameters have clear physical meaning and can be used to investigate the working status of batteries. For example, electrical model parameters, such as the open-circuit voltage (OCV) and equivalent internal resistance, can provide useful information that can be used to estimate the state of charge (SoC) and state of health (SoH) based on the battery’s intrinsic characteristics []. Battery parameters typically rely on many factors, such as the SoC, SoH, internal structure, service time, and operating conditions. Some of these factors are difficult or almost impossible to measure, which may lead to misspecification of the models and cause severe modeling biases. In contrast, the nonparametric modeling approach is useful for exploring hidden structures and reducing modeling biases. For example, ANN-based nonparametric battery models were developed in [] and []; in these reports, variables that are hard to measure were replaced by the weights of the neurons. However, the nonparametric battery models lack direct physical interpretation, which limits their fields of application.
To overcome the above-mentioned disadvantages, this paper presents a semiparametric battery model based on the Thevenin equivalent circuit model, which is a compromise between the nonparametric and parametric battery models. Since the introductory work of Engle in 1986 [], the semiparametric model has been widely studied and applied in many fields, such as applied statistics [], signal processing [,], and dynamic system modeling [,,]. However, to our knowledge, this model has not yet been investigated for use in battery modeling. The proposed semiparametric battery model consists of two major components: a linear parametric component that involves the equivalent circuit parameters (such as ohmic internal resistance, polarization resistance, and polarization capacitance) and a nonparametric component that involves the OCV (because accurate modeling of OCV is a difficult task). In the literature, the semiparametric model described by such a form is also termed the “partially linear model” because of its relationship to the standard linear model []. Compared with the standard linear model, the partially linear model could be more adaptive when it is believed that the response variable has a linear relationship with some covariates but a nonlinear or unknown relationship with others. The proposed semiparametric battery model, hereafter referred to as the partially linear battery model (PLBM), features the flexibility of the nonparametric component while maintaining the direct physical interpretation of the parametric component.
Because the battery parameters cannot be measured directly during the run time, electrical models are often estimated through model-based optimization techniques, such as the use of recursive least square (RLS) estimators [,], sliding-mode observers [], the adaptive control approach [], the subspace identification method [,], and the extended Kalman filter [,]. For the PLBM, an efficient estimation procedure must be developed for both the linear parameters and nonparametric component. Several semiparametric estimators [,,,,] based on basis function expansion methods have been proposed to identify the partially linear model. The current study is concerned with modeling the nonparametric component in the PLBM using the wavelet multiresolution analysis (MRA) expansion due to the wavelet’s good time—frequency localization property. Another advantage of the modeling method is that the nonparametric component can be parsimoniously represented by large timescale wavelet basis functions (or a truncated wavelet MRA expansion) because of the slowly varying behavior of the OCV. Furthermore, the wavelet MRA expansion typically leads to a sparse representation of the original signal [], such as the OCV; this sparsity can be exploited to improve the estimation performance by employing an l1-norm penalized wavelet estimator. However, most existing penalized wavelet estimators of the partially linear model are processed in batch form using iterative algorithms [,,], which are not suitable for online implementation purposes. Recent advances in sparse linear model identification have shown that the cyclic coordinate descent (CCD) algorithm provides an efficient means of solving the penalized least squares (LS) problem [,] and can be implemented online in a recursive fashion [,]. This feature motivates us to extend this algorithm to the wavelet-based partially linear model and develop a recursive penalized wavelet estimator based on a modified online CCD algorithm. The performance of the proposed semiparametric identification approach for lithium-ion batteries is finally investigated by performing simulations and experiments.
2. Modeling of the Lithium-Ion Battery
The modeling of a battery is aimed at investigating the working status of the battery and finding a suitable mathematical expression that can accurately describe its input-to-output dynamics. Accurate electrical battery modeling is difficult to achieve because the electrochemical process is complex and a variety of operating conditions are used. Therefore, many complex electrical modeling methods have been developed to compensate for the modeling errors and uncertainties but at the costs of high computational burden, system complexity, and resource requirements. In this section, we present a simple, flexible, and comprehensive semiparametric battery model based on straightforward circuit analysis of the Thevenin equivalent circuit model.
2.1. Battery Equivalent Circuit Equations
In general, the electrical model is described by an equivalent circuit based on a combination of basic elements, such as voltage sources, resistors, and capacitors, to approximate the electrochemical processes and input-to-output dynamics of the battery. By combining the basic elements in different ways, the electrical models can be further divided into four classes []: the Rint model, radio control model, Thevenin equivalent circuit model, and Partnership for a New Generation of Vehicles model. Among these models, the Thevenin equivalent circuit model is widely employed to model the lithium-ion battery because it has a simple model structure and can capture the battery’s dynamic response well within an acceptable error [,]. Therefore, we select this model as the basic element of our proposed model.
The equivalent circuit model is shown in Figure 1 and consists of three parts: (1) the equivalent ohmic internal resistor Rs; (2) the resistor-capacitor (RC) parallel network Cp // Rp (where Rp is the equivalent polarization resistance and Cp is the equivalent polarization capacitance), which is used to simulate transient responses of the battery during charging–discharging transients; and (3) the OCV voc(h(t)), which is a nonlinear function of SoC h(t). The equivalent circuit model considers the current as the model control input and the terminal voltage as the measured output.
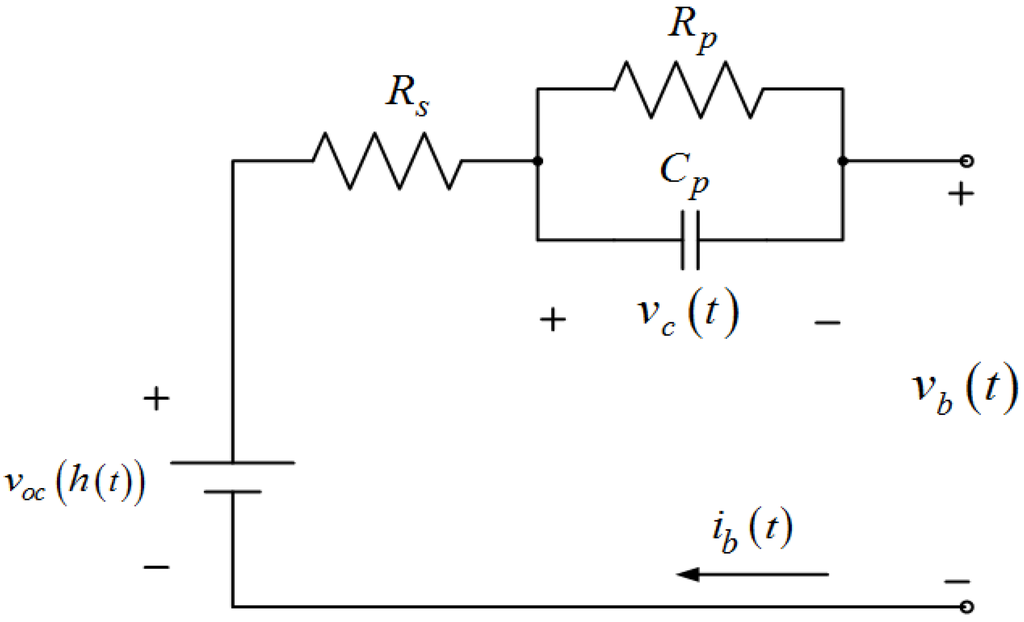
Figure 1.
Equivalent circuit model of the lithium-ion battery.
Theoretically, the equivalent circuit parameters Rs, Rp, and Cp in this model are functions of the temperature and SoC. In fact, because the variations in the SoC and temperature with respect to time are both very small, these parameters can be assumed as quasi-stationary, i.e., time invariant over a short observation time window. Further, for real-time application, parameter identification can only be performed over a finite time sliding window or exponentially decaying time window of the most recent measurement. Thus, within some error tolerance, these parameters can be assumed as constant during the identification. In other words, online identification can capture these parameters faster than the temperature or SoC variations.
The analysis of the equivalent circuit shown in Figure 1 is straightforward. Using Kirchhoff’s law, the dynamics of the circuit can be expressed as follows:
where vb(t) and ib(t) are the terminal voltage and current, respectively; and vc(t) is the voltage across the RC network, which cannot be measured directly.
2.2. PLBM
The OCV of a battery is a nonlinear function of its SoC. Theoretically, if the nonlinear relationship OCV–SoC is obtained prior to the identification procedure, then the model parameters can be directly identified using the LS estimators. Traditionally, this relationship is experimentally established in the offline mode by measuring the OCV at each SoC set point and assuming that it remains the same during the lifetime of the battery. However, in practice, this relationship is not exactly the same for every battery, even if these batteries are part of the same production batch. Moreover, this relationship depends on the number of charge–discharge cycles of the batteries. Therefore, for any online identification algorithms, the a priori OCV–SoC data may lead to an inaccurate identification result. Thus, we should treat voc(h(t)) as an unknown function that belongs to some functional space, which must be identified online, as well as the other model parameters. In this case, voc(h(t)) can be simply represented as voc(t).
As can be seen from Equations (1) and (2), the equivalent circuit equations involve the OCV voc(t) and the polarization voltage vc(t), both of which are unknown. However, the unknown term vc(t) can be removed from these equations based on the following three assumptions []: (1) The variation in SoC with respect to time is very small because the consumed (or regained) energy is very small compared with the total useful capacity; (2) The battery temperature is monitored in real-time and controlled at a predetermined level by a well-designed BMS module. Thus, the temperature variation can be ignored for normal operating conditions; (3) The usage history of the battery has a long-term effect on battery behavior, which can be ignored during on-line identification procedure. These assumptions also have been applied in []. With the unknown term vc(t) removed, the dynamics of the battery model can be approximated as follows:
The Laplace transformation of (3) can be expressed as follows:
Equation (4) is a mathematical model of a continuous system in the s-domain, which can be mapped to its discrete form as follows:
where vb(k) and ib(k) are the samples of vb(t) and ib(t), respectively, at time point tk = kTc and Tc is the sampling period. θ1, θ2, and θ3 are defined as:
and u(k) is defined as:
by letting voc(k) denote the virtual sample of voc(t) at time point tk = kTc , which is assumed to be an unknown function because voc(k) is unknown.
We should note that vb(k) and ib(k) are acquired only via observation, and during the observation, these parameters often suffer additional random disturbance. Let y(k) and x(k) denote the observed values of vb(k) and ib(k), respectively. From (5), the discrete observation equation can be obtained as follows:
where the superscript T denotes the transpose of a vector or matrix, is the measurement vector, is the unknown linear parameter vector, and ε(k) is assumed to be an additive zero-mean white noise error that contains not only the measurement errors of vb(k) and ib(k) but also the interior noise of the battery system.
The battery model (8) is nonlinear because the OCV exhibits a nonlinear relationship with the charging–discharging current. In general, nonlinear system identification and modeling techniques can be classified into three categories: parametric, nonparametric, and, more recently, semiparametric methods. Parametric methods assume that the model structure based on the physical modeling principles is known but that the model parameters are unknown. Parametric methods can provide a direct physical interpretation of the system’s behavior. Conversely, nonparametric methods are necessary when the physical-based model structure is unknown. Nonparametric methods assume a functional relationship between the input and output data. In this case, these methods rely on functional approximators, such as the neural network, the kernel function, or abstract mathematical regression models. However, these methods focus on the input–output representation ability and neglect some important properties of the highly successful parametric modeling, such as the simple model structure involved and clear physical meaning. As an attractive alternative, semiparametric methods offer a compromise between nonparametric and parametric methods, thus reducing the high risk of model misspecification related to the fully parametric methods while simultaneously avoiding some of the disadvantages of fully nonparametric methods. From (8), we can see that the battery model is equipped with a semiparametric, partially linear structure, i.e., the right-hand side of (8) consists of two major components: a linear parametric component involving the parameter vector θ and a nonparametric component u(k) involving the unknown function voc(k). Thus, we can naturally describe the dynamics of the battery using the semiparametric partially linear model; this description is useful not only because our understanding of the OCV does not provide us with a specific function or a parametric model of OCV but also because it provides a better understanding of the model structure and the parameters.
3. Online Identification of the Wavelet-Based PLBM
The goal of our study is to estimate both the unknown linear parameter vector θ and the nonparametric component u(k) from the input–output data. One attractive approach in addressing this problem is to expand the nonparametric component as a linear combination of the parameterized basis functions. The problem is then reduced to a linear estimation problem because the output is linear not only with the linear components but also with the basis functions. The identification method developed in this section is based on the wavelet MRA expansion of the nonparametric component u(k) of the PLBM.
3.1. Wavelet MRA
To make this paper self-contained and improve its readability, we first provide a brief overview of the basic concepts of wavelet MRA theory, which are essential for this paper (the readers are referred to [] and [] for a detailed treatment of this subject). The wavelet MRA expansion has proven to be a powerful tool for parsimoniously representing arbitrary signals because of its inherent property of localization in both time and frequency; wavelet representations have been successfully used in dynamic system identification and modeling [,,,].
The essential idea of the wavelet MRA is to decompose a finite energy signal into a subspace, which is spanned using the scaling and wavelet basis functions at different resolutions. For any signal , the MRA expansion with respect to the mother wavelet ψ(t) and scaling function ϕ(t) can be expressed as []:
where the scaling basis function is the scaled and translated version of ϕ(t); the wavelet basis function is the scaled and translated version of ψ(t); cj0,m and dj,m are respectively termed the scaling and wavelet coefficients at scale levels j0; and j; and j0; is an arbitrary integer that represents the coarsest resolution level (defined by the user). The wavelet MRA representation has localization property in both the time domain (via translations) and the frequency domain (via scale). With this property, wavelets can capture global (low frequency) and local (high frequency) characteristics of any finite energy signal easily.
Theoretically, the resolution level (or timescale) can span from −∞ to ∞. In practice, the observed signals are sampled with finite length. Thus, the MRA expansion can be performed only over a finite number of resolution levels. Without loss of generality, we assume that f(t) is defined over the time window [0,T]. Let f(k) denote the sample of f(t) at time point tk = kTc, k = 1, 2,···, N where N = T / Tc is the length of the sampled signal and assumed to be a power of two for simplicity. Then, the MRA expansion of f(k) can be expressed as:
where j0 ≥ 0 is the coarsest resolution level (or the largest timescale) and jmax = log2 (N) is the finest resolution level (or the smallest timescale) where the sampled signal is originally represented.
From the viewpoint of signal representation, the scaling coefficients carry the approximation information of the original signal at the coarsest scale j0, and the wavelet coefficients at scale j carry the information that is different between two approximations to the original signal at scales j and j − 1. When these smaller timescale components at scale j ≥ J make little contribution to the original signal, the original signal f(k) can be approximated by a truncated MRA expansion from scale j0 up to J as:
where all of the wavelet coefficients at scale J ≤ j < jmax are assumed to be zero. The higher the upper resolution level J, the more accurate the approximation. The truncated MRA representation can describe not only low-frequency fluctuations but also some rapid localized changes. The advantage of the truncated MRA expansion is that it provides a parsimonious approximation representation of the original signal and is particularly suitable for original signals that do not vary significantly during a short time interval.
3.2. Truncated Wavelet MRA Expansion of the Nonparametric Component
As mentioned earlier, the OCV of a battery has a complex nonlinear relationship with its SoC. Obtaining this relationship in real time is difficult because the dynamics of the battery are actually the result of a series of complex electrochemical processes affected by the operating conditions. The variation in SoC with respect to time is very small because the consumed (or regained) energy is very small compared with the total useful capacity. Thus, as a monotonic function with respect to SoC, the OCV is considered to be slowly varying within the battery’s usable capacity region []. Based on this consideration, we assume that the OCV is the superposition of physical and chemical phenomena that occur at larger timescales. In other words, the OCV can be modeled as a signal that belongs to a subspace spanned by large-scale wavelets. Moreover, we assume that (1 − θ1), another part involved in the nonparametric component, is time invariant during the identification process. Thus, an appropriate model for the nonparametric component u(k) in (8) can be provided using a truncated MRA expansion as:
where the truncation parameter J is defined as the finest timescale that characterizes the complexity of the OCV. The truncated MRA expansion leads to a parsimonious model structure that is highly desirable for identification of the wavelet-based, partially linear model discussed in the next section.
The MRA expansion of a signal is not unique and depends on the type of wavelet used. In this study, we use the Haar wavelet because of its simple structure and good localization properties []. Furthermore, the Haar scaling and wavelet basis functions are completely supported and provided explicitly, and these features enable the operations of the MRA expansion of (12) to be more convenient.
The Haar scaling function ϕhaar(t) and mother wavelet ψhaar(t) can be described as:
and:
For notational convenience, we denote ϕhaar(t) and ψhaar(t) as g1(t) and g2(t); that is, g1(t) and g2(t) are the scaling and wavelet basis functions at the coarsest scale of zero, respectively. All other Haar wavelet basis functions derived from g2(t) are denoted as:
where m = 0,1,···,2j − 1 for each scale j = 1,2,···,J. We define g(t) = [g1(t), g2(t),···,gL(t)]T, where L = 2J+1. For example, Figure 2 shows the Haar basis functions of g(t) when J = 3. The discrete representation of g(t) is defined as:
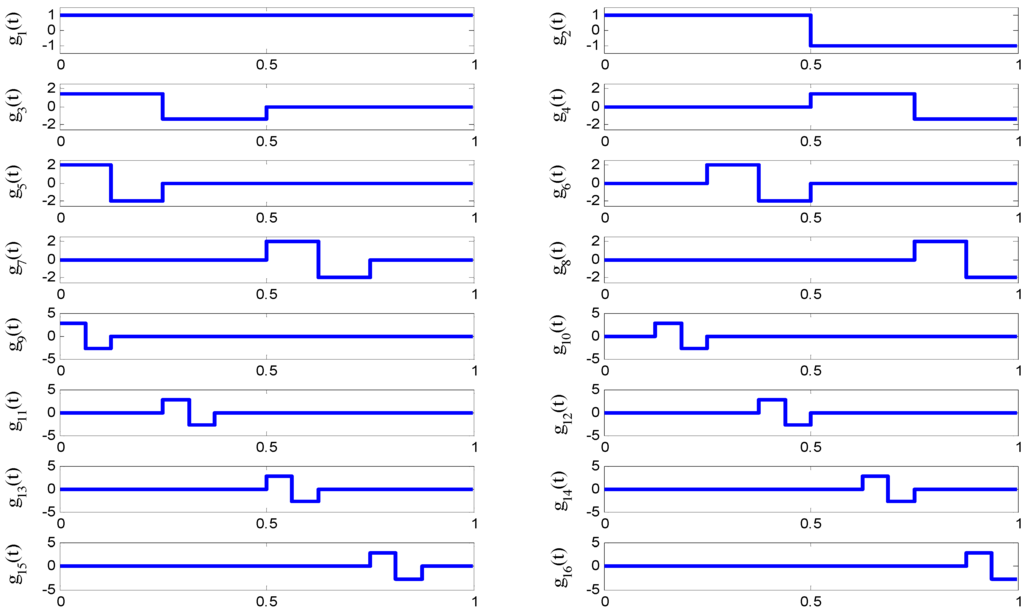
Figure 2.
Haar basis functions.
Using the above notations and from (12), the truncated MRA expansion of u(k) from the initial scale j0 = 0 up to J can be compactly expressed as:
where the expansion coefficient vector is defined as η = [η1,η2,···,ηL]T with ηl as the expansion coefficient that corresponds to the associated Haar wavelet basis function gl(t).
3.3. Recursive Penalized Wavelet Estimator for Online PLBM Identification
By substituting u(k) in (8) with the truncated MRA representation uJ(k), the observation equation can be rewritten as:
where and are both P = 3 + L -dimensional vectors. Comparing (18) with (8), it is seen that the semiparametric identification problem has been transformed into a linear-in-parameter identification problem, which can be solved by the ordinary LS (or RLS) estimator as follows:
The wavelet MRA expansion typically leads to a sparse representation of the original signal [], meaning that most of the wavelet coefficients are zero or close to zero, whereas the important features of the signal are captured by a small number of large coefficients. However, the ordinary LS and RLS estimators cannot account for the underlying sparsity. For the wavelet-based partially linear model (18), the sparsity can be exploited to improve the estimation performance by the penalized wavelet estimator, similar to that in [] and []:
where the cost function is:
where λ is a given penalty factor; and βi is the ith entry of β. In (21), the first summation term measures how well the candidate solution fits the observed data in the LS sense, whereas the second summation term is a regularizer that considers an l1-norm penalty on the wavelet coefficients. λ controls the relative weight of the two terms, which means that the larger λ is, the more the wavelet coefficients will shrink to zero. The penalty term in (21) penalizes only the wavelet coefficients of the nonparametric part of the model and not the scaling coefficients. The penalized wavelet estimator (20) can be regarded as an extension of the wavelet shrinkage estimators, which are typically processed in batch form by iterative soft-thresholding algorithms [,,]. However, the batch estimators suffer from high computational complexity and increased memory requirements as time progresses and are thus not appropriate for online implementation. In contrast to batch estimators, their recursive counterparts offer computational and memory savings and enable tracking of the slowly time-varying system. This feature motivated us to develop a recursive penalized wavelet estimator for PLBM identification.
Now, we consider the recursive solution of (20). Neglecting the constant terms, the cost function (21) at the kth recursive step can be equivalently expressed as follows:
where the matrix R(k) and vector r(k) can be defined recursively as follows:
and:
Unfortunately, the cost function (22) is nondifferentiable and is thus not available in closed-form minimization. One attractive approach to solve such an optimization problem is to run an online CCD algorithm due to its speed and numerical stability [,]. The CCD algorithm separately minimizes the cost function (22) for each entry of β and can admit a closed-form solution.
Let denote the solution of the CCD algorithm at the kth recursive step. The pth entry of is cyclically updated as follows:
In the above expression, only the pth entry of β is currently optimized. We recall that the penalty in (22) is applied only on the wavelet coefficients (β5:βP) and not on the scaling coefficient (β4) or linear parameters (β1:β3). Thus, (25) can be rewritten as:
where R(k)(p,p) is the (p,p)th entry of the matrix R(k) , and is defined as:
where r(k)(p) is the pth entry of r(k). Being a scalar minimization problem, the solution of (26) can be easily obtained in closed form as:
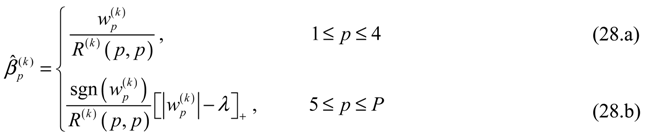 where sgn(a) = a/|a| and [a]+ = max (a,0). Because the Haar wavelet basis functions are compactly supported, local data processing can be employed to reduce the computational burden [], i.e., the wavelet coefficients are updated only when at least one of the incoming inputs falls into the support of the associated wavelet functions. The modified online CCD algorithm for the recursive penalized wavelet estimator is summarized as follows:
where sgn(a) = a/|a| and [a]+ = max (a,0). Because the Haar wavelet basis functions are compactly supported, local data processing can be employed to reduce the computational burden [], i.e., the wavelet coefficients are updated only when at least one of the incoming inputs falls into the support of the associated wavelet functions. The modified online CCD algorithm for the recursive penalized wavelet estimator is summarized as follows:
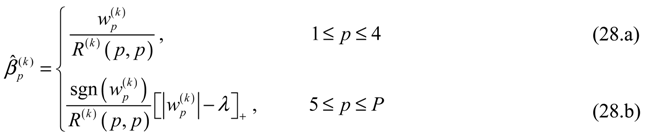
1: Initialize , and .
2: For k = 1,2,...,N do
3: Update R(k) and vector r(k) using (23) and (24), respectively.
4: For p = 1,···,4 do
5: Calculate using (27).
6: Update using (28.a).
7: end for
8: For p = 5,···,P do
9: If gp − 3(k/N) = 0
10: Do not update .
11: else
12: Calculate using (27).
13: Update according to the thresholding rule (28.b).
14: end if
15: end for
16: end for
After acquiring , i.e., and (the recursive estimations of θ and η), the nonparametric component u(k) can be approximately calculated via (17) as follows:
Also, according to (6) and (7), the trajectory of the estimated battery equivalent circuit parameters and OCV can be determined using u(k) and .
4. Simulation and Experimental Results
This section discusses the numerical simulations and experiments performed to verify the accuracy and effectiveness of the proposed identification approach in accordance with the Federal Urban Driving Schedule (FUDS) test. The FUDS test is a standard driving test used by vehicle designers to evaluate performance under urban driving conditions. In all simulations and experiments, the nonparametric components of the PLBM are expanded using the truncated Haar wavelet MRA expansion with the coarsest resolution level j0 = 0 and finest resolution level J = 5. The original input-output data in the observation window [0,T] are normalized into the unit interval [0,1] for convenient implementation [].
4.1. Simulations
We first verify the accuracy of the proposed identification method by performing simulation studies. For all simulations, the input {x(k)} is acquired from one FUDS testing cycle as model excitation, whereas the output {y(k)} is generated according to (5) with an initial value y(0) = 0. The real linear parameters θ1, θ2 and θ3 are generated according to (6) with Rs = 50 mΩ, Rp = 30 mΩ, and Cp = 2500 F. To illustrate the robustness of the proposed identification method, y(k) is corrupted by an additive white Gaussian noise with zero-mean and variance σ2. The signal-to-noise ratio (SNR) is defined as 1/σ2. The OCV is assumed to be monotonically varying throughout the entire simulation process and is modeled as a smooth polynomial for simplicity:
voc (k) = −0.5tk (1.5 − tk) + 41.5, tk = k/N, k = 1,2,···,N
The trajectory of the estimated OCV, Rs, Rp, and Cp are shown individually in Figure 3 in comparison with their real values. The time axis is rescaled according to the inverse time mapping [0,1] → [0,T]. The penalty threshold adopted here is the traditional universal threshold value derived from [] and used in [] and [] for the wavelet semiparametric estimation. The SNR is set at 23 dB. The estimated OCV follows the true OCV variations quite well, and the other estimated parameters all converge to their real values with different convergence speeds. This result demonstrates that the proposed estimator can accurately identify the PLBM and time-invariant linear parameters.
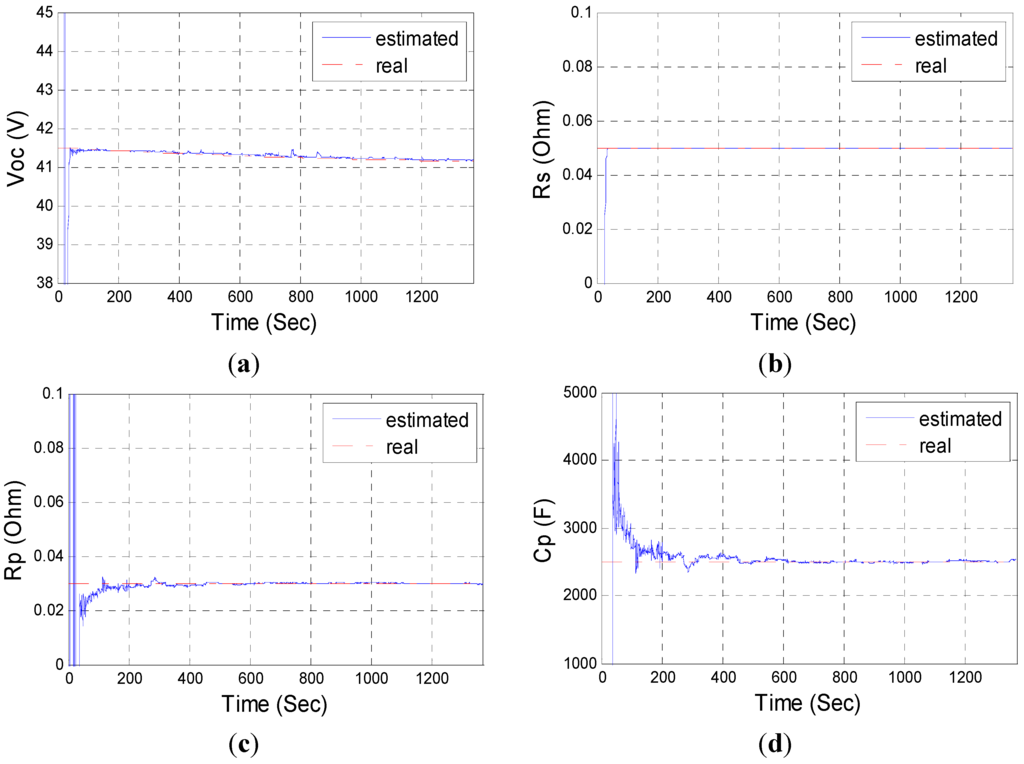
Figure 3.
Real and estimated results of the simulation: (a) OCV; (b) Rs; (c) Rp; (d) Cp.
To illustrate the flexibility of the proposed semiparametric approach, a model bias is first introduced to the OCV model as:
where d is defined as the bias coefficient. Thus, the OCV can be remodeled as:
Assuming the OCV model is known as (30), and from (5) and (6), the parametric model of a battery can be expressed by the following linear regression equation:
[vb(k) − voc(k)] = θ1[vb(k − 1) − voc(k)] + θ2ib(k) + θ3ib(k − 1)
The above parametric model can be identified by standard RLS estimator, and the identification results were compared with the proposed semiparametric approach as shown in Figure 4. As expected, the proposed semiparametric approach can accurately estimate the equivalent circuit parameters since it does not rely on any prior knowledge of OCV model.
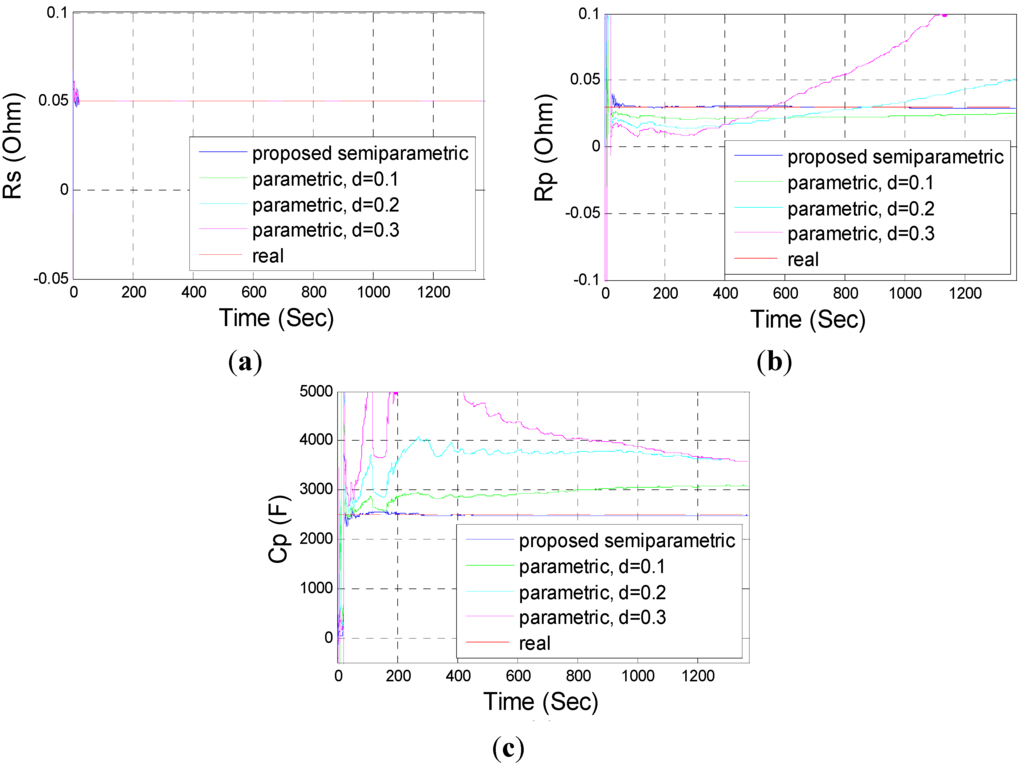
Figure 4.
Estimated results of equivalent circuit parameters with the semiparametric and parametric approaches: (a) Rs; (b) Rp; (c) Cp.
It can be seen from Figure 4a that the parametric approach can also estimate the ohmic internal resistance Rs accurately. This is because the fact that the ohmic internal resistance represents the terminal voltage variation caused by a current variation in the battery and the slowly varying OCV bias has very little effect on the terminal voltage variation. However, as can be seen from Figures 4b,c the parametric approach cannot estimate the equivalent polarization resistance and capacitance accurately, and the larger the model bias (i.e., the larger d), the larger estimation error will be. This result indicates that the polarization parameters are much more sensitive to OCV model bias in comparison with the ohmic internal resistance.
We next compare the performance of the proposed recursive penalized wavelet estimator, the RLS wavelet estimator according to (19), and the adaptive control approach [] with respect to the mean-squared error (MSE) of the OCV, which is defined as:
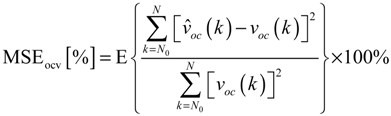 where E{} denotes the expectation operator and the lower bound of the summation is set as N0 = 100 to ensure a fair comparison. To evaluate the MSE, we conducted 500 replicate Monte Carlo simulations for each SNR. Moreover, to clearly illustrate the sensitivity of each approach to observed noise, the input-output data are not pre-filtered. For the adaptive control approach, the OCV was identified based on the discrete version of Equations (11) and (12) in []. The results are shown in Figure 5 and illustrate the sensitivity of the three identification approaches to the observed noise. As expected, the performance of all three approaches increases with the SNR. In the low-SNR regime, the wavelet estimators clearly outperform the adaptive control approach due to the fact that the wavelet estimators identify OCV only using the large scale expansion coefficients as shown in (17), thus the high frequency noise ( spanned by small scale expansion coefficients) can be effectively reduced from the identified OCV. However, the MSE performance of the adaptive control approach increases significantly with increasing SNR. In the high-SNR regime, the MSEs of the adaptive control approach and the proposed recursive penalized wavelet estimator are almost indistinguishable. Additionally, it can be seen that the proposed penalized wavelet estimator outperforms the RLS wavelet estimator because of the power of the l1-norm penalty.
where E{} denotes the expectation operator and the lower bound of the summation is set as N0 = 100 to ensure a fair comparison. To evaluate the MSE, we conducted 500 replicate Monte Carlo simulations for each SNR. Moreover, to clearly illustrate the sensitivity of each approach to observed noise, the input-output data are not pre-filtered. For the adaptive control approach, the OCV was identified based on the discrete version of Equations (11) and (12) in []. The results are shown in Figure 5 and illustrate the sensitivity of the three identification approaches to the observed noise. As expected, the performance of all three approaches increases with the SNR. In the low-SNR regime, the wavelet estimators clearly outperform the adaptive control approach due to the fact that the wavelet estimators identify OCV only using the large scale expansion coefficients as shown in (17), thus the high frequency noise ( spanned by small scale expansion coefficients) can be effectively reduced from the identified OCV. However, the MSE performance of the adaptive control approach increases significantly with increasing SNR. In the high-SNR regime, the MSEs of the adaptive control approach and the proposed recursive penalized wavelet estimator are almost indistinguishable. Additionally, it can be seen that the proposed penalized wavelet estimator outperforms the RLS wavelet estimator because of the power of the l1-norm penalty.
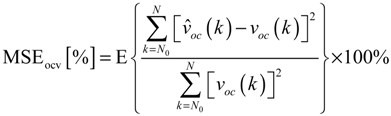
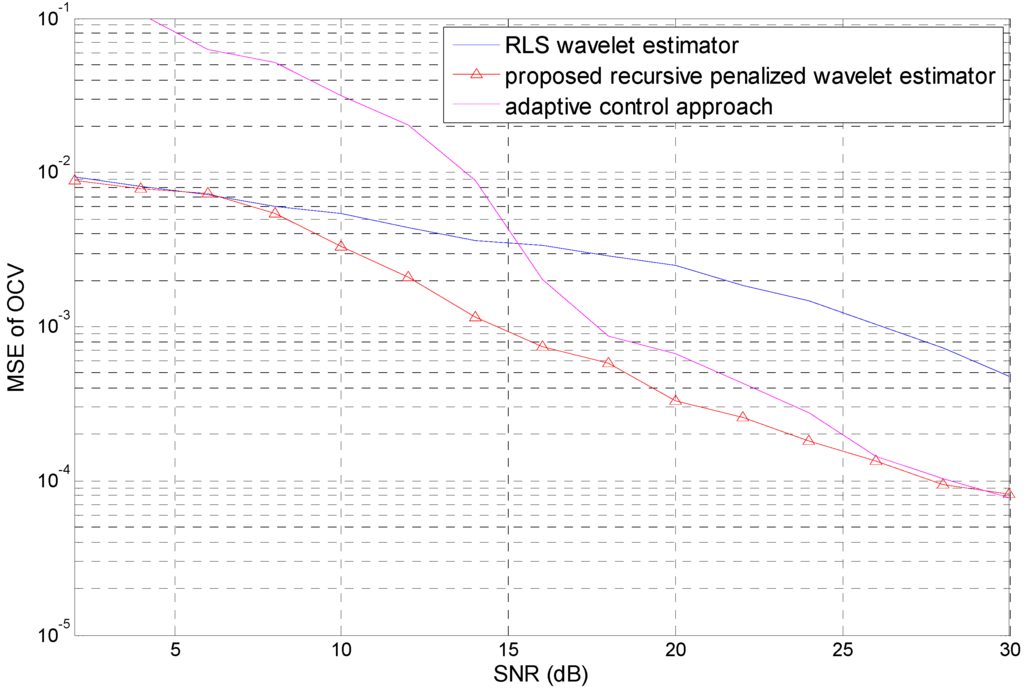
Figure 5.
MSEs of OCV plotted against SNR.
From the above simulation results, it can be seen that the recursive penalized wavelet estimator works well for identifying the equivalent circuit parameters and OCV. The PLBM, as a semiparametric model, combines the simple linear structure and direct physical interpretation ability of the parametric model with the flexibility of the nonparametric model. This is done by modeling the unknown term u(k) in (8) as a nonparametric component, which exhibits high fitting flexibility compared to parametric approaches [,], i.e., the nonparametric approach can be used to accurately identify the OCV without making any prior assumptions on the functional form of OCV (except it is a slowly varying signal). Moreover, unlike the fully nonparametric approaches [,], the proposed semiparametric approach assumes the availability of equivalent circuit model that has explicit physical meaning, i.e., it can directly extracts the equivalent circuit parameters and OCV from the identification results.
It should be pointed out that the wavelet-based PLBM (18) is a generic battery model, which is capable of provide more rich and useful description of battery dynamics in comparison with the baseline model (8). For example, if only the Haar scale basis function at scale zero is used to expand the nonparametric component u(k), the wavelet-based PLBM will be reduced to the baseline model. Since the adaptive identification approaches proposed in [,] are based on the baseline model, a better performance of these adaptive identification approaches could be anticipated by employing the wavelet-based PLBM, which is an interesting topic for future study.
4.2. Experiments
The objective of the experiments is to validate whether the identified results properly represent the real input-to-output behavior of the battery. The experimental studies were conducted on a battery module composed of nine LiMn2O4 lithium-ion cells connected in series Each healthy cell has a nominal voltage of 3.6 V and a nominal capacity of 15 A·h. The experimental setup comprised a Digatron EV battery testing system EVT300-500, a battery management module, a controller area network communication unit, and a host computer running the built-in BMS software BTS-600, as shown in Figure 6. The EVT300-500 system includes a programmable charger/electronic load (which can charge or discharge the battery module with a maximum voltage of 500 V and maximum current of 300 A) and a real-time data acquisition unit that can collect test data, including terminal voltage, outflow current, temperature, and accumulated ampere-hours and watt-hours. The battery management module can also measure the terminal voltage and temperature of each cell in the battery module. The BTS-600 software can deal with the collected data and generate control signals for the EVT300-500 system based on the designed program. To reduce the influence of temperature fluctuation, the experiments were performed under a predefined temperature of 28 °C using a temperature-controlled chamber.
To predict the voltage response of the PLBM, the linear parameters and nonparametric component must first be identified experimentally. After full charging (SoC = 100%) followed by a rest period, the battery module was discharged to 90% SoC at a constant current of 5 A. The terminal voltage and current collected for one FUDS driving cycle are shown in Figure 7a,b, respectively. The sampling period was a half second, and the penalty threshold was empirically chosen as λ = 1.5. The results are shown in Figure 8.
Figures 8a–d show that, given appropriate initial parameter selection, all estimated parameters converged after 400 s. The OCV reduced slowly from its initial value of 34.036 V to the final value of 33.951 V because it decreased as a monotonic function of the SoC. The convergence rate of Rs was much faster than those of the other parameters under a steady value of 25.6 mΩ, which implied that the ohmic internal resistance Rs was less sensitive to the charge–discharge behavior of the lithium-ion battery than the other parameters. The polarized resistance Rp and capacitance Cp converged to 14.3 mΩ and 3900 F, respectively, with some fluctuations.
Based on the previously obtained identification results, we calculated the predicted value of the voltage response of the PLBM using a one-step forward predictor. The voltage response predicted by the model was compared with the measured voltage response as shown in Figure 9a. The relative error analysis result is also shown in Figure 9b. It can be seen that the voltage predicted by the model accurately tracked the measured value despite the large initial value error, and the relative voltage error converged into ± 0.25% of the error band only.
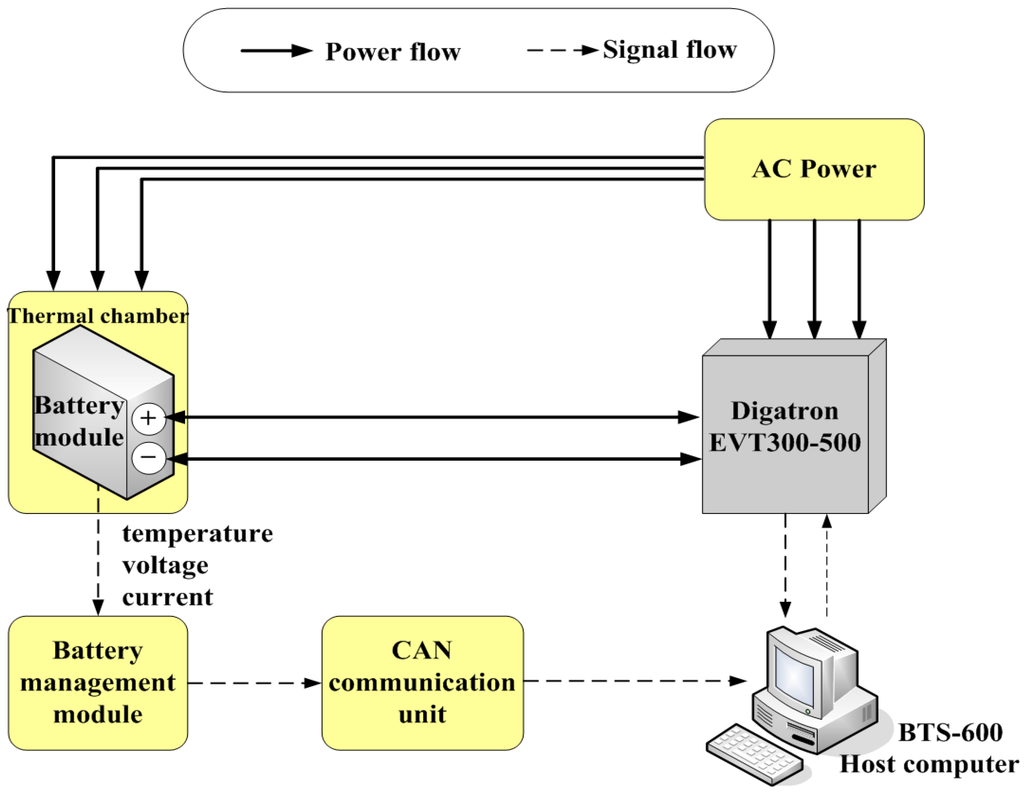
Figure 6.
Schematic diagram of the battery testing system.
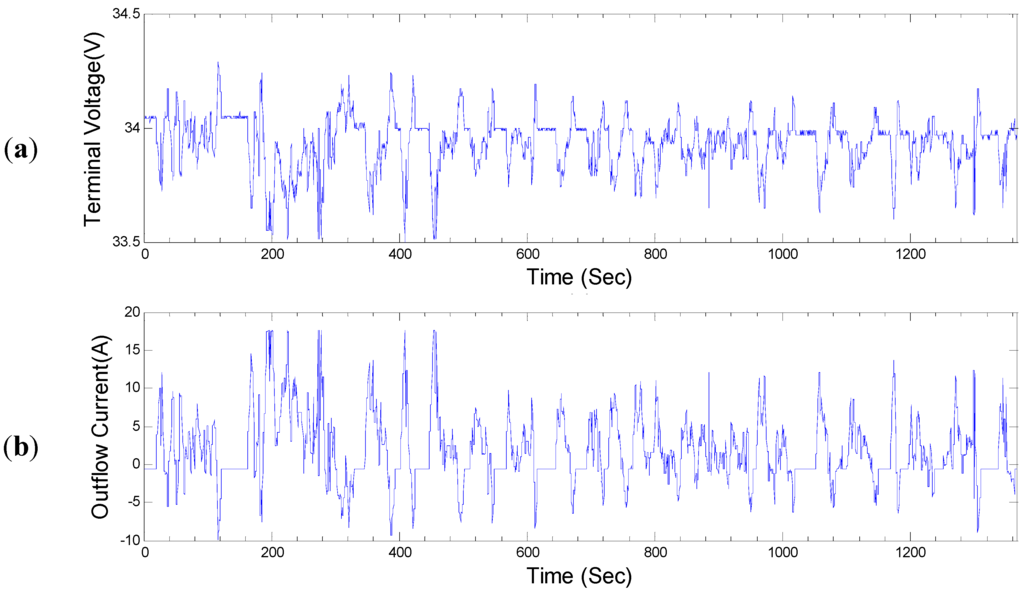
Figure 7.
Measured input–output data in a FUDS cycle: (a) Terminal voltage; (b) Current.
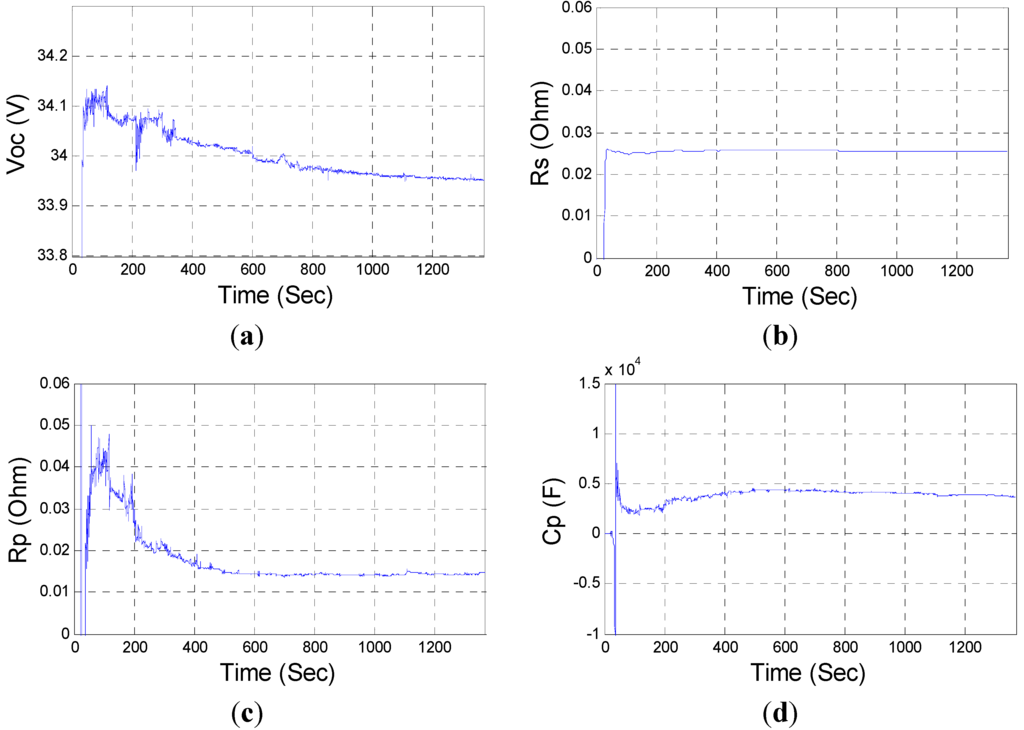
Figure 8.
Identification results for a FUDS cycle: (a) OCV; (b) Rs; (c) Rp; (d) Cp.
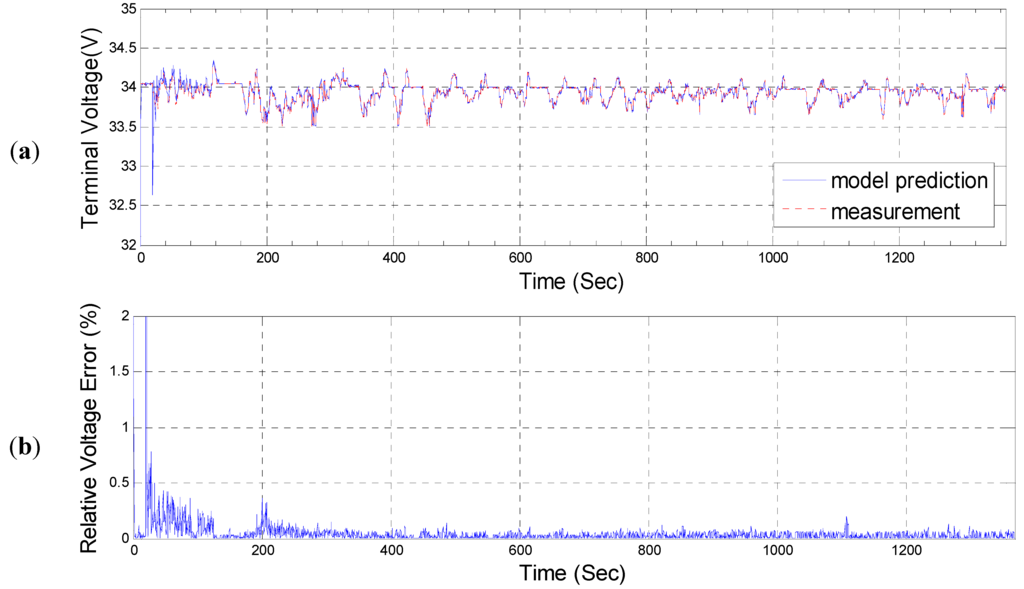
Figure 9.
Validation results of the voltage responses in a FUDS cycle: (a) Measured and predicted battery voltage responses; (b) Relative error rate.
5. Conclusions
To characterize the dynamic behavior of lithium-ion batteries for EVs, this paper has proposed a novel semiparametric identification approach based on the wavelet-based PLBM model. For simplicity, the PLBM developed in this study was based on the first-order equivalent circuit model. However, the analysis results can be easily extended to higher order models. The essential features and advantages of the proposed identification scheme may be summarized as follows:
(1) As a semiparametric model, the PLBM features the flexibility of the nonparametric component while maintaining the direct physical interpretation of the parametric component. Due to its flexible structure, the PLBM can be identified even with poor preliminary knowledge of the OCV.
(2) Because the wavelet method provides a powerful tool for nonstationary signal analysis, we advocate use of the wavelet MRA expansion to model the nonparametric component of the PLBM.
(3) The identification algorithm is very simple because it requires only elementary computations, and simple recursive routines are available for updating both R(k) and r(k), similar to the RLS algorithm.
(4) To exploit the sparsity in the MRA representation and allow for online implementation, a recursive penalized wavelet estimator is proposed, which uses a modified CCD algorithm with l1-norm penalty on the wavelet coefficients to identify the wavelet-based PLBM.
(5) Because the Haar wavelet basis functions are compactly supported, only a small fraction of the wavelet coefficients must be updated for every new measurement data obtained, resulting in low-complexity online computation.
Nomenclature:
| Cp | polarization capacitance |
| cj,m | scaling coefficient of wavelet MRA expansion |
| dj,m | wavelet coefficient of wavelet MRA expansion |
| f | any finite energy signal |
| gi | Haar wavelet basis function |
| h | battery state of charge |
| ib | battery outflow current |
| j | scale level of wavelet MRA expansion |
| j0 | the coarsest scale of wavelet MRA expansion |
| jmax | the finest scale of wavelet MRA expansion |
| J | the truncation scale of truncated wavelet MRA expansion |
| k | discrete time |
| N | length of input/output |
| Rp | polarization resistance |
| Rs | ohmic internal resistance |
| t | continuous time |
| Tc | sampling period |
| u | nonparametric component of PLBM |
| vb | battery terminal voltage |
| vc | polarization voltage |
| voc | open circuit voltage |
| x | observed value of battery terminal voltage |
| y | observed value of battery outflow current |
Greek Symbols
| ε | zero-mean white noise |
| ηi | the ith wavelet expansion coefficient of the nonparametric component of PLBM |
| θi | the ith parameter of the parametric component of PLBM |
| λ | penalty factor |
| ϕ | wavelet scaling function |
| ψ | wavelet mother function |
Acronyms
| CCD | cyclic coordinate descent |
| MRA | multiresolution analysis |
| OCV | open circuit voltage |
| PLBM | partially linear battery model |
| RLS | recursive least square |
| SoC | state of charge |
| SoH | state of health |
Acknowledgments
The work was supported by the National Science Foundation of China (No. 51277010) and the National High Technology Research and Development Program of China (No. 2011AA05A108).
Conflict of Interest
The authors declare no conflict of interest.
References
- Newman, J.; Thomas, K.E.; Hafezi, H.; Wheeler, D.R. Modeling of lithium-ion batteries. J. Power Sources 2003, 119, 838–843. [Google Scholar] [CrossRef]
- Song, L.; Evans, J.W. Electrochemical-thermal model of lithium polymer batteries. J. Electrochem. Soc. 2000, 147, 2086–2095. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 5825–5898. [Google Scholar]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Sitterly, M.; Yin, G.; Wang, C. Enhanced identification of battery models for real-time battery management. IEEE Trans. Sustain. Energy 2011, 2, 300–308. [Google Scholar] [CrossRef]
- Zhang, C.P.; Jiang, J.C.; Zhang, W.G.; Suleiman, M.S. Estimation of state of charge of lithium-ion batteries used in HEV using robust extended Kalman filtering. Energies 2012, 5, 10981–11115. [Google Scholar]
- Sarvi, M.; Ghaffarzadeh, N. A wavelet network based model for Ni-Cd batteries. Int. J. Electrochem. Sci. 2012, 7, 10291–10302. [Google Scholar]
- Shen, Y. Adaptive online state-of-charge determination based on neuro-controller and neural network. Energy Convers. Manag. 2010, 51, 1093–1098. [Google Scholar] [CrossRef]
- Shen, W.; Chan, C.; Lo, E.; Chau, K. A new battery available capacity indicator for electric vehicles using neural network. Energy Convers. Manag. 2002, 43, 817–826. [Google Scholar] [CrossRef]
- Tsang, K.; Sun, L.; Chan, W. Identification and modelling of lithium ion battery. Energy Convers. Manag. 2010, 51, 2857–2862. [Google Scholar] [CrossRef]
- Bhangu, B.; Bentley, P.; Stone, D.; Bingham, C. Nonlinear observers for predicting state-of-charge and state-of-health of lead-acid batteries for hybrid-electric vehicles. IEEE Trans. Veh. Tech. 2005, 54, 783–794. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J.; Rice, J.; Weiss, A. Semiparametric estimates of the relation between weather and electricity sales. J. Am. Stat. Assoc. 1986, 81, 310–320. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Q. Semiparametric partially linear regression models for functional data. J. Stat. Plan. Infer. 2012, 142, 2518–2529. [Google Scholar] [CrossRef]
- Chang, X.W.; Qu, L. Wavelet estimation of partially linear models. Comp.Stat. Data Anal. 2004, 47, 31–48. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y.; Peng, H. Online Estimation of an Electric Vehicle Lithium-Ion Battery Using Recursive Least Squares with Forgetting. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 935–940.
- Kim, I.S. The novel state of charge estimation method for lithium battery using sliding mode observer. J. Power Sources 2006, 163, 584–590. [Google Scholar] [CrossRef]
- Chiang, Y.H.; Sean, W.Y.; Ke, J.C. Online estimation of internal resistance and open-circuit voltage of lithium-ion batteries in electric vehicles. J. Power Sources 2011, 196, 3921–3932. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S. Linear parameter varing battery model identification using subspace methods. J. Power Sources 2011, 196, 2913–2923. [Google Scholar] [CrossRef]
- Gould, C.; Bingham, C.; Stone, D.; Bentley, P. New battery model and state-of-health determination through subspace parameter estimation and state-observer techniques. IEEE Trans. Veh. Tech. 2009, 58, 3905–3916. [Google Scholar] [CrossRef]
- Zhang, C.P.; Zhang, C.N.; Liu, J.Z.; Sharkh, S.M. Identification of dynamic model parameters for lithium-ion batteries used in hybrid electric vehicles. High Technol. Lett. 2010, 16, 6–12. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar] [CrossRef]
- Fadili, J.M.; Bullmore, E. Penalized partially linear models using sparse representations with an application to fMRI time series. IEEE Trans. Signal Process. 2005, 53, 3436–3448. [Google Scholar] [CrossRef]
- Ding, H.; Claeskens, G.; Jansen, M. Variable selection in partially linear wavelet models. Statist. Model. 2011, 11, 409–427. [Google Scholar] [CrossRef]
- Espinoza, M.; Suykens, J.A.K.; de Moor, B. Kernel based partially linear models and nonlinear identification. IEEE Trans. Autom. Control 2005, 50, 1602–1606. [Google Scholar] [CrossRef]
- Yu, Y.; Ruppert, D. Penalized spline estimation for partially linear single-index models. J. Am. Stat. Assoc. 2002, 97, 1042–1054. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Meyer, F.G. Wavelet-based estimation of a semiparametric generalized linear model of fMRI time-series. IEEE Trans. Med. Imag. 2003, 22, 315–322. [Google Scholar] [CrossRef]
- Wu, T.T.; Lange, K. Coordinate descent algorithms for lasso penalized regression. Ann. Appl. Stat. 2008, 2, 224–244. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Höfling, H.; Tibshirani, R. Pathwise coordinate optimization. Ann. Appl. Stat. 2007, 1, 302–332. [Google Scholar] [CrossRef]
- Angelosante, D.; Bazerque, J.A.; Giannakis, G.B. Online adaptive estimation of sparse signals: Where RLS meets the l1-normal. IEEE Trans. Signal Process. 2010, 58, 3436–3447. [Google Scholar] [CrossRef]
- Kekatos, V.; Angelosante, D.; Giannakis, G.B. Sparsity-Aware Estimation of Nonlinear Volterra Kernels. In Proceedings of the 3rd IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Aruba, Dutch Antilles, 13–16 December 2009; pp. 129–132.
- Pawlak, M.; Hasiewicz, Z. Nonlinear system identification by the Haar multiresolution analysis. IEEE Trans. Circuits Syst. I 1998, 45, 945–961. [Google Scholar] [CrossRef]
- Wei, H.; Billings, S. A unified wavelet-based modelling framework for non-linear system identification: The WANARX model structure. Int. J. Control 2004, 77, 351–366. [Google Scholar] [CrossRef]
- Billings, S.A.; Wei, H.L. A new class of wavelet networks for nonlinear system identification. IEEE Trans. Neural Netw. 2005, 16, 862–874. [Google Scholar] [CrossRef] [PubMed]
- Sliwinski, P.; Hasiewicz, Z. Computational algorithms for wavelet identification of nonlinearities in hammerstein systems with random inputs. IEEE Trans. Signal Process. 2008, 56, 846–851. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).