Similarity Analysis in Scaling a Gas Hydrates Reservoir
Abstract
:1. Introduction
2. Experimental Section
2.1. Experimental Apparatus
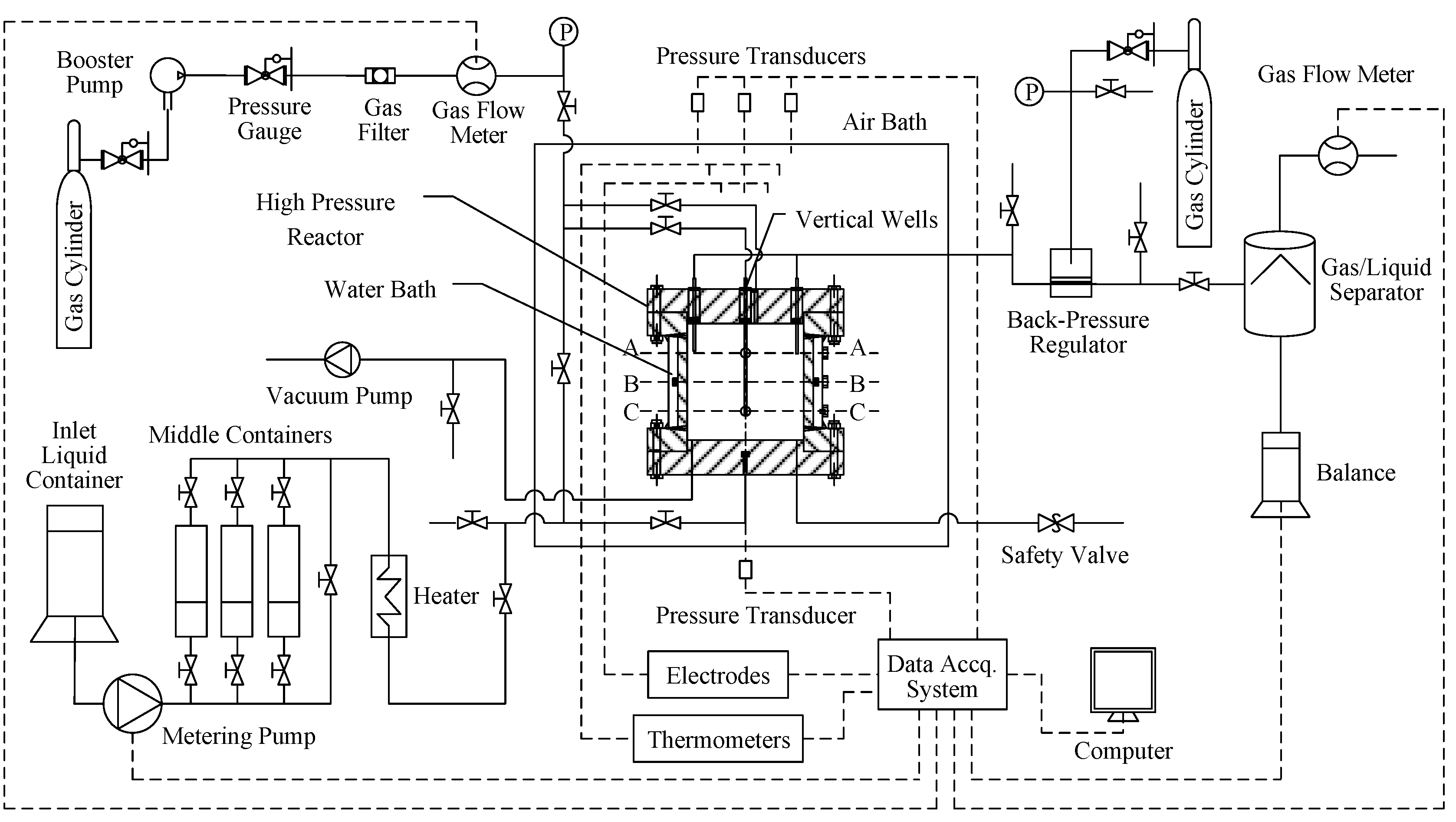
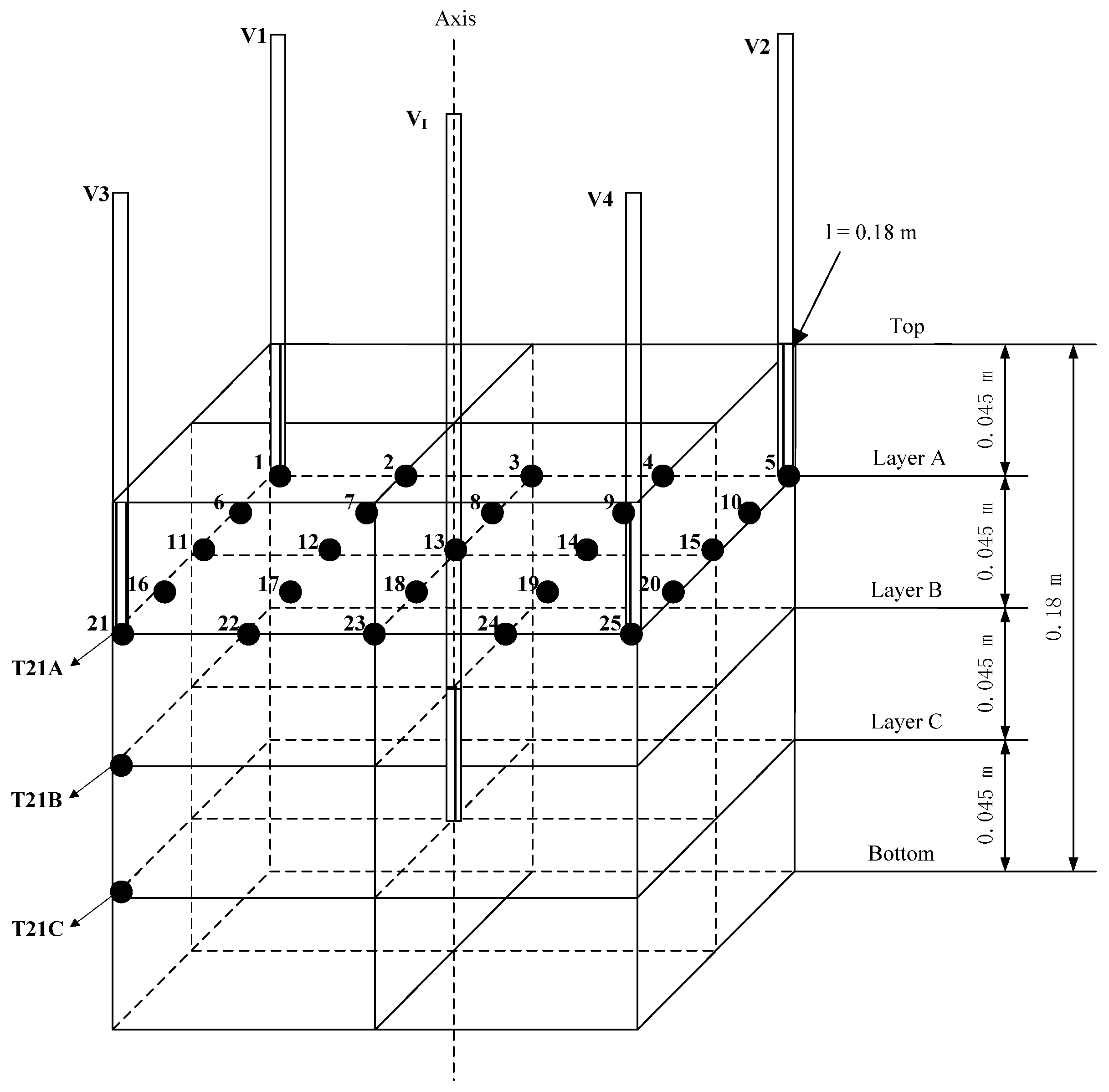
2.2. Experimental Method
3. Scaling Criteria
3.1. Mathematical Model
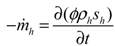
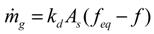
3.2. Calculation
- π1 and π2 are the dimensionless permeabilities of water and gas, respectively;
- π3 is the dimensionless absolutely permeability;
- π4–π11 are the similarities of geometry, well position, and well radius, respectively;
- π12–π14 are the density ratios of hydrate to gas, rock to gas, and water to hydrate, respectively;
- π15–π17 are the conductivity coefficient ratios of gas to water, hydrate to water, and rock to water, respectively;
- π18–π20 are the specific heat ratios of gas to water, hydrate to water, and rock to water, respectively;
- π21 is the dimensionless dissociation heat of hydrate;
- π22 and π23 are the ratios of hydrate equilibrium pressure to gas production pressure, and initial gas pressure to gas production pressure, respectively;
- π24 is the dimensionless temperature in the hydrate reservoir;
- π25 is the dimensionless injection temperature;
- π26 is the dimensionless initial gas saturation;
- π27 is the initial hydrate saturation;
- π28 and π29 are the saturation of residual gas and residual water, respectively;
- π30 is the total porosity;
- π31 is the mobility ratio of the water in residual gas and the gas in residual water;
- π32 is the amount ratio of gas flow per unite area to gas production per unite area in hydrate sediment;
- π33 is the ratio of conduction heat to hydrate dissociation heat per unite time;
- π34 is the ratio of capillary force to gas production pressure;
- π35 is the amount ratio of water flow per unite area to water production per unite area in hydrate sediment;
- π36 is the dimensionless gravity.
4. Results and Discussion
4.1. Production Process
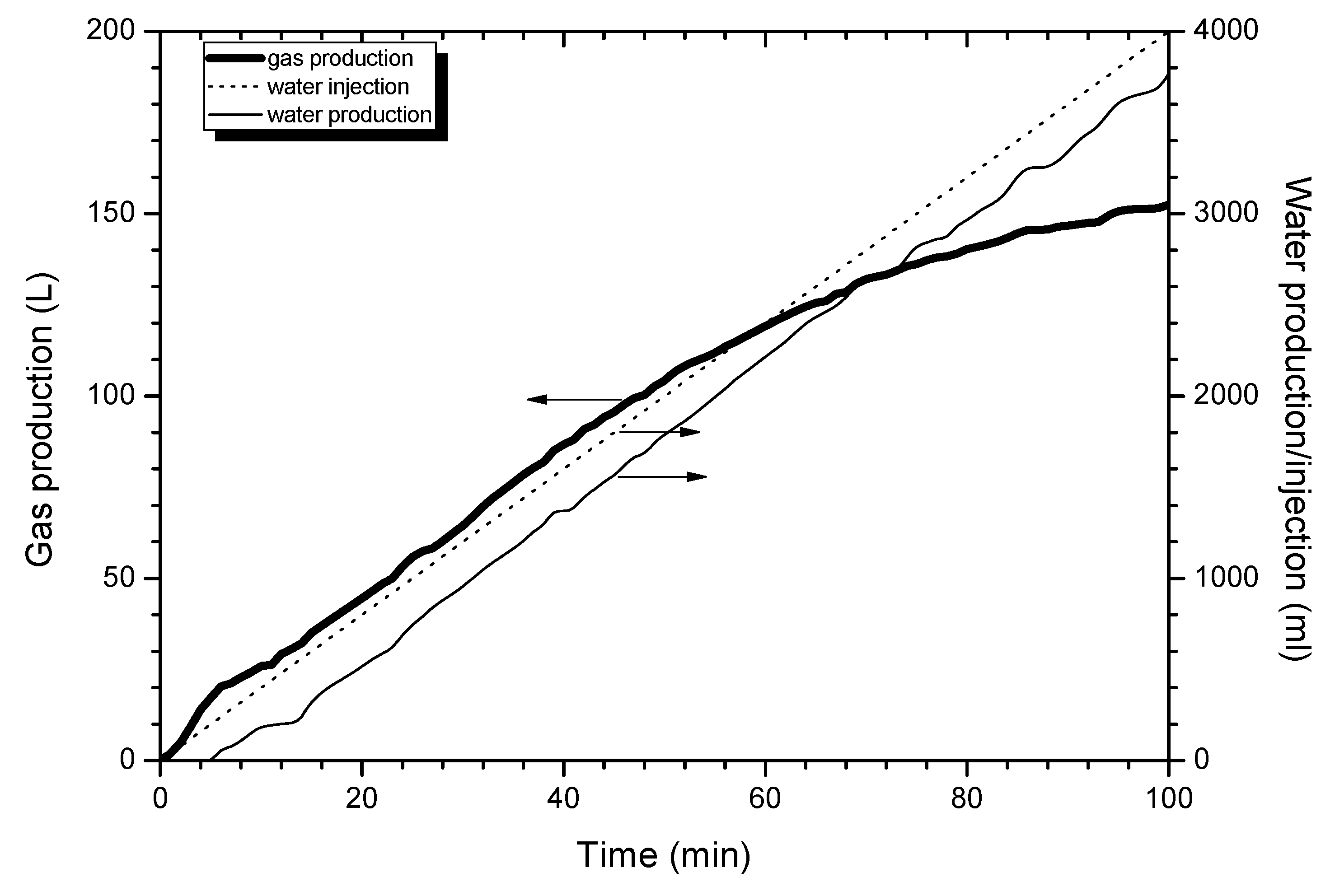
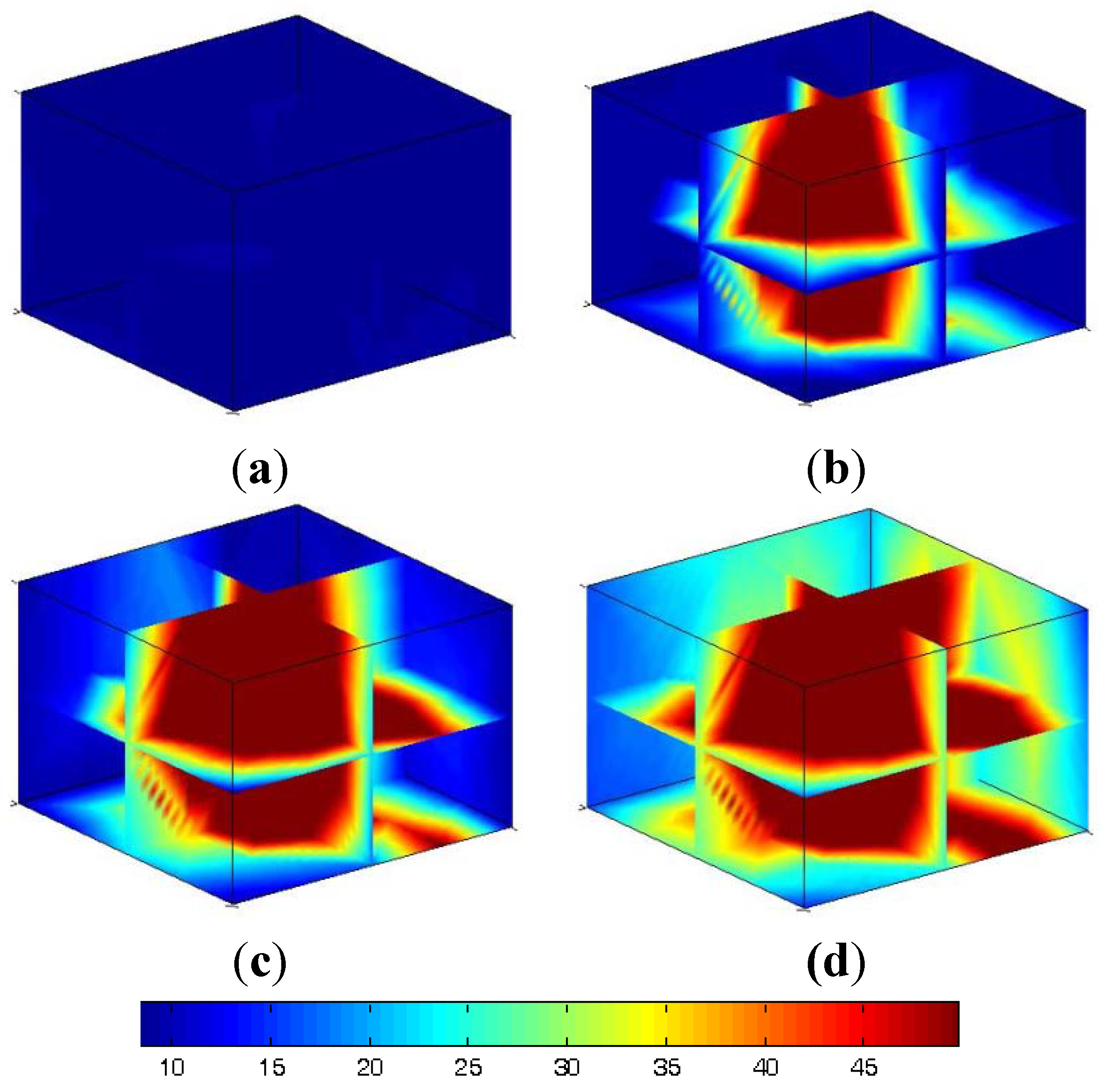
4.2. Similar Model
| Parameters | L/m | H/m | W/m | qI /m3s−1 | r0/m | Sh |
|---|---|---|---|---|---|---|
| CHS | 0.18 | 0.18 | 0.18 | 6.7 × 10−7 | 2 × 10−3 | 0.310 |
| Scaling model | 18 | 18 | 18 | 3.1 × 10−2 | 1 × 10−1 | 0.310 |
| Parameters | TI/°C | ø 0 | Pgp/MPa | g/ms−2 | t/min | Q/m3 |
| CHS | 130 | 0.46 | 6.5 | 9.8 | 100 | 0.152 |
| Scaling model | 130 | 0.46 | 6.5 | 9.8 | 2154 | 1.52 × 105 |
5. Conclusions
Nomenclature
Abbreviation
| CHS | Cubic Hydrate Simulator |
Symbols
| V | wellhead |
| qi | rate of hot water (mL/min) |
| Ti | temperature of hot water (K) |
| x, y, z | coordinates |
| ø | porosity |
| ø0 | total porosity |
| øe | effective porosity |
| s | saturation |
| P | pressure (MPa) |
| µ | viscosity (Pa S) |
| ρ | density (kg m−3) |
| K | permeability (m−2) |
| K0 | maximum absolute permeability (m−2) |
mass rate (m3 s−1) | |
| h | specific heat (J kg−1K−1) |
| λ | conductivity coefficient (w m−1 K−1) |
| q | heat changes on boundary (J) |
| g | the gravitational acceleration (m s−2) |
| xp, yp | coordinates of the production well (m) |
| xI, yI | coordinates of the injection well (m) |
| r0 | well radii (m) |
| re0 | effective radii of well (m) |
| ∆H | enthalpy change of hydrate decomposition (J) |
| M | molecular weight |
| Nh | coefficient of dissociation reaction (5.8) |
| As | specific surface area of porous media (m2) |
| f | gas fugacity (Pa) |
| kd | the dissociation constant |
| L | length (m) |
| H | thickness (m) |
| W | width (m) |
| Q | volume of gas production (m3) |
| σ | gas throttle coefficient |
Subscripts
| i | initial |
| p | production |
| g | gas |
| w | water |
| h | hydrate |
| r | rock |
| eq | phase equilibrium |
| D | dimensionless |
| m | model |
| f | prototype |
Acknowledgments
Conflict of Interest
References
- Sloan, E.D. Fundamental principles and applications of natural gas hydrates. Nature 2003, 426, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Sloan, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gases, 3rd ed.; Taylor and Francis, Inc.: Boca Raton, FL, USA, 2008. [Google Scholar]
- Milkov, A.V. Global estimates of hydrate-bound gas in marine sediments: How much is really out there? Earth-Sci. Rev. 2004, 66, 183–197. [Google Scholar] [CrossRef]
- Klauda, J.B.; Sandler, S.I. Global distribution of methane hydrate in ocean sediment. Energy Fuel 2005, 19, 459–470. [Google Scholar] [CrossRef]
- Kvenvolden, K.A. Methane hydrate-a major reservoir of carbon in the shallow geosphere. Chem. Geol. 1988, 71, 41–51. [Google Scholar] [CrossRef]
- Li, X.S.; Wan, L.H.; Li, G.; Li, Q.P.; Chen, Z.Y.; Yan, K.F. Experimental investigation into the production behavior of methane hydrate in porous sediment with hot brine stimulation. Ind. Eng. Chem. Res. 2008, 47, 9696–9702. [Google Scholar] [CrossRef]
- Sasaki, K.; Ono, S.; Sugai, Y.; Ebinuma, T.; Narita, H.; Yamaguchi, T. Gas production system from methane hydrate layers by hot water injection using dual horizontal wells. J. Can. Petrol. Technol. 2009, 48, 21–26. [Google Scholar] [CrossRef]
- Li, X.S.; Wang, Y.; Li, G.; Zhang, Y.; Chen, Z.Y. Experimental investigation into methane hydrate decomposition during three-dimensional thermal huff and puff. Energy Fuel 2011, 25, 1650–1658. [Google Scholar] [CrossRef]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Bai, Y.H.; Li, J.C.; Zhou, J.F.; Li, Q.P. Sensitivity analysis of the dimensionless parameters in scaling a polymer flooding reservoir. Transp. Porous Med. 2008, 73, 21–37. [Google Scholar] [CrossRef]
- Li, X.S.; Zhang, Y.; Li, G.; Chen, Z.Y.; Wu, H.J. Experimental investigation into the production behavior of methane hydrate in porous sediment by depressurization with a novel three-dimensional cubic hydrate simulator. Energy Fuel 2011, 25, 4497–4505. [Google Scholar] [CrossRef]
- Li, X.S.; Wang, Y.; Li, G.; Zhang, Y. Experimental investigations into gas production behaviors from methane hydrate with different methods in a cubic hydrate simulator. Energy Fuel 2011, 26, 1124–1134. [Google Scholar] [CrossRef]
- Linga, P.; Haligva, C.; Nam, S.C.; Ripmeester, J.A.; Englezos, P. Gas hydrate formation in a variable volume bed of silica sand particles. Energy Fuel 2009, 23, 5496–5507. [Google Scholar] [CrossRef]
- Li, X.S.; Zhang, Y.; Li, G.; Chen, Z.Y.; Yan, K.F.; Li, Q.P. Gas hydrate equilibrium dissociation conditions in porous media using two thermodynamic approaches. J. Chem. Thermodyn. 2008, 40, 1464–1474. [Google Scholar] [CrossRef]
- Civan, F. Scale effect on porosity and permeability: Kinetics, model, and correlation. Aiche J. 2001, 47, 271–287. [Google Scholar] [CrossRef]
- Selim, M.S.; Sloan, E.D. Heat and mass transfer during the dissociation of hydrates in porous media. Aiche J. 1989, 35, 1049–1052. [Google Scholar] [CrossRef]
- Kim, H.C.; Bishnoi, P.R.; Heidemann, R.A.; Rizvi, S.S.H. Kinetics of methane hydrate decomposition. Chem. Eng. Sci. 1987, 42, 1645–1653. [Google Scholar] [CrossRef]
- Makogon, Y.F. Hydrate of Hydrocarbons; Penn Well Publishing Company: Tulsa, OK, USA, 1997. [Google Scholar]
- Liu, Y.; Chen, Y.; Bai, Y.; Li, S. Similarity theory for the physical simulation of natural gas hydrate reservoir development. Min. Sci. Technol. (China) 2010, 20, 782–788. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, Y.; Xu, C.-G.; Li, X.-S.; Li, G.; Chen, Z.-Y. Similarity Analysis in Scaling a Gas Hydrates Reservoir. Energies 2013, 6, 2468-2480. https://doi.org/10.3390/en6052468
Wang Y, Xu C-G, Li X-S, Li G, Chen Z-Y. Similarity Analysis in Scaling a Gas Hydrates Reservoir. Energies. 2013; 6(5):2468-2480. https://doi.org/10.3390/en6052468
Chicago/Turabian StyleWang, Yi, Chun-Gang Xu, Xiao-Sen Li, Gang Li, and Zhao-Yang Chen. 2013. "Similarity Analysis in Scaling a Gas Hydrates Reservoir" Energies 6, no. 5: 2468-2480. https://doi.org/10.3390/en6052468
APA StyleWang, Y., Xu, C.-G., Li, X.-S., Li, G., & Chen, Z.-Y. (2013). Similarity Analysis in Scaling a Gas Hydrates Reservoir. Energies, 6(5), 2468-2480. https://doi.org/10.3390/en6052468







