Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II
Abstract
:1. Introduction
- the criteria for optimization are evaluated on active power distribution systems (containing distributed generators connected directly to the main distribution system and microgrids operated in grid-connected mode);
- the original formulation of the optimization problem, as a Pareto optimal one, with two objective functions (active power losses and system average interruption frequency index);
- an original genetic algorithm (based on NSGA-II) to solve the problem (as a Pareto optimal one) in a non-prohibitive execution time.
2. Problem Formulation
2.1. Criteria for Optimization
2.1.1. Active Power Losses (ΔP)
2.1.2. Reliability of the Distribution System
- Reliability of a particular customer: e.g., the average number of interruptions to the power supply. This index can represent a possible objective and/or constraint in the optimization problem (because some customers can impose maximal/minimal limits in their supply contracts);
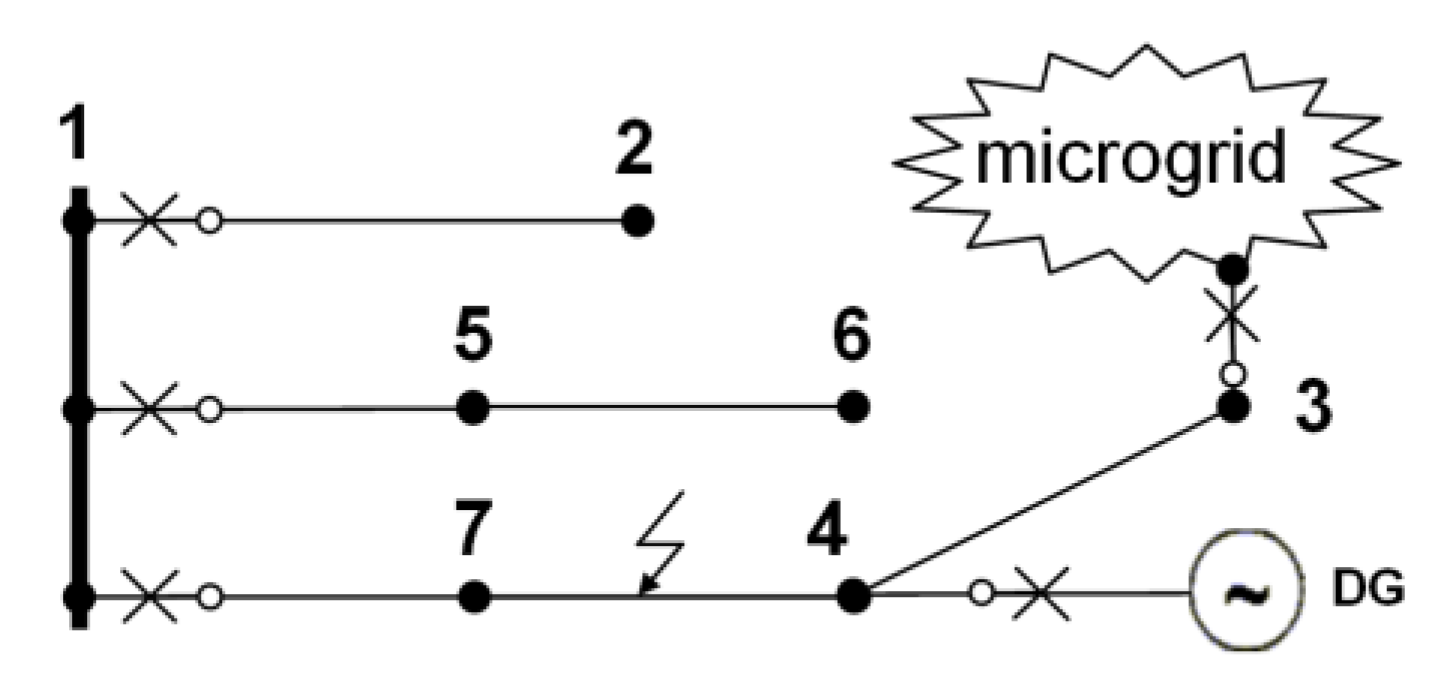
- N = 30 ∙ 6 = 180 (six nodes, 30 customers for each node);
- λt2∙ N2 = 0.5 ∙ 30 = 15;
- λt3∙ N3 = 0.5 ∙ 3 ∙ 0 = 0 (three branches, the microgrid is expected to operate as an island and customers from a microgrid will be supplied even if a fault has occurred in the main distribution system);
- λt4∙ N4 = 0.5 ∙ 3 ∙ 30 = 45 (three branches, if a fault occurs on the path 1-7-4-3, the DG unit will be switched off and the customers will be not supplied);
- λt5∙ N5 = λt6∙ N6 = 0.5 ∙ 2 ∙ 30 = 30 (two branches);
- λt7∙ N7 = 0.5 ∙ 3 ∙ 30 = 45;
- SAIFI = (15 + 0 + 45 + 30 + 30 + 45)/180 = 0.9167.
2.1.3. Other Criteria
- Node Voltages (Vi): Basically, each voltage r.m.s. value of the network nodes must be framed within the allowable limits.
- Branch Load Limits through Lines (Iij): a typical constraint on the reconfiguration problem.
- Safeguard of power supplies for all customers: The attached graph of the electric system should be connected (a tree or a forest).
- Configuration of the Distribution System: Generally, electrical distribution systems are operated in radial configuration. This condition can be expressed as follows:where αij is a binary variable, representing the status of a tie line (0–open, 1–closed); n is the number of electric system nodes; E is the set of power system lines (branches) and p is the number of connected components. In graph theory terms, for a system with one source (p = 1) we are talking about an optimal tree and for a system with more than one feeder (p > 1) we are talking about an optimal forest with a number of trees (connected components) equal to that of source nodes.
2.2. Pareto Optimality Problem Formulation
- Objective function
- Constraints
3. Problem Solving
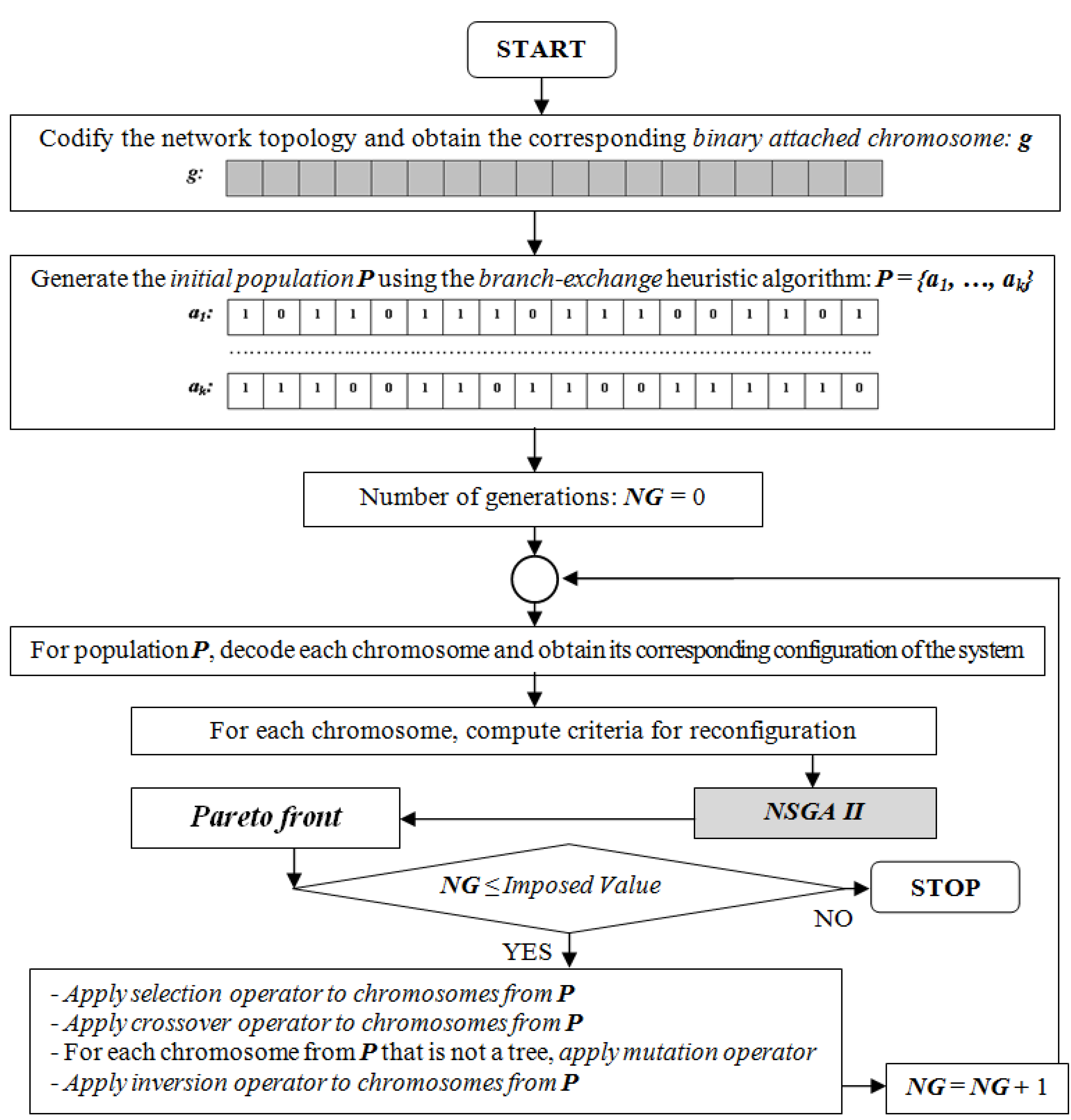
3.1. Genetic Encoding and Decoding of Power Distribution System Topology
3.1.1. Genetic Encoding

3.1.2. Genetic Decoding
3.2. Genetic Operators
3.2.1. Selection
3.2.2. Crossover
3.2.3. Mutation
3.2.4. Inversion
4. Simulation Results
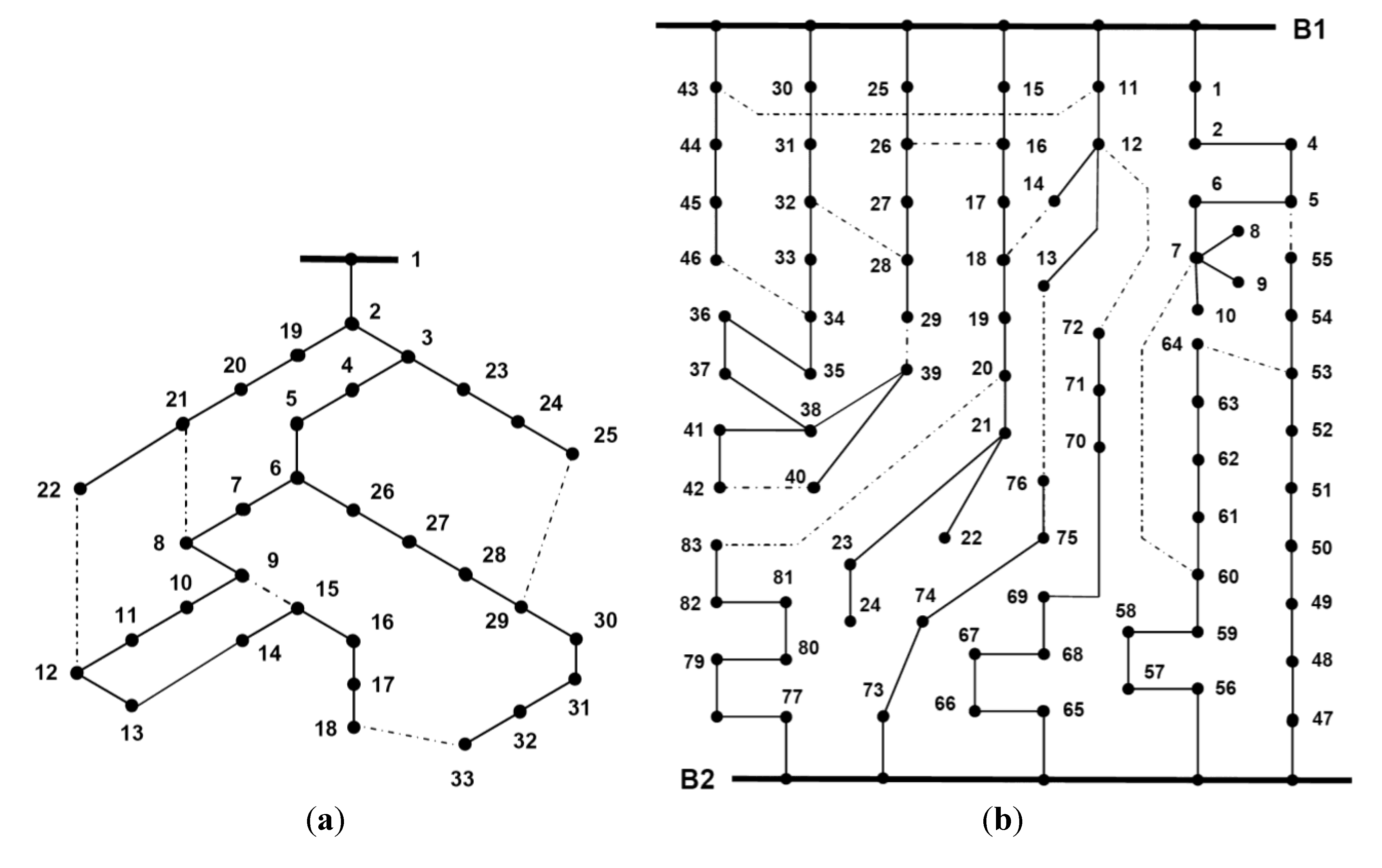
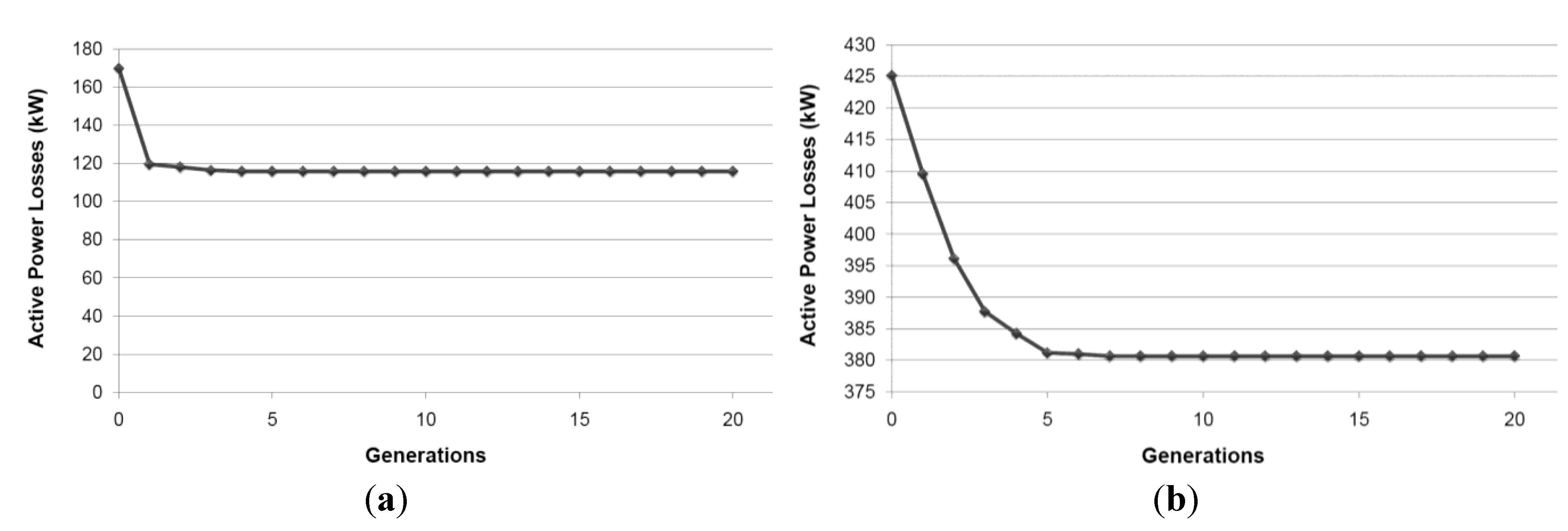
- System A (Figure 5a) [3,27]: There are four DG units installed on nodes 3, 6, 24 and 29 [27]. In the base case, the total active power losses are 169.881 kW. By applying MOReco algorithm (after reconfiguration), the total active power losses are 115.748 kW. The evolution of the active power losses along the searching process is presented in Figure 6a.
- System B (Figure 5b) [27]: In this case, there are eight DG units installed on nodes: 7, 12, 19, 28, 34, 71, 75 and 79 [26]. Before the reconfiguration, the total active power losses are 425.131 kW (as in [26]). After reconfiguration, we obtained a better configuration than the one presented in [26]. The total active power losses are 380.656 kW, therefore smaller than 383.524 kW. The evolution of the active power losses along the searching process is presented in Figure 6b.
| System | Configuration | Open branches (tie lines) | Active power losses | CPU runtime for 100 runs | Population/Generations | |
|---|---|---|---|---|---|---|
| A | Base case | 8–21, 9–15, 12–22, 18–33, 25–29 | 169.881 | kW | - | |
| MOReco | 7–8, 9–10, 14–15, 28–29, 32–33 | 115.748 | kW | Minimum (3 s: 804 ms) Maximum (3 s: 974 ms) Average (3 s: 910 ms) | 10/4 | |
| B | Base case | 5–55, 7–60, 11–43, 12–72, 13–76, 14–18, 16–26, 20–83, 28–32, 29–39, 34–46, 40–42, 53–64 | 425.131 | kW | - | |
| MOReco | 6–7, 12–13, 32–33, 38–39, 41–42, 54–55, 62–63, 71–72, 82–83, 11–43, 14–18, 16–26, 28–32 | 380.656 | kW | Minimum (6 s: 202 ms) Maximum (7 s: 108 ms) Average (6 s: 675 ms) | 10/8 | |
| System | Open branches (tie lines) | Active power losses | SAIFI | CPU runtime for 100 runs | Population/Generations | |
|---|---|---|---|---|---|---|
| B with DGs | 6–7, 12–13, 32–33, 38–39, 41–42, 54–55, 62–63, 71–72, 82–83, 11–43, 14–18, 16–26, 28–32 | 380.656 | kW | 1.143 | Minimum (6 s: 952 ms) Maximum (7 s: 279 ms) Average (7 s: 40 ms) | 10/9 |
| 5–55, 6–7, 11–43, 12–72, 13–76, 14–18, 16–26, 20–83, 28–32, 29–39, 32–33, 40–42, 53–64 | 396.143 | kW | 0.751 | - | ||
| 5–55, 6–7, 11–43, 12–72, 13–76, 14–18, 16–26, 20–83, 28–32, 29–39, 34–46, 40–42, 53–64 | 409.526 | kW | 0.648 | - | ||
| 5–55, 7–60, 11–43, 12–72, 13–76, 14–18, 16–26, 20–83, 28–32, 29–39, 34–46, 40–42, 53–64 | 425.131 | kW | 0.472 | - | ||
| B with microgrids | 6–7, 12–13, 32–33, 38–39, 41–42, 54–55, 62–63, 71–72, 82–83, 11–43, 14–18, 16–26, 28–32 | 380.656 | kW | 0.988 | Minimum (7 s: 114 ms) Maximum (7 s: 342 ms) Average (7 s: 171 ms) | 10/9 |
| 5–55, 6–7, 11–43, 12–72, 13–76, 14–18, 16–26, 20–83, 28–32, 29–39, 32–33, 40–42, 53–64 | 396.143 | kW | 0.619 | - | ||
| 5–55, 7–60, 11–43, 12–72, 13–76, 14–18, 16–26, 20–83, 28–32, 29–39, 34–46, 40–42, 53–64 | 425.131 | kW | 0.427 | - | ||
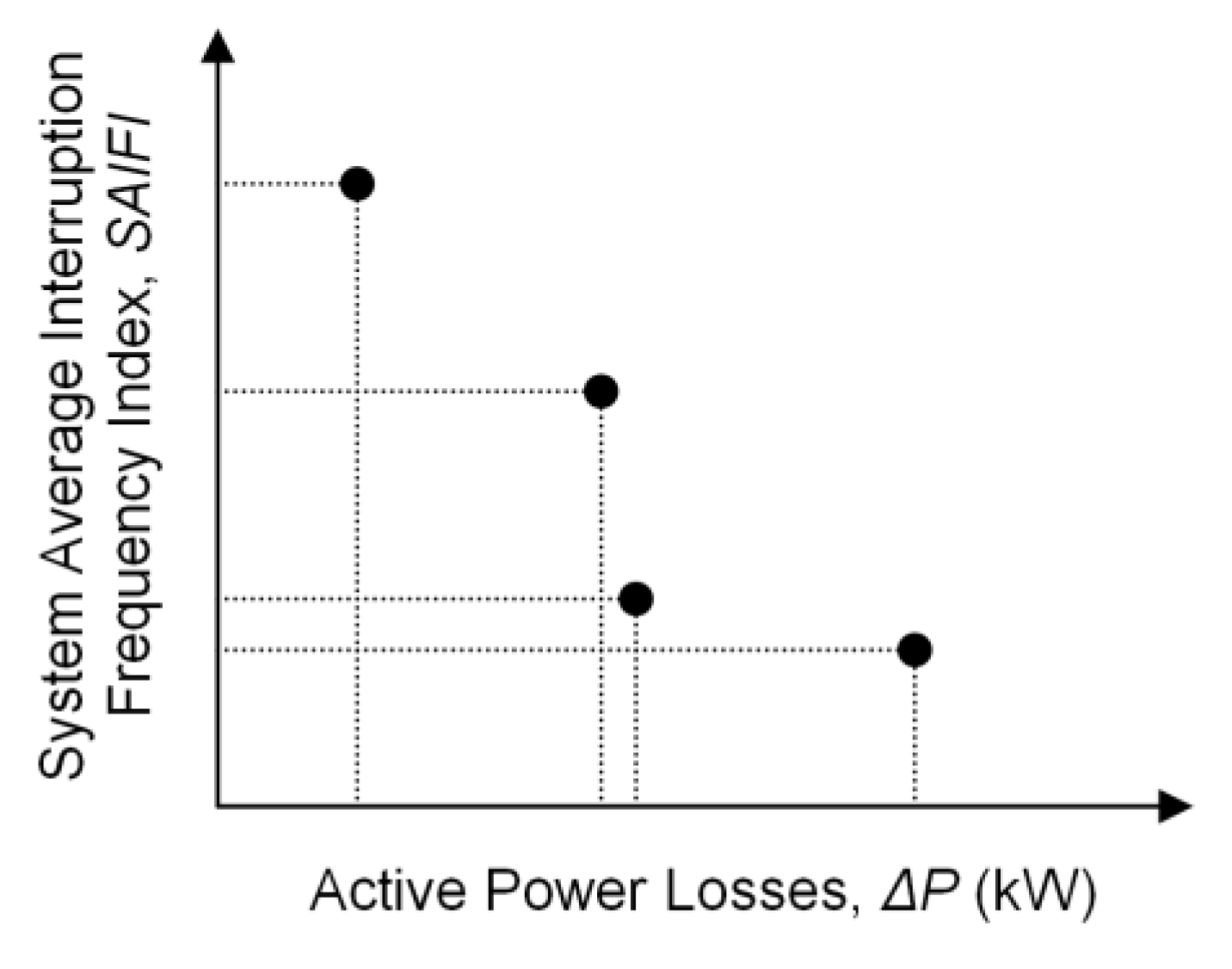
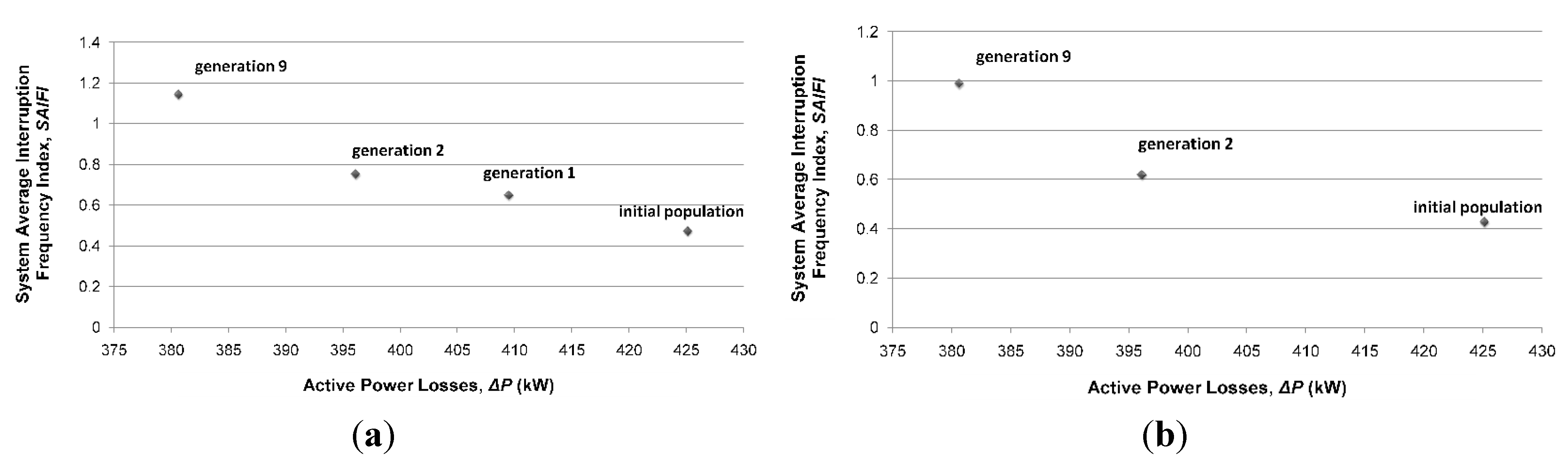
- System B with DG units: The proposed algorithm has obtained a Pareto front with four solutions (Figure 7a). In this case, the first non-dominated solution was obtained from initial population. After the first generation, the algorithm found the second non-dominated solution (the Pareto front contains two solutions). The searching process continued and the third non-dominated solution was found in generation 2 (at the end of generation 2, the Pareto front contains three solutions). The searching process continued, but without finding other non-dominated solutions until generation 9, where the fourth and final non-dominated solution was found. In the end, the Pareto front contains four non-dominated solutions.
- System B with microgrids (instead of DG units, as sources on the points of common coupling): The proposed algorithm obtained a Pareto front with three solutions (Figure 7b). As in the previous case, along the searching process, the Pareto front increases from one solution (from the initial population), to two solutions (generation 2) and, finally, to three solutions (in generation 9). We can observe that the SAIFI index is smaller in the case of existing microgrids than in the case where we consider just distributed generators.
5. Conclusions
Acknowledgments
Appendix
| Branch | i | j | λ [year−1] | Branch | i | j | λ [year−1] | Branch | i | j | λ [year−1] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | B1 | 1 | 0.071 | 37 | 36 | 37 | 0.016 | 73 | B10 | 73 | 0.019 |
| 2 | 1 | 2 | 0.096 | 38 | 37 | 38 | 0.024 | 74 | 73 | 74 | 0.082 |
| 3 | 2 | 3 | 0.078 | 39 | 38 | 39 | 0.064 | 75 | 74 | 75 | 0.009 |
| 4 | 3 | 4 | 0.035 | 40 | 39 | 40 | 0.065 | 76 | 75 | 76 | 0.091 |
| 5 | 4 | 5 | 0.065 | 41 | 38 | 41 | 0.095 | 77 | B11 | 77 | 0.065 |
| 6 | 5 | 6 | 0.082 | 42 | 41 | 42 | 0.046 | 78 | 77 | 78 | 0.017 |
| 7 | 6 | 7 | 0.059 | 43 | B6 | 43 | 0.085 | 79 | 78 | 79 | 0.017 |
| 8 | 7 | 8 | 0.012 | 44 | 43 | 44 | 0.075 | 80 | 79 | 80 | 0.091 |
| 9 | 7 | 9 | 0.012 | 45 | 44 | 45 | 0.062 | 65 | B9 | 65 | 0.042 |
| 10 | 7 | 10 | 0.011 | 46 | 45 | 46 | 0.036 | 66 | 65 | 66 | 0.054 |
| 11 | B2 | 11 | 0.007 | 47 | B7 | 47 | 0.065 | 67 | 66 | 67 | 0.017 |
| 12 | 11 | 12 | 0.039 | 48 | 47 | 48 | 0.093 | 68 | 67 | 68 | 0.016 |
| 13 | 12 | 13 | 0.095 | 49 | 48 | 49 | 0.019 | 69 | 68 | 69 | 0.085 |
| 14 | 12 | 14 | 0.036 | 50 | 49 | 50 | 0.065 | 70 | 69 | 70 | 0.066 |
| 15 | B3 | 15 | 0.048 | 51 | 50 | 51 | 0.017 | 71 | 70 | 71 | 0.052 |
| 16 | 15 | 16 | 0.076 | 52 | 51 | 52 | 0.017 | 72 | 71 | 72 | 0.052 |
| 17 | 16 | 17 | 0.023 | 53 | 52 | 53 | 0.051 | 73 | B10 | 73 | 0.019 |
| 18 | 17 | 18 | 0.094 | 54 | 53 | 54 | 0.026 | 74 | 73 | 74 | 0.082 |
| 19 | 18 | 19 | 0.056 | 55 | 54 | 55 | 0.055 | 75 | 74 | 75 | 0.009 |
| 20 | 19 | 20 | 0.067 | 56 | B8 | 56 | 0.026 | 76 | 75 | 76 | 0.091 |
| 21 | 20 | 21 | 0.099 | 57 | 56 | 57 | 0.017 | 77 | B11 | 77 | 0.065 |
| 22 | 21 | 22 | 0.045 | 58 | 57 | 58 | 0.032 | 78 | 77 | 78 | 0.017 |
| 23 | 21 | 23 | 0.073 | 59 | 58 | 59 | 0.017 | 79 | 78 | 79 | 0.017 |
| 24 | 23 | 24 | 0.046 | 60 | 59 | 60 | 0.068 | 80 | 79 | 80 | 0.091 |
| 25 | B4 | 25 | 0.049 | 61 | 60 | 61 | 0.055 | 84 | 5 | 55 | 0.052 |
| 26 | 25 | 26 | 0.062 | 62 | 61 | 62 | 0.061 | 85 | 7 | 60 | 0.051 |
| 27 | 26 | 27 | 0.066 | 63 | 62 | 63 | 0.098 | 86 | 11 | 43 | 0.072 |
| 28 | 27 | 28 | 0.059 | 64 | 63 | 64 | 0.017 | 87 | 12 | 72 | 0.061 |
| 29 | 28 | 29 | 0.099 | 65 | B9 | 65 | 0.042 | 88 | 13 | 76 | 0.069 |
| 30 | B5 | 30 | 0.034 | 66 | 65 | 66 | 0.054 | 89 | 14 | 18 | 0.049 |
| 31 | 30 | 31 | 0.114 | 67 | 66 | 67 | 0.017 | 90 | 16 | 26 | 0.036 |
| 32 | 31 | 32 | 0.074 | 68 | 67 | 68 | 0.016 | 91 | 20 | 83 | 0.045 |
| 33 | 32 | 33 | 0.065 | 69 | 68 | 69 | 0.085 | 92 | 28 | 32 | 0.066 |
| 34 | 33 | 34 | 0.059 | 70 | 69 | 70 | 0.066 | 93 | 29 | 39 | 0.085 |
| 35 | 34 | 35 | 0.025 | 71 | 70 | 71 | 0.052 | 94 | 34 | 46 | 0.061 |
| 36 | 35 | 36 | 0.026 | 72 | 71 | 72 | 0.052 | 95 | 40 | 42 | 0.042 |
References
- Merlin, A.; Back, H. Search for a Minimal-Loss Operating Spanning Tree Configuration in an Urban Power Distribution System. In Proceedings of the 1975 Fifth Power Systems Computer Conference (PSCC), Cambridge, UK, 1–5 September 1975; pp. 1–18.
- Civanlar, S.; Grainger, J.J.; Yin, H.; Lee, S.S.H. Distribution feeder reconfiguration for loss reduction. IEEE Trans. Power Deliv. 1988, 3, 1217–1223. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Shirmohammadi, D.; Hong, H.W. Reconfiguration of electric distribution networks for resistive line losses reduction. IEEE Trans. Power Deliv. 1989, 4, 1492–1498. [Google Scholar] [CrossRef]
- Chiang, H.D.; Jean-Jumeau, R. Optimal network reconfigurations in distribution systems: Part 2: Solution algorithms and numerical results. IEEE Trans. Power Deliv. 1990, 5, 1568–1574. [Google Scholar] [CrossRef]
- Nara, K.; Shiose, A.; Kitagawa, M.; Ishihara, T. Implementation of genetic algorithm for distribution systems loss minimum re-configuration. IEEE Trans. Power Systems 1992, 7, 1044–1051. [Google Scholar] [CrossRef]
- Sárfi, R.J.; Salama, M.M.A.; Chinchani, A.Y. Distribution system reconfiguration: An algorithm based on network partitioning theory. IEEE Trans. Power Syst. 1996, 11, 504–510. [Google Scholar] [CrossRef]
- Sárfi, R.J.; Salama, M.M.A.; Chinchani, A.Y. System optimization of electrical distribution networks: A new nonlinear formulation. Int. J. Power Energy Syst. 1997, 17, 169–174. [Google Scholar]
- Lin, W.M.; Chin, H.C. A new approach for distribution feeder reconfiguration for loss reduction and service restoration. IEEE Trans. Power Deliv. 1998, 13, 870–875. [Google Scholar] [CrossRef]
- Morton, A.; Mareels, M.Y. An efficient brute-force solution to the network reconfiguration problem. IEEE Trans. Power Deliv. 2000, 15, 996–1000. [Google Scholar] [CrossRef]
- Ramos, E.R.; Martinez-Ramos, J.L.; Exposito, A.G.; Salado, A.J.U. Optimal Reconfiguration of Distribution Networks for Power Loss Reduction. In Proceedings of the IEEE Porto Power Tech Conference, Porto, Portugal, 10–13 September 2001.
- Radha, B.; Ah. King, R.T.F.; Rughooputh, H.C.S. Optimal Network Reconfiguration of Electrical Distribution Systems. In Proceedings of the International Conference on Industrial Technology (ICIT 2003), Maribor, Slovenia, 10–12 December 2003; pp. 66–71.
- Oliveira, M.E.; Ochoa, L.F.; Padilha-Feltrin, A.; Mantovani, J.R.S. Network Reconfiguration and Loss Allocation for Distribution Systems with Distributed Generation. In Proceedings of the 2004 IEEE/PES Transmission & Distribution Conference & Exposition: Latin America, San Paulo, Brazil, 8–11 November 2004; pp. 206–211.
- Queiroz, L.M.O.; Lyra, C. Adaptive hybrid genetic algorithm for technical loss reduction in distribution networks under variable demands. IEEE Trans. Power Syst. 2006, 24, 445–453. [Google Scholar] [CrossRef]
- Carpaneto, E.; Chicco, G. Distribution System Minimum Reconfiguration in the Hyper-Cube Ant Colony Optimization Framework. In Proceedings of the Sixth World Energy System Conference (WESC 2006), Torino, Italy, 10–12 July 2006; pp. 167–174.
- Guimaraes, M.A.N.; Castro, C.; Romero, R. Reconfiguration of Distribution Systems by a Modified Genetic Algorithm. In Proceedings of the IEEE PowerTech’07, Lausanne, Switzerland, 1–5 July 2007.
- Yang, L.; Guo, Z. Reconfiguration of Electric Distribution Networks for Energy Losses Reduction. In Proceedings of the International Conference on Deregulation and Restructuring and Power Technologies (DRPT 2008), Nanjing, China, 6–9 April 2008; pp. 662–666.
- Enacheanu, B.; Raison, B.; Caire, R.; Devaux, O.; Bienia, W.; Hadjsaid, N. Radial network reconfiguration using genetic algorithm based on the matroid theory. IEEE Trans. Power Syst. 2008, 23, 186–195. [Google Scholar] [CrossRef]
- Carreno, E.M.; Romero, R.; Padilha-Feltrin, A. An efficient codification to solve distribution network reconfiguration for loss reduction problem. IEEE Trans. Power Syst. 2008, 23, 1542–1551. [Google Scholar] [CrossRef]
- Chouhan, S.; Hui, W.; Lai, H.J.; Feliachi, A.; Choudhry, M.A. Intelligent Reconfiguration of Smart Distribution Network Using Multi-Agent Technology. In Proceedings of the 2009 IEEE Power and Energy Society General Meeting, Calgary, Canada, 26–30 July 2009; pp. 1–6.
- Ababei, C.; Kavasseri, R. Efficient network reconfiguration using minimum cost maximum flow-based branch exchanges and random walks-based loss estimations. IEEE Trans. Power Syst. 2011, 26, 30–37. [Google Scholar] [CrossRef]
- Martinez-Rojas, M.; Sumper, A.; Gomis-Bellmunt, O.; Sudrià-Andreu, A. Reactive power dispatch in wind farms using particle swarm optimization technique and feasible solutions search. Appl. Energy 2011, 88, 4678–4686. [Google Scholar] [CrossRef]
- Roytelman, I.; Melnik, V.; Lee, S.S.H.; Lugtu, R.L. Multi-objective Feeder Reconfiguration by Distribution Management System. IEEE Trans. Power Syst. 1996, 11, 661–667. [Google Scholar] [CrossRef]
- Huang, Y.-C. Enhanced Genetic Algorithm-based Fuzzy Multi-objective Approach to Distribution Network Reconfiguration. IEE Proc. Gener. Transm. Distrib. 2002, 149, 615–620. [Google Scholar] [CrossRef]
- Asakura, T.; Genji, T.; Yura, T.; Hayashi, N.; Fukuyama, Y. Long-term distribution network expansion planning by network reconfiguration and generation of construction plans. IEEE Trans. Power Syst. 2003, 18, 1196–1204. [Google Scholar] [CrossRef]
- Tsai, M.-S.; Hsu, F.-Y. Application of grey correlation analysis in evolutionary programming for distribution system feeder reconfiguration. IEEE Trans. Power Syst. 2010, 25, 1126–1133. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Lee, C.-Y.; Liu, L.-C.; Tsai, S.-H. Study of reconfiguration for the distribution system with distributed generators. IEEE Trans. Power Deliv. 2010, 25, 1678–1685. [Google Scholar] [CrossRef]
- Singh, D.; Misra, R.K. Multi-objective feeder reconfiguration in different tariff structures. IET Gener. Transm. Distrib. 2010, 4, 974–988. [Google Scholar] [CrossRef]
- Santos, A.C.; Delbem, A.C.B.; London, J.B.A.; Bretas, N.G. Node-depth encoding and multiobjective evolutionary algorithm applied to large-scale distribution system reconfiguration. IEEE Trans. Power Syst. 2010, 25, 1254–1265. [Google Scholar] [CrossRef]
- Guimaraes, M.A.N.; Castro, C.A.; Romero, R. Distribution systems operation optimisation through reconfiguration and capacitor allocation by a dedicated genetic algorithm. IET Gener. Transm. Distrib. 2010, 4, 1213–1222. [Google Scholar] [CrossRef]
- Mendoza, J.E.; Lopez, M.E.; Coello, C.A.; Lopez, E.A. Microgenetic multiobjective reconfiguration algorithm considering power losses and reliability indices for medium voltage distribution network. IET Gener. Transm. Distrib. 2009, 3, 825–840. [Google Scholar] [CrossRef]
- Bernardon, D.P.; Garcia, V.J.; Ferreira, A.S.Q.; Canha, L.N. Multicriteria distribution network reconfiguration considering subtransmission analysis. IEEE Trans. Power Deliv. 2010, 25, 2684–2691. [Google Scholar] [CrossRef]
- Amanulla, B.; Chakrabarti, S.; Singh, S.N. Reconfiguration of power distribution systems considering reliability and power loss. IEEE Trans. Power Deliv. 2012, 27, 918–926. [Google Scholar] [CrossRef]
- Chiang, H.D.; Baran, M. On the existence and uniqueness of load flow solution for radial distribution power network. IEEE Trans. Circuits Syst. 1990, 37, 410–416. [Google Scholar] [CrossRef]
- IEEE Guide for Electric Power Distribution Reliability Indices. IEEE Standard 1366-2003. December 2003.
- Heggie, G.; Yip, H.T. A Multi-Function Relay for Loss of Mains Protection. In Proceedings of the 1998 IEE Colloquium on System Implications of Embedded Generation and Its Protection and Control, London, UK, 25 February 1998; pp. 5/1–5/4.
- Colet-Subirachs, A.; Ruiz-Alvarez, A.; Gomis-Bellmunt, O.; Alvarez-Cuevas-Figuerola, F.; Sudria-Andreu, A. Centralized and distributed active and reactive power control of a utility connected microgrid using IEC61850. IEEE Syst. J. 2012, 6, 58–67. [Google Scholar] [CrossRef]
- Tomoiagă, B.; Chindriş, M.; Sumper, A.; Sudrià-Andreu, A.; Marzband, M. Fuzzy Numbers Based Algorithm for Interruptions Frequency Estimation on Distribution Smart Grids. In Proceedings of the 2012 International Conference and Exposition on Electrical and Power Engineering (EPE 2012), Iasi, Romania, 25–27 October 2012; pp. 237–241.
- Fonseca, C.; Fleming, P.J. Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion, Generalization. In Proceedings of the 5th International Conference on Genetic Algorithms, San Mateo, CA, USA, 17–21 July 1993; pp. 416–423.
- Horn, J.; Nafpliotis, N.; Goldberg, D.E. A Niched Pareto Genetic Algorithm for Multiobjective Optimization. In Proceedings of the 1st IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, Piscataway, NJ, USA, 27–29 June 1994; Volume 1, pp. 82–87.
- Zitzler, E.; Thiele, L.; Bader, J. On set-based multiobjective optimization. IEEE Trans. Evol. Comput. 2010, 14, 58–79. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Richardson, J. Genetic Algorithms with Sharing for Multimodal Function Optimization. In Proceedings of the 2nd International Conference on Genetic Algorithms and Their Applications, Hillsdale, NJ, USA, 28–31 July 1987; pp. 41–49.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tomoiagă, B.; Chindriş, M.; Sumper, A.; Sudria-Andreu, A.; Villafafila-Robles, R. Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II. Energies 2013, 6, 1439-1455. https://doi.org/10.3390/en6031439
Tomoiagă B, Chindriş M, Sumper A, Sudria-Andreu A, Villafafila-Robles R. Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II. Energies. 2013; 6(3):1439-1455. https://doi.org/10.3390/en6031439
Chicago/Turabian StyleTomoiagă, Bogdan, Mircea Chindriş, Andreas Sumper, Antoni Sudria-Andreu, and Roberto Villafafila-Robles. 2013. "Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II" Energies 6, no. 3: 1439-1455. https://doi.org/10.3390/en6031439
APA StyleTomoiagă, B., Chindriş, M., Sumper, A., Sudria-Andreu, A., & Villafafila-Robles, R. (2013). Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II. Energies, 6(3), 1439-1455. https://doi.org/10.3390/en6031439