Harmonic Current Predictors for Wind Turbines
Abstract
:1. Introduction
2. Field Measurements of Wind Turbine

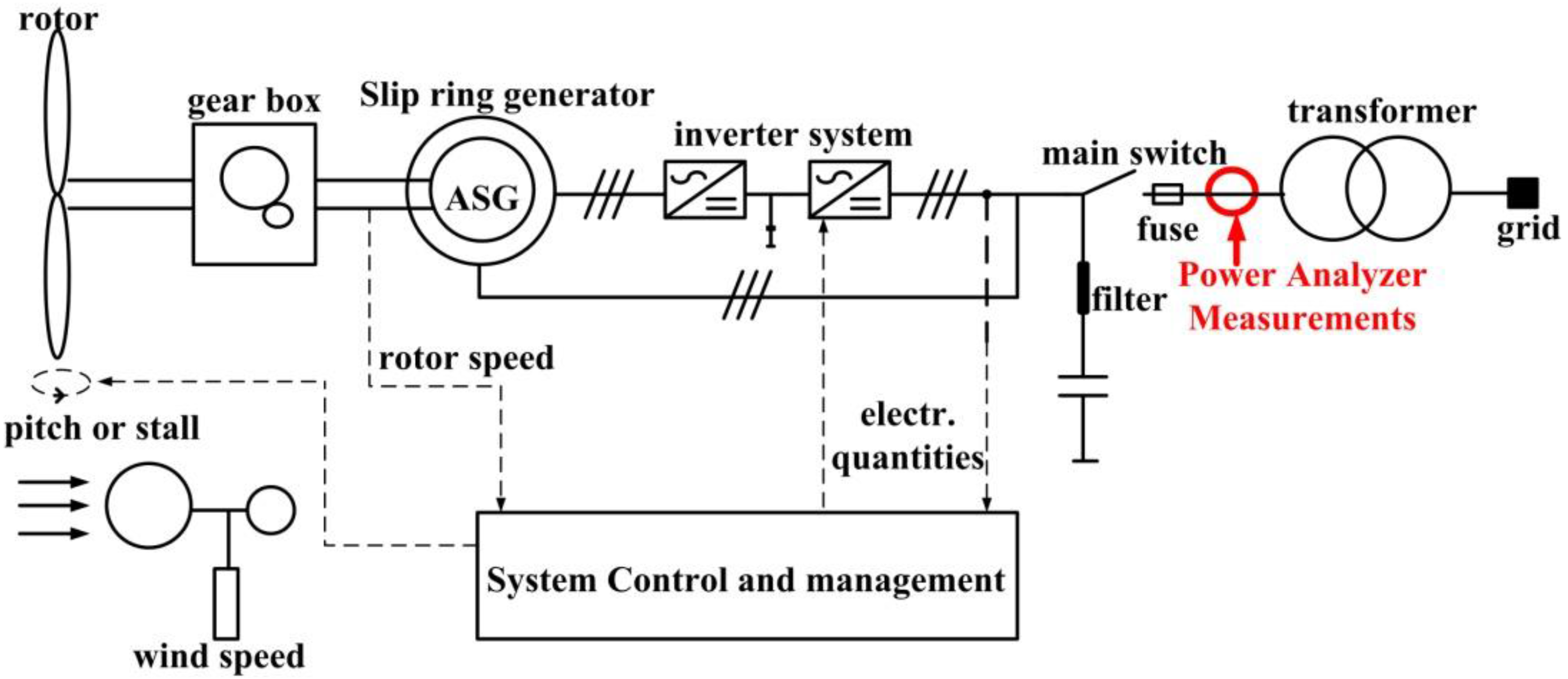
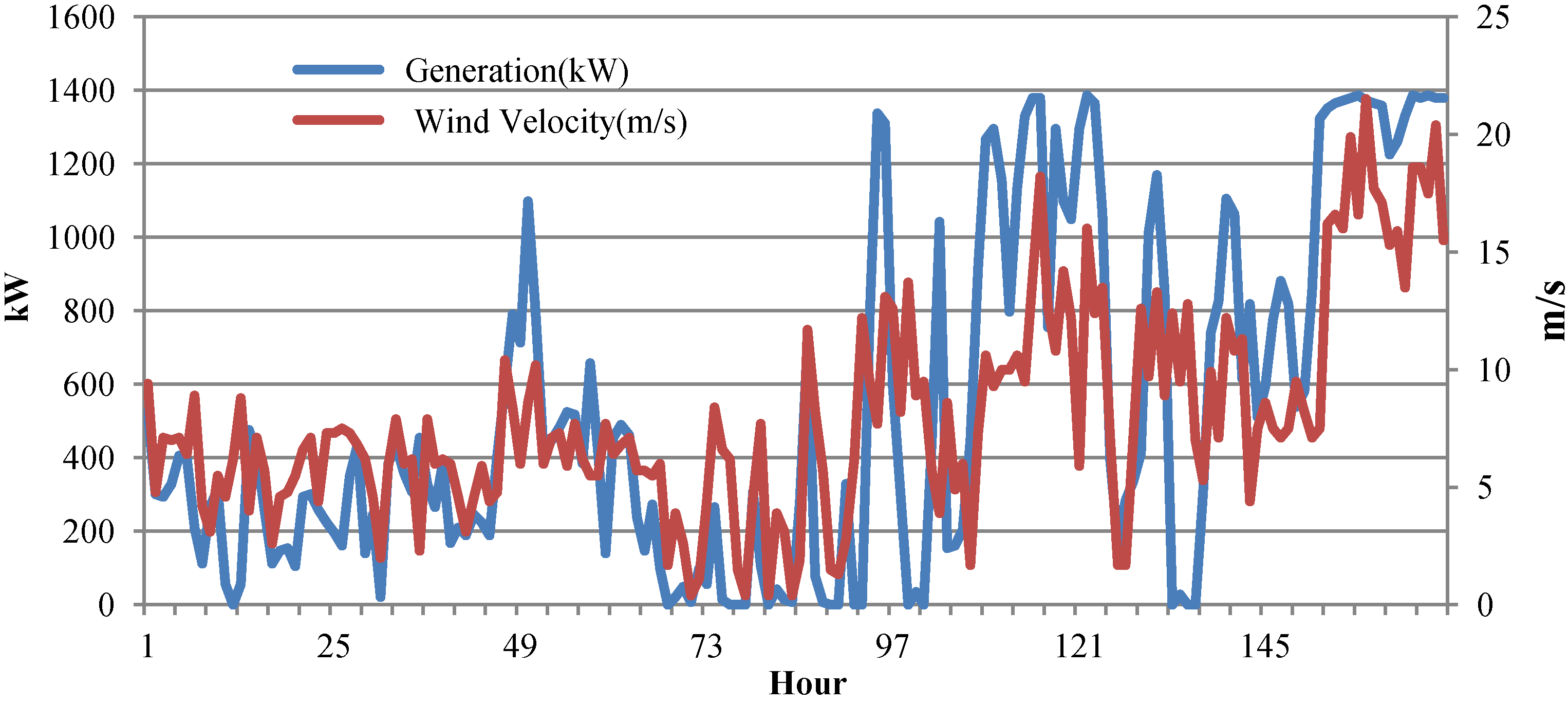
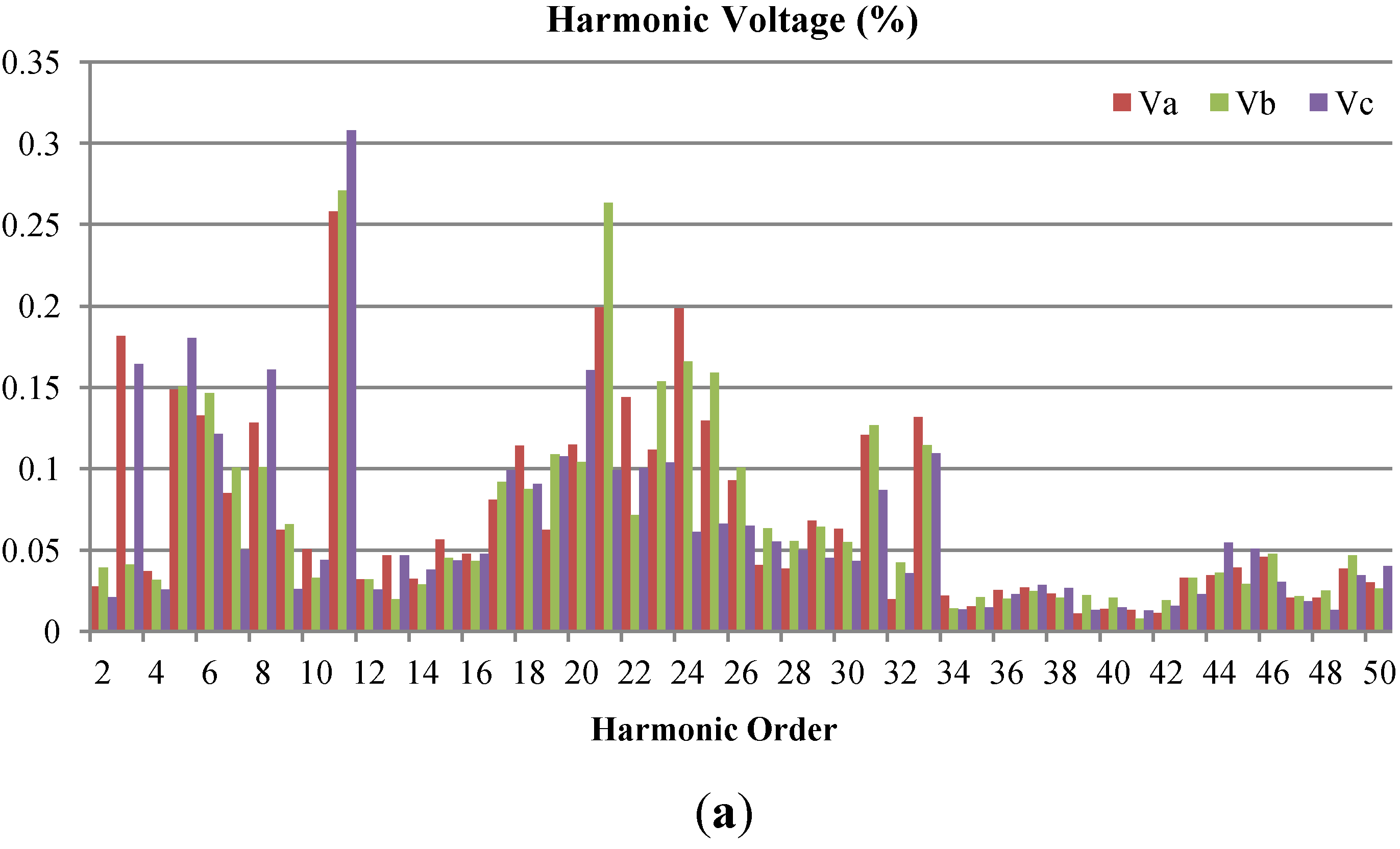
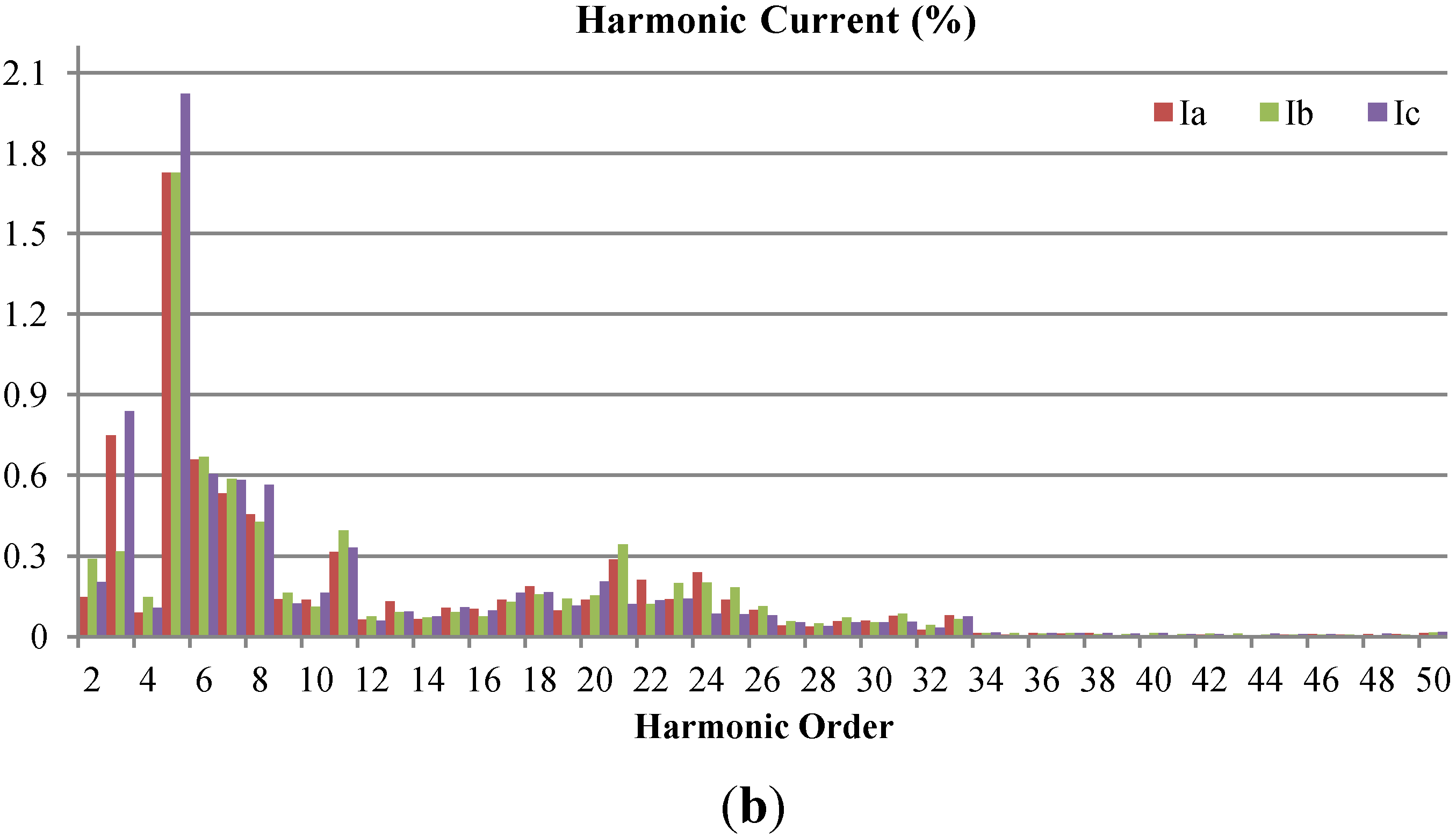
3. Harmonic Current Predictor for Wind Turbines
3.1. ARMA-Based Harmonic Current Predictor
3.2. Stochastic Harmonic Current Predictor Based on Probability Density Distributions of Harmonic Currents
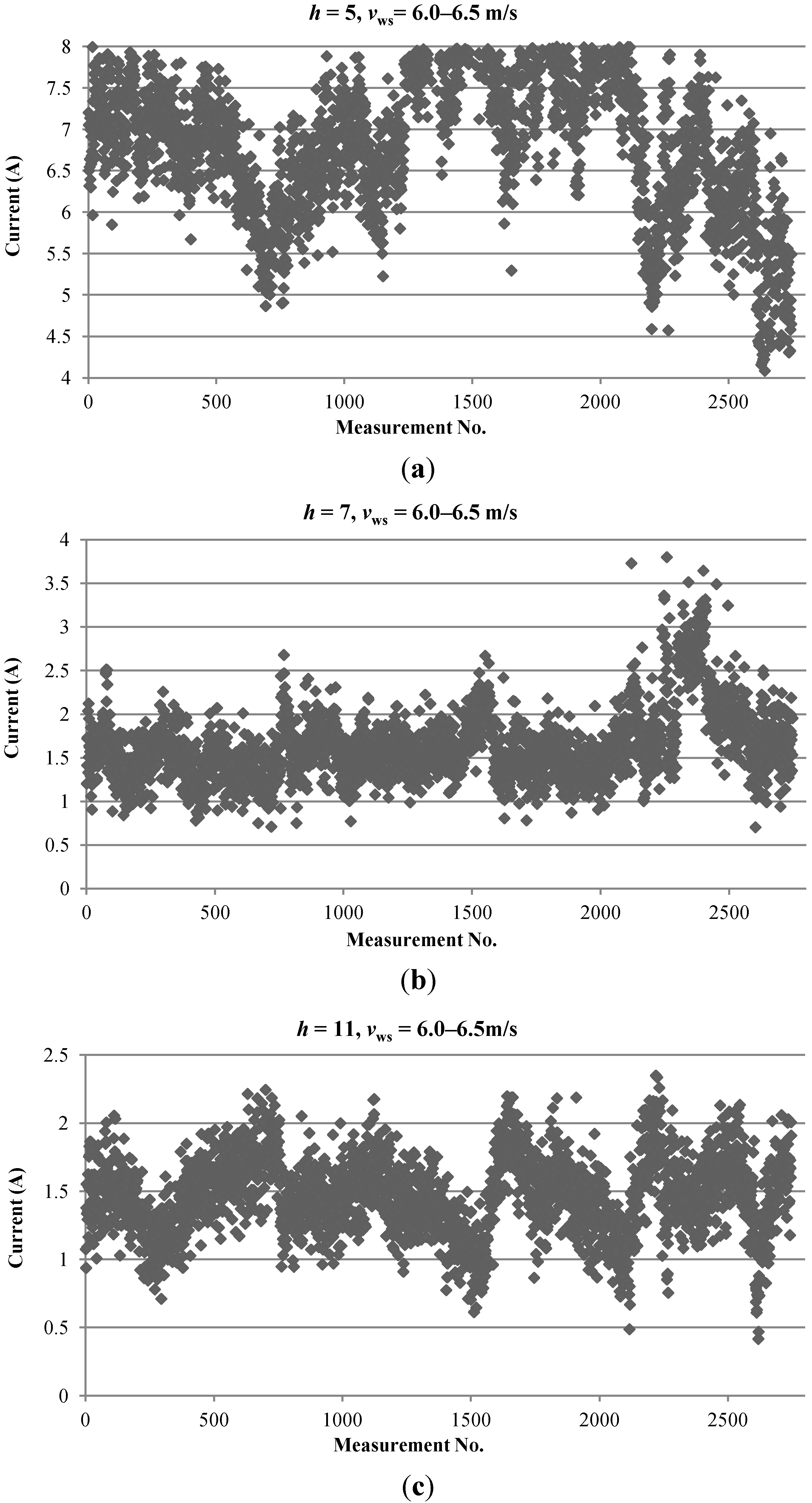
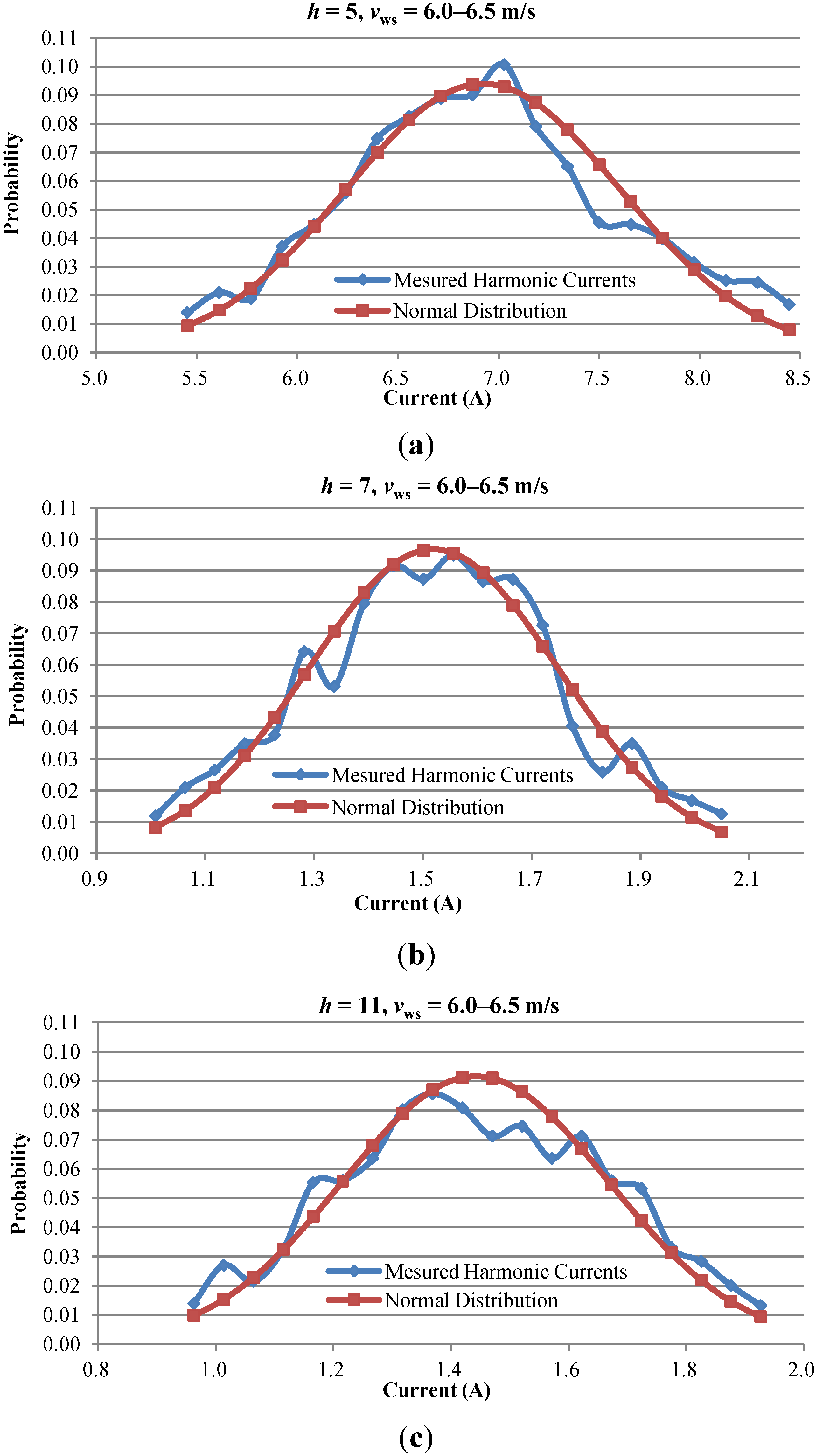
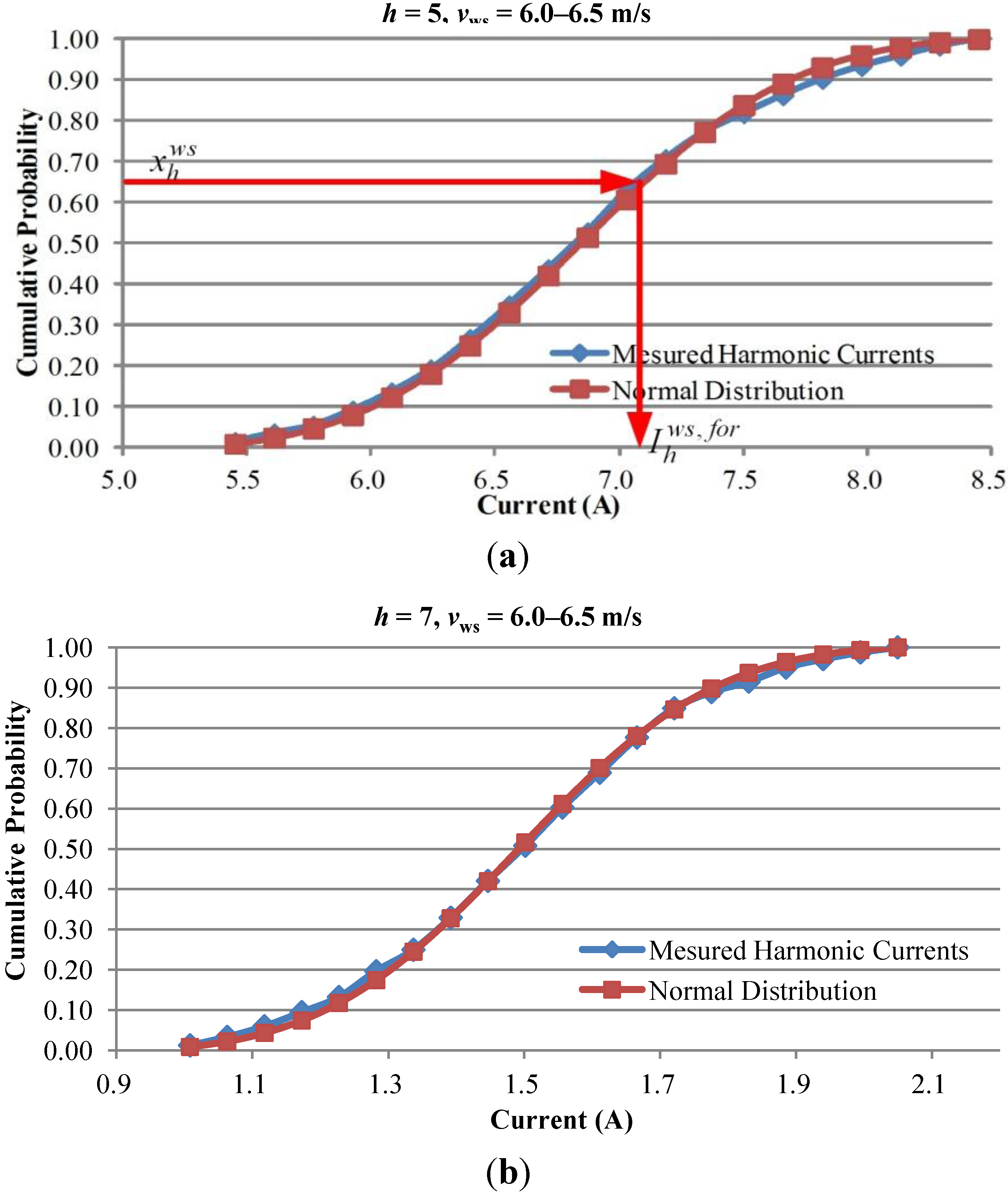
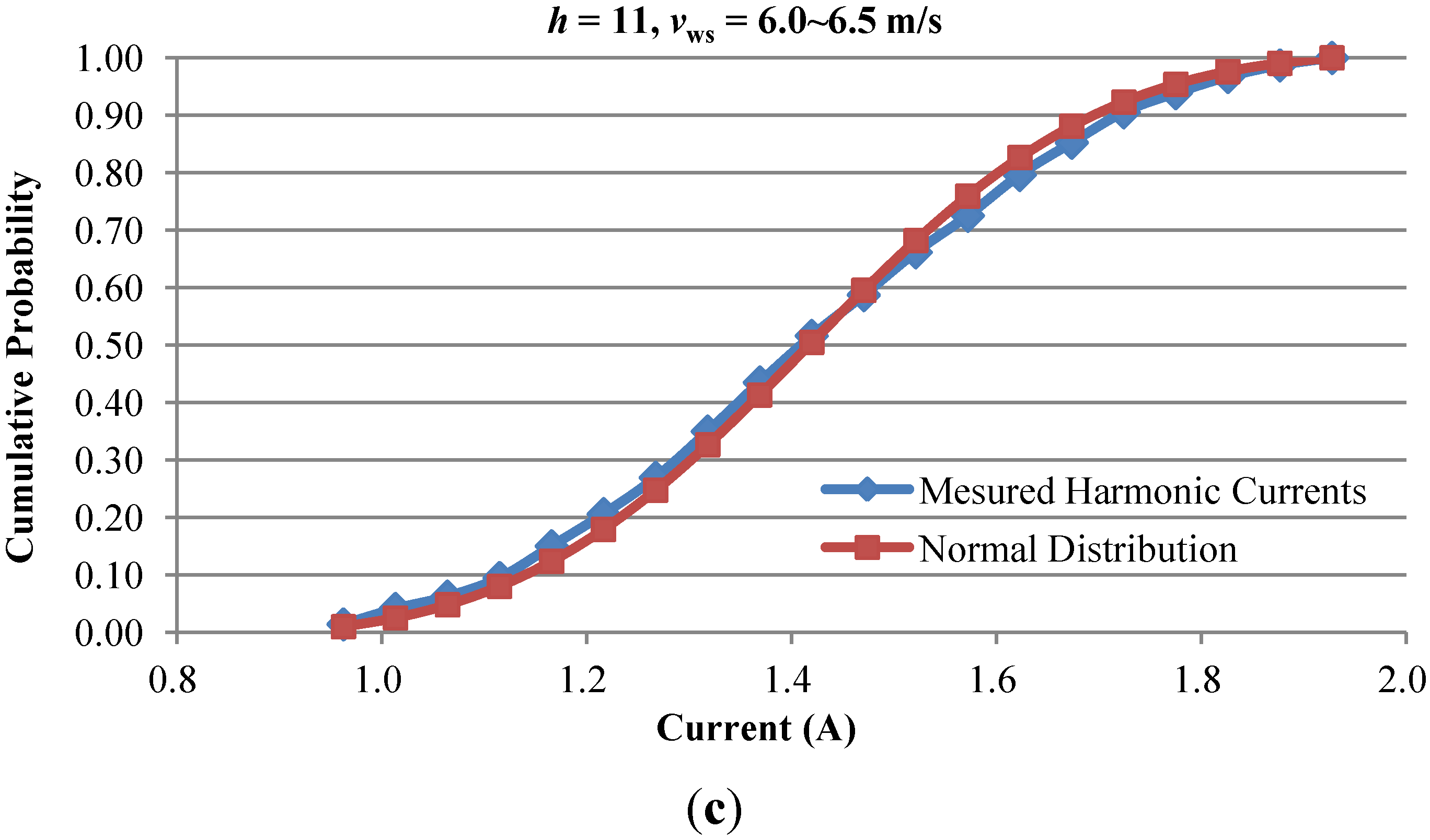
4. Test Results and Discussions
4.1. Prediction Results of ARMA-based Harmonic Current Predictor
| Harmonic order | Parameters | |
|---|---|---|
| φ1 | θ1 | |
| 5 | 0.99132 | 0.871431 |
| 7 | 0.994271 | 0.927426 |
| 11 | 0.997019 | 0.914273 |
| 13 | 0.993054 | 0.977224 |
| 17 | 0.993752 | 0.976071 |
| 19 | 0.988407 | 0.963316 |
| Harmonic Order | Error | |||
|---|---|---|---|---|
| Max. | Min. | Average | Standard deviation | |
| 5 | 82.62430 | 0.0007 | 7.4293 | 7.2188 |
| 7 | 332.3400 | 0.0027 | 15.0743 | 17.1146 |
| 11 | 259.0560 | 0.0041 | 13.9408 | 13.8874 |
| 13 | 336.1530 | 0.0056 | 35.5855 | 37.6699 |
| 17 | 495.9790 | 0.0057 | 31.0665 | 35.0412 |
| 19 | 2524.9900 | 0.0027 | 48.7375 | 85.6002 |
| Harmonic Order | Error | |||
|---|---|---|---|---|
| Max. | Min. | Average | Standard deviation | |
| 5 | 77.7710 | 0.0042 | 7.4070 | 7.2547 |
| 7 | 328.0160 | 0.0070 | 15.1540 | 17.0847 |
| 11 | 256.9150 | 0.0062 | 13.9424 | 13.9027 |
| 13 | 333.1270 | 0.0133 | 35.5394 | 37.5889 |
| 17 | 491.7180 | 0.0032 | 30.9229 | 34.8254 |
| 19 | 2761.8000 | 0.0165 | 48.0389 | 81.9972 |
4.2. Prediction Results of Stochastic Harmonic Current Predictor
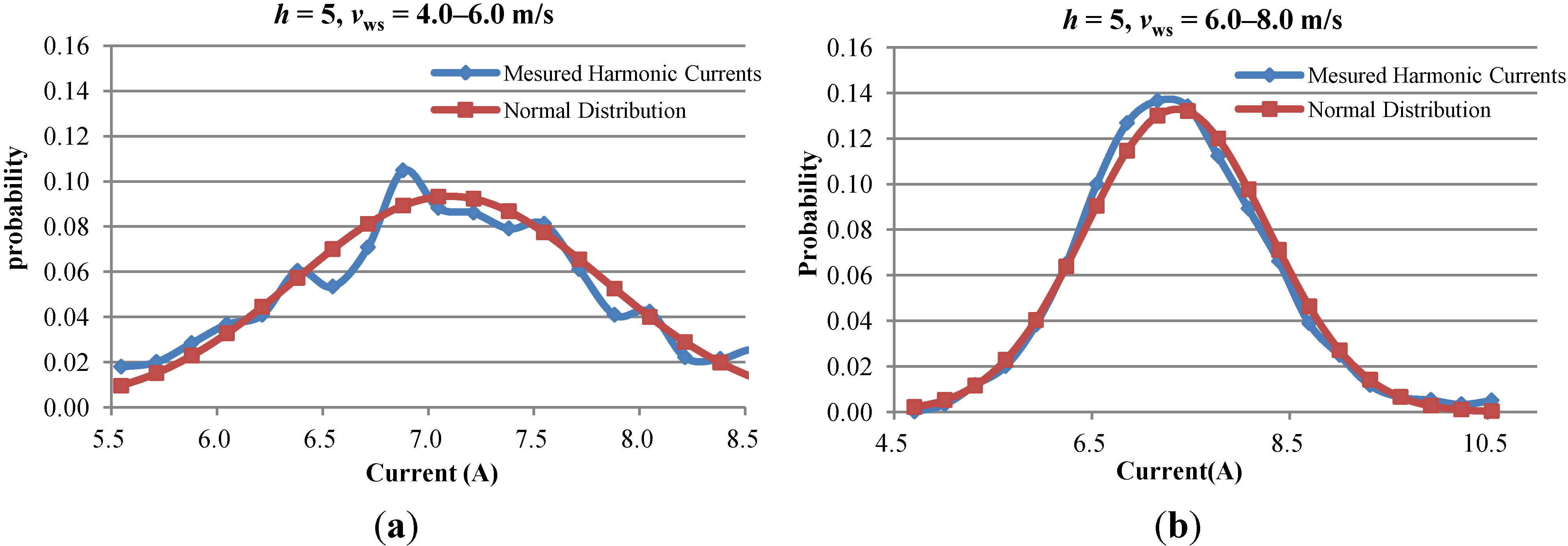
| Harmonic order | Wind speed (4–6 m/s) | Wind speed (6–8 m/s) | ||
|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard deviation | |
| 5 | 7.0997 | 0.7278 | 7.3567 | 0.9232 |
| 7 | 1.3728 | 0.2725 | 1.6626 | 0.5240 |
| 11 | 1.4312 | 0.2451 | 1.5279 | 0.2729 |
| 13 | 0.5777 | 0.1431 | 0.5532 | 0.1767 |
| 17 | 0.5014 | 0.1362 | 0.5850 | 0.2505 |
| 19 | 0.6556 | 0.1659 | 0.8099 | 0.3825 |
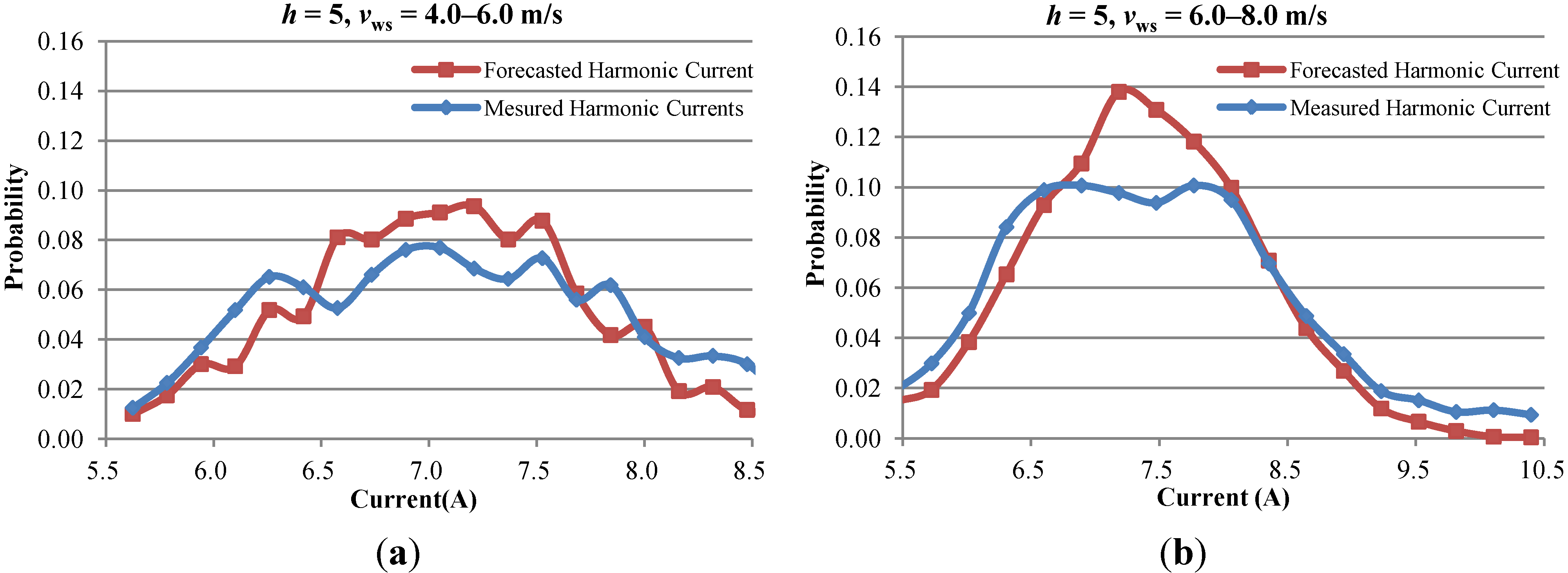
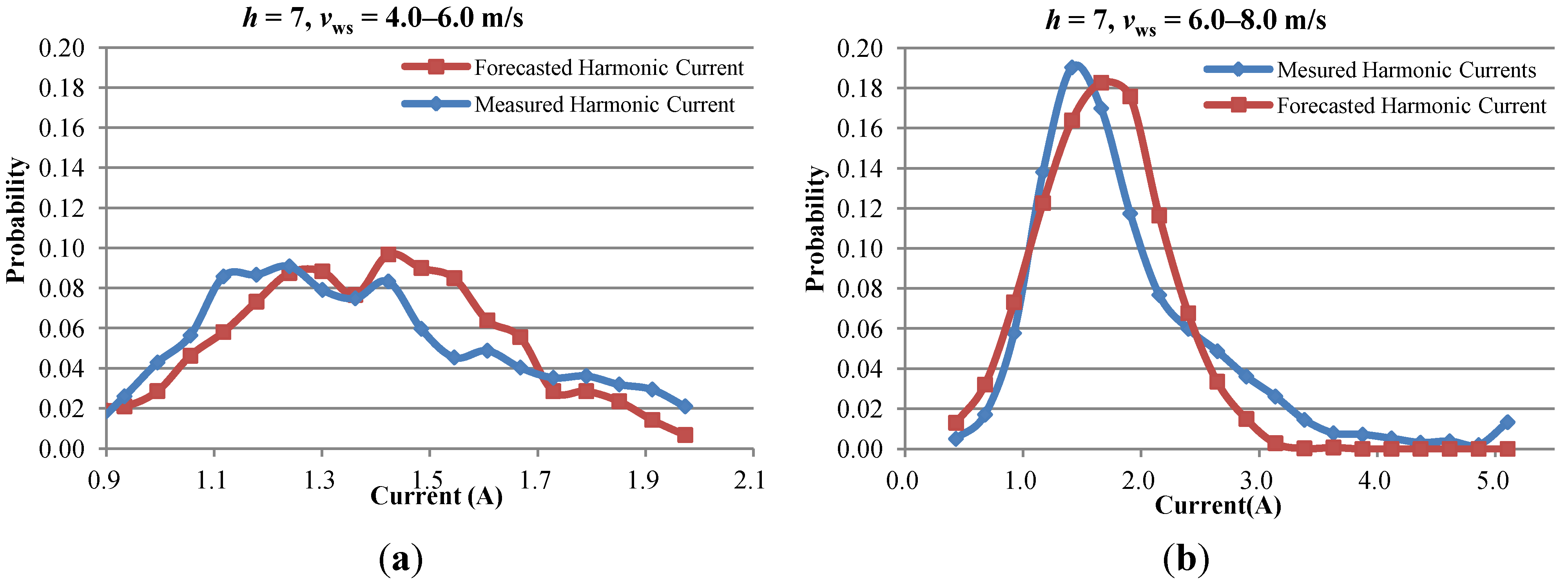
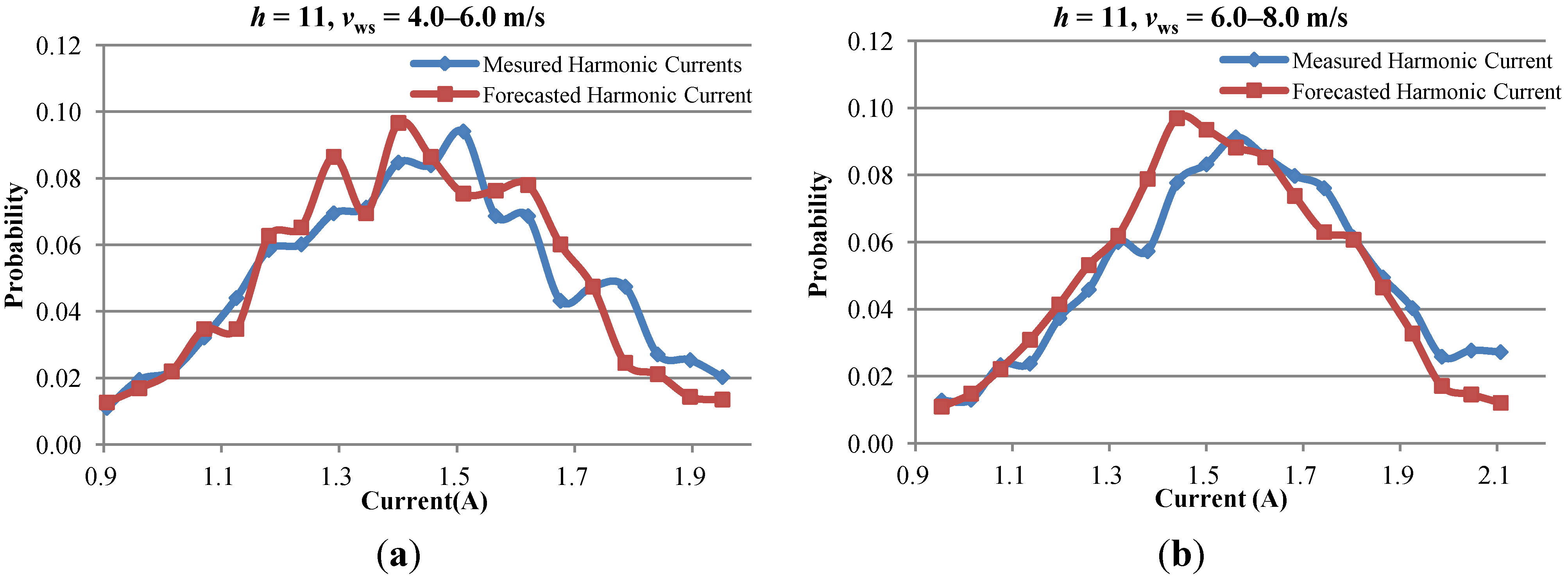
5. Conclusions
Acknowledgement
References
- Wind Turbine Generator Systems-Part 21: Measurement and Assessment of Power Quality Characteristic of Grid Connected Wind Turbines; IEC 61400-21; IEC Standard, 2001.
- Feijoo, A.E.; Cidras, J. Modeling of wind farms in the load flow analysis. IEEE Trans. Power Syst. 2000, 15, 110–115. [Google Scholar] [CrossRef]
- Chen, Z.; Spooner, E. Grid power quality with variable speed wind turbines. IEEE Trans. Energy Convers. 2001, 16, 148–154. [Google Scholar] [CrossRef]
- Larsson, A. Flicker emission of wind turbines caused by switching operations. IEEE Trans. Energy Convers. 2002, 17, 119–123. [Google Scholar] [CrossRef]
- Mohammed, H.; Nwankpa, C.O. Stochastic analysis and simulation of grid-connected wind energy conversion system. IEEE Trans. Energy Convers. 2000, 15, 85–90. [Google Scholar] [CrossRef]
- Tenca, P.; Rockhill, A.A.; Lipo, T.A. Wind turbine current-source converter providing reactive power control and reduced harmonics. IEEE Trans. Ind. Appl. 2007, 43, 1050–1060. [Google Scholar] [CrossRef]
- Tentzerakis, S.T.; Papathanassiou, S.A. An Investigation of the harmonic emissions of wind turbines. IEEE Trans. Energy Convers. 2007, 22, 150–158. [Google Scholar] [CrossRef]
- Melicio, R.; Mendes, V.M.F.; Catalao, J.P.S. Harmonic assessment of variable-speed wind turbines considering a converter control malfunction. IET Renew. Power Gener. 2010, 4, 139–152. [Google Scholar] [CrossRef]
- Herrera, J.I.; Reddoch, T.W.; Lawler, J.S. Harmonics generated by two variable speed wind generating systems. IEEE Trans. Energy Convers. 1988, 3, 267–273. [Google Scholar] [CrossRef]
- Papathanassiou, S.A.; Papadopoulos, M.P. Harmonic analysis in a power system with wind generation. IEEE Trans. Power Deliv. 2006, 21, 2006–2016. [Google Scholar] [CrossRef]
- Cavallini, A.; Langella, R.; Testa, A.; Ruggiero, F. Gaussian modeling of harmonic vectors in power systems. In Proceedings of 8th IEEE International Conference Harmonics Quality Power (ICHQP), Athens, Greece, 14–16 October 1998.
- Pierrat, L.; Wang, Y.-J. Summation of randomly varying harmonics—towards a univariate distribution function using generalized Gamma distribution. In Proceedings of 5th International Conference Probabilistic Methods Applied to Power System (PMAPS), Vancouver, BC, Canada, 21–25 September 1997.
- Sainz, L.; Mesas, J.J.; Teodorescu, R.; Rodriguez, P. Deterministic and stochastic study of wind farm harmonic currents. IEEE Trans. Energy Convers. 2010, 25, 1071–1080. [Google Scholar] [CrossRef]
- Mazumdar, J.; Harley, R.G.; Lambert, F.C.; Venayagamoorthy, G.K. Neural network based method for predicting nonlinear load harmonics. IEEE Trans. Power Electron. 2007, 22, 1036–1045. [Google Scholar] [CrossRef]
- Lin, H.C. Intelligent neural network-based fast power system harmonic detection. IEEE Trans. Ind. Electron. 2007, 54, 43–52. [Google Scholar] [CrossRef]
- Mazumdar, J.; Harley, R.G. Recurrent neural networks trained with back propagation through time algorithm to estimate nonlinear load harmonic currents. IEEE Trans. Ind. Electron. 2008, 55, 3484–3491. [Google Scholar] [CrossRef]
- ARMA Model Specifications. MathWorks, Inc. Available online: http://www.mathworks.com/help/econ/arma-models.html (accessed on 18 December 2012).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Teng, J.-H.; Leou, R.-C.; Chang, C.-Y.; Chan, S.-Y. Harmonic Current Predictors for Wind Turbines. Energies 2013, 6, 1314-1328. https://doi.org/10.3390/en6031314
Teng J-H, Leou R-C, Chang C-Y, Chan S-Y. Harmonic Current Predictors for Wind Turbines. Energies. 2013; 6(3):1314-1328. https://doi.org/10.3390/en6031314
Chicago/Turabian StyleTeng, Jen-Hao, Rong-Ceng Leou, Chuo-Yean Chang, and Shun-Yu Chan. 2013. "Harmonic Current Predictors for Wind Turbines" Energies 6, no. 3: 1314-1328. https://doi.org/10.3390/en6031314
APA StyleTeng, J.-H., Leou, R.-C., Chang, C.-Y., & Chan, S.-Y. (2013). Harmonic Current Predictors for Wind Turbines. Energies, 6(3), 1314-1328. https://doi.org/10.3390/en6031314






