Submarine Slope Failure Primed and Triggered by Bottom Water Warming in Oceanic Hydrate-Bearing Deposits
Abstract
:1. Introduction
1.1. Gas Hydrate Dissociation as a Trigger or Primer for Slope Failure
| Area | Features | Possible Primer or Triggers | References |
|---|---|---|---|
| Storegga Slide | Gradient = 10–20° Maximum thickness = 200 m Area = 34,000 km2 Volume of loss = 5500 km3 | - Earthquake - Methane hydrate dissociation due to bottom water warming | Bugge et al. [25] Canals et al. [26] Vogt and Jung [8] |
| Buford Sea Margin (Alaska) | Width = 500 km Length = 40–50 km Thickness = 100–150 m | - Methane hydrate dissociation due to sea-level lowering | Kayen and Lee [10] |
| Blake Ridge | Subsidence by seafloor collapse Area = 100 km2 Volume of loss = 13 km3 | - Overpressurized free gas beneath gas hydrate zone | Dillon et al. [27] Holbrook [28] |
| Northern East Sakhalin Margin | Gradient = 2.5° Length = 70 km Volume of mass wasting = 660 km3 | - Shallow earthquakes - Methane hydrate dissociation due to sea-level lowering | Wong et al. [7] |
| Tokai Thrust in Eastern Nankai Wedge | Gradient = 2°–8° Failure layer concurs with BSR | - Methane hydrate dissociation due to plate uplift caused by subduction of paleo-Zenisu ridge | Cochonat et al. [6] |
| Amazon Fan | Gradient = less than 1° Area = 15,000 km2 Thickness = 200 m | - Methane hydrate dissociation due to sea-level lowering - Overburdening by Amazon River sediment discharge during deglacial time | Maslin et al. [4] |
| Balearic Basin of the Western Mediterranean Sea | Volume of mass wasting = 500 km3 | - Methane hydrate dissociation due to sea-level lowering | Rothwell et al. [5] |
1.2. Bottom Water Warming—Past History and Current Trend
2. Gas Hydrate Dissociation in Sediments
2.1. Thermal Dissociation of Gas Hydrate

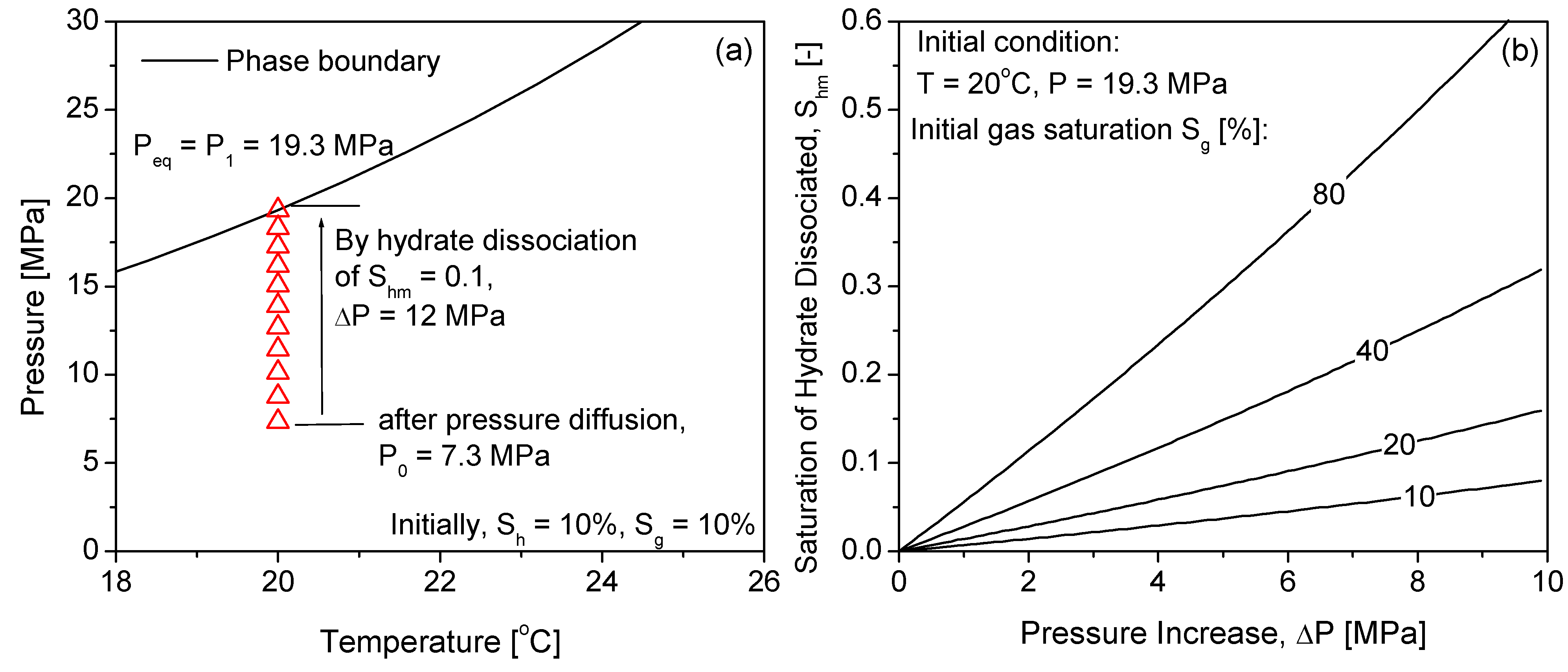
2.2. Hydrate Dissociation by Pressure Diffusion
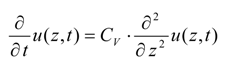
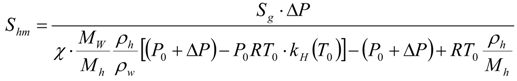
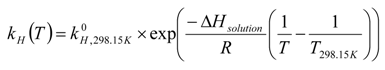
3. Numerical Analysis—Effect of Bottom Water Warming
3.1. Scope of Numerical Analysis
3.2. Algorithm for Sequentially Coupled T-H-M Analysis
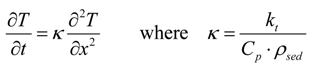
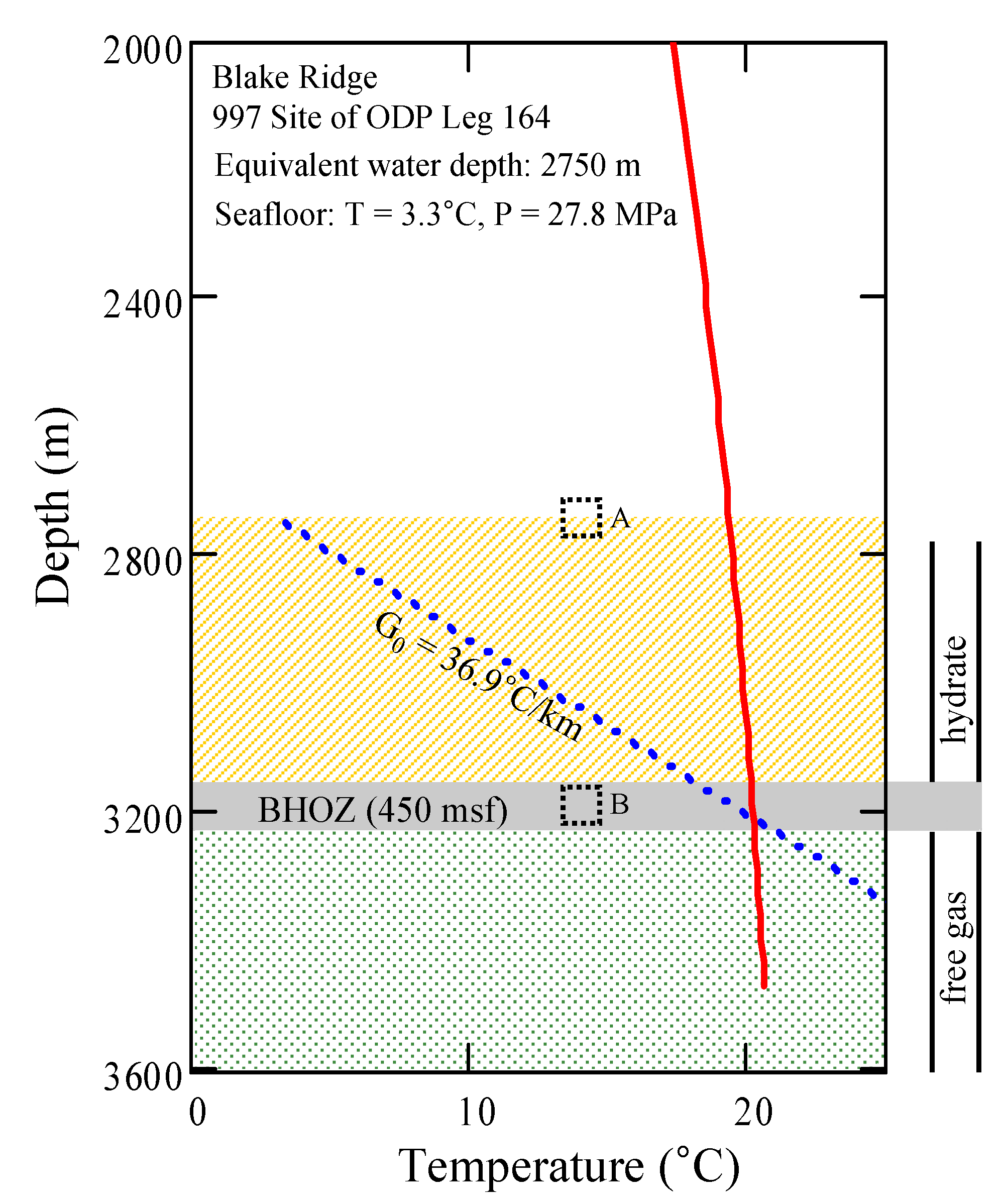
3.3. Geological Conditions and Input Properties
| Property | Values |
|---|---|
| Hydrostatic pressure at the seafloor [MPa] a,b | 27.8 |
| Temperature at the seafloor [°C] a,c | 3.3 |
| Geothermal gradient [°C·km−1] a,c | 36.9 |
| Depth of the base of the hydrate occurrence zone (BHOZ) [mbsf] a,b | 450 |
| Pore volume fraction of methane hydrate in hydrate layer [%] a,b | 10 |
| Pore volume fraction of methane gas in free gas layer [%] a,d | 10 |
| Thermal diffusivity of hydrate-bearing sediments [m2·s−1] e | 10−6 |
| Coefficient of consolidation of hydrate-bearing sediments [m2·s−1] | 10−8 |
| Coefficient of consolidation of gassy sediments [m2·s−1] | 10−7 |
| Mass density of water-saturated sediments [g·cm−3] | 1.8 |
| Friction angle of sediments at critical state [°] | 30 |
4. Analysis Results
4.1. Thermal Responses at the Base of Hydrate Occurrence Zone (BHOZ)
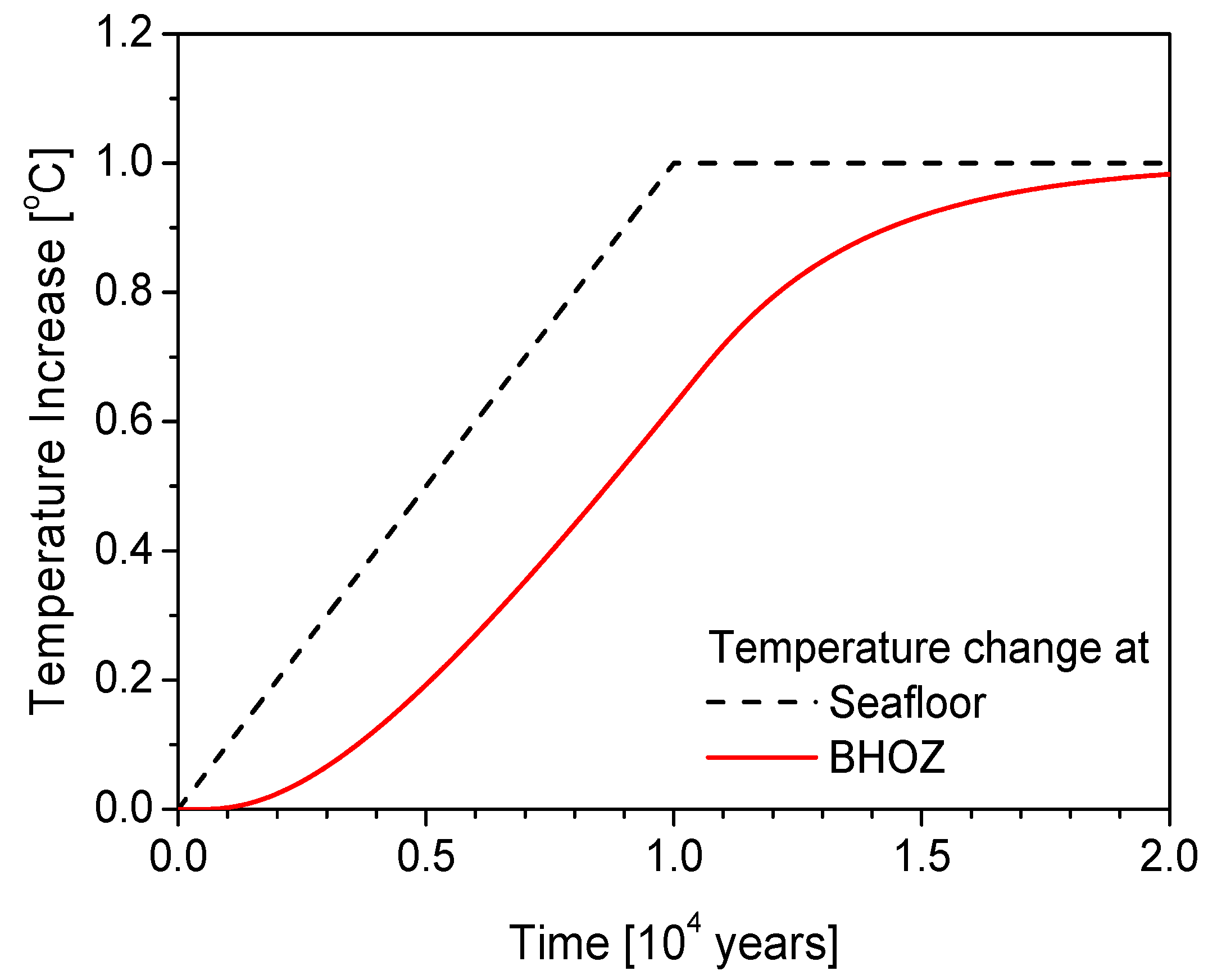
4.2. Generation of Excess Pore Pressure and Pressure Diffusion
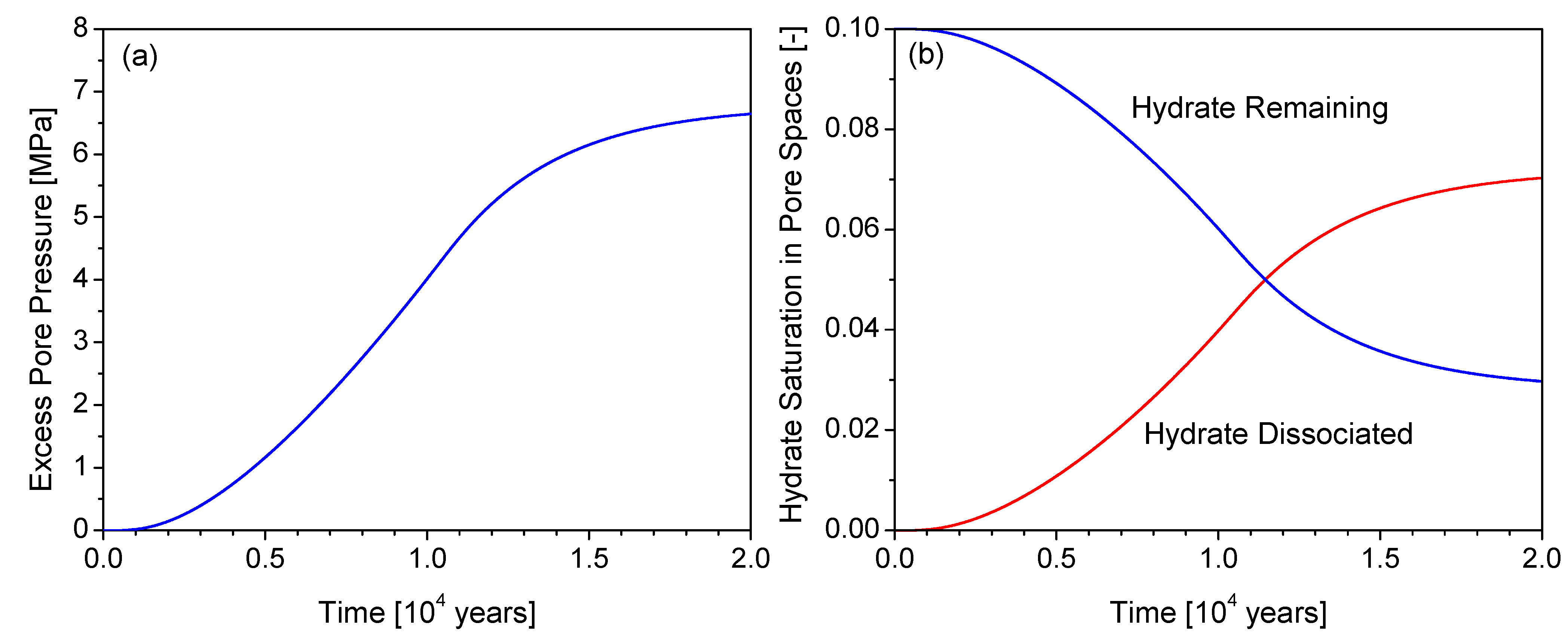
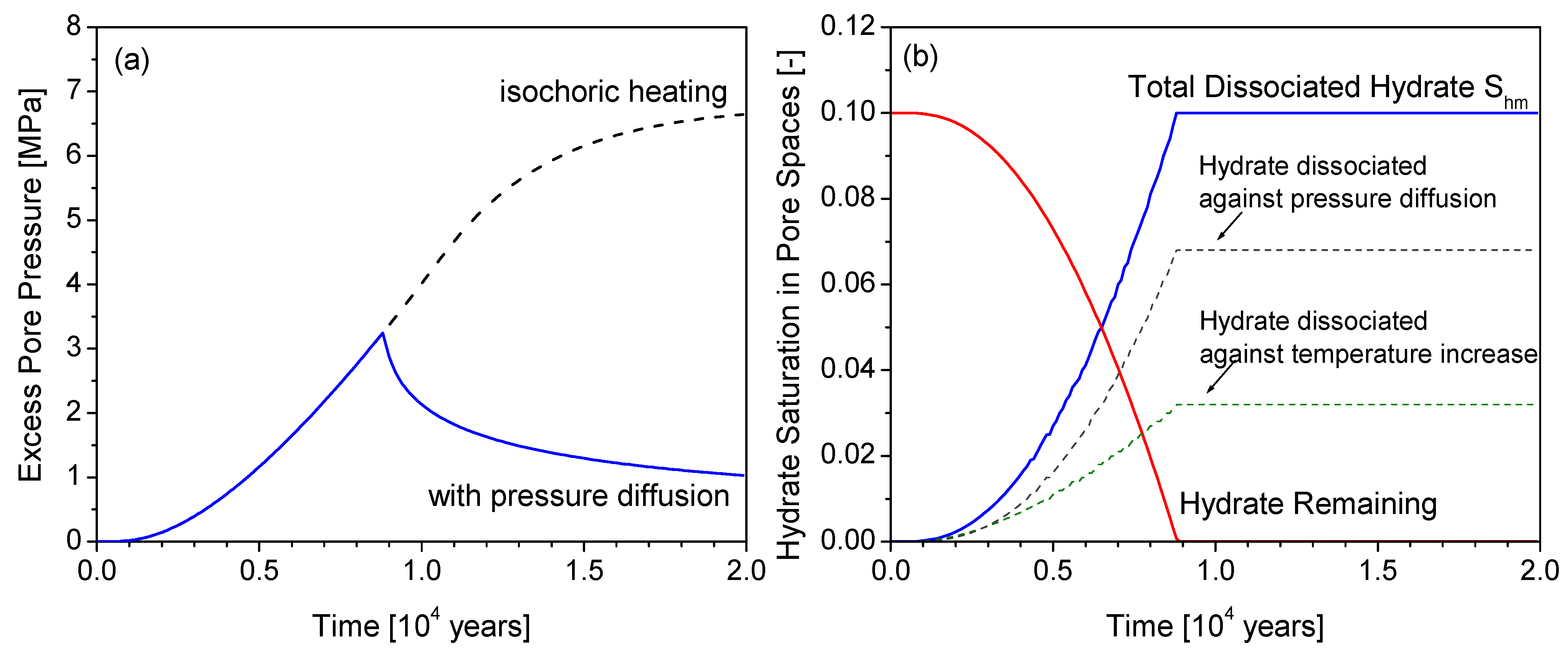
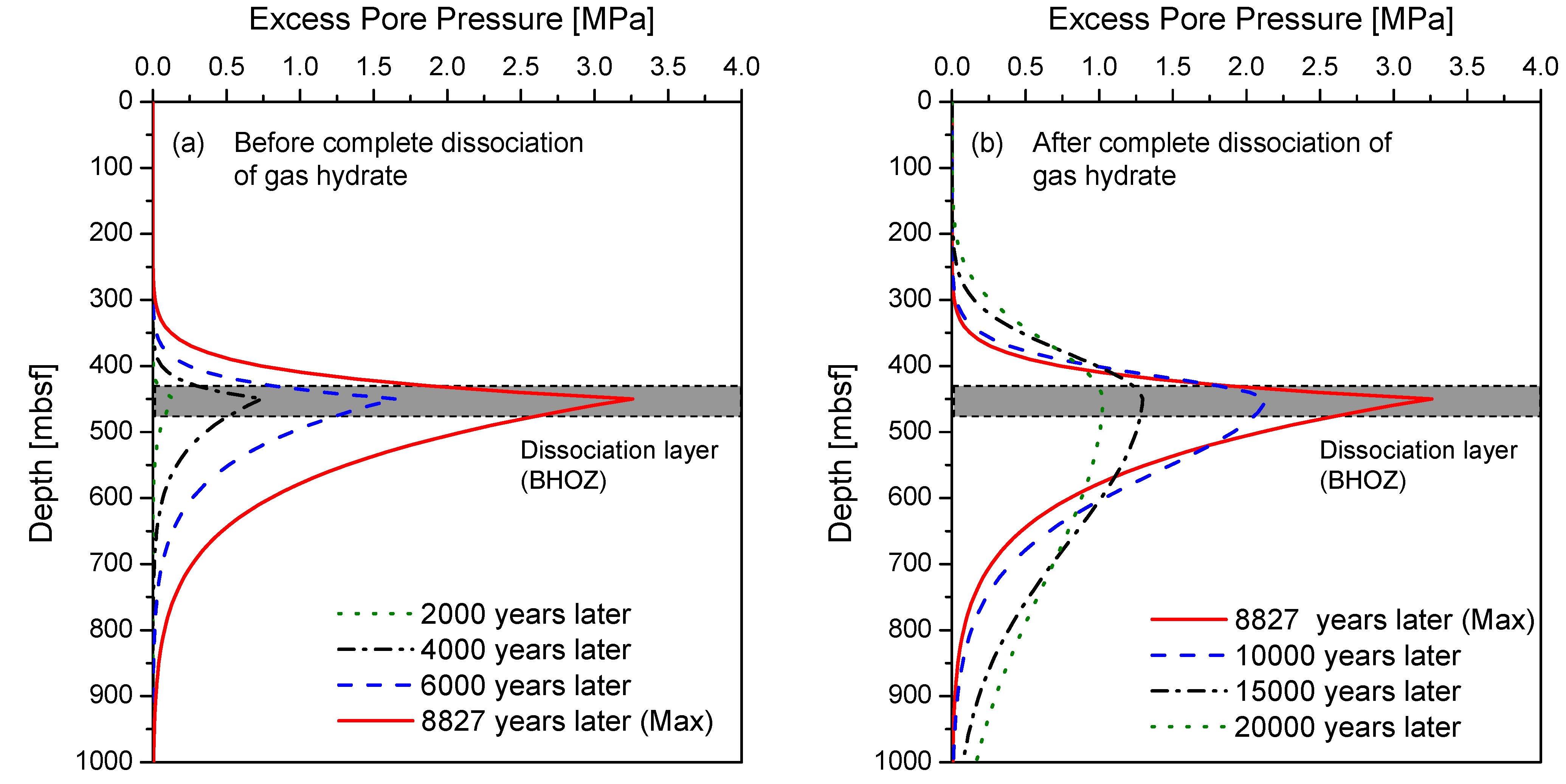
4.3. Factor of Safety (FS)
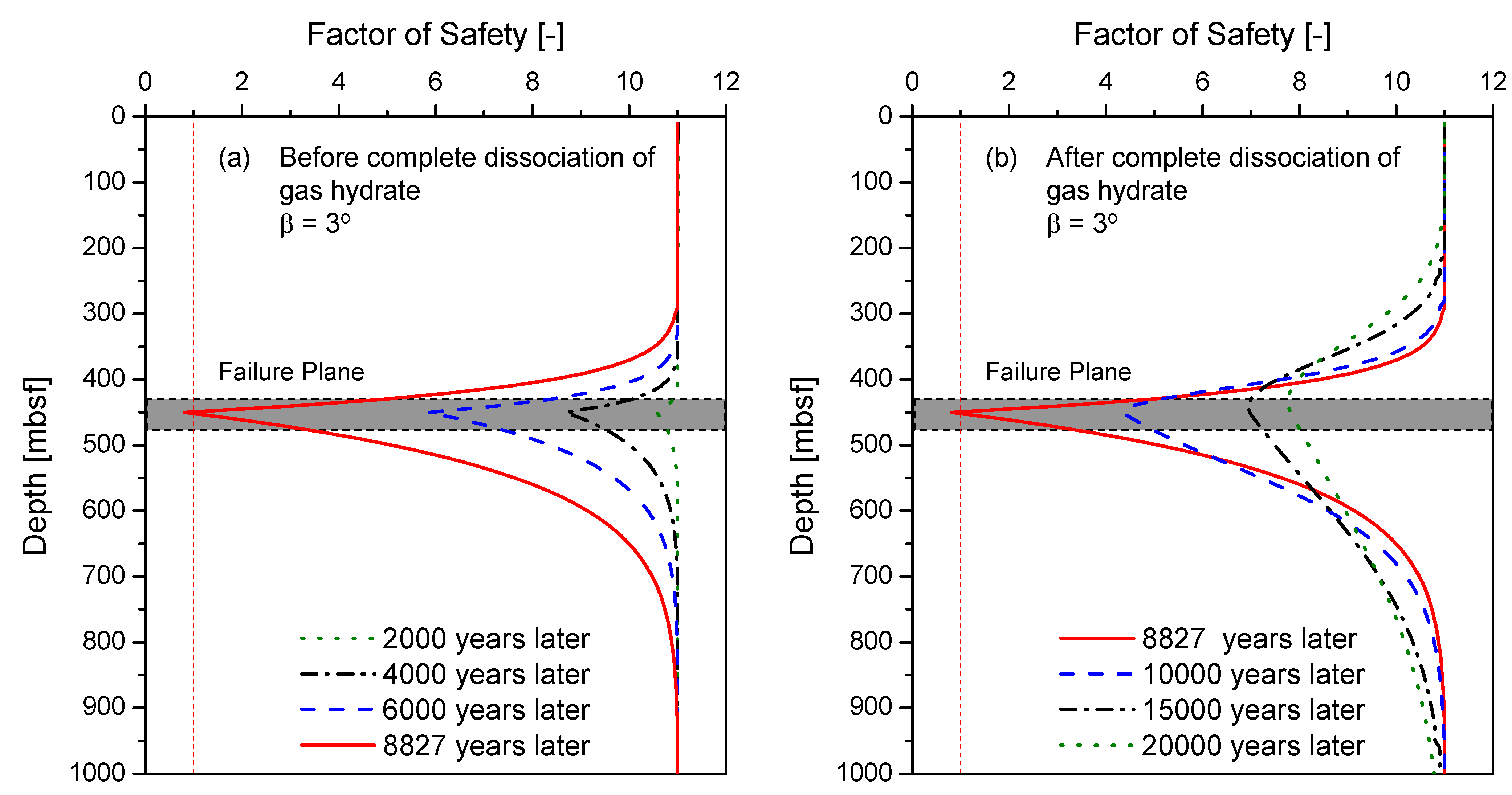
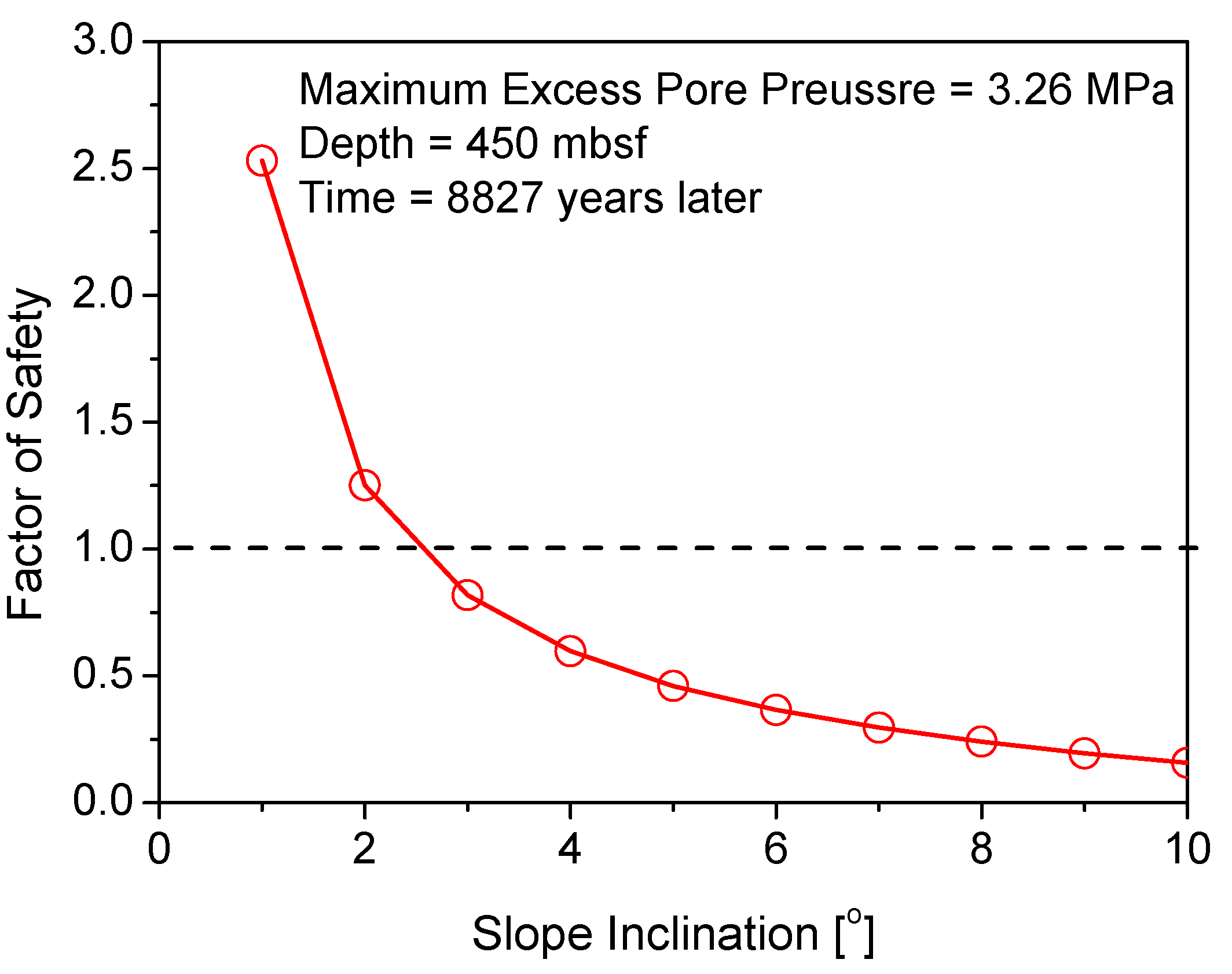
5. Discussion and Implications
5.1. Parametric Study
| Case | Thermal diffusivity [m−2·s−1] | Coefficient of consolidation above BHOZ [m−2·s−1] | Hydrate saturation [%] | Gas Saturation [%] |
|---|---|---|---|---|
| REF | 10−6 | 10−8 | 10 | 10 |
| TH1 | 10−5 | 10−8 | 10 | 10 |
| TH2 | 5 × 10−7 | 10−8 | 10 | 10 |
| TH3 | 10−7 | 10−8 | 10 | 10 |
| HP1 | 10−6 | 10−9 | 10 | 10 |
| HP2 | 10−6 | 10−7 | 10 | 10 |
| HP3 | 10−6 | 10−6 | 10 | 10 |
| SH1 | 10−6 | 10−8 | 5 | 10 |
| SH2 | 10−6 | 10−8 | 20 | 10 |
| SH3 | 10−6 | 10−8 | 10 | 30 |
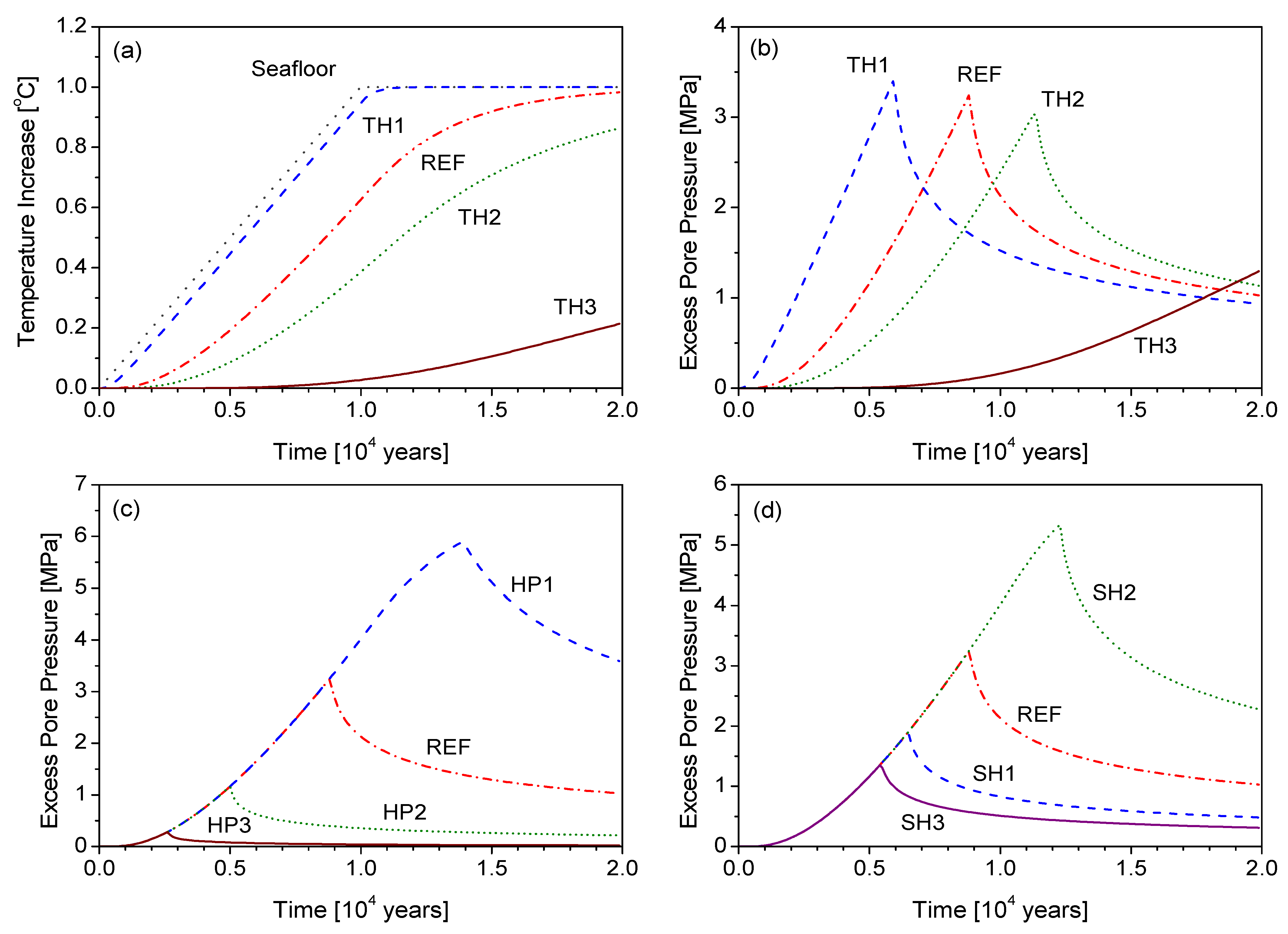
5.2. Thermal Destabilization of Hydrate-Bearing Sediments
5.3. Shallow Methane Hydrate Deposits
5.4. Implications for Sea-Level Lowering
6. Conclusions
Acknowledgments
References
- Sultan, N.; Cochonat, P.; Cayocca, F.; Bourillet, J.F.; Colliat, J.L. Analysis of submarine slumping in the Gabon continental slope. AAPG Bull. 2004, 88, 781–799. [Google Scholar] [CrossRef]
- Sultan, N.; Cochonat, P.; Foucher, J.P.; Mienert, J. Effect of gas hydrates melting on seafloor slope instability. Mar. Geol. 2004, 213, 379–401. [Google Scholar] [CrossRef]
- Davies, R.J.; Clark, I.R. Submarine slope failure primed and triggered by silica and its diagenesis. Basin Res. 2006, 18, 339–350. [Google Scholar] [CrossRef]
- Maslin, M.; Mikkelsen, N.; Vilela, C.; Haq, B. Sea-level- and gas-hydrate-controlled catastrophic sediment failures of the Amazon Fan. Geology 1998, 26, 1107–1110. [Google Scholar] [CrossRef]
- Rothwell, R.G.; Thomson, J.; Kahler, G. Low-sea-level emplacement of a very large Late Pleistocene ‘megaturbidite’ in the western Mediterranean Sea. Nature 1998, 392, 377–380. [Google Scholar] [CrossRef]
- Cochonat, P.; Cadet, J.P.; Lallemant, S.J.; Mazzotti, S.; Nouze, H.; Fouchet, C.; Foucher, J.P. Slope instabilities and gravity processes in fluid migration and tectonically active environment in the eastern Nankai accretionary wedge (KAIKO-Tokai ’96 cruise). Mar. Geol. 2002, 187, 193–202. [Google Scholar] [CrossRef]
- Wong, H.K.; Ludmann, T.; Baranov, B.V.; Karp, B.Y.; Konerding, P.; Ion, G. Bottom current-controlled sedimentation and mass wasting in the northwestern Sea of Okhotsk. Mar. Geol. 2003, 201, 287–305. [Google Scholar] [CrossRef]
- Vogt, P.R.; Jung, W.Y. Holocene mass wasting on upper non-Polar continental slopes—Due to post-Glacial ocean warming and hydrate dissociation? Geophys. Res. Lett. 2002, 29, 1341. [Google Scholar] [CrossRef]
- Jahren, A.H.; Conrad, C.P.; Arens, N.C.; Mora, G.; Lithgow-Bertelloni, C. A plate tectonic mechanism for methane hydrate release along subduction zones. Earth Planet. Sci. Lett. 2005, 236, 691–704. [Google Scholar] [CrossRef]
- Kayen, R.E.; Lee, H.J. Pleistocene slope instability of gas hydrate-laden sediment on the Beaufort sea margin. Mar. Geotechnol. 1991, 10, 125–141. [Google Scholar] [CrossRef]
- Kleinberg, R.L.; Flaum, C.; Griffin, D.D.; Brewer, P.G.; Malby, G.E.; Peltzer, E.T.; Yesinowski, J.P. Deep sea NMR: Methane hydrate growth habit in porous media and its relationship to hydraulic permeability, deposit accumulation, and submarine slope stability. J. Geophys. Res. 2003, 108, 2508. [Google Scholar] [CrossRef]
- Xu, W.Y.; Germanovich, L.N. Excess pore pressure resulting from methane hydrate dissociation in marine sediments: A theoretical approach. J. Geophys. Res. Solid Earth 2006, 111, B01104. [Google Scholar]
- Moridis, G.J.; Kowalsky, M.B. Response of oceanic hydrate-bearing sediments to thermal stresses. SPE J. 2007, 12, 253–268. [Google Scholar] [CrossRef]
- Nixon, M.F.; Grozic, J.L.H. Submarine slope failure due to gas hydrate dissociation: A preliminary quantification. Can. Geotech. J. 2007, 44, 314–325. [Google Scholar] [CrossRef]
- Kwon, T.H.; Cho, G.C.; Santamarina, J.C. Gas hydrate dissociation in sediments: Pressure-temperature evolution. Geochem. Geophys. Geosyst. 2008, 9, Q03019. [Google Scholar] [CrossRef]
- Kwon, T.H.; Lee, K.; Cho, G.C.; Lee, J.Y. Geotechnical properties of deep oceanic sediments recovered from the hydrate occurrence regions in the Ulleung Basin, East Sea, Offshore Korea. Mar. Pet. Geol. 2011, 28, 1870–1883. [Google Scholar] [CrossRef]
- Francisca, F.; Yun, T.S.; Ruppel, C.; Santamarina, J.C. Geophysical and geotechnical properties of near-seafloor sediments in the northern Gulf of Mexico gas hydrate province. Earth Planet. Sci. Lett. 2005, 237, 924–939. [Google Scholar] [CrossRef]
- Yun, T.S.; Fratta, D.; Santamarina, J.C. Hydrate-bearing sediments from the Krishna-Godavari basin: Physical characterization, pressure core testing and scaled production monitoring. Energy Fuels 2010, 24, 5972–5983. [Google Scholar] [CrossRef]
- Jang, J.; Santamarina, J.C. Recoverable gas from hydrate-bearing sediments: Pore network model simulation and macroscale analyses. J. Geophys. Res. 2011, 116, B08202. [Google Scholar]
- Holtzman, R.; Juanes, R. Thermodynamic and hydrodynamic constraints on overpressure caused by hydrate dissociation: A pore-scale model. J. Geophys. Res. 2011, 38, L14308. [Google Scholar]
- Birchwood, R.; Noeth, S.; Hooyman, P. Wellbore stability model for marine sediments contanining gas hydrates. In Proceedings of the AADE 2005 National Technical Conference and Exhibition, Houston, TX, USA, 5–7 April 2005. AADE-05-NTCE-13.
- Freij-Ayoub, R.; Tan, C.; Clennell, B.; Tohidi, B.; Yang, J.H. A wellbore stability model for hydrate bearing sediments. J. Pet. Sci. Eng. 2007, 57, 209–220. [Google Scholar] [CrossRef]
- Rutqvist, J.; Moridis, G.J. Numerical studies on the geomechanical stability of hydrate-bearing sediments. SPE J. 2009, 14, 267–282. [Google Scholar] [CrossRef]
- Kwon, T.H.; Song, K.I.; Cho, G.C. Destabilization of marine gas hydrate-bearing sediments induced by a hot wellbore: A numerical approach. Energ. Fuel 2010, 24, 5493–5507. [Google Scholar] [CrossRef]
- Bugge, T.; Befring, S.; Belderson, R.H.; Eidvin, T.; Jansen, E.; Kenyon, N.H.; Holtedahl, H.; Sejrup, H.P. A giant three-stage submarine slide off Norway. Geo-Mar. Lett. 1987, 7, 191–198. [Google Scholar] [CrossRef]
- Canals, M.; Lastras, G.; Urgeles, R.; Casamor, J.L.; Mienert, J.; Cattaneo, A.; De Batist, M.; Haflidason, H.; Imbo, Y.; Laberg, J.S.; et al. Slope failure dynamics and impacts from seafloor and shallow sub-seafloor geophysical data: Case studies from the COSTA project. Mar. Geol. 2004, 213, 9–72. [Google Scholar] [CrossRef]
- Dillon, W.P.; Nealon, J.W.; Taylor, M.H.; Lee, M.W.; Drury, R.M.; Anton, C.H. Seafloor collapse and methane venting associated with gas hydrate on the Blake ridge—Causes and implications to seafloor stability and methane release. Geophys. Monogr. Ser. 2001, 124, 211–233. [Google Scholar]
- Holbrook, W.S. Seismic studies of the Blake ridge: Implications for hydrate distribution, methane expulsion, and free gas dynamics. Geophys. Monogr. Ser. 2001, 124, 234–256. [Google Scholar]
- Levitus, S.; Antonov, J.; Boyer, T. Warming of the world ocean, 1955–2003. Geophys. Res. Lett. 2005, 32, L02604. [Google Scholar]
- Dickens, G.R. Carbon cycle—The blast in the past. Nature 1999, 401, 752–755. [Google Scholar] [CrossRef]
- Kennett, J.P.; Stott, L.D. Abrupt deep-sea warming, palaeoceanographic changes and benthic extinctions at the end of the Palaeocene. Nature 1991, 353, 225–229. [Google Scholar] [CrossRef]
- Dickens, G.R.; Castillo, M.M.; Walker, J.C.G. A blast of gas in the latest Paleocene: Simulating first-order effects of massive dissociation of oceanic methane hydrate. Geology 1997, 25, 259–262. [Google Scholar] [CrossRef] [PubMed]
- Norris, R.D.; Rohl, U. Carbon cycling and chronology of climate warming during the Palaeocene/Eocene transition. Nature 1999, 401, 775–778. [Google Scholar] [CrossRef]
- Bains, S.; Corfield, R.M.; Norris, R.D. Mechanisms of climate warming at the end of the Paleocene. Science 1999, 285, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Bice, K.L.; Marotzke, J. Could changing ocean circulation have destabilized methane hydrate at the Paleocene/Eocene boundary? Paleoceanography 2002, 17, 1818. [Google Scholar]
- Svensen, H.; Planke, S.; Malthe-Sorenssen, A.; Jamtveit, B.; Myklebust, R.; Eidem, T.R.; Rey, S.S. Release of methane from a volcanic basin as a mechanism for initial Eocene global warming. Nature 2004, 429, 542–545. [Google Scholar] [CrossRef] [PubMed]
- Hesselbo, S.P.; Grocke, D.R.; Jenkyns, H.C.; Bjerrum, C.J.; Farrimond, P.; Bell, H.S.M.; Green, O.R. Massive dissociation of gas hydrate during a Jurassic oceanic anoxic event. Nature 2000, 406, 392–395. [Google Scholar] [CrossRef] [PubMed]
- Katz, M.E.; Cramer, B.S.; Mountain, G.S.; Katz, S.; Miller, K.G. Uncorking the bottle: What triggered the Paleocene/Eocene thermal maximum methane release? Paleoceanography 2001, 16, 549–562. [Google Scholar] [CrossRef]
- Kvenvolden, K.A. Methane hydrates and global climate. Glob. Biogeochem. Cycles 1988, 2, 221–229. [Google Scholar] [CrossRef]
- Walter, K.M.; Zimov, S.A.; Chanton, J.P.; Verbyla, D.; Chapin, F.S., III. Methane bubbling from Siberian thaw lakes as a positive feedback to climate warming. Nature 2006, 443, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Zimov, S.A.; Schuur, E.A.G.; Chapin, F.S., III. Permafrost and the global carbon budget. Science 2006, 312, 1612–1613. [Google Scholar] [CrossRef] [PubMed]
- Shakhova, N.; Semiletov, I.; Salyuk, A.; Yusupov, V.; Kosmach, D.; Gustafsson, O. Extensive methane venting to the atmosphere from sediments of the East Siberian Arctic Shelf. Science 2010, 327, 1246–1250. [Google Scholar] [CrossRef] [PubMed]
- Westbrook, G.K.; Thatcher, K.E.; Rohling, E.J.; Piotrowski, A.M.; Pälike, H.; Osborne, A.H.; Nisbet, E.G.; Minshull, T.A.; Lanoisellé, M.; James, R.H.; et al. Escape of methane gas from the seabed along the West Spitsbergen continental margin. Geophys. Res. Lett. 2009, 36, L15608. [Google Scholar] [CrossRef]
- Kerr, R.A. “Arctic Armageddon” needs more science, less hype. Science 2010, 329, 620–621. [Google Scholar] [CrossRef] [PubMed]
- Biastoch, A.; Treude, T.; Rüpke, L.H.; Riebesell, U.; Roth, C.; Burwicz, E.B.; Park, W.; Latif, M.; Böning, C.W.; Madec, G.; et al. Rising Arctic ocean temperatures cause gas hydrate destabilization and ocean acidification. Geophys. Res. Lett. 2011, 38, L08602. [Google Scholar] [CrossRef]
- Houghton, J. Global warming. Rep. Prog. Phys. 2005, 68, 1343–1403. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Stephens, C. Warming of the world ocean. Science 2000, 287, 2225–2229. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.E.; Locarnini, R.A.; Mishonov, A.V.; Reagan, J.R.; Seidov, D.; Yarosh, E.S.; et al. World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys. Res. Lett. 2012, 39, L10603. [Google Scholar] [CrossRef]
- Purkey, S.G.; Johnson, G.C. Warming of global abyssal and deep southern ocean waters between the 1990s and 2000s: Contributions to global heat and sea level rise budgets. J. Clim. 2010, 23, 6336–6351. [Google Scholar] [CrossRef]
- Robertson, R.; Visbeck, M.; Gordon, A.L.; Fahrbach, E. Long-term temperature trends in the deep waters of the Weddell Sea. Deep Sea Res. Part II Top. Stud. Oceanogr. 2002, 49, 4791–4806. [Google Scholar] [CrossRef]
- Anderson, R.; Llamedo, M.; Tohidi, B.; Burgass, R.W. Experimental measurement of methane and carbon dioxide clathrate hydrate equilibria in mesoporous silica. J. Phys. Chem. B 2003, 107, 3507–3514. [Google Scholar] [CrossRef]
- Kwon, T.H.; Kim, H.S.; Cho, G.C. Dissociation behavior of CO2 hydrate in sediments during isochoric heating. Environ. Sci. Technol. 2008, 42, 8571–8577. [Google Scholar] [CrossRef] [PubMed]
- Sloan, E.D. Clathrate Hydrates of Natural Gas, 2nd ed.; Dekker: New York, NY, USA, 1998. [Google Scholar]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; Wiley: New York, NY, USA, 1948. [Google Scholar]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 78th ed.; CRC Press Inc.: Boca Raton, FL, USA, 1997. [Google Scholar]
- Paull, C.K.; Matsumoto, R.; Wallace, P.J.; Dillon, W.P. (Eds.) Proceedings of the Ocean Drilling Program, Scientific Results; Ocean Drilling Program: College Station, TX, USA, 2000; Volume 164. [CrossRef]
- Dickens, G.R.; Paull, C.K.; Wallace, P. Direct measurement of in situ methane quantities in a large gas-hydrate reservoir. Nature 1997, 385, 426–428. [Google Scholar] [CrossRef]
- Clennell, M.; Hovland, M.; Booth, J.S.; Henry, P.; Winters, W.J. Formation of natural gas hydrates in marine sediments 1: Conceptual model of gas hydrate growth conditioned by host sediment properties. J. Geophys. Res. 1999, 104, 22985–23003. [Google Scholar] [CrossRef]
- Xu, W.Y.; Ruppel, C. Predicting the occurrence, distribution, and evolution of methane gas hydrate in porous marine sediments. J. Geophys. Res. 1999, 104, 5081–5095. [Google Scholar] [CrossRef]
- Yun, T.S.; Santamarina, J.C.; Ruppel, C. Mechanical properties of sand, silt, and clay containing tetrahydrofuran hydrate. J. Geophys. Res. 2007, 112, B04106. [Google Scholar]
- Mesri, G. Discussion on “New design procedure for stability of soft clays”. J. Geotech. Eng. ASCE 1975, 101, 409–412. [Google Scholar]
- Mesri, G. A Reevaluation of Su(Mob) = 0.22σ'p using laboratory shear tests. Can. Geotech. J. 1989, 26, 162–164. [Google Scholar] [CrossRef]
- Henninges, J.; Huenges, E.; Burkhardt, H. In situ thermal conductivity of gas-hydrate-bearing sediments of the Mallik 5L-38 well. J. Geophys. Res. 2005, 110, B11206. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Ruppel, C. The impact of hydrate saturation on the mechanical, electrical, and thermal properties of hydrate-bearing sand, silts, and clay. In Proceedings of the 6th International Conference on Gas Hydrates, Vancouver, Canada, 6–10 July 2008.
- Cortes, D.D.; Martin, A.I.; Yun, T.S.; Francisca, F.M.; Santamarina, J.C.; Ruppel, C. Thermal conductivity of hydrate-bearing sediments. J. Geophys. Res. 2009, 114, B11103. [Google Scholar] [CrossRef]
- Waite, W.F.; Santamarina, J.C.; Cortes, D.D.; Dugan, B.; Espinoza, D.N.; Germaine, J.; Jang, J.; Jung, J.W.; Kneafsey, T.J.; Shin, H.; et al. Physical properties of hydrate-bearing sediments. Rev. Geophys. 2009, 47, RG4003. [Google Scholar] [CrossRef]
- MacDonald, I.R.; Bender, L.C.; Vardaro, M.; Bernard, B.; Brooks, J.M. Thermal and visual time-series at a seafloor gas hydrate deposit on the Gulf of Mexico slope. Earth Planet. Sci. Lett. 2005, 233, 45–59. [Google Scholar] [CrossRef]
- Nimblett, J.; Ruppel, C. Permeability evolution during the formation of gas hydrates in marine sediments. J. Geophys. Res. 2003, 108, 2420. [Google Scholar] [CrossRef]
- Johnson, A.; Patil, S.; Dandekar, A. Experimental investigation of gas-water relative permeability for gas-hydrate-bearing sediments from the Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope. Mar. Pet. Geol. 2011, 28, 419–426. [Google Scholar] [CrossRef]
- Seol, Y.; Kneafsey, T.J. Methane hydrate induced permeability modification for multiphase flow in unsaturated porous media. J. Geophys. Res. 2011, 116, B08102. [Google Scholar]
- Peltzer, E.P.; Brewer, P.G. Practical physical chemistry and empirical predictions of methane hydrate stability. In Natural Gas Hydrate in Oceanic and Permafrost Environments; Max, M.D., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000; pp. 17–28. [Google Scholar]
- Henry, P.; Thomas, M.; Clennell, M.B. Formation of natural gas hydrates in marine sediments 2: Thermodynamic calculations of stability conditions in porous sediments. J. Geophys. Res. 1999, 104, 23005–23022. [Google Scholar] [CrossRef]
- Ruppel, C. Anomalously cold temperatures observed at the base of the gas hydrate stability zone on the US Atlantic passive margin. Geol. 1997, 25, 699–702. [Google Scholar] [CrossRef]
- Briaud, J.L.; Chaouch, A. Hydrate melting in soil around hot conductor. J. Geotech. Geoenviron. Eng. 1997, 123, 645–653. [Google Scholar] [CrossRef]
- Zatsepina, O.Y.; Buffett, B.A. Phase equilibrium of gas hydrate: Implications for the formation of hydrate in the deep sea floor. Geophys. Res. Lett. 1997, 24, 1567–1570. [Google Scholar] [CrossRef]
- Seo, Y.; Lee, H.; Ryu, B.J. Hydration number and two-phase equilibria of CH4 hydrate in the deep ocean sediments. Geophys. Res. Lett. 2002, 29, 1244. [Google Scholar] [CrossRef]
- Davie, M.K.; Zatsepina, O.Y.; Buffett, B.A. Methane solubility in marine hydrate environments. Mar. Geol. 2004, 203, 177–184. [Google Scholar] [CrossRef]
- Waite, W.F.; Stern, L.A.; Kirby, S.H.; Winters, W.J.; Mason, D.H. Simultaneous determination of thermal conductivity, thermal diffusivity and specific heat in sI methane hydrate. Geophys. J. Int. 2007, 169, 767–774. [Google Scholar] [CrossRef]
- Hornbach, M.J.; Saffer, D.M.; Holbrook, W.S. Critically pressured free-gas reservoirs below gas-hydrate provinces. Nature 2004, 427, 142–144. [Google Scholar] [CrossRef] [PubMed]
- Cabanes, C.; Cazenave, A.; Le Provost, C. Sea level rise during past 40 years determined from satellite and in situ observations. Science 2001, 294, 840–842. [Google Scholar] [CrossRef] [PubMed]
- Peltier, W.R. Global sea level rise and glacial isostatic adjustment. Global Planet. Chang. 1999, 20, 93–123. [Google Scholar] [CrossRef]
- Yokoyama, Y.; De Deckker, P.; Lambeck, K.; Johnston, P.; Fifield, L.K. Sea-level at the Last Glacial Maximum: Evidence from northwestern Australia to constrain ice volumes for oxygen isotope stage 2. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2001, 165, 281–297. [Google Scholar] [CrossRef]
- Fleming, K.; Johnston, P.; Zwartz, D.; Yokoyama, Y.; Lambeck, K.; Chappell, J. Refining the eustatic sea-level curve since the Last Glacial Maximum using far- and intermediate-field sites. Earth Planet. Sci. Lett. 1998, 163, 327–342. [Google Scholar] [CrossRef]
- Camoin, G.F.; Montaggioni, L.F.; Braithwaite, C.J.R. Late glacial to post glacial sea levels in the Western Indian Ocean. Mar. Geol. 2004, 206, 119–146. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kwon, T.-H.; Cho, G.-C. Submarine Slope Failure Primed and Triggered by Bottom Water Warming in Oceanic Hydrate-Bearing Deposits. Energies 2012, 5, 2849-2873. https://doi.org/10.3390/en5082849
Kwon T-H, Cho G-C. Submarine Slope Failure Primed and Triggered by Bottom Water Warming in Oceanic Hydrate-Bearing Deposits. Energies. 2012; 5(8):2849-2873. https://doi.org/10.3390/en5082849
Chicago/Turabian StyleKwon, Tae-Hyuk, and Gye-Chun Cho. 2012. "Submarine Slope Failure Primed and Triggered by Bottom Water Warming in Oceanic Hydrate-Bearing Deposits" Energies 5, no. 8: 2849-2873. https://doi.org/10.3390/en5082849
APA StyleKwon, T.-H., & Cho, G.-C. (2012). Submarine Slope Failure Primed and Triggered by Bottom Water Warming in Oceanic Hydrate-Bearing Deposits. Energies, 5(8), 2849-2873. https://doi.org/10.3390/en5082849





