Exergy Analysis of Overspray Process in Gas Turbine Systems
Abstract
:1. Introduction
2. System Analysis
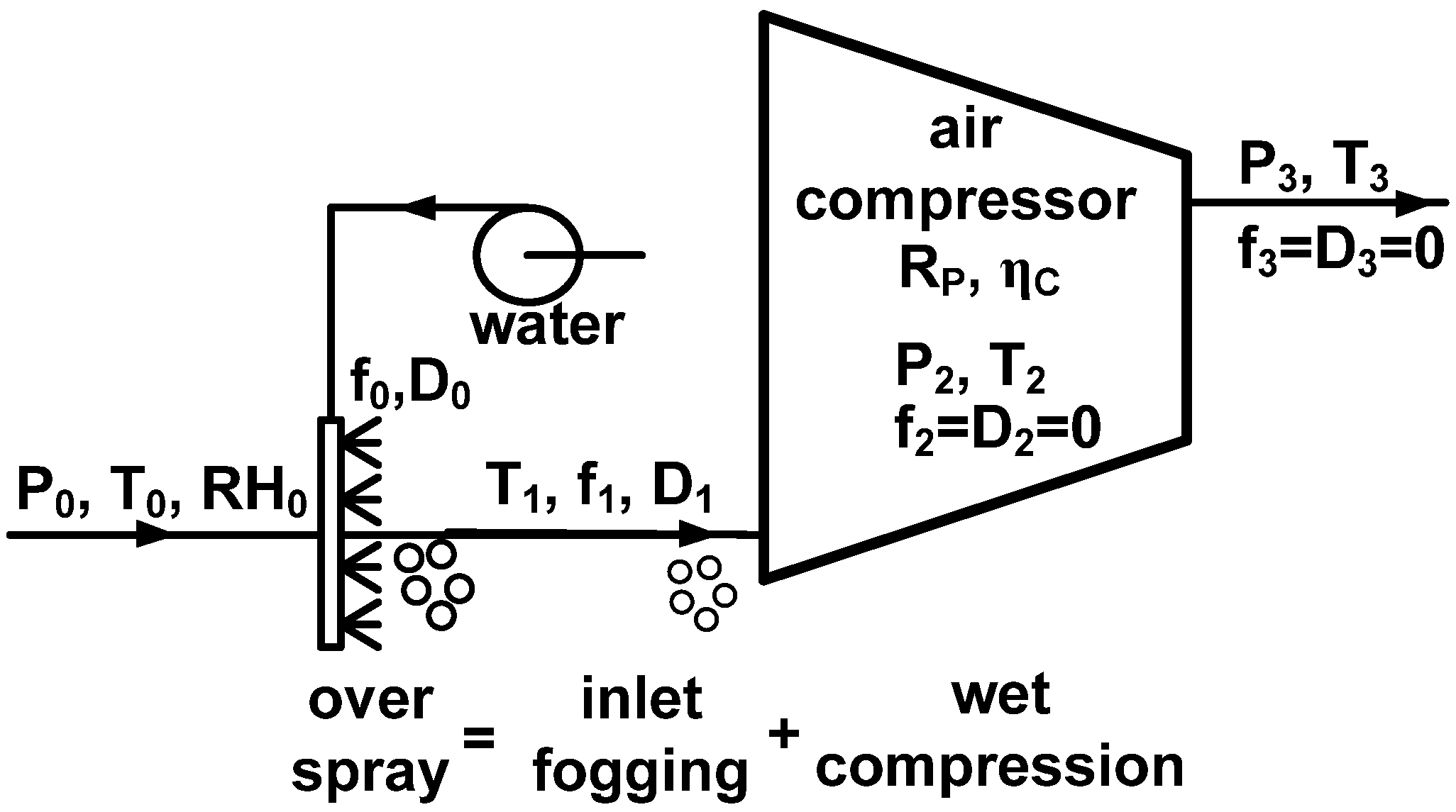
3. Results and Discussion
3.1. Effects of Pressure Ratio
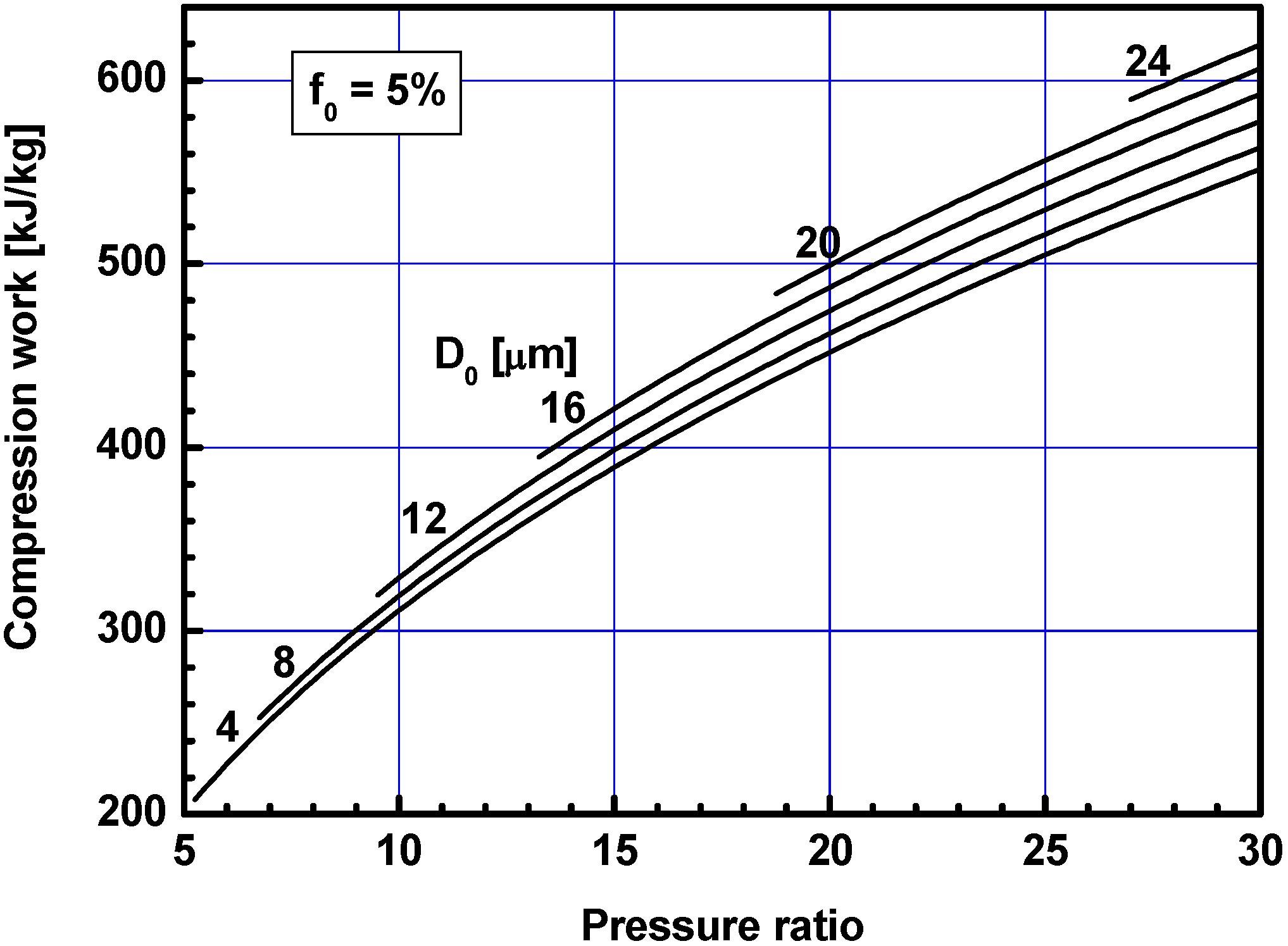
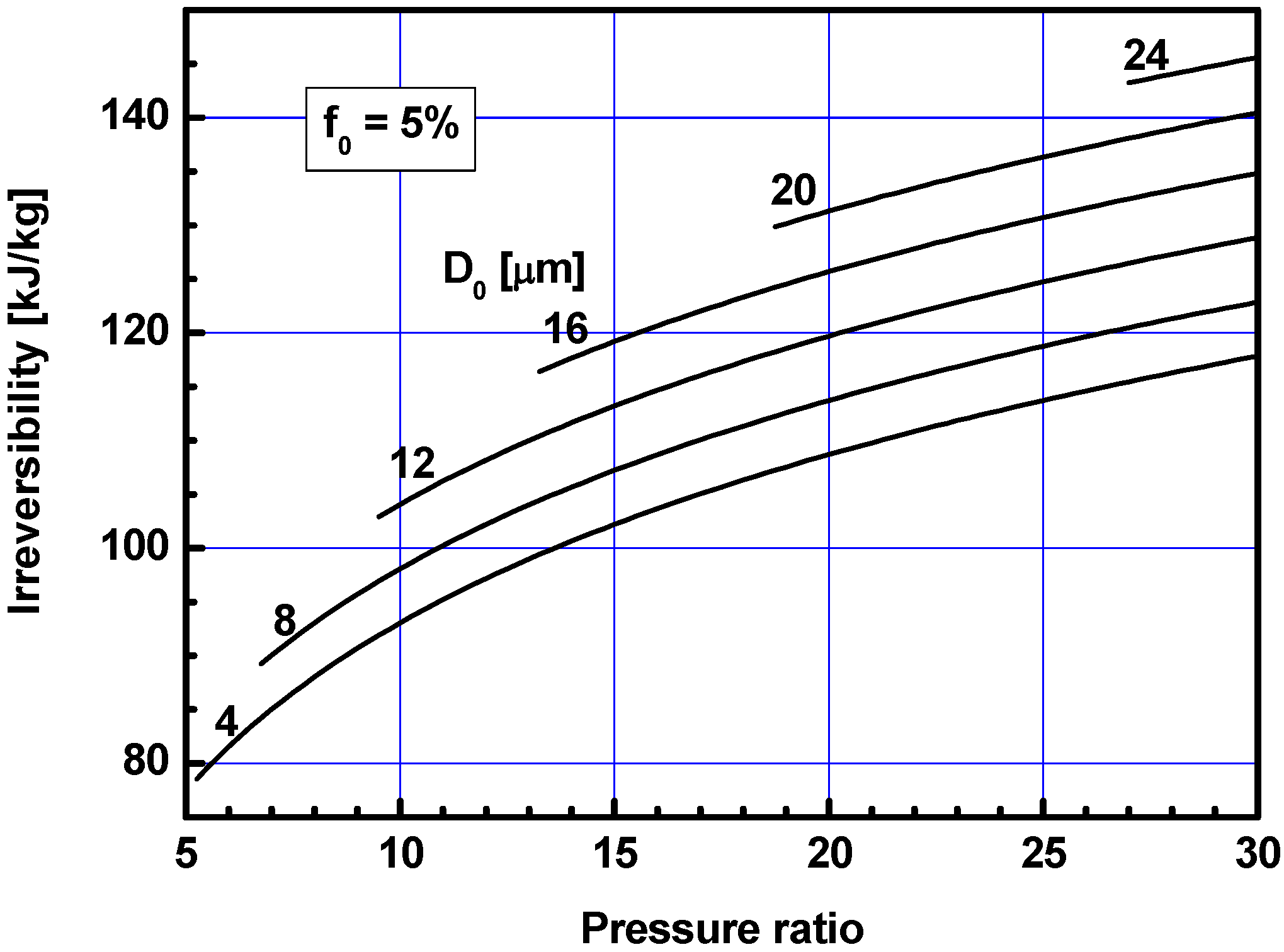
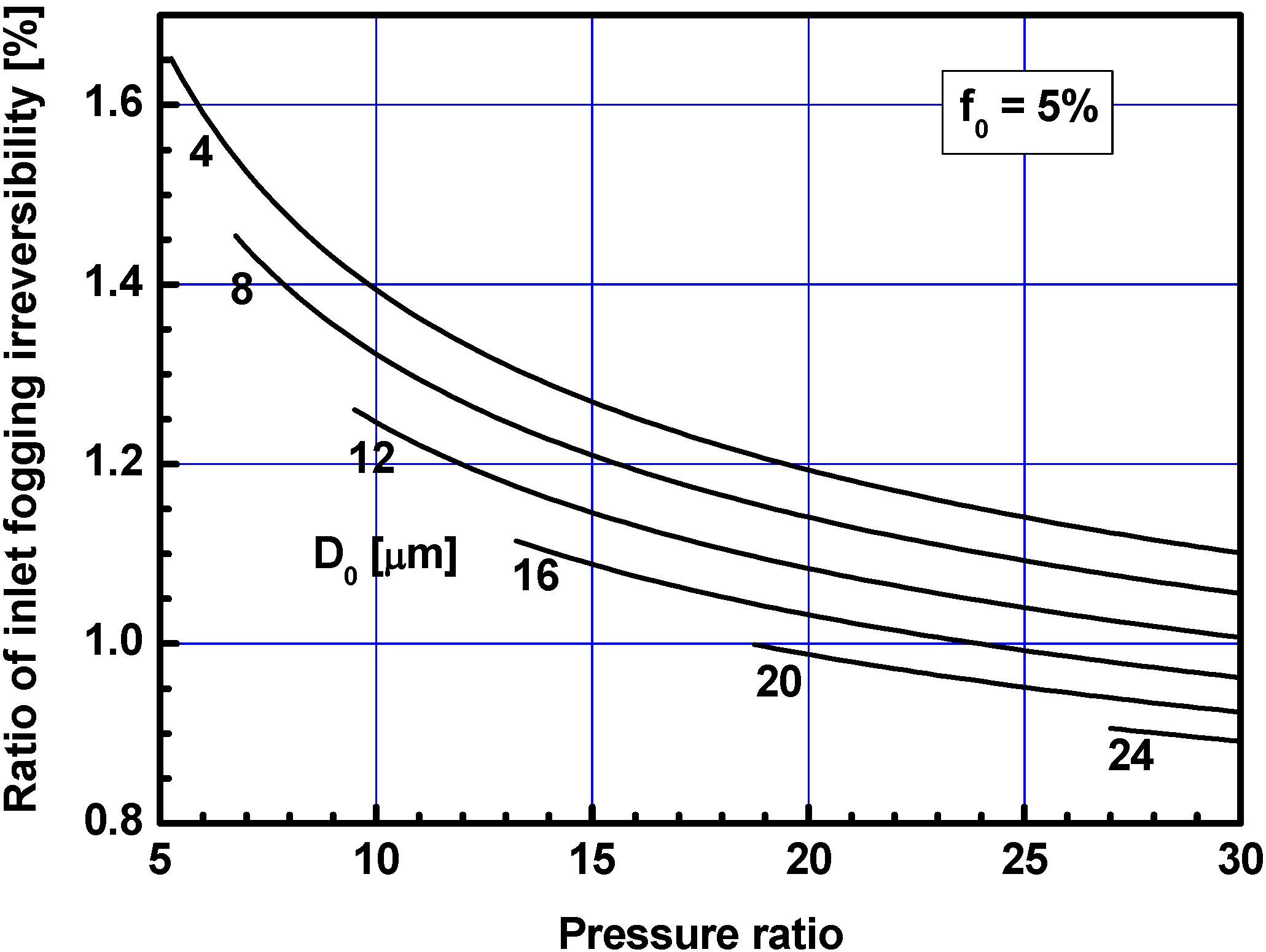
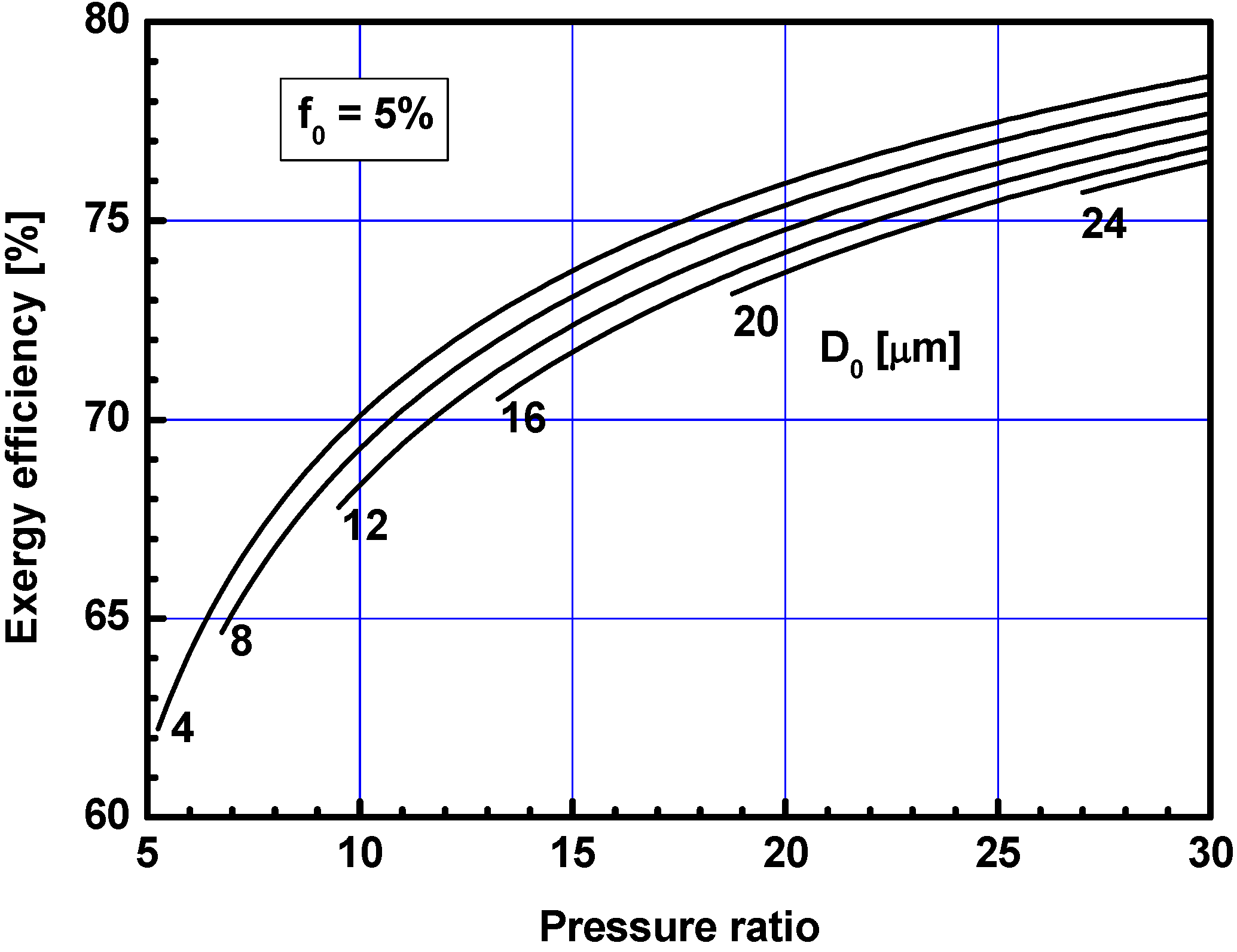
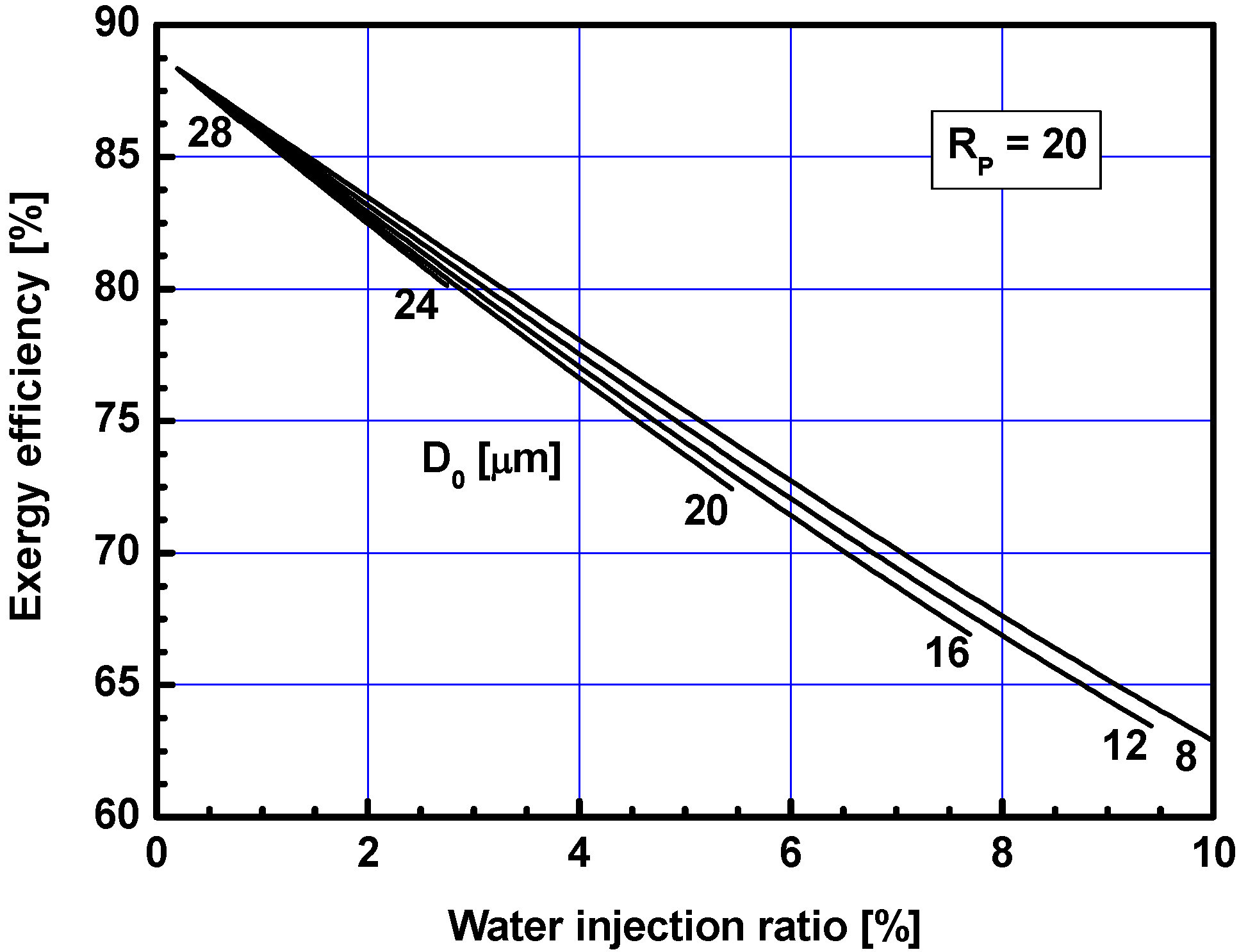
3.2. Effects of Water Injection Ratio
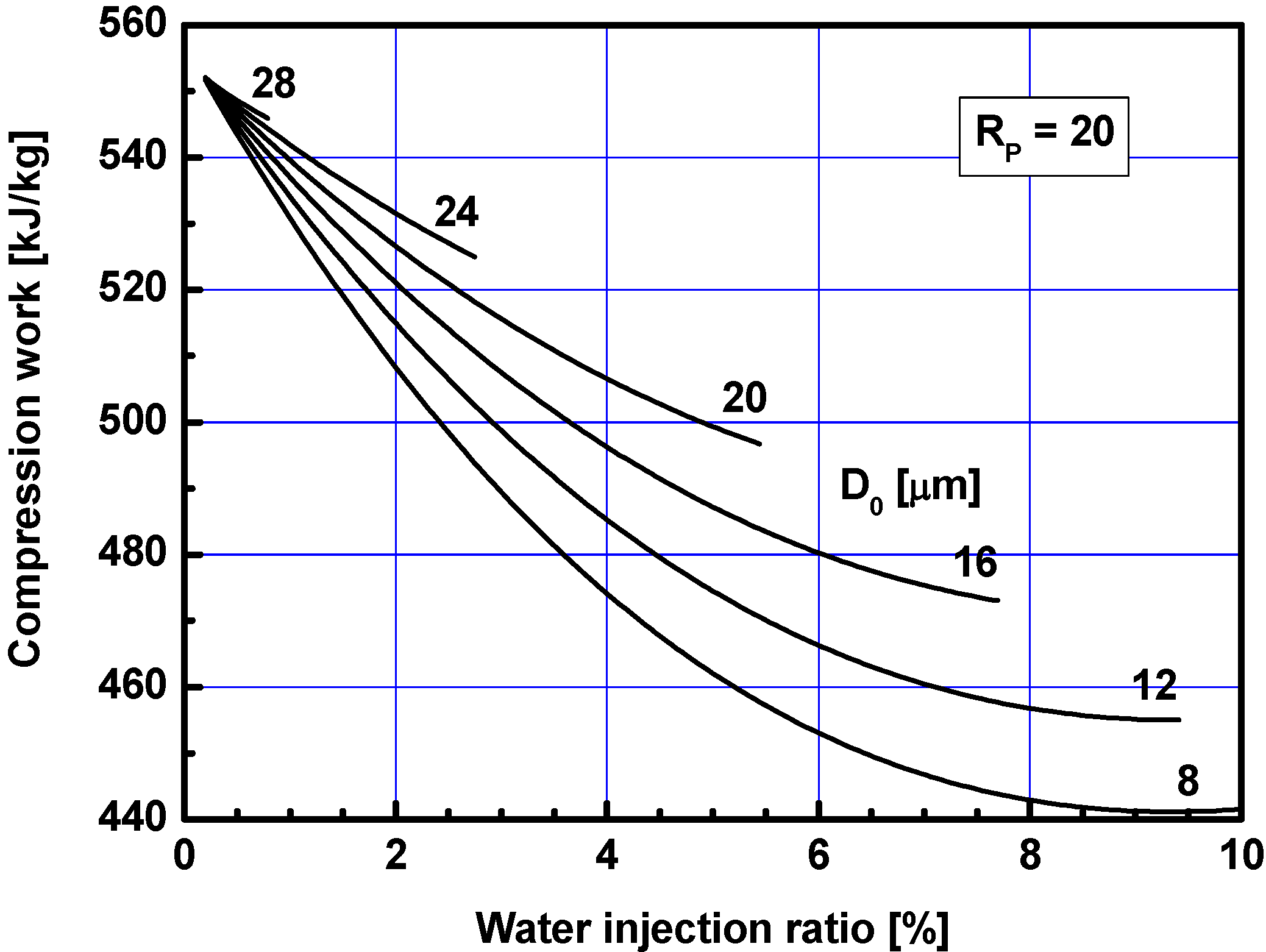
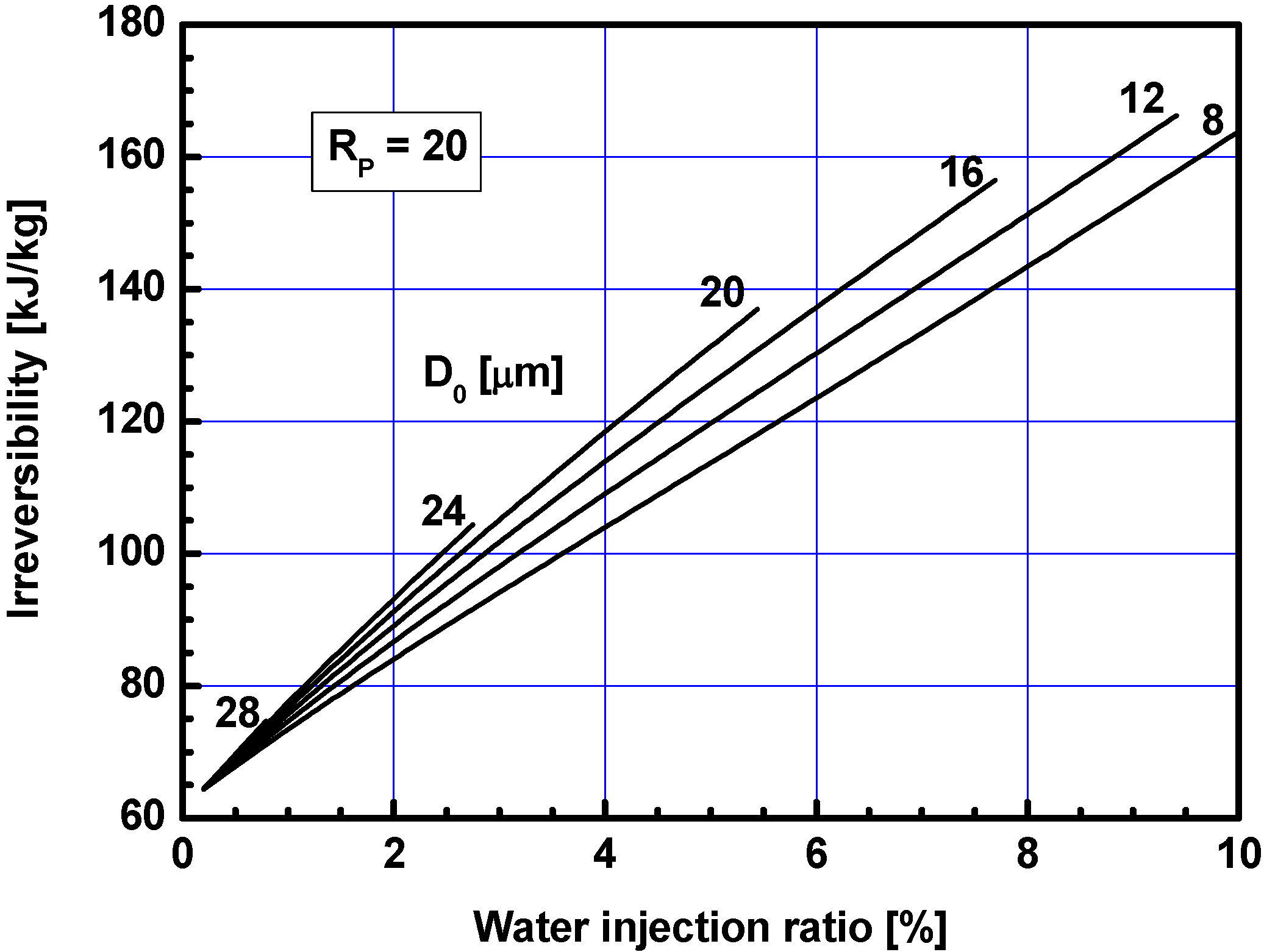
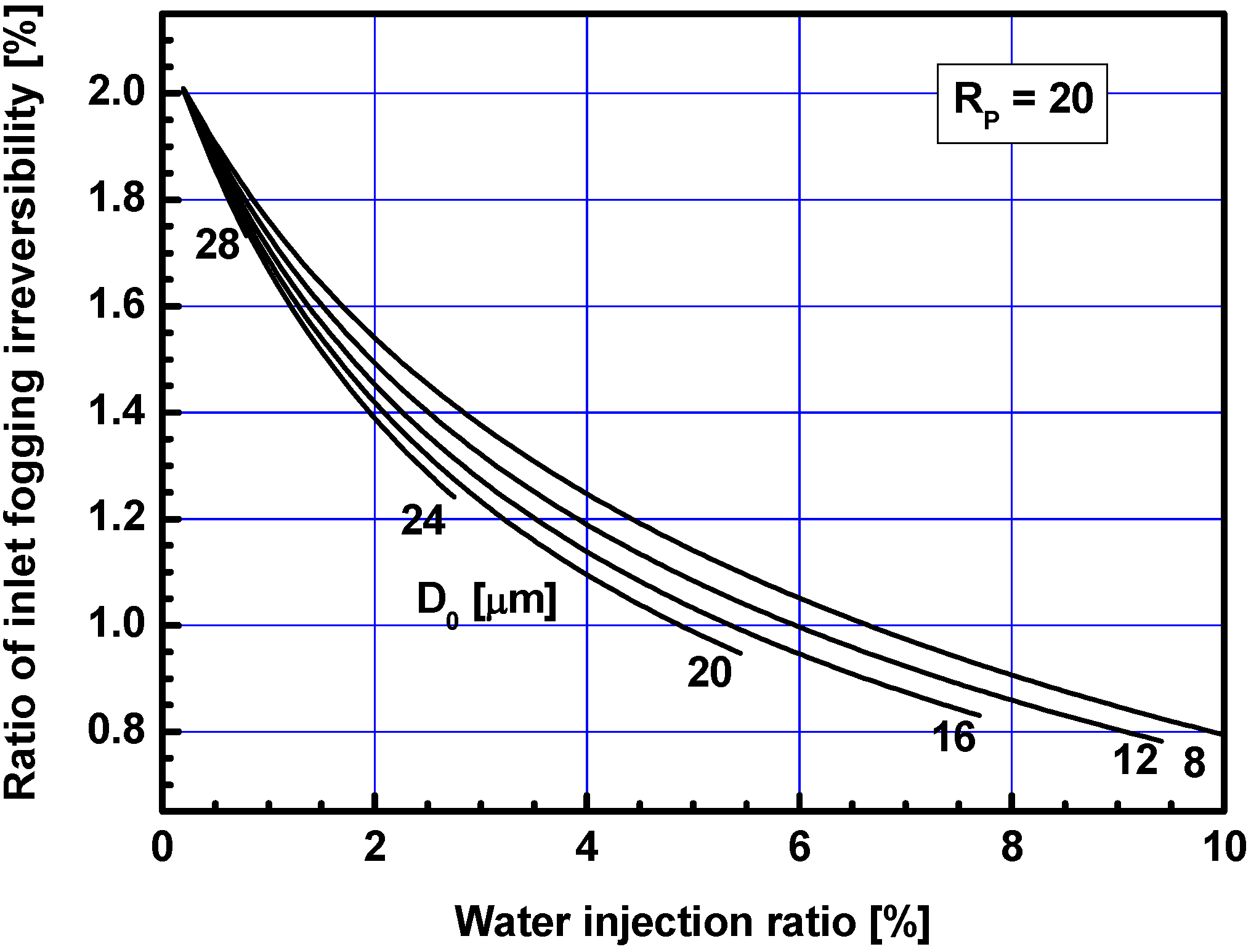
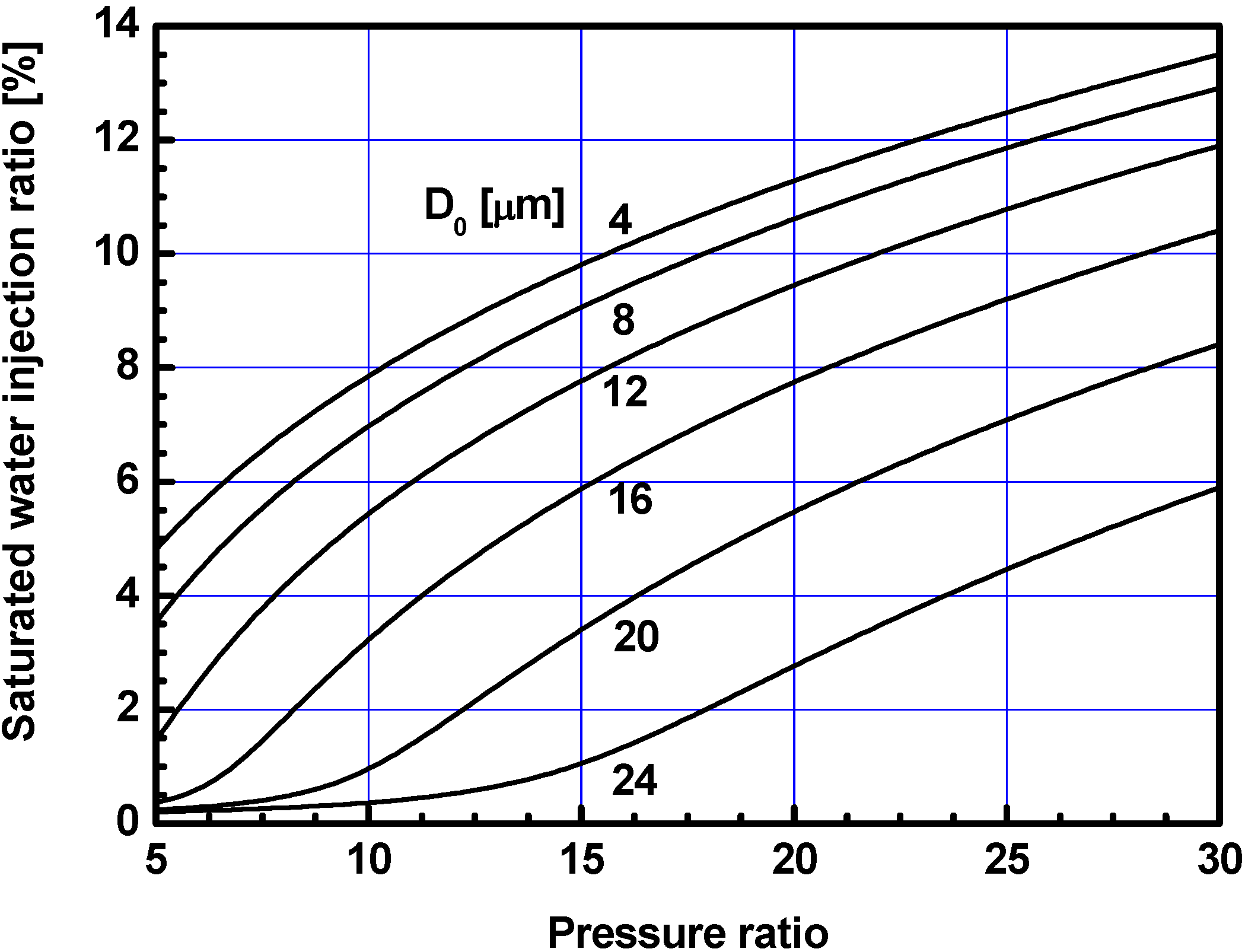
3.3. Results with Saturated Water Injection Ratios
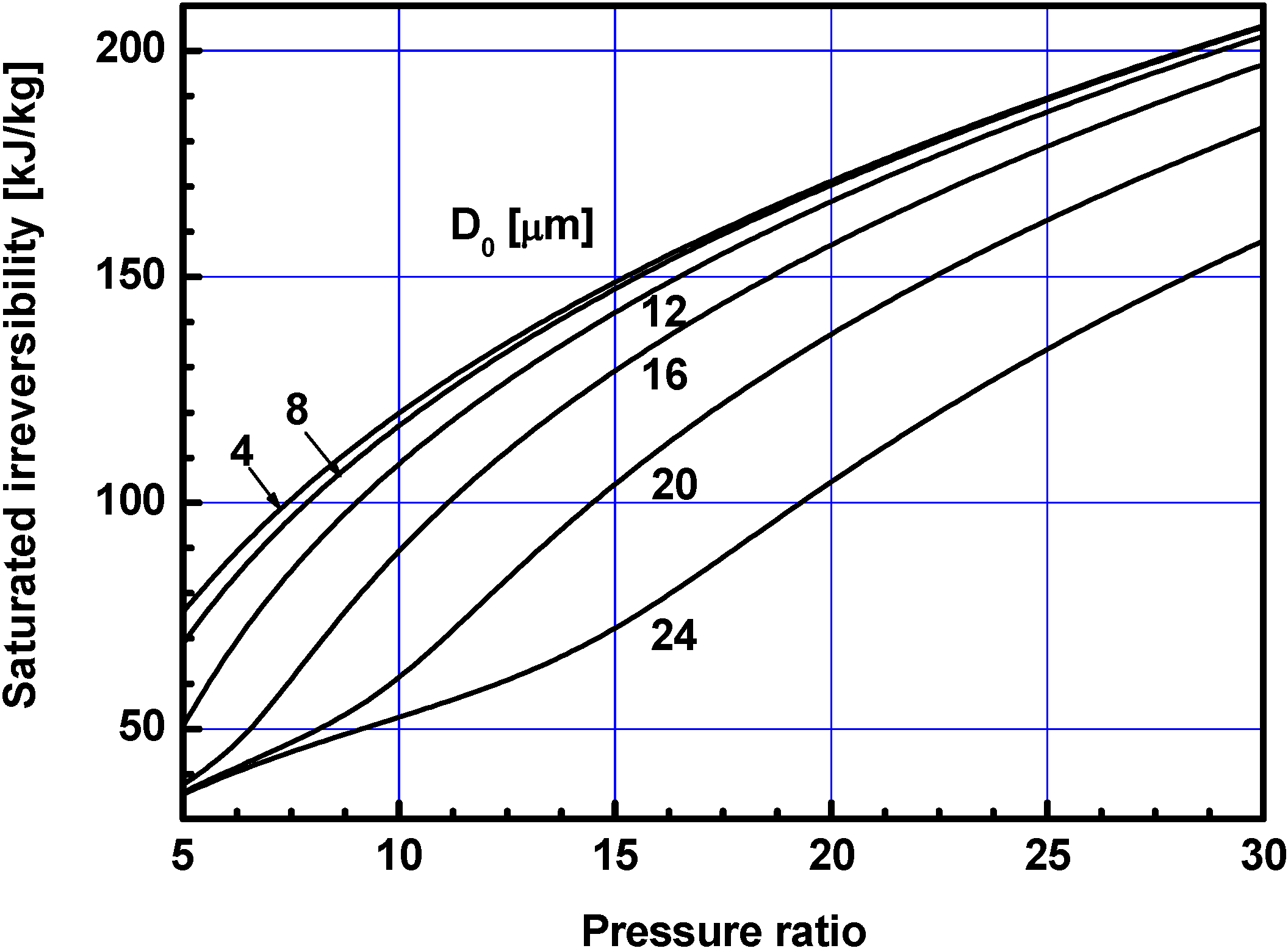
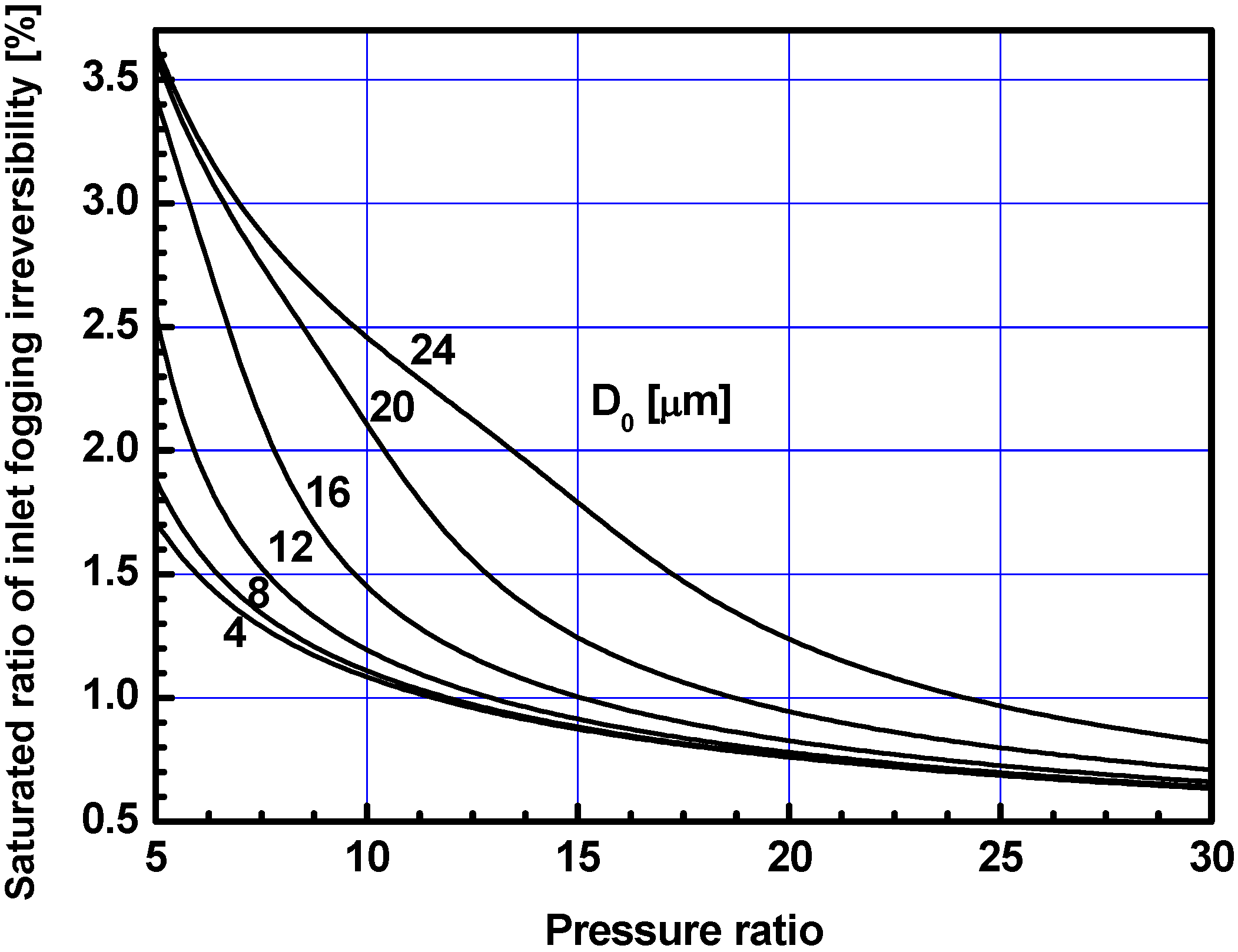
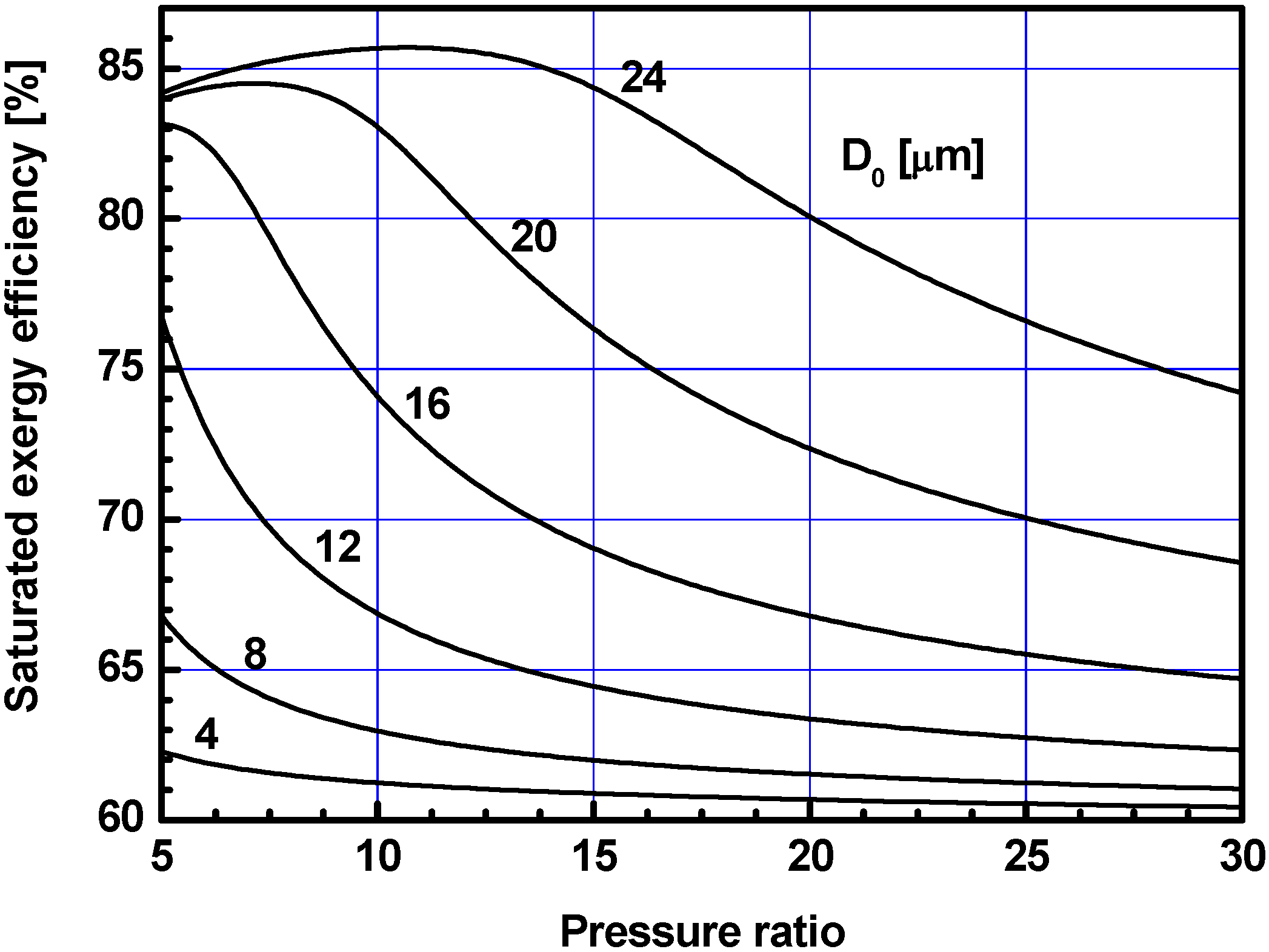
4. Conclusions
Acknowledgments
References
- Sorensen, H.A. Energy Conversion Systems; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Lanzi, E.; Verdolini, E.; Hascic, I. Efficiency-improving fossil fuel technologies for electricity generation: Data selection and trends. Energy Policy 2011, 39, 7000–7014. [Google Scholar] [CrossRef]
- Poullikkas, A. An overview of current and future sustainable gas turbine technologies. Renew. Sustain. Energy Rev. 2005, 9, 409–443. [Google Scholar] [CrossRef]
- Jonsson, M.; Yan, J. Humidified gas turbines—a review of proposed and implemented cycles. Energy 2005, 30, 1013–1078. [Google Scholar] [CrossRef]
- Kakaras, E.; Doukelis, A.; Karellas, S. Compressor intake-air cooling in gas turbine plants. Energy 2004, 29, 2347–2358. [Google Scholar] [CrossRef]
- Chaker, C.B.; Meher-Homji, C.B.; Mee, T., III. Inlet fogging of gas turbine engines—Part I: Fog droplet thermodynamics, heat transfer, and practical considerations. J. Eng. Gas Turbines Power 2004, 126, 545–558. [Google Scholar] [CrossRef]
- Chaker, C.B.; Meher-Homji, C.B.; Mee, T., III. Inlet fogging of gas turbine engines—Part II: Fog droplet sizing analysis, nozzle types, measurement, and testing. J. Eng. Gas Turbines Power 2004, 126, 559–570. [Google Scholar] [CrossRef]
- Chaker, C.B.; Meher-Homji, C.B.; Mee, T., III. Inlet fogging of gas turbine engines—Part III: Fog behavior in inlet ducts, computational fluid dynamics analysis, and wind tunnel experiments. J. Eng. Gas Turbines Power 2004, 126, 571–580. [Google Scholar] [CrossRef]
- Utamura, M. Empirical correlations for predicting key performance parameters due to inlet fogging. In Proceedings of 2005 ASME Turbo Expo Conference, Reno-Tahoe, NV, USA, 6–9 June 2005; pp. 201–208.
- Bhargava, R.K.; Meher-Homji, C.B.; Chaker, M.A.; Bianchi, M.; Melino, F.; Peretto, A.; Ingistov, S. Gas turbine fogging technology: A state of the art review Part I: Inlet evaporative fogging—analytical and experimental aspects. In Proceedings of 2005 ASME Turbo Expo Conference, Reno-Tahoe, NV, USA, 6–9 June 2005; pp. 71–82.
- Belarbi, R.; Ghihaus, C.; Allard, F. Modeling of water spray evaporation: Application to passive cooling of buildings. Sol. Energy 2006, 80, 1540–1552. [Google Scholar] [CrossRef]
- Yang, C.; Yang, Z.; Cai, R. Analytical method for evaluation of gas turbine inlet air cooling in combined cycle power plant. Appl. Energy 2009, 86, 848–856. [Google Scholar] [CrossRef]
- Farzaneh-Gord, M.; Deymi-Dashtebayaz, M. Effects of various inlet air cooling methods on gas turbine performance. Energy 2011, 36, 1196–1205. [Google Scholar] [CrossRef]
- Kim, K.H.; Ko, H.J.; Kim, K.; Perez-Blanco, H. Analysis of water droplet evaporation in a gas turbine inlet fogging process. Appl. Therm. Eng. 2012, 33–34, 62–69. [Google Scholar]
- Utamura, M.; Takkaki, K.; Murata, H.; Nubuyuki, H. Effects of intensive evaporative-cooling on performance characteristics of a land-based gas turbine. In Proceedings of ASME International Joint Power Generation Conference, San Francisco, CA, USA, 25–28 July 1999; Volume 34, pp. 321–328.
- Zheng, Q.; Sun, Y.; Li, Y.; Wnag, Y. Thermodynamic analyses of wet compression process in the compressor of gas turbine. J. Turbomach. 2003, 125, 489–496. [Google Scholar] [CrossRef]
- White, A.J.; Meacock, A.J. An evaluation of the effects of water injection on compressor performance. J. Eng. Gas Turbines Power 2004, 126, 748–754. [Google Scholar] [CrossRef]
- Kim, K.H.; Perez-Blanco, H. Potential of regenerative gas-turbine systems with high fogging compression. Appl. Energy 2007, 84, 16–28. [Google Scholar] [CrossRef]
- Perez-Blanco, H.; Kim, K.H.; Ream, S. Evaporatively-cooled compression using a high-pressure refrigerant. Appl. Energy 2007, 84, 1028–1043. [Google Scholar] [CrossRef]
- Bracco, S.; Pierfederici, A.; Trucco, A. The wet compression technology for gas turbine power plants: Thermodynamic model. Appl. Therm. Eng. 2007, 27, 699–704. [Google Scholar] [CrossRef]
- Roumeliotis, I.; Mathioudakis, K. Evaluation of water injection effect on compressor and engine performance and operability. Appl. Energy 2010, 87, 1207–1216. [Google Scholar] [CrossRef]
- Johnson, M.V.; Zhu, G.S.; Aggarwal, S.K.; Goldsborough, S.S. Droplet evaporation characteristics due to wet compression under RCM conditions. Int. J. Heat Mass Transfer 2010, 53, 1100–1111. [Google Scholar] [CrossRef]
- Goldborough, S.S.; Johnson, M.V.; Zhu, G.S.; Aggarwal, S.K. Gas-phase saturation and evaporative cooling effects during wet compression of a fuel aerosol under RCM conditions. Combust. Flame 2011, 158, 57–68. [Google Scholar] [CrossRef]
- Kim, K.H.; Ko, H.J.; Perez-Blanco, H. Analytical modeling of wet compression of gas turbine systems. Appl. Therm. Eng. 2011, 31, 834–840. [Google Scholar] [CrossRef]
- Chiang, H.W.; Wang, P.Y.; Tsai, B.J. Gas turbine power augmentation by overspray inlet fogging. J. Energy Eng. 2007, 133, 224–235. [Google Scholar] [CrossRef]
- Sanaye, S.; Rezazadeh, H.; Aghazeynali, M. Effects of inlet fogging and wet compression on gas turbine performance. In Proceedings of 2006 ASME Turbo Expo Conference, Barcelona, Spain, 8–11 May 2006; pp. 769–776.
- Sanaye, S.; Tahani, M. Analysis of gas turbine operating parameters with inlet fogging and wet compression processes. Appl. Therm. Eng. 2010, 30, 234–244. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Huerdogan, E.; Buyuekalaka, O.; Hepbasli, A.; Yilmaz, T. Exergetic modeling and experimental performance assessment of a novel desiccant cooling system. Energy Build. 2011, 43, 1489–1498. [Google Scholar] [CrossRef]
- Ehyaei, M.A.; Mozafari, A.; Alibiglou, M.H. Exergy, economic & environmental (3E) analysis of inlet fogging for gas turbine power plant. Energy 2011, 36, 6851–6861. [Google Scholar]
- Kim, K.H.; Ko, H.J.; Perez-Blanco, H. Exergy analysis of gas-turbine systems with high-fogging compression. Int. J. Exergy 2011, 8, 16–32. [Google Scholar] [CrossRef]
- Bianchi, M.; Chaker, M.; De Pascale, A.; Peretto, A.; Spina, P.R. CFD Simulation of water injection in GT inlet duct using spray experimentally tuned data: Nozzle spray simulation model and results for an application to a heavy-duty gas turbine. In Proceedings of 2007 ASME Turbo Expo Conference, Montreal, Canada, 14–17 May 2007; pp. 629–642.
- Nikolaidis, T.; Pilidis, P.; Teixeira, J.A.; Pachidis, V. Water film formation on an axial flow compressor rotor blade. In Proceedings of 2008 ASME Turbo Expo Conference, Reno-Tahoe, Berlin, Germany, 9–13 June 2008; pp. 79–87.
- Sun, L.; Zheng, Q.; Luo, M.; Li, Y.; Bhargava, L. On the behavior of water droplets when moving onto blade surface in a wet compression transonic compressor. J. Eng. Gas Turbines Power 2011, 133, 082001.1–082001.10. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kim, K.H.; Kim, K. Exergy Analysis of Overspray Process in Gas Turbine Systems. Energies 2012, 5, 2745-2758. https://doi.org/10.3390/en5082745
Kim KH, Kim K. Exergy Analysis of Overspray Process in Gas Turbine Systems. Energies. 2012; 5(8):2745-2758. https://doi.org/10.3390/en5082745
Chicago/Turabian StyleKim, Kyoung Hoon, and Kyoungjin Kim. 2012. "Exergy Analysis of Overspray Process in Gas Turbine Systems" Energies 5, no. 8: 2745-2758. https://doi.org/10.3390/en5082745
APA StyleKim, K. H., & Kim, K. (2012). Exergy Analysis of Overspray Process in Gas Turbine Systems. Energies, 5(8), 2745-2758. https://doi.org/10.3390/en5082745



