Collector Efficiency in Downward-Type Double-Pass Solar Air Heaters with Attached Fins and Operated by External Recycle
Abstract
:1. Introduction
2. Theoretical Analysis
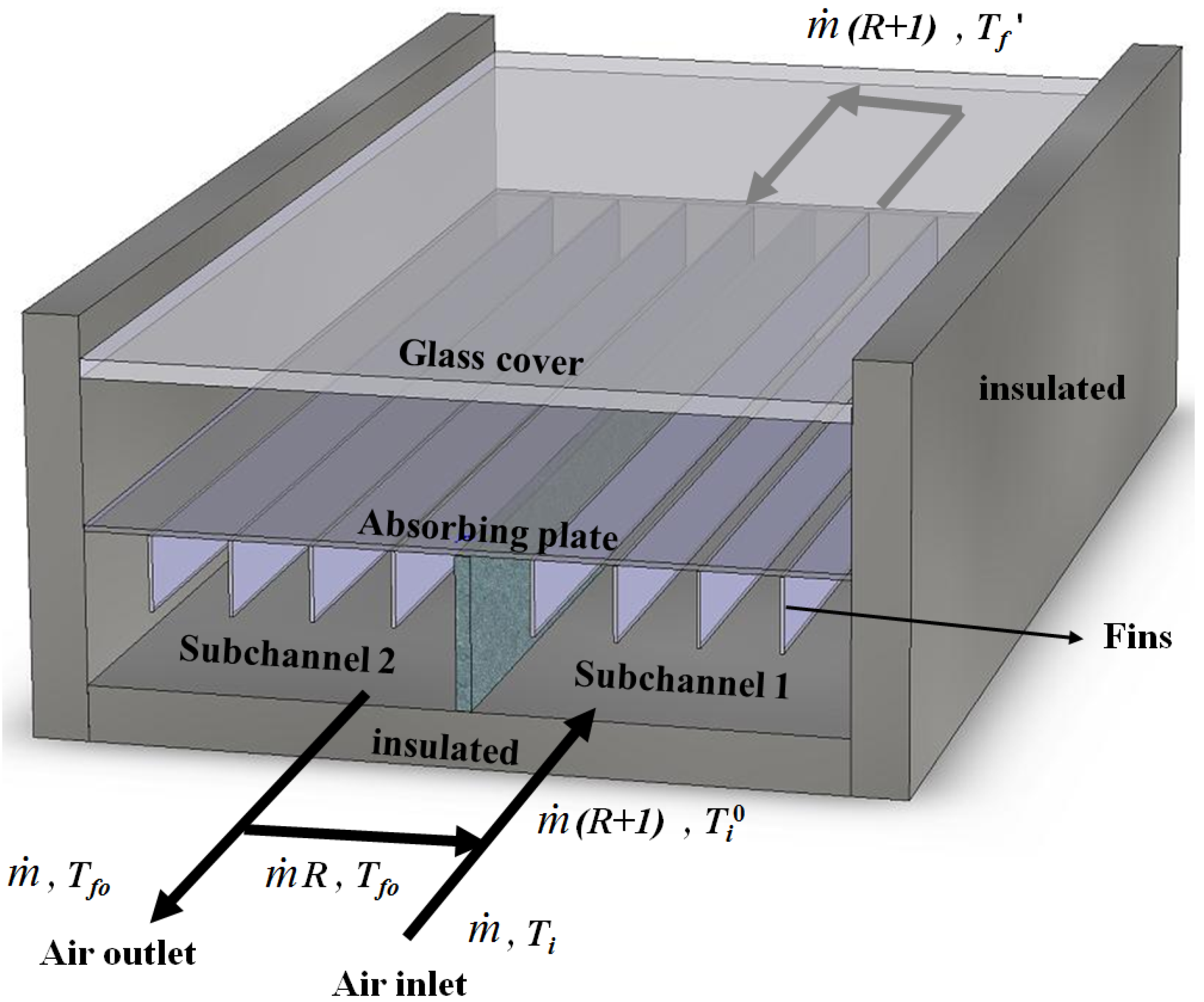
2.1. Temperature Distribution for the Fluid in Subchannel 1
2.2. Temperature Distribution for the Fluid in Subchannel 2
2.3. Collector Efficiency and Fluid Outlet Temperature
2.4. Mean Fluid and Absorbing-Plate Temperatures
2.5. Heat-Transfer Coefficients
2.6. Calculation Method for ηcf and Tfo
3. Results and Discussion
3.1. Numerical Example
| T (K) | ρ (kg/m3) | Cp (J/kg K) | k (W/m K) | μ (kg/m s) |
|---|---|---|---|---|
| 273 | 1.292 | 1006 | 0.0242 | 1.72 × 10−5 |
| 293 | 1.204 | 1006 | 0.0257 | 1.81 × 10−5 |
| 313 | 1.127 | 1007 | 0.0272 | 1.90 × 10−5 |
| 333 | 1.059 | 1008 | 0.0287 | 1.99 × 10−5 |
| 353 | 0.999 | 1010 | 0.0302 | 2.09 × 10−5 |
3.2. Effects of Operating Parameters on Collector Efficiency
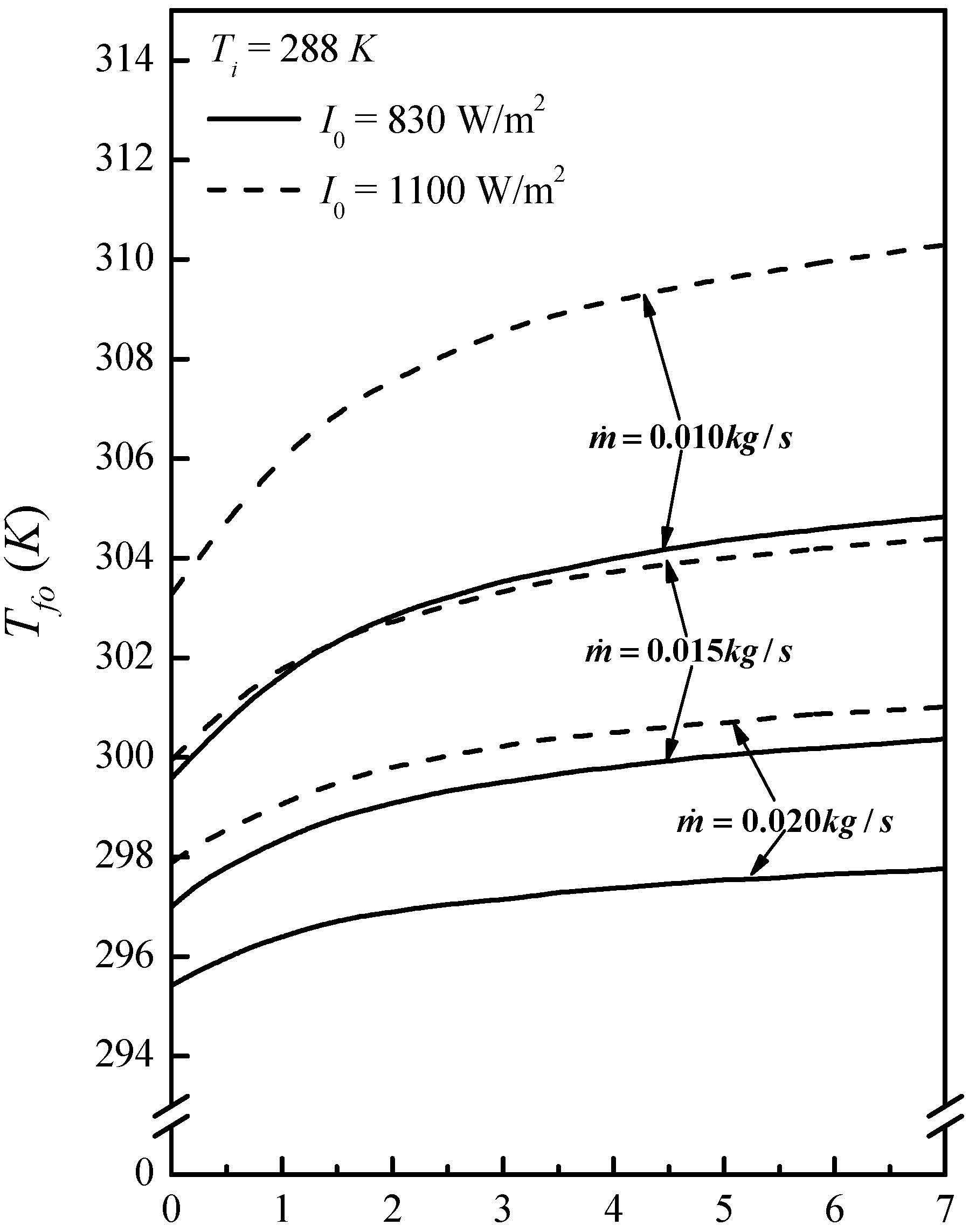

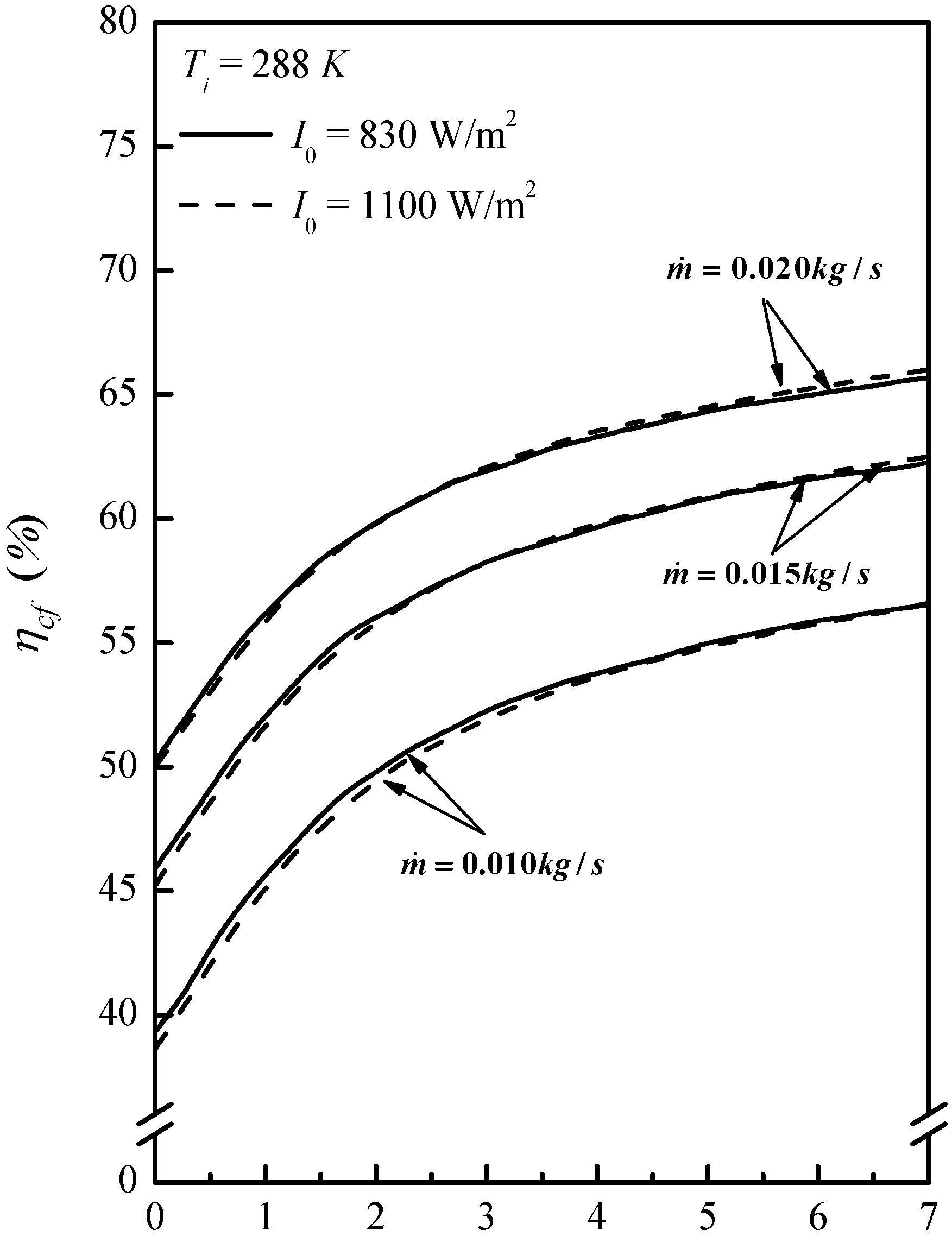
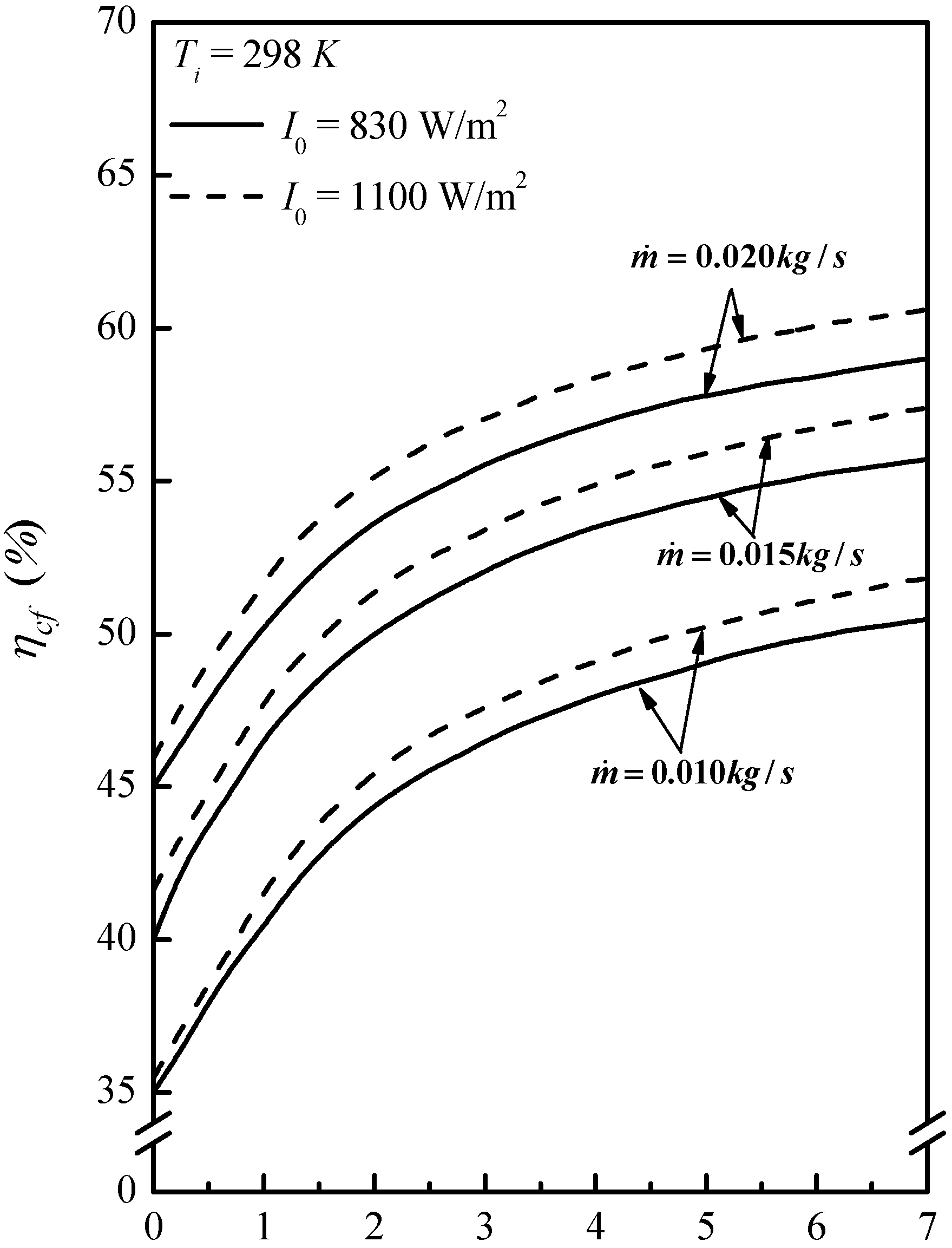
3.3. Improvement in Performance by Recycling
| Ti (K) | (kg/s) | (%) | If (%) | I (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R = 0 | R = 1 | R = 3 | R = 5 | R = 0 | R = 1 | R = 3 | R = 5 | |||||
| (a) | 288 | 0.01 | 24.60 | 58.94 | 88.30 | 111.92 | 123.02 | 36.49 | 68.91 | 97.68 | 111.97 | |
| 0.015 | 30.35 | 50.37 | 73.58 | 91.67 | 99.99 | 31.04 | 57.63 | 80.42 | 91.90 | |||
| 0.02 | 34.65 | 44.47 | 63.88 | 78.66 | 85.35 | 27.32 | 50.30 | 69.63 | 79.00 | |||
| 293 | 0.01 | 23.28 | 58.94 | 88.40 | 119.22 | 123.34 | 36.52 | 69.34 | 97.93. | 112.71 | ||
| 0.015 | 28.75 | 50.41 | 73.76 | 92.01 | 100.42 | 31.10 | 58.08 | 80.90 | 92.56 | |||
| 0.02 | 32.84 | 44.50 | 64.07 | 79.02 | 85.79 | 27.40 | 50.67 | 70.29 | 79.82 | |||
| 298 | 0.01 | 21.96 | 58.85 | 88.39 | 112.26 | 123.49 | 36.51 | 69.40 | 98.25 | 112.82 | ||
| 0.015 | 27.14 | 50.30 | 73.77 | 92.15 | 100.63 | 31.12 | 58.09 | 81.16 | 93.01 | |||
| 0.02 | 31.02 | 44.41 | 64.11 | 79.20 | 86.05 | 27.42 | 50.69 | 70.30 | 79.95 | |||
| (b) | 288 | 0.01 | 23.92 | 61.21 | 92.15 | 117.08 | 119.03 | 36.49 | 68.85 | 97.53 | 111.77 | |
| 0.015 | 29.73 | 52.32 | 76.71 | 95.70 | 104.45 | 31.04 | 57.63 | 80.28 | 91.70 | |||
| 0.02 | 34.11 | 46.09 | 66.39 | 81.85 | 88.85 | 27.32 | 50.23 | 69.48 | 78.82 | |||
| 293 | 0.01 | 22.90 | 61.29 | 92.34 | 117.39 | 129.17 | 36.52 | 69.19 | 97.61 | 112.27 | ||
| 0.015 | 28.48 | 52.42 | 83.39 | 96.01 | 104.92 | 31.10 | 57.94 | 80.60 | 92.15 | |||
| 0.02 | 32.69 | 46.25 | 66.71 | 82.33 | 89.41 | 27.40 | 50.52 | 69.98 | 79.42 | |||
| 298 | 0.01 | 21.87 | 61.38 | 92.52 | 117.69 | 129.54 | 36.51 | 69.17 | 97.75 | 112.16 | ||
| 0.015 | 27.21 | 52.58 | 77.23 | 96.52 | 105.43 | 31.12 | 57.88 | 80.70 | 92.37 | |||
| 0.02 | 31.26 | 46.33 | 66.92 | 82.69 | 89.85 | 27.42 | 50.49 | 69.86 | 79.38 | |||
3.4. Effect of Fin Attached on Device Performance
| Ti (K) | (kg/s) | E (%) | ||||
|---|---|---|---|---|---|---|
| R = 0 | R = 1 | R = 3 | R = 5 | |||
| (a) | 288 | 0.01 | 16.45 | 11.48 | 7.20 | 5.21 |
| 0.015 | 14.75 | 10.12 | 6.24 | 4.22 | ||
| 0.02 | 13.47 | 9.04 | 5.32 | 3.55 | ||
| 298 | 0.01 | 16.37 | 11.21 | 7.07 | 5.01 | |
| 0.015 | 14.63 | 9.92 | 6.07 | 3.95 | ||
| 0.02 | 13.33 | 8.91 | 5.23 | 3.39 | ||
| (b) | 288 | 0.01 | 18.11 | 13.80 | 9.90 | 7.96 |
| 0.015 | 16.24 | 12.10 | 8.55 | 6.64 | ||
| 0.02 | 14.74 | 10.76 | 7.30 | 5.57 | ||
| 298 | 0.01 | 18.22 | 13.80 | 10.08 | 8.19 | |
| 0.015 | 16.37 | 12.26 | 8.75 | 6.79 | ||
| 0.02 | 14.84 | 10.92 | 7.55 | 5.84 | ||
4. Conclusions
Nomenclature
| Ac | surface area of the absorbing plate, BL (m2) |
| B | the width of absorber surface area, nw1 (m) |
| Cp | specific heat of air at constant pressure (J/kg K) |
| De | equivalent diameter of the channel (m) |
| E | further improvement in collector efficiency |
| F' | efficiency factor of the solar air heater |
| FR | heat-removal factor for the solar air heater |
| H | height of the air tunnel in the solar collector, or the distance between glass cover and absorbing plate (m) |
| h | convective feat-transfer coefficient for fluid flowing over the plate of duct (W/m2 K) |
| hp−R | radiant heat-transfer coefficient between two parallel plates (W/m2 K) |
| hw | convective heat-transfer coefficient between glass cover and ambient (W/m2 K) |
| I | improvement in collector efficiency in the device without fins |
| If | improvement in collector efficiency in the device with fins attached |
| Io | solar radiation incident (W/m2) |
| k | thermal conductively of air (W/m K) |
| ks | thermal conductivity of absorbing plate and fins (W/m K) |
| L | collector length (m) |
mass flow-rate of air (kg/s) | |
| M | quantity defined by Equation (6) |
| n | fin number |
| Nu | Nusselt number |
| Qu | useful gain of energy carried away by air per unit time (W) |
| R | reflux ratio |
| Re | Reynolds number of flow channel |
| T | temperature (K) |
| t | fin thickness (m) |
| Ut | loss coefficient from the top of solar collector to the ambient (W/m2 K) |
average air velocity in the flow channel (m/s) | |
| V | wind velocity (m/s) |
| w1 | distance between fins (m) |
| w2 | height of fin (m) |
| z | axis along the flow direction (m) |
Greek Letters
| η | collector efficiency |
| σ | the Stefan–Boltzmann constant (W/m2 K4) |
| εg | emissivity of glass cover |
| εp | emissivity of absorbing plate |
| εR | emissivity of bottom plate |
| τg | transmittance of glass cover |
| ϕ | dimensionless quantity defined by Equation (4) |
| αp | absorptivity of the absorbing plate |
Subscripts
| a | ambient |
| f | fluid |
| i | inlet |
| m | mean value |
| o | outlet at subchannel 2 (z = 0), or single-pass operation without recycle |
| p | absorbing plate |
| R | bottom plate |
| 1,2 | subchannel 1, subchannel 2 |
Superscripts
| 0 | mixed |
| ' | outlet at the first pass or inlet at subchannel 2 (z = L) |
Acknowledgments
References
- Yeh, H.M.; Ting, Y.C. Effects of free convection on collector efficiencies of solar air heaters. Appl. Energy 1986, 22, 145–155. [Google Scholar] [CrossRef]
- Yeh, H.M.; Lin, T.T. The effect of collector aspect ratio on the collector efficiency of flat-plate solar air heaters. Energy 1995, 20, 1041–1047. [Google Scholar] [CrossRef]
- Forson, F.K.; Nazha, M.A.A.; Rajakaruna, H. Experimental and simulation studies on a single pass, double duct solar air heater. Energy Convers. Manag. 2003, 44, 1209–1227. [Google Scholar] [CrossRef]
- Naphon, P. On the performance and entropy generation of the double-pass solar air heater with longitudinal fins. Renew. Energy 2005, 30, 1345–1357. [Google Scholar] [CrossRef]
- Yeh, H.M.; Ho, C.D.; Lin, C.Y. Effect of collector aspect ratio on the collector efficiency of upward type baffled solar air heaters. Energy Convers. Manag. 2000, 41, 971–981. [Google Scholar] [CrossRef]
- Sharma, V.K.; Sharma, S.; Mahajan, R.B.; Garg, H.P. Evaluation of a matrix solar air heater. Energy Convers. Manag. 1990, 30, 1–8. [Google Scholar] [CrossRef]
- Yeh, H.M.; Chen, C.H.; Yeh, T.Y. Influence of channel-width ratio on solvent extraction through a double-pass parallel-plate membrane module. J. Membr. Sci. 2004, 230, 13–19. [Google Scholar] [CrossRef]
- Yeh, H.M.; Hung, F.C.; Chen, C.H.; Hung, C.R. Effect of recycle-barrier location on membrane extraction in a parallel-flow rectangular module with internal reflux. J. Membr. Sci. 2005, 60, 167–177. [Google Scholar]
- Yeh, H.M. Effects of reflux and reflux-barrier location on solvent extraction through cross-flow flat-plate membrane modules with internal reflux. J. Membr. Sci. 2006, 269, 133–141. [Google Scholar] [CrossRef]
- Korpijarvi, J.; Oinas, P.; Reunaneu, J. Hydrodynamics and mass transfer in airlift reactor. Chem. Eng. Sci. 1998, 54, 2255–2262. [Google Scholar] [CrossRef]
- Santacesaria, E.; Di Serio, M.; Iengo, P. Mass transfer and kinetics in ethoxylation spray tower loop reactors. Chem. Eng. Sci. 1999, 54, 1499–1504. [Google Scholar] [CrossRef]
- Atwnas, M.; Clark, M.; Lazarova, V. Holdup and liquid circulation velocity in a rectangular air-lift bioreactor. Ind. Eng. Chem. Res. 1999, 38, 944–949. [Google Scholar] [CrossRef]
- Yeh, H.M.; Tsai, S.W.; Lin, C.S. A study of the separation efficiency in thermal diffusion column with a vertical permeable barrier. AIChE J. 1986, 32, 971–980. [Google Scholar] [CrossRef]
- Yeh, H.M.; Tsai, S.W.; Chiang, C.L. Recycle effects on heat and mass transfer through a parallel-plate channel. AIChE J. 1987, 33, 1743–1746. [Google Scholar] [CrossRef]
- Ho, C.D.; Yeh, H.M.; Sheu, W.S. An analytical study of heat and mass transfer through a parallel-plate channel with recycle. Int. J. Heat Mass Transf. 1998, 41, 2589–2599. [Google Scholar] [CrossRef]
- Ho, C.D.; Yeh, H.M.; Sheu, W.S. The influence of recycle on double-pass heat and mass transfer through a parallel-plate. Int. J. Heat Mass Transf. 1999, 42, 1707–1722. [Google Scholar] [CrossRef]
- Yeh, H.M.; Ho, C.D. Solar Air Heaters with External Recycle. Appl. Therm. Eng. 2009, 29, 1694–1701. [Google Scholar] [CrossRef]
- Yeh, H.M.; Ho, C.D. Heat-transfer enhancement of double-pass solar air heaters with external recycle. Appl. Therm. Eng. 2011, 42, 793–800. [Google Scholar]
- Bennett, C.O.; Myers, J.E. Momentum, Heat and Mass Transfer, 2nd ed.; McGraw-Hill Inc.: New York, NY, USA, 1974; p. 445. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 2nd ed.; Wiley: New York, NY, USA, 1991. [Google Scholar]
- McAdams, W.H. Heat Transmission, 3rd ed.; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Klein, S.A. Calculation of flat-plate loss coefficients. Sol. Energy 1975, 17, 79–80. [Google Scholar] [CrossRef]
- Hottel, H.C.; Woertz, B.B. Performance of flat-plate solar-heat collector. Trans. ASME 1942, 64, 91–104. [Google Scholar]
- Kays, W.M.; Crawford, M.E. Convective Heat- and Mass-Transfer, 2nd ed.; McGraw-Hill: New York, NY, USA, 1980; p. 245. [Google Scholar]
Appendix
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yeh, H.-M.; Ho, C.-D. Collector Efficiency in Downward-Type Double-Pass Solar Air Heaters with Attached Fins and Operated by External Recycle. Energies 2012, 5, 2692-2707. https://doi.org/10.3390/en5082692
Yeh H-M, Ho C-D. Collector Efficiency in Downward-Type Double-Pass Solar Air Heaters with Attached Fins and Operated by External Recycle. Energies. 2012; 5(8):2692-2707. https://doi.org/10.3390/en5082692
Chicago/Turabian StyleYeh, Ho-Ming, and Chii-Dong Ho. 2012. "Collector Efficiency in Downward-Type Double-Pass Solar Air Heaters with Attached Fins and Operated by External Recycle" Energies 5, no. 8: 2692-2707. https://doi.org/10.3390/en5082692
APA StyleYeh, H.-M., & Ho, C.-D. (2012). Collector Efficiency in Downward-Type Double-Pass Solar Air Heaters with Attached Fins and Operated by External Recycle. Energies, 5(8), 2692-2707. https://doi.org/10.3390/en5082692





