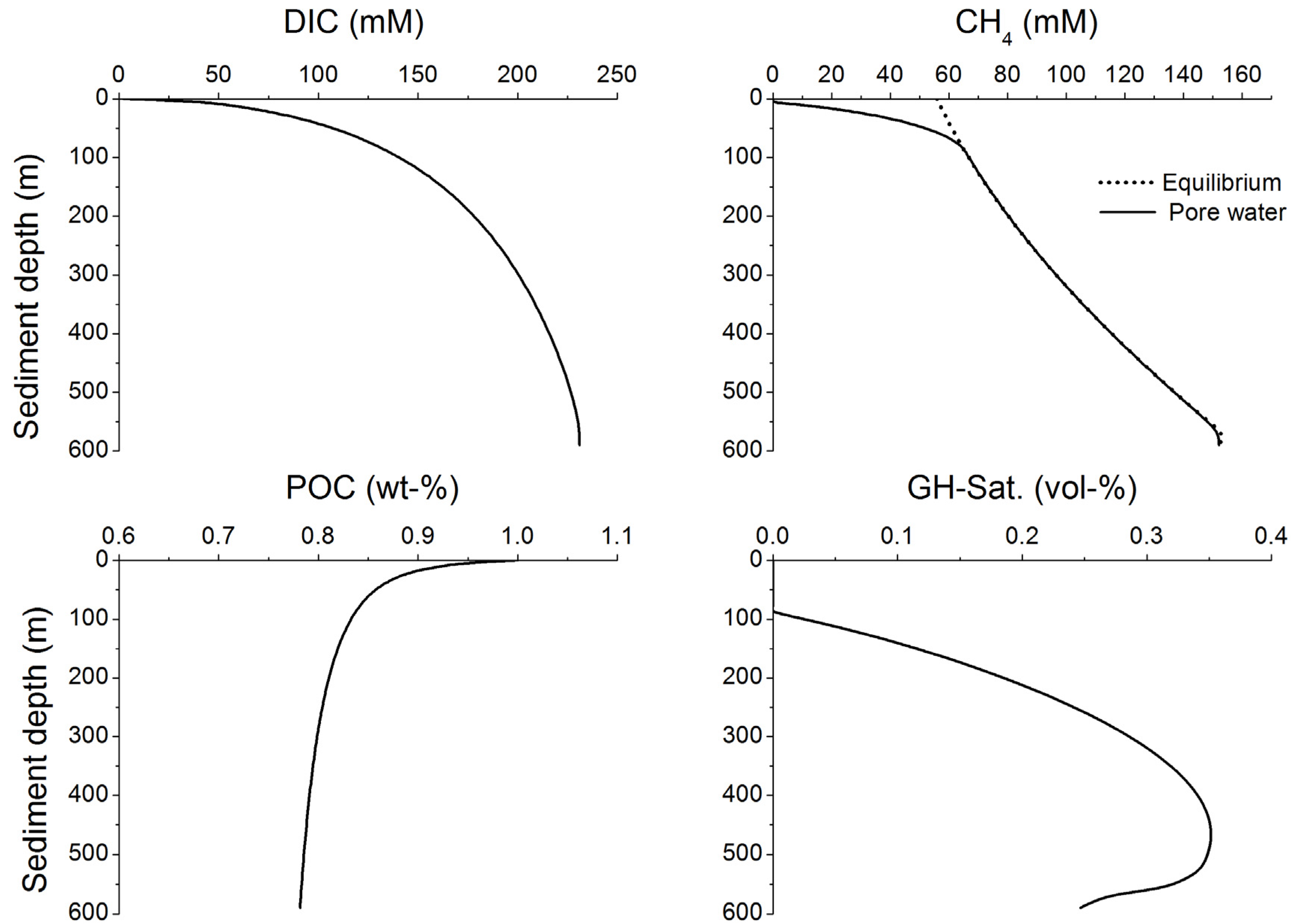
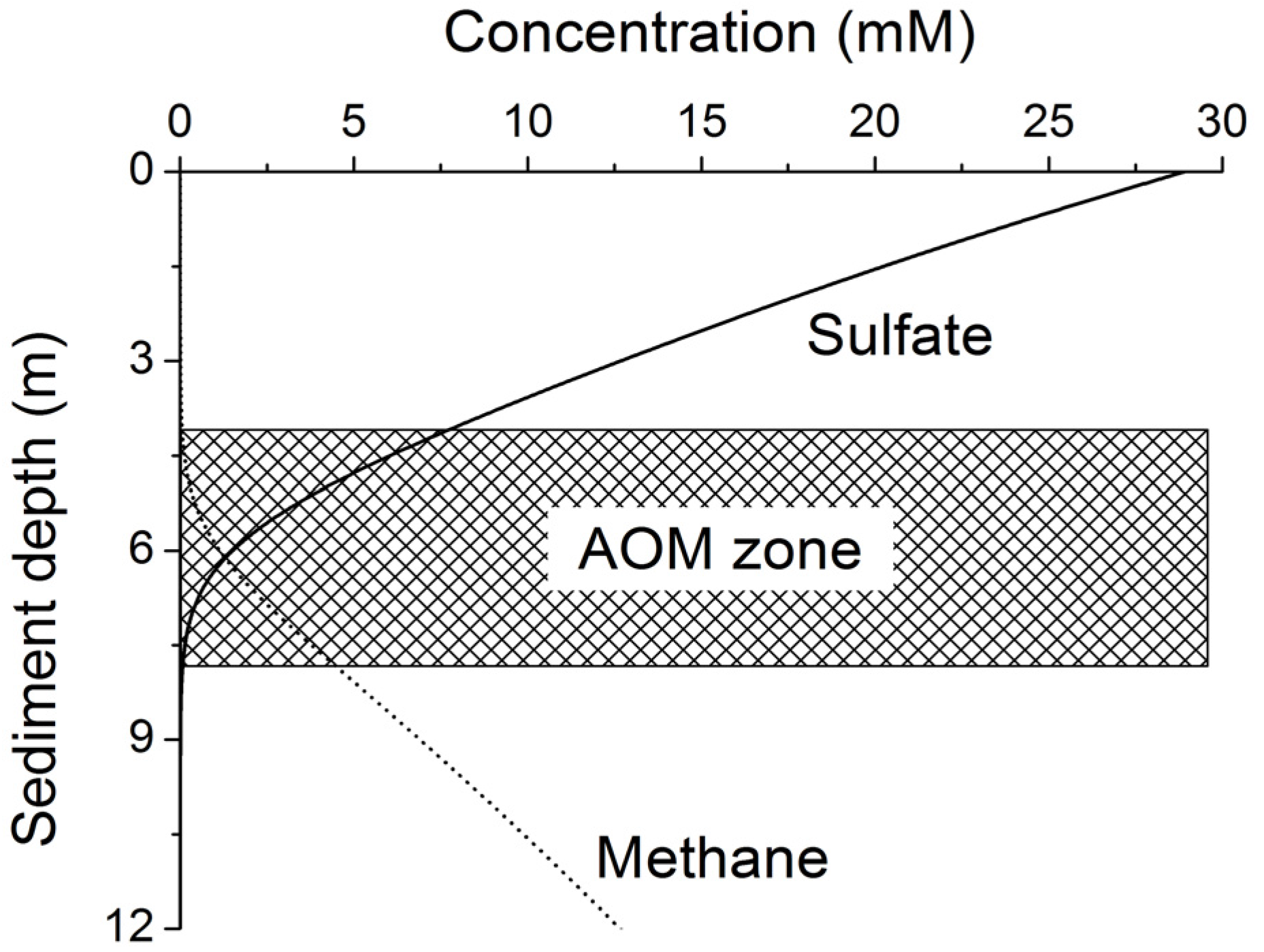
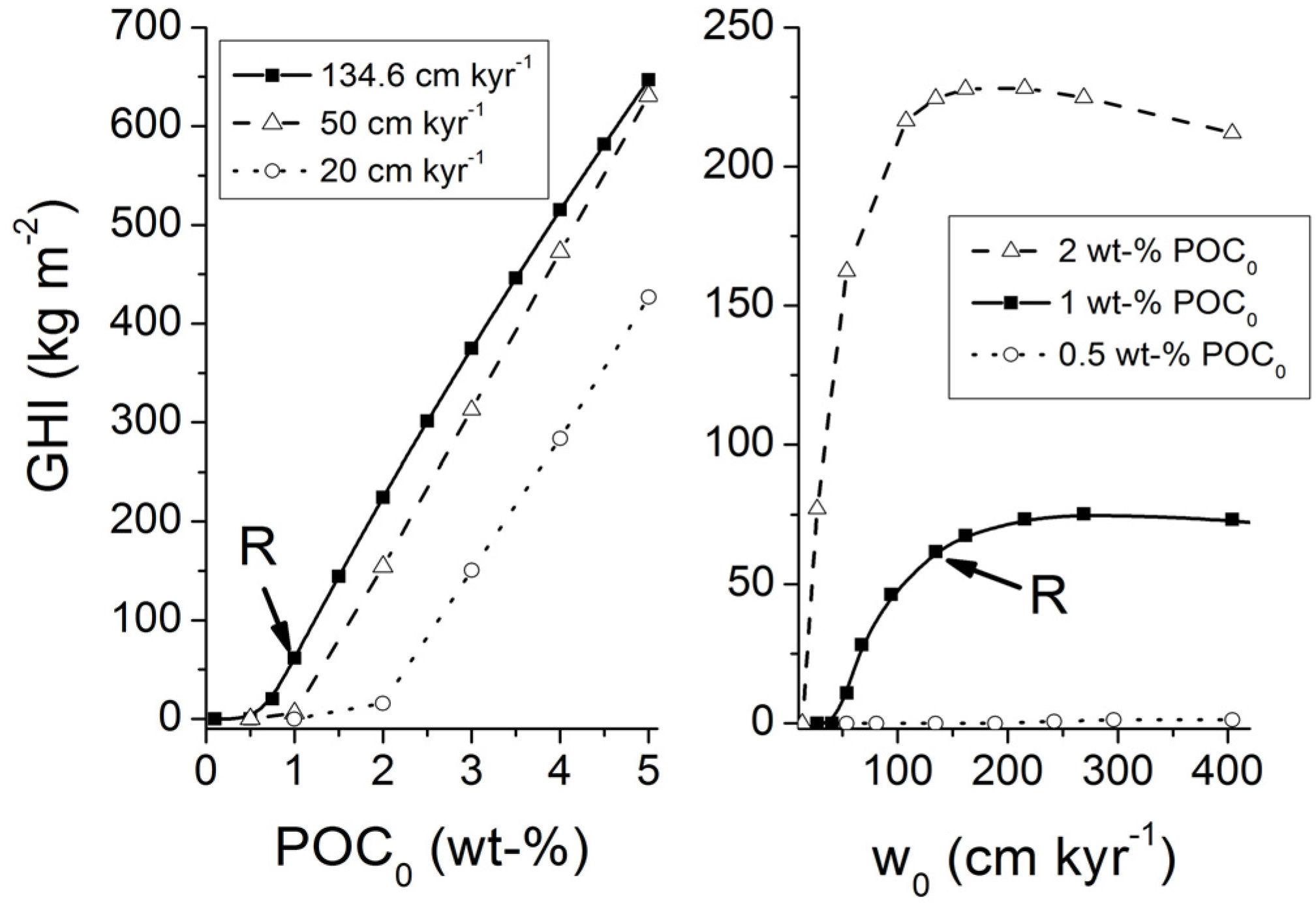
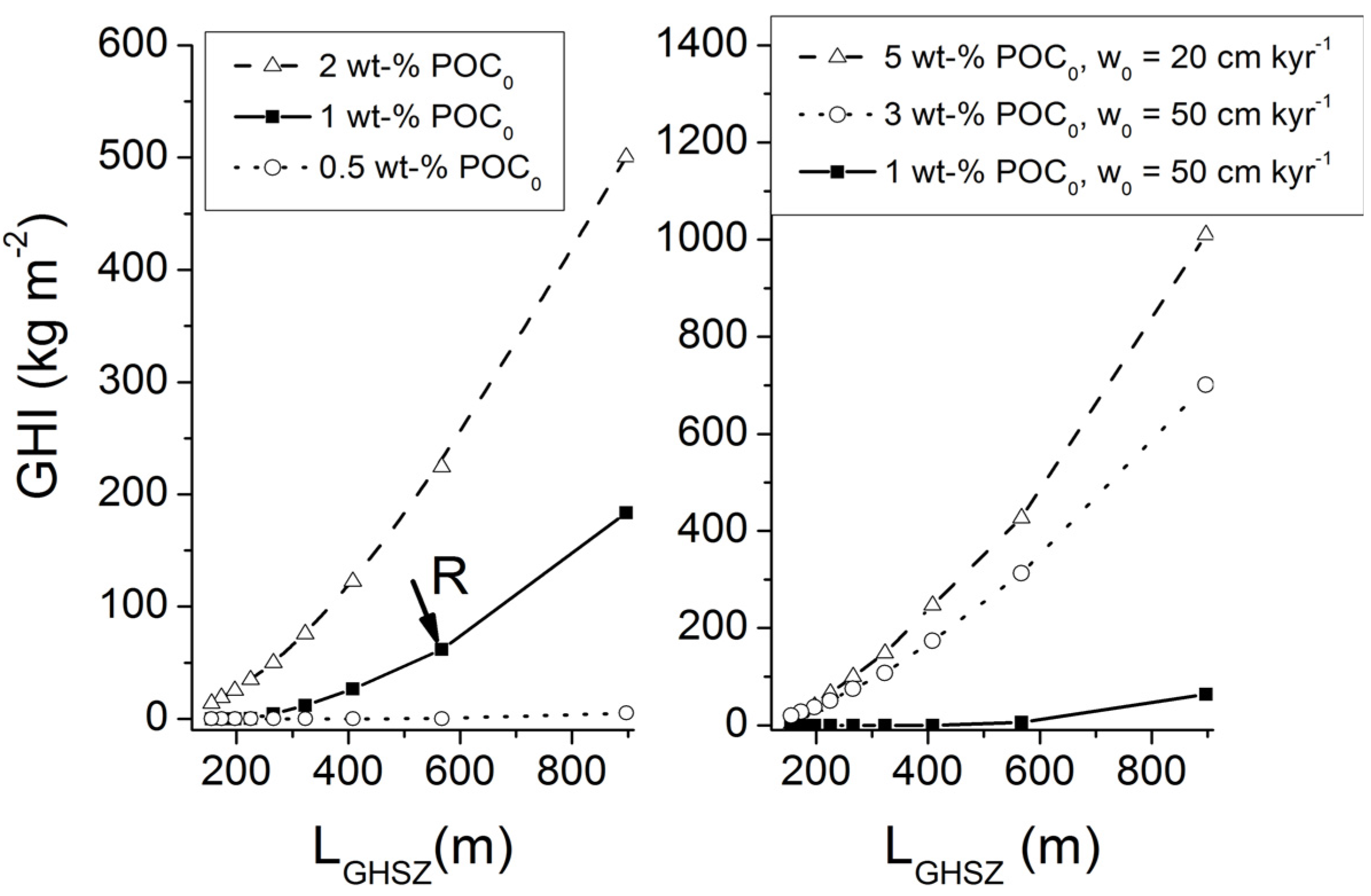
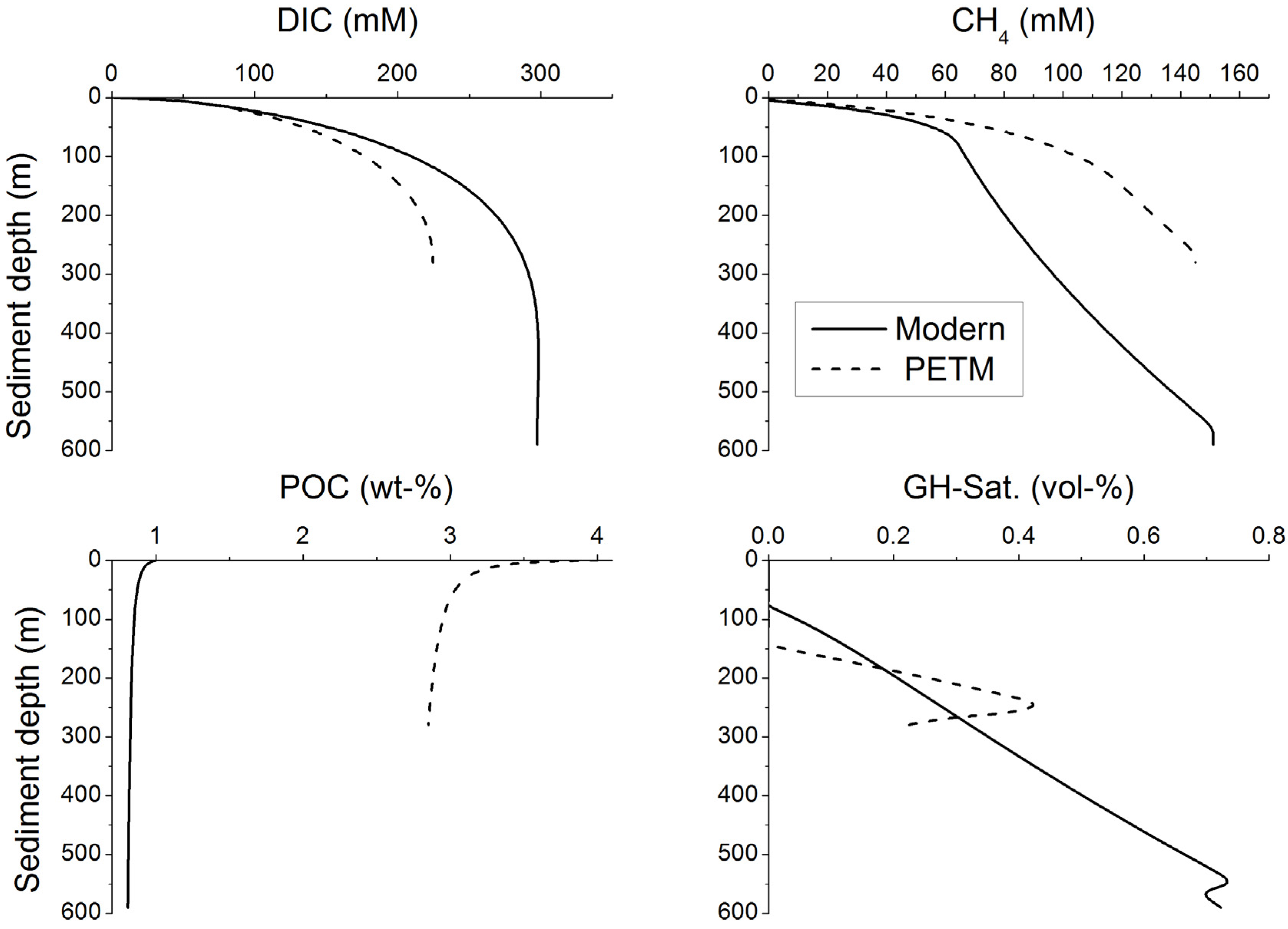
3. Microbial Degradation of Organic Matter and Methane Formation in Marine Sediments
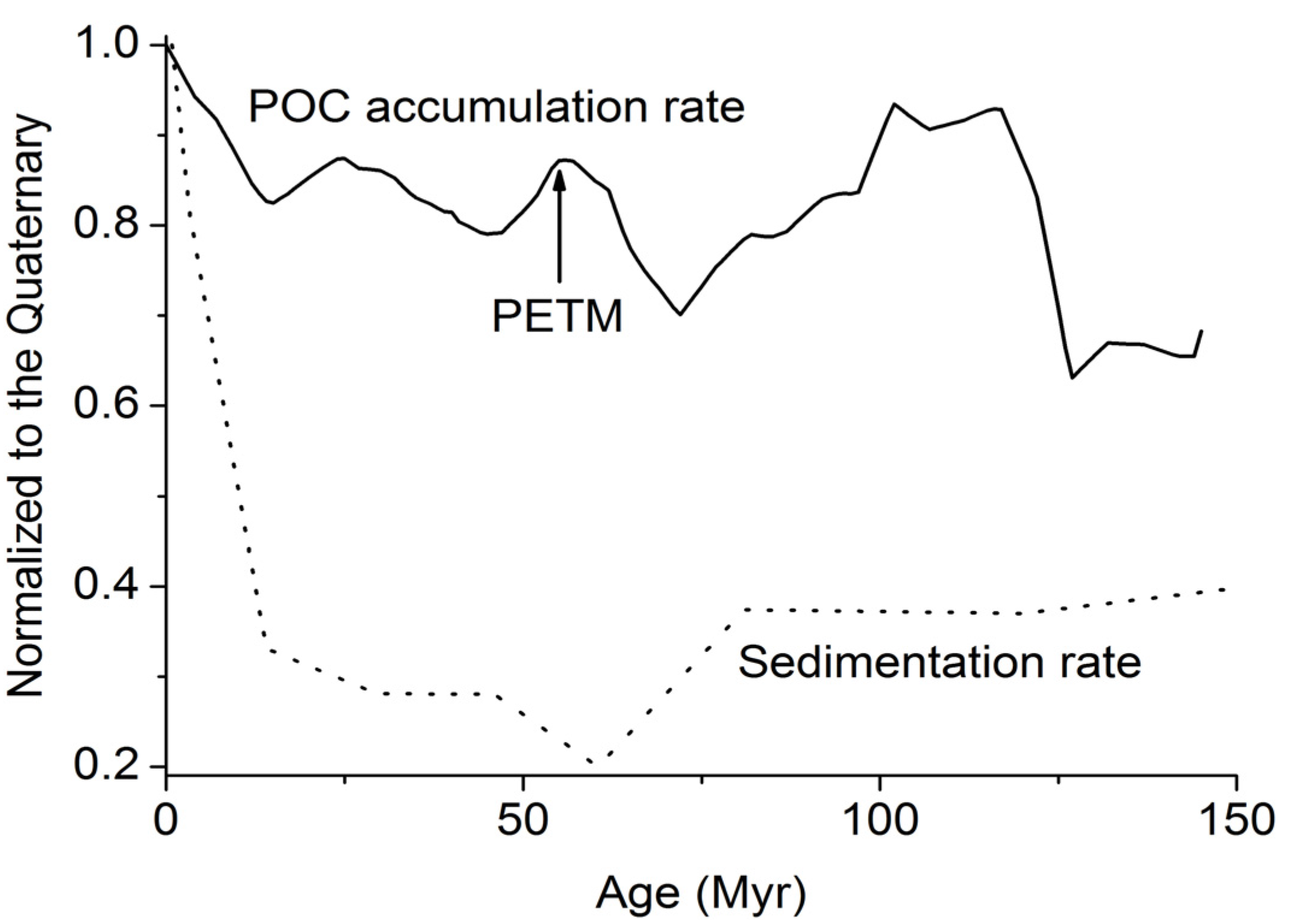
Stable carbon isotope data show that methane hydrates are usually formed from biogenic methane produced by the anaerobic degradation of organic matter in the deep marine biosphere. It is thus important to understand the mechanisms and kinetics of organic matter degradation and microbial methane formation in the marine subsurface. Organic matter deposited at the seabed is degraded by microorganisms and other benthic biota using oxygen as terminal electron acceptor. The remaining organic matter is degraded by anaerobic bacteria and archaea using dissolved nitrate and manganese (+IV) and iron (+III) minerals as oxidizing agents [
19]. These additional electron acceptors are usually consumed within the bioturbated surface layer (0–10 cm sediment depth). Field data show that only a small fraction of the POC raining to the seafloor is buried below 10 cm depth [
20]. The data reveal a marked contrast between fine-grained continental margin and deep-sea sediments [
21]. While at continental margins about 10% of the POC raining to the seabed is conserved and buried below 10 cm sediment depth, this fraction is reduced to about 1% at the deep-sea floor [
20]. Due to the very low preservation of POC in open ocean environments, gas hydrates are usually not found in pelagic sediments but only at continental margins where a significant POC fraction is buried and therefore available for microbial methane formation in the deep subsurface.
POC buried below the bioturbated surface layer is further degraded by anaerobic bacteria and archaea using dissolved sulfate as electron acceptor:
where C(H
2O) represents sedimentary POC.
Microbial methane production and accumulation starts below the depth of sulfate penetration. Several steps are needed before methane is finally produced as stable end product of anaerobic microbial POC degradation. In a first step, biogenic polymers are hydrolyzed and converted into monomers. These monomers (sugars, amino acids, lipids,
etc.) are then fermented into CO
2, H
2 and a number of organic acids. Methane is finally formed by methanogenic microorganisms converting CO
2 and H
2 into methane [
22]:
The stoichiometry of the overall process of organic matter degradation and methanogenesis is given by the following reaction:
Equation (5) does not imply that methane is directly formed by POC degradation. It rather defines the substrate and the final products. The intermediate steps including fermentation and CO
2 reduction with H
2 are included in the overall stoichiometry [
23].
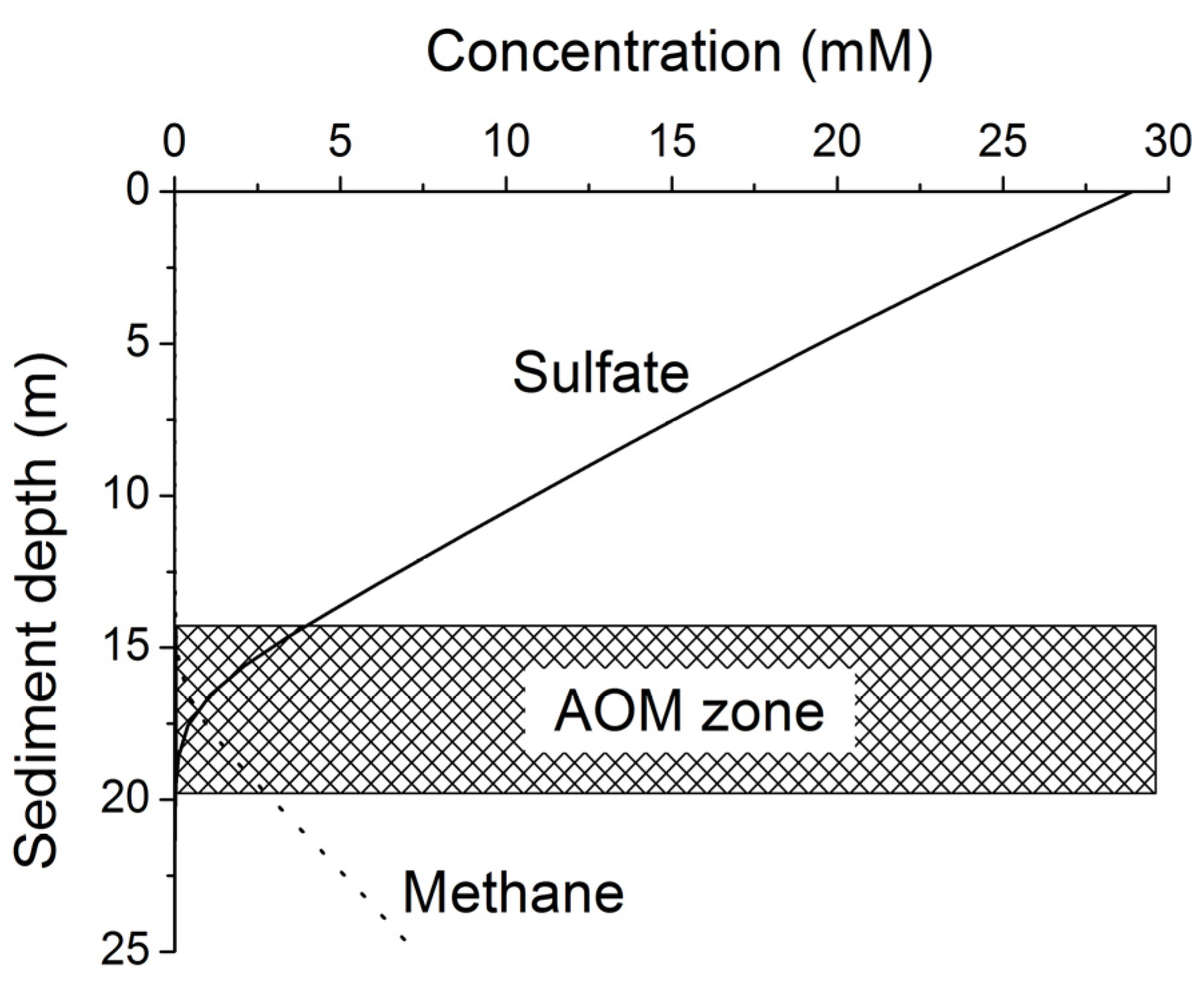
Methane formed at depth is transported upwards into the sulfate-methane transition zone (SMTZ) via molecular diffusion and advection. Within this zone, methane is oxidized by consortia of bacteria and archaea using sulfate as terminal electron acceptor [
24]. The overall stoichiometry of anaerobic oxidation of methane (AOM) within the SMTZ is given by:
Considering this complex network of microbial processes, the key questions that need to be answered to estimate the global rate of methane formation may be formulated as: How much POC is reaching the methanogenic zone and how much of that POC can be microbially converted into methane? To answer these questions not only the POC burial rates but also the down-core changes in POC reactivity need to be defined. Since more than three decades marine geochemists and microbiologists have observed that the POC reactivity decreases strongly with sediment age and depth. In his classical paper on POC degradation kinetics in marine sediments Middelburg showed that the down-core decrease in POC reactivity can be represented by the following equation [
25]:
where
kage is the age-dependent reactivity (in yr
−1) and
age0 is the initial age of POC (in yr). The rate of POC degradation (
RPOC in g C g
−1 yr
−1) is calculated as:
where
CPOC is the POC concentration (in g C per g of dry sediment). The equation was calibrated by a large number of rate measurements showing that the reactivity of POC decreases by 10 orders of magnitude going from fresh marine plankton to POC buried in deep-sea sediments. More recently, ODP drilling confirmed the presence of living microorganisms in pelagic and terrigenous sediments down to the underlying oceanic crust [
26,
27,
28,
29]. The number of prokaryotic cells (bacteria and archaea) decreases from more than 10
8 cm
−3 in the upper few meter of the sediment column to less than 10
6 cm
−3 at depth [
26,
30]. The logarithmic down-core decrease in cell numbers and the microbial POC degradation rates in the deep subsurface are broadly consistent with the rates predicted by the Middelburg model [
27,
31,
32].
The main uncertainty of the Middleburg model is associated with the initial age parameter (
age0) defined as the average age of POC buried below the bioturbated zone. Initial ages of 300–30,000 yrs were applied to reproduce the pore water profiles in sediment cores retrieved from the Sakhalin slope [
23]. An even larger range of 800–180,000 yrs was needed to reproduce pore water profiles measured in ODP sediment cores [
33]. These large ranges probably reflect the ambient variability in burial velocity, the deposition of refractory organic matter and the possible loss of surface sediments during core retrieval [
23]. The largest initial ages were observed at Blake Ridge where drift sediments are deposited containing pre-aged organic matter of terrigenous and marine origin [
23,
33].
Equations (7,8) can be combined and solved to estimate the POC loss within the sulfate reduction zone and thereby the input of POC into the methanogenic zone. The fraction of POC reaching the methanogenic zone results in:
where
texp is the sulfate exposure time and
fMI is the concentration of POC in sediments reaching the methanogenic zone divided by the POC concentration in sediments buried below the bioturbated zone at 0.1 m depth. The sulfate exposure time depends on sulfate penetration depth (
zS in m) and burial velocity (w in m yr
−1):
Burial velocities at the deep-sea floor typically range from 0.1 to 10 cm kyr
−1 [Equation (2)] while sulfate penetrates usually more than 100 m into pelagic sediment. A compilation of sulfate penetration depths in open ocean sediments confirmed that sulfate is usually not fully depleted in these pelagic deposits [
32]. This observation is partly explained by the deep penetration of dissolved oxygen into pelagic sediments [
29] and the delivery of sulfate through the base of the sediment column via sulfate-rich fluids circulating through the underlying oceanic crust. Deep-sea sediments are thus typically exposed to sulfate over their entire life span (up to ~150 Myr). Microbial rate measurements and pore water profiles obtained in pelagic sediments revealed that methanogenesis may occur already within the sulfate-bearing sediment horizons [
27]. Methane produced by this process is, however, consumed within the sulfate-bearing zone via AOM. Methane concentrations in pelagic sediments are therefore several orders of magnitude lower than the ambient saturation value with respect to methane hydrate [
34]. Due to this strong undersaturation of pore fluids, methane hydrates have never been documented in pelagic sediments.
In most continental margin settings, sulfate dissolved in ambient pore fluids is completely consumed at 10–100 m sediment depth [
32,
35]. The sulfate exposure time results as
texp = 10
4–10
6 yr for burial velocities of 10–100 cm kyr
−1. Thus, about 30–90% of the buried POC is reaching the methanogenic zone in continental margin sediments (
Figure 5). The microbial degradation of POC delivered to the sulfate-free methanogenic zone may lead to the accumulation of methane in pore fluids and to the formation of methane hydrates pending on the rate of methane formation and the local pressure and temperature conditions.
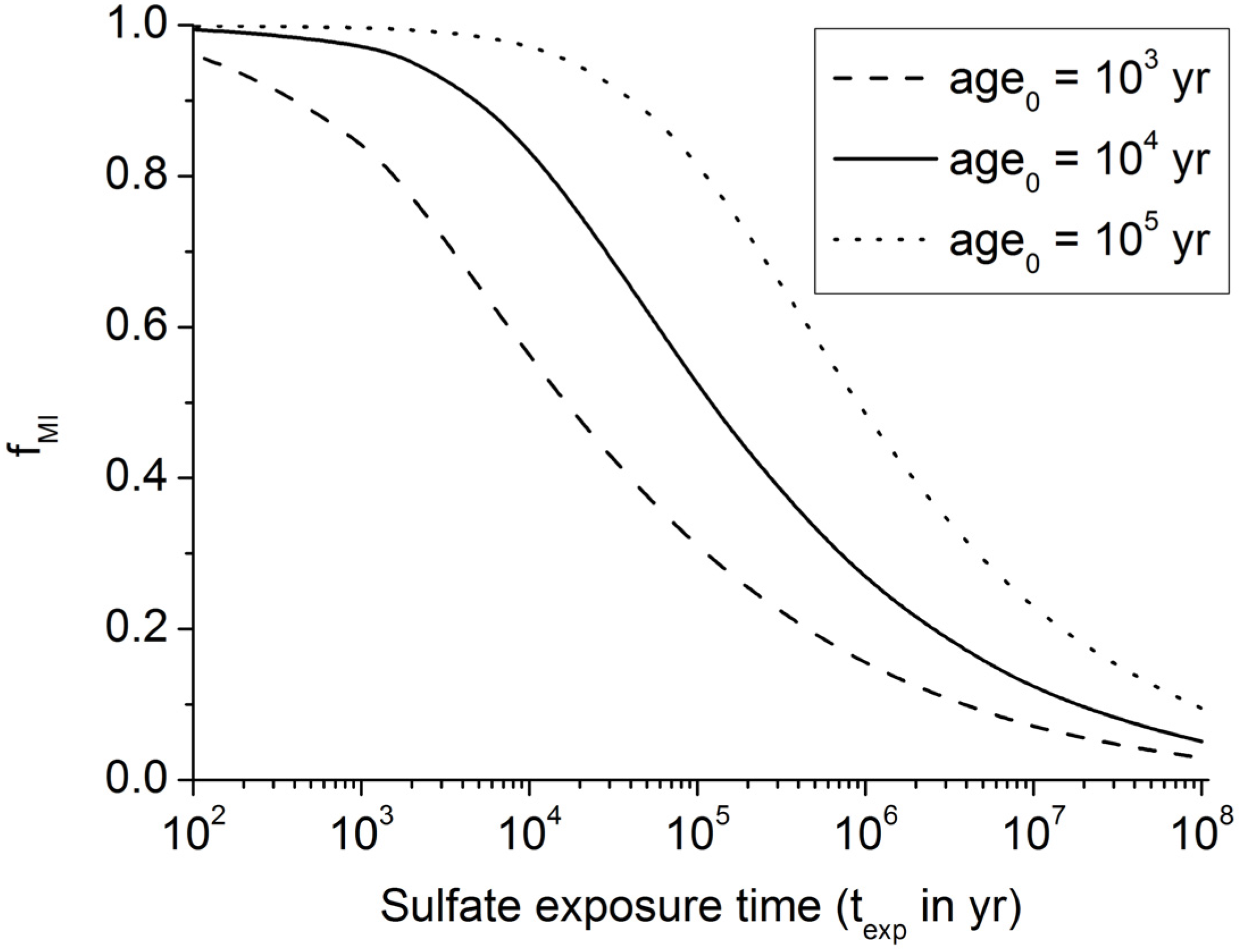
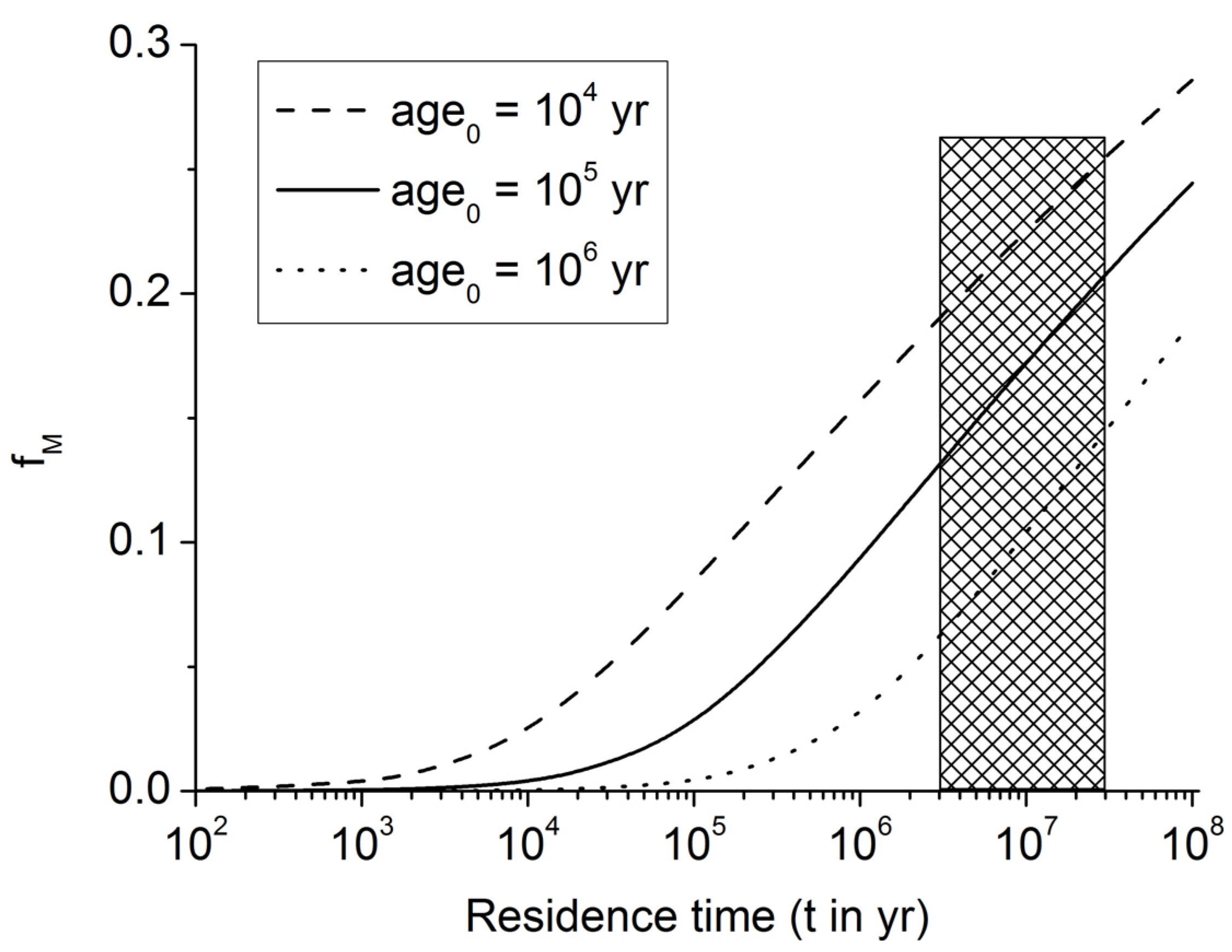
Figure 5.
Fraction of buried POC entering the methanogenic zone (fMI) as calculated from Equation (9) for initial ages of 1000 yrs, 10,000 yrs, and 100,000 yrs.
Figure 5.
Fraction of buried POC entering the methanogenic zone (fMI) as calculated from Equation (9) for initial ages of 1000 yrs, 10,000 yrs, and 100,000 yrs.
Dissolved sulfate profiles often show an almost linear decrease with sediment depth suggesting that only a minor sulfate fraction is used for POC degradation while most of the sulfate is consumed via AOM in the underlying sulfate-methane transition zone [
36,
37]. Equation (9) implies that only 10% of the POC buried in continental margin sediments is consumed via microbial sulfate reduction where pre-aged organic matter (
age0 = 10
5 yr) is deposited at the seabed (
Figure 5). It is thus likely that linear sulfate profiles are induced by the deposition of old POC at the seabed. Terrestrial POC delivered to the margins by continental erosion is a likely source for this pre-aged material. However, sulfate profiles with significant curvature documenting strong sulfate depletion via anaerobic POC degradation are also commonly observed [
23]. They probably reflect the deposition of young marine organic matter since Equation (9) implies that up to 80% of this young POC (
age0 = 10
3 yr) is consumed via microbial sulfate reduction (
Figure 5).
The kinetics of microbial methane formation in marine sediments was studied in detail by Wallmann
et al. [
23]. Evaluating pore water and sediment data from the Sakhalin Slope and the Blake Ridge, the authors showed that the rate of methane formation within the methanogenic zone (
RCH4 in g of methane carbon g
−1 yr
−1) can be calculated as:
where
KC is an inhibition constant (
KC = 30–50 mM), C
DIC is the concentration of dissolved inorganic carbon in ambient pore fluids and
CCH4 the dissolved methane concentration (in mM). The factor 0.5 defines the fraction of POC being converted into methane. The remaining POC fraction is decomposed into carbon dioxide for sedimentary POC with an oxidation state of carbohydrates [Equation (5)]. This extension of the Middelburg model was subsequently tested and applied at a number of ODP drill sites in prominent gas hydrate provinces [
33]. The evaluation of pore water profiles showed that kinetic Equation (11) gives indeed a good approximation of the down-core changes in microbial methane formation within the GHSZ.
Equation (11) can be solved to calculate the fraction of POC being converted into methane carbon within the methanogenic zone:
where
t is the residence time of sedimentary POC within the methanogenic zone while age
0 is the initial age of POC entering the methanogenic zone from above. The organic matter entering the methanogenic zone of typical margin sediments has initial ages of 10
4–10
6 yr considering ambient sedimentation rates and sulfate exposure times. Methane formation is further inhibited by the accumulation of dissolved metabolites (DIC and CH
4) within ambient pore fluids. Assuming typical concentrations of
CDIC =
CCH4 = 50 mM and an inhibition constant of
KC = 40 mM, Equation (12) can be applied to calculate the POC fraction being converted into methane within the sulfate-free methanogenic zone (
Figure 6).
Figure 6.
Fraction of POC converted into methane carbon within the methanogenic zone of continental margin sediments (fM). The marked area indicates the range of POC residence times (t = 3–30 Myr) within the methanogenic zone at continental margins.
Figure 6.
Fraction of POC converted into methane carbon within the methanogenic zone of continental margin sediments (fM). The marked area indicates the range of POC residence times (t = 3–30 Myr) within the methanogenic zone at continental margins.
The residence time of sediments within the methanogenic zone is limited by the geothermal gradient since microbial methane formation cannot proceed at temperatures above ~100 °C. Assuming a geothermal gradient of 30–40 °C/km, the deep biosphere may extend to a sediment depth of about 3 km. At continental margins with typical burial velocities of 10–100 cm kyr
−1, the residence time within the methanogenic zone may thus fall into a range of
t = 3–30 Myr.
Figure 6 and Equation (12) show that about 10%–20% of the POC entering the methanogenic zone is microbially converted into methane under these assumptions (for
age0 = 10
5 yr). Since 30–90% of POC buried below the bioturbated surface zone of continental margin sediments is reaching the methanogenic zone (
Figure 5), about 3%–18% of the buried POC is converted into methane by the deep biosphere residing in underlying sulfate-depleted sediment layers.
Considering the arguments and equations presented above it is now possible to estimate the rate of microbial methane formation in continental margin sediments at global scale (
Table 1).
Table 1.
Quaternary POC and methane balance for global continental margins.
Table 1.
Quaternary POC and methane balance for global continental margins.
| | Range | Best Estimate |
|---|
| POC burial at continental margins (1014 g C yr−1) | 1.21–1.39 | 1.3 |
| Fraction of buried POC reaching the methanogenic zone (%) | 30–90 | 50 |
| Fraction of buried POC microbially converted into methane (%) | 3–18 | 8 |
| Microbial methane production rate (1012 g C yr−1) | 4–25 | 10 |
This new estimate of microbial methane production in margin sediments (4–25 Tg C yr
−1,
Table 1) is significantly lower than previous estimates of the global microbial methane production ranging from 60 Tg C yr
−1 [
38] to 240 Tg C yr
−1 [
39]. These previous estimates approach or even exceed the global rate of POC burial below the bioturbated zone. Our best estimate of ~10 Tg C yr
−1 would lead to an accumulation of up to 100,000 Gt CH
4-C over an accumulation period of 10 Myr if none of the methane would be lost by upward diffusion, AOM, fluid flow and gas ascent. However, field data clearly show that a large fraction of methane is lost by upward diffusion and fluid flow into the overlying sulfate-bearing zone where methane is consumed by microbial consortia using sulfate as terminal electron acceptor [
24]. The biogenic methane inventory is thus certainly much smaller than the time-integrated rate of biogenic methane formation derived above. Nevertheless, the number of 100,000 Gt C is a useful upper limit for biogenic methane accumulation. Interestingly, the global methane hydrate inventory estimated by Klauda and Sandler [
4] approaches this upper limit value.
The kinetic models of Middelburg and Wallmann can also be used to estimate the total POC degradation rate within the deep marine biosphere. The Middelburg model [Equation (8)] yields a rate of 1.2 × 1014 g yr−1 applying a mean POC input flux of 1.4 × 1014 g yr−1, an initial age of 104 yr and a POC residence time in the deep biosphere of 10 Myr. It predicts that almost 90% of the buried POC would be consumed within the deep biosphere. Applying the same parameter values, an inhibition constant of 40 mM and mean methane and CO2 concentrations of 50 mM, the Wallmann model [Equation (11)] predicts a POC consumption rate of 0.7 × 1014 g yr−1 corresponding to ~50% of the burial flux. The remaining POC is further decomposed below the deep biosphere via chemical processes yielding thermogenic gas, oil, kerogen and other products of high-temperature (>100 °C) thermal maturation. It should, however, be noted that the numbers given above are very rough estimates since microbial organic matter degradation in the deep biosphere is a very complex and poorly understood process.
4. Thickness of the Gas Hydrate Stability Zone
Methane hydrates are only stable at low temperatures and high pressures. The stability field of structure type-I methane hydrate is well defined [
40]. Pitzer equations can be used to constrain the effects of seawater salinity and porewater composition on methane hydrate stability [
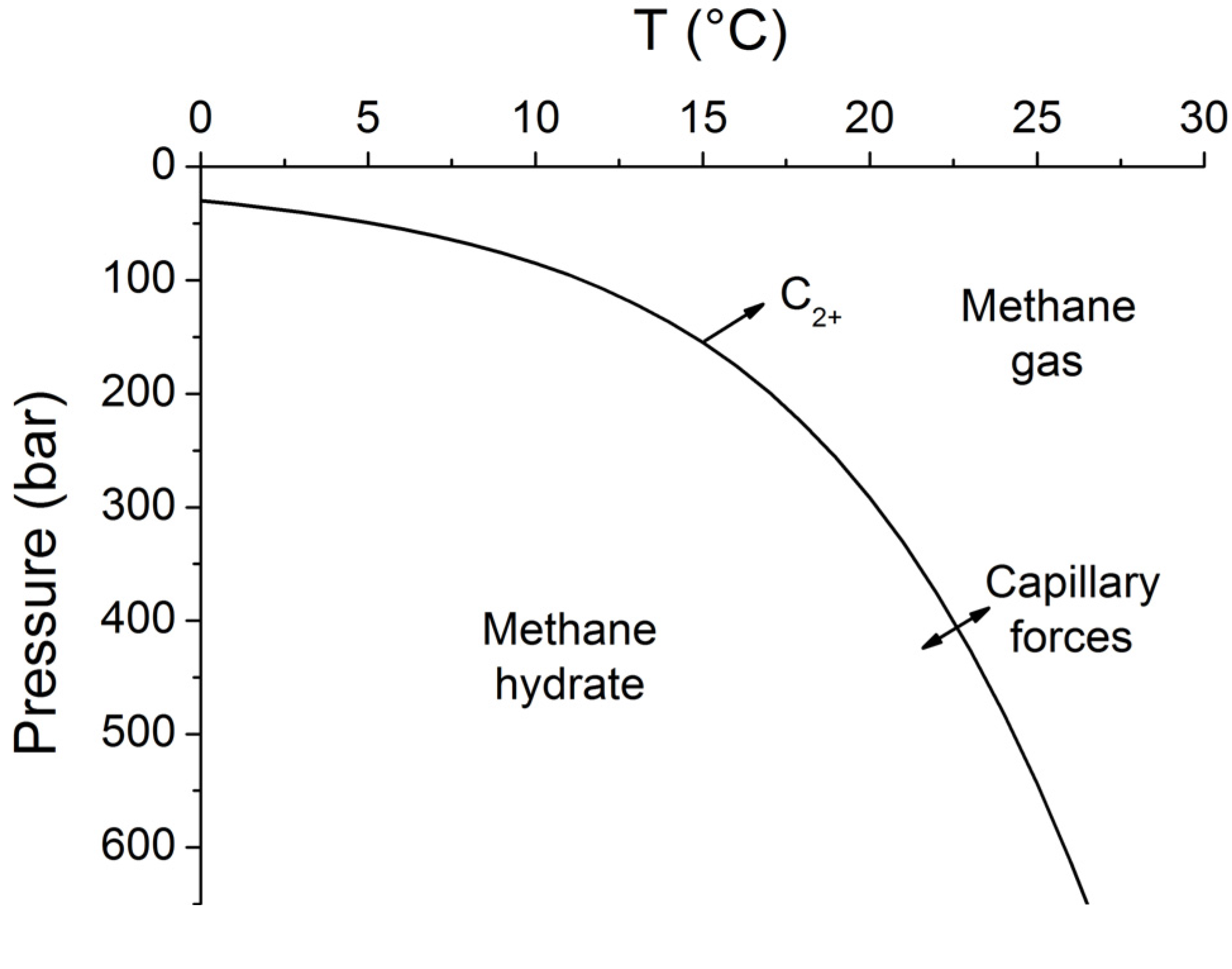
34]. The stability field for sulfate-free seawater with a salinity of 35 PSU is shown in
Figure 7. The sharp phase boundary depicted in
Figure 7 is however not strictly valid for sediments and other porous media. Capillary forces acting on gas hydrates and free gas residing in sediment pores of different sizes create a broad transition zone where free gas and gas hydrate coexist [
41]. The thickness of this zone has been estimated as 20–28 m for Hydrate Ridge and Blake Ridge [
41]. The seismic bottom simulating reflector (BSR) indicating the top of the free gas occurrence zone is therefore often located at shallower depths than predicted by the bulk phase boundary. Moreover, the composition of the hydrate-forming natural gas has a strong effect on the positioning of the phase boundary. Biogenic gas formed by the microbial degradation of organic matter is composed of methane and CO
2 and contains only trace amounts of higher hydrocarbons (C
2+). CO
2 hydrates are usually not formed in marine sediments since their solubility clearly exceeds the CO
2 concentration in ambient pore fluids. Methane hydrates are less soluble and therefore the major product of biogenic gas formation in marine sediments. The hydrate-bound gas thus typically contains more than 99.9% methane with only trace amounts of CO
2 and C
2+ [
42]. The low abundance of higher hydrocarbons in biogenic gas supports the formation of structure type I methane hydrate. However, thermogenic gas ascending from larger sediment depths contains significant amounts of C
2+ favoring the formation of structure type II and/or the inclusion of C
2+-components in structure type I methane hydrate. These hydrates are stable over a significantly broader P-T range and thus induce a down-core displacement of the phase boundary [
40].
Figure 7.
Phase diagram for methane hydrate (structure type I) for sulfate-free seawater with a salinity of 35 [
34]. Arrows indicate the formation of a transition zone by capillary forces and the broadening of the gas hydrate stability zone by higher hydrocarbon compounds (C
2+).
Figure 7.
Phase diagram for methane hydrate (structure type I) for sulfate-free seawater with a salinity of 35 [
34]. Arrows indicate the formation of a transition zone by capillary forces and the broadening of the gas hydrate stability zone by higher hydrocarbon compounds (C
2+).
The thickness of the gas hydrate stability zone (GHSZ) in marine sediments is usually estimated considering the temperature (T) and pressure (P) conditions at the seabed and the increase in T and P with sediment depth. High-resolution data sets are available to define temperatures and pressures at the seafloor on global scale [
6] while the conductive heat flux has been measured at more than 9000 sites [
43]. Most of these heat flow data have been generated by measuring the temperature gradient within the upper few meters of the sediment column. The conductive heat flux (
qH) is then calculated from the temperature gradient considering the ambient thermal conductivity of bulk sediments (λ
B):
Heat flow data rather than temperature gradients (d
T/d
z) have been compiled at global scale [
43]. Geothermal gradients defining the thickness of the gas hydrate stability zone, thus, need to be derived from the heat flux data applying appropriate estimates for ambient thermal conductivity. Thermal conductivities of bulk sediments quantify the efficiency of heat transport which involves transport (1) from grain to grain; (2) from grain to liquid to grain; and (3) through pore-filling liquid [
44]. Rather than calculate the contribution of each heat transport path explicitly, thermal conductivity is often estimated using a two-phase mixing model to combine the thermal conductivities of the sediment grains with the pore fluid. The thermal conductivities of methane hydrate and water differ by <10% at the temperatures found in hydrate-bearing sediments [
44]. For this reason, first-order thermal conductivity estimates can neglect the presence of methane hydrate and assume that the sediment pore space contains only water [
45]. The following two-phase mixing model provides a reasonable approximation for thermal conductivity in the uppermost 500–1000 m of the sediment column [
45]:
where λ
B, λ
W, and λ
S are thermal conductivities of bulk sediment, seawater and solids, respectively. The thermal conductivity of seawater increases with pressure and temperature [
46]. It varies from 0.56 to 0.60 W m
−1 K
−1 over the P-T range encountered within the GHSZ [
46]. A mean value of λ
W = 0.58 W m
−1 K
−1 is thus representative for the marine hydrate stability zone. Quartz has a conductivity of 7.7–8.4 W m
−1 K
−1 [
44] while calcite has an average conductivity of 3.6 W m
−1 K
−1 [
47]. Thermal conductivities of clay minerals vary from 5.2 W m
−1 K
−1 for chlorite to 1.8–2.7 W m
−1 K
−1 for smectite, illite and kaolinite [
47]. Data measured in ODP cores retrieved at various continental margin sites indicate a mean value of λ
S = 2.5 W m
−1 K
−1 for the dry solids in fine-grained margin sediments [
45]. The average porosity within the upper few meter of the sediment column is typically close to 0.75 [
45]. Applying Equation (14), the thermal conductivity of clay-rich surface sediments results as λ
B = 0.836 W m
−1 K
−1 for λ
W = 0.58 W m
−1 K
−1 and λ
S = 2.5 W m
−1 K
−1. The geothermal gradient in surface sediments is thus derived by dividing the ambient heat flux data by λ
B = 0.836 W m
−1 K
−1 [Equation (13)].
Thermal conductivity changes, however, with sediment depth due to the compaction of sediments inducing a down-core decrease in porosity. Porosity change is often described by the following equation [
19]:
where
Φ0 is the porosity at the sediment surface,
Φf the porosity at the base of the sediment column and
p is an attenuation coefficient. The mean porosity profile observed in ODP cores can be approximated applying
Φ0 = 0.74,
Φ0 = 0.3 and
p = 1/600 m
−1 [
48].
The steady-state temperature profile in marine sediments is usually controlled by heat conduction. Neglecting heat production and convection, it can be described by the following differential equation [
49]:
This equation can be solved applying the following boundary conditions at the top of the sediment column at
z = 0:
where
TGrad is the temperature gradient recorded in surface sediments,
qH is the heat flow calculated from the gradient and the thermal conductivity of surface sediments while
TBW is the temperature of ambient bottom water. The solution of this equation for constant λ
B results as:
The equation can also be solved for variable λ
B considering the down-core changes in porosity and λ
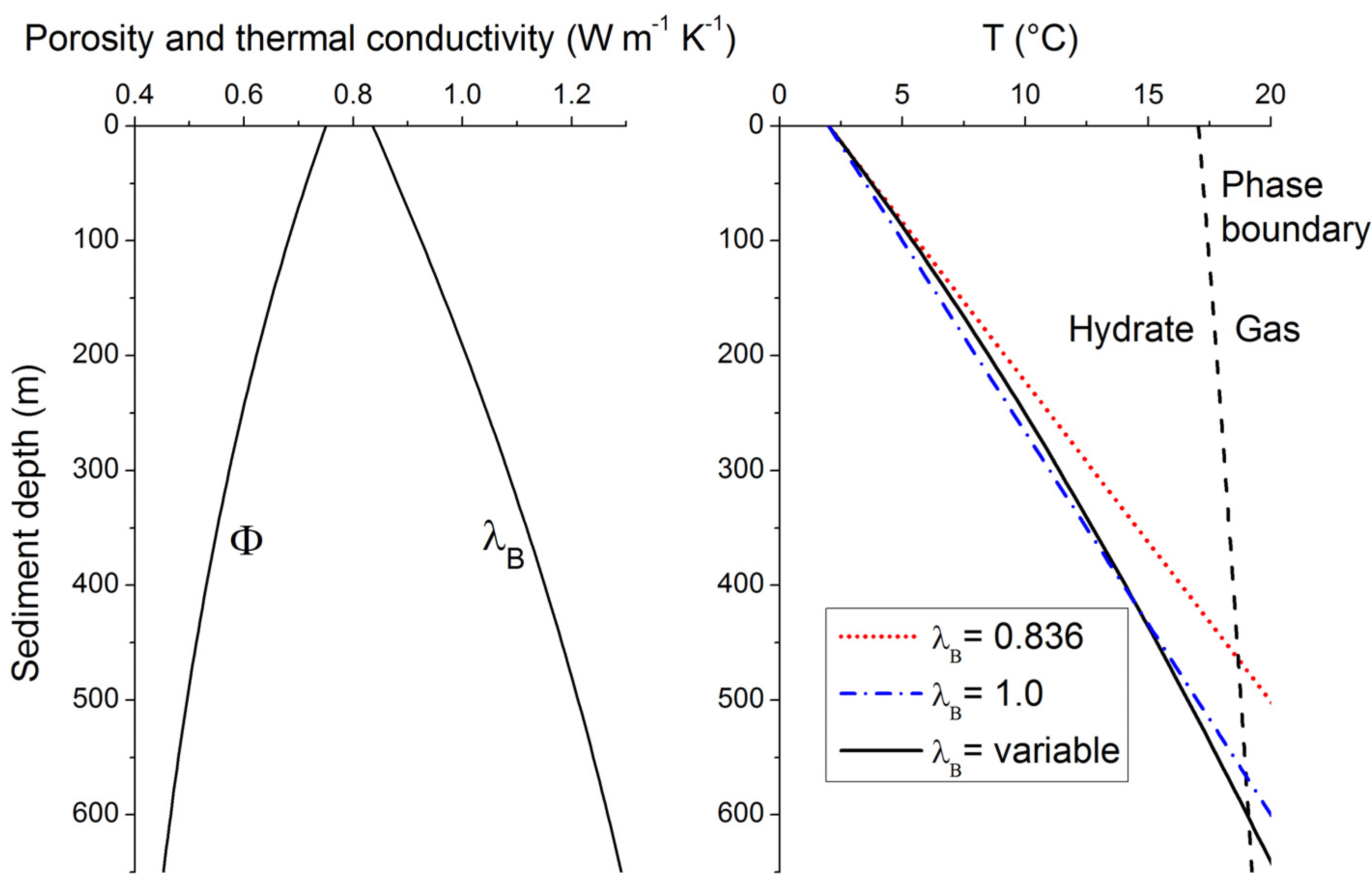
B defined in Equations (14,15). The resulting temperature profile is depicted in
Figure 8 for typical continental margin sediments (solid black line in the right panel). It shows a clearly non-linear shape since the down-core decrease in porosity induces a significant λ
B increase with depth (left panel in
Figure 8). The linear profile calculated from the λ
B value in surface sediments [λ
B = 0.836 W m
−1 K
−1, red dotted line in the left panel, Equation (16)] overestimates sediment temperatures at depth and thus underestimates the thickness of the GHSZ by almost 150 m (
Figure 8). It is thus important to consider the non-linear nature of sedimentary temperature profiles. The temperature profile and GHSZ thickness can, however, be approximated applying a constant λ
B of 1 W m
−1 K
−1 (blue dotted-broken line in right panel of
Figure 8). This mean value is thus often applied to estimate the vertical extent of the GHSZ in marine sediments [
45].
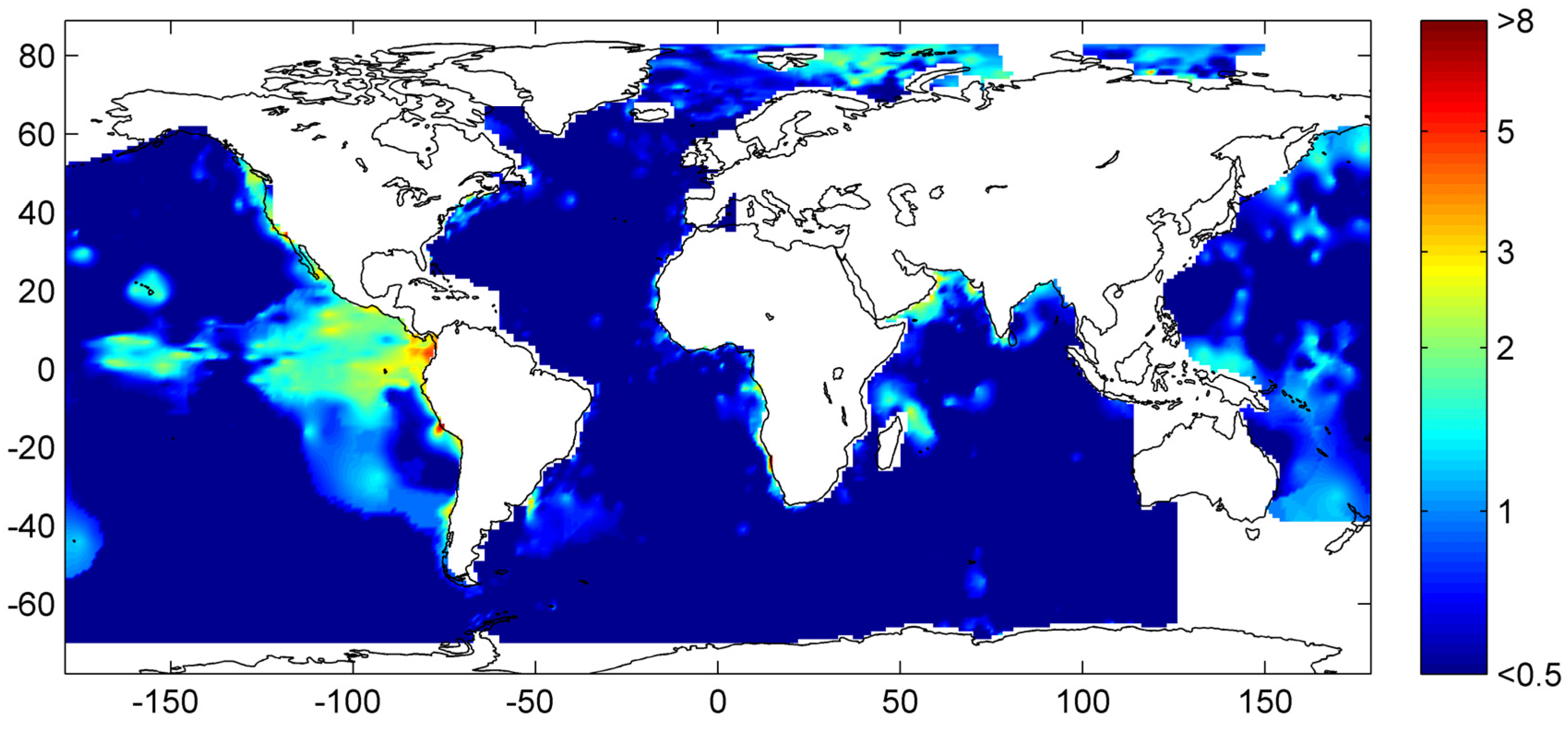
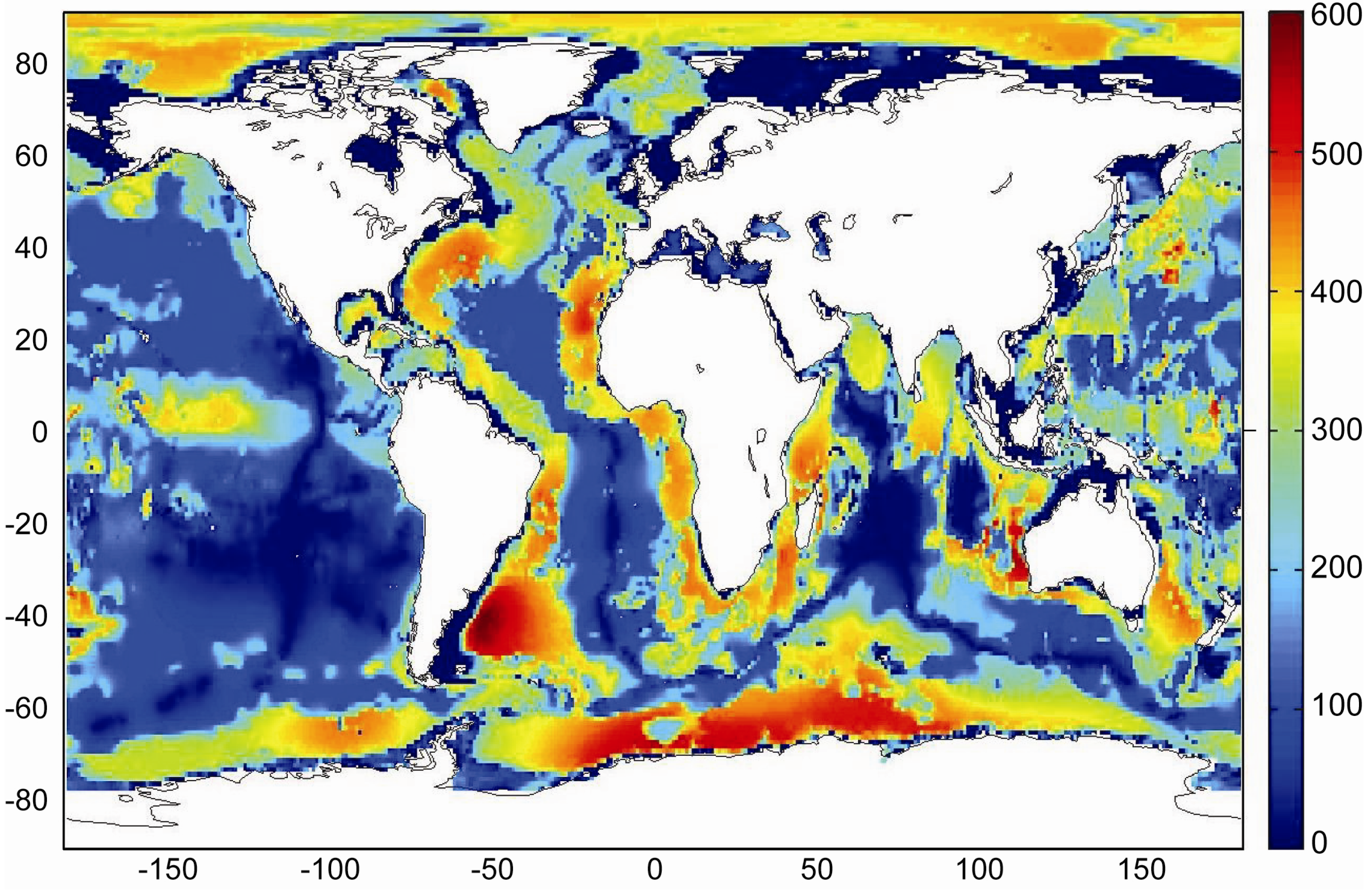
Global maps of the GHSZ thickness were produced by Burwicz
et al. [
6] and Pinero
et al. [
50] assuming constant temperature gradients and applying the same global data sets for water depth, bottom water temperature, heat flow and sediment thickness. The base of the GHSZ is defined by the intersection of the sedimentary temperature profile and the phase boundary for sulfate-free pore water (
Figure 8). Pinero
et al. [
50] assumed a constant thermal conductivity of λ
B = 1.0 W m
−1 K
−1 over the entire ocean. The map produced under this assumption gives a good approximation for the GHSZ thickness in fine-grained continental margin sediments (
Figure 9). The vertical extend of the GHSZ is, however, underestimated where sediments are dominated by sand, chlorite and calcite since sedimentary bulk conductivity is strongly enhanced by these components [
47]. Moreover, the map is based on a thermodynamic model valid for pure methane hydrate of structure type I [
34]. It may thus underestimate the vertical extent of the GHSZ where methane hydrate is stabilized by C
2+ components entrained into the GHSZ by the ascent of thermogenic gas (
Figure 7). Burwicz
et al. [
6] applied a constant λ
B value of 1.5 W m
−1 K
−1 which over-predicts the GHSZ thickness in margin sediments composed of smectite, illite and kaolinite but may give a better approximation for pelagic sediments. Both maps show an extended and deep-reaching GHSZ at high latitudes and around passive continental margins whereas a thin GHSZ is derived for the open ocean where the thickness of the GHSZ is limited by the thin sedimentary cover.
Figure 8.
Down-core change in porosity [
Φ, Equation (15)], thermal conductivity of bulk sediment [λ
B, Equation (14)] and temperature [T, Equation (16)] in typical continental margin sediments (
Φ0 = 0.74,
Φf = 0.3 and
p = 1/600 m
−1,
qH = 0.03 W m
−2, λ
W = 0.58 W m
−1 K
−1, λ
S = 2.5 W m
−1 K
−1). The phase boundary for methane hydrate (structure type I) shown in the right panel (black broken line) is calculated for sediments deposited at 2000 m water depth, hydrostatic pressure conditions and sulfate-free sediment porewater with a salinity of 35 [
34].
Figure 8.
Down-core change in porosity [
Φ, Equation (15)], thermal conductivity of bulk sediment [λ
B, Equation (14)] and temperature [T, Equation (16)] in typical continental margin sediments (
Φ0 = 0.74,
Φf = 0.3 and
p = 1/600 m
−1,
qH = 0.03 W m
−2, λ
W = 0.58 W m
−1 K
−1, λ
S = 2.5 W m
−1 K
−1). The phase boundary for methane hydrate (structure type I) shown in the right panel (black broken line) is calculated for sediments deposited at 2000 m water depth, hydrostatic pressure conditions and sulfate-free sediment porewater with a salinity of 35 [
34].
Figure 9.
Thickness of the gas hydrate stability zone calculated from global heat flux data [
43] considering bathymetry, bottom water temperature, sediment thickness data and a bulk thermal conductivity of 1.0 W m
−1 K
−1 [
50].
Figure 9.
Thickness of the gas hydrate stability zone calculated from global heat flux data [
43] considering bathymetry, bottom water temperature, sediment thickness data and a bulk thermal conductivity of 1.0 W m
−1 K
−1 [
50].
The global volume of the GHSZ is estimated to be 67 × 10
15 m
3 integrating the data shown in
Figure 9. This value should be considered as a minimum estimate since the thickness of the GHSZ may be underestimated in those areas where solid phases with high thermal conductivity and C
2+-bearing gas hydrates are deposited. The pore space available for gas hydrate accumulation amounts to 44 × 10
15 m
3 considering the decay of porosity over the sediment column [
Figure 8, Equation (15)]. Up to 4 × 10
21 g CH
4-C could reside in the GHSZ if the entire pore space (44 × 10
15 m
3) would be filled by methane hydrate. This maximum estimate clearly exceeds the total methane pool generated via microbial POC degradation over a period of 10 Myr (1.0 × 10
20 g CH
4-C, see section 3). Thus, only 2.5% of the global GHSZ pore space could be occupied by gas hydrates if the entire biogenic methane pool would be fixed as gas hydrate.
6. Sediment Compaction, Fluid Flow and Gas Ascent
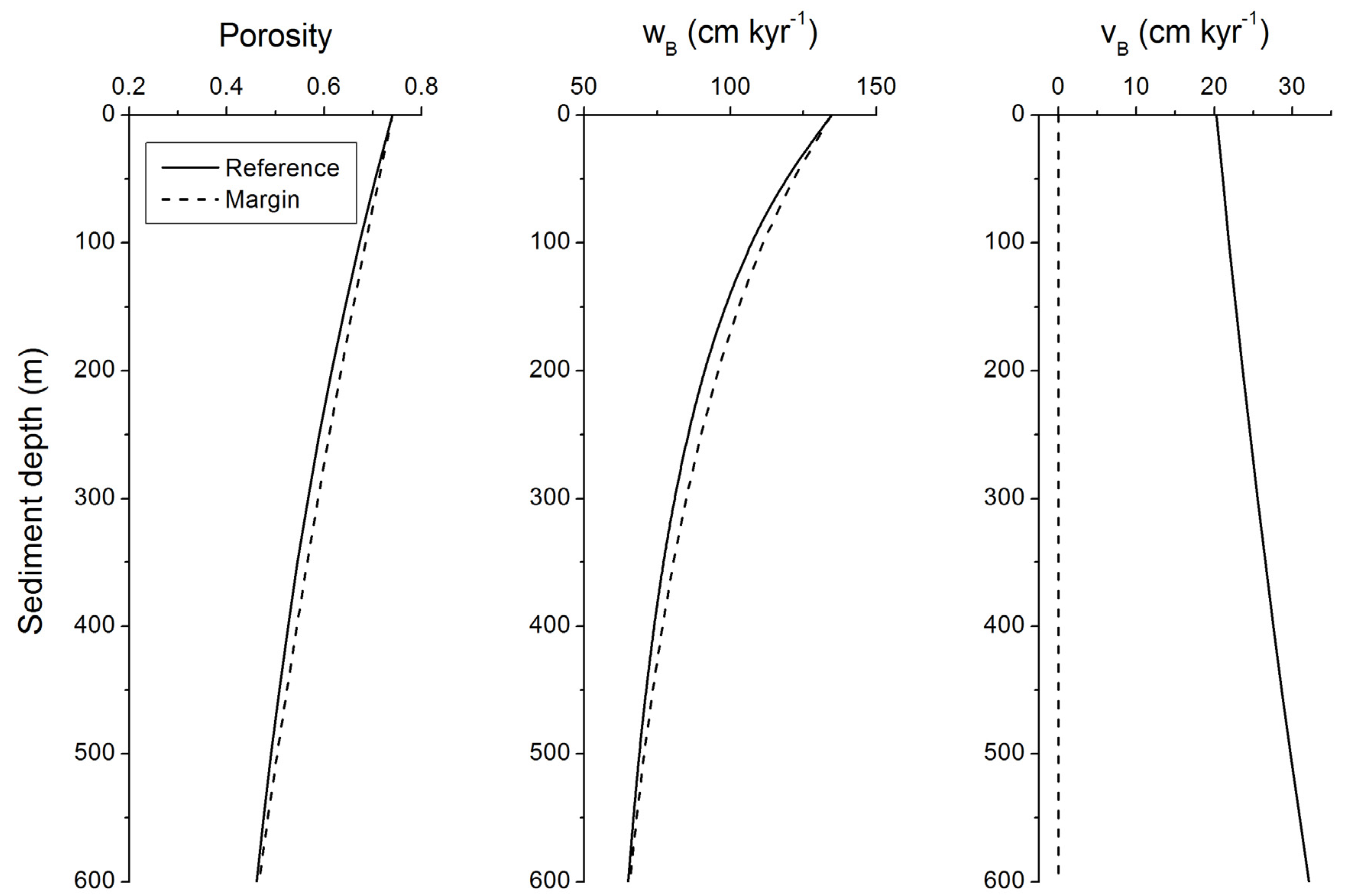
Gas hydrates are formed from methane being produced within the GHSZ (section 3) and by methane ascending into the GHSZ from below. Upward flow of methane is induced by numerous processes including sediment compaction, tectonic over-pressuring and the buoyancy of methane gas and methane charged fluids. Sediment compaction is driven by the overburden load of younger sediments being continuously deposited at the seabed [
48]. In most marine settings, it induces an exponential decrease in porosity (
Φ) and water content with sediment depth (
Figure 8). Therefore, exponential equations such as Equation (15) are used to describe the compaction-driven down-core decrease in porosity. Applying Equations (1,15), the burial velocity of pore water (
vB) and solids (
wB) are calculated as [
19]:
The equations above are valid for steady state conditions,
i.e., for homogenous deposits formed by continuous sedimentation. The porosity of marine sediments deposited on oceanic crust is usually not completely eliminated by compaction. The residual porosity at the base of the sediment column (
i.e., the crust-sediment interface) is given by
Φf while w
f is the burial velocity of water and solids which is attained after the porosity has been reduced to
Φf via steady-state compaction. Compaction promotes the burial of solids while pore water burial is diminished since water is expelled and transported upwards due to the down-core reduction in pore space (
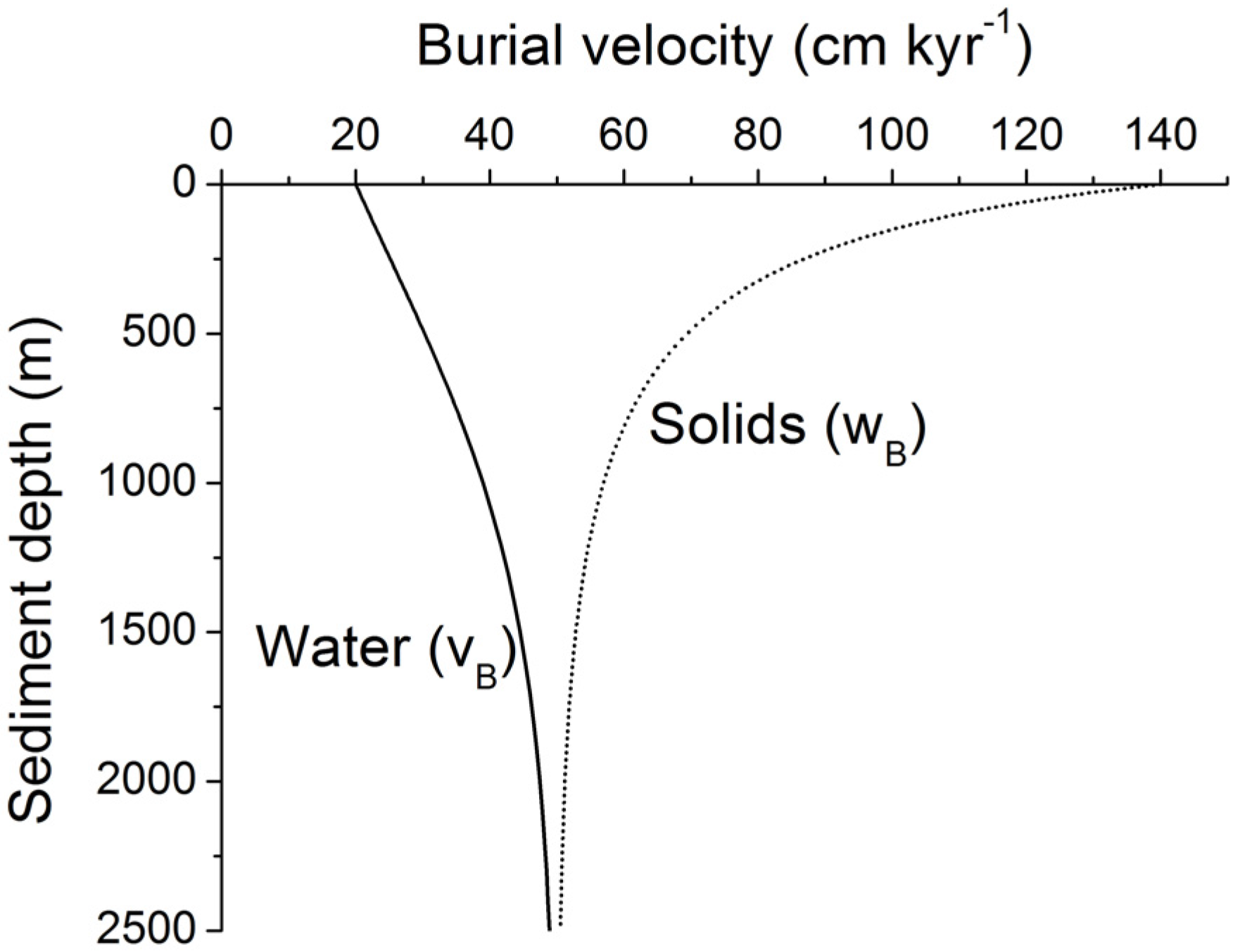
Figure 11). However, steady-state compaction does not induce a flow of water into the overlying water column: The pore fluids do not escape into the bottom water since the pore water burial velocity induced by the continuous deposition of young sediments at the seabed exceeds the velocity of the compaction-driven upward fluid flow.
Figure 11.
Burial velocity of pore fluids (vB) and solids (wB) in marine sediments subject to steady-state compaction. Velocities are calculated applying Equation (19) with Φ0 = 0.74, Φf = 0.3, p = 1/600 m−1, and wf = 50 cm kyr−1.
Figure 11.
Burial velocity of pore fluids (vB) and solids (wB) in marine sediments subject to steady-state compaction. Velocities are calculated applying Equation (19) with Φ0 = 0.74, Φf = 0.3, p = 1/600 m−1, and wf = 50 cm kyr−1.
Seepage of pore fluids is frequently observed at continental margins where sediments are compressed by tectonic forces [
52] since marine sediments subducted below continental crust and accreted at active continental margins are over-pressured and dewatered to such an extent that pore fluids escape into the bottom water [
53,
54,
55,
56]. Salt diapirism, sediment erosion and slope failure induce additional fluid seepage at passive and active continental margins. Upward fluid flow is ultimately driven by excess pressures as described by the Darcy equation [
57]:
where the Darcy flow
u (m
3 m
−2 yr
−1) is the volume of water (m
3) being transported through a cross-sectional sediment area (m
2) over a period of time (yr). Upward fluid flow occurs when the sedimentary pressure gradient (
in Pa m
−1) exceeds the hydrostatic pressure gradient defined as product of water density (
ρW in kg m
−3) and gravitational acceleration (
g = 9.81 Pa m
2 kg
−1). The velocity of fluid flow is modulated by the intrinsic permeability of bulk sediments (
k in m
2) and the viscosity of water (
µw ≈ 10
−3 Pa s). The intrinsic permeability of marine sediment varies over several orders of magnitude. It increases with porosity and grain size: Terrigenous marine sediments containing fine-grained clay have typical permeability values of 10
−18–10
−14 m
2 while clean sands have values of 10
−12–10
−10 m
2 [
57].
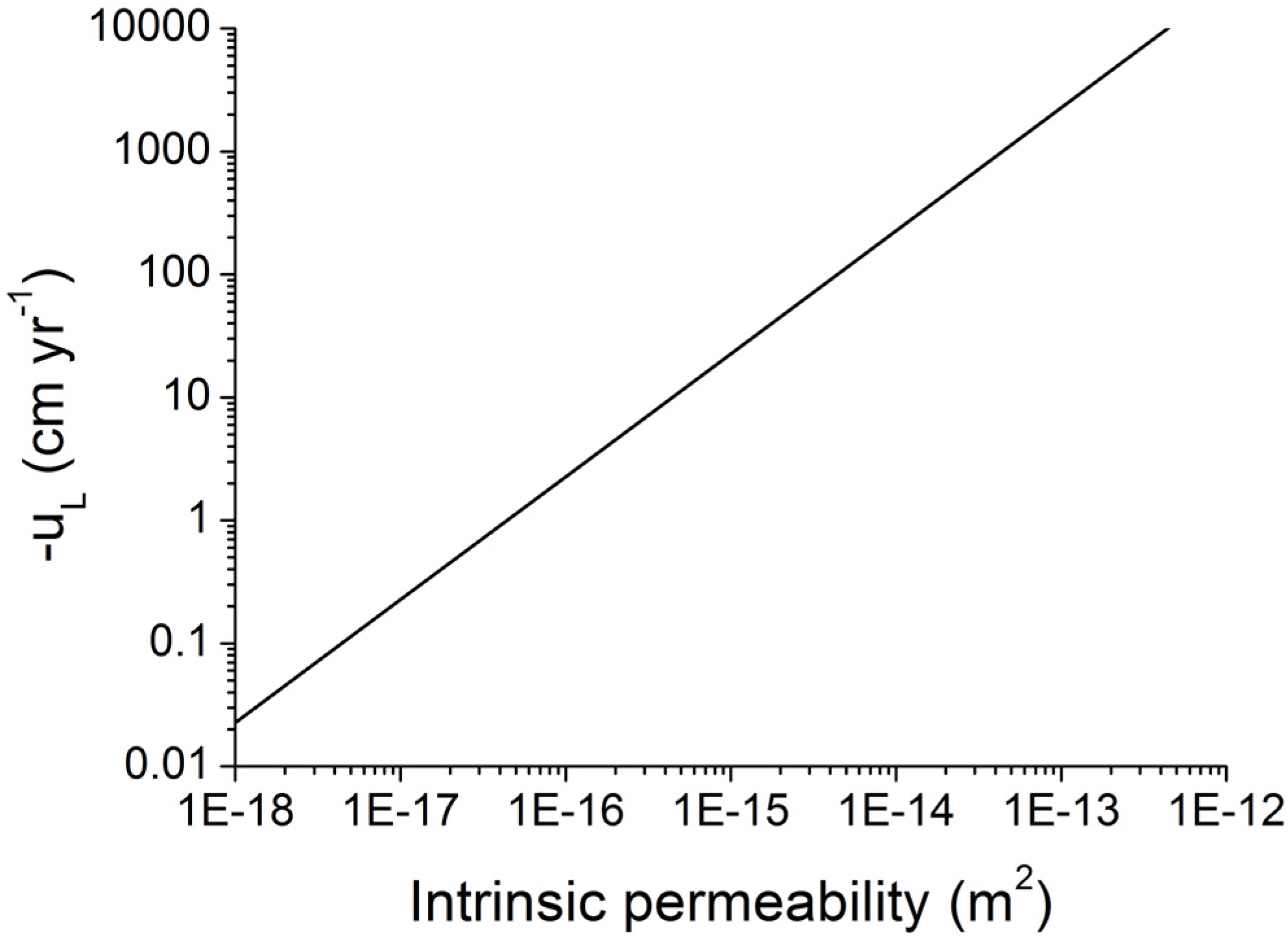
The sedimentary pressure gradient is enhanced in compressive tectonic settings and may approach the lithostatic pressure gradient defined as the product of g and the bulk density of sediments. The bulk density of sediments ρ
B is calculated as:
The Darcy flow at lithostatic pressure
uL is thus calculated as:
The inter-granular fluid flow velocity v is related to the Darcy flow velocity u as:
Both velocities,
u and
v, attain a positive sign for a downward movement with respect to the sediment-water interface while a negative sign indicates the ascent of pore fluids towards the sediment surface. Fluids ascending through a constantly growing homogenous sediment deposit subject to steady-state compaction have an inter-granular fluid flow velocity of:
Fluids are thus expelled across the sediment-water interface into the overlying water column when the velocity of fluids infiltrating the sediment column from below (
v) exceeds the burial velocity of pore fluids (
vB). Upward fluid flow velocities (
v) have been measured at various cold seep sites and mud volcanoes located at active and passive continental margins [
53,
54,
58,
59,
60,
61,
62,
63]. They typically range from 0.1 to 100 cm yr
−1. These flow velocities are consistent with
uL values predicted for over-pressured clay-bearing sediments deposited at continental margins (
Figure 12).
Figure 12.
Velocity of Darcy fluid flow at lithostatic pressure (uL) in marine sediments as function of intrinsic permeability. Darcy flow is calculated applying density values of ρW = 1036 kg m−3 and ρS = 2500 kg m−3 and a porosity of Φ = 0.5.
Figure 12.
Velocity of Darcy fluid flow at lithostatic pressure (uL) in marine sediments as function of intrinsic permeability. Darcy flow is calculated applying density values of ρW = 1036 kg m−3 and ρS = 2500 kg m−3 and a porosity of Φ = 0.5.
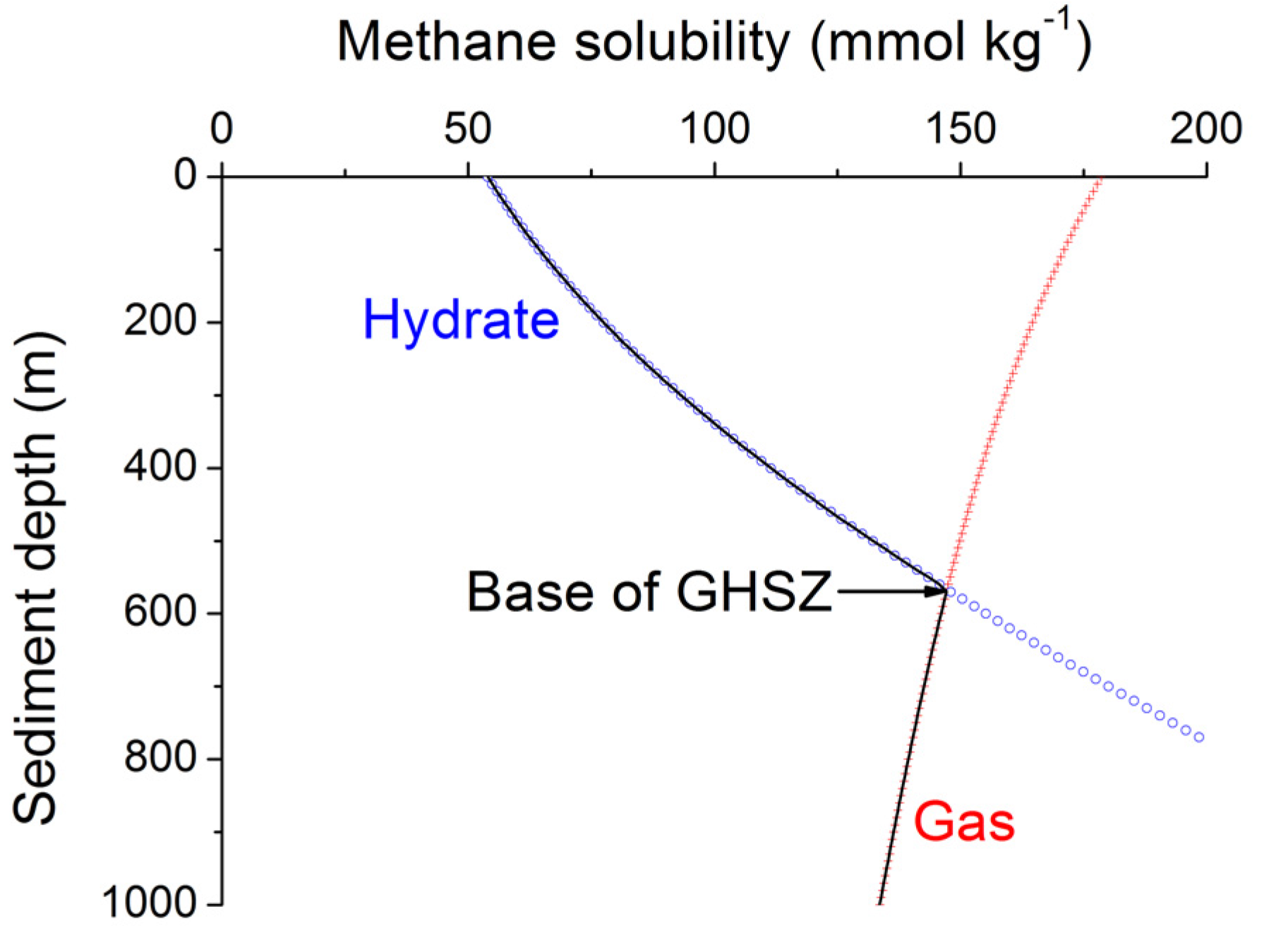
Gaseous methane occurs below the GHSZ and in the transition zone at the base of the GHSZ. The bottom simulating reflector (BSR) observed in many seismic surveys marks the boundary between hydrate-bearing sediments and the underlying gas-bearing sediment zone. The density of methane gas is lower than the density of pore fluids. Therefore buoyancy forces may induce an upward flow of gas into the GHSZ. For sediments containing both gas and water, Darcy’s law is formulated as [
57]:
where the subscripts W and G indicate water and gas, respectively. Relative permeability appears as additional non-dimensional parameter in the equations above (
kRW and
kRG). Various equations have been proposed to quantify the relative permeability of water and gas in marine sediments at different saturation values [
44,
57]. One of the more commonly used forms is given by [
64]:
where m is the pore-size-distribution index. The normalized water saturation
SWN is defined as:
where
SW is the water saturation,
i.e., fraction of pore space occupied by water (
SW = 1 −
SG). The irreducible water saturation has a typical value of
SWC = 0.3 while the corresponding gas saturation falls into the range of
SGC = 0.01–0.1 [
65]. The irreducible gas saturation is the most critical parameter for the prediction of upward gas migration in marine sediments since gas migration occurs only when the gas saturation
SG exceeds
SGC. A high
SGC value of 0.1 indicates that gas migration is inhibited if less than 10% of the pore space is occupied by gas [
SG < 0.1,
SWN = 1,
kRG = 0,
qG = 0, s. Equations (25–27)]. This would imply that gas migration across the BSR is effectively suppressed since the methane gas produced by microbial POC degradation below the GHSZ rarely builds up to saturations of
SG > 0.1. The BSR is produced by the strong seismic contrast between gas below the GHSZ and gas hydrate within the GHSZ. Seismic surveys show a wide-spread occurrence of the BSR indicating that a significant fraction of methane gas is not mobile but retained and buried in sediments underlying the GHSZ. However, seismic chimneys indicating the ascent of free gas are also frequently observed at continental margins and are often associated with high gas hydrate saturations in the overlying GHSZ. It thus seems that the free gas is usually immobile but locally mobilized and transported into the GHSZ. The controls on gas migration into the GHSZ are poorly understood and this lack of physical understanding causes a large degree of uncertainty in the prediction of gas hydrate accumulation in marine sediments.
The gas pressure
PG is related to the water pressure
PW as [
57]:
where
PC is the capillary pressure.
PC may be calculated as [
66]:
where
PCC has a value of 13,300 Pa in low permeability sediments while npc takes a value of 1.7 [
66].
Darcy gas flow at constant gas saturation (
) and hydrostatic pressure (
) can be calculated as function of gas saturation (
SG) and intrinsic permeability to quantify the buoyancy driven gas ascent into the GHSZ:
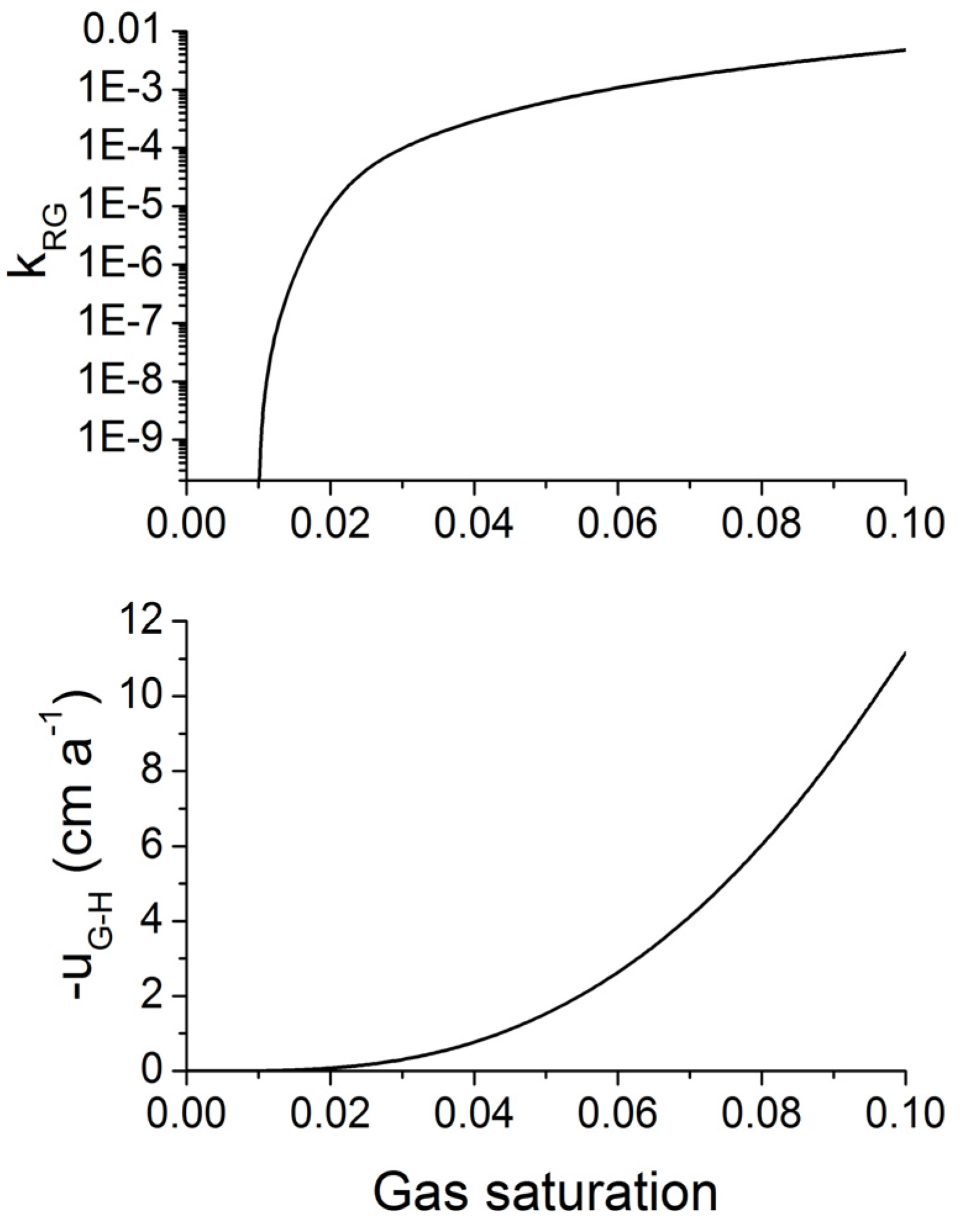
Figure 13 shows this buoyancy driven flux for typical continental margin sediments deposited at 2000 m water depth. Applying a geothermal gradient of 30 °C/km, the temperature at the base of the GHSZ is 19.1 °C while the hydrostatic pressure at the phase boundary amounts to 257 bar (
Figure 8). The densities of methane gas and water are
ρG = 198 kg m
−3 [
67] and
ρW = 1036 kg m
−3 [
68] under these P-T conditions while the dynamic viscosity of methane gas amounts to
µG = 11 × 10
−6 Pa s [
69]. The gas flow is completely inhibited at
SG <
SGC and increases rapidly with increasing
SG at
SG >
SGC. Buoyancy forces would thus induce a rapid ascent of gas into the GHSZ if the gas saturation exceeds the critical value. Under these conditions the methane hydrates buried and dissociated below the GHSZ would not be lost from the system but would be constantly recycled into the GHSZ via upward gas migration. The methane hydrate inventory would expand over time until the pore space available for gas migration is clocked by methane hydrate. Very high methane hydrate saturations could be attained by this recycling mechanism.
Figure 13.
Relative permeability of gas [kRG, upper panel, Equation (26)] and buoyancy-driven gas flow (uG-H, lower panel, Equation 30) in fine-grained marine sediments as function of gas saturation (SG = 1 − SW). kRG is calculated applying Equations 26 and 27 with SWC = 0.3, SGC = 0.01 and m = 0.75. The gas flux is calculated for hydrostatic pressure conditions applying Equation 30 with ρW = 1036 kg m−3, ρG = 198 kg m−3, k = 10−15 m2, µG = 11 × 10−6 Pa s and the relative gas permeability depicted in the upper panel.
Figure 13.
Relative permeability of gas [kRG, upper panel, Equation (26)] and buoyancy-driven gas flow (uG-H, lower panel, Equation 30) in fine-grained marine sediments as function of gas saturation (SG = 1 − SW). kRG is calculated applying Equations 26 and 27 with SWC = 0.3, SGC = 0.01 and m = 0.75. The gas flux is calculated for hydrostatic pressure conditions applying Equation 30 with ρW = 1036 kg m−3, ρG = 198 kg m−3, k = 10−15 m2, µG = 11 × 10−6 Pa s and the relative gas permeability depicted in the upper panel.
It is important to note that gas ascent is a much more efficient mechanism for the transport of methane into the GHSZ than fluid flow. For the conditions shown in
Figure 13, an upward Darcy gas flow of 1 cm yr
−1 introduces a methane flux of 1980 g m
−2 yr
−1 (for
ρG = 198 kg m
−3) while a corresponding water flow of 1 cm yr
−1 induces a methane flux of only 24 g m
−2 yr
−1 at a dissolved methane concentration of 150 mM (
Figure 10).
The POC accumulation rates that are fueling methane production at depth rarely exceed 10 g m
−2 yr
−1 (
Figure 3). The entire methane pool potentially formed by the microbial and thermal decomposition of buried POC would thus be transported into the GHSZ at gas and water flow velocities as low as
uG ≈ 0.002 cm yr
−1 and
uW ≈ 0.2 cm yr
−1.
A better understand of the physical controls on gas and water ascent into the GHSZ is thus a high priory requirement for the prediction of gas hydrate accumulation at local and global scale.
8. Constraining the Global Methane Hydrate Inventory in the Modern Ocean
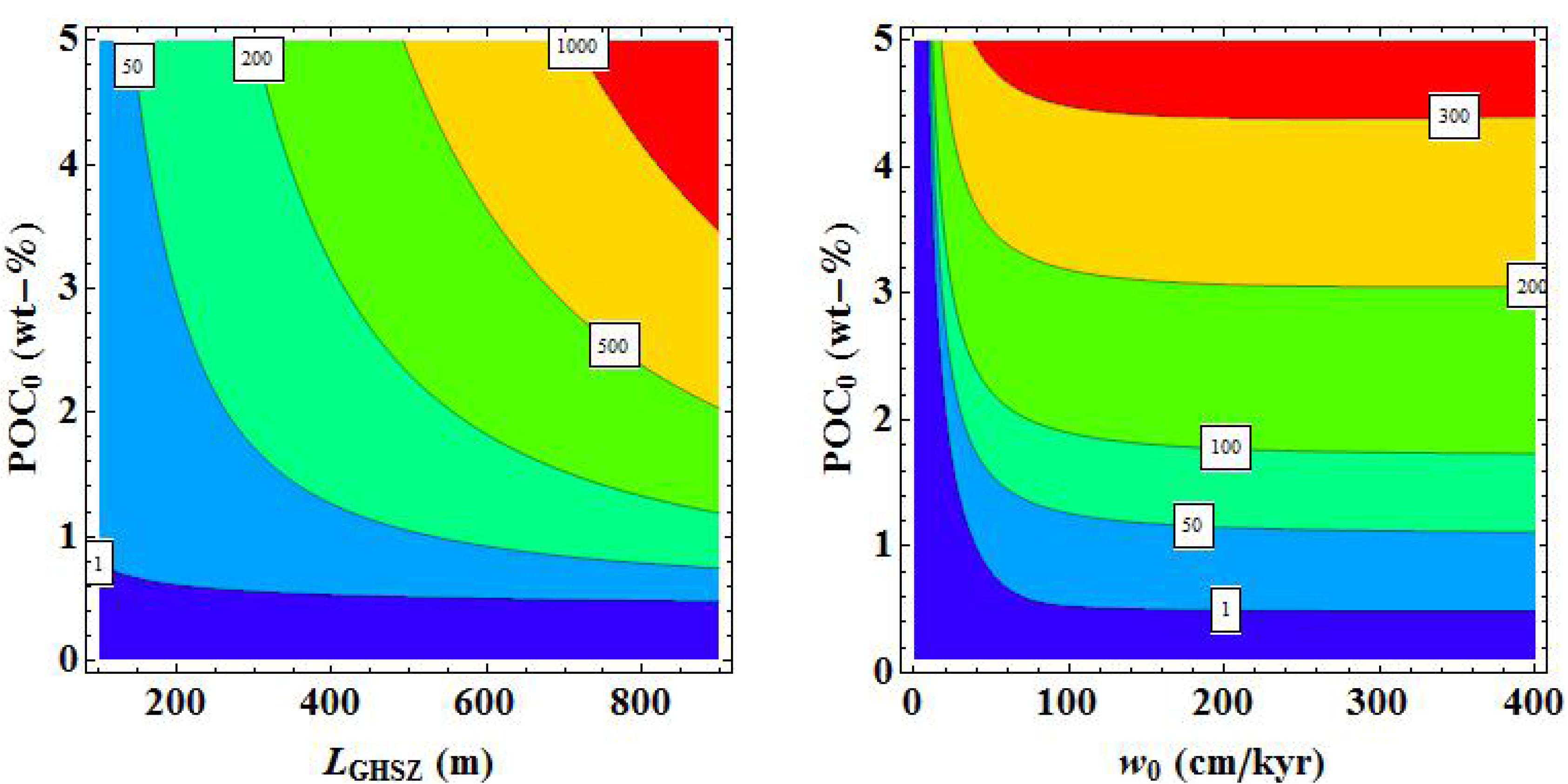
In the following section, the transfer functions derived in
Section 7.2 and
Section 7.3 are applied on a global grid to estimate the abundance and distribution of methane hydrate in marine sediments. The global grid was defined by the POC concentrations in marine surface sediments (
POC0) and burial velocities (
w0) reported in Burwicz
et al. [
6] and the GHSZ map (
LGHSZ) shown in
Figure 9.
Transfer function Equation (31) which is valid for sediments experiencing a low degree of compaction was applied with Holocene burial velocities to provide a minimum estimate for the accumulation of gas hydrates in marine sediments. The global inventory of methane hydrates in marine sediments amounts to only 3 Gt of C under these boundary conditions. Low-grade gas hydrate occurrences are predicted for some high productivity areas with depth-integrated hydrate inventories of less than 40 kg m
−2. These low values are consistent with the previous model results for Holocene boundary conditions presented by Burwicz
et al. [
6] yielding a global gas hydrate inventory of only 4 Gt of C.
The transfer function valid for low compaction [Equation (31)] was also applied on a grid with Quaternary burial velocities to consider the down-slope transport of sediments during glacial sea-level low-stands (
Figure 30). The global inventory of methane hydrates in marine sediments expands to 122 Gt of C due to the increase in burial velocity. The map shows extended hydrate-bearing areas at productive continental margins. Elevated inventories of up to 230 kg m
−2 are found at the highly productive margin off Peru.
Figure 30.
Global distribution of methane hydrate in marine sediments. The map was calculated applying low compaction [Equation (31)] and Quaternary burial velocities. The color coding indicates depth-integrated hydrate inventories in kg C m−2.
Figure 30.
Global distribution of methane hydrate in marine sediments. The map was calculated applying low compaction [Equation (31)] and Quaternary burial velocities. The color coding indicates depth-integrated hydrate inventories in kg C m−2.
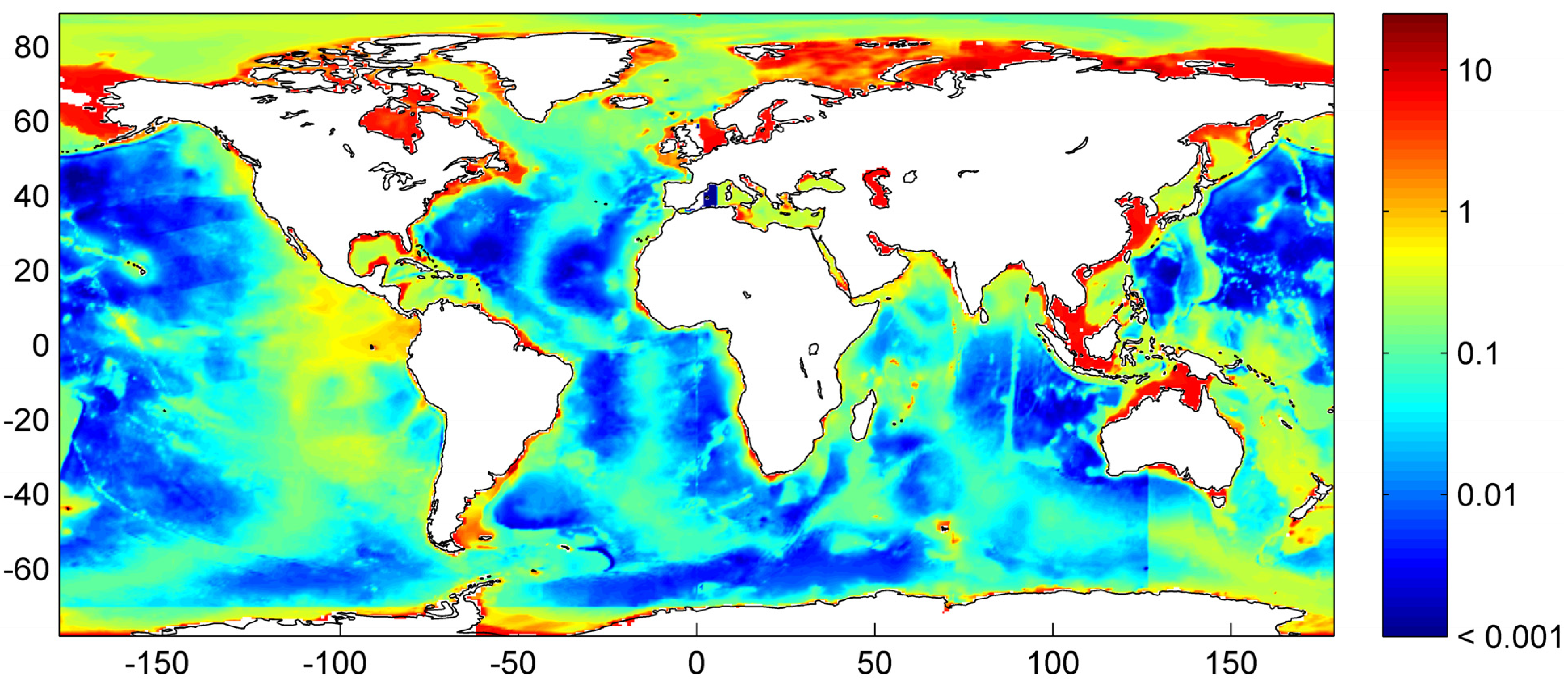
Our best estimate of the global distribution of marine sediments is shown in
Figure 31. It is based on the assumptions that margin sediments are completely compacted at large sediment depths and that shelf sediments are eroded and deposited on the continental slope and rise under glacial conditions. The global inventory of gas hydrates derived from our best estimate map (
Figure 31) is 455 Gt of C. The map predicts gas hydrate accumulations of ~10 kg m
−2 over extended margin areas with elevated values of >100 kg m
−2 in high productivity zones at the western continental margins and in the Arabian Sea. High values are also calculated at the Argentinean margin and north of Madagascar. The background concentration of methane hydrates in margin sediments of ~10 kg m
−2 corresponds to very low gas hydrate saturations of less than 0.1 Vol.% which are not resolved by geophysical methods and drilling. The true distribution of gas hydrates is probably patchier than the distribution shown in
Figure 31 since sediments are not always experiencing full compaction such that dissolved methane is buried and lost below the GHSZ. Fluid flow is implicitly considered in the map since pore fluids are not buried below the GHSZ. This approach is probably valid for passive continental margins. However, it does not consider the additional fluid flow at active margins where pore fluids of the incoming oceanic plate are mobilized and released into the GHSZ. The gas hydrate abundance at active margins is thus systematically underestimated in
Figure 31.
Figure 31.
Global distribution of methane hydrate in marine sediments. The map was calculated applying complete compaction [Equation (32)] and Quaternary burial velocities. The color coding indicates depth-integrated hydrate inventories in kg C m−2.
Figure 31.
Global distribution of methane hydrate in marine sediments. The map was calculated applying complete compaction [Equation (32)] and Quaternary burial velocities. The color coding indicates depth-integrated hydrate inventories in kg C m−2.
It should also be noted that steady-state conditions were applied in all model runs. The models were run over a period of several million years until the depth-integrated inventory of gas hydrates reached a constant value. It was assumed that geothermal gradients and POC accumulation rates at the seafloor have been constant over the entire model period. Thus, the model runs do not consider subsidence, thermal evolution and the changes in POC accumulation during basin formation.
Gas ascent and focused fluid flow at active continental margins are not considered in the map. These processes are responsible for the formation of high-grade gas hydrate accumulations which have been documented at an ever increasing number of sites [
78,
79]. The global picture that emerges from our modeling exercise may be summarized as: Gas hydrates occur at many continental margin sites at very low saturations of less than 0.1%. Higher saturations of 1%–3% appear at productive continental margins where abundant organic matter is delivered to the seabed by the sinking of biogenic detritus. High-grade deposits with saturations of >3% are formed only where fluid and/or gas have migrated into the GHSZ. These deposits are not shown on the map since it is currently not possible to constrain the global distribution of these high-grade gas hydrate deposits.
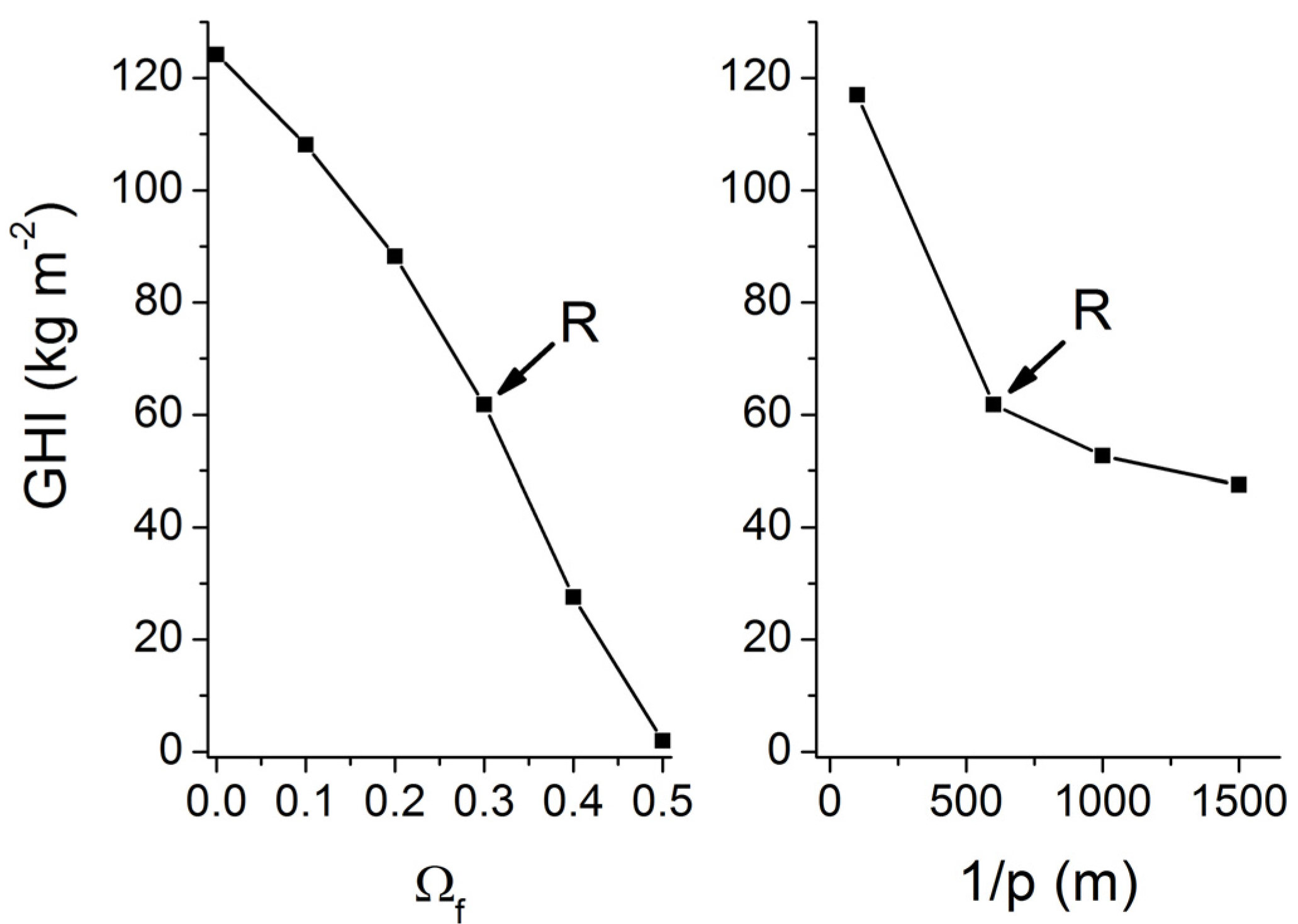
Our estimate of the global abundance of marine gas hydrates is certainly too low since gas ascent and focused fluid flow are not considered. Fluid and gas flow have an enormously strong effect on gas hydrate accumulation. The gas hydrate inventory is enhanced by about two orders magnitude already at very low velocities of fluid and gas ascent (
uw < 2 cm kyr
−1;
uG < 0.02 cm kyr
−1, s.
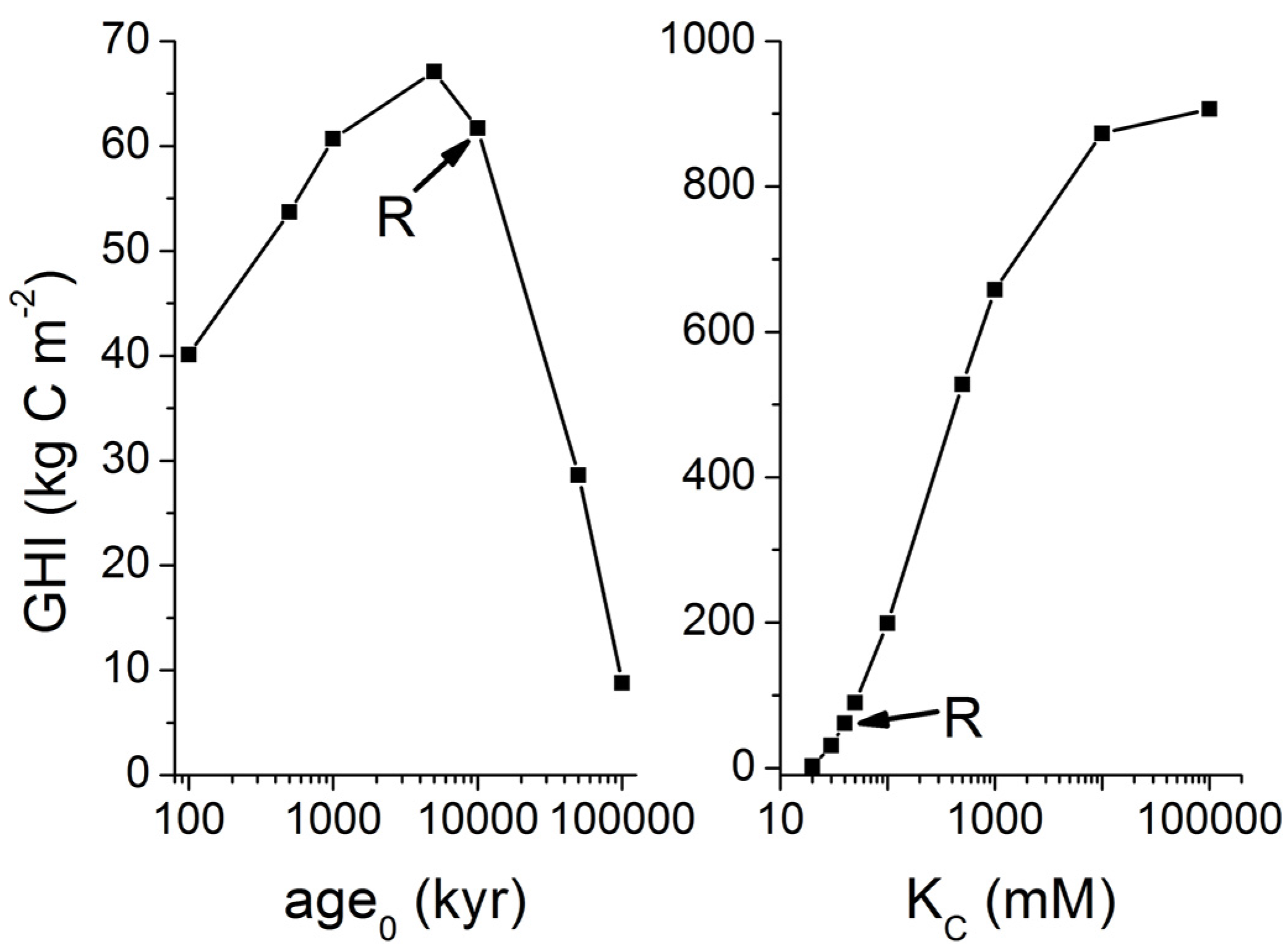
Figure 25). It is currently not possible to constrain the global number and abundance of these hot spots for gas hydrate accumulation. However, the modeling presented in this contribution suggests that the global inventory of methane in these hot spot areas may exceed the global hydrate inventory of low-grade deposits if only 1% of the global seafloor would be affected by upward gas or fluid flow.
The gas hydrate distribution shown in
Figure 31 may be used for prospection purposes while Equation (32) can be applied to estimate the gas hydrate inventory where ambient data for
w0,
LGHSZ and
POC0 are available. It should, however, be noted that detailed local surveys will almost certainly reveal inventories differing considerably from the predicted values since the regional basin evolution and the local pathways for fluid and gas flow are not resolved in our global estimates. Seismic surveys and drilling data are needed to constrain local gas hydrate inventories. Moreover, new 3-D basin modeling tools have recently been developed that can be used to better constrain gas hydrate inventories in well characterized sedimentary basins [
80]. These models can be used to simulate in detail the thermal and sedimentary history and the ascent of gas and fluids through faults and fractures at selected sites. However, it will not be possible to apply these basin models at global scale in the foreseeable future.
The first model-based estimate of the global methane hydrate inventory under Holocene boundary conditions was presented by Buffett and Archer [
3]. They used the POC rain rate to the seabed as a major external driving force for the simulation of hydrate formation in marine sediments. The rain rate was calculated as a function of water depth and applied as an upper boundary condition for an early diagenesis model simulating the degradation of POC in the top meter of the sediment column [
81]. The POC burial rate at 1 m sediment depth calculated with this “muds” model was applied as upper boundary condition for the simulation of methane turnover in the underlying sediment sequence. The later simulations consider the microbial degradation of POC via sulfate reduction and methanogenesis and the anaerobic oxidation of methane within the sulfate-methane transition zone [
82,
83]. POC was separated into an inert fraction and a labile fraction that was degraded over the top km of the sediment column following first order reaction kinetics (rate constant 3 × 10
−13 s
−1). The model also considers an externally imposed rate of upward fluid flow. It was calibrated using field data obtained at Blake Ridge (a passive margin site) and the Cascadia margin (active continental margin). The best fit to observations was obtained assuming that the 25% of the total POC is labile and using upward fluid flow velocities of 0.23 mm yr
−1 (passive margin) to 0.4 mm yr
−1 (active margin). Applying these parameter values on a global grid and assuming a compensating downward fluid flow over 50% of the global seafloor area resulted in a total methane hydrate inventory of 3000 Gt C. The hydrate inventory was to a large degree controlled by the velocity of upward fluid flow. Without imposed fluid flow, the global hydrate inventory was reduced to 600 Gt C. Subsequently, the authors discovered an extrapolation error in the calculation of POC rain rates as function of water depth [
5]. The model-based estimate of the global hydrate inventory was reduced from 3000 Gt C to approximately 700–900 Gt C after correction for this error [
5].
Klauda and Sandler [
4] used a modified version of the Davie and Buffett model [
82,
83] to estimate the global marine hydrate inventory under Holocene boundary conditions. The entire POC pool was assumed to be completely degradable with a reduced decay constant of 1.5 × 10
−14 s
−1. The upper boundary of the model domain was constrained by field data. POC concentrations measured in surface sediments and Holocene sedimentation rates averaged over the major ocean basins were applied to define the POC burial flux at the sediment surface. The global hydrate inventory estimated with this approach was surprisingly high (55–700 Gt C) even though the model was run without imposing upward fluid flow. Unfortunately, Klauda and Sandler [
4] did not consider POC degradation via sulfate reduction. The large difference to our estimate may be explained by the neglect of microbial sulfate reduction and AOM since the accumulation of methane in pore fluids and gas hydrates is strongly diminished by these processes.
Burwicz
et al. [
6] performed the first simulation of gas hydrate formation under Quaternary boundary conditions at global scale. Their estimate of the global gas hydrate inventory in marine sediments (995 Gt C) is larger than our Quaternary estimates for low and complete compaction (122 Gt C and 455 Gt C, respectively). Burwicz
et al. [
6] applied a different compaction law and assumed very low porosities for GHSZ sediments. Moreover, they used a significantly higher value for the mean thermal conductivity of marine sediments (1.5 W m
−1 K
−1) resulting in a very strong expansion of the GHSZ with respect to our modeling (s. discussion in section 4). To test the effect of the GHSZ expansion, we applied their GHSZ grid in an additional model run. We obtained a global GHI value of 937 Gt C for Quaternary conditions and full compaction [Equation (32)] which is close to the value derived by Burwicz
et al. [
6] (995 Gt C). We conclude that the difference between our best estimate (455 Gt C) and the previous estimate (995 Gt C) by Burwicz
et al. [
6] is mainly caused by the different choice of thermal conductivity values. The maps presented by Burwicz
et al. [
6] were produced by performing a full-scale 1-D transport-reaction simulation at each grid point. They are thus more precise than our estimates which are affected by additional errors introduced by the transfer functions. However, the available data strongly suggest that the thermal conductivity of most continental margin sediments is smaller than 1.5 W m
−1 K
−1 and close to the value applied in our modeling (1.0 W m
−1 K
−1). We thus conclude that the gas hydrate distribution shown in
Figure 31 and our new best estimate of the global gas hydrate abundance (455 Gt C) are more realistic than previous results.