Advanced Thermodynamic Analysis and Evaluation of a Supercritical Power Plant
Abstract
:1. Introduction
2. Methodology
2.1. Conventional Exergy Analysis
2.2. Advanced Exergy Analysis
2.2.1. Endogenous/Exogenous Exergy Destruction
2.2.3. Combination of the splitting
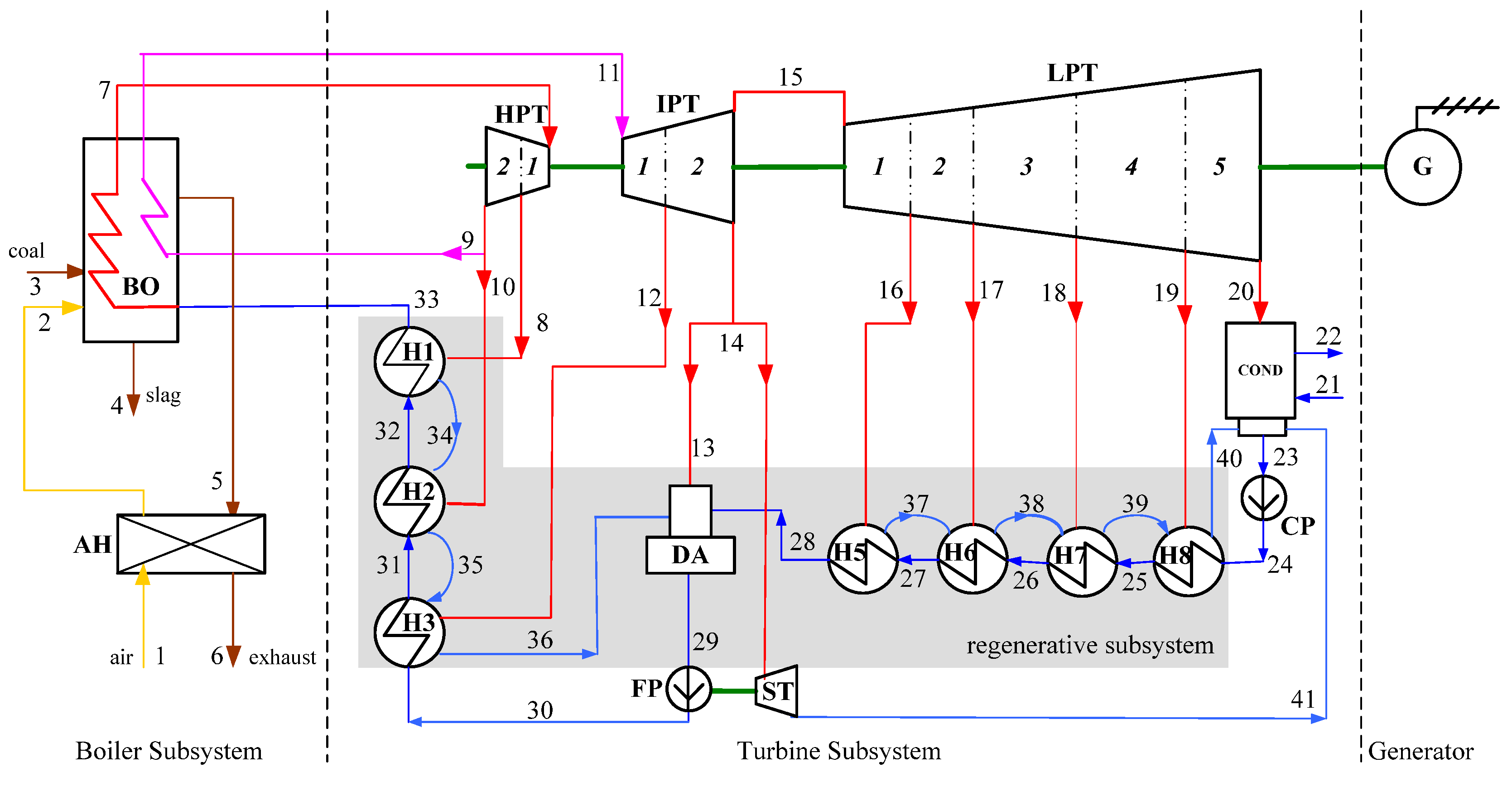
3. Plant Descriptions
| Item | Value | Item | Value | Item | Value | Item | Value |
|---|---|---|---|---|---|---|---|
| Moisture | 2.10% | Carbon | 57.52% | Oxygen | 2.78% | Sulphur | 2.00% |
| Ash | 23.70% | Hydrogen | 3.11% | Nitrogen | 0.99% | LHV | 21981 kJ/kg |
| No | , kg/s | , °C | , bar | , MW | No | , kg/s | , °C | , bar | , MW |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 619.385 | 25.00 | 1.002 | 0.85 | 22 | 29813.6 | 30.79 | 1.000 | 81.39 |
| 2 | 619.385 | 330.41 | 1.000 | 61.40 | 23 | 395.497 | 35.79 | 0.059 | 1.27 |
| 3 | 68.802 | 25.00 | 1.000 | 1603.07 | 24 | 395.497 | 35.94 | 17.24 | 1.96 |
| 4 | 15.980 | 600.00 | 1.000 | 15.97 | 25 | 395.497 | 58.16 | 15.84 | 4.41 |
| 5 | 670.831 | 394.00 | 0.998 | 133.39 | 26 | 395.497 | 85.41 | 14.54 | 10.46 |
| 6 | 670.831 | 127.00 | 0.978 | 48.85 | 27 | 395.497 | 105.06 | 12.94 | 16.63 |
| 7 | 522.217 | 571.00 | 254.0 | 806.90 | 28 | 395.497 | 143.24 | 11.44 | 32.57 |
| 8 | 39.407 | 364.23 | 67.97 | 46.81 | 29 | 522.217 | 180.06 | 10.04 | 69.16 |
| 9 | 438.914 | 304.98 | 43.00 | 474.94 | 30 | 522.217 | 185.59 | 308.7 | 87.76 |
| 10 | 43.896 | 304.98 | 43.00 | 47.50 | 31 | 522.217 | 211.95 | 303.7 | 109.57 |
| 11 | 438.914 | 569.00 | 41.10 | 632.49 | 32 | 522.217 | 253.27 | 298.4 | 149.16 |
| 12 | 19.400 | 459.68 | 20.58 | 23.45 | 33 | 522.217 | 284.05 | 293.5 | 183.29 |
| 13 | 24.018 | 362.68 | 10.44 | 24.20 | 34 | 39.407 | 258.82 | 64.97 | 11.05 |
| 14 | 28.702 | 362.68 | 10.44 | 28.92 | 35 | 83.303 | 217.50 | 41.00 | 16.41 |
| 15 | 366.794 | 362.68 | 10.44 | 369.52 | 36 | 102.702 | 191.14 | 19.08 | 15.45 |
| 16 | 25.599 | 253.53 | 4.374 | 20.12 | 37 | 25.599 | 110.61 | 4.174 | 1.19 |
| 17 | 12.993 | 128.72 | 1.333 | 7.01 | 38 | 38.592 | 90.96 | 1.333 | 1.13 |
| 18 | 17.286 | 88.19 | 0.655 | 7.27 | 39 | 55.878 | 63.71 | 0.655 | 0.68 |
| 19 | 13.574 | 60.94 | 0.208 | 3.41 | 40 | 69.452 | 41.49 | 0.208 | 0.30 |
| 20 | 297.343 | 35.79 | 0.059 | 23.80 | 41 | 28.702 | 39.68 | 0.073 | 3.20 |
| 21 | 29813.6 | 25.00 | 1.000 | 74.47 |
4. Simulations for the Advanced Exergy Analysis
4.1. Theoretical Conditions
5. Results and Discussion
| Comp. | , MW | , MW | , % | , % | Comp. | ,MW | , MW | , % | , % |
|---|---|---|---|---|---|---|---|---|---|
| HPT1 | 186.55 | 175.69 | 0.72 | 94.2 | H7 | 7.72 | 6.05 | 0.11 | 78.4 |
| HPT2 | 51.10 | 47.63 | 0.23 | 93.2 | H6 | 7.07 | 6.17 | 0.06 | 87.2 |
| IPT1 | 101.99 | 98.2 | 0.25 | 96.3 | H5 | 18.93 | 15.93 | 0.20 | 84.2 |
| IPT2 | 84.41 | 81.36 | 0.20 | 96.4 | DA | 22.86 | 19.81 | 0.20 | 86.7 |
| LPT1 | 81.28 | 78.22 | 0.20 | 96.2 | FP | 20.80 | 18.6 | 0.15 | 89.4 |
| LPT2 | 83.93 | 81.56 | 0.16 | 97.2 | H3 | 24.41 | 21.81 | 0.17 | 89.4 |
| LPT3 | 39.13 | 36.5 | 0.17 | 93.3 | H2 | 42.14 | 39.6 | 0.17 | 94.0 |
| LPT4 | 52.63 | 39.89 | 0.85 | 75.8 | H1 | 35.76 | 34.13 | 0.11 | 95.4 |
| LPT5 | 50.94 | 41.95 | 0.60 | 82.4 | ST | 25.72 | 20.8 | 0.33 | 80.9 |
| COND | 26.03 | - | 1.27 | - | GT | 681.00 | 671.21 | 0.65 | 98.6 |
| CP | 0.86 | 0.69 | 0.01 | 80.5 | BO | 1483.04 | 781.16 | 46.57 | 52.7 |
| H8 | 3.79 | 2.46 | 0.09 | 64.8 | AH | 84.54 | 60.55 | 1.59 | 71.6 |
| Comp. | ||||||||
|---|---|---|---|---|---|---|---|---|
| HPT1 | 9.90 | 0.96 | 7.25 | 3.61 | 6.67 | 3.23 | 0.38 | 0.58 |
| HPT2 | 3.05 | 0.42 | 2.16 | 1.31 | 1.87 | 1.18 | 0.13 | 0.29 |
| IPT1 | 3.64 | 0.16 | 2.59 | 1.21 | 2.47 | 1.17 | 0.04 | 0.12 |
| IPT2 | 2.69 | 0.37 | 2.04 | 1.01 | 1.77 | 0.92 | 0.09 | 0.28 |
| LPT1 | 2.78 | 0.28 | 2.38 | 0.68 | 2.10 | 0.68 | 0.00 | 0.28 |
| LPT2 | 2.13 | 0.24 | 1.92 | 0.46 | 1.65 | 0.48 | −0.02 | 0.26 |
| LPT3 | 2.31 | 0.31 | 1.92 | 0.70 | 1.72 | 0.59 | 0.11 | 0.20 |
| LPT4 | 11.46 | 1.29 | 6.28 | 6.46 | 5.72 | 5.74 | 0.72 | 0.56 |
| LPT5 | 7.84 | 1.15 | 7.15 | 1.84 | 6.23 | 1.61 | 0.23 | 0.92 |
| COND | 15.30 | 3.81 | - | - | - | - | - | - |
| CP | 0.15 | 0.02 | 0.12 | 0.05 | 0.10 | 0.04 | 0.01 | 0.01 |
| H8 | 1.18 | 0.16 | 1.12 | 0.21 | 0.99 | 0.19 | 0.03 | 0.13 |
| H7 | 1.21 | 0.46 | 1.41 | 0.26 | 1.15 | 0.06 | 0.20 | 0.26 |
| H6 | 0.61 | 0.29 | 0.71 | 0.19 | 0.54 | 0.07 | 0.12 | 0.17 |
| H5 | 2.17 | 0.83 | 2.47 | 0.53 | 2.02 | 0.15 | 0.38 | 0.45 |
| DA | 2.03 | 1.02 | 2.89 | 0.16 | 2.12 | −0.09 | 0.25 | 0.78 |
| FP | 1.70 | 0.50 | 1.72 | 0.49 | 1.34 | 0.37 | 0.12 | 0.38 |
| H3 | 2.28 | 0.32 | 2.16 | 0.44 | 1.96 | 0.33 | 0.11 | 0.20 |
| H2 | 1.58 | 0.96 | 1.99 | 0.55 | 1.45 | 0.13 | 0.42 | 0.54 |
| H1 | 1.15 | 0.49 | 1.25 | 0.38 | 1.00 | 0.15 | 0.24 | 0.25 |
| ST | 3.20 | 1.72 | 3.50 | 1.42 | 2.31 | 0.89 | 0.53 | 1.19 |
| GT | 9.79 | 0.00 | 1.35 | 8.45 | 1.35 | 8.45 | 0.00 | 0.00 |
| BO | 615.20 | 86.68 | 676.29 | 25.60 | 608.98 | 6.23 | 19.37 | 67.31 |
| AH | 16.91 | 7.09 | 11.46 | 12.53 | 11.56 | 5.34 | 7.19 | −0.10 |
5.1. Conventional Analysis
5.2. Advanced Analysis
5.2.1. Interactions among Components
5.2.2. Endogenous/Exogenous Exergy Destruction
| k | r | HPT1 | HPT2 | IPT1 | IPT2 | LPT1 | LPT2 | LPT3 | LPT4 | LPT5 | COND | CP | H8 | H7 | H6 | H5 | DA | FP | H3 | H2 | H1 | ST | GE | BO | AH |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HPT1 | 9.90 | 0.08 | 0.06 | 0.04 | 0.04 | 0.03 | 0.04 | 0.18 | 0.12 | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 | 0.01 | 0.00 | 0.03 | 0.04 | 0.03 | −0.09 | 0.06 | 0.15 | 0.05 | 0.00 | |
| HPT2 | 0.14 | 3.05 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.05 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.02 | −0.03 | 0.00 | 0.02 | 0.04 | 0.02 | 0.00 | |
| IPT1 | 0.10 | 0.03 | 3.64 | 0.02 | 0.02 | 0.01 | 0.01 | 0.07 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | −0.05 | −0.01 | 0.01 | 0.02 | 0.05 | −0.21 | 0.00 | |
| IPT2 | 0.08 | 0.02 | 0.02 | 2.69 | 0.01 | 0.01 | 0.01 | 0.05 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 | 0.01 | 0.00 | 0.00 | 0.01 | 0.01 | 0.04 | 0.02 | 0.00 | |
| LPT1 | 0.08 | 0.02 | 0.03 | 0.02 | 2.78 | 0.01 | 0.01 | 0.05 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.03 | 0.00 | −0.01 | 0.00 | 0.00 | 0.01 | −0.02 | 0.04 | 0.01 | 0.00 | |
| LPT2 | 0.06 | 0.02 | 0.03 | 0.02 | 0.02 | 2.13 | 0.01 | 0.04 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 | 0.00 | 0.00 | −0.01 | 0.00 | 0.00 | 0.01 | −0.02 | 0.03 | 0.01 | 0.00 | |
| LPT3 | 0.07 | 0.02 | 0.03 | 0.02 | 0.02 | 0.02 | 2.31 | 0.04 | 0.03 | 0.00 | 0.00 | 0.00 | −0.01 | 0.00 | 0.01 | 0.00 | −0.01 | 0.00 | 0.00 | 0.01 | −0.02 | 0.03 | 0.01 | 0.00 | |
| LPT4 | 0.33 | 0.10 | 0.15 | 0.11 | 0.11 | 0.08 | 0.09 | 11.46 | 0.14 | 0.00 | 0.00 | −0.06 | −0.01 | 0.01 | 0.03 | 0.01 | −0.06 | 0.02 | 0.01 | 0.04 | −0.10 | 0.17 | 0.06 | 0.00 | |
| LPT5 | 0.23 | 0.07 | 0.10 | 0.08 | 0.07 | 0.06 | 0.06 | 0.31 | 7.84 | 0.00 | 0.00 | −0.01 | 0.01 | 0.01 | 0.02 | 0.00 | −0.04 | 0.01 | 0.00 | 0.03 | −0.07 | 0.11 | 0.04 | 0.00 | |
| COND | 0.43 | 0.13 | 0.18 | 0.13 | 0.14 | 0.10 | 0.11 | 0.57 | 0.39 | 15.30 | 0.00 | 0.03 | 0.01 | 0.02 | 0.03 | 0.01 | 0.16 | 0.03 | 0.01 | 0.03 | 0.30 | 0.22 | 0.24 | 0.00 | |
| CP | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| H8 | 0.03 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | 0.00 | −0.01 | 1.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.01 | 0.02 | 0.01 | 0.00 | |
| H7 | 0.04 | 0.01 | 0.01 | 0.01 | 0.01 | 0.00 | 0.01 | 0.02 | 0.02 | 0.00 | 0.00 | 0.25 | 1.21 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.01 | 0.02 | 0.01 | 0.00 | |
| H6 | 0.02 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.17 | 0.61 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | |
| H5 | 0.06 | 0.02 | 0.05 | 0.04 | 0.04 | 0.00 | 0.01 | 0.04 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.30 | 2.17 | 0.00 | 0.01 | 0.00 | 0.00 | 0.01 | 0.01 | 0.03 | 0.04 | 0.00 | |
| DA | 0.06 | 0.02 | 0.04 | 0.03 | −0.01 | 0.01 | 0.01 | 0.04 | 0.02 | 0.00 | 0.00 | −0.04 | −0.03 | −0.06 | 0.62 | 2.03 | 0.00 | −0.02 | 0.00 | 0.00 | 0.01 | 0.03 | 0.04 | 0.00 | |
| FP | 0.05 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.03 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 1.70 | 0.01 | 0.00 | −0.01 | 0.01 | 0.02 | 0.27 | 0.00 | |
| H3 | 0.06 | 0.02 | 0.08 | 0.01 | 0.01 | 0.01 | 0.01 | 0.04 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.18 | −0.12 | 2.28 | −0.05 | −0.01 | 0.01 | 0.03 | 0.00 | 0.00 | |
| H2 | 0.09 | 0.03 | −0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.03 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.03 | 0.02 | 0.61 | 1.58 | −0.03 | 0.01 | 0.02 | −0.01 | 0.00 | |
| H1 | 0.07 | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | 0.00 | 0.02 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.02 | 0.22 | 1.15 | 0.01 | 0.02 | 0.00 | 0.00 | |
| ST | 0.09 | 0.03 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.06 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.63 | 0.01 | 0.01 | -0.03 | 3.20 | 0.05 | 0.50 | 0.00 | |
| GE | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.79 | 0.00 | 0.00 | |
| BO | 7.00 | 2.11 | 3.39 | 2.63 | 2.66 | 2.03 | 2.21 | 10.93 | 7.48 | 0.00 | −0.01 | 0.33 | 0.23 | 0.30 | 0.64 | 0.12 | 1.84 | 0.32 | −0.04 | 1.37 | 3.67 | 8.98 | 615.20 | 19.25 | |
| AH | 0.26 | 0.07 | 0.10 | 0.07 | 0.07 | 0.06 | 0.06 | 0.30 | 0.21 | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.02 | 0.00 | 0.04 | 0.01 | 0.03 | −0.20 | 0.09 | 0.25 | 4.74 | 16.91 | |
5.2.4. Combined Analysis
5.3. Improvement Strategy
6. Conclusions
- The ratio of exogenous exergy destruction differs quite a lot from component to component. In general, inherent irreversibilities in turbines contribute more or less 90% to their total exergy destruction, while this proportion drops down to 70% when it comes to feedwater preheaters. The boiler subsystem also has a large amount of exergy destruction caused by the inefficiencies in other components.
- The boiler subsystem still has the largest avoidable exergy destruction; however, the enhancement efforts should be made not only to its inherent irreversibilities but also to inefficiencies of the remaining components. Moreover, around 60% of the avoidable exergy destruction of feedwater preheaters is exogenous. For the remaining components efforts should mainly focus on improving the components themselves.
- Due to the interactions among components, the improvement priorities refer not only to the components that should be modified, but also to the sequence for optimization. We believe that the improvement of the boiler subsystem will be more meaningful if the remaining important components are improved first and can provide persuading good performances.
Acknowledgments
References
- Energy Information Administration (EIA). International Energy Annual Website. Available online: http://www.eia.doe.gov/iea (accessed on 10 September 2011).
- Som, S.K.; Datta, A. Thermodynamic irreversibilities and exergy balance in combustion processes. Prog. Energy Combut. Sci. 2008, 34, 351–376. [Google Scholar] [CrossRef]
- Tsatsaronis, G.; Cziesla, F. Thermoeconomics. In Encyclopedia of Physical Science and Technology; Meyers, R.A., Ed.; Academic Press: New York, NY, USA, 2001; pp. 659–680. [Google Scholar]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Rosen, M.A. Energy and exergy-based comparison of coal-fired and nuclear steam power plants. Exergy Int. J. 2001, 1, 180–192. [Google Scholar] [CrossRef]
- Sengupta, S.; Datta, A.; Duttagupta, S. Exergy analysis of a coal-based 210 MW thermal power plant. Int. J. Energy Res. 2007, 31, 14–28. [Google Scholar] [CrossRef]
- Aljundi, I.H. Energy and exergy analysis of a steam power plant in Jordan. Appl. Therm. Eng. 2009, 29, 324–328. [Google Scholar] [CrossRef]
- Ameri, M.; Ahmadi, P.; Hamidi, A. Energy, exergy and exergoeconomic analysis of a steam power plant: A case study. Int. J. Energy Res. 2009, 33, 499–512. [Google Scholar] [CrossRef]
- Regulagadda, P.; Dincer, I.; Naterer, G.F. Exergy analysis of a thermal power plant with measured boiler and turbine losses. Appl. Therm. Eng. 2010, 30, 970–976. [Google Scholar] [CrossRef]
- Tsatsaronis, G.; Morosuk, T. A General Exergy-Based Method for Combining a Cost Analysis with an Environmental Impact Analysis, Part I—Theoretical Development. In Proceedings of ASME 2008 International Mechanical Engineering Congress and Exposition (IMECE 2008), Boston, MA, USA, 2–6 November 2008.
- Tsatsaronis, G.; Morosuk, T. A General Exergy-Based Method for Combining a Cost Analysis with an Environmental Impact Analysis, Part II—Application to a Cogeneration System. In Proceedings of ASME 2008 International Mechanical Engineering Congress and Exposition (IMECE 2008), Boston, MA, USA, 2–6 November 2008.
- Kelly, S. Energy System Improvements Based on Endogenous and Exogenous Exergy Destruction. Ph.D. Thesis, Technische Universitat Berlin, Berlin, Germany, 2008. [Google Scholar]
- Morosuk, T.; Tsatsaronis, G. Advanced exergy analysis for chemically reacting systems—Application to a simple open gas-turbine system. Int. J. Thermodyn. 2009, 12, 105–111. [Google Scholar]
- Kelly, S.; Tsatsaronis, G.; Morosuk, T. Advanced exergetic analysis: Approaches for splitting the exergy destruction into endogenous and exogenous parts. Energy 2009, 34, 384–391. [Google Scholar] [CrossRef]
- Morosuk, T.; Tsatsaronis, G. Advanced exergetic evaluation of refrigeration machines using different working fluids. Energy 2009, 34, 2248–2258. [Google Scholar] [CrossRef]
- Petrakopoulou, F.; Tsatsaronis, G.; Morosuk, T. Conventional and Advanced Exergetic Analysis Applied to a Combined Cycle Power Plant. In Proceedings of 2010 International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS 2010), Lausanne, Switzerland, 14–17 June 2010.
- Tsatsaronis, G.; Morosuk, T. Advanced exergetic analysis of a novel system for generating electricity and vaporizing liquefied natural gas. Energy 2010, 35, 820–829. [Google Scholar] [CrossRef]
- Petrakopoulou, F.; Tsatsaronis, G.; Morosuk, T.; Carassai, A. Advanced Exergoeconomic Analysis: Applied to a Complex Energy Conversion System. In Proceedings of ASME 2010 International Mechanical Engineering Congress and Exposition (IMECE 2010), Vancouver, Canada, 12–18 November 2010.
- Tsatsaronis, G. Design Optimization Using Exergoeconomic. In Thermodynamic Optimization of Complex Energy Systems; Bejan, A., Mamut, E., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 101–117. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, L.; Yang, Y.; Morosuk, T.; Tsatsaronis, G. Advanced Thermodynamic Analysis and Evaluation of a Supercritical Power Plant. Energies 2012, 5, 1850-1863. https://doi.org/10.3390/en5061850
Wang L, Yang Y, Morosuk T, Tsatsaronis G. Advanced Thermodynamic Analysis and Evaluation of a Supercritical Power Plant. Energies. 2012; 5(6):1850-1863. https://doi.org/10.3390/en5061850
Chicago/Turabian StyleWang, Ligang, Yongping Yang, Tatiana Morosuk, and George Tsatsaronis. 2012. "Advanced Thermodynamic Analysis and Evaluation of a Supercritical Power Plant" Energies 5, no. 6: 1850-1863. https://doi.org/10.3390/en5061850
APA StyleWang, L., Yang, Y., Morosuk, T., & Tsatsaronis, G. (2012). Advanced Thermodynamic Analysis and Evaluation of a Supercritical Power Plant. Energies, 5(6), 1850-1863. https://doi.org/10.3390/en5061850






