Online Estimation of Peak Power Capability of Li-Ion Batteries in Electric Vehicles by a Hardware-in-Loop Approach
Abstract
:1. Introduction
2. Online Parameters Identification Method
2.1. The EP Model
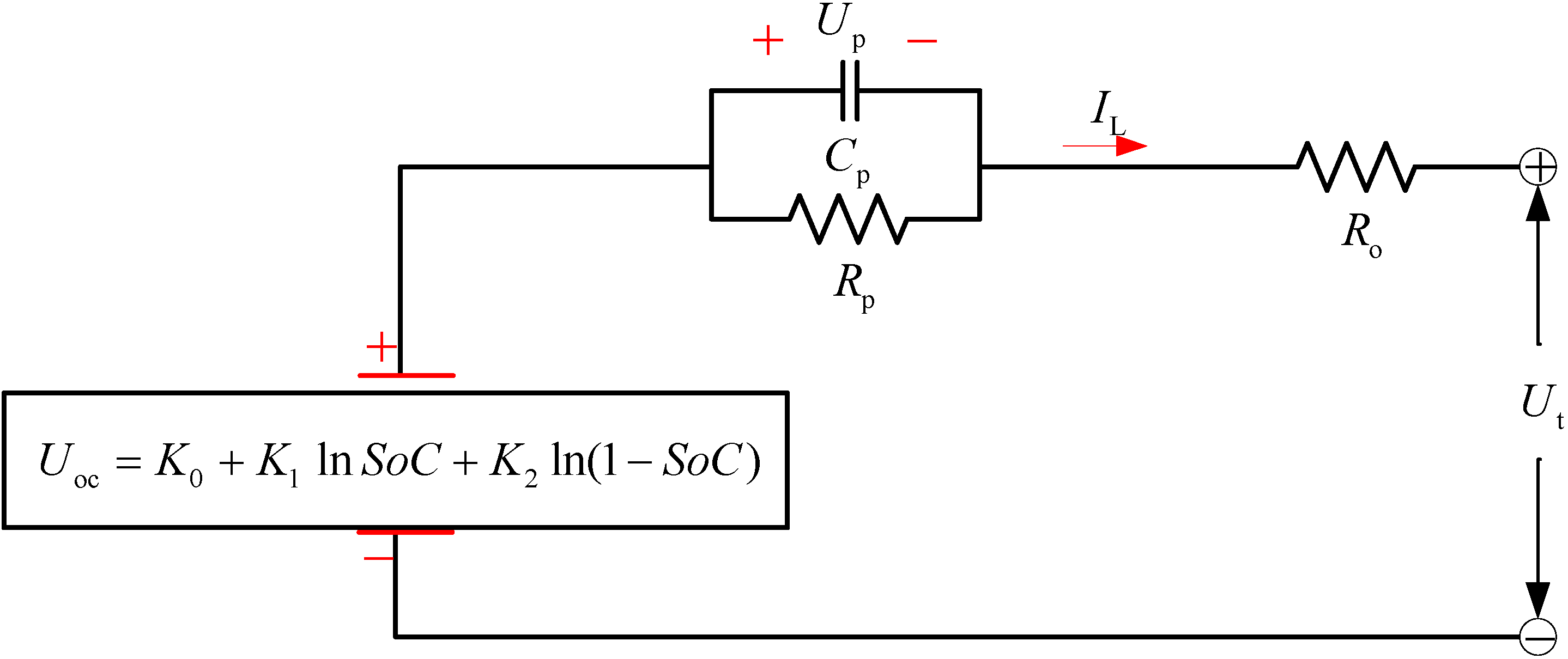
2.2. The Recursive Least Square Method with an Optimal Forgetting Factor
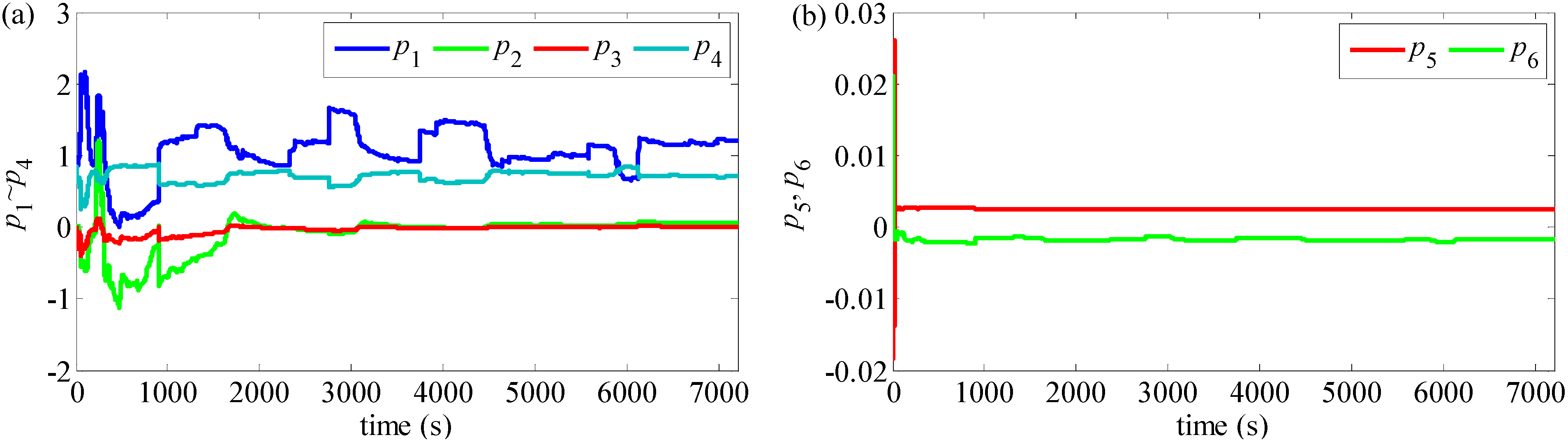
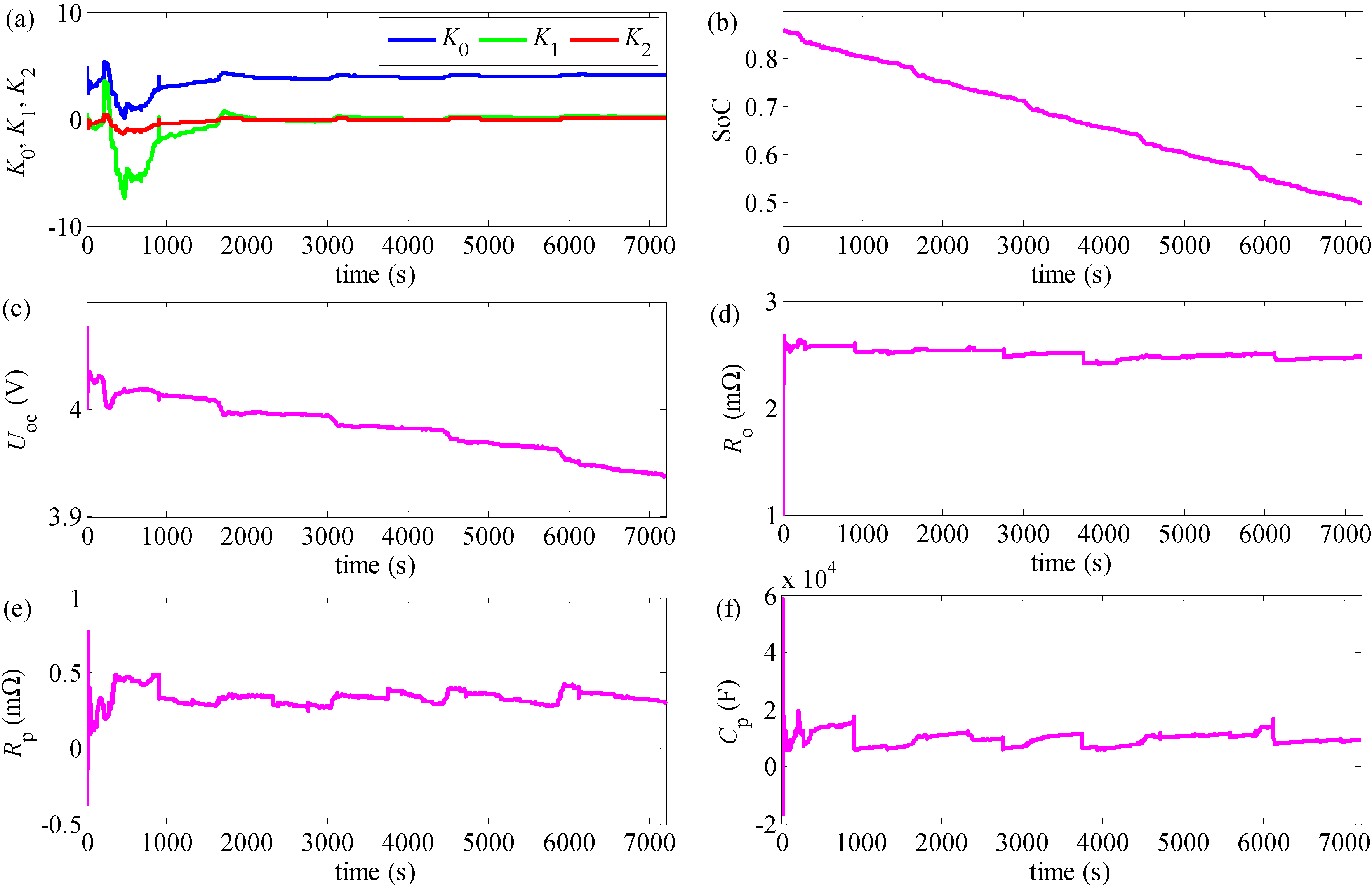
2.3. The Online Parameters Identification Method for the EP Model
3. Battery Online Peak Power Capability Estimation Method
3.1. Online Peak Power Capability Estimation Method
3.1.1. The HPPC Method
3.1.2. The SoC-Limited Method
3.1.3. The EP Dynamic Model-Based Method
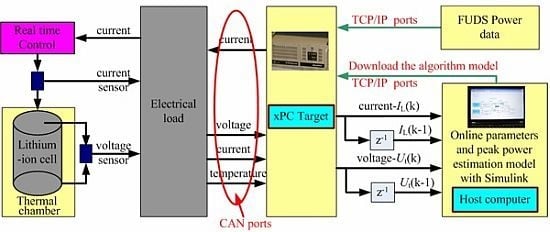
3.2. The Hardware-in-Loop Test Bench Design
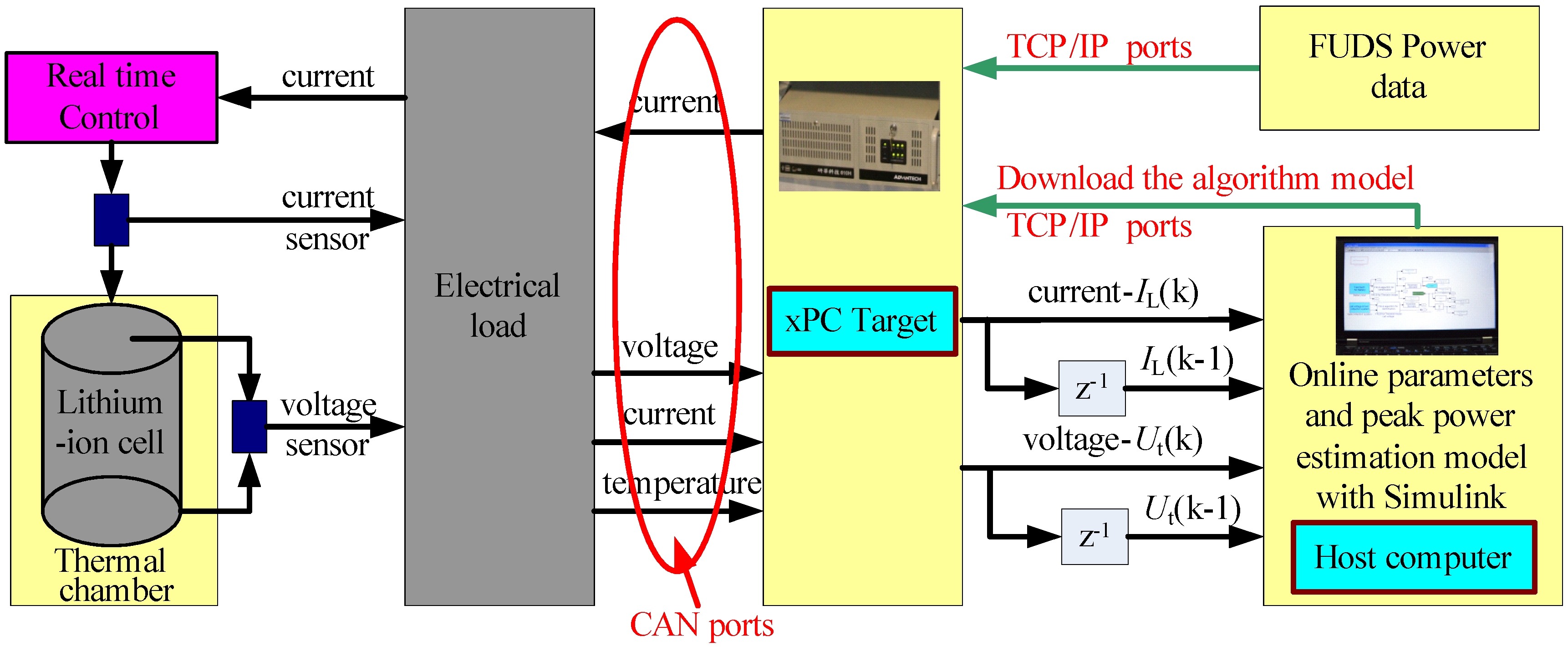
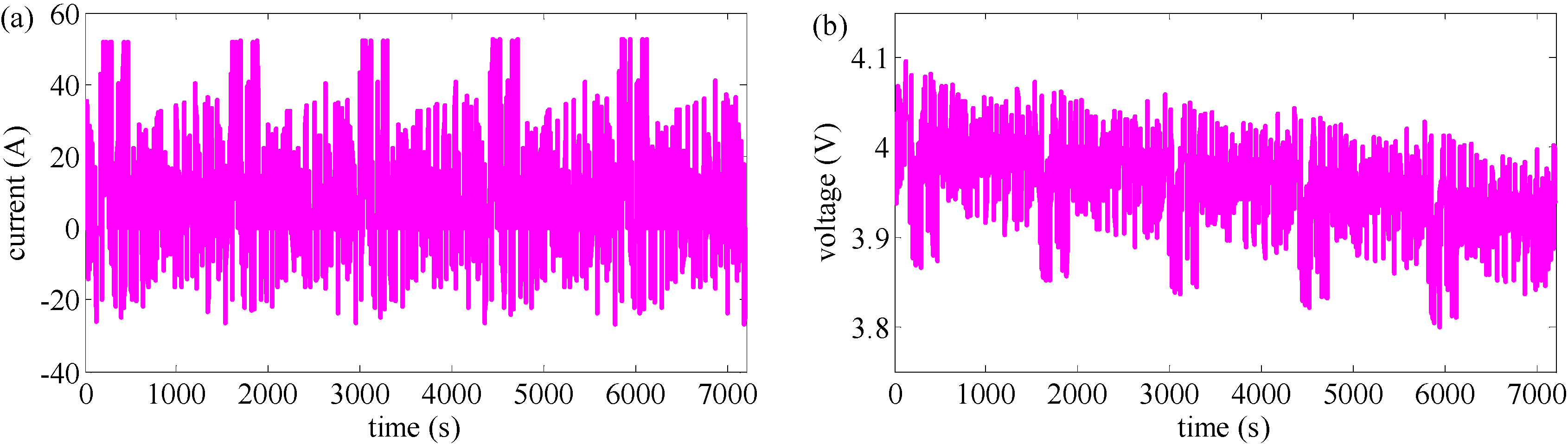
4. Results and Discussion
| Parameters | Value |
|---|---|
| Maximum load current /A | 350 |
| Minimum load current /A | 175 |
| Maximum terminal voltage /V | 4.2 |
| Minimum terminal voltage /V | 3.0 |
| Peak discharge power /W | 1500 |
| Peak charge power /W | −700 |
| SoC operation range for HEVs | 0.35–0.85 |
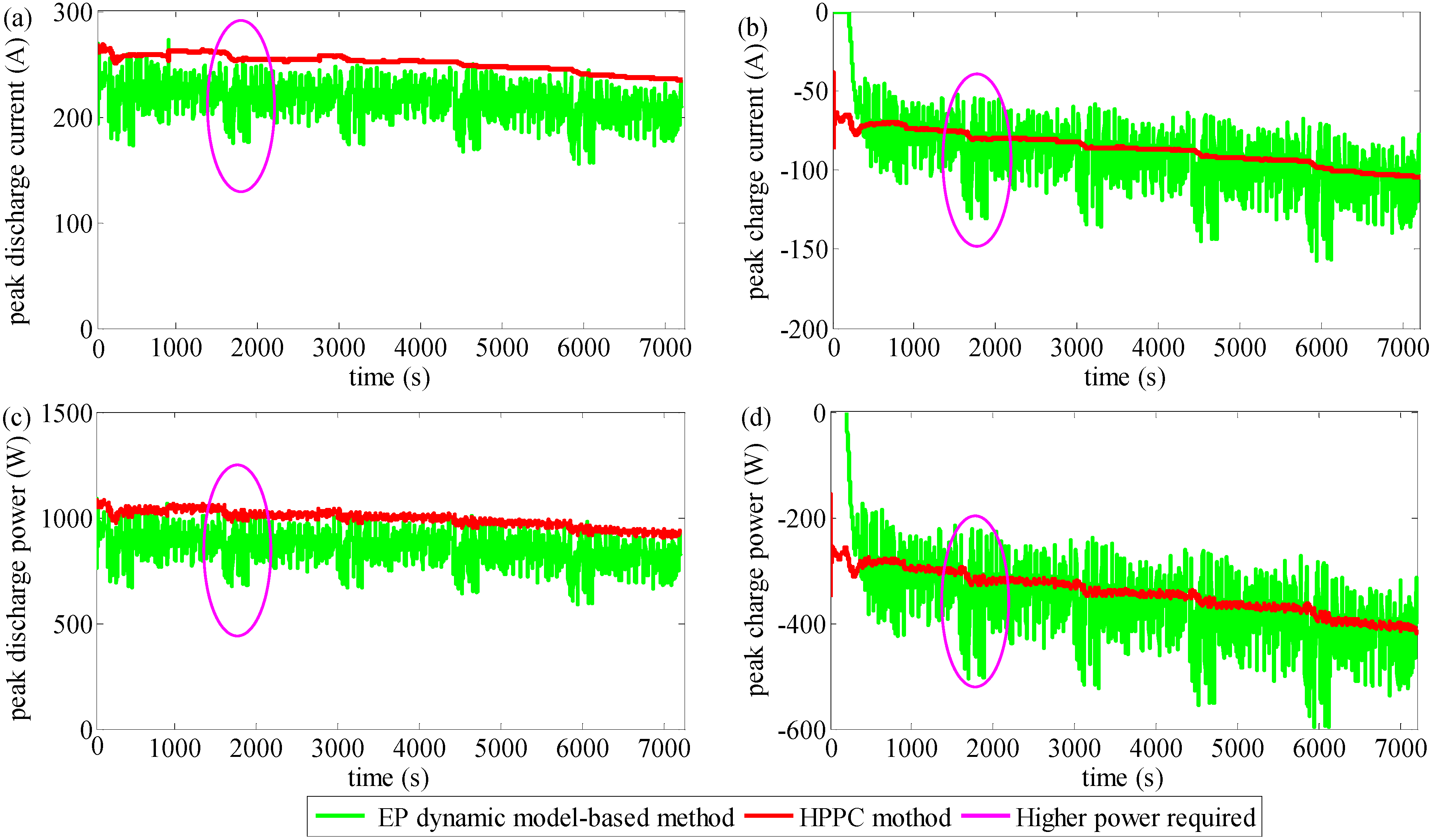
5. Conclusions
- (1)
- In order to avoid time-consuming, laborious and error-prone experiments for determining the tabulated OCV-SoC data, the EP model, which uses the Nernst model to define the open circuit voltage, is applied to model the lithium-ion battery.
- (2)
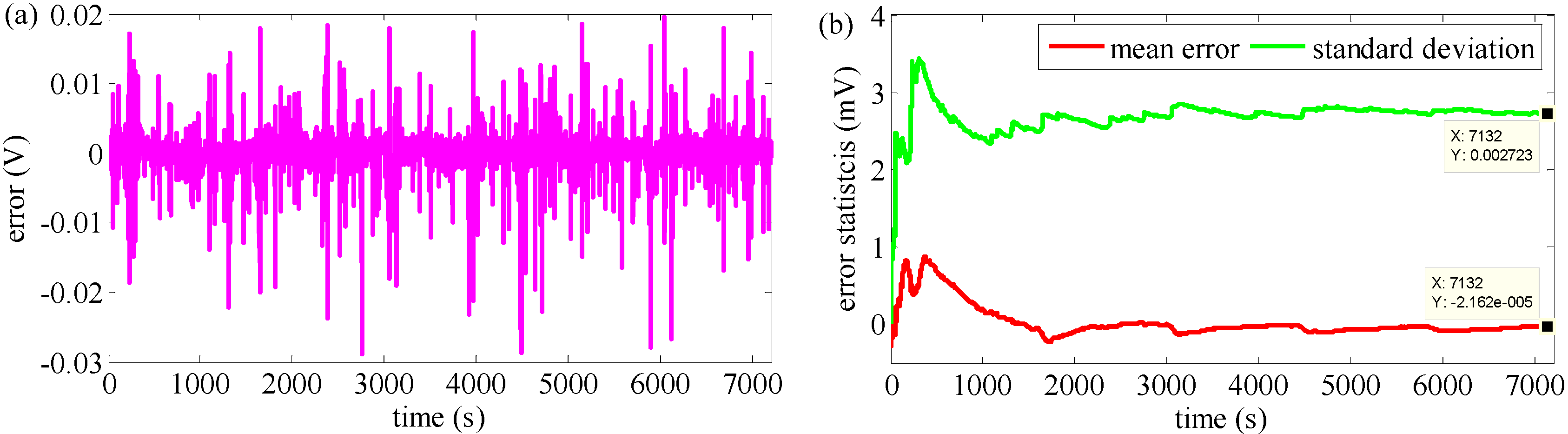
- For improving the dynamic performance of the EP model, the RLSF algorithm is applied to identify online the EP model’s parameters; the model’s accuracy is verified by the hardware-in-loop test, and the maximum error of the estimated terminal voltage is within 1% of its nominal voltage.
- (3)
- Compared with the HPPC method, the proposed peak power capability estimation method takes the cell voltage, current, SoC and power as its constraints; which can simulate the relaxation effect well. The evaluation results based on the HIL test show that the proposed method gives a more reliable estimation, especially when the load current changes suddenly or strongly. More importantly, when the SoC is high and low, the proposed method can give a more accurate estimate; avoiding overcharging or overdischarging.
- (4)
- The HIL test data has provided critical guidance for further development and improvement of the peak power capability estimation approach. This accelerates the overall system development process and reduces the cost of the EVs development.
Acknowledgments
References
- Su, M.; Liang, C.; Chen, B.; Chen, S.; Yang, Z. Low-carbon development patterns: Observations of typical Chinese cities. Energies 2012, 5, 2913–2904. [Google Scholar] [CrossRef]
- He, H.W.; Xiong, R.; Chang, Y.H. Dynamic modeling and simulation on hybrid power system for electric vehicle application. Energies 2010, 3, 1821–1830. [Google Scholar] [CrossRef]
- He, H.W.; Yan, S.; Xiao, Z. Integrated control method for a fuel cell hybrid system. Asia-Pac. J. Chem. Eng. 2009, 4, 68–72. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 5825–5898. [Google Scholar]
- Kim, J.; Lee, S.; Cho, B.H. Discrimination of Li-ion batteries based on hamming network using discharging–charging voltage pattern recognition for improved state-of-charge estimation. J. Power Sources 2011, 196, 2227–2240. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H.; Li, W.; Aussems, J. Model-based dynamic multi-parameter method for peak power estimation of lithium-ion batteries. Appl. Energy 2012, 96, 3773–3785. [Google Scholar] [CrossRef]
- Idaho National Engineering & Environmental Laboratory. Battery Test Manual for Plug-In Hybrid Electric Vehicles; Assistant Secretary for Energy Efficiency and Renewable Energy (EE) Idaho Operations Office: Idaho Falls, ID, USA, 2010. [Google Scholar]
- Zhang, C.; Zhang, C.; Sharkh, S. Estimation of real-time peak power capability of a traction battery pack used in an HEV. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference (APPEEC), Chengdu, China; 2010; pp. 1–6. [Google Scholar]
- Gregory, L. High-performance battery-pack power estimation using a dynamic cell model. IEEE Trans. Veh. Tech. 2004, 53, 15861–15893. [Google Scholar]
- Low, K.; Wang, H.; Wang, M. On the development of a real time control system by using xPC target: Solution to robotic system control. In Proceedings of the 2005 IEEE International Conference on Automation Science and Engineering, Edmonton, Canada, 1–2 August 2005; pp. 3453–3450.
- Shiakolas, P.; Piyabongkarn, D. On the development of a realtime digital control system using xPC target and magnetic levitation device. In Proceedings of the International Conference on Decision and Control, Orlando, FL, USA; 2001; pp. 1384–1353. [Google Scholar]
- He, Y.; Liu, W.; Brain, J. Battery algorithm verification and development using hardware-in-the-loop testing. J. Power Sources 2010, 195, 2969–2974. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Guo, H.; Ding, Y. Modeling for lithium-ion battery used in electric vehicles. Procedia Eng. 2011, 15, 2869–2874. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Sin, K.S. Adaptive Filtering, Prediction and Control; Prentice-Hall: Upper Saddle River, NJ, USA, 1984. [Google Scholar]
- Ho, Y.; Farouq, S.; Yeoh, H. Recursive least squares-based adaptive control of a biodiesel transesterification reactor. Ind. Eng. Chem. Res. 2010, 49, 11434–11442. [Google Scholar] [CrossRef]
- Yi-Hsien, C.; Wu-Yang, S.; Jia-Cheng, K. Online estimation of internal resistance and opencircuit voltage of lithium-ion batteries in electric vehicles. J. Power Sources 2011, 196, 3921–3932. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar] [CrossRef]
- Kruse, R.; Huls, T. Development of the federal urban driving schedule. SAE Tech. Pap. 1973. [Google Scholar] [CrossRef]
- Zhang, C.P.; Jiang, J.C.; Zhang, W.G.; Suleiman, M.S. Estimation of state of charge of lithium-ion batteries used in HEV using robust extended Kalman filtering. Energies 2012, 5, 10981–11115. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xiong, R.; He, H.; Sun, F.; Zhao, K. Online Estimation of Peak Power Capability of Li-Ion Batteries in Electric Vehicles by a Hardware-in-Loop Approach. Energies 2012, 5, 1455-1469. https://doi.org/10.3390/en5051455
Xiong R, He H, Sun F, Zhao K. Online Estimation of Peak Power Capability of Li-Ion Batteries in Electric Vehicles by a Hardware-in-Loop Approach. Energies. 2012; 5(5):1455-1469. https://doi.org/10.3390/en5051455
Chicago/Turabian StyleXiong, Rui, Hongwen He, Fengchun Sun, and Kai Zhao. 2012. "Online Estimation of Peak Power Capability of Li-Ion Batteries in Electric Vehicles by a Hardware-in-Loop Approach" Energies 5, no. 5: 1455-1469. https://doi.org/10.3390/en5051455
APA StyleXiong, R., He, H., Sun, F., & Zhao, K. (2012). Online Estimation of Peak Power Capability of Li-Ion Batteries in Electric Vehicles by a Hardware-in-Loop Approach. Energies, 5(5), 1455-1469. https://doi.org/10.3390/en5051455