Numerical Modelling of Mutual Effect among Nearby Needles in a Multi-Needle Configuration of an Atmospheric Air Dielectric Barrier Discharge
Abstract
:1. Introduction
2. Simulation Model
2.1. Geometry Models in the Simulation
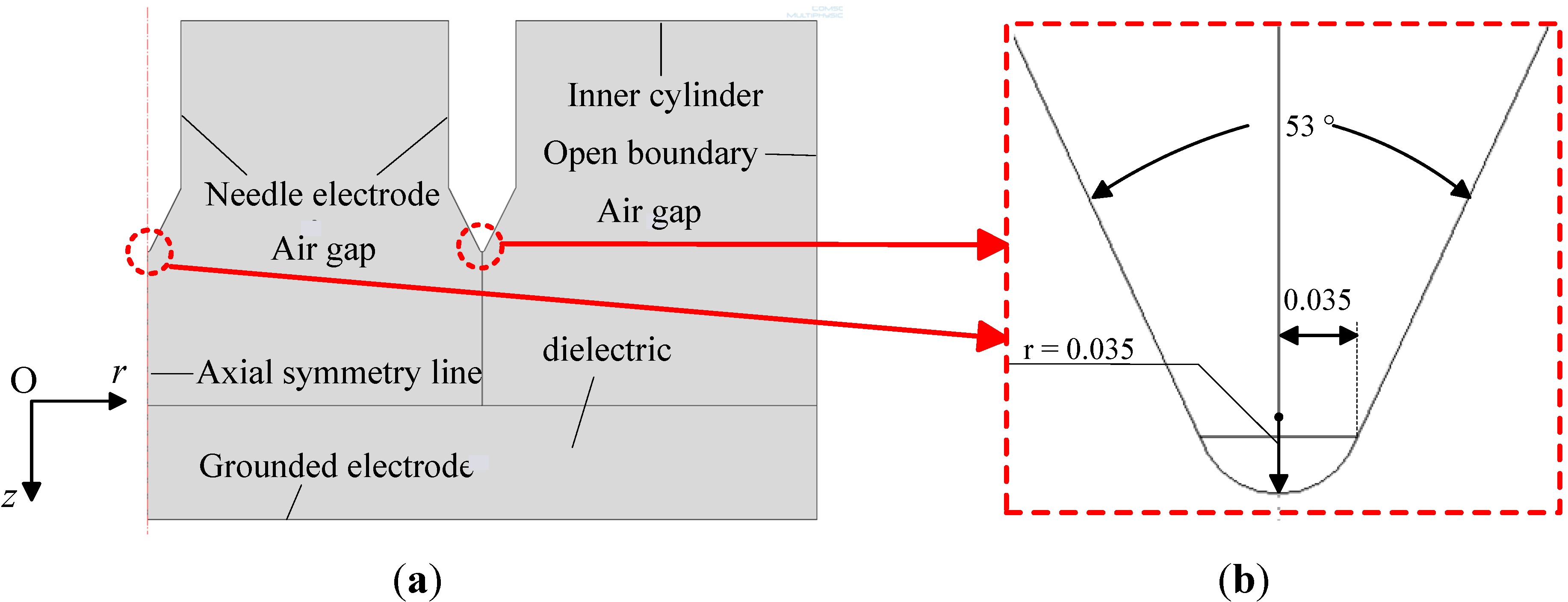
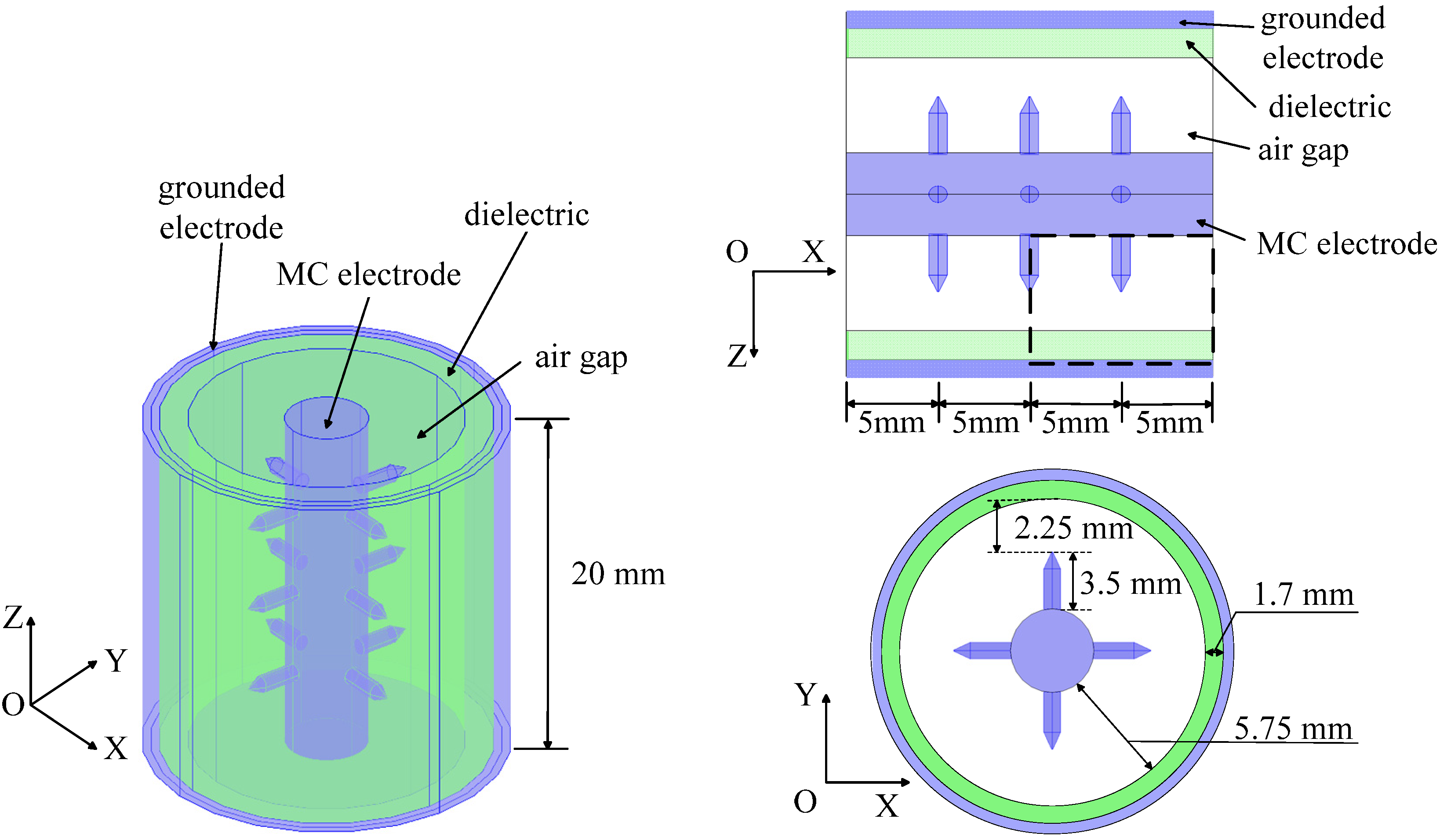
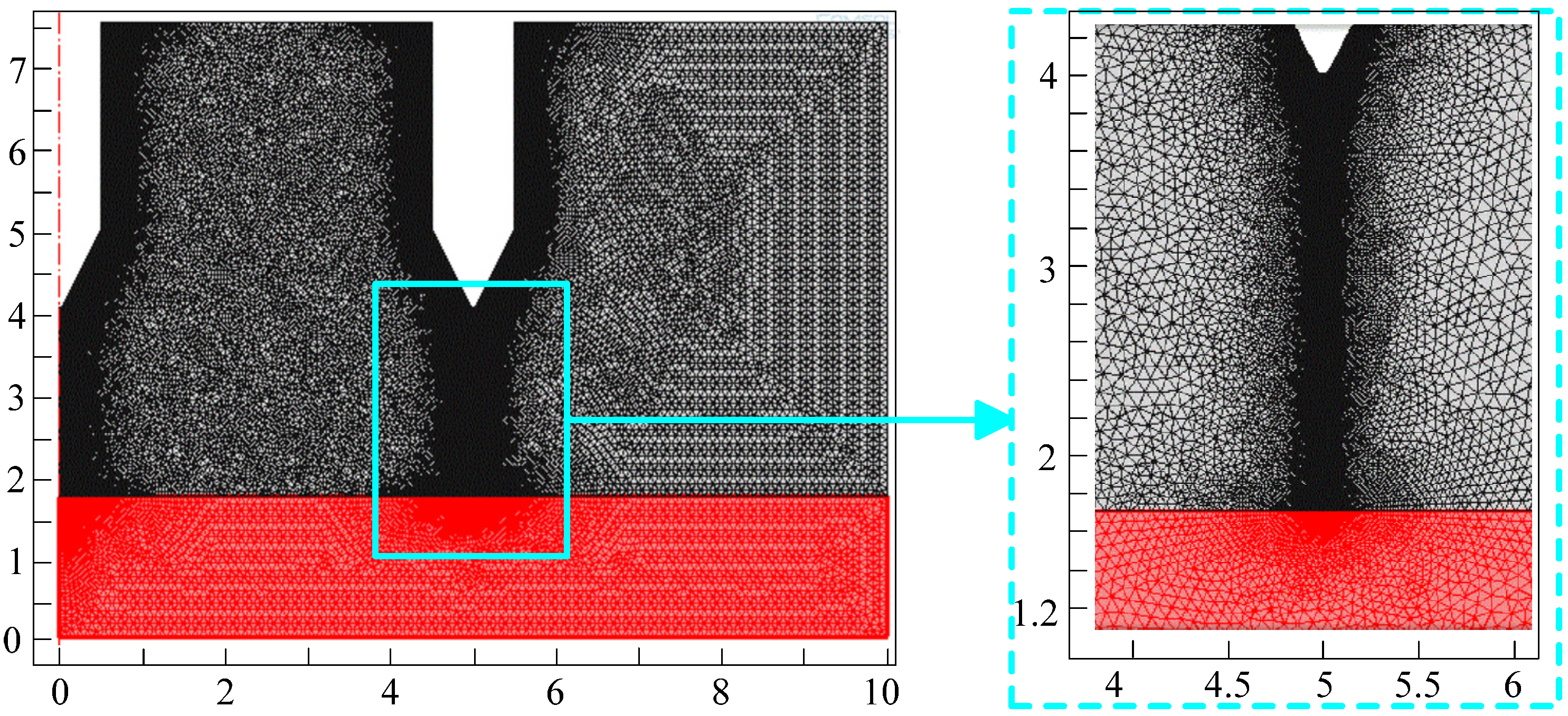
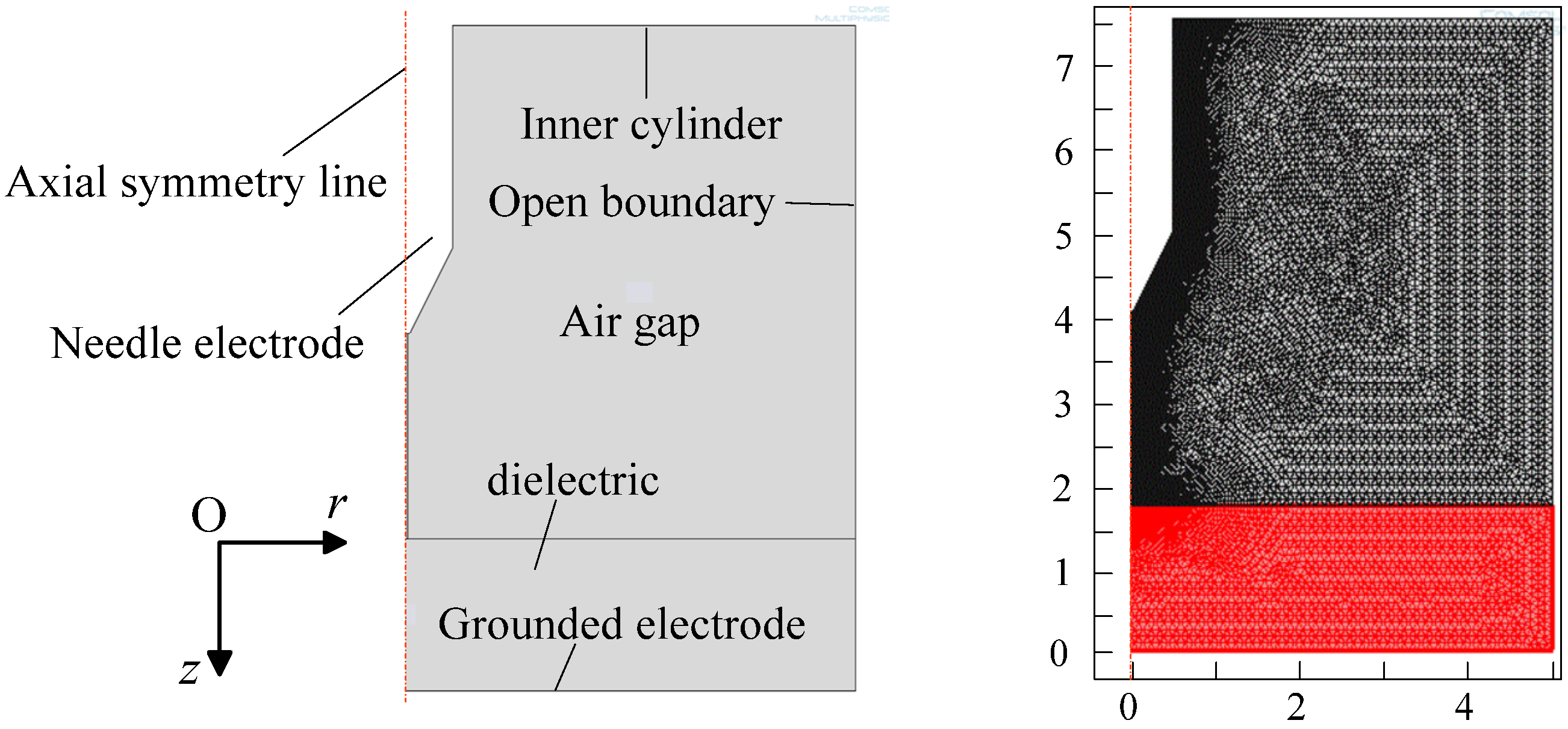
| Mesh parameter | Results |
|---|---|
| Triangular elements | 113,554 |
| Edge elements | 2,755 |
| Minimum element quality | 0.6566 |
| Average element quality | 0.9635 |
| Element area ratio | 4.298 × 10−11 |
| Mesh area | 7.0 × 10−5 m2 |
2.2. Mathematical Model
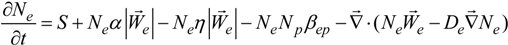
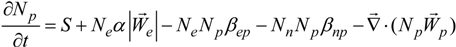
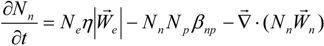
| Properties | Functions |
|---|---|
| α (cm−1) | 3500exp(−1.65 × 105E−1) |
| η (cm−1) | 15exp(−2.5 × 104E−1) |
| βep = βnp / cm3·s−1) | 2 × 10−7 [42] |
| We (cm·s−1) | −6060E0.75 |
| Wp (cm·s−1) | 2.43E |
| Wn (cm·s−1) | −2.7E |
| D (cm2·s−1) | 1800 |
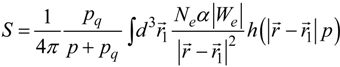
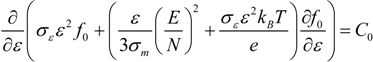
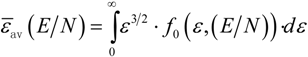
2.3. Boundary and Initial Conditions
| Application mode | Convection and diffusion Ne | Convection and diffusion Np | Convection and diffusion Nn | Electrostatics φ |
|---|---|---|---|---|
| Inner cylinder electrode | Flux | Nn = 0 | U(t) ** | |
| Needle electrode | Nn = 0 | U(t) ** | ||
| Dielectric upper surface | * | |||
| Open boundaries | * | |||
| Ground boundary | Np = 0 | 0 |
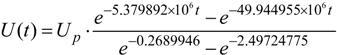
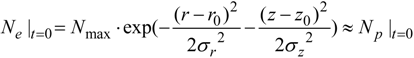
3. Results and Discussion
3.1. Electric Field Distribution and Streamer Propagation Velocity
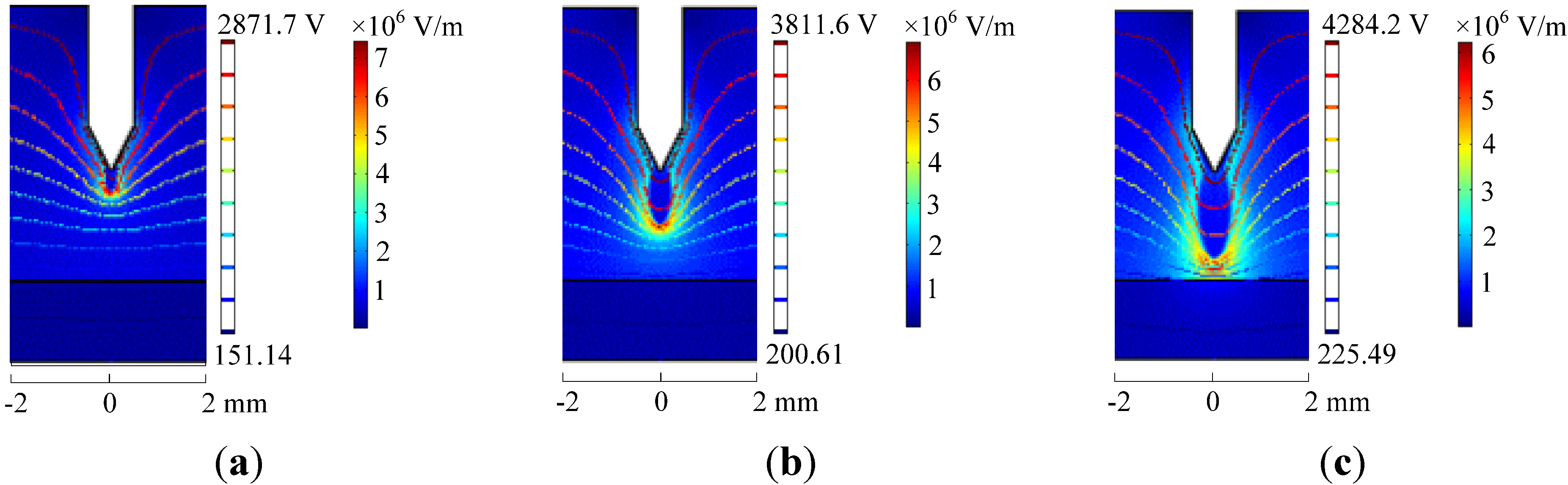
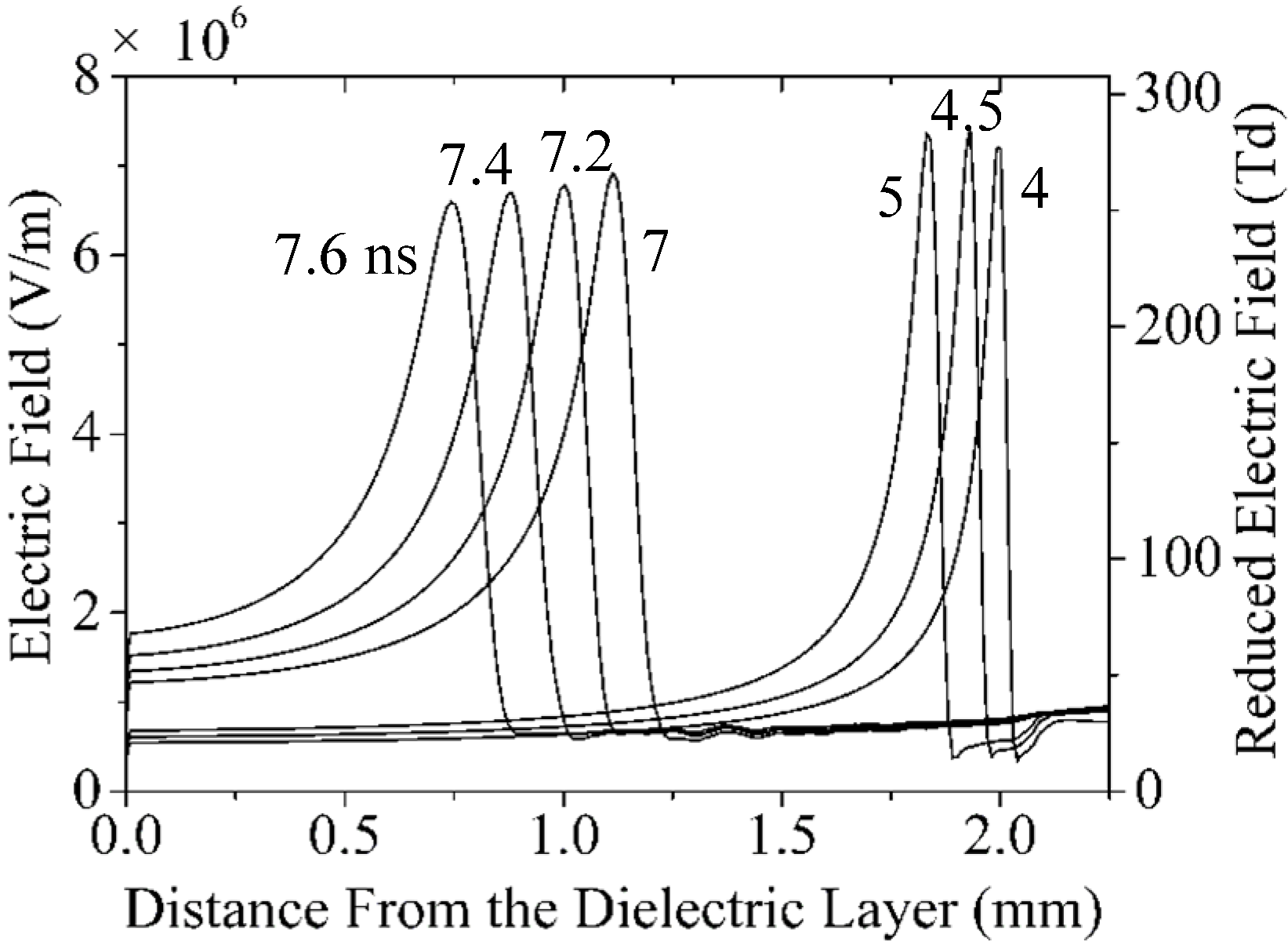
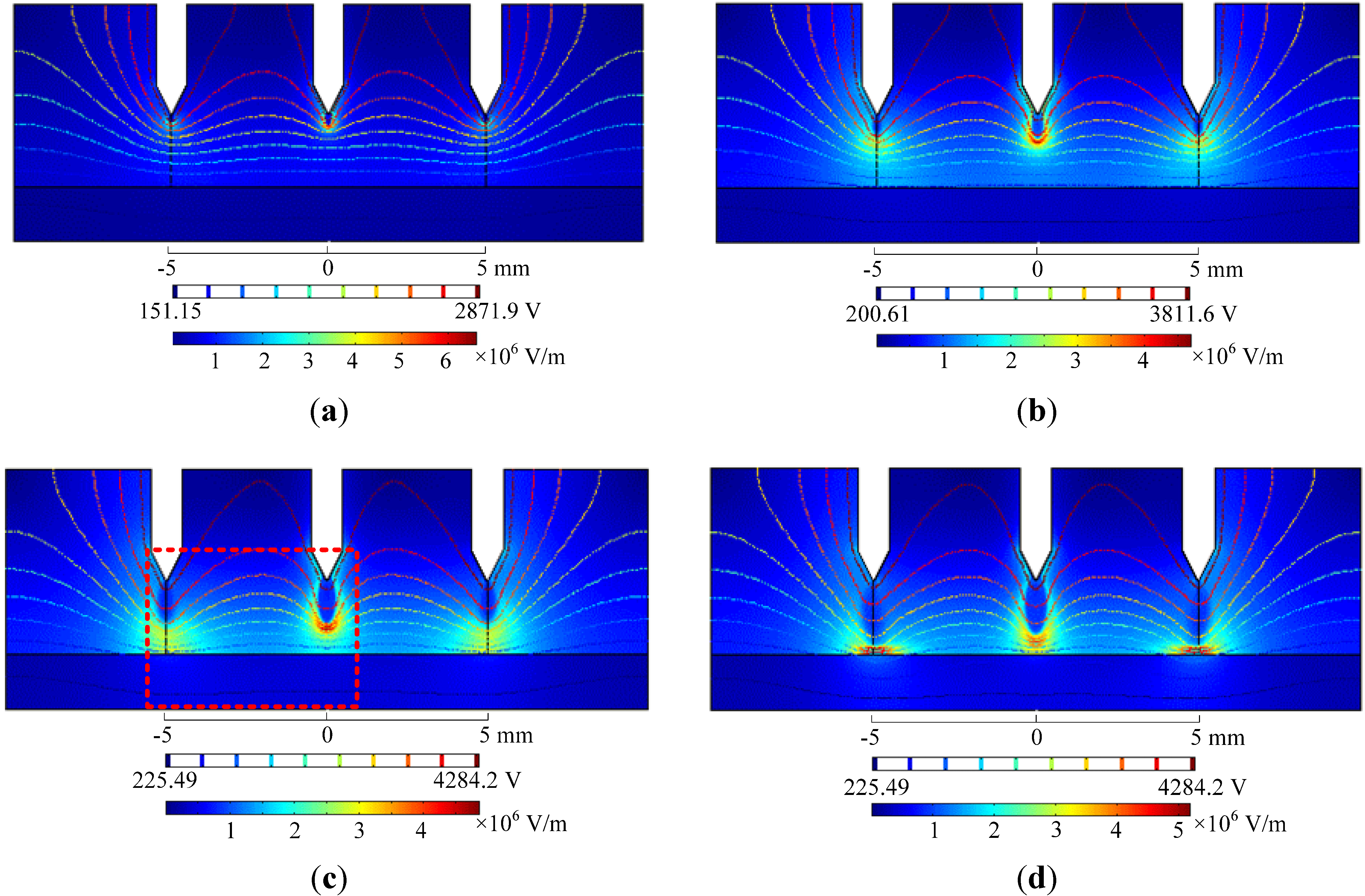
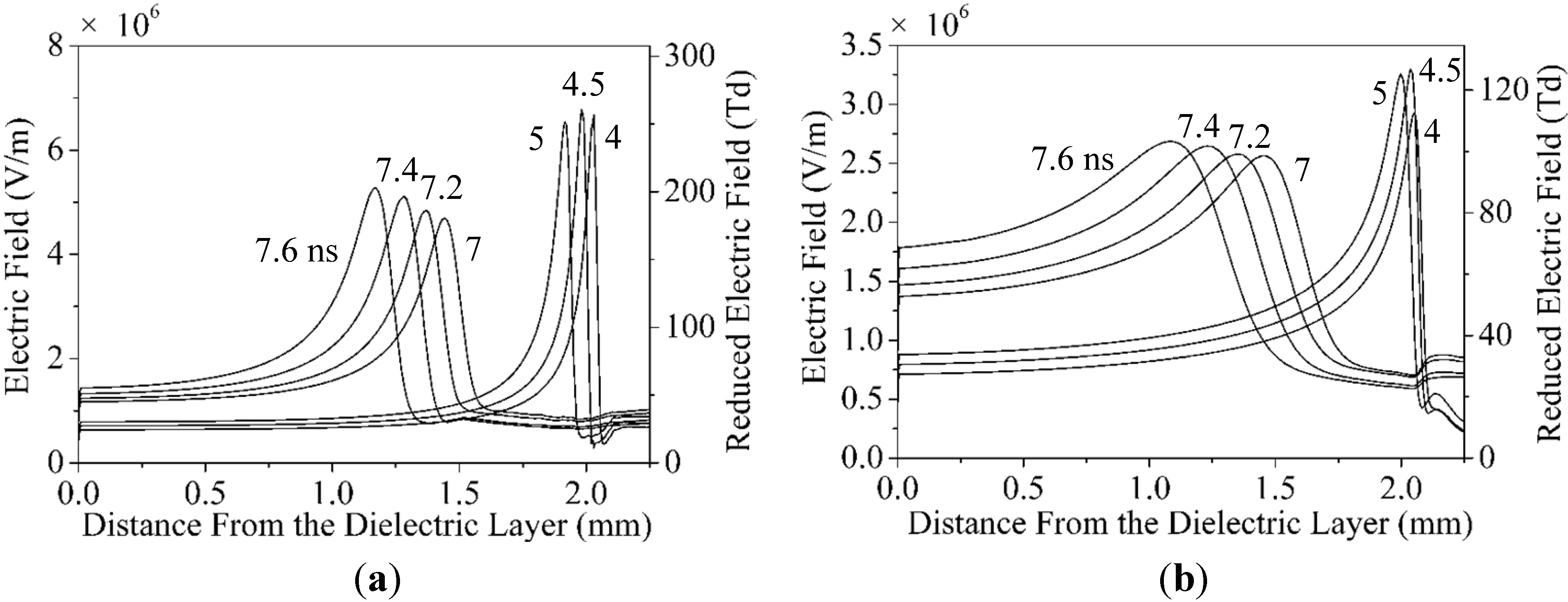
| Time (ns) | The amplitude value of the applied voltage (V) | Calculated voltage at the streamer head (V) | Distance from the dielectric layer (mm) |
|---|---|---|---|
| 5 | 2871.7 | 2267.2 | 1.85 |
| 7 | 3811.6 | 2206.7 | 1.1 |
| 8.1 | 4284.2 | 1578.4 | 0.4 |
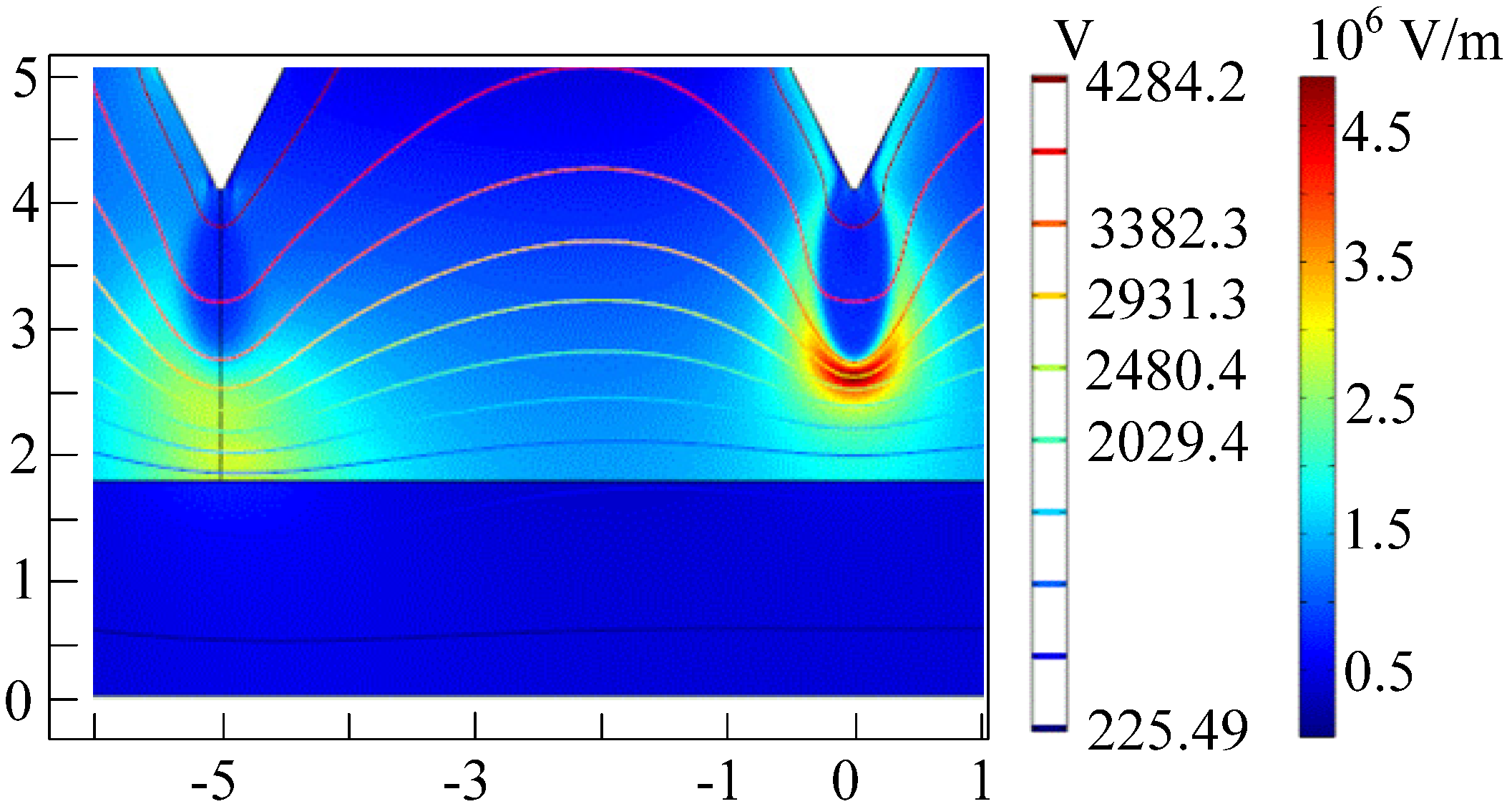
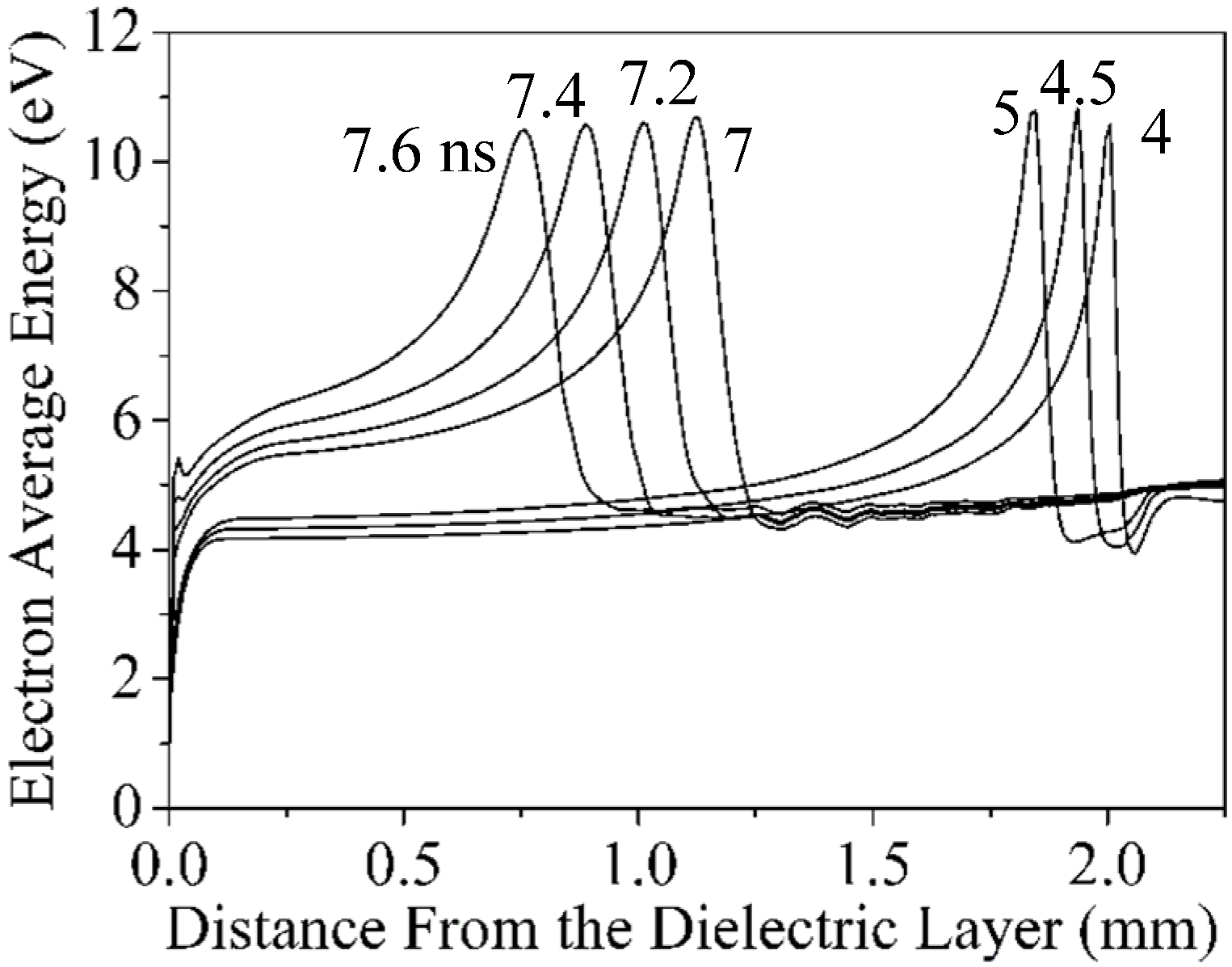
3.2. Electron Average Energy Profile
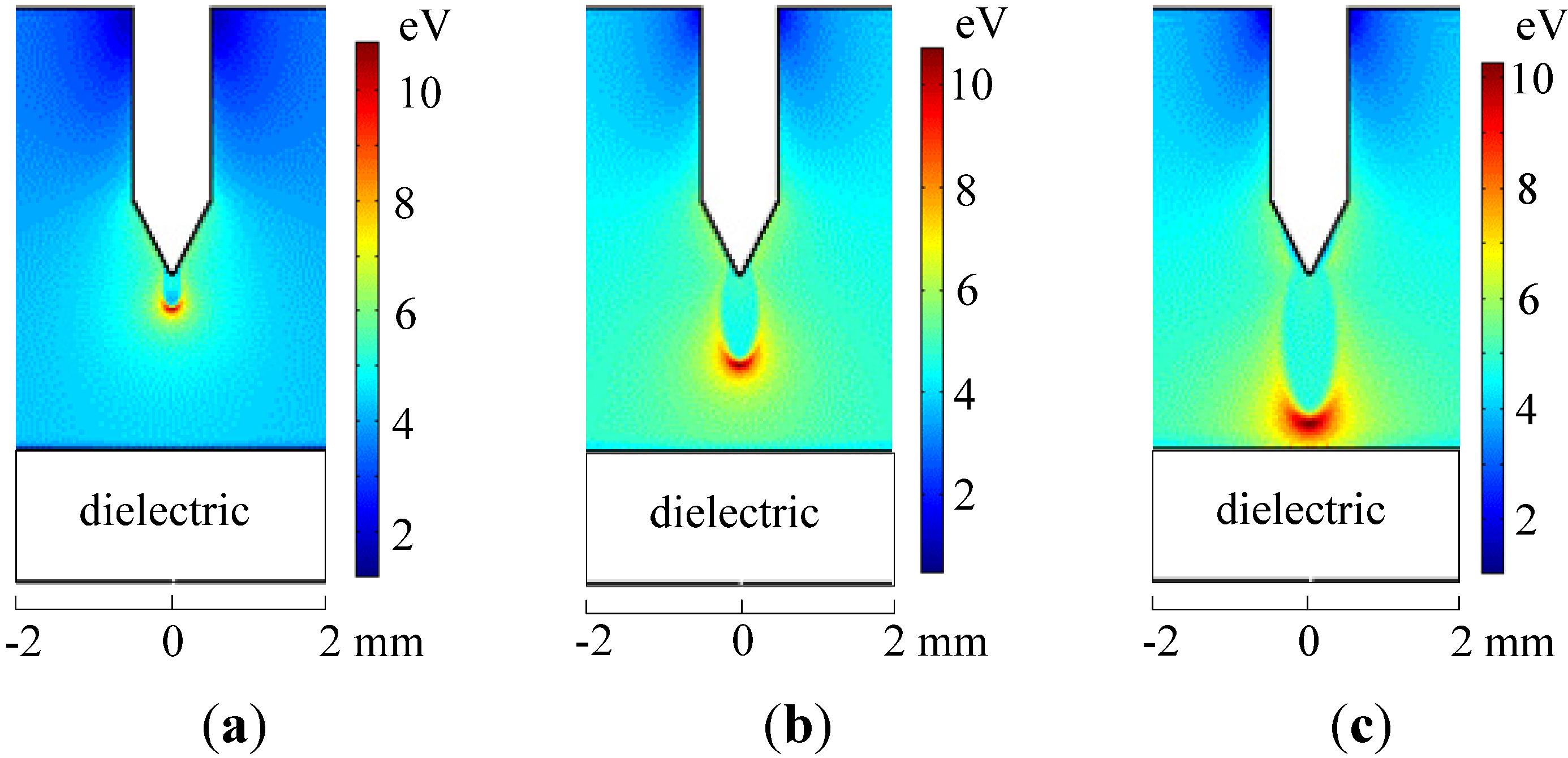
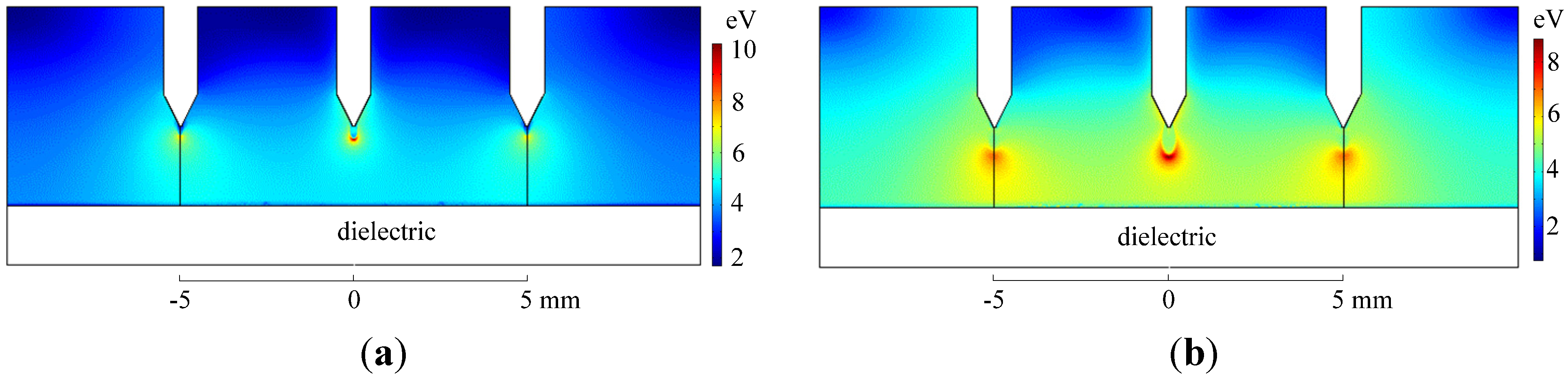
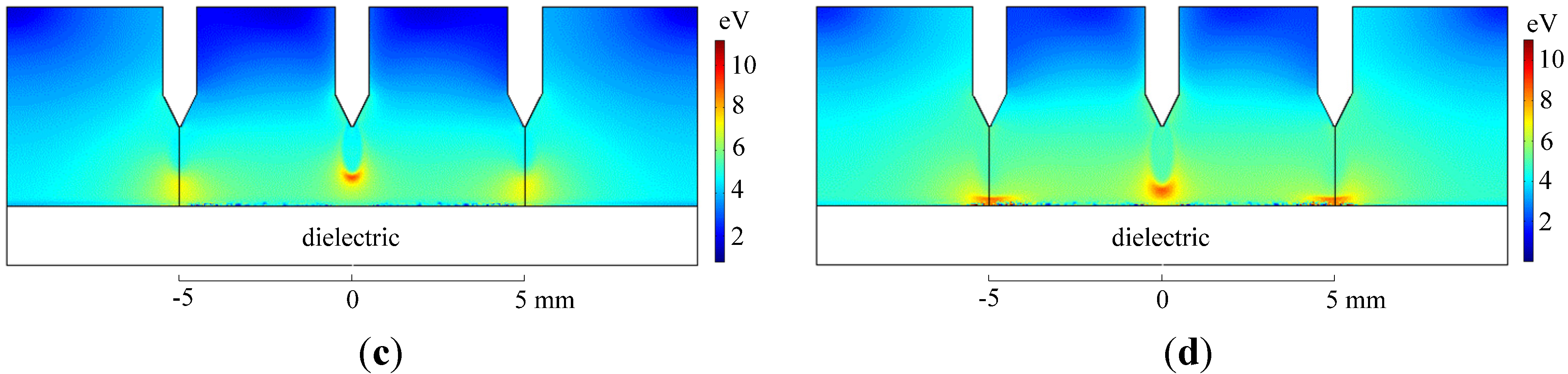

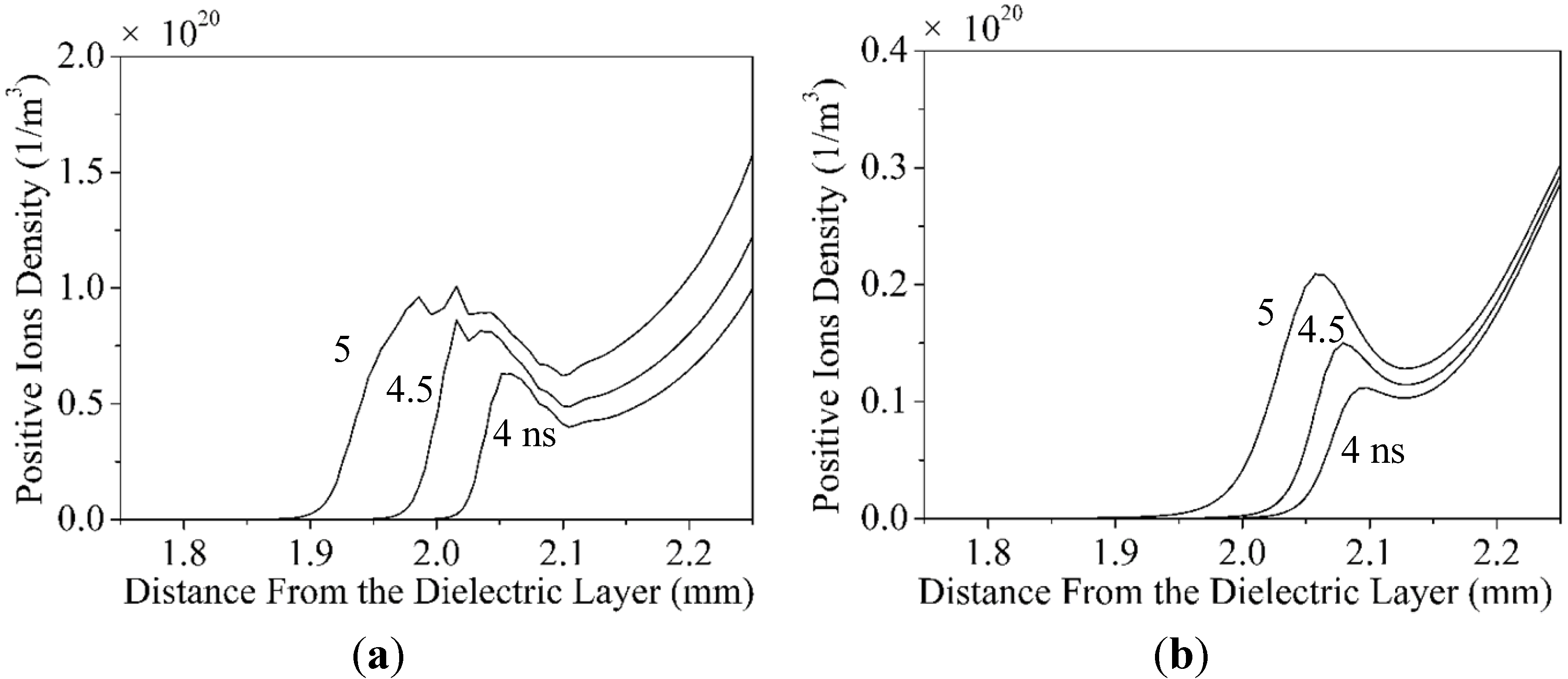
3.3. Distribution of Electron and Positive Ions
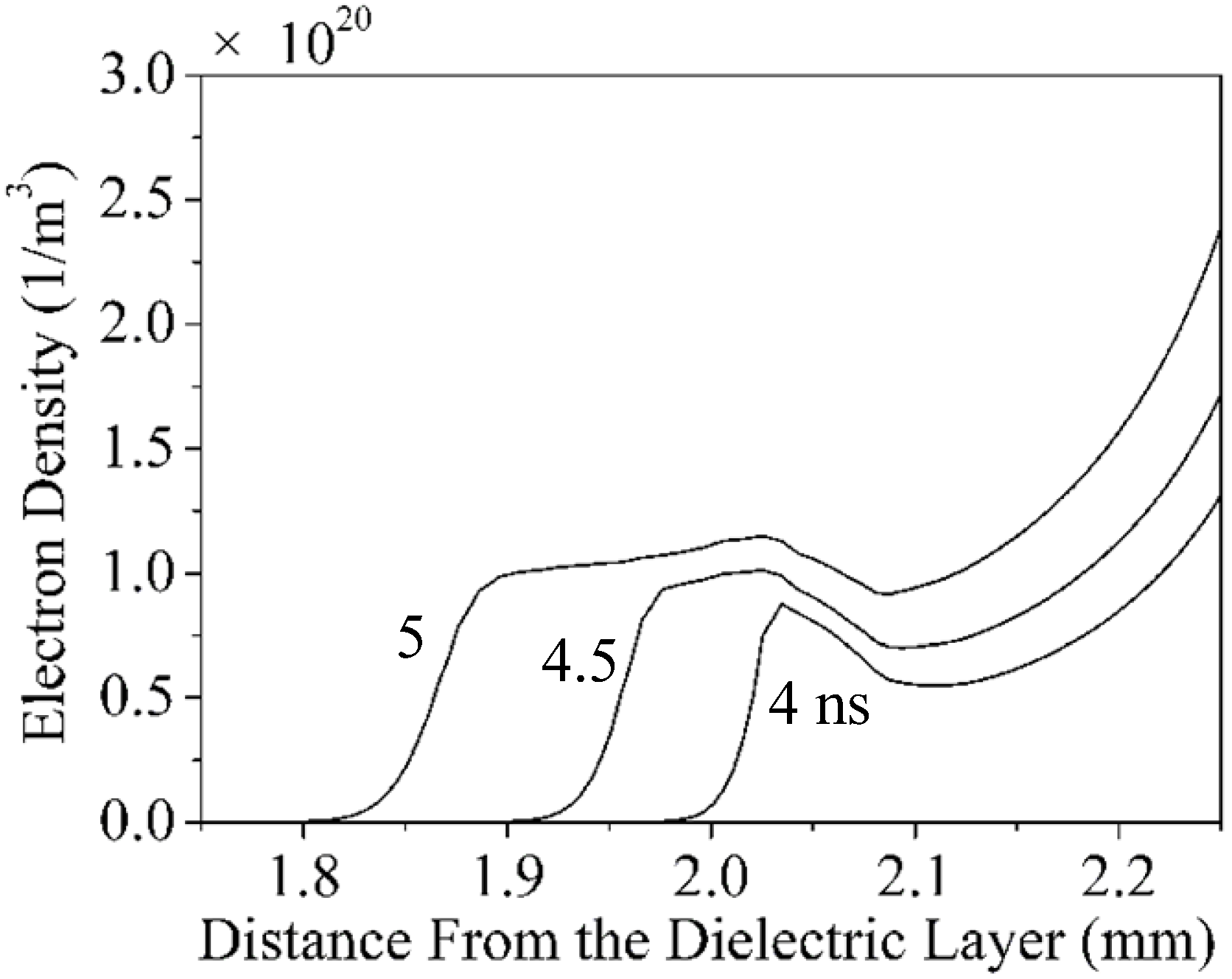
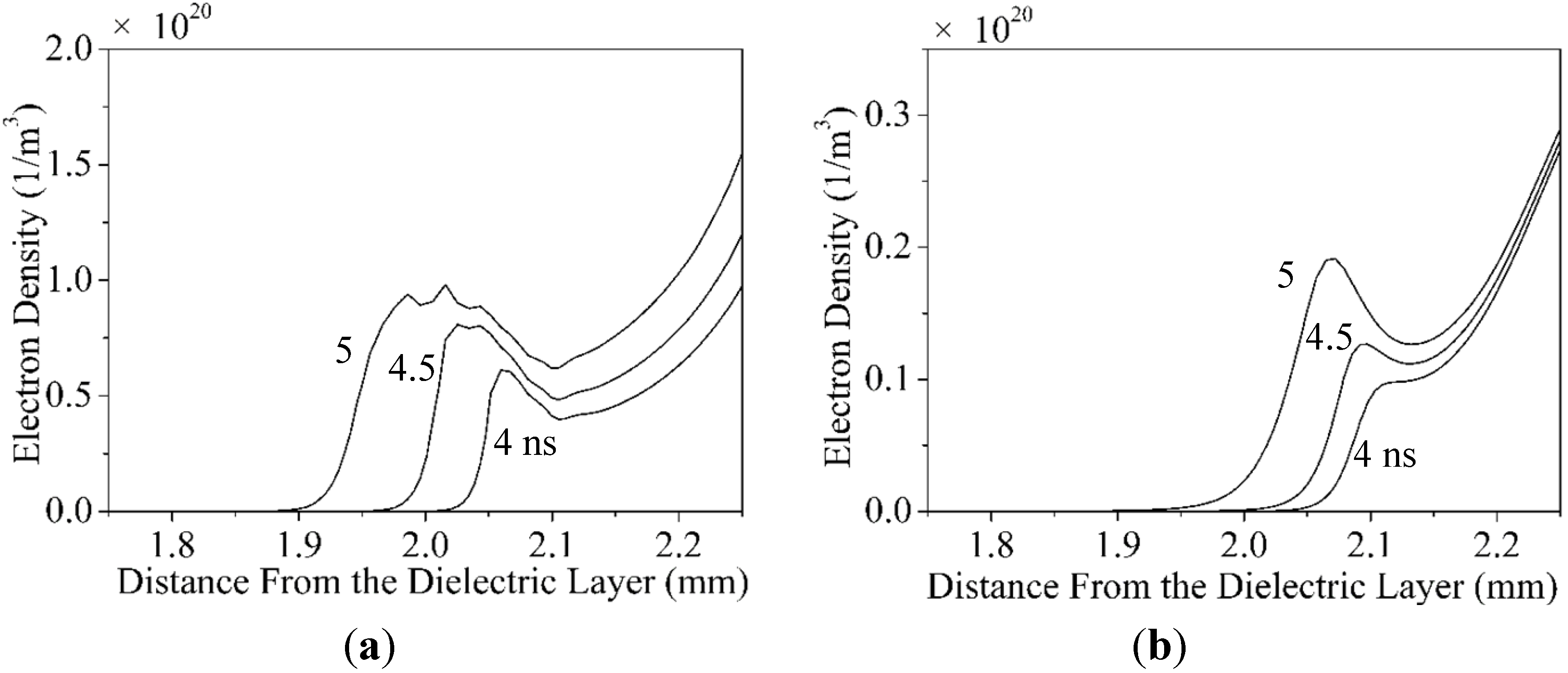
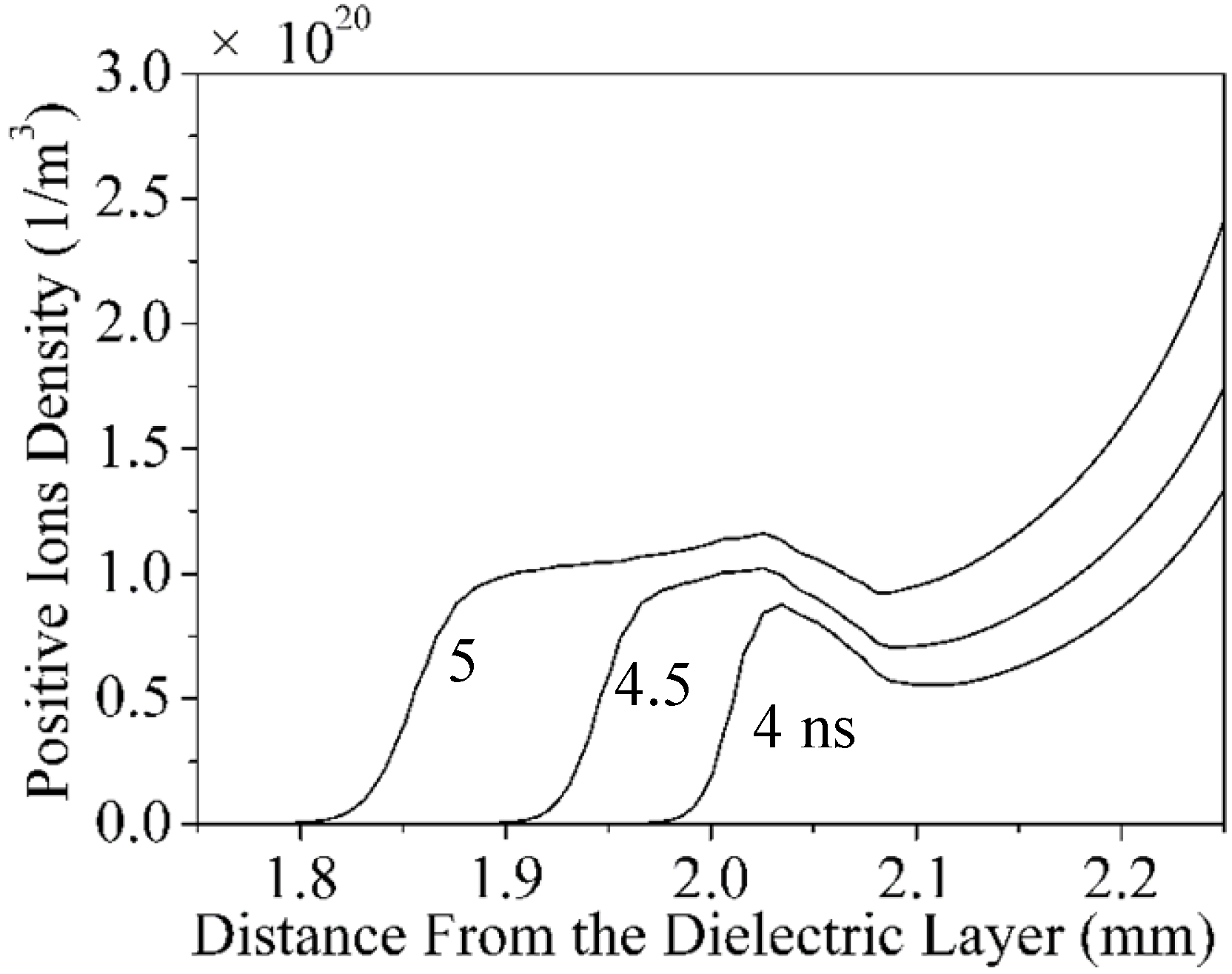
4. Conclusions
Acknowledgments
References
- Kogelschatz, U. Dielectric-barrier discharges: Their history, discharge physics, and industrial applications. Plasma Chem. Plasma Process. 2003, 23, 1–46. [Google Scholar] [CrossRef]
- Palaskar, S.; Kale, K.H.; Nadiger, G.S.; Desai, A.N. Dielectric barrier discharge plasma induced surface modification of polyester/cotton blended fabrics to impart water repellency using HMDSO. J. Appl. Polym. Sci. 2011, 122, 1092–1100. [Google Scholar] [CrossRef]
- De Geyter, N.; Morent, R.; van Vlierberghe, S.; Frere-Trentesaux, M.; Dubruel, P.; Payen, E. Effect of electrode geometry on the uniformity of plasma-polymerized methyl methacrylate coatings. Prog. Org. Coating 2011, 70, 293–299. [Google Scholar] [CrossRef]
- An, H.T.Q.; Huu, T.P.; Le van, T.; Cormier, J.M.; Khacef, A. Application of atmospheric non thermal plasma-catalysis hybrid system for air pollution control: Toluene removal. Catal. Today 2010, 176, 474–477. [Google Scholar]
- Rong, M.; Liu, D.; Wang, D.; Su, B.; Wang, X.; Wu, Y. A new structure optimization method for the interneedle distance of a multineedle-to-plane barrier discharge reactor. IEEE Trans. Plasma Sci. 2010, 38, 966–972. [Google Scholar] [CrossRef]
- Ono, R.; Oda, T. Ozone production process in pulsed positive dielectric barrier discharge. J. Phys. D Appl. Phys. 2007, 40, 176–182. [Google Scholar] [CrossRef]
- Daou, F.; Vincent, A.; Amouroux, J. Point and multipoint to plane barrier discharge process for removal of NOx from engine exhaust gases: Understanding of the reactional mechanism by isotopic labeling. Plasma Chem. Plasma Process. 2003, 23, 309–325. [Google Scholar] [CrossRef]
- Dang, X.Q.; Huang, J.Y.; Chen, L.; Liu, X.; Kang, L. Research on removal of dilute gaseous toluene using dielectric barrier discharge with TiO2 photocatalyst. In Proceedings of the 2010 IEEE International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 2026–2031.
- Wang, X.; Sun, C. Formation conditions for transported charges of multineedle-to-cylinder dielectric barrier discharge based on the orthogonal design and lissajous figures. In Proceedings of the 2011 International Conference on Information Science and Engineering Application, Chongqing, China, 21–23 October 2011.
- Bhoj, A.N.; Kushner, M.J. Multi-scale simulation of functionalization of rough polymer surfaces using atmospheric pressure plasmas. J. Phys. D Appl. Phys. 2006, 39, 1594–1598. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Q.; Yao, C.; Zhang, X.; Sun, C. Dielectric barrier discharge characteristics of multineedle-to-cylinder configuration. Energies 2011, 4, 2133–2150. [Google Scholar] [CrossRef]
- Takaki, K.; Fujiwara, T. Multipoint barrier discharge process for removal of NOx from diesel engine exhaust. IEEE Trans. Plasma Sci. 2001, 29, 518–523. [Google Scholar] [CrossRef]
- Takaki, K.; Jani, M.A.; Fujiwara, T. Removal of nitric oxide in flue gases by multipoint to plane dielectric barrier discharge. IEEE Trans. Plasma Sci. 1999, 27, 1137–1145. [Google Scholar] [CrossRef]
- Jani, M.A.; Takaki, K.; Fujiwara, T. Low-voltage operation of a plasma reactor for exhaust gas treatment by dielectric barrier discharge. Rev. Sci. Instr. 1998, 69, 1847–1849. [Google Scholar] [CrossRef]
- Jani, M.A.; Takaki, K.; Fujiwara, T. Streamer polarity dependence of NOx removal by dielectric barrier discharge with a multipoint-to-plane geometry. J. Phys. D Appl. Phys. 1999, 32, 2560–2567. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, X.-J.; Sun, C.-X. Effect of electrode structure on the parameters of dielectric barrier discharge. High Volt. Appl. 2010, 46, 31–34. [Google Scholar]
- Kang, W.S.; Park, J.M.; Kim, Y.; Hong, S.H. Numerical study on influences of barrier arrangements on dielectric barrier discharge characteristics. IEEE Trans. Plasma Sci. 2003, 31, 504–510. [Google Scholar] [CrossRef]
- Massines, F.; Segur, P.; Gherardi, N.; Khamphan, C.; Ricard, A. Physics and chemistry in a glow dielectric barrier discharge at atmospheric pressure: Diagnostics and modelling. Surf. Coat. Technol. 2003, 174, 8–14. [Google Scholar] [CrossRef]
- Dorai, R.; Kushner, M.J. A model for plasma modification of polypropylene using atmospheric pressure discharges. J. Phys. D Appl. Phys. 2003, 36, 666–685. [Google Scholar] [CrossRef]
- Massines, F.; Rabehi, A.; Decomps, P.; Gadri, R.B.; Segur, P.; Mayoux, C. Experimental and theoretical study of a glow discharge at atmospheric pressure controlled by dielectric barrier. J. Appl. Phys. 1998, 83, 2950–2957. [Google Scholar] [CrossRef]
- Kogelschatz, U. Filamentary, patterned, and diffuse barrier discharges. IEEE Trans. Plasma Sci. 2002, 30, 1400–1408. [Google Scholar] [CrossRef]
- Babaeva, N.Y.; Kushner, M.J. Intracellular electric fields produced by dielectric barrier discharge treatment of skin. J. Phys. D Appl. Phys. 2010, 43, 185206. [Google Scholar] [CrossRef]
- Georghiou, G.E.; Papadakis, A.P.; Morrow, R.; Metaxas, A.C. Numerical modelling of atmospheric pressure gas discharges leading to plasma production. J. Phys. D Appl. Phys. 2005, 38, R303–R328. [Google Scholar] [CrossRef]
- Babaeva, N.Y.; Kushner, M.J. Ion energy and angular distributions onto polymer surfaces delivered by dielectric barrier discharge filaments in air: I. Flat surfaces. Plasma Sources Sci. Technol. 2011, 20, 035017–035027. [Google Scholar] [CrossRef]
- Zhuang, Y.; Chen, G.; Rotaru, M. Numerical modelling of needle-grid electrodes for negative surface corona charging system. J. Phys. Conf. Ser. 2011, 310. [Google Scholar] [CrossRef]
- Kumara, S.; Serdyuk, Y.V.; Gubanski, S.M. Charging of polymeric surfaces by positive impulse corona. IEEE Trans. Dielect. Electr. Insul. 2009, 16, 726–733. [Google Scholar] [CrossRef]
- Storch, D.G.; Kushner, M.J. Destruction mechanisms for formaldehyde in atmospheric-pressure low-temperature plasmas. J. Appl. Phys. 1993, 73, 51–55. [Google Scholar] [CrossRef]
- Georghiou, G.E.; Morrow, R.; Metaxas, A.C. The effect of photoemission on the streamer development and propagation in short uniform gaps. J. Phys. D Appl. Phys. 2001, 34, 200–208. [Google Scholar] [CrossRef]
- Kushner, M.J. Hybrid modelling of low temperature plasmas for fundamental investigations and equipment design. J. Phys. D Appl. Phys. 2009, 42, 194013–194032. [Google Scholar] [CrossRef]
- Raether, H. Development of electron avalanche in the radio channel. Zeitschrift Fur Physik 1939, 112, 464–489. [Google Scholar] [CrossRef]
- Loeb, L.B.; Meek, J.M. The mechanism of spark discharge in air at atmospheric pressure. I. J. Appl. Phys. 1940, 11, 438–447. [Google Scholar] [CrossRef]
- Li, C.; Ebert, U.; Hundsdorfer, W. Spatially hybrid computations for streamer discharges: II. Fully 3D simulations. J. Comput. Phys. 2012, 231, 1020–1050. [Google Scholar] [CrossRef]
- Li, C.; Ebert, U.; Hundsdorfer, W. Spatially hybrid computations for streamer discharges with generic features of pulled fronts: I. Planar fronts. J. Comput. Phys. 2010, 229, 200–220. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Ebert, U.; Hundsdorfer, W. 3D hybrid computations for streamer discharges and production of runaway electrons. J. Phys. D Appl. Phys. 2009, 42, 202003:1–4: 202003. [Google Scholar]
- Li, C.; Ebert, U.; Brok, W.J.M.; Hundsdorfer, W. Spatial coupling of particle and fluid models for streamers: where nonlocality matters. J. Phys. D Appl. Phys. 2008, 41, 032005:1–4:032005. [Google Scholar]
- Li, C.; Brok, W.J.M.; Ebert, U.; van der Mullen, J.J.A.M. Deviations from the local field approximation in negative streamer heads. J. Appl. Phys. 2007, 101, 123305:1–17:123305. [Google Scholar]
- Farouk, T.; Farouk, B.; Staack, D.; Gutsol, A.; Fridman, A. Simulation of dc atmospheric pressure argon micro glow-discharge. Plasma Sources Sci. Technol. 2006, 15, 676–688. [Google Scholar] [CrossRef]
- Pancheshnyi, S.; Nudnova, M.; Starikovskii, A. Development of a cathode-directed streamer discharge in air at different pressures: Experiment and comparison with direct numerical simulation. Phys. Rev. E 2005, 71, 016407:1–12:016407. [Google Scholar] [CrossRef]
- Georghiou, G.E.; Morrow, R.; Metaxas, A.C. Two-dimensional simulation of streamers using the FE-FCT algorithm. J. Phys-D-Appl. Phys. 2000, 33, L27–L32. [Google Scholar]
- Georghiou, G.E.; Morrow, R.; Metaxas, A.C. An improved finite-element flux-corrected transport algorithm. J. Comput. Phys. 1999, 148, 605–620. [Google Scholar] [CrossRef]
- Nagayama, K.; Farouk, B.; Lee, Y.H. Particle simulation of radio-frequency plasma discharges of methane for carbon film deposition. IEEE Trans. Plasma Sci. 1998, 26, 125–134. [Google Scholar] [CrossRef]
- Morrow, R.; Lowke, J.J. Streamer propagation in air. J. Phys-D-Appl. Phys. 1997, 30, 614–627. [Google Scholar]
- Nagayama, K.; Farouk, B.; Lee, Y.H. Neutral and charged particle simulation of RF Ar plasma. Plasma Sources Sci. Technol. 1996, 5, 685–695. [Google Scholar] [CrossRef]
- Bourdon, A.; Pasko, V.P.; Liu, N.Y.; Célestin, S.; Segur, P.; Marode, E. Efficient models for photoionization produced by non-thermal gas discharges in air based on radiative transfer and the Helmholtz equations. Plasma Sources Sci. Technol. 2007, 16, 656–678. [Google Scholar] [CrossRef]
- Célestin, S.; Bonaventura, Z.; Zeghondy, B.; Bourdon, A.; Ségur, P. Influence of surface charges on the structure of a dielectric barrier discharge in air at atmospheric pressure: Experiment and modeling. Eur. Phys. J. Appl. Phys. 2009, 47. [Google Scholar] [CrossRef]
- Célestin, S.; Bonaventura, Z.; Zeghondy, B.; Bourdon, A.; Ségur, P. The use of the ghost fluid method for Poisson's equation to simulate streamer propagation in point-to-plane and point-to-point geometries. J. Phys. D Appl. Phys. 2009, 42, 065203:1–14:065203. [Google Scholar]
- Guo, J.-M.; Wu, C.-H.J. Two-dimensional nonequilibrium fluid models for streamers. IEEE Trans. Plasma Sci. 1993, 21, 684–695. [Google Scholar] [CrossRef]
- Eichwald, O.; Ducasse, O.; Merbahi, N.; Yousfi, M.; Dubois, D. Effect of order fluid models on flue gas streamer dynamics. J. Phys. D Appl. Phys. 2006, 39, 99–107. [Google Scholar] [CrossRef]
- Sakiyama, Y.; Graves, D.B. Finite element analysis of an atmospheric pressure RF-excited plasma needle. J. Phys. D Appl. Phys. 2006, 39, 3451–3456. [Google Scholar] [CrossRef]
- Dhali, S.K.; Williams, P.F. Two-Dimensional Studies of Streamers in Gases. J. Appl. Phys. 1987, 62, 4696–4707. [Google Scholar] [CrossRef]
- Wang, M.C.; Kunhardt, E.E. Streamer dynamics. Phys. Rev. A 1990, 42, 2366–2373. [Google Scholar] [CrossRef] [PubMed]
- Kulikovsky, A.A. Positive streamer between parallel plate electrodes in atmospheric pressure air. J. Phys. D Appl. Phys. 1997, 30, 441–450. [Google Scholar] [CrossRef]
- Vitello, P.A.; Penetrante, B.M.; Bardsley, J.N. Simulation of negative-streamer dynamics in nitrogen. Phys. Rev. E 1994, 49, 5574–5598. [Google Scholar] [CrossRef]
- Pancheshnyi, S.V.; Starikovskaia, S.M.; Starikovskii, A.Y. Role of photoionization processes in propagation of cathode-directed streamer. J. Phys. D Appl. Phys. 2001, 34, 105–115. [Google Scholar] [CrossRef]
- Liu, N.Y.; Pasko, V.P. Effects of photoionization on propagation and branching of positive and negative streamers in sprites. J. Geophys. Res. Space Phys. 2004, 109(A4), A04301:1–17:A04301. [Google Scholar] [CrossRef]
- Zheleznyak, M.B.; Mnatsakarian, A.K.; Sizyka, S.V. Photoionization of nitrogen and oxygen mixtures by radiation from gas discharges. High Temp. 1982, 20, 357–362. [Google Scholar]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- BOLSIG + 2005 CPAT. Available online: http://www.codiciel.fr/plateforme/plasma/bolsig/bolsig.php (accessed on 30 April 2009).
- Lee, S.-H.; Lee, S.-Y.; Park, I.-H. Finite-element analysis of corona discharge onset in air with artificial diffusion scheme and under Fowler-Nordheim electron emission. IEEE Trans. Magn. 2007, 43, 1453–1456. [Google Scholar] [CrossRef]
- Gupta, D.K.; Mahajan, S.; John, P.I. Theory of step on leading edge of negative corona current pulse. J. Phys. D Appl. Phys. 2000, 33, 681–691. [Google Scholar] [CrossRef]
- Morrow, R. Theory of negative corona in oxygen. Phys. Rev. A 1985, 32, 1799–1809. [Google Scholar] [CrossRef] [PubMed]
- Pancheshnyi, S.V.; Starikovskii, A.Y. Two-dimensional numerical modelling of the cathode-directed streamer development in a long gap at high voltage. J. Phys. D Appl. Phys. 2003, 36, 2683–2691. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, D. Gas Discharge Physics; Fudan Univresity Publisher: Shanghai, China, 1996. [Google Scholar]
- Liang, X.; Chen, C.; Zhou, Y. High Voltage Engineering; Tsinghua University Press: Beijing, China, 2003; pp. 16–22. [Google Scholar]
- Sima, W.; Peng, Q.; Yang, Q.; Yuan, T.; Shi, J. Study of the characteristics of a streamer discharge in air based on a plasma chemical model. IEEE Trans. Dielect. Electr. Insul. 2012, 19, 660–670. [Google Scholar] [CrossRef]
- Ducasse, O.; Papageorghiou, L.; Eichwald, O.; Spyrou, N.; Yousfi, M. Critical analysis on two-dimensional point-to-plane streamer simulations using the finite element and finite volume methods. IEEE Trans. Plasma Sci. 2007, 35, 1287–1300. [Google Scholar] [CrossRef]
- Yi, W.J.; Williams, P.F. Experimental study of streamers in pure N-2 and N-2/O-2 mixtures and an approximate to 13 cm gap. J. Phys. D Appl. Phys. 2002, 35, 205–218. [Google Scholar] [CrossRef]
- Sigmond, R.S. The residual streamer channel-return strokes and secondary streamers. J. Appl. Phys. 1984, 56, 1355–1370. [Google Scholar] [CrossRef]
- Raizer, Y.P.; Allen, J.E.; Kisin, V.I. Gas Discharge Physics; Springer-Verlag: Berlin, Germany, 1991; pp. 357–358. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, X.; Yao, C.; Sun, C.; Yang, Q.; Zhang, X. Numerical Modelling of Mutual Effect among Nearby Needles in a Multi-Needle Configuration of an Atmospheric Air Dielectric Barrier Discharge. Energies 2012, 5, 1433-1454. https://doi.org/10.3390/en5051433
Wang X, Yao C, Sun C, Yang Q, Zhang X. Numerical Modelling of Mutual Effect among Nearby Needles in a Multi-Needle Configuration of an Atmospheric Air Dielectric Barrier Discharge. Energies. 2012; 5(5):1433-1454. https://doi.org/10.3390/en5051433
Chicago/Turabian StyleWang, Xiaojing, Chenguo Yao, Caixin Sun, Qing Yang, and Xiaoxing Zhang. 2012. "Numerical Modelling of Mutual Effect among Nearby Needles in a Multi-Needle Configuration of an Atmospheric Air Dielectric Barrier Discharge" Energies 5, no. 5: 1433-1454. https://doi.org/10.3390/en5051433




