A General Mathematical Framework for Calculating Systems-Scale Efficiency of Energy Extraction and Conversion: Energy Return on Investment (EROI) and Other Energy Return Ratios
Abstract
:1. Introduction
2. Energy Ratios and Their Uses
2.1. Development of Energy Return Ratios
2.2. The Usefulness of Energy Return Ratios
2.3. The Limitations of Energy Return Ratios
2.4. Existing NEA Methods
3. Developing a General Bottom-Up Model of ERRs
3.1. Types of Processing Stages
- Harvesting, capturing, or gathering of the primary energy carrier (the initial form of the principal energy flow) from the natural environment. This might include the lifting of crude oil from the subsurface or the conversion of energy contained in photons to electrical energy in a PV panel.
- Shifting energy availability in space. This includes the transport of a principal energy flow from one location in space to another, as in the movement of crude oil from an oil field to a refinery via pipeline or the transport of solar PV electricity from generators to consumers.
- Shifting energy availability in time. This is the shifting of a principal energy flow from one time period to another later time period (storage). Examples include the storage of solar-PV-generated electricity in batteries for use at night, or the storage of crude oil in oil tanks before processing.
- Upgrading or improvement in the quality of a principal energy flow. This is a chemical or physical conversion that does not change the fundamental character of the energy type, but improves its usefulness or quality. An example might be an oil refinery hydrotreating unit that removes sulfur from distillate fuels (e.g., creating ultra-low-sulfur diesel fuel from conventional diesel fuel). Another example might be the transformation of DC solar PV electricity to AC power in an inverter.
- Conversion from one fundamental energy type to another. This is the use of a technology to convert the principal energy flow from one physical form to another. This is typically a more profound and fundamental change than upgrading the principal energy flow. For example, this might involve the conversion from chemical potential energy in gasoline (which exists due to hydrocarbons being out of equilibrium with an oxygen-rich atmosphere) to rotational kinetic energy using a heat engine.
3.1.1. Example of a Processing Stage
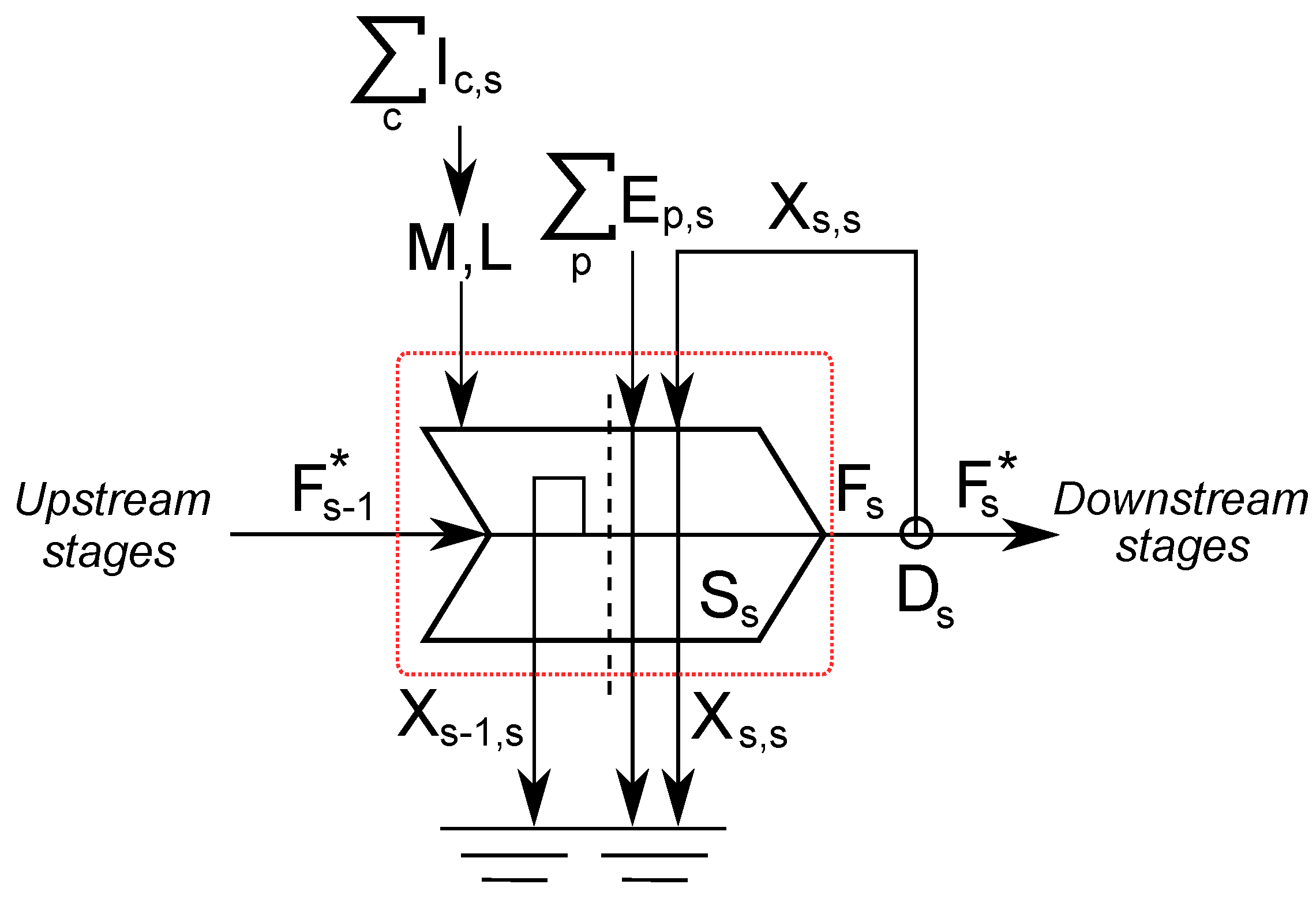
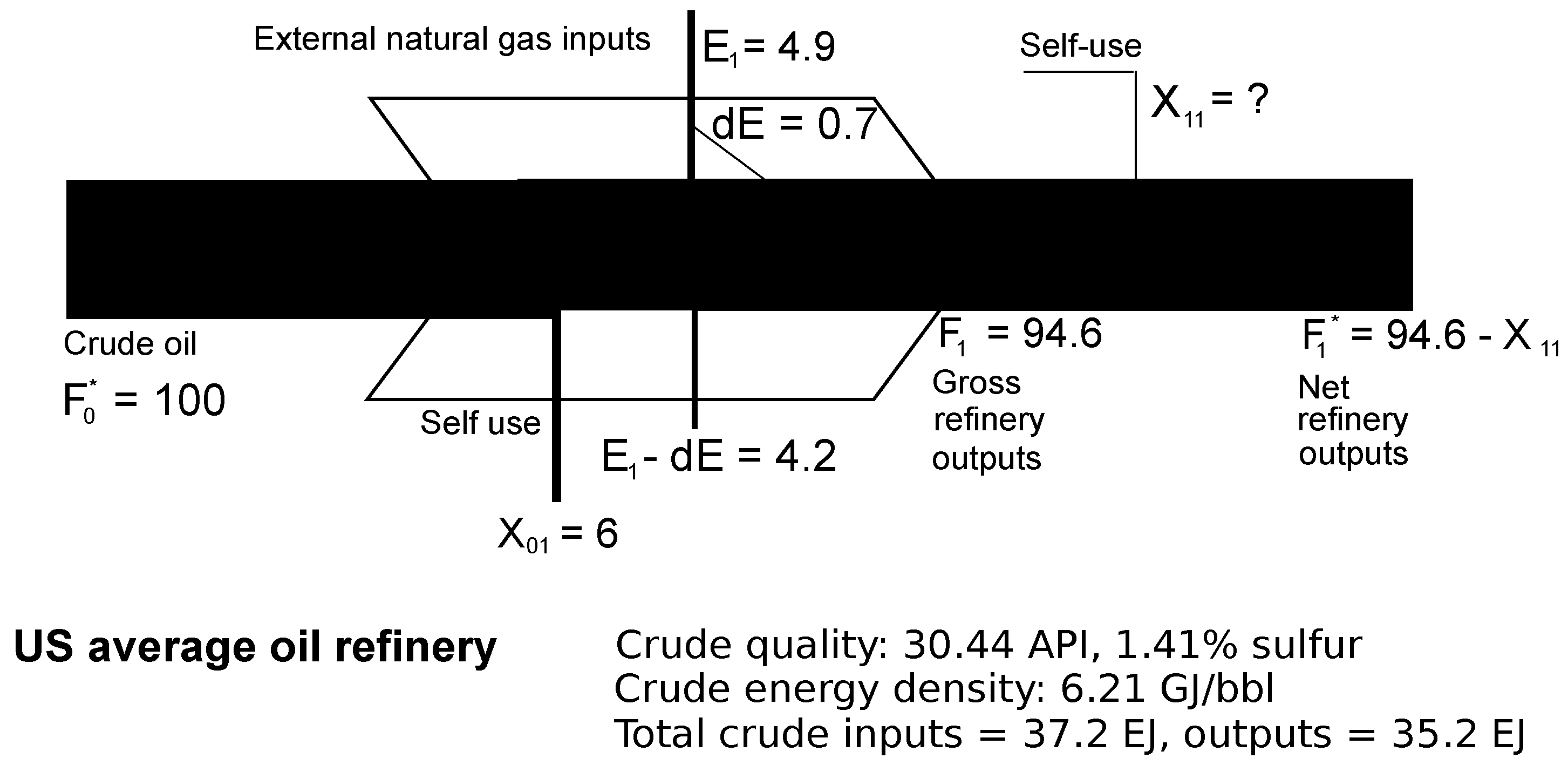
3.1.2. Processing Stage Efficiency
3.2. Energy Pathway Analysis
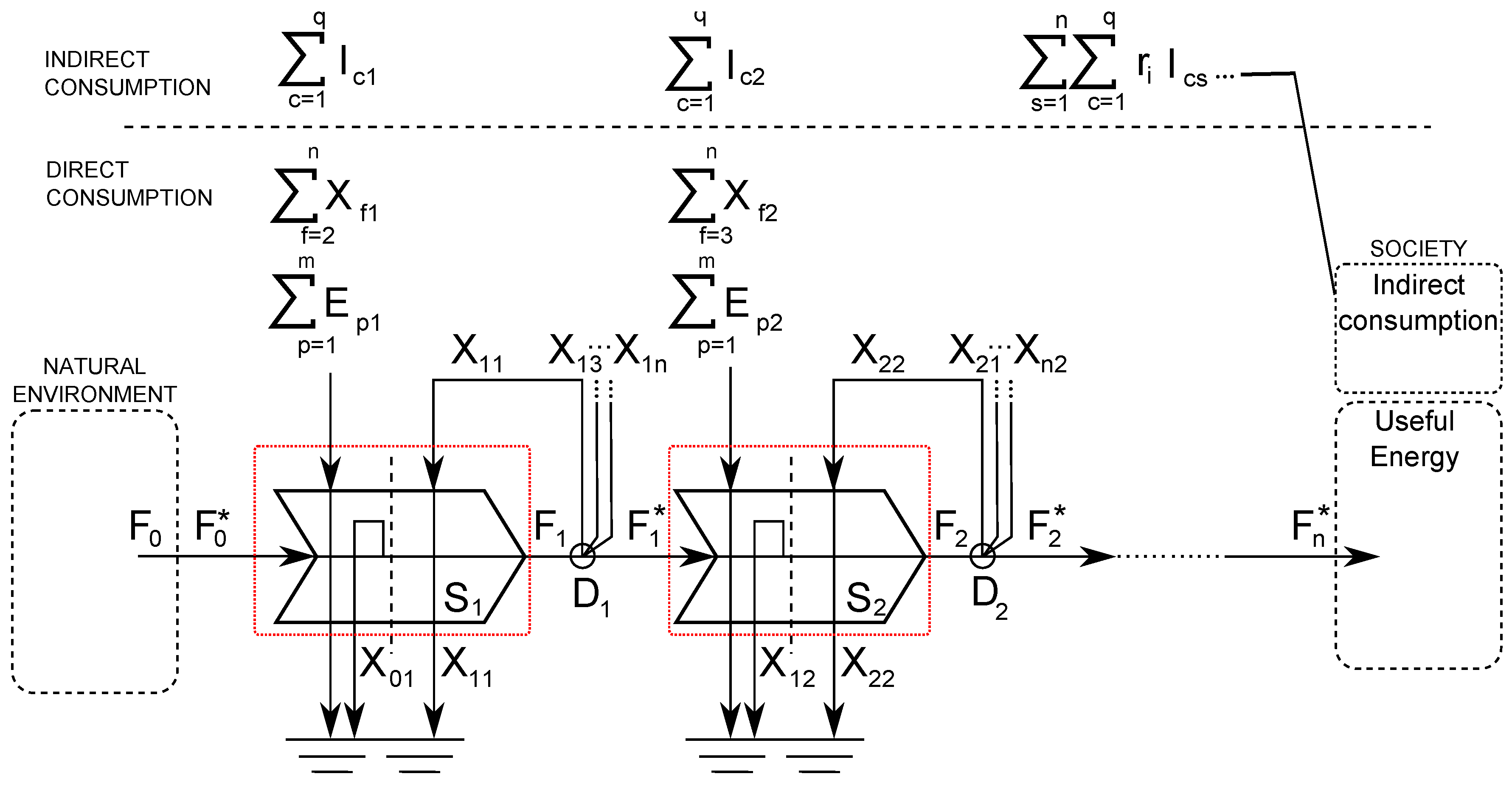
- The flow of principal energy type leaving a given processing stage s;
- The total self consumption inputs to a stage s from all other stages within the pathway ();
- The total external inputs to a stage s from all external energy types (adjusted for indirect consumption, );
- The total embodied energy induced in all economic sectors c due to external energy and materials consumed in stage s ().
| ERR Type | Net Energy Return (NER) | Gross Energy Return (GER) |
|---|---|---|
| Consumptive (Flow) | ||
| Consumptive (Efficiency) | ||
| External (Flow) | ||
| External (Efficiency) | ||
| Life cycle (Flow) [EROI] | ||
| Life cycle (Efficiency) |
| ERR Type | Net External Energy Return (NEER) | Gross External Energy Return (GEER) |
|---|---|---|
| Consumptive (Flow) | ||
| Consumptive (Efficiency) | ||
| External (Flow) | ||
| External (Efficiency) | ||
| Life cycle (Flow) [EROI] | ||
| Life cycle (Efficiency) |
| Stages and Flows | ||||
|---|---|---|---|---|
| Pathways | m other energy extraction and conversion pathways, with counter index p | Energy extraction and processing pathways | ||
| Stages | n stages counted with counter index s (or ) | Energy extraction and processing stages | ||
| Distribution points | n distribution points counted with counter index s | Energy distribution points for principal energy flows | ||
| Flows | n flows leaving energy extraction and processing stages (counter index s) | Flows of principal energy (MJ of principal energy type s) | ||
| Self consumption | flows leaving energy extraction and processing stage f and going into stage t (, ) | Flows of principal energy (MJ of principal energy type f) | ||
| External consumption | flows leaving energy extraction and conversion pathway m into stage s | Flows of principal energy of type m (MJ of principal energy type m) | ||
| Indirect consumption | flows induced in economic sector c due to direct consumption of materials and energy in stage s | Indirect consumption of all energy types in sector c (MJ of all energy types) | ||
| Dependent Variables and Efficiencies | ||||
| Distribution fraction | , , …, | Ratio of outflow from distribution point s to inflow | Dimensionless ratio | |
| Flow efficiency | , , …, | Ratio of outflow from stage s to inflow | Dimensionless ratio | |
| Consumptive efficiency | , , …, | Ratio of outflow from stage to sum of inflow and energy consumed from within pathway () | Dimensionless ratio | |
| External efficiency | , , …, | Ratio of outflow from stage to sum of inflow and energy consumed from within pathway () and from outside the pathway () | Dimensionless ratio | |
| Life cycle efficiency | , , …, | Ratio of outflow from stage to sum of inflow and energy consumed from within pathway () and from outside the pathway () as well as indirect consumption in other economic sectors () | Dimensionless ratio | |
| Indirect self-use ratio | – | The fraction of indirect energy consumed that originally arose from the pathway in question. Can be determined using society-wide energy mix or sector-specific energy mixes. | Dimensionless ratio | |
4. Results and Discussion
4.1. A Simple Applied Example: Solar Photovoltaic Energy Capture and Processing
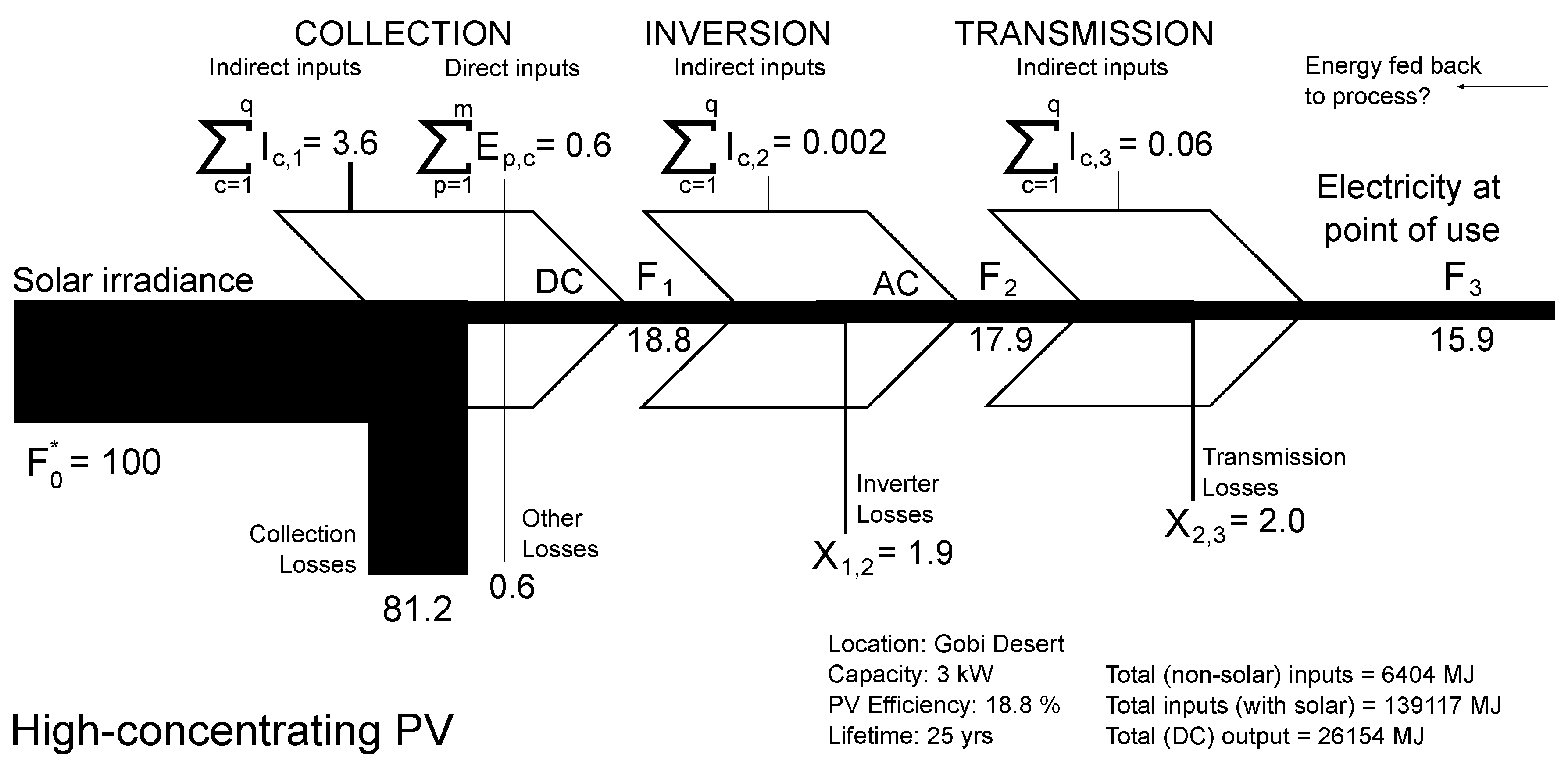
| System Boundary | ||||
|---|---|---|---|---|
| Ratios | α | β | γ | δ |
| - | ||||
| - | ||||
| - | ||||
| - | ∞ | |||
4.2. Application of Mathematical form to a Generic Energy Processing Chain
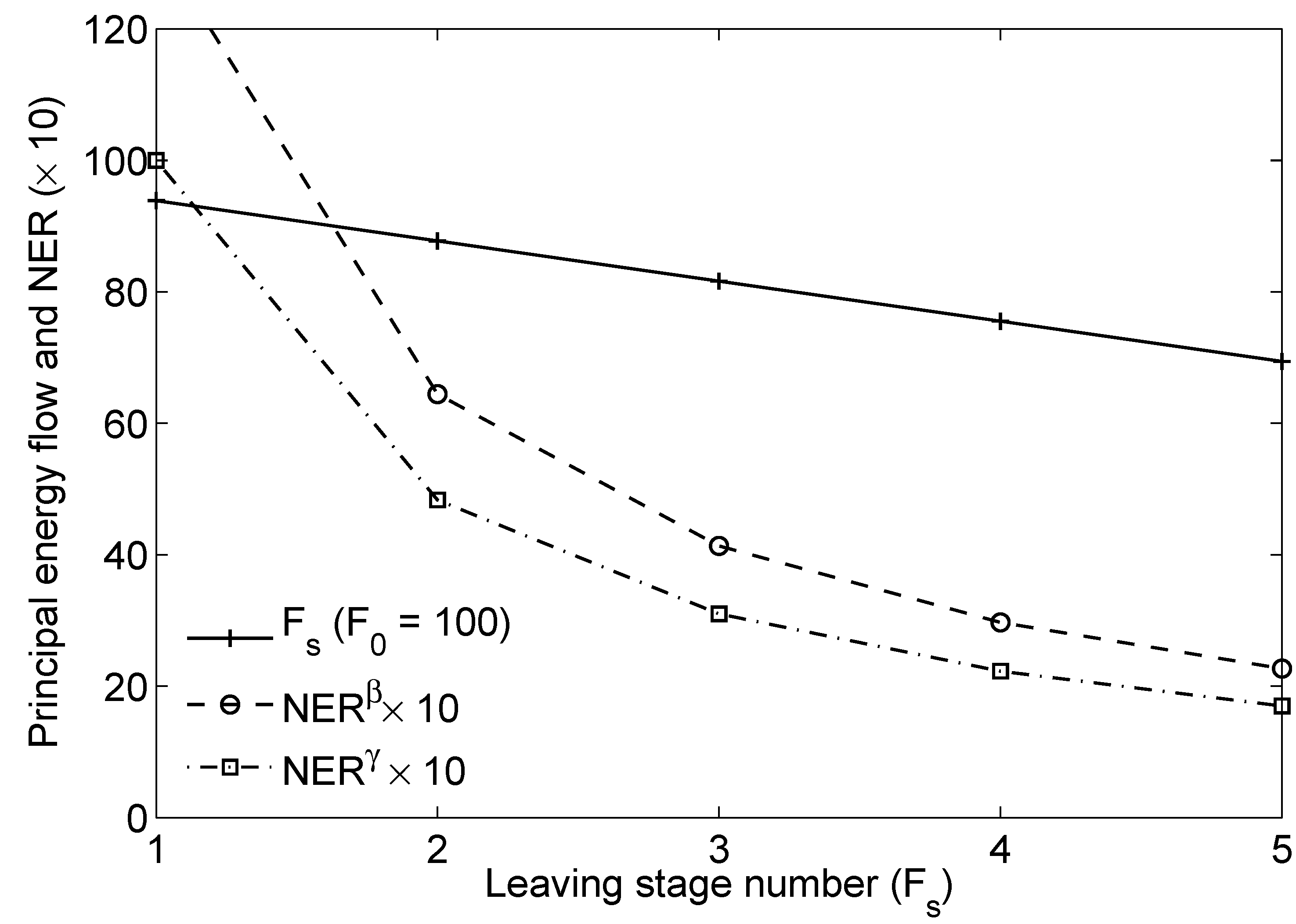
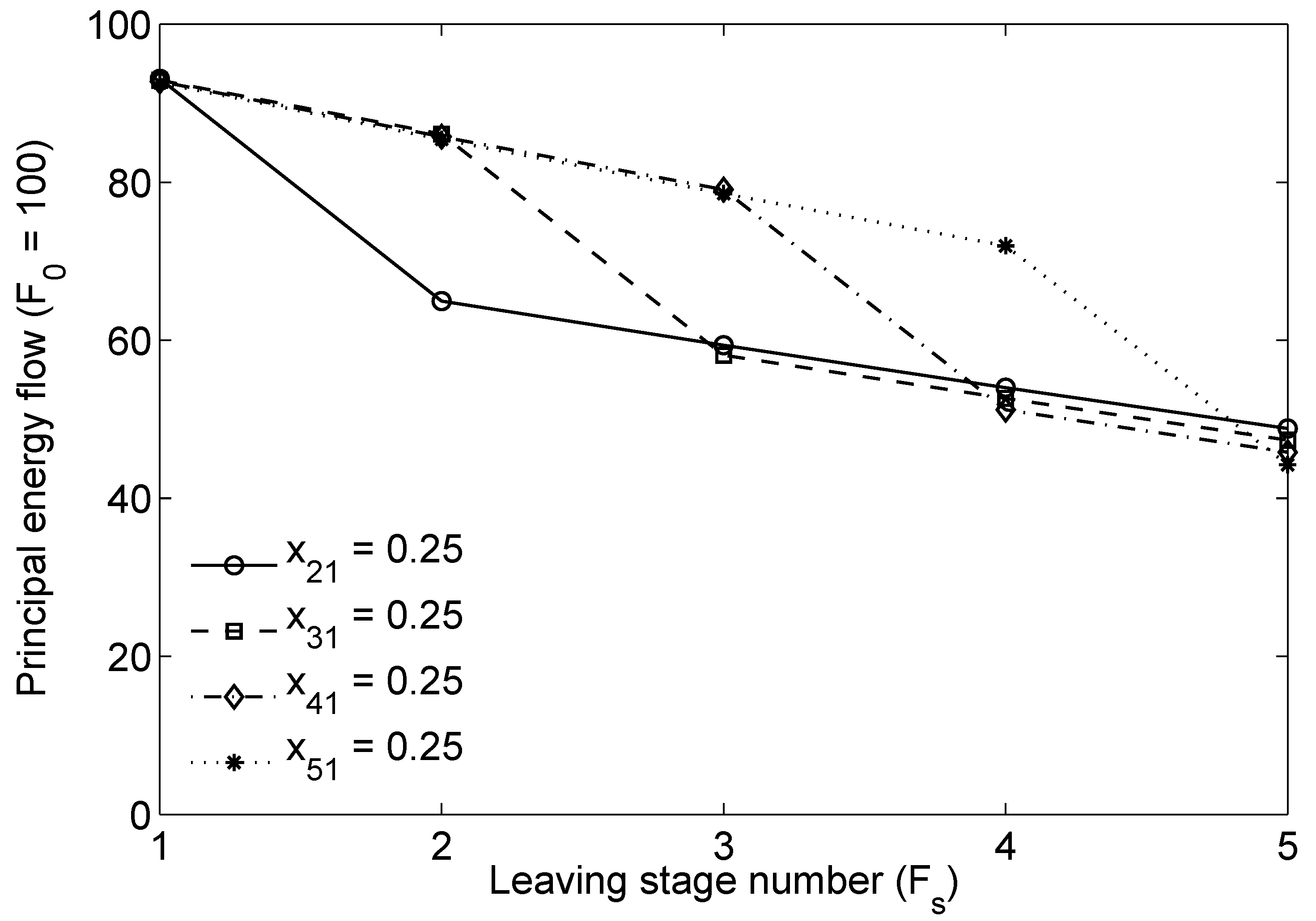
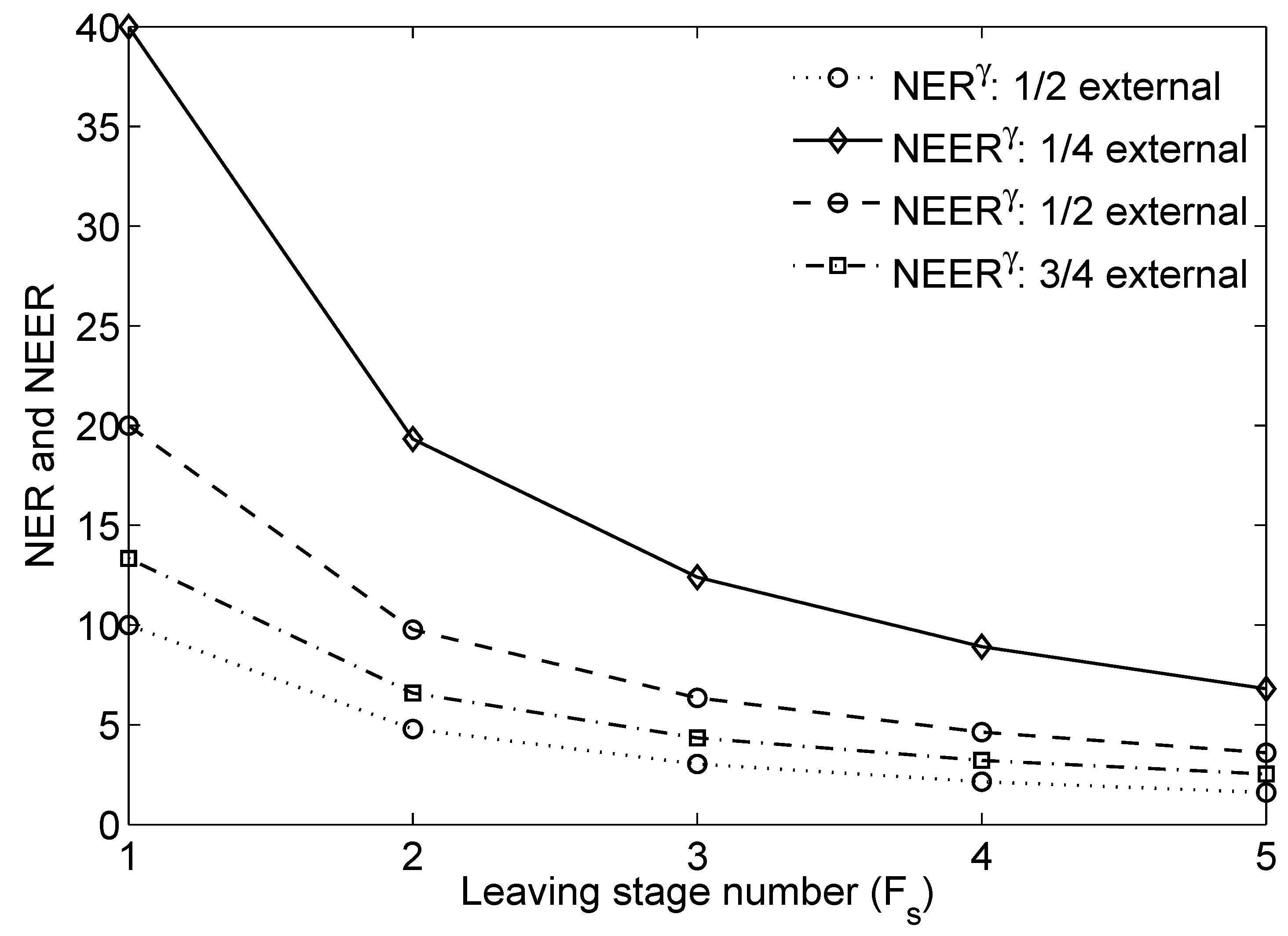
5. Discussion of Formulation Limitations and Next Steps
6. Appendix: Derivation of Multi-Stage, Single-Pathway Models
6.1. Two Stage Pathways with Only Internal Consumption
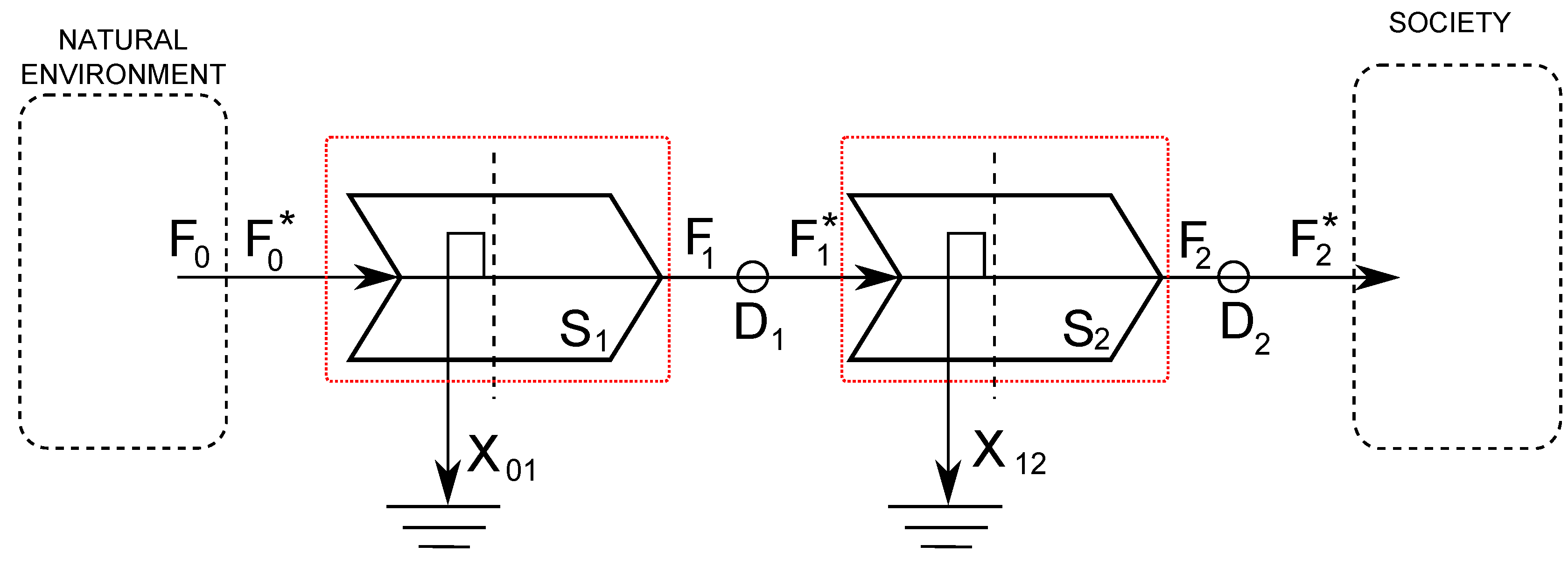
6.1.1. Energy Balance
6.1.2. Efficiencies
6.1.3. Net Energy Ratio and Other Energy Return Ratios
6.2. Two Stage Pathways with only Within-Pathway Consumption

6.2.1. Energy Balance
6.2.2. Efficiencies
6.2.3. Net Energy Ratio and Other Energy Return Ratios
6.3. One Pathway, n Stages
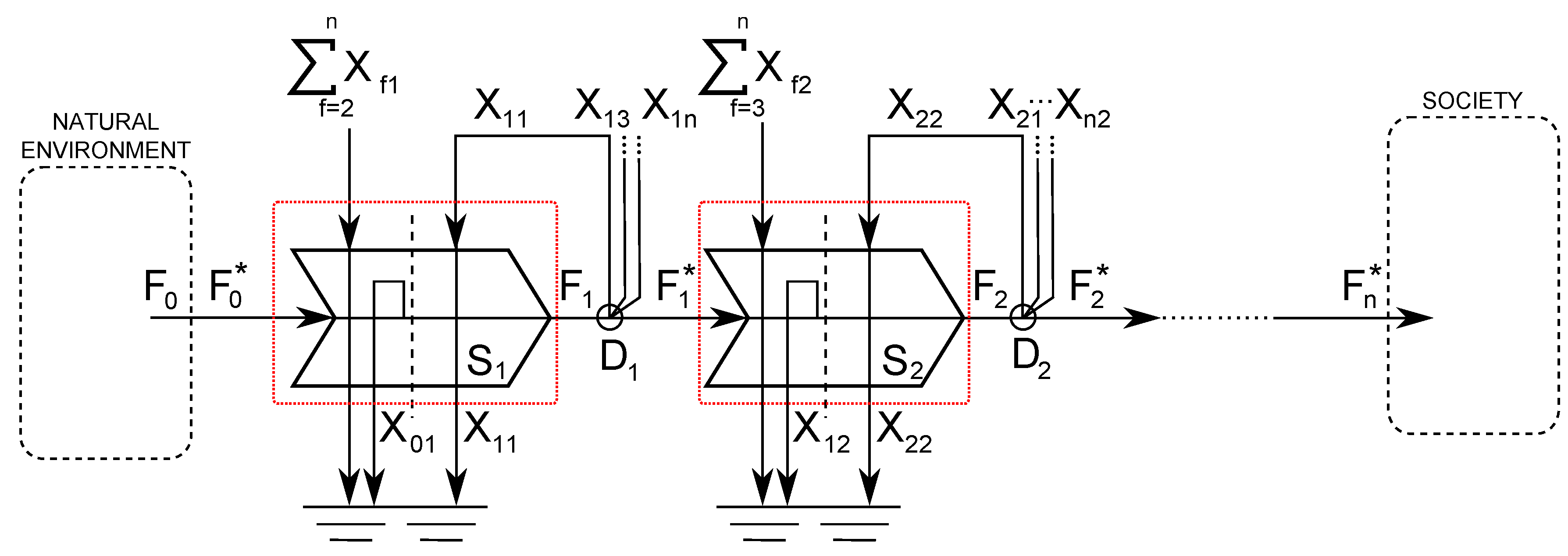
6.3.1. Energy Balance
6.3.2. Efficiencies and Normalized Quantities
6.3.3. Energy Return Ratios
6.4. One Pathway, n Stages, with External Energy Inputs
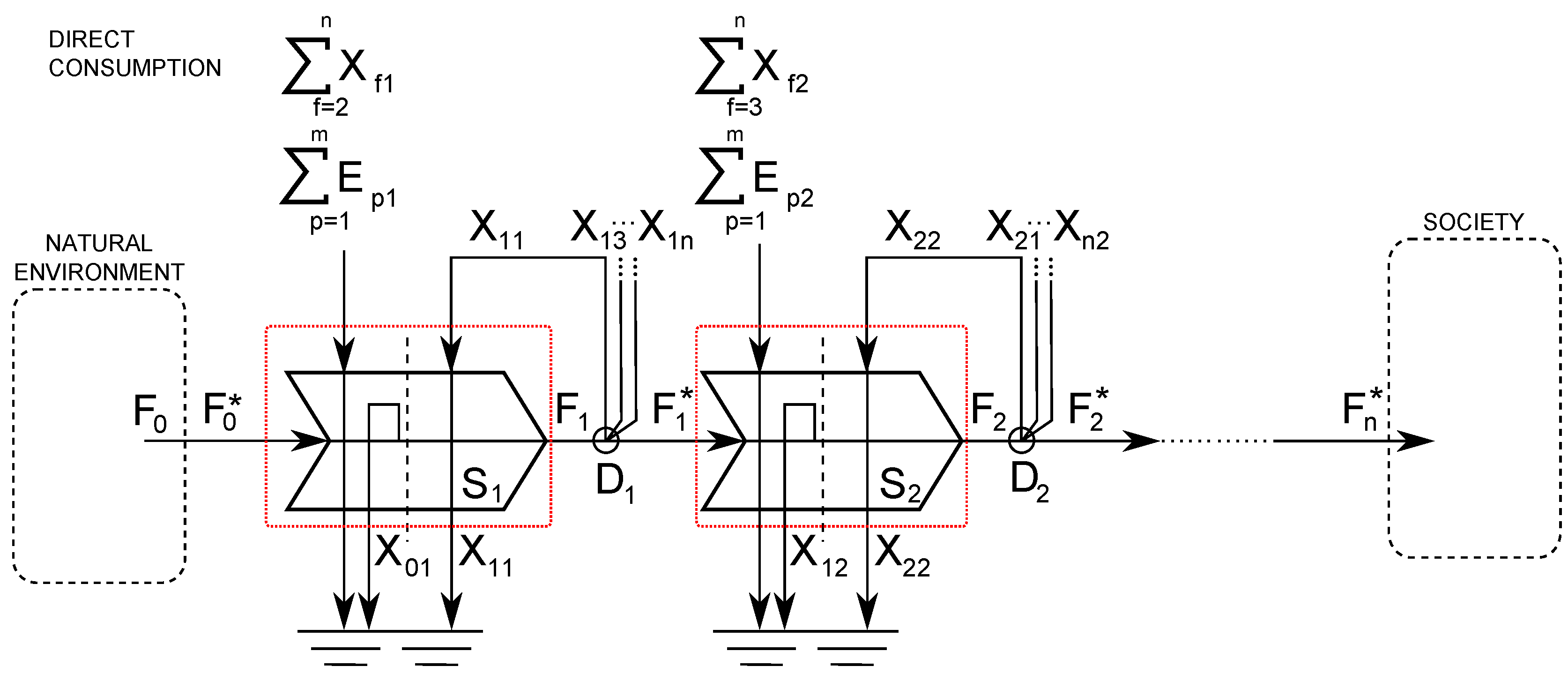
6.4.1. Energy Balance
6.4.2. Efficiencies
6.4.3. Net Energy Ratio
6.4.4. Pathways with Indirect Consumption of Energy
- Indirect consumption of all energy types due to external energy consumption;
- Indirect consumption of all energy types due to materials consumption in the energy system.
- Indirect consumption of all energy types must be added to the denominator of the NER, GER and EER equivalents;
- Indirect consumption of the principal energy flow must be subtracted from that energy available due to the production process (e.g., must be removed from the numerator of the ratios).
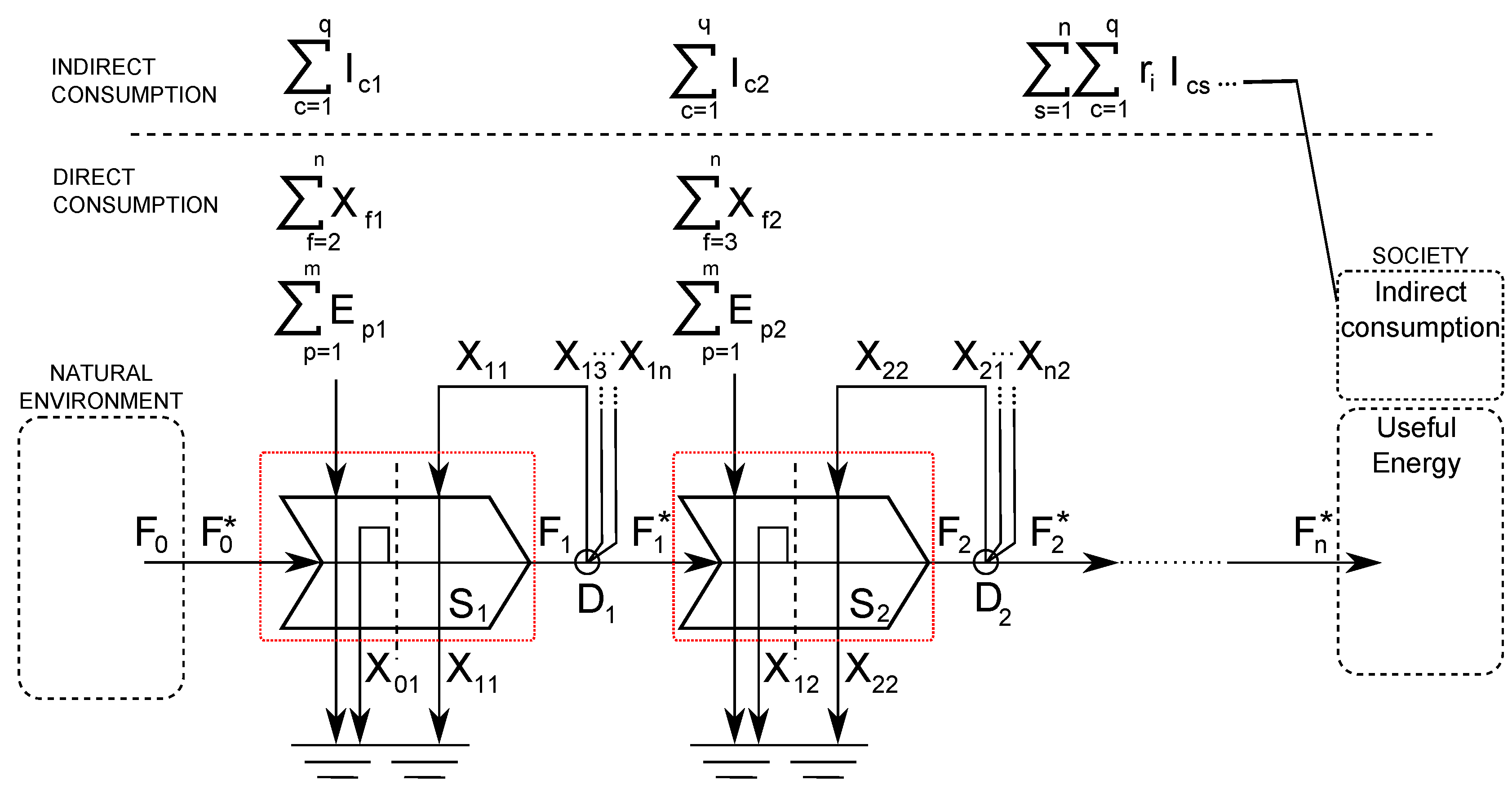
6.4.5. Energy Balance
6.4.6. Efficiencies
6.4.7. Net Energy Ratio and Gross Energy Ratio
6.4.8. External Energy Ratio
Acknowledgements
References and Notes
- Herendeen, R.A. Net energy analysis: Concepts and methods. In Encyclopedia of Energy; Ayres, R.U., Costanza, R., Goldemberg, J., Ilic, M.D., Jochem, E., Kaufmann, R., Lovins, A.B., Munasinghe, M., Pachauri, R.K., Pardo, C.S., Peterson, P., Schipper, L., Slade, M., Smil, V., Worrell, E., Cleveland, C.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Huettner, D.A. Net energy analysis: An economic assessment. Science 1976, 192, 101–104. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, C.J. Energy quality and energy surplus in the extraction of fossil fuels in the US. Ecol. Econ. 1992, 1992, 139–162. [Google Scholar] [CrossRef]
- Cleveland, C.J. Net energy from the extraction of oil and gas in the United States. Energy 2005, 30, 769–782. [Google Scholar] [CrossRef]
- Pacca, S.; Sivaraman, D.; Keoleian, G.A. Parameters affecting the life cycle performance of PV technologies and systems. Energy Policy 2007, 35, 3316–3326. [Google Scholar] [CrossRef]
- Knapp, K.; Jester, T. Empirical investigation of the energy payback time for photovoltaic modules. Sol. Energy 2001, 71, 165–172. [Google Scholar] [CrossRef]
- EROI is sometimes called the energy return on energy invested, or EROEI.
- Hall, C.A.S.; Balogh, S.; Murphy, J. What is the minimum EROI that a sustainable society must have? Energies 2009, 2, 25–47. [Google Scholar] [CrossRef]
- Odum, H.T. Environment, Power, and Society; Wiley-Interscience: New York, NY, USA, 1971. [Google Scholar]
- CERI. Net Energy Analysis: An Energy Balance Study of Fossil Fuel Resources; Colorado Energy Research Institute: Golden, CO, USA, 1976. [Google Scholar]
- Spreng, D.T. Net Energy Analysis and the Energy Requirements of Energy Systems; Praeger Publishers: New York, NY, USA, 1988. [Google Scholar]
- Hannon, B. Energy discounting. In Energetics and Systems; Mitsch, W.J., Ragade, R., Bosserman, R.W., Dillion, J.A.J., Eds.; Ann Arbor Science: Ann Arbor, MI, USA, 1982. [Google Scholar]
- Spitzley, D.V.; Keoleian, G. Life Cycle Environmental and Economic Assessment of Willow Biomass Electricity: A Comparison with Other Renewable and Non-Renewable Sources; Technical Report CSS04-05R; University of Michigan: Ann Arbor, MI, USA, 2004. [Google Scholar]
- Mulder, K.; Hagens, N.J. Energy return on investment: Toward a consistent framework. AMBIO: J. Hum. Environ. 2008, 37, 74–79. [Google Scholar] [CrossRef]
- Murphy, D.J.; Hall, C.A.S.; Cleveland, C.J. Order from chaos: A preliminary protocol for determining EROI for fuels. In Presented at the Association for Study of Peak Oil-USA Conference, Boston, MA, USA, 25–27 October 2006.
- Brandt, A.R. Converting oil shale to liquid fuels: Energy inputs and greenhouse gas emissions of the Shell in situ conversion process. Environ. Sci. Technol. 2008, 42, 7489–7495. [Google Scholar] [CrossRef] [PubMed]
- Brandt, A.R. Converting oil shale to liquid fuels with the Alberta Taciuk Processor: Energy inputs and greenhouse gas emissions. Energy & Fuels 2009, 23, 6253–6258. [Google Scholar]
- Norgaard, R.B. Output, Input and Productivity Change in U.S. Petroleum Development: 1939–1968. Ph.D. Thesis, University of Chicago, Chicago, IL, USA, 1971. [Google Scholar]
- Norgaard, R.B. Resource scarcity and new technology in U.S. petroleum development. Nat. Resour. J. 1975, 15, 265–282. [Google Scholar]
- Norgaard, R.B.; Leu, G.J. Petroleum accessibility and drilling technology-an analysis of United-States development costs from 1959 to 1978. Land Econ. 1986, 62, 14–25. [Google Scholar] [CrossRef]
- Livernois, J.R. Empirical-evidence on the characteristics of extractive technologies-the case of oil. J. Environ. Econ. Manag. 1987, 14, 72–86. [Google Scholar] [CrossRef]
- Livernois, J.R.; Uhler, R.S. Extraction costs and the economics of nonrenewable resources. J. Political Econ. 1987, 95, 195–203. [Google Scholar] [CrossRef]
- Ayres, R.; Warr, B. Accounting for growth: The role of physical work. Struct. Change Econ. Dyn. 2005, 16, 181–209. [Google Scholar] [CrossRef]
- Ayres, R. Exergy, power and work in the US economy, 1900–1998. Energy 2003, 28, 219–273. [Google Scholar] [CrossRef]
- Ayres, R.U. Energy efficiency, sustainability, and economic growth. Energy 2007, 32, 634–638. [Google Scholar] [CrossRef]
- Sorrell, S. Energy, Growth, and Sustainability: Five Propositions; SPRU-Science and Technology Policy Research: Colorado, CO, USA, 2010. [Google Scholar]
- King, C.; Zarnikau, J.; Henshaw, P. Defining a Standard Measure for Whole System EROI Combining Economic “Top-Down” and LCA “Bottom-Up” Accounting. In Proceedings of the ASME 2010 4th International Conference on Energy Sustainability (ES2010), Phoenix, AZ, USA, 17–22 May 2010.
- Henshaw, P.; King, C.; Zarnikau, J. System energy assessment (SEA), defining a standard measure of EROI for energy businesses as whole systems. Sustainability 2011, in press. [Google Scholar] [CrossRef]
- Boulding, K. The unimportance of energy. In Energetics and Systems; Mitsch, W.J., Ragade, R., Bosserman, R.W., Dillion, J.A.J., Eds.; Ann Arbor Science: Ann Arbor, MI, USA, 1982. [Google Scholar]
- Boulding [29] cites 7 basic “factors” or elements that are of fundamental value to an economy (or an organism): space, time, matter, energy, information, “know-how”, and “know-what”. These factors are traded off by organisms and economies, such that a company might deploy capital (at matter and energy cost) to save human labor (time). Note that fundamental theories of value can be constructed around a number of of these factors (e.g., labor theory of value).
- Leach, G. Net energy analysis-is it any use? Energy Policy 1975, 1975, 332–344. [Google Scholar] [CrossRef]
- Reap, J.; Roman, F.; Duncan, S.; Bras, B. A survey of unresolved problems in life cycle assessment—Part 1: Goal and scope and inventory analysis. Int. J. Life Cycle Assess. 2008, 13, 290–300. [Google Scholar] [CrossRef]
- Reap, J.; Roman, F.; Duncan, S.; Bras, B. A survey of unresolved problems in life cycle assessment—Part 2: Impact assessment and interpretation. Int. J. Life Cycle Assess. 2008, 13, 374–388. [Google Scholar] [CrossRef]
- The issue of worker food consumption raises important systems boundary questions. Does one count the energy content of the workers’ food (i.e., food calories), the embodied fossil energy in the food (e.g., fertilizer energy inputs), or neither input because the worker would have eaten anyway without the energy project?
- Bullard, C.W.; Penner, P.S.; Pilati, D.A. Net energy analysis: Handbook for combining process and input-output analysis. Resour. Energy 1978, 1, 267–313. [Google Scholar] [CrossRef]
- An excellent analysis of the effect of system boundaries on internal vs. external accounting is given by CERI [10] (p. III-25).
- Hendrickson, C.T.; Horvath, A.; Joshi, S.; Klausner, M.; Lave, L.B.; McMichael, F.C. Comparing two life cycle assessment approaches: A process model-vs. economic input-output-based assessment. Proceedings of the 1997 IEEE International Symposium on Electronics and the Environment 1997, 412, 176–181. [Google Scholar]
- Hendrickson, C.T.; Lave, L.B.; Scott, M.H. Environmental Life Cycle Assessment of Goods and Services: An Input-Output Approach; Resources for the Future: Washington, DC, USA, 2006. [Google Scholar]
- Herendeen, R.A. Input-output techniques and energy cost of commodities. Energy Policy 1978, 6, 162–165. [Google Scholar] [CrossRef]
- It is noted here that energy is never truly “consumed” due to the first law of thermodynamics. This terminology is used throughout to refer to the degradation of useful energy to waste heat, or the destruction of exergy during an energy conversion process.
- Note that we assume that no external energy inputs Ep end up contained within the principal energy flow Fs. This is a simplification made for ease of exposition and solution of the resulting mathematics. Also, we note that flow Xs,s also cannot be incorporated into the output energy stream. In some real-world cases, this assumption is violated, as when an oil refinery incorporates energy from natural-gas-derived hydrogen into the finished product stream.
- Using the EIO LCA tool, very little biomass energy is consumed indirectly in natural gas production. In rounding to two significant figures, no biomass energy is consumed.
- CMU-GDI. Economic Input-Output Life Cycle Assessment (EIO-LCA). US 2002 Industry Benchmark model. 2008. Available online: http://www.eiolca.net/ (accessed on 17 Auguest 2011).
- If we were building a simultaneous multi-pathway model, the specific types of secondary energy resources consumed would have to be accounted in the model through other pathways. Also, thermal energy could be weighted by a physical or economic quality-weighting factor (see discussion below).
- Wang, M.Q. Estimation of Energy Efficiencies of U.S. Petroleum Refineries (Plus Associated Spreadsheet); Center for Transportation Research, Argonne National Laboratory: Argonne, IL, USA, 2008.
- Denholm, P.; Kulcinski, G.L. Life cycle energy requirements and greenhouse gas emissions from large scale energy storage systems. Energy Convers. Manag. 2004, 45, 2153–2172. [Google Scholar] [CrossRef]
- ηα is derived from an energy balance on a pathway with no external consumption, as illustrated in the appendix.
- This quantity has been called by a number of names, including Process Net Energy Ratio (PNER) [10], energy yield ratio (EYR) and net energy ratio (NER). The same CERI report also defines a related metric called the Resource Net Yield Ratio that includes in the denominator energy lost or rendered unrecoverable through the extraction process. Metrics also differ by whether they consider the gross or net output from a process.
- In other studies, this quantity is variously called the incremental energy ratio, or IER [1], or the external net energy ratio (ENER) [10].
- Note that methods for calculating EROI have varied significantly to date, but this metric seems the most congruent with the general goals of EROI analysis.
- Tzimas, E.; Georgakaki, A.; Cortes, C.; Peteves, S. Enhanced Oil Recovery using Carbon Dioxide in the European Energy System; Report EUR 21895 EN; European Commission Joint Research Centre: Brussels, Belgium, December 2005. [Google Scholar]
- Green, D.; Willhite, G. Enhanced Oil Recovery; Society of Petroleum Engineers: Richardson, TX, UAS, 1998. [Google Scholar]
- Since there are no measured Xj,k flows between stages within the pathway under study, ηα = ηβ. Likewise, the NER, GER and the NEER and GEER are equal, since X3,j flows are unknown.
- Ray, S. Electrical Power Systems: Concepts, Theory and Practice; Printice-Hall of India: New Delhi, India, 2007. [Google Scholar]
- Nishimura, A.; Hayashi, Y.; Tanaka, K.; Hirota, M.; Kato, S.; Ito, M.; Araki, K.; Hu, E. Life cycle assessment and evaluation of energy payback time on high-concentration photovoltaic power generation system. Appl. Energy 2010, 87, 2797–2807. [Google Scholar] [CrossRef]
- King, D.; Gonzalez, S.; Galbraith, G.; Boyson, W. Performance Model for Grid-Connected Photovoltaic Inverters; Sandia Report, SAND2007-5036; Sandia National Laboratories: Livermore, CA, USA, 2007. [Google Scholar]
- Hermann, W. Quantifying global exergy resources. Energy 2006, 31, 1349–1366. [Google Scholar] [CrossRef]
- Cleveland, C.J.; Kaufman, R.K.; Stern, D.I. Aggregation and the role of energy in the economy. Ecol. Econ. 2000, 32, 301–317. [Google Scholar] [CrossRef]
- Cleveland, C.J.; Kaufmann, R.K.; Stern, D.L. Aggregation of energy. In Encyclopedia of Energy; Ayres, R.U., Costanza, R., Goldemberg, J., Ilic, M.D., Jochem, E., Kaufmann, R., Lovins, A.B., Munasinghe, M., Pachauri, R.K., Pardo, C.S., Peterson, P., Schipper, L., Slade, M., Smil, V., Worrell, E., Cleveland, C.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; Volume 1. [Google Scholar]
- This is a common feature of mathematical models with “recycle” loops (e.g., chemical engineering systems with recycle of unreacted product).
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Brandt, A.R.; Dale, M. A General Mathematical Framework for Calculating Systems-Scale Efficiency of Energy Extraction and Conversion: Energy Return on Investment (EROI) and Other Energy Return Ratios. Energies 2011, 4, 1211-1245. https://doi.org/10.3390/en4081211
Brandt AR, Dale M. A General Mathematical Framework for Calculating Systems-Scale Efficiency of Energy Extraction and Conversion: Energy Return on Investment (EROI) and Other Energy Return Ratios. Energies. 2011; 4(8):1211-1245. https://doi.org/10.3390/en4081211
Chicago/Turabian StyleBrandt, Adam R., and Michael Dale. 2011. "A General Mathematical Framework for Calculating Systems-Scale Efficiency of Energy Extraction and Conversion: Energy Return on Investment (EROI) and Other Energy Return Ratios" Energies 4, no. 8: 1211-1245. https://doi.org/10.3390/en4081211
APA StyleBrandt, A. R., & Dale, M. (2011). A General Mathematical Framework for Calculating Systems-Scale Efficiency of Energy Extraction and Conversion: Energy Return on Investment (EROI) and Other Energy Return Ratios. Energies, 4(8), 1211-1245. https://doi.org/10.3390/en4081211





