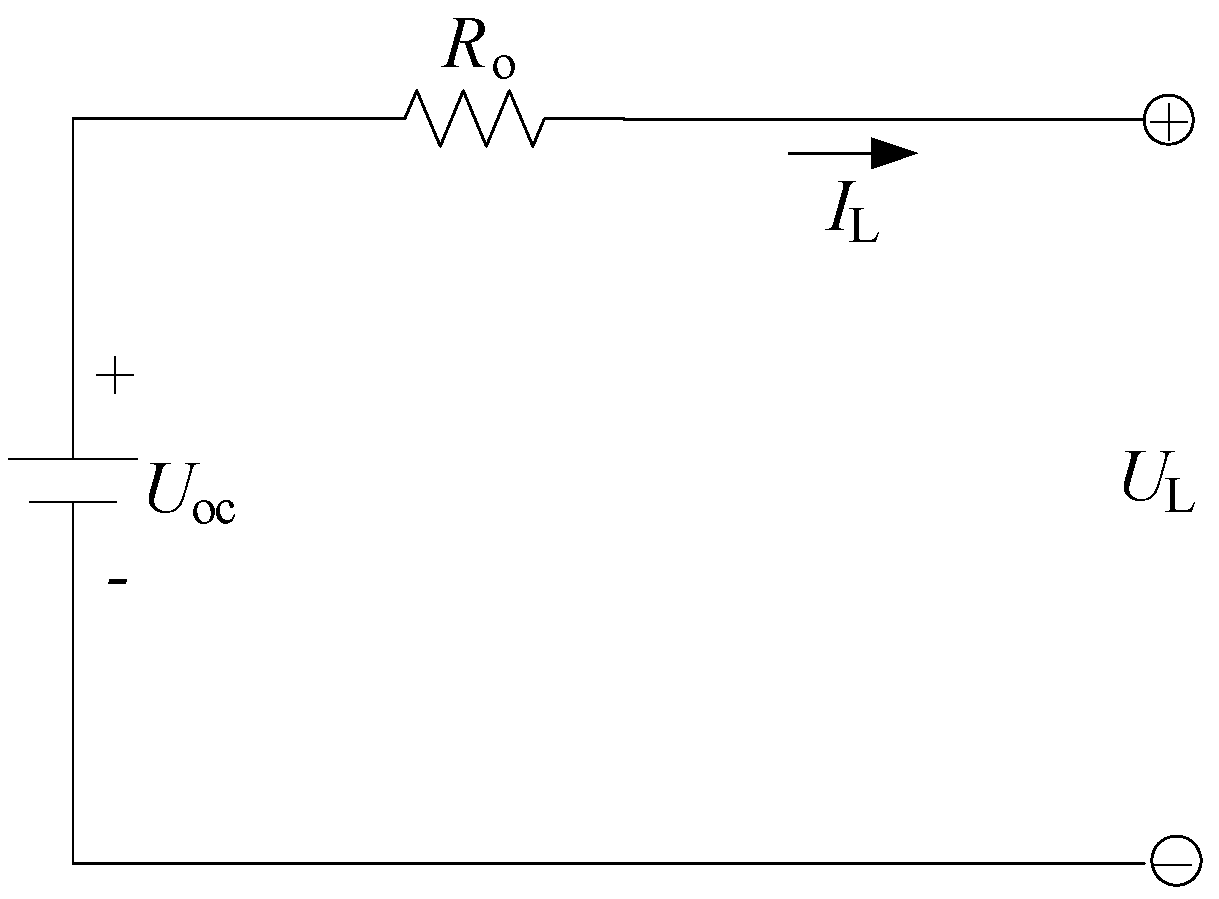
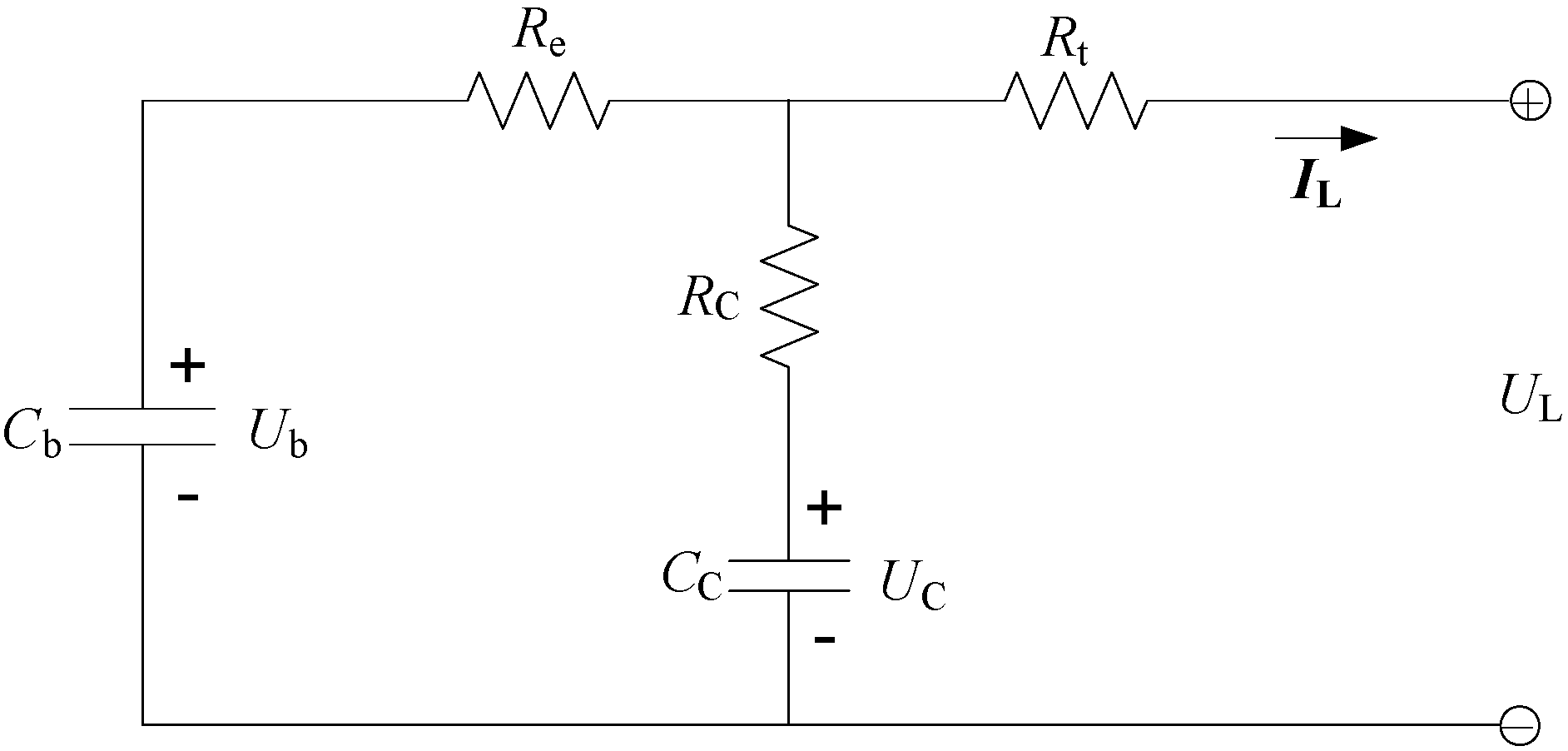
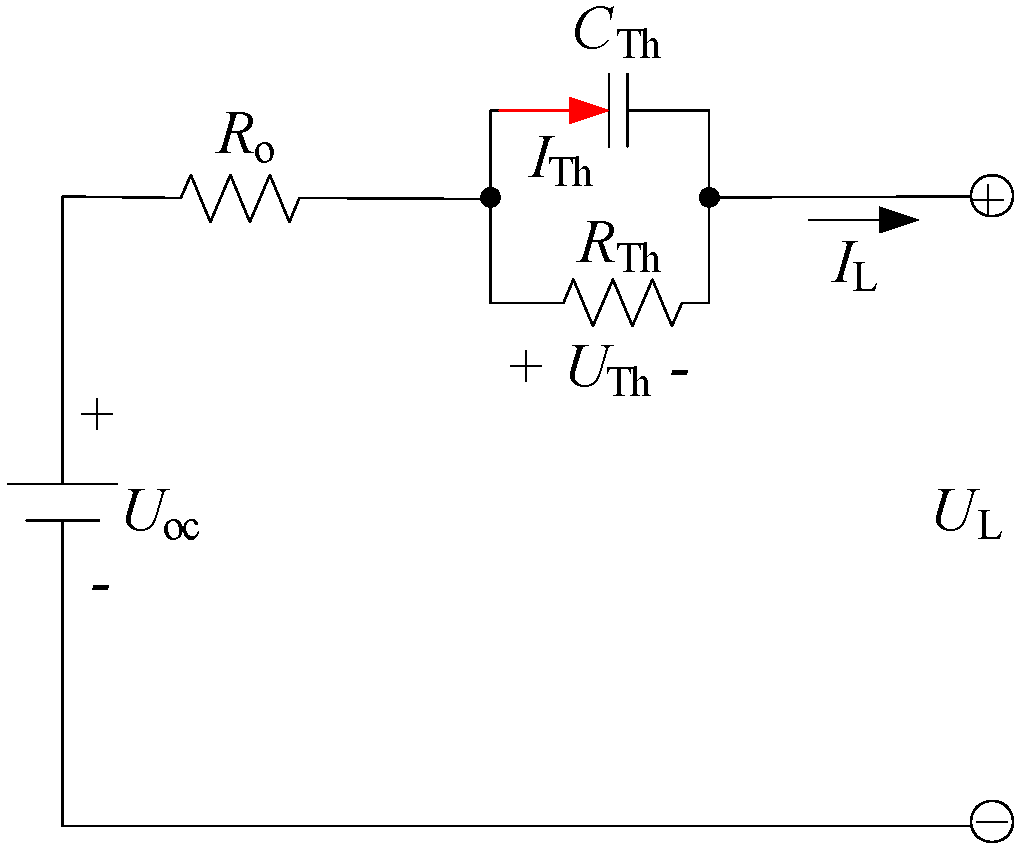
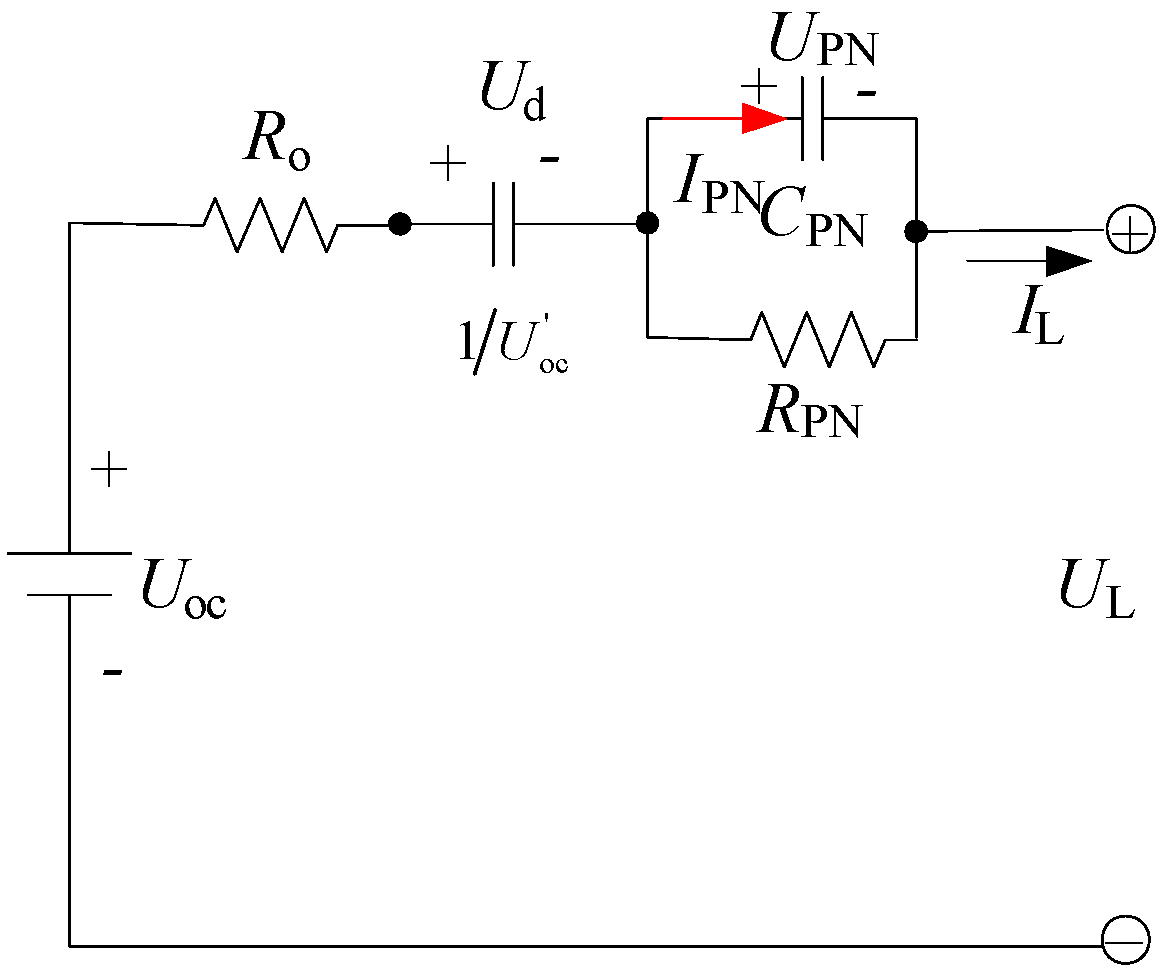
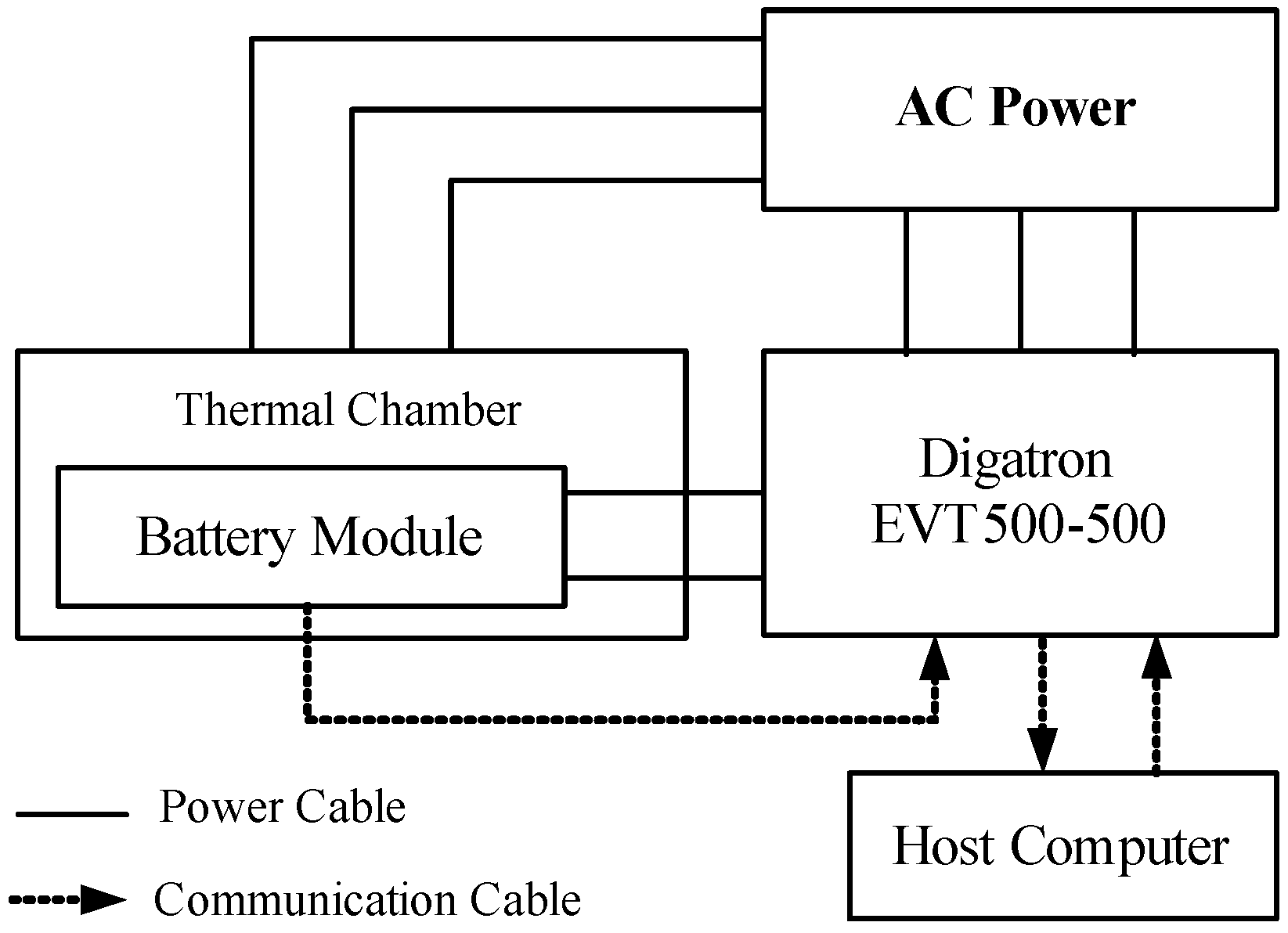
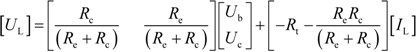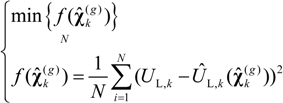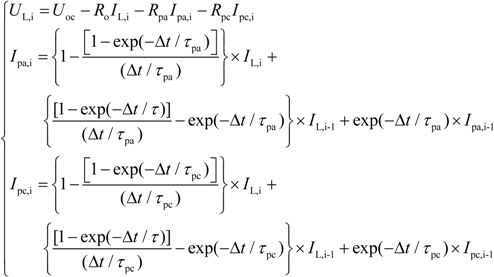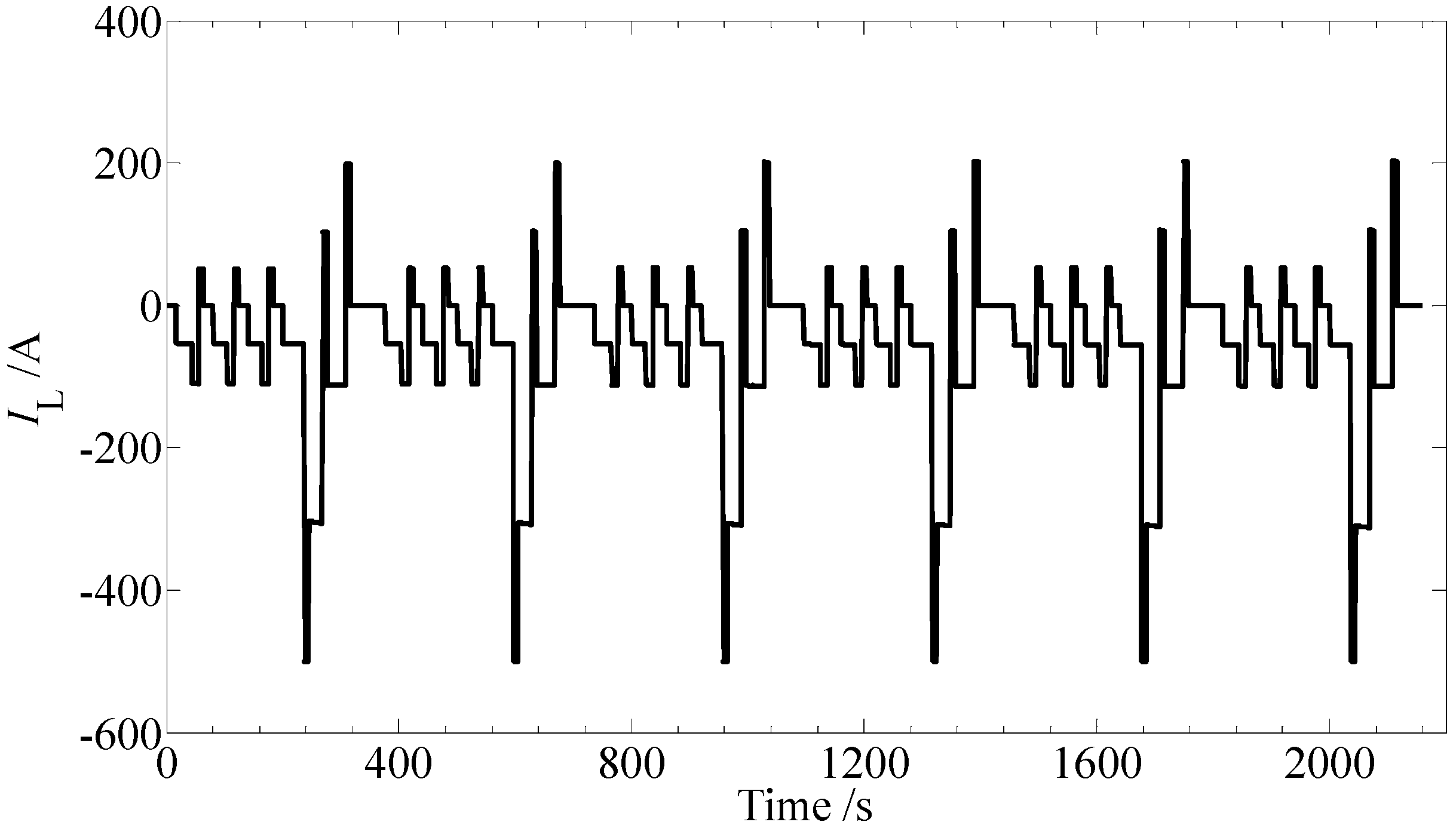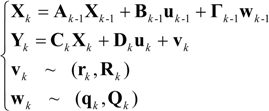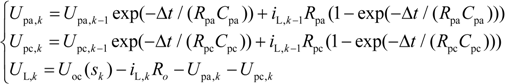4.1. Model Verification
To evaluate the validity of the battery models, six consecutive Dynamic Stress Test (DST) cycles [
16] which is a standard testing program of the EVT500-500, are adopted as the input for both the lithium-ion battery module and the battery models, as shown in
Figure 8. The initial SoC is 100%. The parameters of the battery models as a function of SoC are updated via linear lookup table and extrapolation.
Figure 8.
The load current profiles of 6 DST testing cycles.
Figure 8.
The load current profiles of 6 DST testing cycles.
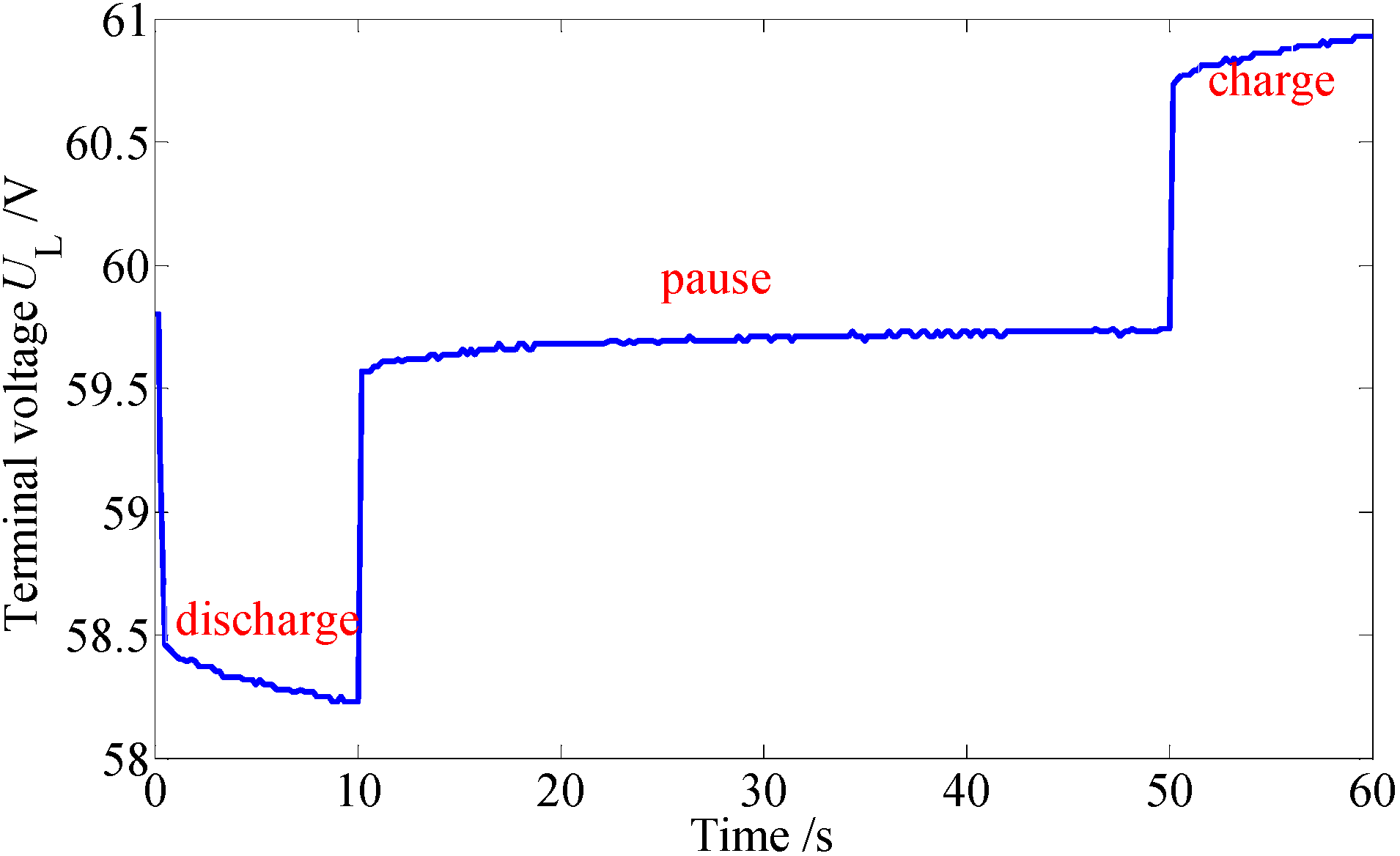
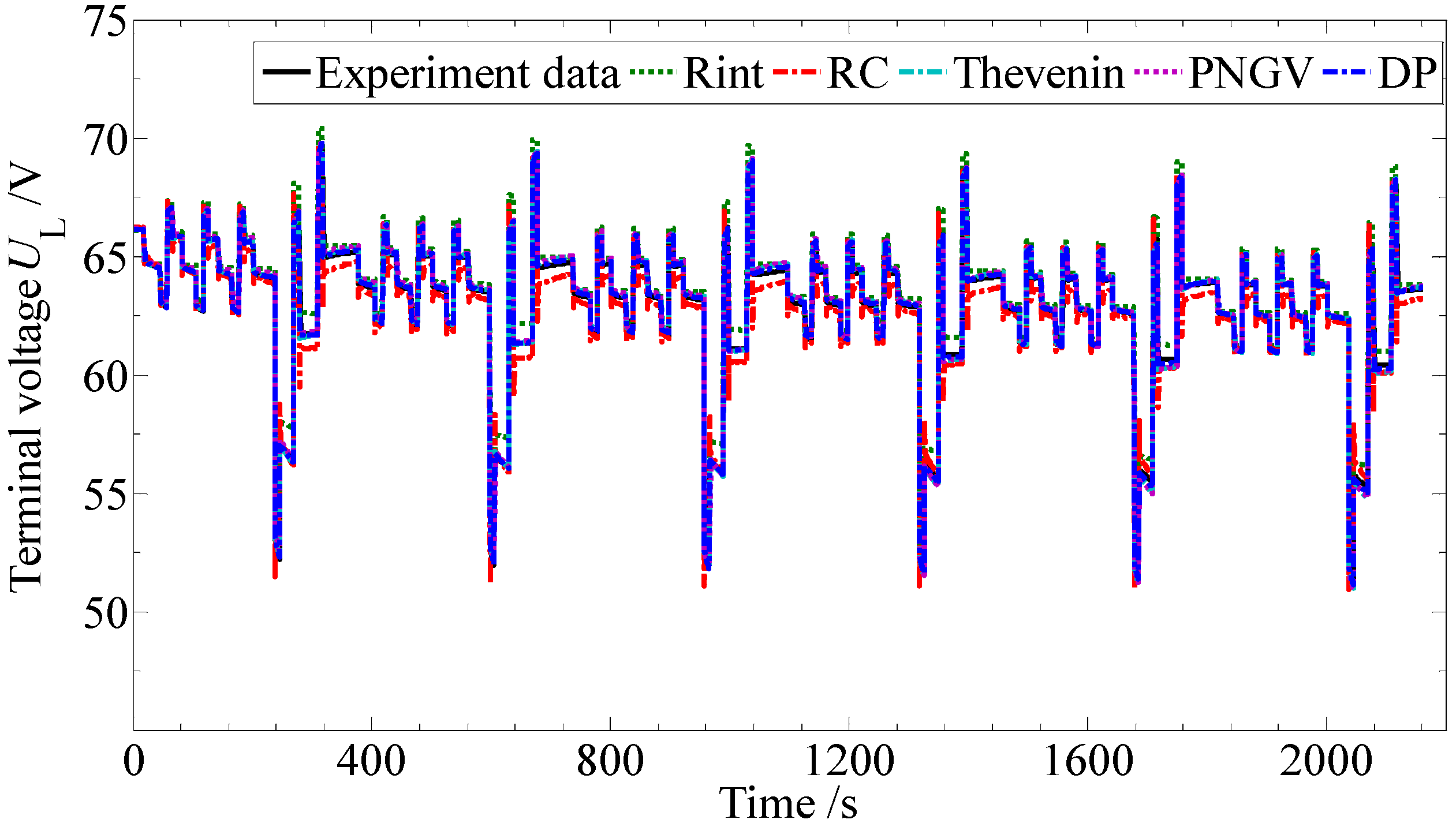
Figure 9 presents the terminal voltage curves of the experimental data and the model-based simulation data.
Figure 9.
The terminal voltage profiles of the model-based simulation and experiment.
Figure 9.
The terminal voltage profiles of the model-based simulation and experiment.
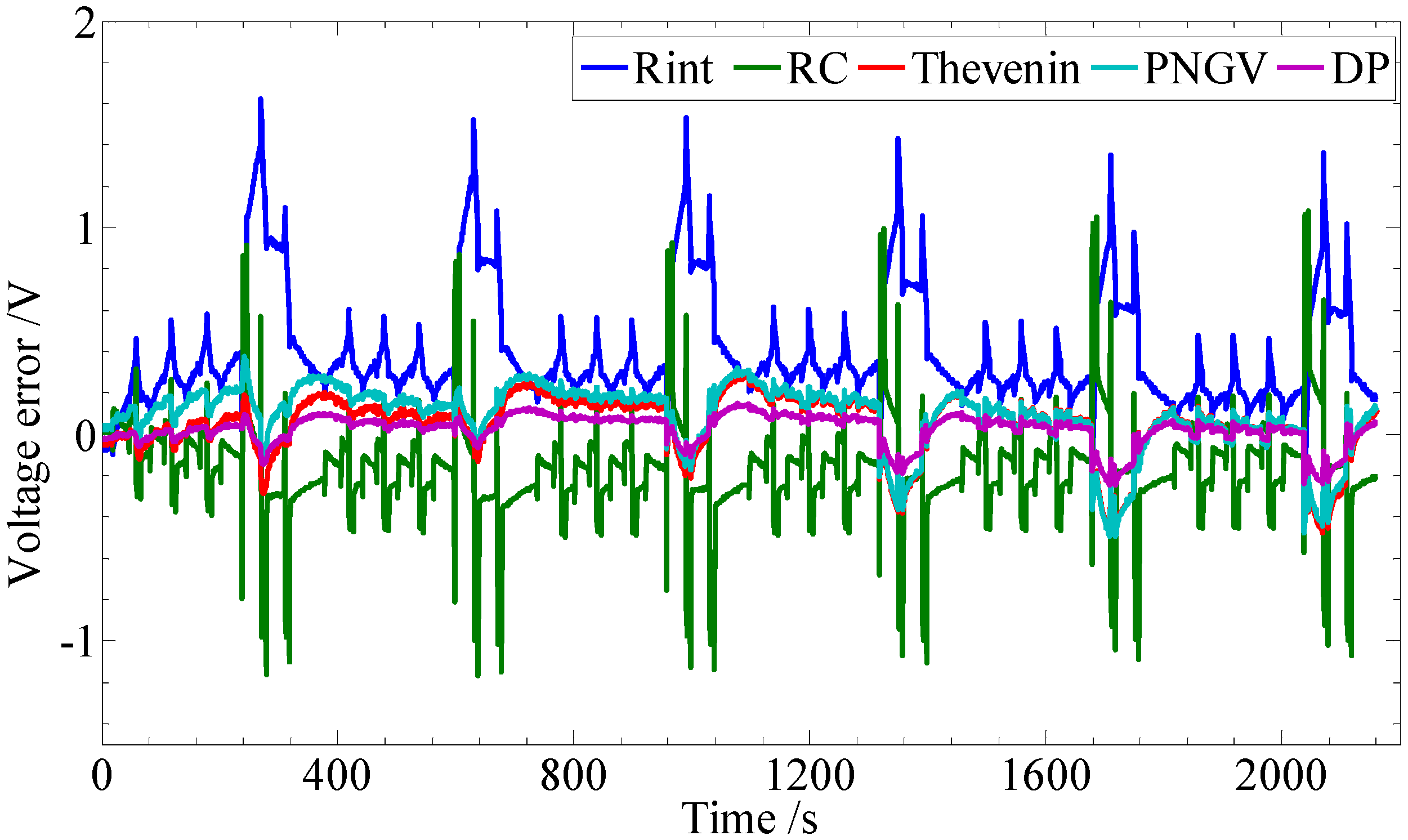
The comparison curves of the terminal voltage between the experimental data and the model-based simulation data are drawn as shown in
Figure 10.
Figure 10.
The terminal voltage error curves between the simulation and experiment.
Figure 10.
The terminal voltage error curves between the simulation and experiment.
It can be concluded that all five equivalent circuit models simulate the dynamic characteristics to some extent, albeit with different accuracy. Both the DP model and the Thevenin model have better dynamic simulation results, which indicates that these two models are more suitable for the modeling of lithium-ion batteries.
4.3. Evaluation on the Adaptability of the Battery Models for SoC Estimation
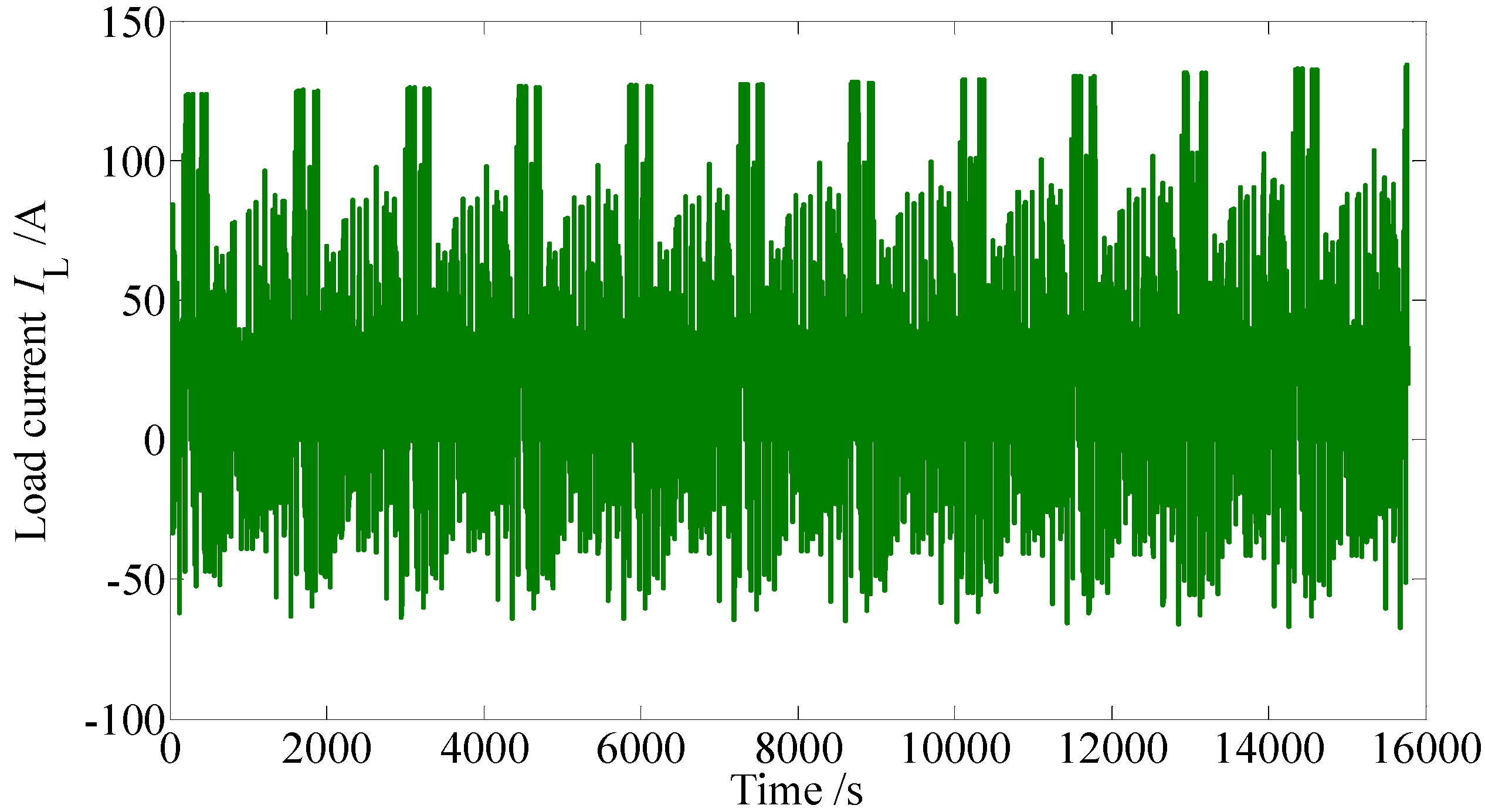
The Federal Urban Driving Schedules (FUDS) is a typical driving cycle which is often used to evaluate various SoC estimation algorithms. In this paper, eleven consecutive FUDS were employed to verify the SoC estimation approach, and the sampled current profiles are shown in
Figure 11.
Figure 11.
Load Current profile sampled during eleven consecutive FUDS cycles.
Figure 11.
Load Current profile sampled during eleven consecutive FUDS cycles.
The model-based SoC estimation greatly depends on the algorithms and this may lead to a fluctuant, even divergent result. The Kalman filter algorithm can reduce the fluctuation by adjusting the gain matrix based on the error between the model-observed value and the actual value of the terminal voltage, and gradually make the SoC estimation approach the true value. Meanwhile, another feature of the Kalman filter is its strong dependence on the model accuracy [
14,
16]. In order to reduce the dependence of the Kalman filter on uncertain factors, a robust extended Kalman filter (REKF) algorithm is selected and designed for the implementation of the SoC estimation [
19,
20].
The SoC estimations with REKF algorithm were conducted for the five models. A detailed description with the DP model taken as an example follows:
The state equation and observation equation of the discrete system of interest with REKF algorithm is as follows:
where
X is a
n × 1 state matrix;
Y is a
m × 1 observe matrix;
A,
B,
C,
D and
Γ are
n ×
n,
n × 1,
m ×
n,
m × 1 and
n ×
n matrix respectively;
wk is a process noise with mean of
qk and covariance of
Qk;
vk is the measurement noise with mean of
rk and covariance of
RkTransform the Equation (6) to a discrete system:
Define state matrix
X and SoC as:
Then, the matrix
A,
B,
C and
D can be written as follows:
where,
s is the abbreviation of SoC, Δ
t is the sample step,
η is the coulombic efficiency,
CN is the nominal capacity of the battery.
The experimental data of the coulombic efficiency under different charging/discharging current for the lithium-ion battery module are shown in
Table 7, which shows that the coulombic efficiency decreases with the increase of the discharge current and it is necessary to limit the discharge current range for a higher efficiency.
Set the initial values as:
X0 = [0 0 1]
T;
R = 10;
Q = diag (0.00001, 0.00001, 0.00001, 0.00001, 0.00001);
P0 = diag (1, 0.1, 0.1, 0.1, 0.1) (herein,
P is the covariance matrix of
X). The DP model-based SoC estimation results with REKF are shown in
Figure 12.
Table 7.
Coulombic efficiency list of the lithium-ion battery module.
Table 7.
Coulombic efficiency list of the lithium-ion battery module.
| Current (A) | 30 | 50 | 100 | 150 | 200 | 300 |
|---|
| Coulombic efficiency in discharging process (%) | 100 | 99.3 | 98.5 | 98.1 | 97.4 | 95.2 |
| Coulombic efficiency in charging process (%) | 100 | 98.5 | 97.4 | 96.0 | 94.0 | - |
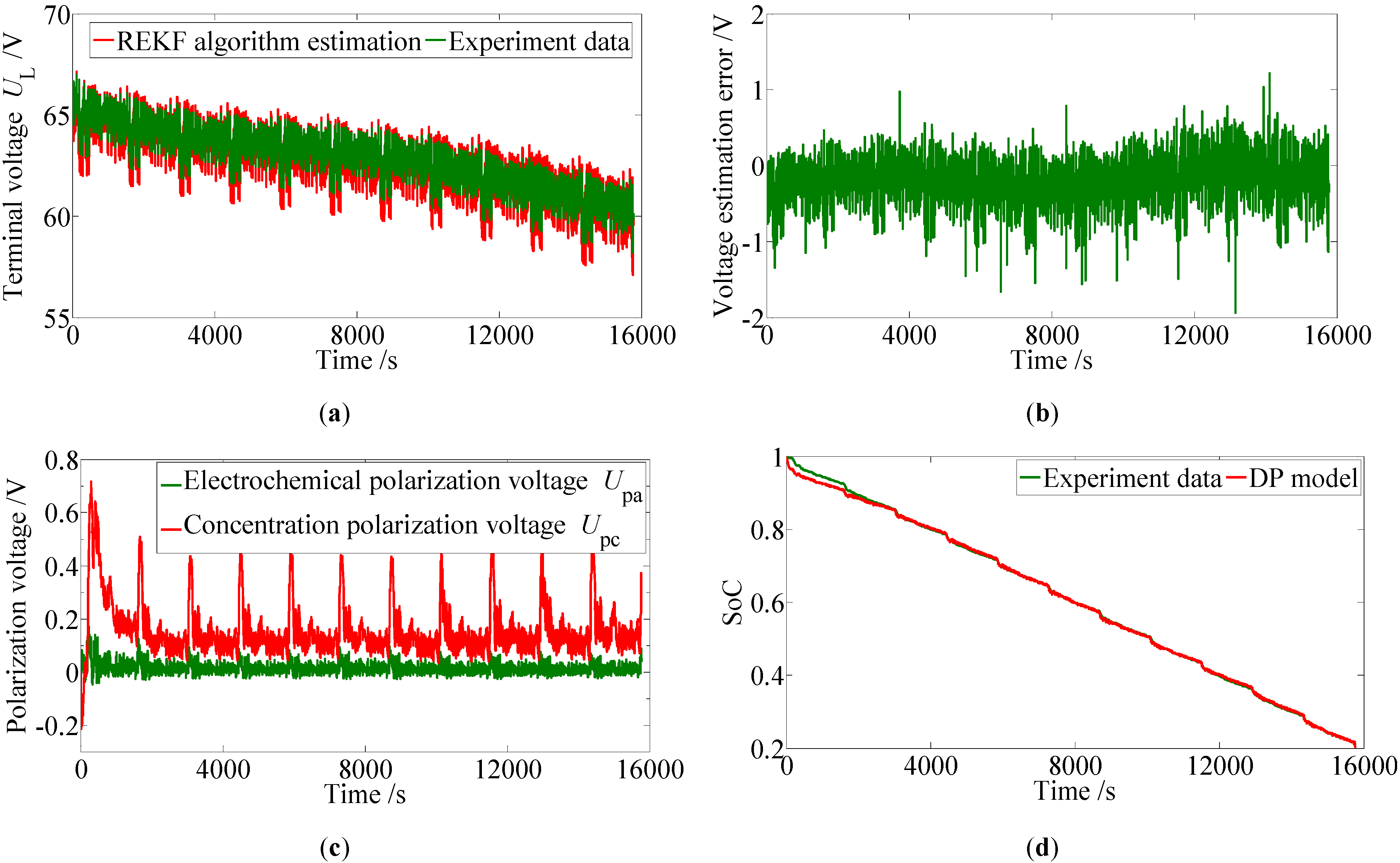
Figure 12.
The DP model-based SoC estimation results with REKF: (a) Terminal voltage; (b) Voltage estimation error; (c) Polarization voltages; (d) SoC.
Figure 12.
The DP model-based SoC estimation results with REKF: (a) Terminal voltage; (b) Voltage estimation error; (c) Polarization voltages; (d) SoC.
4.3.1. SoC Estimation Accuracy
Figure 12(d) shows the experimental SoC data based on the Digatron EVT 500-500 test bench results after proper adjustments as follows: in order to get the true SoC by an experimental approach, firstly, the battery module is fully charged to make sure the initial SoC is 1.0; after the eleven consecutive FUDS test is finished, the battery module is rested for at least 2 hours and a further discharge experiment with nominal current is conducted until the battery module is fully discharged, and then the true value of the terminal SoC can be calculated according to the definition of SoC. Since the true values of the initial SoC and the terminal SoC are determined, the simple Ah counting method is used to calculate the experimental SoC based on the load current profile and the coulomb efficiency map, also a proper adjustment coefficient, which is calculated based on the true values of the initial SoC and terminal SoC, is applied during the calculation. The Ah counting method with an adjustment approach based on a further discharging experiment can only be used in laboratory. Herein, it is used to provide a true SoC profile for comparison purposes. The results of the SoC estimation with REKF for the five models are shown in
Figure 13 and the comparisons between the estimations and the experiment are shown in
Figure 14. A statistic analysis on the absolute SoC estimation errors is conducted and the results including the terminal SoC error are list in
Table 8.
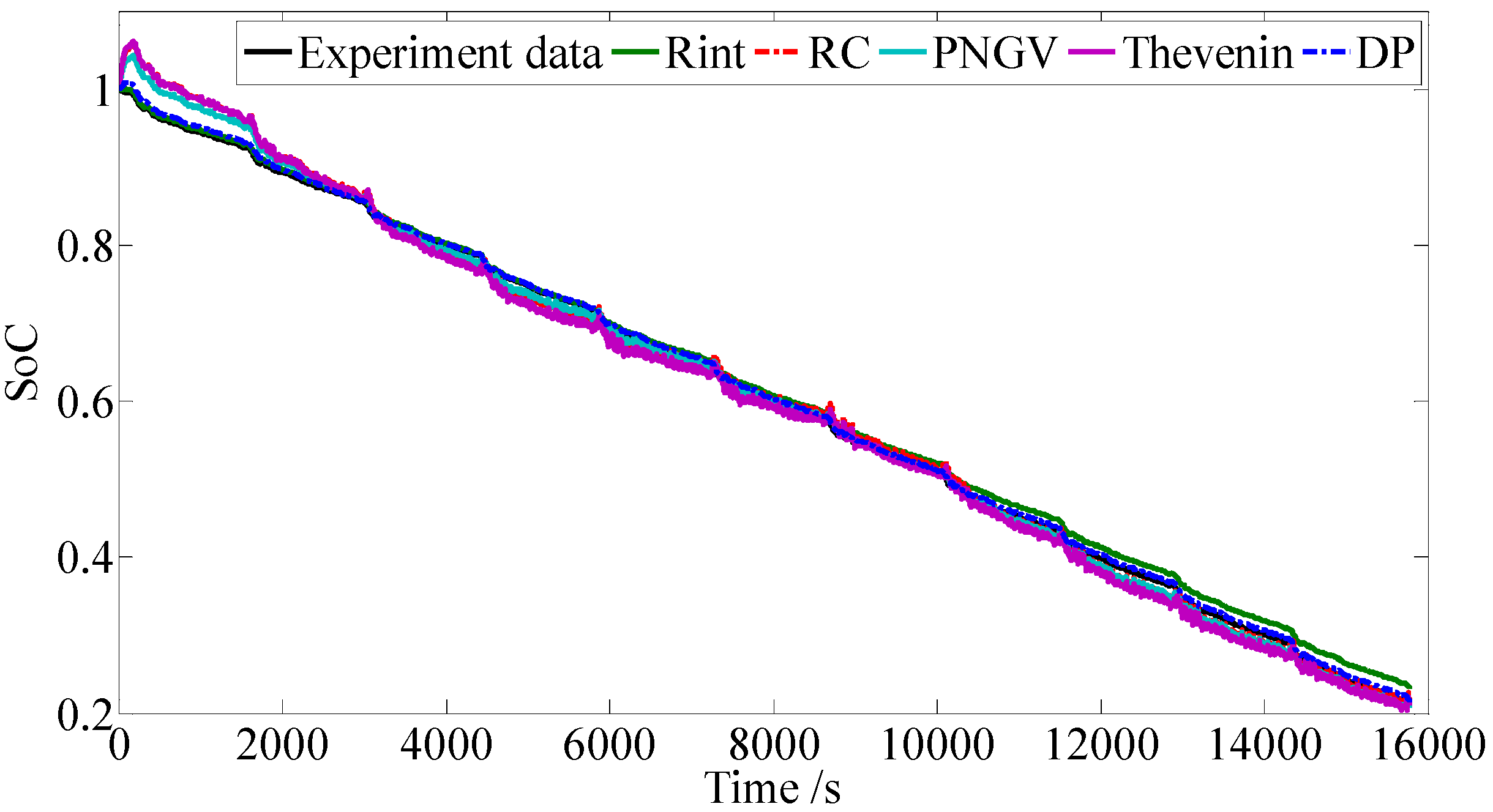
Figure 13.
SoC estimation profiles based on FUDS cycles.
Figure 13.
SoC estimation profiles based on FUDS cycles.
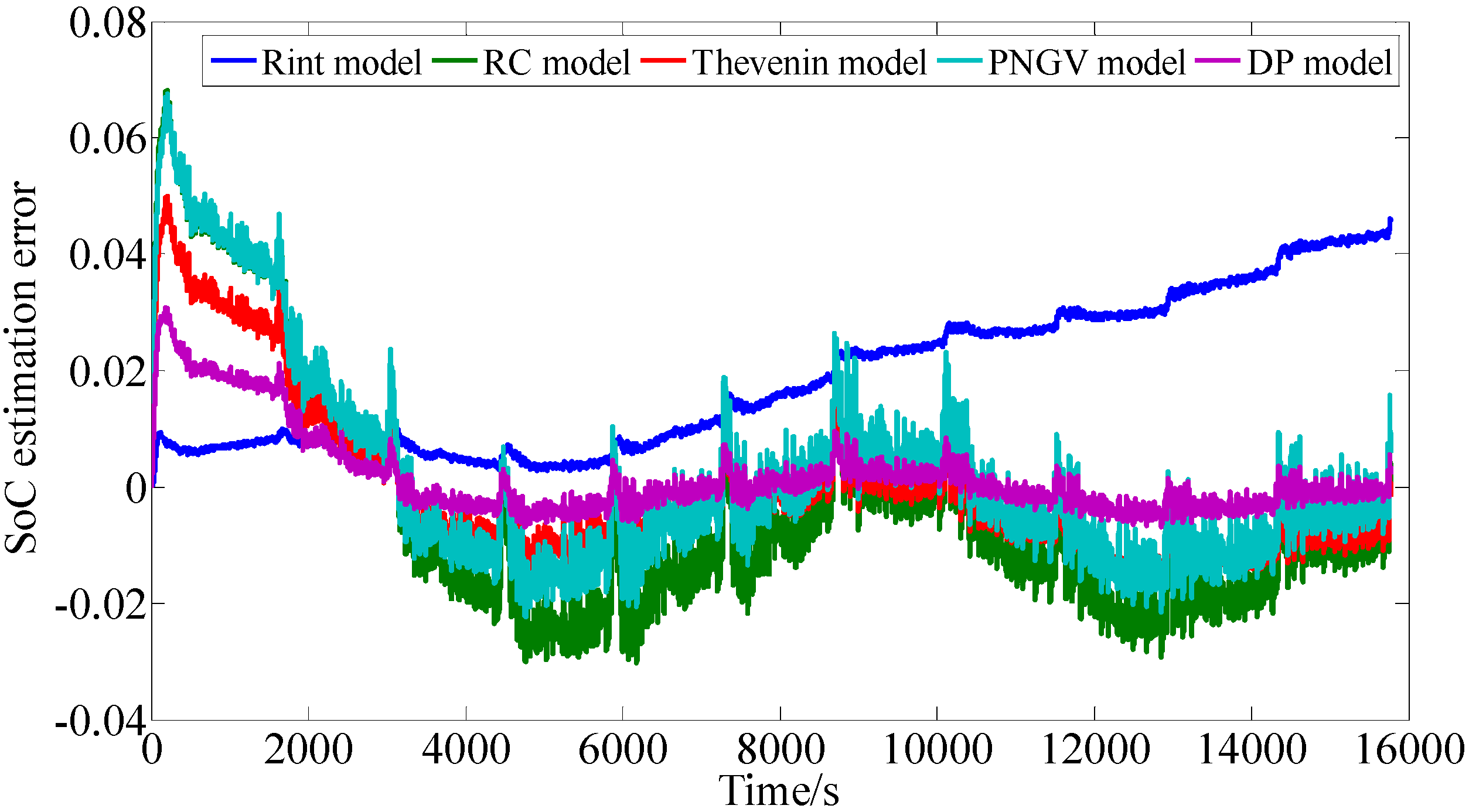
Figure 14.
The SoC estimation error profiles based on FUDS cycles.
Figure 14.
The SoC estimation error profiles based on FUDS cycles.
Table 8.
The statistic list of the absolute SoC estimation error and the terminal SoC error.
Table 8.
The statistic list of the absolute SoC estimation error and the terminal SoC error.
| Model | Maximum | Mean | Variance | Terminal |
|---|
| Rint Model | 0.0462 | 0.0186 | 0.0012 | 0.046 |
| RC Model | 0.0681 | 0.0167 | 0.0009 | 0.013 |
| Thevenin Model | 0.0500 | 0.0101 | 0.0004 | −0.016 |
| PNGV Model | 0.0675 | 0.0126 | 0.0005 | −0.017 |
| DP Model | 0.0309 | 0.0047 | 0.00004 | −0.005 |
According to
Figure 14 and
Table 8, it can be seen that for the Rint model, due to the precise initial SoC and Ah counting method, a minimal SoC error is achieved for the first 2020 s, however, an accumulation error appears and a maximum SoC error is obtained at the end of the calculation due to the lower accuracy of this model. For the other four models with the considerations of the polarization characteristics, there appears a similar fluctuation and tendency, which shows that the SoC error reaches a maximum in the first stage and reduces quickly toward the true SoC during the calculation process with different accuracy. The fact that the maximum of SoC error appears at the first stage for the DP model, the RC model, the Thevenin model, the PNGV model, while that appears at the final stage for the Rint model, shows that the Rint model is not suitable for long time application in SoC estimation except for timely revision of the initial SoC, while the other four models have good performance in SoC estimation especially for long time periods. By comparison, the SoC error for the DP model always stays at a minimum, except for the first 2020 s; this also verifies that the DP model has the highest accuracy for SoC estimation.
4.3.2. Evaluation on the SoC Estimation Accuracy Influenced by Its Initial Value
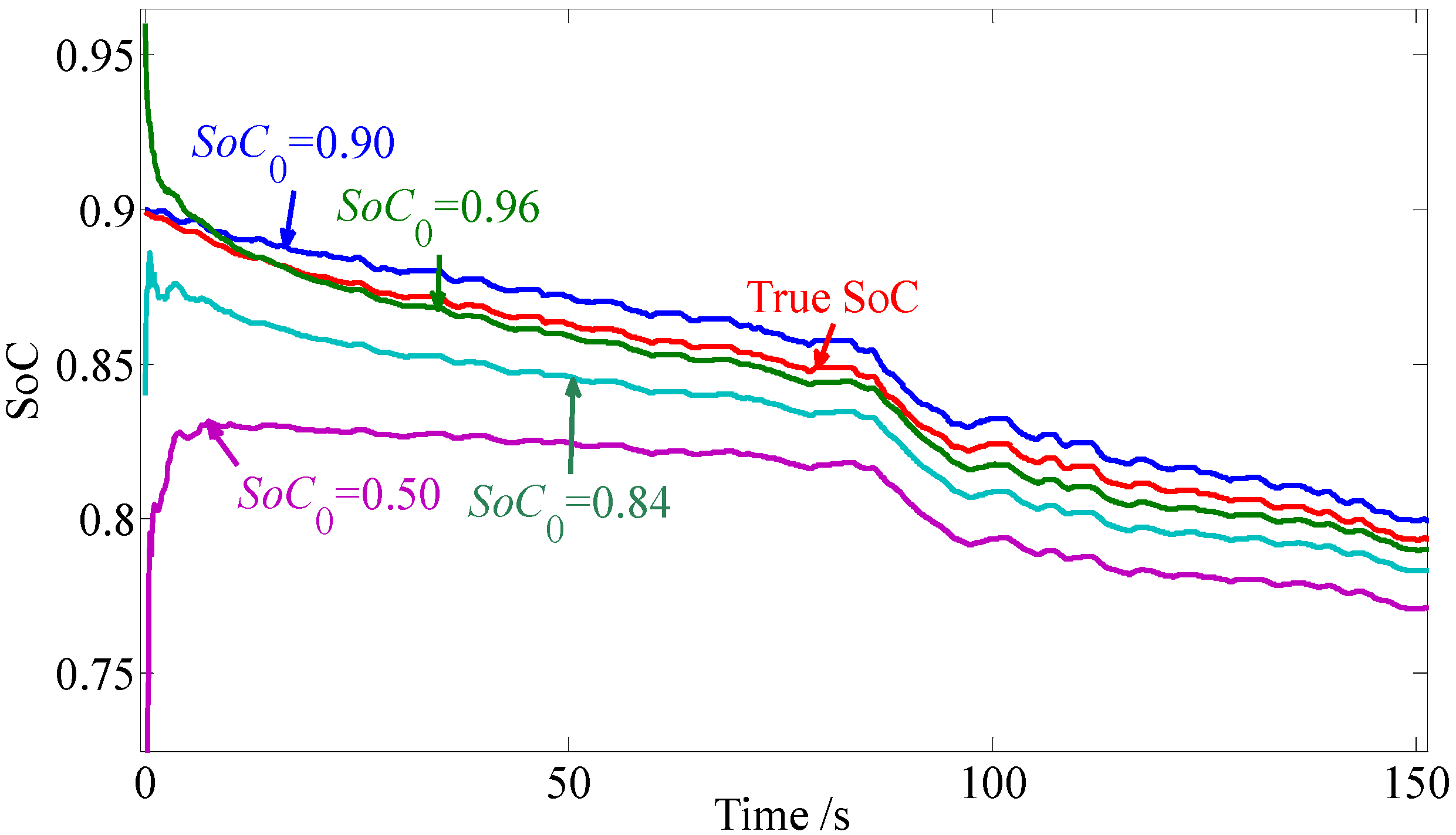
An accurate SoC estimation depends on two aspects according the definition of SoC given by Equation (15), one is the initial SoC, and the other is the calculation of SoC consumption. From the comparison in
Section 4.3.1, the DP model has the highest accuracy for the SoC estimation under the assumption of a precise initial SoC value. In order to investigate whether the SoC estimation with REKF algorithm and the DP model, can effectively solve the initial estimation inaccuracy of SoC, a further simulation analysis is conducted. Four different SoC initial values, 0.90, 0.96, 0.84 and 0.50, are preset and the corresponding SoC estimations are performed based on the FUDS cycles, at the same time, a true SoC is calculated with the true initial SoC of 0.899 based on the FUDS test data. The results are shown in
Figure 15 for the first 150 s and the results of the statistic analysis on the absolute SoC estimation error between the true value and the estimation during 151 s~15775 s are listed in
Table 9. It can be seen that the estimated SoC can effectively converge around the true SoC within 150 s, no matter which initial SoC value is used and its terminal error is within 1.56%.
Figure 15.
The SoC estimation profiles with different SoC initial values.
Figure 15.
The SoC estimation profiles with different SoC initial values.
Table 9.
The statistical list of absolute SoC estimation errors with different initial SoC values after 150 s and the terminal error.
Table 9.
The statistical list of absolute SoC estimation errors with different initial SoC values after 150 s and the terminal error.
| SoC0 | Maximum | Mean | Variance | Terminal Error |
|---|
| 0.90 | 0.0098 | 0.0051 | 2.65 × 10−5 | 0.0070 |
| 0.96 | 0.0181 | 0.0080 | 1.79 × 10−5 | 0.0073 |
| 0.84 | 0.0279 | 0.0105 | 7.40 × 10−5 | 0.0103 |
| 0.50 | 0.0352 | 0.0144 | 3.68 × 10−4 | 0.0156 |