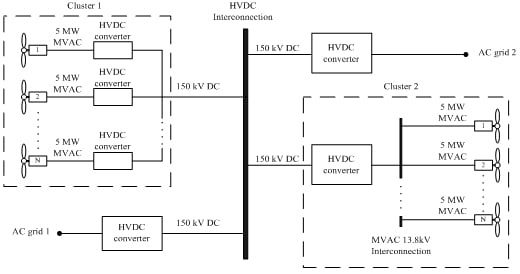
An Examination of AC/HVDC Power Circuits for Interconnecting Bulk Wind Generation with the Electric Grid
Abstract
:1. Introduction
2. HVDC Converter Topologies, a Brief Review
2.1. Current Sourced Converter (CSC)
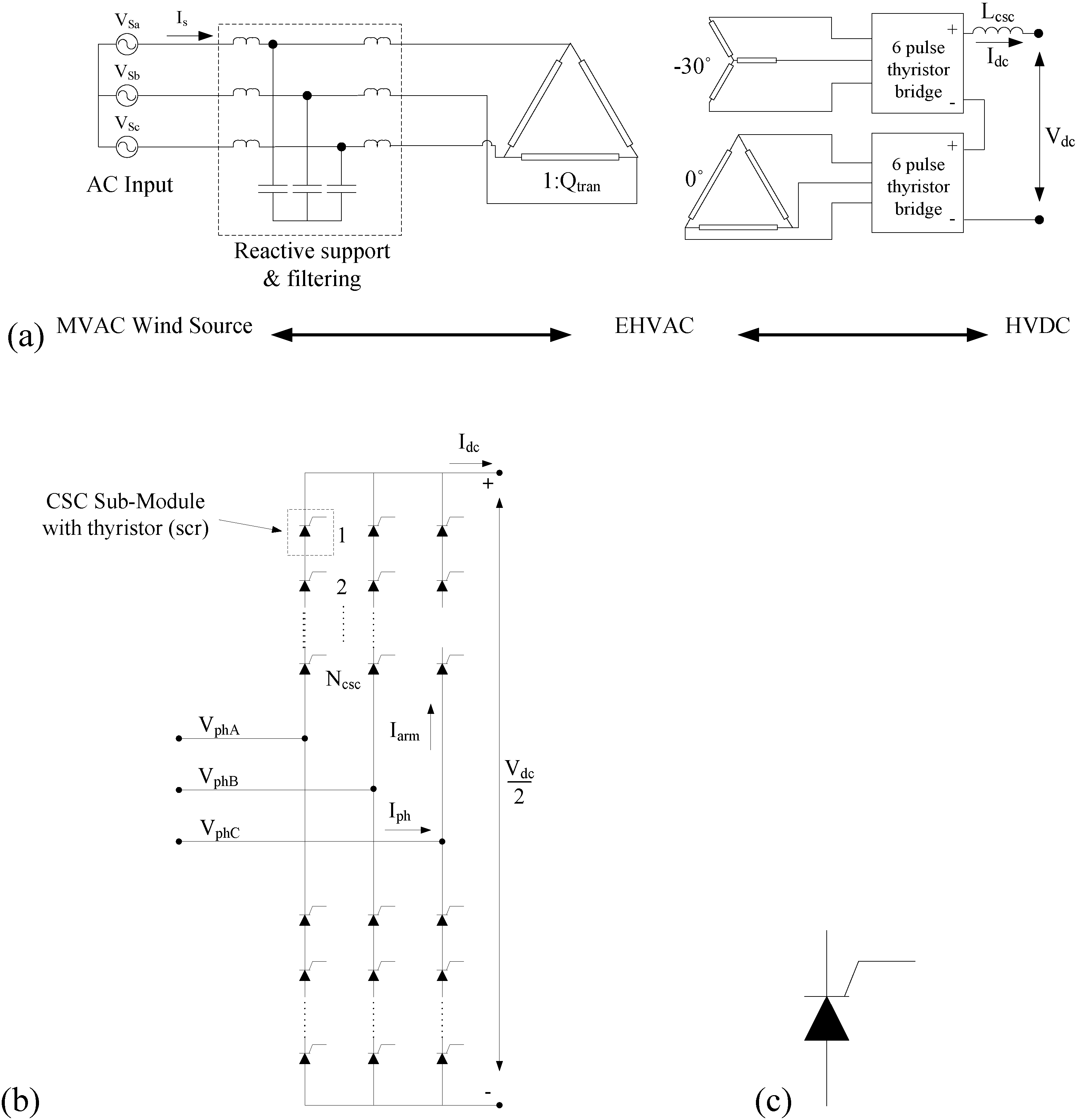
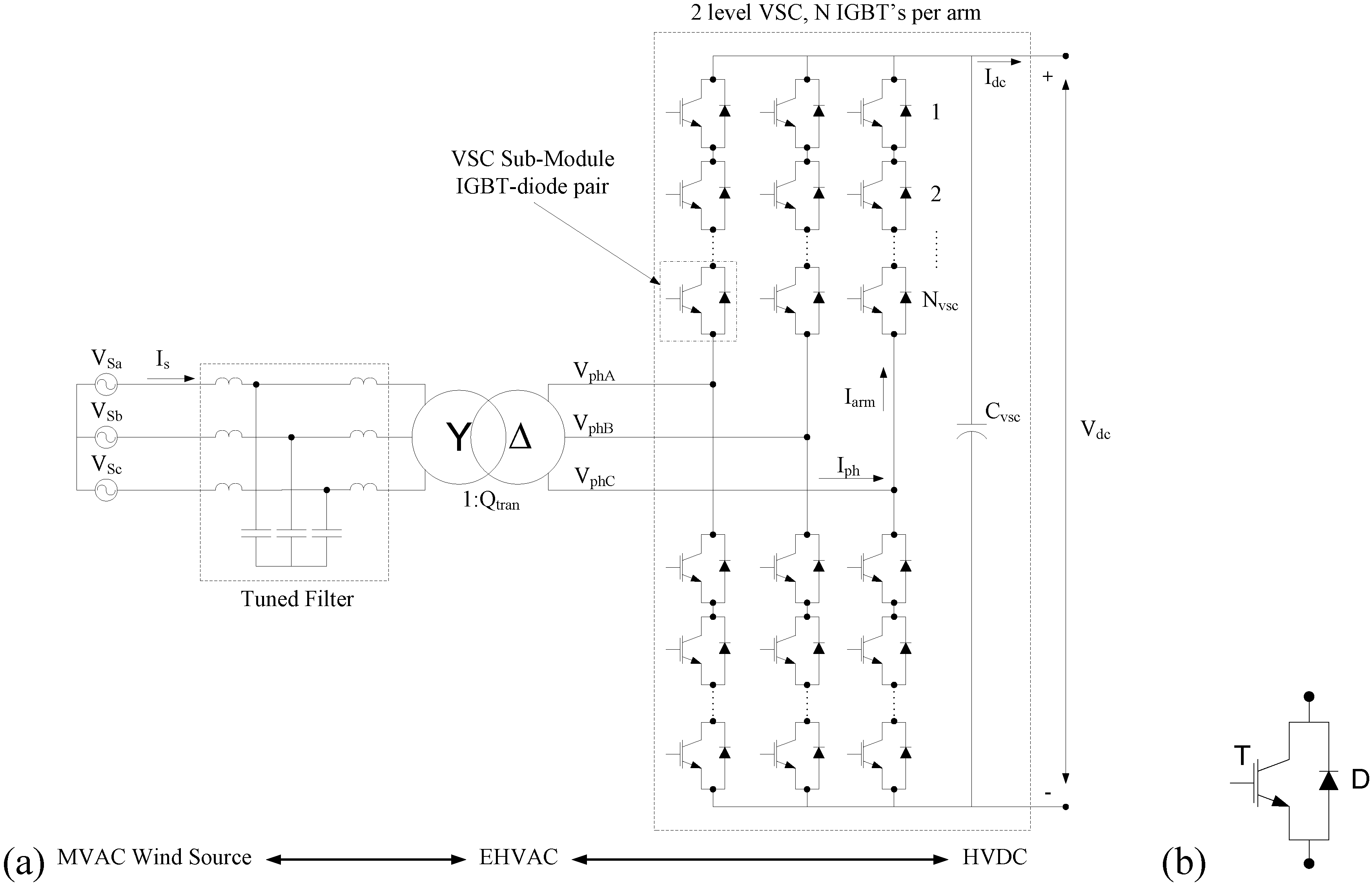
2.2. Voltage Sourced Converter (VSC)
2.3. Bridge of Bridge Converter (BoBC)
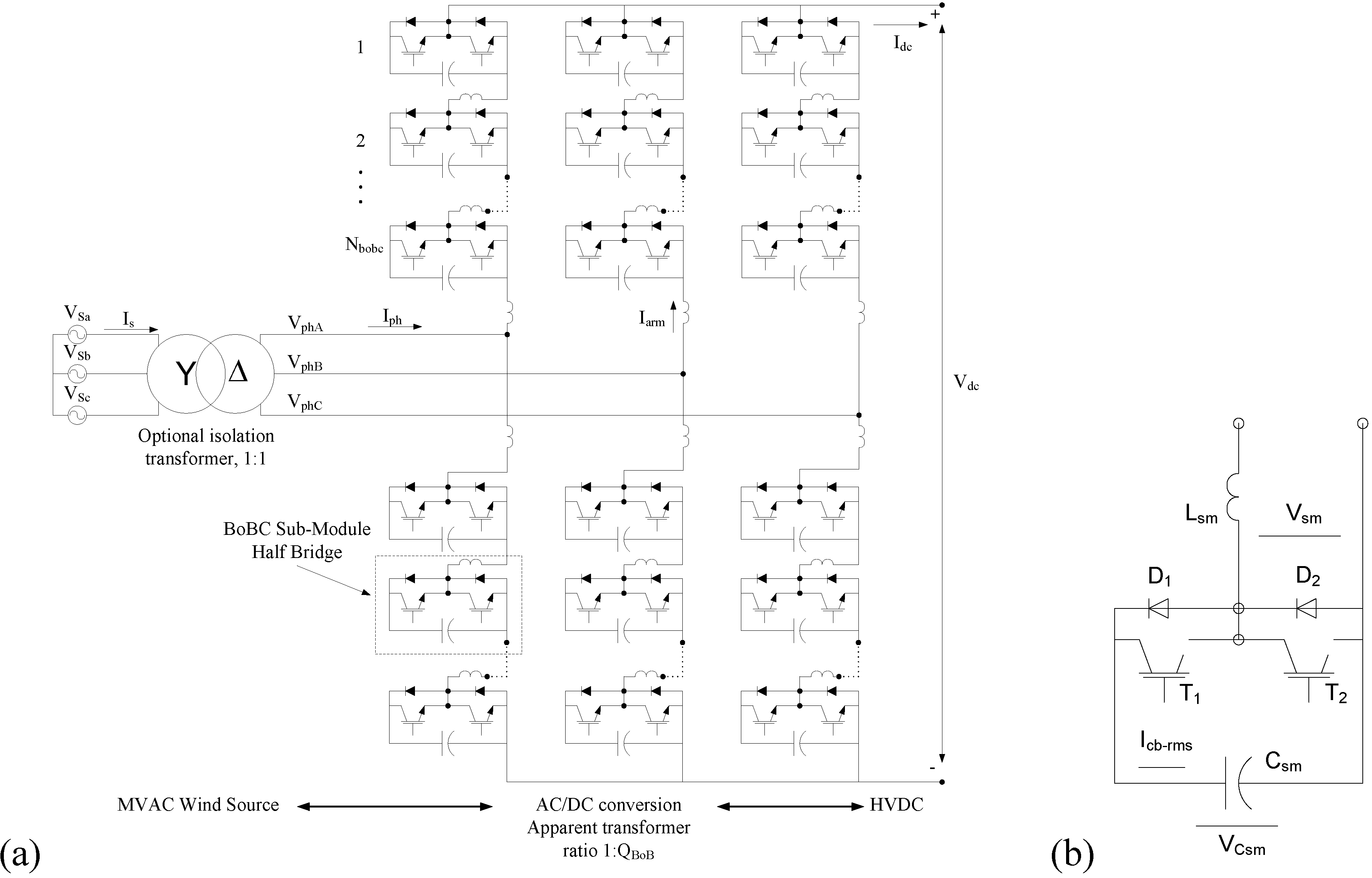
3. Converter Comparison
3.1. Power Semiconductor Requirements
| CSC | VSC | BoBC | |
|---|---|---|---|
| Device type | SCR | IGBT | IGCT |
| CSC | VSC | BoBC |
|---|---|---|
| CSC | VSC | BoBC | |
|---|---|---|---|
| Device Type | Thyristor (SCR) | IGBT-diode pair | IGCT –diode pair |
| Blocking voltage (kV) | 6.5 | 6.5 | 4.5 |
| Part number | ABB 5STP 03X6500 | ABB 5SNA 0400J650100 | ABB 5SHX 14H4510 |
| De-rated application voltage Vca(kV) | 3.3 | 3 | 2.8 |
| Number of series sub-modules per arm | |||
| Total number of devices | 276 thyristors | 228 IGBT-diode pairs | 330 IGCT-diode pairs |
| Total semiconductor MVA (p.u.) | 4.1 | 6.6 | 17.8 |
3.2. Reactive Component Requirements & Waveform Quality
3.2.1. AC side Reactive Components
| CSC | VSC | BoBC | |
|---|---|---|---|
| Transformer rating MVA (p.u) | 1.1 | 1.04 | 1.0 (optional) |
| Lowest harmonic number Pulse Number, Npulse | |||
| Switching frequency filter MVA (p.u) | 0.35 | 0.25 | 0 |
| Displacement power factor correction MVA (p.u) | 0.5 | 0 | 0 |
| Total ac side reactive component MVA (p.u.) | 1.95 | 1.29 | (optional) |
3.2.2. Sub-Module Reactive Components
| Inductor size, Larm_pu | 0.031 |
| Inductor RMS current, Iarm | 0.5 |
| BoBC total inductor MVA | 0.028 |
| Capacitor size, Csm | 70 |
| Capacitor RMS current, icb-rms | 0.25 |
| BoBC total capacitor MVA | 9.3 |
| Sub-module stored energy | 0.13 |
| BoBC total stored energy | 43 |
3.2.3. DC Side Reactive Components
| CSC | VSC | |
|---|---|---|
| Inductor size, Lcsc | 1.3 | ---- |
| Average inductor current, Idc | 1 | ---- |
| Inductor MVA | 1 | ---- |
| Capacitor size, Cvsc | ---- | 1.7 |
| Capacitor RMS current, icv-rms | ---- | 0.58 |
| Capacitor MVA | ---- | 0.58 |
| Total converter stored energy | 0.104 | 0. 126 |
3.3. System Operating Losses
| CSC | VSC | BoBC | |
|---|---|---|---|
| Device Conduction Losses (p.u.) | 0.0026 | 0.0031 | 0.024 |
| Device Switching Losses (p.u.) | ---- | 0.023 | 0.0084 |
| Total Semiconductor Losses (p.u.) | 0.0026 | 0.026 | 0.033 |
| Transformer & Filter Losses (p.u.) | 0.01 | 0.01 | 0.01 |
| Total Capacitor Losses (p.u.) | ---- | 3·10-5 | 4.7·10-4 |
| Total losses (p.u.) | 0.013 | 0.036 | 0.043 |
| Efficiency (%) | 98.7 | 96.5 | 95.7 |
3.4. Multi-terminal Operation
| CSC | VSC | BoBC | |
|---|---|---|---|
| Multi-terminal Operation | 0 | 0 | 0 |
| Weak ac network compatibility | 1 | 0 | 0 |
| Multi-terminal rank | 2nd | 1st | 1st |
3.5. Fault Tolerance
| CSC | VSC | BoBC | |
|---|---|---|---|
| Controllable HVDC fault current | 0 | 1 | 0 |
| HVDC breakers necessary? | 0 | 1 | 0 |
| Possible HV Transformer Fault? | 1 | 1 | 0 |
| Fast Dynamic response? | 1 | 0 | 0 |
| Fault tolerance rank | 2nd | 3rd | 1st |
3.6. Modularity & Complexity
| CSC | VSC | BoBC | |
|---|---|---|---|
| Degree of Modularity | 1 | 1 | 0 |
| Stand Alone Sub-Module | 1 | 1 | 0 |
| Ease of integration | 0 | 1 | 0 |
| Relative control complexity | 0 | 0 | 1 |
| Modularity & integration rank | 2nd | 3rd | 1st |
4. Conclusions
| CSC | VSC | BoBC | |
|---|---|---|---|
| Semiconductor MVA | 4.1 (p.u.) | 6.6 (p.u.) | 17.8 (p.u.) |
| Total capacitor MVA | ---- | 0.58 (p.u.) | 9.3 (p.u.) |
| Total inductor MVA | 1 (p.u.) | ---- | 0.028 (p.u.) |
| AC filter/reactor & transformer MVA | 1.95 (p.u.) | 1.29 (p.u.) | 1 (p.u.) optional |
| Stored energy | 0.104 (p.u.) | 0.126 (p.u.) | 43 (p.u.) |
| Converter losses | 0.013 (p.u.) | 0.036 (p.u.) | 0.043 (p.u.) |
| Converter efficiency | 98.7% | 96.5% | 95.7% |
| CSC | VSC | BoBC | |
|---|---|---|---|
| Multi-terminal operation rank | 2nd | 1st | 1st |
| Fault tolerance rank | 2nd | 3rd | 1st |
| Modularity & integration rank | 2nd | 3rd | 1st |
| Technology maturity level | 1st | 2nd | 3rd |
Acknowledgements
Nomenclature
| VS | Source rms phase voltage, [kV] |
| Vph | converter rms phase voltage, [kV] |
| Vdc | HVDC output voltage, [kV] |
| VCsm | BoBC sub-module dc bus voltage [kV] |
| Vsm | BoBC sub-module output voltage [kV] |
| Vca | Thyristor cathode-anode voltage [kV] |
| Vce | IGBT collected-emitter voltage [kV] |
| Vca_i | IGCT cathode-anode voltage [kV] |
| Qtran | CSC & VSC transformer turns ratio |
| Qbobc | BoBC apparent transformer turns ratio |
| α | CSC thyristor firing angle |
| m | VSC modulation index |
| dsm | BoBC sub-module duty cycle |
| IS | Source rms phase current, [A] |
| Iph | Converter rms phase current, [A] |
| Idc | HVDC output current, [A] |
| Iarm | Converter rms arm current, [A] |
| icv-rms | VSC rms capacitor current, [A] |
| icb-rms | BoBC rms capacitor current, [A] |
| Cvsc | VSC dc bus capacitance, [μF] |
| Csm | BoBC sub-module capacitance, [μF] |
| Lcsc | CSC HVDC line inductance, [H] |
| Lsm | BoBC sub-module inductance, [μH] |
| Larm | BoBC arm inductance, [μH] |
| Ncsc | Number of sub-modules, CSC |
| Nvsc | Number of sub-modules, VSC |
| Nbobc | Number of sub-modules, BoBC |
| fsw | Switching frequency |
| fp | Power frequency |
| Npulse | Lowest harmonic pulse number |
Appendix: Per-Unit base quantities and selected derivations
| Power base, PB | 50 MVA |
| Frequency base, fB, ωB | 60 Hz, 377 rads/s |
| Energy base, EB | = 833 kJ |
| AC source voltage base, VBs | 13.8 kV rms |
| Converter AC voltage base, VBph | 117 kV rms |
| DC voltage base, VBdc | 150 kV |
| AC source current base, IBs | = 2092 A rms |
| DC current base, IBdc | = 333 A |
| AC Impedance base, ZBac | = 6.6 Ω |
| DC Impedance base, ZBdc | = 450 Ω |
| AC Inductance base, LBac | = 17.5 mH |
| DC Inductance base, LBdc | = 1.2 H |
| AC Capacitance base, CBac | = 400 μF |
| DC Capacitance base, CBdc | = 5.9 μF |
Current Sourced Converter semiconductor selected derivations
Voltage Sourced Converter semiconductor device current and voltage derivations
Bridge of Bridge Converter semiconductor device current and voltage derivations
References
- Prasai, A.; Yim, J.; Divan, D.; Bendre, A.; Sul, S. A new architecture for offshore wind farms. IEEE Trans. Power Electr. 2008, 23, 1198–1204. [Google Scholar] [CrossRef]
- Jovcic, D.; Strachan, N. Offshore wind farm with centralised power conversion and DC interconnection. Generat. Transmis. Distribut. IET. 2009, 3, 586–595. [Google Scholar] [CrossRef]
- Jovcic, D.; Milanovic, J.V. Offshore wind farm based on variable frequency mini-grids with multiterminal DC interconnection. In AC and DC Power Transmission Conference, London, UK, March 2006.
- Jovcic, D. Interconnecting offshore wind farms using multiterminal VSC-based HVDC. In Presented at IEEE Power Engineering Society General Meeting, Montreal, QB, Canada, October 2006.
- Kling, W.L.; Hendriks, R.L.; den Boon, J.H. Advanced transmission solutions for offshore wind farms. In Presented at IEEE Power and Energy Society General Meeting—Conversion And Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, July 2008.
- Cole, S.; van Hertem, D.; Meeus, L; Belmans, R. Technical developments for the future transmission grid. In Presented at Future Power Systems Conference, Amsterdam, The Netherlands, November 2005.
- Bresesti, P; Kling, W.L.; Hendriks, R.L.; Vailati, R. HVDC connection of offshore wind farms to the transmission system. IEEE Trans. Energy Convers. 2007, 22, 37–43. [Google Scholar]
- Chaudhary, S.K.; Teodorescu, R.; Rodriguez, P. Wind farm grid integration using VSC based HVDC transmission—An overview. In Presented at IEEE Energy 2030 Conference, Atlanta, GA, USA, November 2008.
- Kirby, N.M.; Xu, L.; Luckett, M.; Siepmann, W. HVDC transmission for large offshore wind farms. Power Eng. J. 2002, 16, 135–141. [Google Scholar] [CrossRef]
- Morton, A.B.; Cowdroy, S.; Hill, J.R.A.; Halliday, M.; Nicholson, G.D. AC or DC? Economics of grid connection design for offshore wind farms. In Presented at AC and DC Power Transmission Conference, London, UK, March 2006.
- Cole, S.; Belmans, R. Transmission of Bulk Power. IEEE Industr. Electr. Mag. 2009, 3, 19–24. [Google Scholar] [CrossRef]
- Flourentzou, N.; Agelidis, V.G.; Demetriades, G.D. VSC-Based HVDC power transmission systems: An overview. IEEE Trans. Power Electr. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Allebrod, S.; Hamerski, R.; Marquardt, R. New transformerless, scalable modular multilevel converters for HVDC-transmission. In Presented at IEEE PESC, Rhodes, Greece, March 2008.
- Faulstich, A.; Stinke, J.K.; Wittwer, F. Medium voltage converter for permanent magnet wind power generators up to 5 MW. In Presented at Power Electronics and Applications, Dresden, Germany, August 2006.
- Zargari, N.R.; Xiao, Y.; Wu, B. A multi-level thyristor rectifier with improved power factor. IEEE IAS 1996, 2, 967–972. [Google Scholar]
- Li, R.; Bozhko, S.; Asher, G.M.; Clare, J.C.; Yao, L.; Sasse, C. Grid frequency control design for offshore wind farms with naturally commutated HVDC link connection. IEEE Industr. electr. 2006, 2, 1595–1600. [Google Scholar]
- Foster, S.; Xu, L.; Fox, B. Control of an LCC HVDC system for connecting large offshore wind farms with special consideration of grid fault. In IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, July 2008.
- Bozhko, S.V.; Blasco-Gimenez, R.; Li, R.; Clare, J.C.; Asher, G.M. Control of offshore DFIG-based wind farm grid with line-commutated HVDC connection. IEEE Trans. Energy Convers. 2007, 22, 71–78. [Google Scholar] [CrossRef]
- Bozhko, S.; Li, R.; Blasco-Gimenez, R.; Asher, G.M.; Clare, J.C.; Yao, L.; Sasse, C. STATCOM-controlled HVDC power transmission for large offshore wind farms: Engineering issues. In Presented at IECON, Paris, France, November 2006.
- Sood, V.A. HVDC and FACTS Controllers, Applications of Static Converters in Power Systems; Pai, M.A., Stankovic, A., Eds.; Kluwer Academic Publishers: Norwell, MA, USA, 2004. [Google Scholar]
- Krein, P.T. Elements of Power Electronics; van Valkenburg, M., Sedra, A.S., Lightner, M.R., Eds.; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- de la Villa, J.A.; Acha, E.; Exposito, A.G. Voltage Source Converter Modeling for Power System State Estimation: STATCOM and VSC-HVDC. IEEE Trans. Power Syst. 2008, 23, 1552–1559. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Dynamic model and control of the NPC-based back-to-back HVDC system. IEEE Trans. Power Deliv. 2006, 21, 414–424. [Google Scholar] [CrossRef]
- Yao, X.; Sui, H.; Xing, Z. The study of VSC-HVDC transmission system for offshore wind power farm. In Presented at The International Conference on Electrical Machines and Systems, Seoul, South Korea, October, 2007.
- Xu, L.; Agelidis, V.G. VSC transmission system using flying capacitor multilevel converters and hybrid PWM control. IEEE Trans. Power Deliv. 2007, 22, 693–702. [Google Scholar] [CrossRef]
- Saeedifard, M.; Iravani, R.; Pou, J. A Space Vector Modulation Strategy for a Back-to-Back Five-Level HVDC Converter System. IEEE Trans. Industr. Electr. 2009, 56, 452–466. [Google Scholar] [CrossRef]
- Lee, G.B.; Engelbrecht, F.; Beukes, H.J. Series-stacked and neutral point clamped multilevel converter topologies for MVDC transmission. IEEE Conf. Afr. 2002, 2, 735–741. [Google Scholar]
- Zhou, K.; Fu, X.; Cheng, M.; Zhu, X.; Wang, W.; Wang, T. Topologies and control of VSC-HVDC systems for grid connection of large-scale off-shore wind farms. In The International Conference on Electrical Machines and Systems, Wuhan, China, February 2009; pp. 2357–2361.
- Ludois, D.C.; Reed, J.; Venkataramanan, G. Hierarchical control of bridge of bridge multilevel power converters. IEEE Trans. Industr. Electr. 2010, in press. [Google Scholar] [CrossRef]
- Maharjan, L.; Inoue, S.; Akagi, H.; Asakura, J. A transformerless battery energy storage system based on a multilevel cascade PWM converter. In IEEE Power Electronics Specialists Conference, Rhodes, Greece, June 2008.
- Maharjan, L.; Inoue, S.; Akagi, H. A transformerless energy storage system based on a cascade multilevel PWM converter with star configuration. IEEE Trans. Industr. Appl. 2008, 44, 1621–1630. [Google Scholar] [CrossRef]
- Hagiwara, M.; Akagi, H. PWM control and experiment of modular multilevel converters. In Presented at IEEE Power Electronics Specialists Conference, June 2008; Rhodes, Greece.
- Glinka, M.; Marquardt, R. A new AC/AC multilevel converter family. IEEE Trans. Industr. Electr. 2005, 52, 662–669. [Google Scholar] [CrossRef]
- Erickson, R.W.; Al-Naseem, O.A. A new family of matrix converters. IEEE Industr. Electr. Soc. 2001, 2, 1515–1520. [Google Scholar]
- Ding, G.; Tang, G.; He, Z.; Ding, M. New technologies of voltage source converter (VSC) for HVDC transmission system based on VSC. In IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, July 2008.
- Baek, J.W.; Yoo, D.W.; Kim, H.G. High voltage switch using series-connected IGBTs with simple auxiliary circuit. In IEEE Industry Applications Conference, Rome, Italy, October 2000.
- Bhattacharya, S. Series connected IGCT based high power three-level neutral point clamped voltage source inverter pole for FACTS applications. In IEEE Power Electronics Specialists Conference, Pittsburgh, PA, USA, July 2005.
- Staff of RSMeans. RSMeans Electrical Cost Data, 29th ed.; Reed Construction Data: Kingston, MA, USA, 2006. [Google Scholar]
- IEEE Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems; IEEE Standard 519-1992; IEEE: New York, NY, USA, 1993.
- ABB Online Library. Bernt Bergdahl R.D. AC-DC harmonic filters for three Gorges-Changzhou 500 kV HVDC project. Available online: http://www.abb.com (accessed on 9 June 2010).
- Rockhill, A.A.; Liserre, M.; Teodorescu, R.; Rodriguez, P. Grid filter design for a multi-megawatt medium voltage voltage source inverter. IEEE Trans. Industr. Electr. 2010, in press. [Google Scholar]
- Nian, M.; Yinhong, L.; Xianzhong, D.; Jiang, Y.; Chuang, F. Study on high voltage capacitor unbalance protection in HVDC projects. In Asia-Pacific Power And Energy Engineering Conference, Wuhan, China, March 2009.
- Kolar, J.W.; Round, S.D. Analytical calculation of the RMS current stress on the DC-link capacitor of voltage-PWM converter systems. In IEE Proceedings: Electric Power Applications Conference, Canterbury, UK, September 2006.
- Cornell Dubilier Staff. Application Guide to Aluminum Electrolytic Capacitors. Available online: http://www.abb.com (accessed on 9 June 2010).
- ABB Staff. Product Guide LV Products and Systems Power Quality Product Data. Available online: http://www.abb.com (accessed on 9 June 2010).
- Saint, B. DOE distribution transformer efficiency standards. In Presented at IEEE Rural Electric Power Conference, Charleston, SC, USA, April 2008.
- Siemens MV Drive Product Guide. ROBICON Perfect Harmony, Answers for Industry. Available online: http://www.sea.siemens.com (accessed on 9 June 2010).
- Bhuvaneswari, G; Mahanta, B.C. Analysis of converter transformer failure in HVDC systems and possible solutions. IEEE Trans. Power Deliv. 2009, 24, 814–821. [Google Scholar]
- Meyer, C.; Schroder, S.; De Doncker, R.W. Solid-state circuit breakers and current limiters for medium-voltage systems having distributed power systems. IEEE Trans. Power Electr. 2004, 19, 1333–1340. [Google Scholar] [CrossRef]
- Meyer, C.; De Doncker, R.W. Solid-state circuit breaker based on active thyristor topologies. IEEE Trans. Power Electr. 2006, 21, 450–458. [Google Scholar] [CrossRef]
- Tang, L.; Ooi, B. Protection of VSC-multi-terminal HVDC against DC faults. In Presented at IEEE Power Electronics Specialists Conference, Cairns, Queensland, Australia, June 2002.
- Power Transmission & Distribution: High Power Direct-Light-Triggered Thyristor Valve Technology. Available online: http:// www.sea.siemens.com (accessed on 9 June 2010).
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ludois, D.; Venkataramanan, G. An Examination of AC/HVDC Power Circuits for Interconnecting Bulk Wind Generation with the Electric Grid. Energies 2010, 3, 1263-1289. https://doi.org/10.3390/en3061263
Ludois D, Venkataramanan G. An Examination of AC/HVDC Power Circuits for Interconnecting Bulk Wind Generation with the Electric Grid. Energies. 2010; 3(6):1263-1289. https://doi.org/10.3390/en3061263
Chicago/Turabian StyleLudois, Daniel, and Giri Venkataramanan. 2010. "An Examination of AC/HVDC Power Circuits for Interconnecting Bulk Wind Generation with the Electric Grid" Energies 3, no. 6: 1263-1289. https://doi.org/10.3390/en3061263
APA StyleLudois, D., & Venkataramanan, G. (2010). An Examination of AC/HVDC Power Circuits for Interconnecting Bulk Wind Generation with the Electric Grid. Energies, 3(6), 1263-1289. https://doi.org/10.3390/en3061263