The WRF Model Forecast-Derived Low-Level Wind Shear Climatology over the United States Great Plains
Abstract
:1. Introduction and Motivation
| Turbine Manufacturer | Turbine Ratings (MW) | Diameter of Rotors (m) | Hub Height (m) | Max. Reach of Blades (m) |
| Mitsubishi | 1 | 57–61.4 | 45–69 | 99.7 |
| Suzlon | 1.25 | 64–66 | 56–74 | 107 |
| GE | 1.5 | 70.5–77 | 61–100 | 138.5 |
| Gamesa | 2 | 80–90 | 60–100 | 145 |
| Siemens | 2.3 | 93 | 70–80 | 126.5 |
| Vestas | 3 | 90 | 80–105 | 150 |
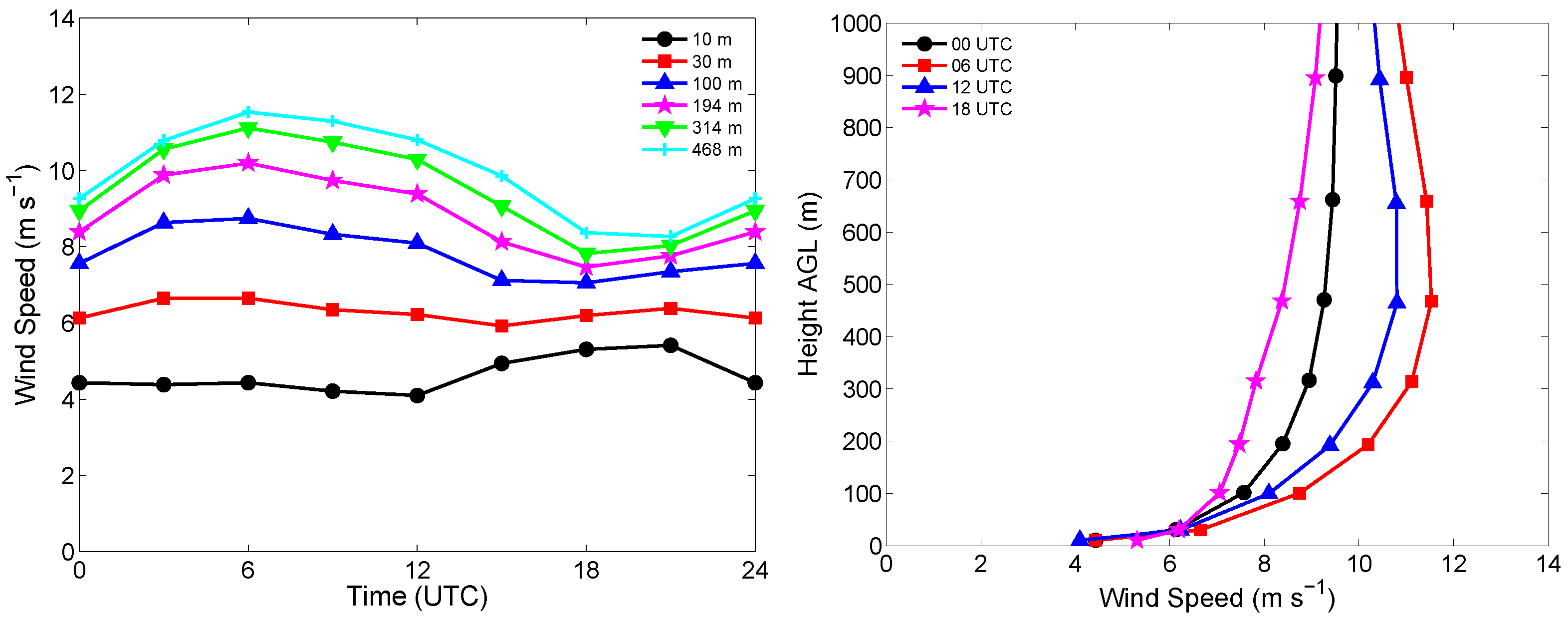
2. Wind Shear
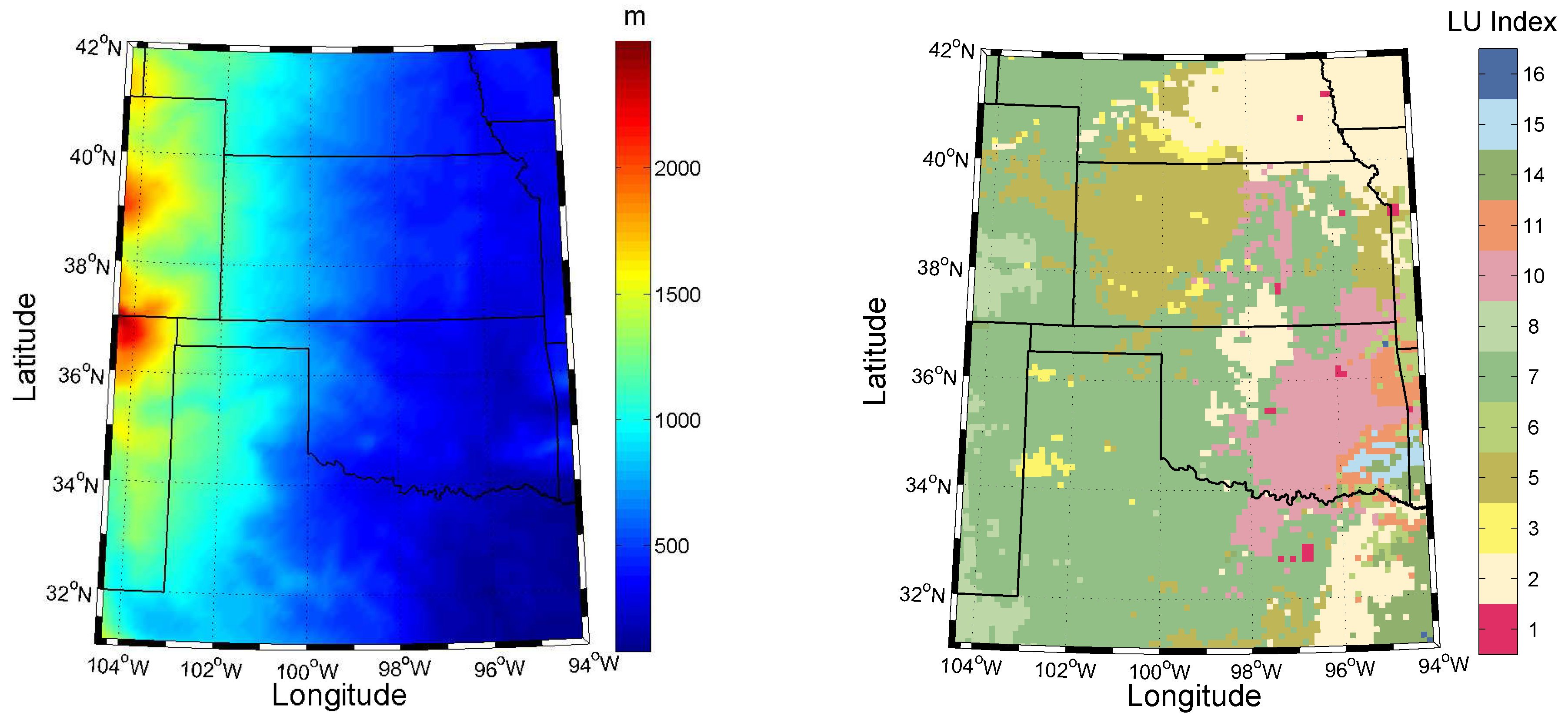
3. Data and Methodology
3.1. Operational WRF Model Forecasts
| Model Run | WRF Version | Horizontal Grid Spacing (km) | Initial and Boundary Data | PBL Scheme | Output Frequency (h) |
| WRF-NCAR | 2.1, 2.2 | 36/12 | AWIP | YSU | 3 |
| WRF-YSU-NARR | 3.1.1 | 27/9 | NARR | YSU | 1 |
| WRF-MYJ-NARR | 3.1.1 | 27/9 | NARR | MYJ | 1 |
| WRF-QNSE-NARR | 3.1.1 | 27/9 | NARR | QNSE | 1 |
| WRF-ACM2-NARR | 3.1.1 | 27/9 | NARR | ACM2 | 1 |
| WRF-YSU-NNRP | 3.1.1 | 27/9 | NNRP | YSU | 1 |
| WRF-YSU-FNL | 3.1.1 | 27/9 | FNL | YSU | 1 |
| WRF-YSU-AWIP | 3.1.1 | 27/9 | AWIP | YSU | 1 |
3.2. Sensitivity Studies Using the WRF Model
3.3. Observational Data
- Tall-tower observations are basically point measurements. In contrast, the WRF model forecast-derived statistics correspond to a spatial grid of 12 km (in the case of the operational WRF-NCAR run) or 9 km (in the case of the sensitivity study runs) resolution.
- While the WRF model forecasts represent instantaneous values (1 or 3 hourly), most of the observed wind speed values utilized by us and SE06 (personal communication, Elliot and Schwartz, 2007) were 10 minute averages.
- Data from the directional sectors affected by the tower structure (shadowing effects) were not considered by us and SE06. However, we analyzed all the directional sectors from the WRF model forecasts.
4. Results and Discussions
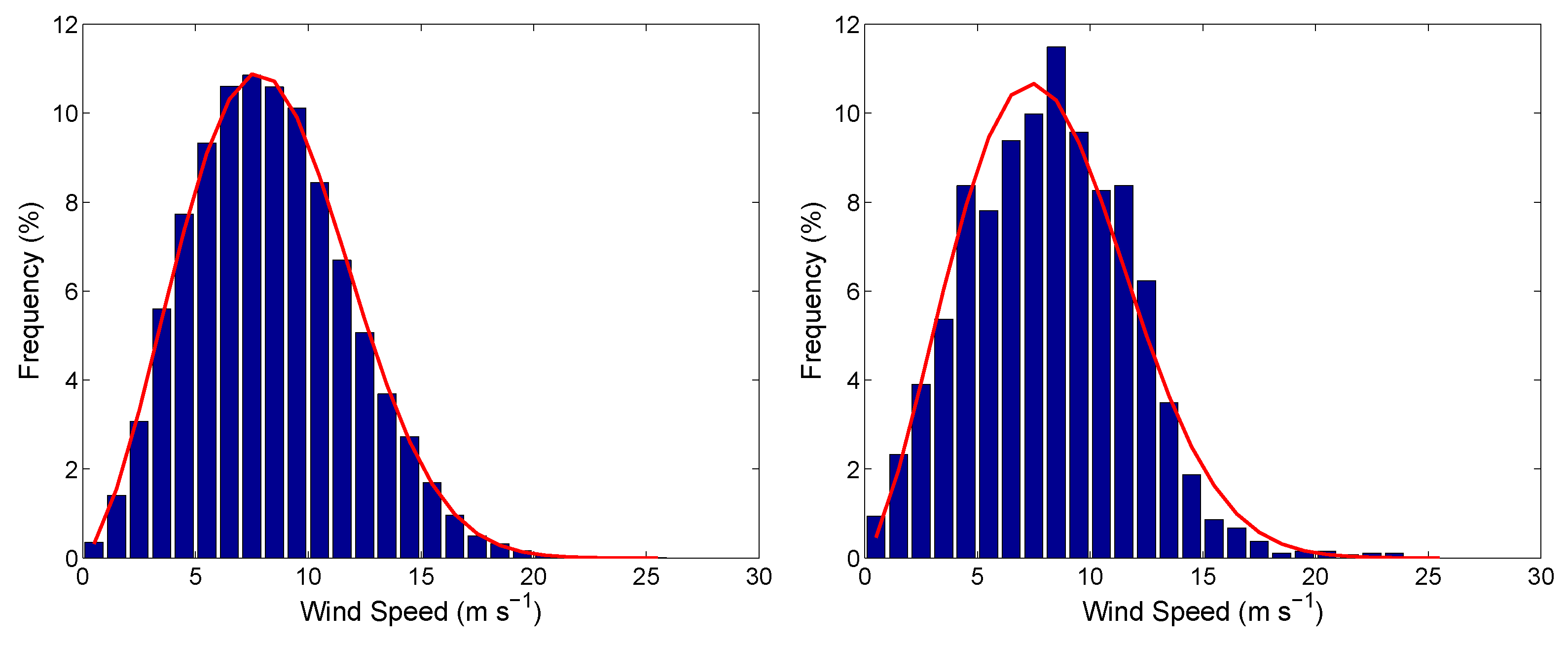
4.1. Wind Characteristics at Sweetwater, TX
| (m s) | c (m s) | k | (m s) | (m s) | (W m) | |
| Observation | 8.36 | 9.42 | 2.56 | 7.76 | 11.80 | 544.09 |
| WRF-NCAR | 8.18 | 9.21 | 2.42 | 7.39 | 11.80 | 526.98 |
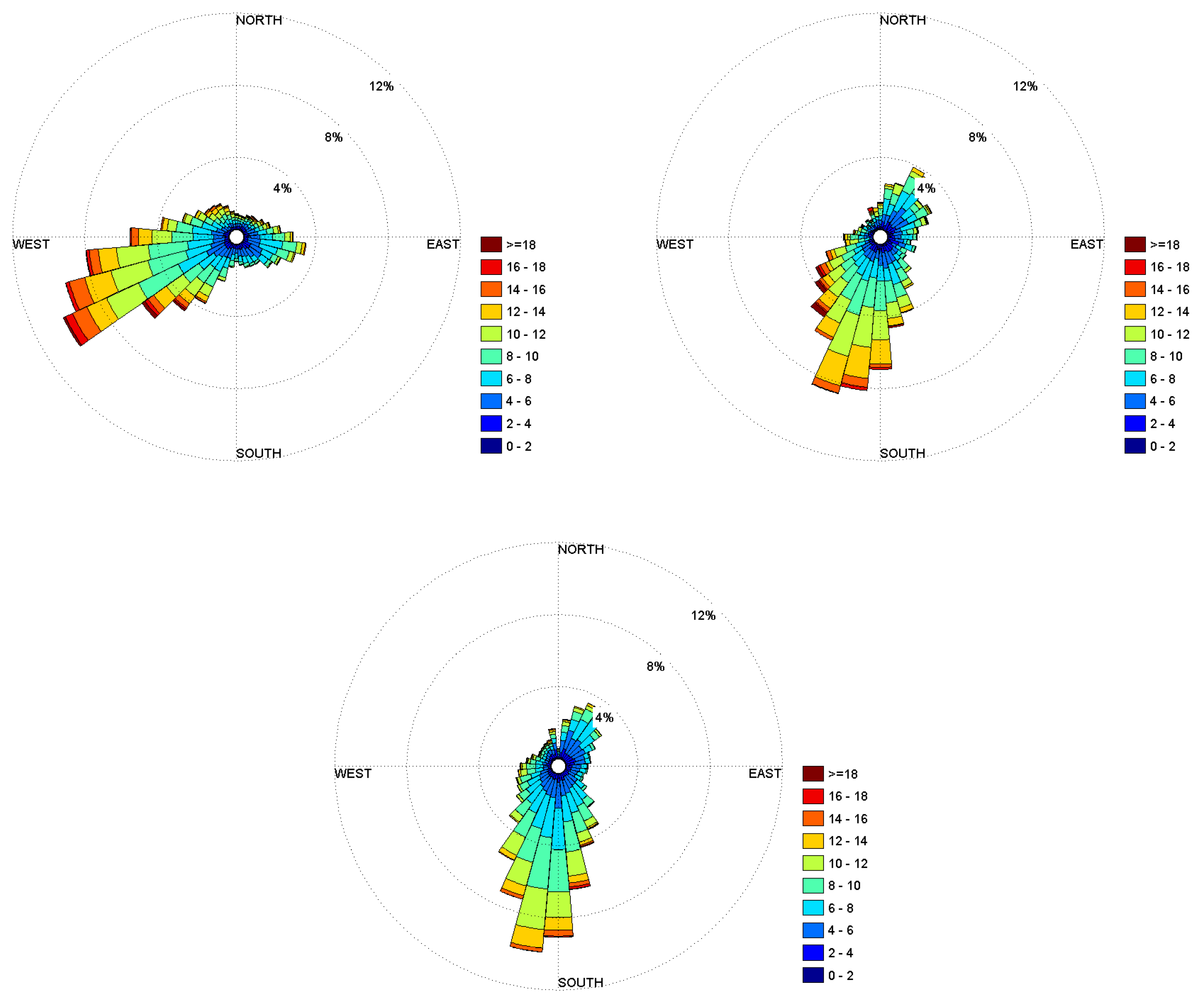
| Anemometer | Observed | Observed | Observed | WRF Grid | WRF | WRF | WRF | WRF | WRF |
| Heights (m) | Levels (m) | ||||||||
| 50, 100 | 0.169 | 0.136 | 0.182 | 30, 101 | 0.168 | 0.072 | 2.22 | 3.42 | 0.177 |
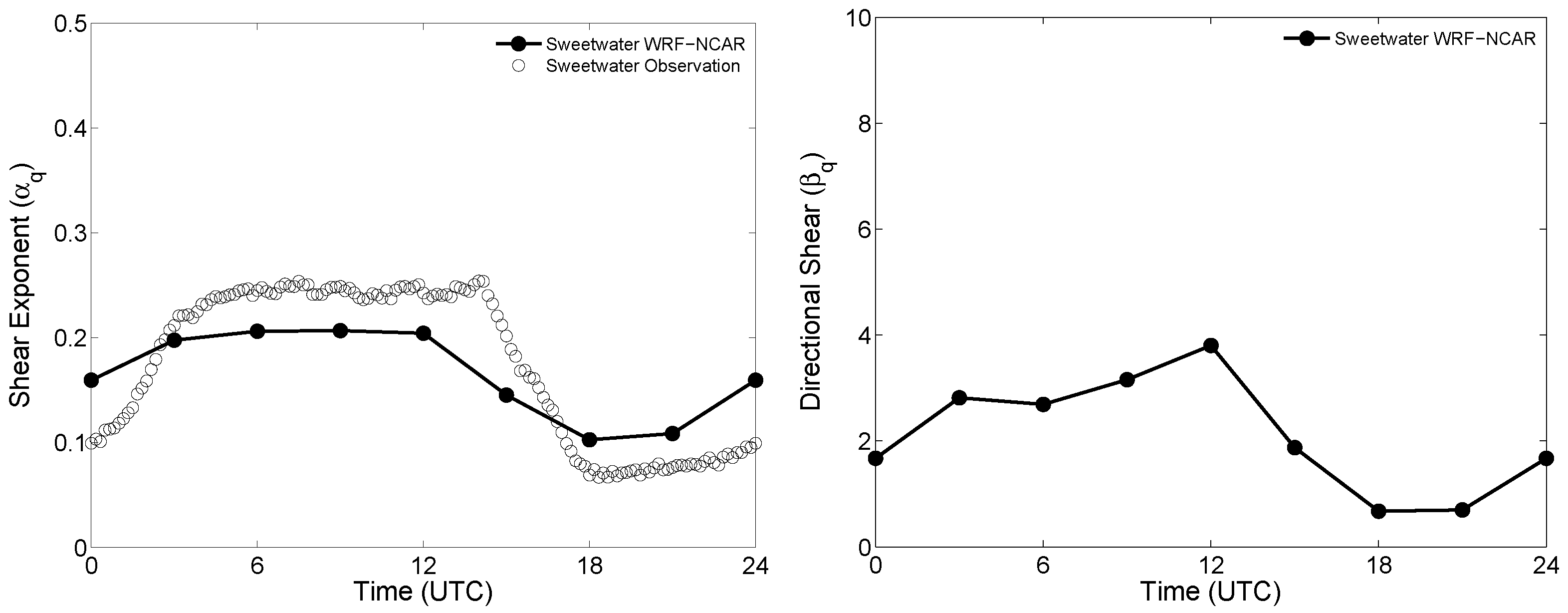
4.2. Wind Shear Values at a Few USGP Sites
| Anemometer | Observed | WRF Grid | WRF | WRF | WRF | WRF | WRF | |
| Site Name | Heights (m) | α | Levels (m) | |||||
| Elk City, OK | 40, 70 | 0.227 | 30, 101 | 0.174 | 0.076 | 2.51 | 3.48 | 0.180 |
| Ellsworth, KS | 50, 110 | 0.165 | 30, 100 | 0.178 | 0.077 | 2.99 | 3.76 | 0.185 |
| Hobart, OK | 40, 70 | 0.195 | 30, 101 | 0.175 | 0.076 | 2.58 | 3.66 | 0.182 |
| Jewell, KS | 50, 110 | 0.206 | 30, 99 | 0.175 | 0.073 | 2.93 | 3.71 | 0.180 |
| Kearny, KS | 50, 80 | 0.138 | 30, 99 | 0.171 | 0.078 | 3.34 | 4.11 | 0.176 |
| Lamar, CO | 52, 113 | 0.150 | 29, 98 | 0.152 | 0.086 | 4.11 | 5.18 | 0.163 |
| Logan, KS | 50, 80 | 0.179 | 30, 99 | 0.172 | 0.080 | 3.02 | 3.86 | 0.179 |
| Ness, KS | 50, 110 | 0.223 | 30, 100 | 0.172 | 0.078 | 3.00 | 3.79 | 0.178 |
| Sumner, KS | 50, 80 | 0.254 | 30, 100 | 0.177 | 0.078 | 3.04 | 3.79 | 0.182 |
| Sweetwater, TX | 50, 100 | 0.220 | 30, 101 | 0.168 | 0.072 | 2.22 | 3.42 | 0.177 |
| Washburn, TX | 50, 75 | 0.170 | 30, 100 | 0.172 | 0.075 | 2.61 | 3.47 | 0.180 |
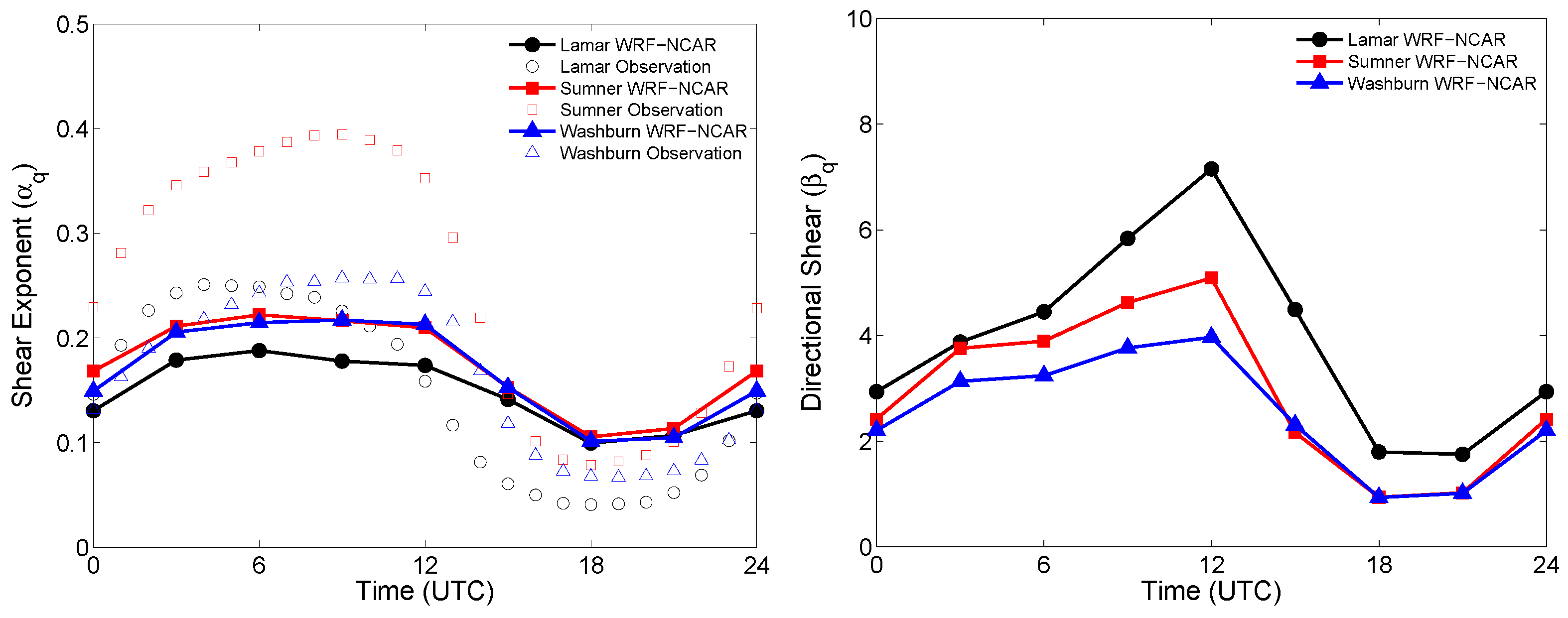
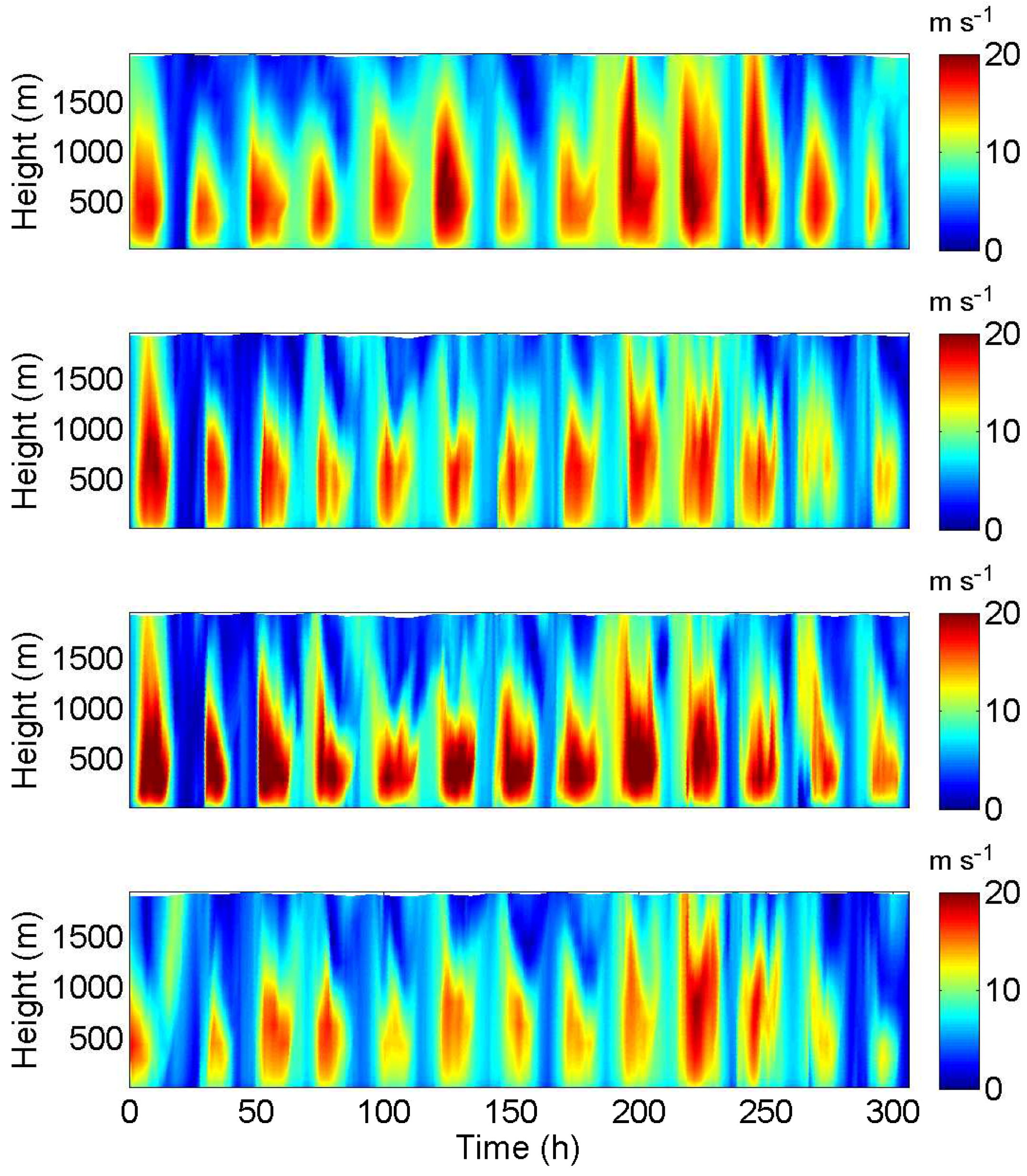
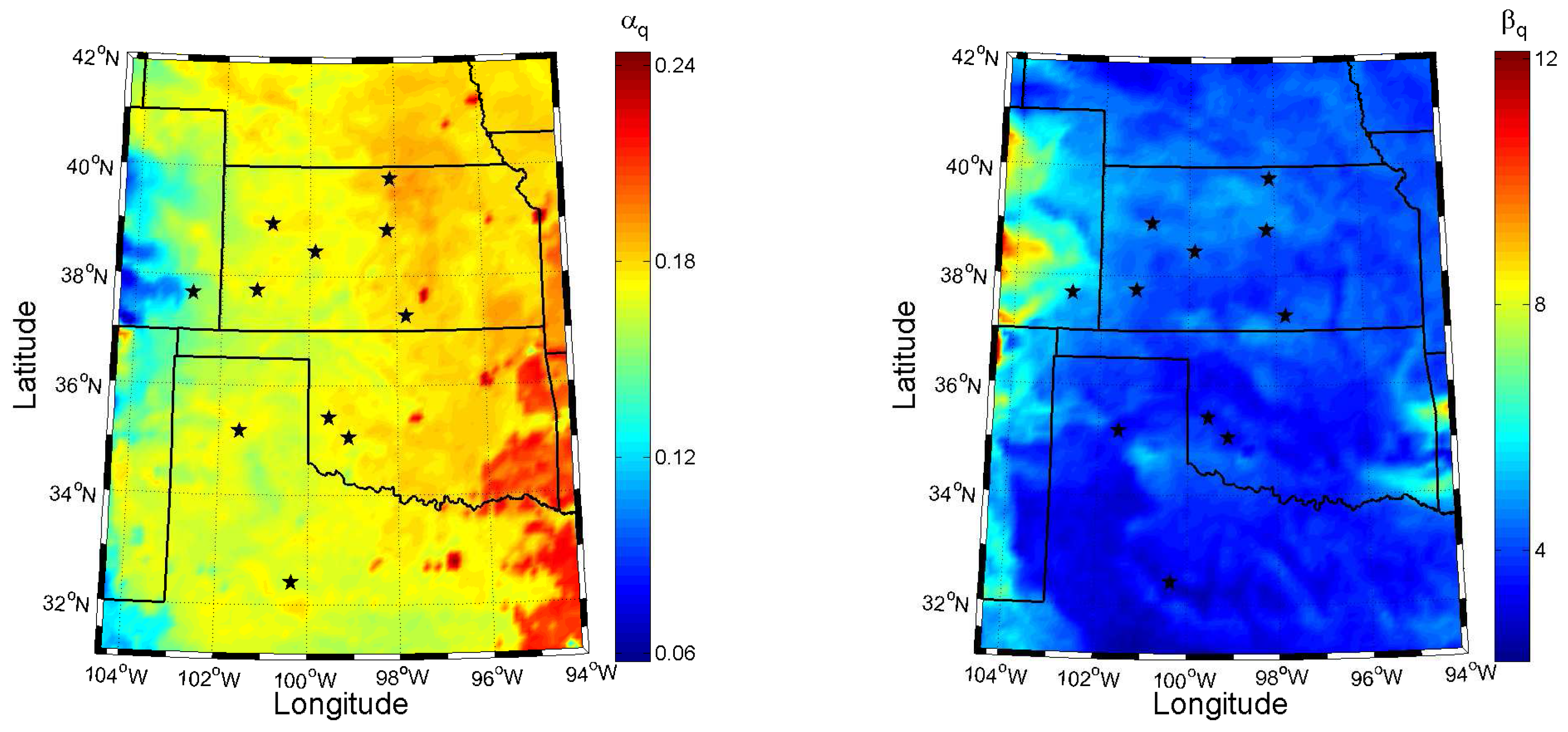
4.3. Spatial Distribution of Wind Shear Values over the USGP
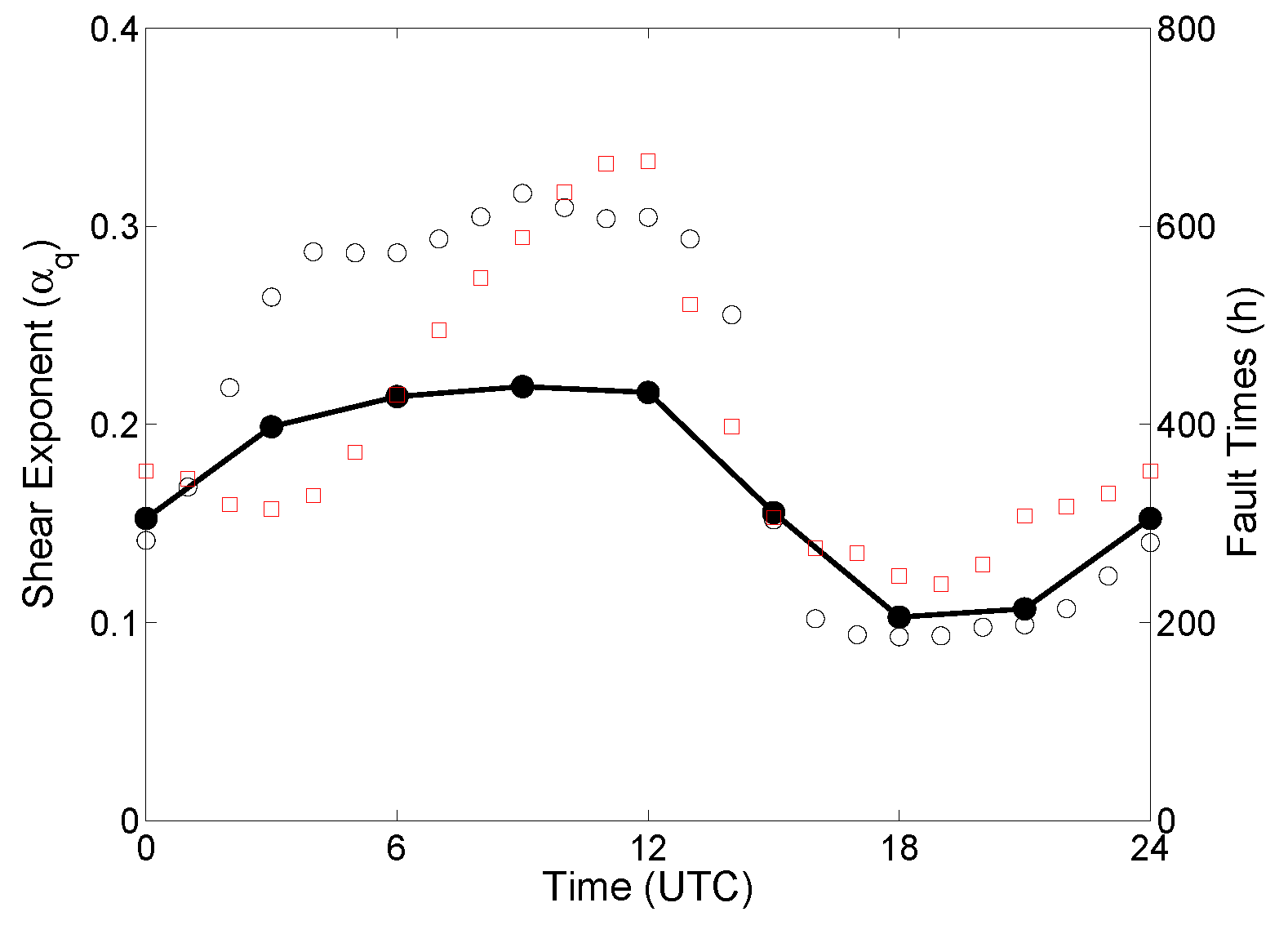
4.4. Sensitivity Studies
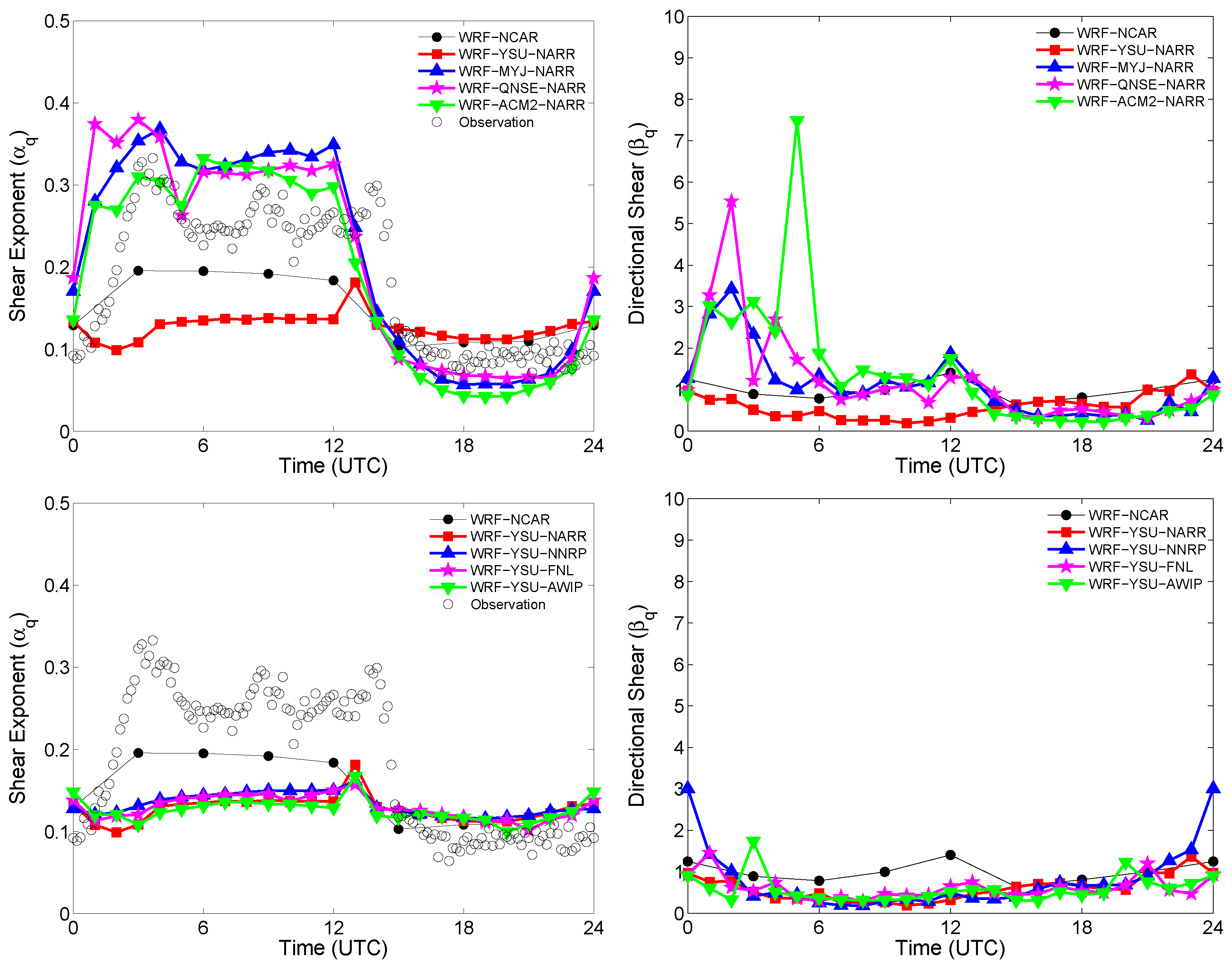
- The model forecast-derived shear exponents are significantly more sensitive to the PBL schemes than the initial-boundary data;
- All the model runs capture the daytime wind speed shear exponents quite well;
- The model runs using the MYJ, QNSE, and ACM2 PBL schemes significantly overestimates the nighttime wind speed shear exponents;
- The model runs using the YSU PBL scheme severely underestimates the nighttime wind speed shear exponents;
- The model runs using the MYJ, QNSE, and ACM2 PBL schemes produce significantly higher directional shear during nighttime hours in comparison to the runs based on the YSU scheme.
5. Concluding Remarks
Acknowledgements
References and Notes
- AWEA Homepage. Available online: http://www.awea.org (accessed 10 February 2010).
- Bonner, W.D. Climatology of the low-level jet. Mon. Wea. Rev. 1968, 96, 833–850. [Google Scholar] [CrossRef]
- Mitchell, M.J.; Arritt, R.W.; Labas, K. A climatology of the warm season Great Plains low-level jet using wind profiler observations. Wea. Forecast. 1995, 10, 576–591. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Bian, X.; Zhong, S. Low-level jet climatology from enhanced rawinsonde observations at a site in the Southern Great Plains. J. Appl. Meteorol. 1997, 36, 1363–1376. [Google Scholar] [CrossRef]
- Song, J.; Liao, K.; Coulter, R.L.; Lesht, B.M. Climatology of the low-level jet at the Southern Great Plains atmospheric boundary layer experiments site. J. Appl. Meteorol. 2005, 44, 1593–1606. [Google Scholar] [CrossRef]
- Blackadar, K. Boundary layer wind maxima and their significance for the growth of nocturnal inversions. Bull. Amer. Meteorol. Soc. 1957, 38, 283–290. [Google Scholar]
- Holton, J.R. The diurnal boundary layer wind oscillation above sloping terrain. Tellus 1967, 19, 199–205. [Google Scholar] [CrossRef]
- Reiter, E.R. Jet Stream Meteorology; University of Chicago Press: Chicago, IL, USA, 1963. [Google Scholar]
- Kelley, N.; Shirazi, M.; Jager, D.; Wilde, S.; Adams, J.; Buhl, M.; Sullivan, P.; Patton, E. Lamar Low-Level Jet Project Interim Report; NREL/TP-500-34593; National Renewable Energy Laboratory: Golden, CO, USA, 2004.
- Wind Turbine Generator System Part 1: Design Requirements, 3rd ed.; IEC 61400-1; International Electrotechnical Commission: Geneva, Switzerland, 2005.
- Kelley, N.D.; Jonkman, B.J.; Scott, G.N. The Great Plains Turbulence Environment: Its Origins, Impact and Simulation; NREL/CP-500-40176; National Renewable Energy Laboratory: Golden, CO, USA, 2006.
- Hand, M.M. Mitigation of Wind Turbine/Vortex Interaction Using Disturbance Accomodating Control; NREL/TP-500-35172; National Renewable Energy Laboratory: Golden, CO, USA, 2003.
- Smith, K.; Randall, G.; Malcolm, D.; Kelley, N.; Smith, B. Evaluation of wind shear patterns at Midwest wind energy facilities. In Proceedings of the American Wind Energy Association (AWEA) Windpower 2002 Conference, Portland, OR, USA, June 2002.
- Holtslag, A.A.M. Estimates of diabatic wind speed profiles from near-surface weather observations. Boundary-Layer Meteorol. 1984, 29, 225–250. [Google Scholar] [CrossRef]
- Giebel, G.; Gryning, S.E. Shear and Stability in High Met Masts, and How WAsP Treats It; Risφ National Laboratory: Roskilde, Denmark, 2004.
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. Description of the Advanced Research WRF Version 2; NCAR/TN-468+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2005. [Google Scholar]
- Schlichting, H. Boundary-layer theory, 6th ed.; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Arya, S.P. Air Pollution Meteorology and Dispersion; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Frost, R. The velocity profile in the lowest 400 feet. Meteorol. Mag. 1947, 76, 14–17. [Google Scholar]
- Sisterson, D.L.; Frenzen, P. Nocturnal boundary-layer wind maxima and the problem of wind power assessment. Environ. Sci. Tech. 1978, 12, 218–221. [Google Scholar] [CrossRef]
- Irwin, J. A theoretical variation of the wind profile power-law exponent as a function of surface roughness and stability. Atmos. Environ. 1979, 13, 191–194. [Google Scholar] [CrossRef]
- Schwartz, M.; Elliot, D. Wind shear characteristics at central plains tall towers. In Proceedings of the American Wind Energy Association (AWEA) Windpower 2006 Conference, Pittsburg, PA, USA; 2006. [Google Scholar]
- van Ulden, A.P.; Holtslag, A.A.M. Estimation of atmospheric boundary layer parameters for diffusion applications. J. Clim. Appl. Meteorol. 1985, 24, 1196–1207. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Dudhia, J.; Chen, S.-H. A revised approach to ice-microphysical processes for the bulk parameterization of cloud and precipitation. Mon. Wea. Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface hydrology model with the Penn State - NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Wea. Rev. 2001, 129, 569–585. [Google Scholar]
- Kain, J.S.; Fritsch, J.M. Convective parameterization for mesoscale models: The Kain-Fritsch scheme. In The Representation of Cumulus Convection in Numerical Models of the Atmosphere; Emanuel, K., Raymond, D.J., Eds.; American Meteorological Society: Boston, MA, USA, 1993; pp. 165–170. [Google Scholar]
- Kain, J.S. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Janjic, Z.I. Nonsingular implementation of the Mellor-Yamada level 2.5 scheme in the NCEP Meso model; Office Note #437; National Centers for Environmental Prediction: Camp Springs, MD, USA, 2001.
- Sukoriansky, S.; Galperin, B.; Perov, V. A quasi-normal scale elimination model of turbulence and its application to stably stratified flows. Nonlinear Process. Geophys. 2006, 13, 9–22. [Google Scholar] [CrossRef]
- Pleim, J.E. A combined local and nonlocal closure model for the atmospheric boundary layer. Part I: Model description and testing. J. Appl. Meteorol. Clim. 2007, 46, 1383–1395. [Google Scholar] [CrossRef]
- Tjernström, M.; Zagar, M.; Svensson, G.; Cassano, J.J.; Pfeifer, S.; Rinke, A.; Wyser, K.; Dethloff, K.; Jones, C.; Semmler, T.; Shaw, M. Modelling the arctic boundary layer: An evaluation of six ARCMIP regional-scale models using data from the SHEBA project. Boundary-Layer Meteorol. 2004, 117, 337–381. [Google Scholar] [CrossRef]
- Mathew, S. Wind Energy: Fundamentals, Resource Analysis and Economics; Springer: Berlin, Germany, 2006. [Google Scholar]
- Beljaars, A.; Viterbo, P. The role of the boundary layer in a numerical weather prediction model. In Clear and Cloudy Boundary Layers; Holtslag, A.A.M., Duynkerke, P.G., Eds.; Royal Netherlands Academy of Arts and Sciences: Amsterdam, The Netherlands, 1998; pp. 297–304. [Google Scholar]
- Viterbo, P.; Beljaars, A.; Mahfouf, J.-F.; Teixeira, J. The representation of soil moisture freezing and its impact on the stable boundary layer. Quart. J. Royal Meteorol. Soc. 1999, 125, 2401–2426. [Google Scholar] [CrossRef]
- Cuxart, J.; Holtslag, A.A.M.; Beare, R.J.; Bazile, E.; Beljaars, A.; Cheng, A.; Conangla, L.; Ek, M.; Freedman, F.; Hamdi, R.; Kerstein, A.; Kitagawa, H.; Lenderink, G.; Lewellen, D.; Mailhot, J.; Mauritsen, T.; Perov, V.; Schayes, G.; Steeneveld, G.-J.; Svensson, G.; Taylor, P.; Weng, W.; Wunsch, S.; Xu, K.-M. Single-column model intercomparison for a stably stratified atmospheric boundary layer. Boundary-Layer Meteorol. 2006, 118, 273–303. [Google Scholar] [CrossRef]
- Zehnder, J.A. Simple modifications to improve fifth-generation Pennsylvania State University-National Center for Atmospheric Research Mesoscale Model performance for the Phoenix, Arizona, metropolitan area. J. Appl. Meteorol. 2002, 41, 971–979. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Kim, S.-W. Stable Boundary Layer Mixing in a Vertical Diffusion Scheme. In Proceedings of 9th WRF Users’ Workshop, Boulder, CO, USA; 2008. [Google Scholar]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Storm, B.; Basu, S. The WRF Model Forecast-Derived Low-Level Wind Shear Climatology over the United States Great Plains. Energies 2010, 3, 258-276. https://doi.org/10.3390/en3020258
Storm B, Basu S. The WRF Model Forecast-Derived Low-Level Wind Shear Climatology over the United States Great Plains. Energies. 2010; 3(2):258-276. https://doi.org/10.3390/en3020258
Chicago/Turabian StyleStorm, Brandon, and Sukanta Basu. 2010. "The WRF Model Forecast-Derived Low-Level Wind Shear Climatology over the United States Great Plains" Energies 3, no. 2: 258-276. https://doi.org/10.3390/en3020258
APA StyleStorm, B., & Basu, S. (2010). The WRF Model Forecast-Derived Low-Level Wind Shear Climatology over the United States Great Plains. Energies, 3(2), 258-276. https://doi.org/10.3390/en3020258




