A Proposal of Ecologic Taxes Based on Thermo-Economic Performance of Heat Engine Models
Abstract
:1. Introduction
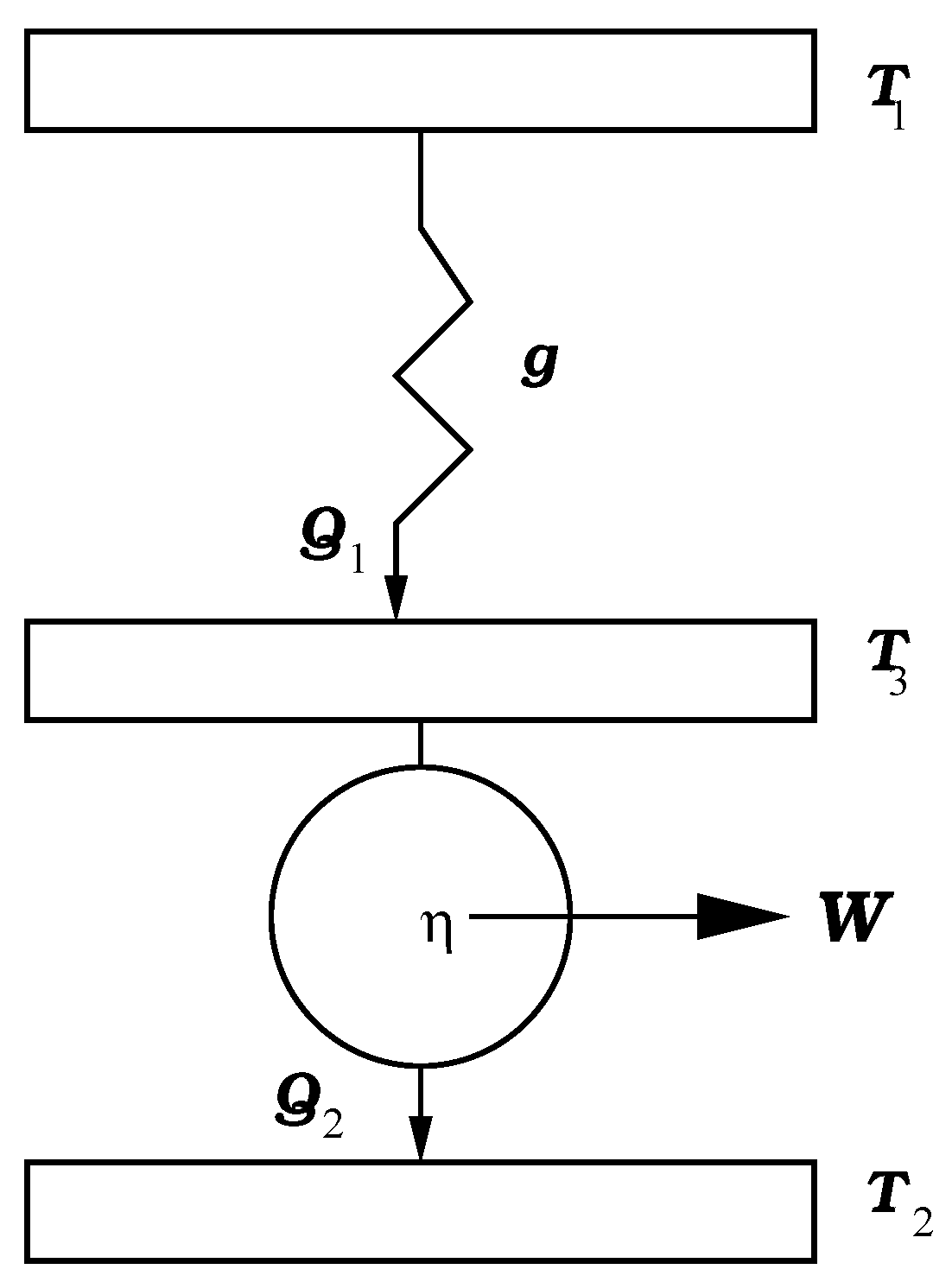
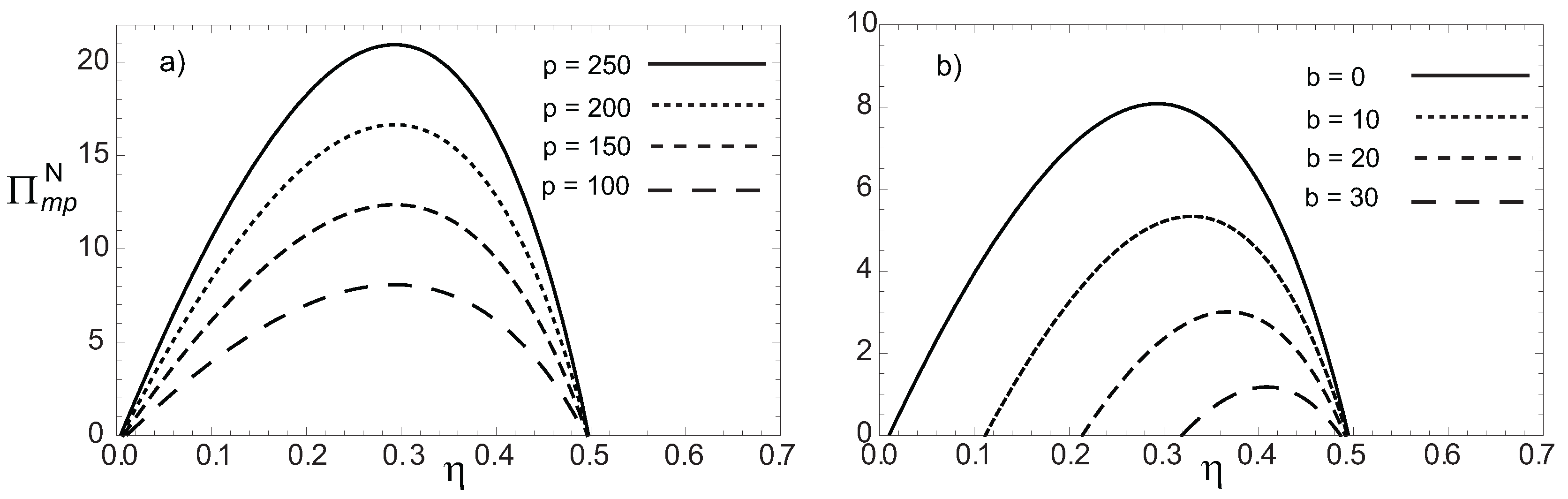
2. Optimization of the Profit Function: Newtonian Heat Transfer Law Case
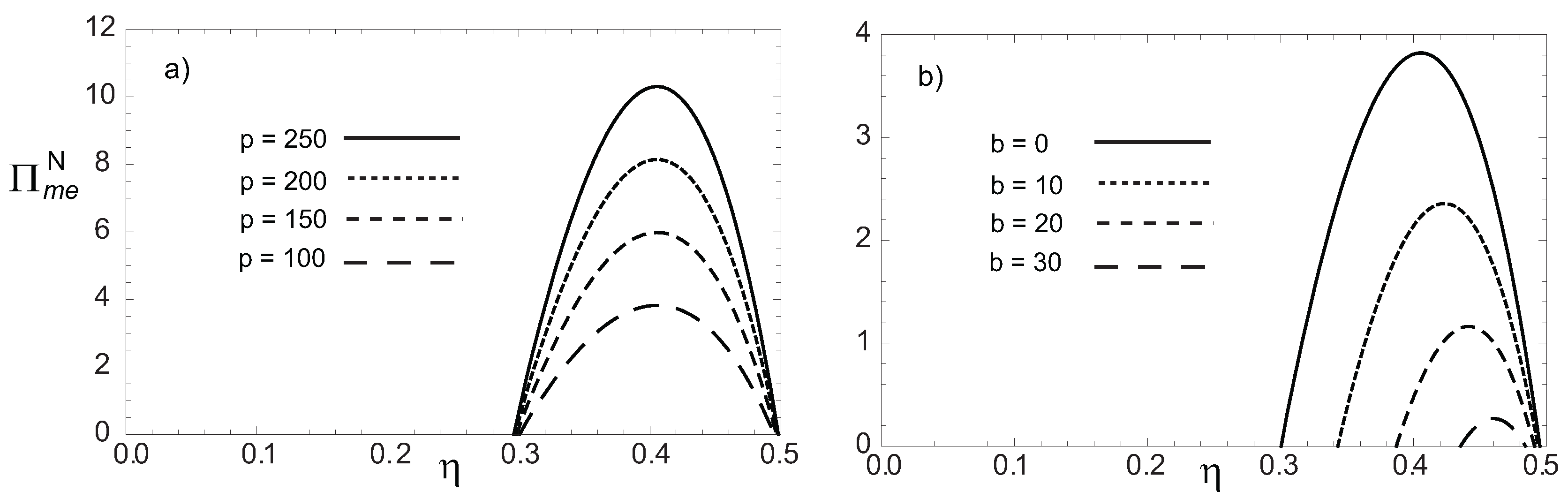
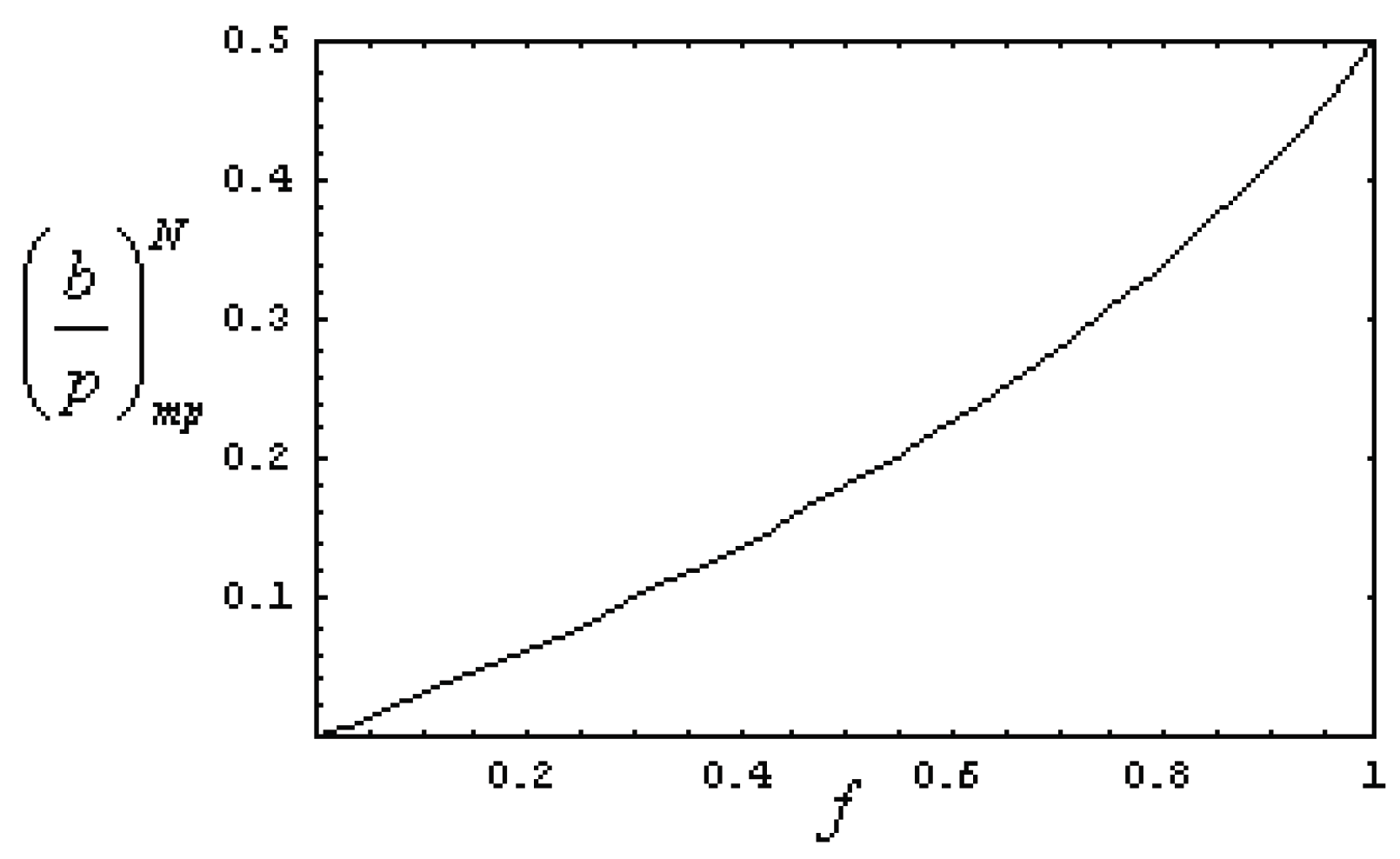
3. Optimization of the Profit Function: Dulong-Petit Heat Transfer Law Case
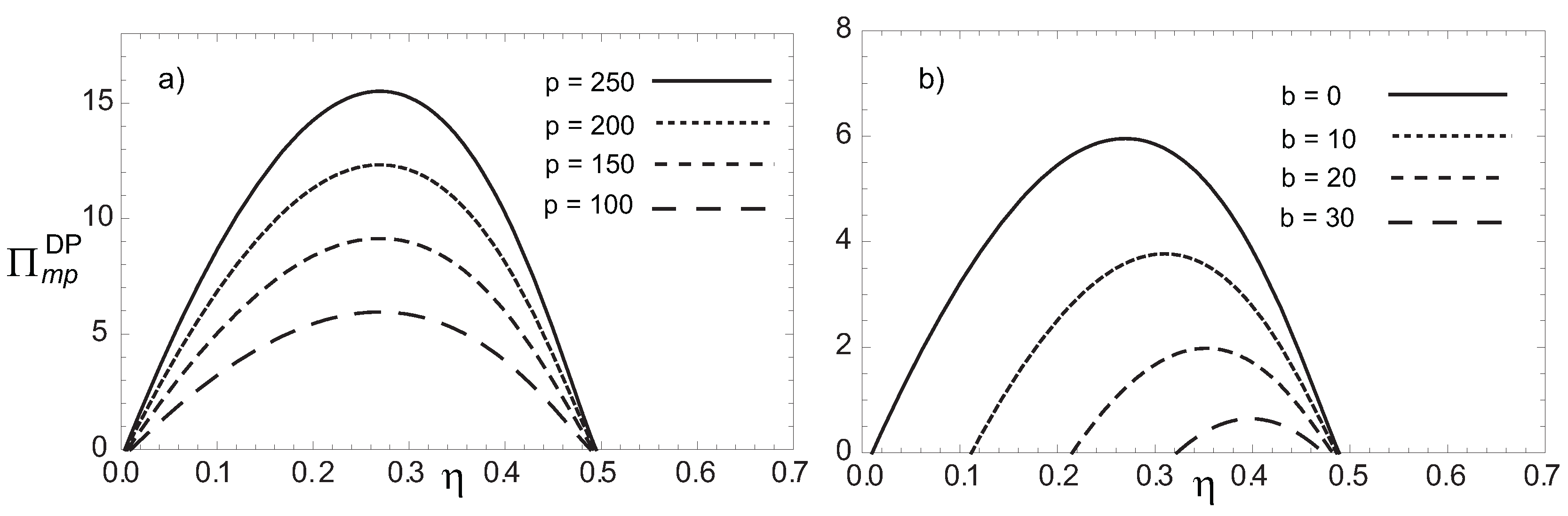
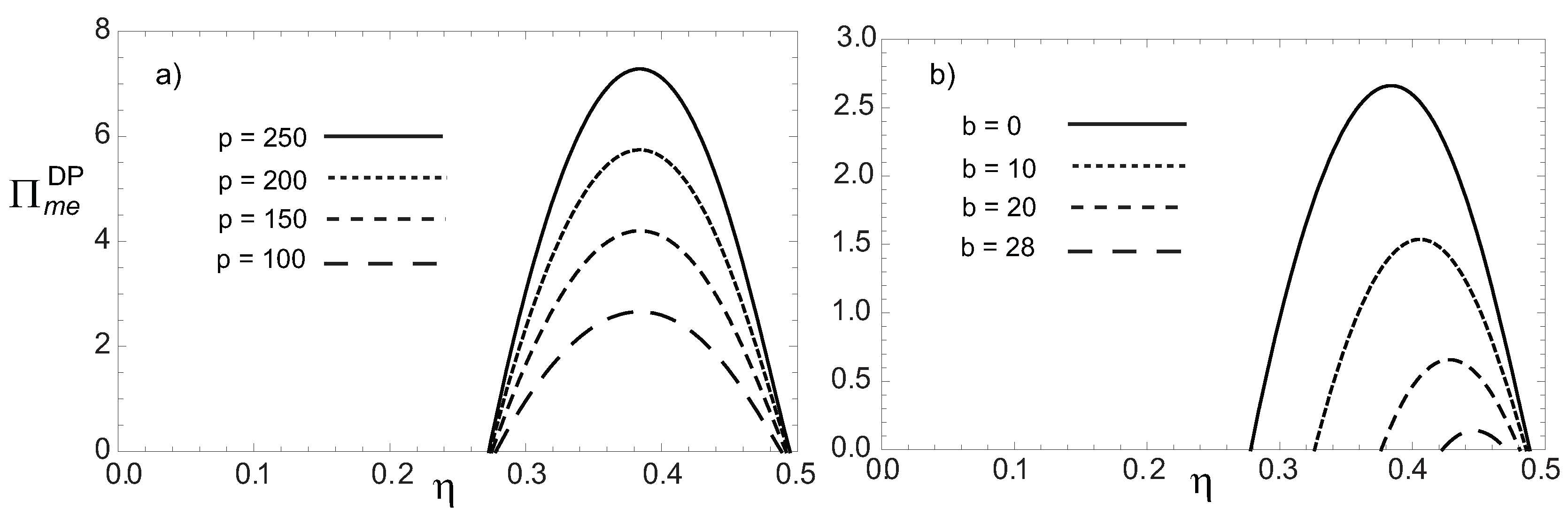
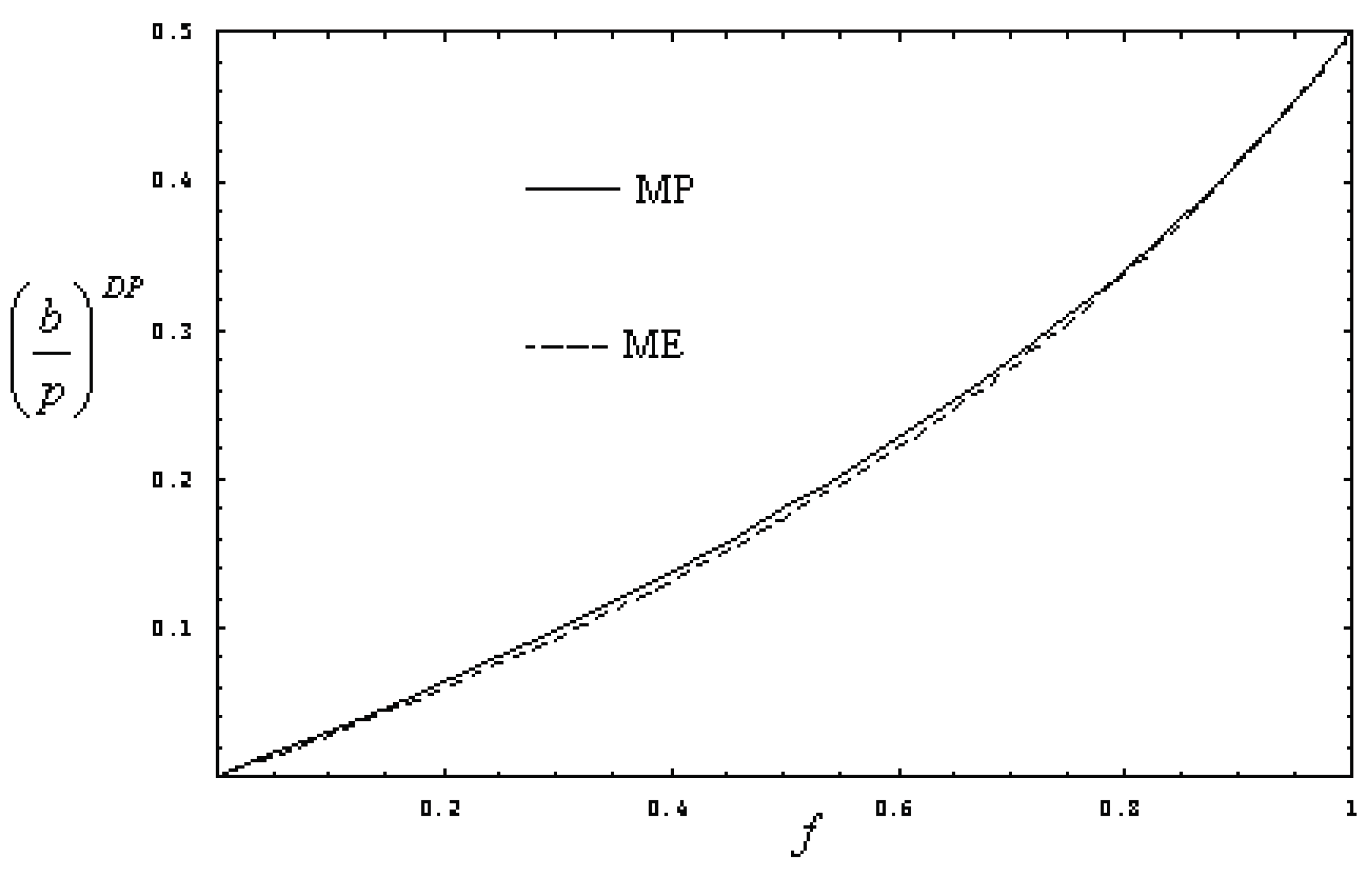
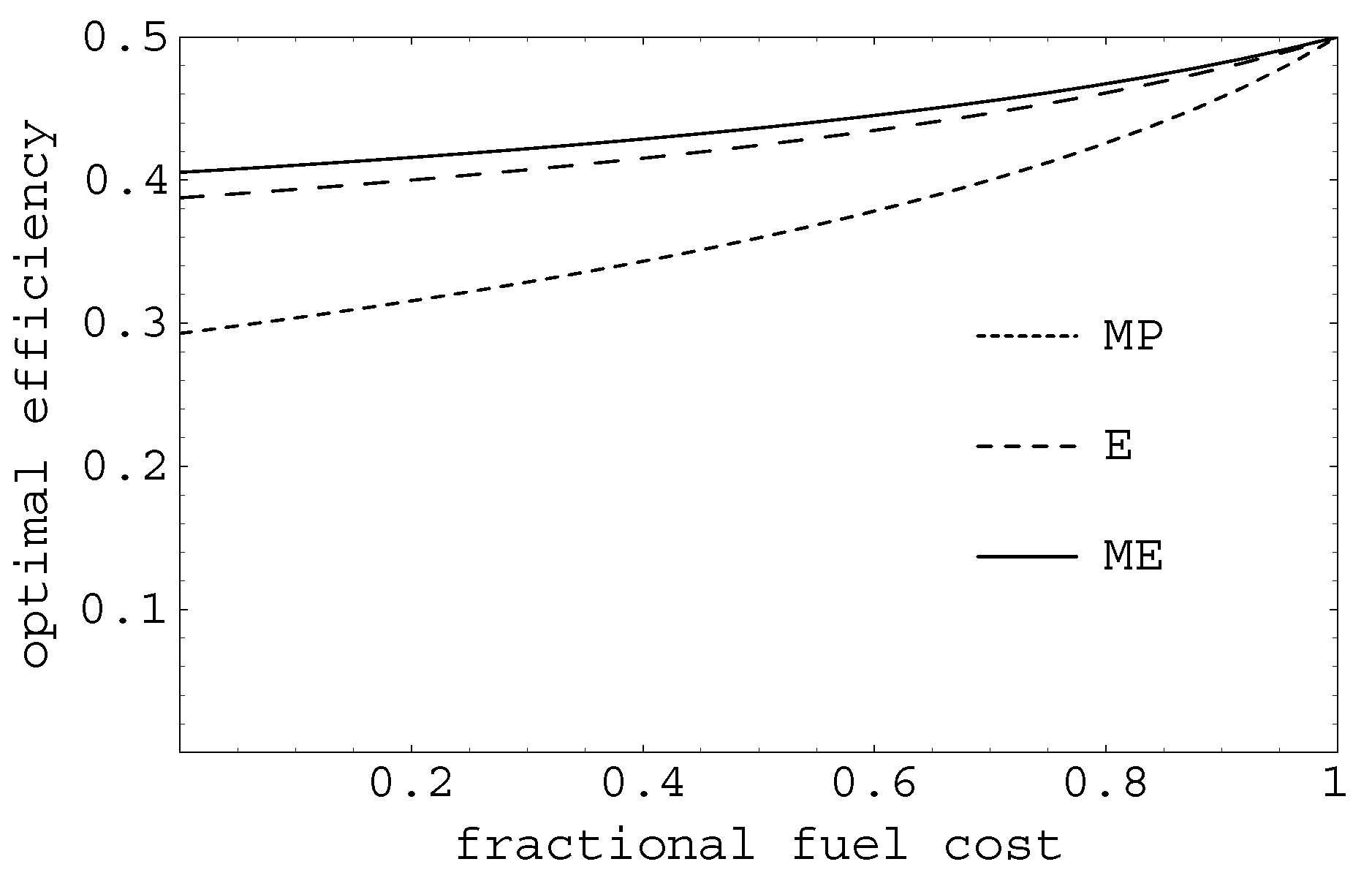
4. Proposal of an Ecological Lax
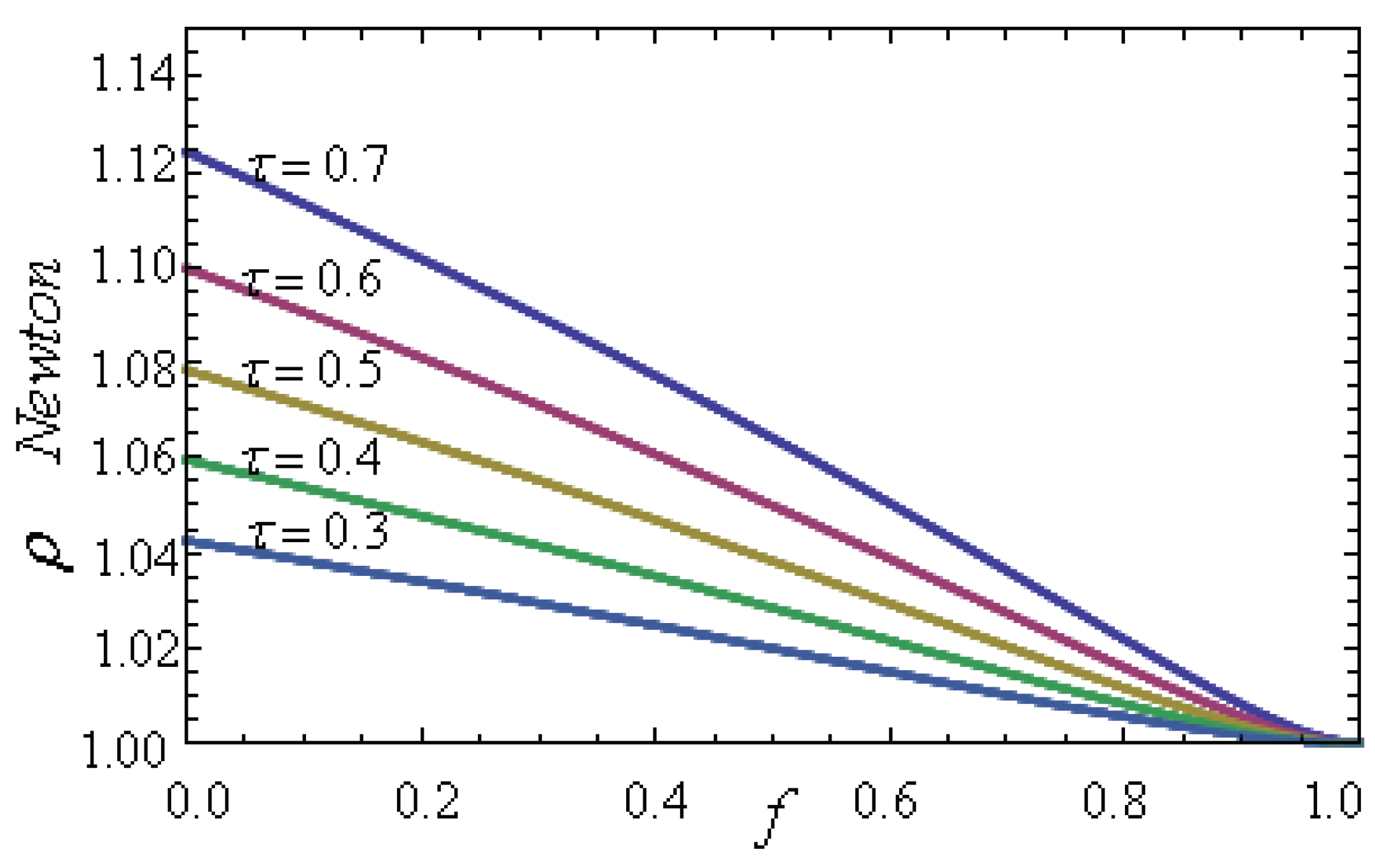
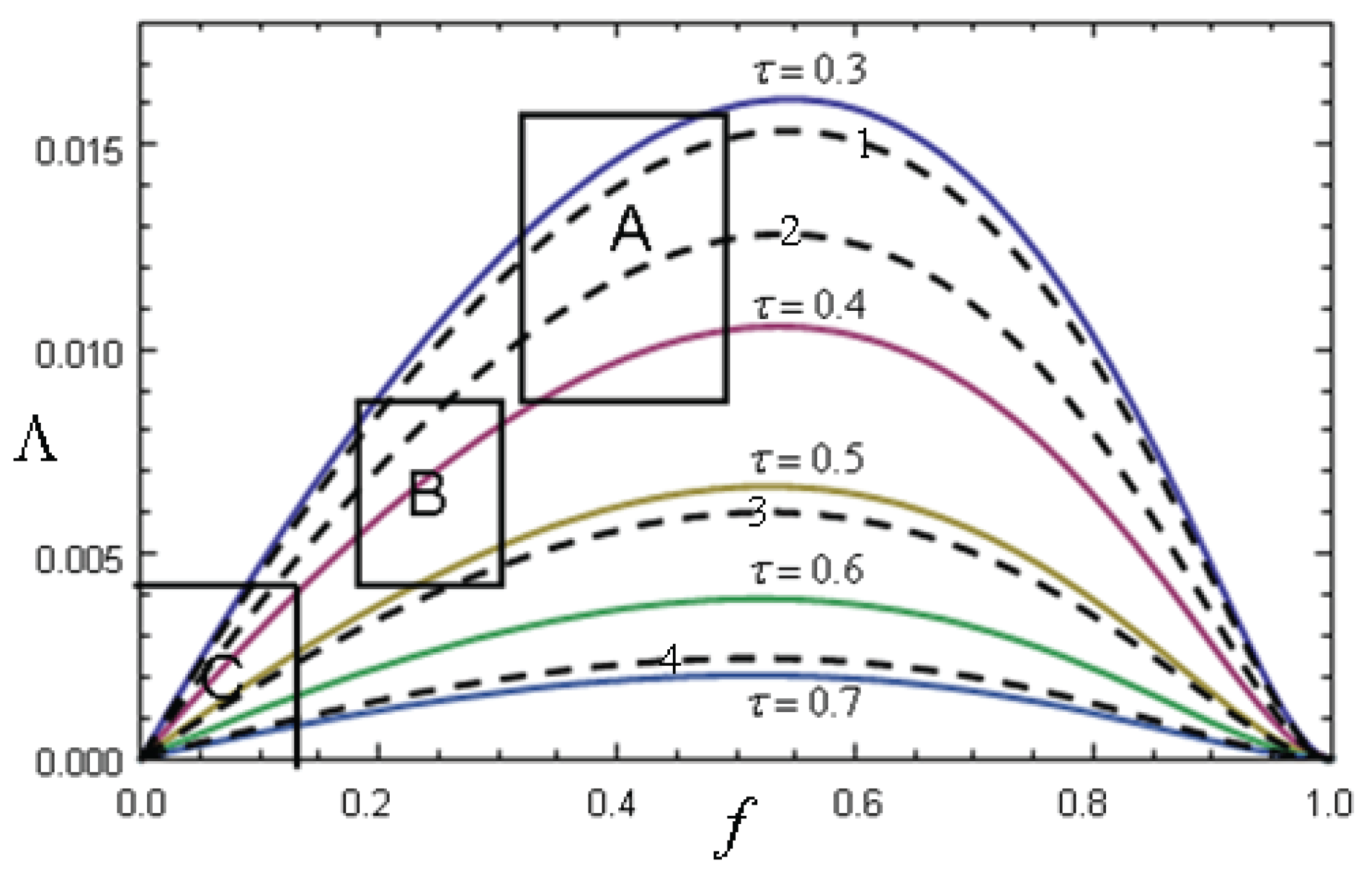
5. Conclusions
Acknowledgements
References and Notes
- Fisher, M.; Hoffmann, K.H. Can a quantitative simulation of an otto engine be accurately rendered by a simple novikov model with heat leak. J. Non-Equil. Thermodyn. 2004, 29, 9–28. [Google Scholar] [CrossRef]
- Curto-Risso, P.L.; Medina, A.; Calvo-Hernández, A. Theoretical and simulated models for an irreversible otto cycle. J. Appl. Phys. 2008, 104. [Google Scholar] [CrossRef]
- Salamon, P.; Nitzan, A. Finite time optimizations of a newton’s law carnot cycle. J. Chem. Phys. 1981, 74, 3546–3560. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F.; Chen, W. Finite time exergoeconomic performance bound and optimization criteria for two-heat-reservoir refrigerators. Chin. Sci. Bull. 1991, 36, 156–157. [Google Scholar]
- Chen, L.; Sun, F.; Wu, C. Maximum profit performance of an absorption refrigerator. Int. J. Energ. Environ. Econom. 1996, 4, 1–7. [Google Scholar]
- Wu, F.; Chen, L.; Sun, F.; Wu, C. Finite-time exergoeconomic performance bound for a quantum stirling engine. Int. J. Eng. Sci. 2000, 38, 239–247. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F.; Wu, C. Maximum profit performance for generalized irreversible carnot engines. Appl. Energy 2004, 79, 15–25. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, L.; Sun, F.; Wu, C. Maximum profit performance for a class of universal steady flow endoreversible heat engine cycles. Int. J. Ambient Energy 2007, 27, 29–36. [Google Scholar] [CrossRef]
- Wu, C.; Chen, L.; Sun, F. Effect of heat transfer law on finite time exergoeconomic performance of heat engines. Energy Int. J. 1996, 21, 1127–1134. [Google Scholar] [CrossRef]
- Wu, C.; Chen, L.; Sun, F. Effect of heat transfer law on finite time exergoeconomic performance of a carnot heat pump. Energ. Convers. Manage. 1998, 39, 579–588. [Google Scholar] [CrossRef]
- Chen, L.; Wu, C.; Sun, F. Effect of heat transfer law on finite time exergoeconomic performance of a carnot refrigerator. Exergy Int. J. 2001, 1, 295–302. [Google Scholar] [CrossRef]
- de Vos, A. Endoreversible thermoeconomics. Energ. Conv. Manage. 1995, 36, 1–5. [Google Scholar] [CrossRef]
- Novikov, I.I. The efficiency of atomic power stations (a review). Atomimaya Energiya 1957, 3, 409. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermoeconomic optimisation of novikov power plant model under maximum ecological conditions. J. Energy Inst. 2007, 80, 96–104. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Angulo-Brown, F.; Arias-Hernández, L.A. A replay to comments on a general property of endoreversible thermal engines. J. Appl. Phys. 2001, 89, 1520–1521. [Google Scholar] [CrossRef]
- Angulo-Brown, F.; Arias-Hernández, L.A.; Santillán, M. On some connections between first order irreversible thermodynamics and finite-time thermodynamics. Revista Mexicana de Física 2002, 48-S, 182–192. [Google Scholar]
- Barranco-Jiménez, M.A.; Sánchez-Salas, N. On thermodynamic optimisation of solar collector model under maximum ecological conditions. J. Energy Inst. 2008, 81, 164–167. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Sánchez-Salas, N.; Angulo-Brown, F. On the optimum operation conditions of an endoreversible heat engine with different heat transfer laws in the thermal couplings. Revista Mexicana de Física 2008, 54, 284–292. [Google Scholar]
- Velasco, S.; Rocco, J.M.; Medina, A.; White, J.A.; Calvo-Hernández, A. Optimization of heat engines including the saving of natural resources and the reduction of thermal pollution. J. Phys-D-Appl. Phys. 2000, 33, 355–359. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A. Modelos endorreversibles para la conversión de energía solar en energía de viento y análisis termo-económico de plantas de potencia . PhD thesis, Autonomous University of the State of Mexico, Mexico City, México, 2005. [Google Scholar]
- Sahin, B.; Kodal, A. Performance analysis of an endoreversible heat engines based on a new thermoeconomic optimization criterion. Energ. Convers. Manage. 2001, 42, 1085–1093. [Google Scholar] [CrossRef]
- Sahin, B.; Kodal, A. Finite time thermoeconomic optimization for endoreversible refrigerators and heat pumps. Energ. Convers. Manage. 1999, 40, 951–960. [Google Scholar] [CrossRef]
- Sahin, B.; Kodal, A. Thermoeconomic optimization of two-stage combined refrigeration systems: a finite time approach. Int. J. Refrig. 2002, 25, 872–877. [Google Scholar] [CrossRef]
- Kodal, A.; Sahin, B.; Oktem, A.S. Performance analysis of two stage combined heat pump system based on thermoeconomic optimization criterion. Energ. Convers. Manage. 2000, 41, 1989–2008. [Google Scholar] [CrossRef]
- Kodal, A.; Sahin, B. Finite tiem thermoeconomic optimization for ireversible heat engines. Int. J. Therm. Sci. 2003, 42, 777–782. [Google Scholar] [CrossRef]
- Kodal, A.; Sahin, B.; Yilmaz, T. Effects of internal irreversibility and heat leakage on the finite time thermoeconomic performance of refrigerators and heat pumps. Energ. Convers. Manage. 2000, 41, 607–619. [Google Scholar] [CrossRef]
- Sahin, B.; Kodal, A.; Koyun, A. Optimal performance characteristics of a two-stage irreversible combined refrigeration system under maximum cooling load per unit total cost conditions. Energ. Convers. Manage. 2001, 42, 451–465. [Google Scholar] [CrossRef]
- Kodal, A.; Sahin, B.; Erdil, A. Performance analysis of a two-stage irreversible heat pump under maximum heating load per unit total cost conditions. Int. J. Exergy 2002, 2, 109–123. [Google Scholar] [CrossRef]
- Kodal, A.; Sahin, B.; Ekmekci, I.; Yilmaz, T. Thermoeconomic optimization for irreversible absorption refrigerators and heat pumps. Energ. Convers. Manage. 2003, 44, 109–123. [Google Scholar] [CrossRef]
- Qin, X.; Chen, L.; Sun, F.; Wu, C. Thermoeconomic optimization of an endoreversible four-heat-reservoir absorption-refrigerator. Appl. Energy 2005, 81, 420–433. [Google Scholar] [CrossRef]
- Kreps, D.M. A Course in Microeconomic Theory; Princeton University Press: New York, NY, USA, 1990. [Google Scholar]
- Tirole, J. The Theory of Industrial Organization; MIT Press Cambridge Mass: London, UK, 1988. [Google Scholar]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermoeconomical optimization of an endoreversible power plant model. Revista Mexicana de Física 2005, 51, 49–56. [Google Scholar]
- Gutowicz-Krusin, D.; Procaccia, J.; Ross, J. On the efficiency of rate processes: Power and efficiency of heat engines. J. Chem. Phys. 1978, 69, 3898–3906. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F.; Chen, W. Influence of heat transfer law on the performance of a carnot engine. Chin. J. Engng. Thermophys. 1990, 11, 241–243. [Google Scholar] [CrossRef]
- O’Sullivan, C.T. Newton’s law of cooling - a critical assessment. Amer. J. Phys. 1990, 58, 956–960. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Proceedings of 17th Conference on Efficiency, Costs, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS 2004), Guanajuato, México, 7–9 July 2004; Instituto Mexicano del Petróleo: Distrito Federal, México, 2004; pp. 351–357.
- Bejan, A. Advanced Engineering Thermodynamics; Addison Wiley: New York, NY, USA, 1988. [Google Scholar]
- de Vos, A. Endoreversible Thermodynamics of Solar Energy Conversion; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barranco-Jiménez, M.A.; Ramos-Gayosso, I.; Rosales, M.A.; Angulo-Brown, F. A Proposal of Ecologic Taxes Based on Thermo-Economic Performance of Heat Engine Models. Energies 2009, 2, 1042-1056. https://doi.org/10.3390/en20401042
Barranco-Jiménez MA, Ramos-Gayosso I, Rosales MA, Angulo-Brown F. A Proposal of Ecologic Taxes Based on Thermo-Economic Performance of Heat Engine Models. Energies. 2009; 2(4):1042-1056. https://doi.org/10.3390/en20401042
Chicago/Turabian StyleBarranco-Jiménez, Marco A., Israel Ramos-Gayosso, Marco A. Rosales, and Fernando Angulo-Brown. 2009. "A Proposal of Ecologic Taxes Based on Thermo-Economic Performance of Heat Engine Models" Energies 2, no. 4: 1042-1056. https://doi.org/10.3390/en20401042
APA StyleBarranco-Jiménez, M. A., Ramos-Gayosso, I., Rosales, M. A., & Angulo-Brown, F. (2009). A Proposal of Ecologic Taxes Based on Thermo-Economic Performance of Heat Engine Models. Energies, 2(4), 1042-1056. https://doi.org/10.3390/en20401042



