Abstract
This paper deals with the economics of gasification facilities in general and IGCC power plants in particular. Regarding the prospects of these systems, passing the technological test is one thing, passing the economic test can be quite another. In this respect, traditional valuations assume constant input and/or output prices. Since this is hardly realistic, we allow for uncertainty in prices. We naturally look at the markets where many of the products involved are regularly traded. Futures markets on commodities are particularly useful for valuing uncertain future cash flows. Thus, revenues and variable costs can be assessed by means of sound financial concepts and actual market data. On the other hand, these complex systems provide a number of flexibility options (e.g., to choose among several inputs, outputs, modes of operation, etc.). Typically, flexibility contributes significantly to the overall value of real assets. Indeed, maximization of the asset value requires the optimal exercise of any flexibility option available. Yet the economic value of flexibility is elusive, the more so under (price) uncertainty. And the right choice of input fuels and/or output products is a main concern for the facility managers. As a particular application, we deal with the valuation of input flexibility. We follow the Real Options approach. In addition to economic variables, we also address technical and environmental issues such as energy efficiency, utility performance characteristics and emissions (note that carbon constraints are looming). Lastly, a brief introduction to some stochastic processes suitable for valuation purposes is provided.
1. Introduction
From an economic point of view, perhaps the best suited description of gasification is the following: “Gasification is a flexible, commercially proven, and efficient technology that produces the building blocks for a range of high-value products from a variety of low-value feedstocks” (Gasification Technologies Council [1]). In view of that, this work focuses on system flexibility issues optimizing inputs and outputs in addition to gasifier designs and processes. As stated at the very start in Trigeorgis [2]: “Flexibility has value”. Assessing its value at the applied level, though, is far from obvious.
Regarding energy investments, first we note the random character of both input and output prices. Second, scientific and technological developments take place continuously in unpredictable ways. Third, the institutional framework within which relevant players operate changes from time to time in response to new circumstances. On the other hand, these investments are at least partially irreversible, i.e., should market conditions turn, the firm cannot “uninvest” and recover the full expenditure. Further, usually the firm has the opportunity (not the obligation) to invest in a project over some pre-specified period of time; i.e., it has to decide whether and when to invest. In the particular case of gasification facilities, this scenario combines with other options to manage the energy project in flexible ways.
Under these circumstances, valuation techniques based on the methods for pricing options (such as Contingent Claims Analysis or Dynamic Programming) are superior to the traditional approaches that are based on discounted cash flows (see, for instance, Dixit and Pindyck [3]; Sick [4]; Trigeorgis [2]). Specific applications to energy investments can be found in Ronn [5], and the Real Options Group web site (http://www.realoptions.org). Now in this paper we address the main elements to be considered in an economic valuation of gasification technologies in general, and Integrated Gasification Combined Cycle (IGCC) power plants in particular. The particular choice between burning coal or natural gas for producing power has been previously analyzed in Abadie and Chamorro [6]. These investments enjoy a long useful life but require some non-negligible time to build. In the medium to long term, their ultimate fate will depend on their economic profitability. In this respect, any economic assessment should take into account both the potential profits and risks inherent to these technologies.
Some of the advantages can be directly measured. Thus, most importantly, gasification technologies allow choosing the cheapest fuel from a range of alternatives. This is in stark contrast to pricier resources for inflexible technologies, such as natural gas-fired combined cycles (NGCC) in power production. Since investments in power generation involve long-lived assets, a proper valuation of this fuel price gap in the future is crucial. Note, though, that there may not be markets for some of the commodities involved in exploiting these technologies, despite the fact that they do have an economic value. For instance, municipal and industrial wastes could be deemed worthless (or even costly to store or treat), but they can be transformed into high-value products. The same can also apply to certain pollutant emissions if a market for them is (still) in the offing. This possibility should not be overlooked.
As mentioned above, not only returns are important but risks as well. Whatever their nature happens to be (financial, operational, regulatory, ...), these risks must be quantified. Needless to say, any measure targeted at reducing them will contribute to the development of this technology. Some major aspects on risk management are highlighted below:
- Risk related to the possibility of more stringent environmental regulations. They could result in a higher operating cost for coal-based technologies as compared with competing low-emission (natural gas) or clean technologies (nuclear, wind, solar). In countries with this kind of regulation in place, future regulatory developments always spell uncertainty and therefore volatility in the emission allowance price.
- Risk related to the identity of the marginal technology in power production. Natural gas-fired plants are usually the marginal technology; as such, they set the market price of electricity according to their short-term marginal costs. In particular, lower carbon emissions from gas plants (relative to coal plants) mean that these plants need less emissions allowances per unit of electricity. Therefore, the price of electricity would partially reflect their lower emissions. In other words, this price would be “unduly low” from coal plants’ perspective. These plants could thus find it difficult to recover some fraction of their costs through the electricity price (the more so if carbon prices rise). One possible reaction would be to retrofit them for capturing carbon.
- Risk related to the development of the gasification technology because of a lack of standards and modularization.
This paper is organized as follows:
- Section 2 introduces gasification processes and technologies; special focus is placed on the flexibilities that are available to the managers.
- Coal, one of several feedstocks suitable for gasification, is briefly addressed in Section 3.
- If we are assessing a potential investment in this technology we need to identify the more relevant issues. Section 4 is devoted to those issues for which markets are particularly worth considering. This clearly holds for primary energy markets. Coal and natural gas prices are regularly determined on futures markets, and the information they convey cannot be overlooked. Of course, identifying the cheapest fuel is important when, from the outset, the plant is restricted to use one single fuel; and, at least in this case, it is also relatively simple. When there is flexibility, though, this important issue becomes more complex. This is because the cheapest fuel can change from time to time and fuel switching costs may be a barrier to seize this opportunity. Next, the market for electricity is relevant from the revenue side. However, (futures) markets for electricity are not as developed as those for oil, coal or natural gas. In spite of this, electricity prices play a crucial role in the economics of a given power station: the merit order influences dispatch of every plant, which in turn affects its availability rate. Moreover, the utilities that operate under environmental restrictions must closely watch emissions markets (for sulfur, carbon, etc.). In addition to variable costs and revenues, construction costs are of paramount importance for the profitability of these capital-intensive plants.
- Then Section 5 addresses other relevant issues in less detail. They range from the plant’s intrinsic concerns (e.g., process efficiency) to issues of public policy (e.g., support measures).
- For those readers with an interest in more rigorous analysis, in Section 6 we briefly introduce some stochastic processes that are used in capital budgeting decisions regarding energy assets.
2. Brief Description of the Gasification Technology
The starting point is an initial (low-grade) hydrocarbon material or “feedstock”. This fuel must undergo a preparation process that is very important for the reliability and the availability of the system, because of the impact it can have on the life of the gasifier feed injectors1. The particular feed material chemically reacts with oxygen and steam at high temperatures to generate a synthesis gas (or syngas). The following (exothermic) reactions provide heat through partial combustion of coal2:
This energy allows some further (endothermic) reactions whereby various syngas components are generated:
Depending on the type of gasifier, additional chemical reactions can give rise to amounts of methane:
The syngas consists primarily of carbon monoxide (CO) and hydrogen (). It can be subjected to a cleanup process in the pre-combustion stage. This process could allow separation of some and more cheaply than during post-combustion. Similarly, since carbon dioxide () is more concentrated, it would be easier to separate than during post-combustion; this is relevant if the owners of the plant are trying to decide whether to build a carbon capture and storage (CCS) unit. Some gasifiers’ syngas contains tars, which must be condensed and recycled; tars complicate downstream gas cleaning.
There are three major types of gasifiers: fixed bed3, fluidized bed, and entrained flow gasifier. These process technologies allow a large variety of plant configurations. The range of objectives includes: hydrogen, methanol or dimethyl ether, ammonia, Fischer-Tropsch liquids, power only without capture, power only with capture, power and co-production of hydrogen. As Holt [7] points out, the best gasification technology for a given application will depend on the project objectives and the range of coal or other feedstocks available. In addition, a gasification plant can be designed to produce more than one product at a time (co-production or “polygeneration”), such as the production of electricity, steam, and chemicals. This polygeneration flexibility allows a facility to increase its efficiency and to improve the economics of its operation.
Gasification has been used since 1950, with 19 plants currently operating in the U.S. The last one started operation in 2002. Table 1 shows location, fuel type, and the output of these plants4. More than 140 gasification plants are deployed over the world5. The majority of them are designed to produce chemicals and fertilizers. The current product market share consists of 45% chemicals, 30% liquid fuel, 19% power, and 6% gaseous fuel. In terms of feedstock, some of them are based on solid feedstock (coal and petroleum coke), others on refinery of high-sulfur heavy-oil. Only a small number of them are based on coal.

Table 1.
Gasification plants in the U.S.
| Syngas | |||||
|---|---|---|---|---|---|
| Plant Name | Location | Year | Main Product | Feed Class | Output (*) |
| Houston Oxochemicals Plant | Houston, TX | 1977 | Chemicals | Gas | 287 |
| Baton Rouge Oxochemicals Plant | Baton Rouge, LA | 1978 | Chemicals | Petroleum | 78 |
| LaPorte Syngas Plant | Deer Park, TX | 1979 | Chemicals | Gas | 656 |
| Hoechst Oxochemicals Plant | Bay City, TX | 1979 | Chemicals | Petroleum | 68 |
| Kingsport Integrated Coal Gasific. | Kingsport, TN | 1983 | Chemicals | Coal | 219 |
| Sunoco Oxochemicals Plant | Texas | 1983 | Chemicals | Gas | 55 |
| Texas City Dow Syngas Plant | Texas City, TX | 1983 | Chemicals | Gas | 114 |
| Great Plains Synfuels Plant | Bismarck, ND | 1984 | Gaseous fuels | Coal | 1900 |
| Convent H2 Plant | Convent, LA | 1984 | Chemicals | Petroleum | 257 |
| Wabash River Energy Ltd. | West Terre Haute, IN | 1995 | Power | Petcoke | 591 |
| Taft Syngas Plant | Taft, LA | 1995 | Chemicals | Gas | 59 |
| LaPorte Syngas Plant | LaPorte, TX | 1996 | Chemicals | Gas | 253 |
| Texas City Praxair Syngas Plant | Texas City, TX | 1996 | Chemicals | Gas | 278 |
| Polk County IGCC Project | Mulberry, FL | 1996 | Power | Coal | 451 |
| Oxochemicals Plant | Texas | 1998 | Chemicals | Gas | 48 |
| Coffeyville Syngas Plant | Coffeyville, KS | 2000 | Chemicals | Petcoke | 293 |
| Baytown Syngas Plant | Baytown, TX | 2000 | Gaseous fuels | Petroleum | 347 |
| Delaware Clean Energy Cogener. | Delaware City, DE | 2002 | Power | Petcoke | 520 |
| Longview Gasification Plant | Longview, TX | 2002 | Chemicals | Gas | 213 |
Source: World Gasification Database; Gasification Technologies Council.
(*) Syngas output in megawatts thermal.
There are also 15 power plants across the world, with an installed capacity of 4,107 MW (Gasification Technologies Council [1]). Entrained-flow gasifiers have been selected for the majority of commercial-sized IGCC project applications. Among them, IGCC power plants at Buggenum (the Netherlands), Wabash River (Indiana, U.S.), Polk County (Florida, U.S.), and Puertollano (Spain) are of particular interest because they are based on coal as primary fuel.
Electricity generation requires burning the syngas in an internal combustion engine or a gas turbine (Brayton cycle) to produce electricity. The post-combustion flue gases are used to produce steam which can be utilised in steam turbines (Rankine cycle). This additional power output improves the efficiency considerably. In the absence of any requirement or regulation for capture, the selection for IGCC is more open to all types of gasifier and would be evaluated presumably based on the traditional criteria of CoE (cost of electricity) and perception of risk and availability. The choice will also be markedly affected by coal type. If the requirement for capture could be relaxed, then a wider range of gasifiers could be used in polygeneration or co-production mode. However, each technology must be evaluated on its total characteristics rather than efficiency alone.
According to Franco and Diaz [8], IGCC technology holds great promise for the future due to the flexible feedstock, process options, and products and opens new markets for coal (syn-fuels, chemicals, fertilizers). It also provides the only feasible bridge from coal to hydrogen (directly converts coal to hydrogen). But in the meantime new barriers are growing against deployment of IGCC. The first is the power industry culture (IGCC is basically a chemical plant, and power companies do not like chemical units). Moreover there are a lot of technical and financial risks. Finally, companies do not understand why they should build IGCC when it is possible to get a permit for a conventional coal plant.
Frequently coal gasification has also appeared as a substitute product for natural gas. The price gap between gas and coal can determine in many instances the viability of gasification-based facilities. Some of the main variables to be taken into account are: output prices, installation costs, input prices, thermal efficiency of the transformation process, environmental impacts and related costs. They all will be considered in Section 4 and Section 56.
Similarly, gasification is the starting point for getting transportation fuels. There are basically two methods:
- The Fischer-Tropsch (FT) liquefaction technology was developed in 1920 by Franz Fischer and Hans Tropsch. It was later used during the II World War by Germany and Japan. More lately, it has been intensely used in South Africa, where it provides some 28% of the diesel and gasoline needs. The FT process is also used for converting syngas to other products such as naphtha, waxes, ammonia, hydrogen and methane. The syngas is reacted in the presence of an iron or cobalt catalyst7.
- Another process is the so-called Methanol to Gasoline (MTG). The syngas is first transformed into methanol and this in turn into gasoline. This technology was developed for use by ExxonMobil in New Zealand during the 1980s and can produce commercial levels of transportation fuels.
Figure 1 shows entry and exit flexibility for both gasification and liquefaction processes. This flexibility has important economic consequences which are explored in this paper.
3. Coal Reserves and World Consumption: The Security of Supply
Coal reserves represent about 70% of the world’s proven fossil resources, and they are geographically more delocalized than gas or oil (see Table 2)8. Its usage can improve the security of energy supply, for example when it comes to the reduction in natural gas imports. The extended utilisation of coal could also alleviate the pressure on the demand for other alternative fuels like natural gas. To make this possible, though, the gasification technology needs to be further developed and optimized.
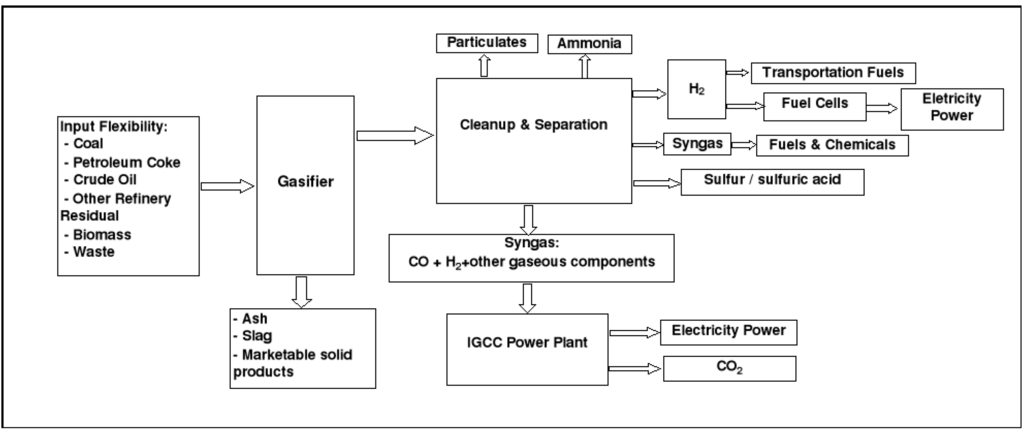
Figure 1.
Input and output flexibility in gasification technology.
The ratio of proven reserves to production (R/P) at the end of 2008 appears in Table 3 for different geographic areas (BP [9]). We also include the R/P ratio for natural gas since we will refer to this fuel in Section 4.
As can be seen in Figure 2, coal consumption has increased substantially at the world level. Countries such as China satisfy a significant part of their energy needs with coal. Right now efficiency enhancement ranks higher than before. This is for the sake of lower coal consumption and specific emission, as well as better economics.
With regard to future consumption, according to the Reference Scenario in IEA [10] coal sees the biggest increase in demand in absolute terms, jumping by 73% between 2005 and 2030 and pushing its share of total energy demand up from 25% to 28%. Similarly, in the EIA [11] reference case, world coal consumption increases by 49% from 2006 to 2030, and coal’s share of world energy consumption increases from 27% in 2006 to 28% in 2030.
4. Relevant Issues for an Economic Assessment
From an economic viewpoint, the following issues are relevant when assessing gasification: (a) the price of the input fuels9; (b) the efficiency of the generation processes; (c) the flexibility regarding alternative fuels; (d) the flexibility concerning output products; (e) the availability and reliability of the system; (f) the environmental costs related to gasification technologies; (g) the option to install a CCS facility alongside the gasification plant; (h) the total capital cost; (i) construction time10; (j) annual maintenance costs; (k) the project lifetime; (l) other additional items (water consumption, disposal of pollutants such as mercury, etc.). These aspects are elaborated below.
4.1. Fuel cost without entry flexibility in an IGCC plant
Before addressing the valuation of input flexibility, first we consider the case in which only one fuel can be used as feed material in the IGCC power plant. It could be coal or any other fuel input; for example, refineries produce amounts of crude oil residual. This low-cost fuel might be used in the IGCC plant to produce only power or both power and hydrogen (in this case there would be output flexibility).

Table 2.
Recoverable coal resources around the world (million short tons). Source: see note 8.
| Country | Anthracite and | Lignite and | Total |
|---|---|---|---|
| Bituminous | Subbituminous | Recoverable Coal | |
| Canada | 3,826 | 3,425 | 7,251 |
| United States | 122,001 | 141,780 | 263,781 |
| Others North America | 948 | 589 | 1,537 |
| North America | 126,776 | 145,793 | 272,569 |
| Brazil | 0 | 7,791 | 7,791 |
| Colombia | 7,251 | 420 | 7,671 |
| Others Central & South America | 718 | 1,761 | 2,479 |
| Central & South America | 7,969 | 9,973 | 17,941 |
| Former Serbia and Montenegro | 7 | 15,299 | 15,306 |
| Germany | 168 | 7,227 | 7,394 |
| Poland | 6,627 | 1,642 | 8,270 |
| Others Europe | 2,495 | 17,317 | 19,812 |
| Europe | 9,296 | 41,485 | 50,781 |
| Kazakhstan | 31,052 | 3,450 | 34,502 |
| Russia | 54,110 | 118,964 | 173,074 |
| Ukraine | 16,922 | 20,417 | 37,339 |
| Others Eurasia | 1,102 | 3,100 | 4,202 |
| Eurasia | 103,186 | 145,931 | 249,117 |
| Middle East (Iran) | 1,528 | 0 | 1,528 |
| South Africa | 52,911 | 0 | 52,911 |
| Others Africa | 1,577 | 192 | 1,769 |
| Africa | 54,488 | 192 | 54,680 |
| Australia | 40,896 | 43,541 | 84,437 |
| China | 68,564 | 57,651 | 126,215 |
| India | 57,585 | 4,694 | 62,278 |
| Others Asia & Oceania | 2,950 | 7,927 | 10,877 |
| Asia & Oceania | 169,994 | 113,813 | 283,807 |
| World Total | 473,236 | 457,186 | 930,423 |
Even when the IGCC plant is designed to run on a single fuel, it would be possible to choose fuels that are less suited for plants that burn pulverized coal (PC). For instance, PC plants—to comply with environmental regulations—would be required to use coal with a low sulfur content, or to adopt post combustion removal systems (such as flue gas desulphurizer or spray dry scrubber). On the other hand, IGCC technology allows for a cheaper capture of carbon (or sulfur). In connection with this technology, the type of fuel burnt can affect both capital costs and operation costs of the plant.

Table 3.
Proven reserves to production ratio () at end of 2008.
| Area | Coal | Area | N.Gas |
|---|---|---|---|
| Total North America | 216 | Total North America | 10.9 |
| Total S. & Cent. America | 172 | Total S. & Cent. America | 46.0 |
| Total Europe & Eurasia | 218 | Total Europe & Eurasia | 57.8 |
| Total Middle East & Africa | 131 | Total Middle East | >100 |
| Total Asia Pacific | 64 | Total Africa | 68.2 |
| TOTAL WORLD | 122 | Total Asia Pacific | 37.4 |
| of which: European Union | 51 | TOTAL WORLD | 60.4 |
| OECD | 164 | of which: European Union | 15.1 |
| Former Soviet Union | 433 | OECD | 14.6 |
| Other Emerging Mkt. Econ. | 60 | Former Soviet Union | 71.8 |
Source: BP Statistical Review of World Energy 2009.
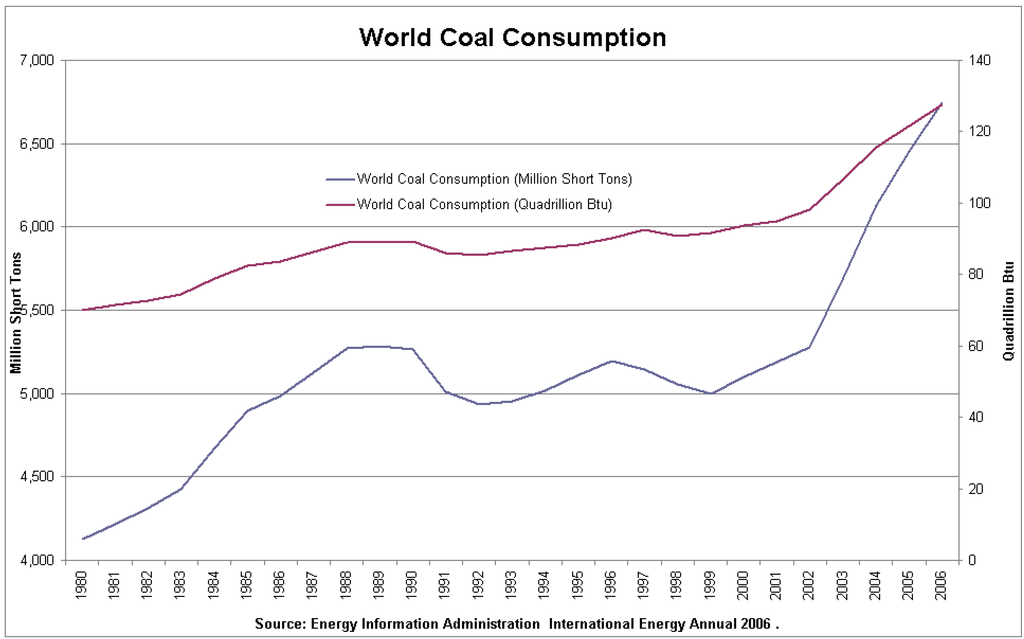
Figure 2.
World consumption of coal. Source: EIA.
The price of the fuel used to produce one megawatt-hour (MWh) of electricity is one of the main advantages of the IGCC technology over other competing alternatives. Figure 3 shows the costs of U.S. power plants in nominal U.S. dollars. Coal and petroleum coke (or petcoke) enjoy a significant advantage over natural gas for a given power generation efficiency. This comparative advantage has increased steeply over the last years11.
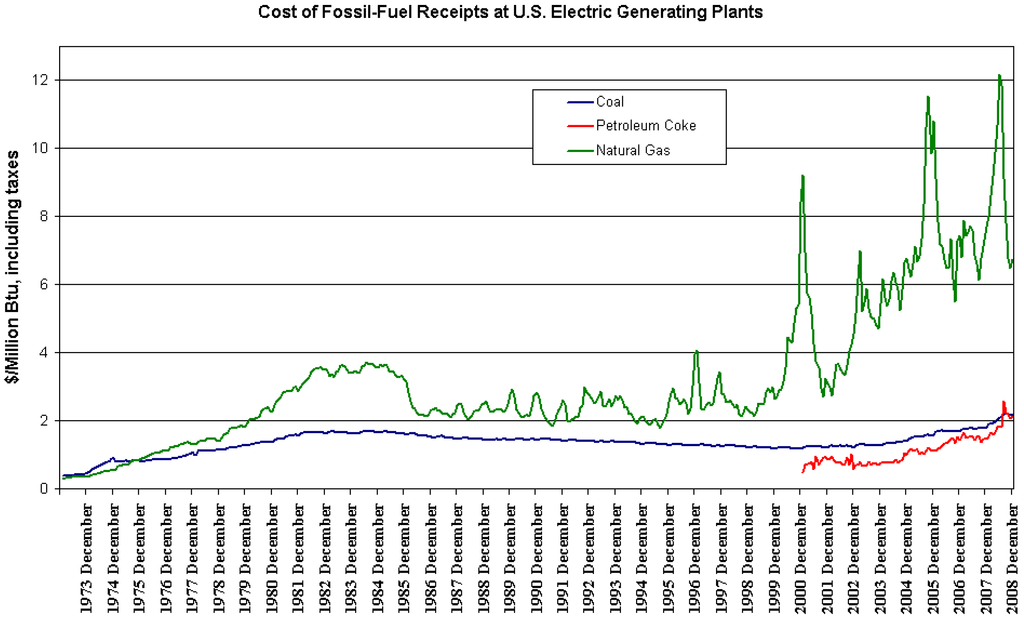
Figure 3.
Cost of several fossil fuel inputs to electricity production in the U.S. Source: U.S. DoE.
Figure 4 shows the fuel price gap (again in nominal U.S. dollars) between coal and natural gas for producing one MWh with standard efficiency levels at both IGCC and NGCC power plants, 42.5% and 55% respectively. It can be seen that high gas prices impact strongly this technology’s variable costs, a fact which is not offset by its higher efficiency level.
The greater fuel flexibility afforded by gasification technologies can be an important source of value: at any time it allows choosing the cheapest alternative (within the limits established by the specific design of each gasification plant). The IGCC technology must incur lower variable costs linked to fuel consumption than the NGCC technology; in particular, the fuel costs of producing one unit of electricity must be lower. At the same time, by using a gas turbine and a steam turbine, the IGCC plant reaches higher efficiencies than a conventional coal-fired plant. Thus we have:
where and denote the price of natural gas and coal, respectively. and stand for the thermal efficiency of a NGCC plant and a PC plant, while applies to the IGCC plant. For the sake of simplicity, we assume that all the prices have been converted into $/MWh (or €/MWh).
Therefore, the difference measures the relative (cost) advantage of an IGCC plant over an NGCC plant in terms of the fuel used. Its advantage over a PC plant is attributed to its higher efficiency: 12. The advantage provided by the fuel price gap (adjusted for relative efficiencies) must be assessed numerically as an input to decision making process. Especially, it is important to know if this advantage, when added to any other that could be exploited, allows to compensate for some disadvantages, such as the higher investment costs. Specific items to be considered include fuel prices, installations’ efficiencies, and their expected useful lives.
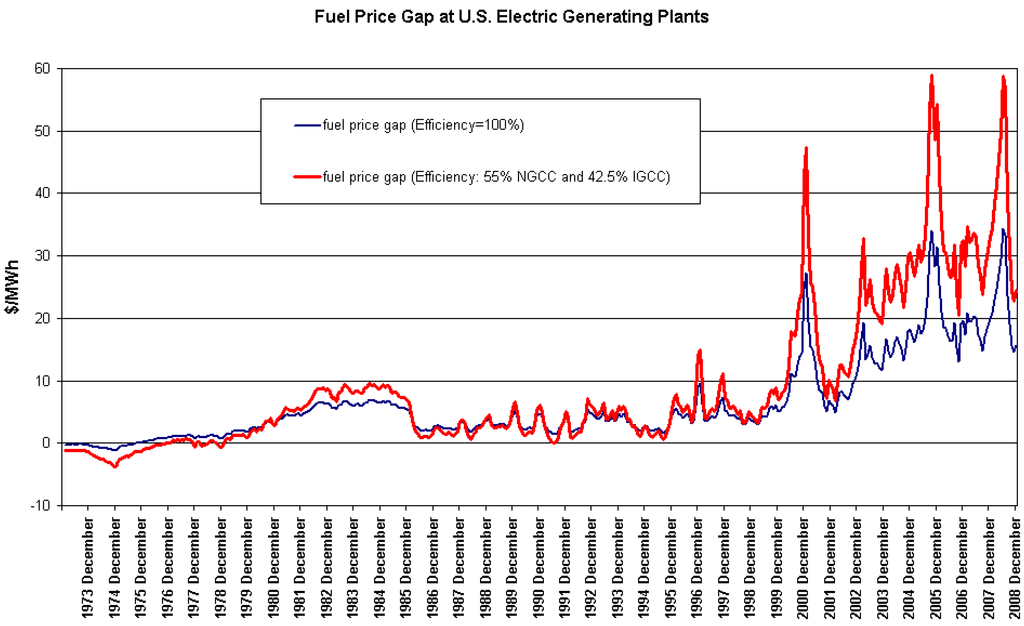
Figure 4.
Fuel price gap between natural gas and coal.
Obviously, since we are dealing with long-lived facilities, their value depends not only on current prices and price gaps for producing one MWh, but on their future levels as well. Present and future coal reserves, refinery production processes, the evolution of demand and extraction costs, they all affect the future price gap, which can turn out to be very different from that prevailing in the spot market currently. Futures markets can be particularly helpful in this respect.
Figure 5 shows the prices of futures contracts on natural gas and coal on the New York Mercantile Exchange (NYMEX). As could be expected, natural gas prices display a prominent seasonal pattern on any given day. However, in a long-term evaluation, when gas is consumed on a uniform basis to produce electricity, using the deseasonalised series (also shown) would be enough. Currently traded contracts’ maturities go beyond 2020. Note also that these prices depend on local conditions and can be the object of speculation to some degree.
Futures prices are not the spot prices expected to prevail in the physical or actual world in the future, which are harder to estimate (because of the risk premium embedded in actual prices). A standard result in Finance textbooks is that the futures price for a given maturity is equal to the spot price expected to prevail at that time if market agents are assumed to be risk neutral. Thus, the futures price provides the expected value of the future spot price in a risk-neutral world; and it can be properly discounted to the present at the risk-free interest rate. Figure 6 shows the futures price gap for the same efficiency levels as before (namely 42.5% and 55%). Therefore, the gap in this figure corresponds to the gap in a risk-neutral world. The fuel price gap is given by:
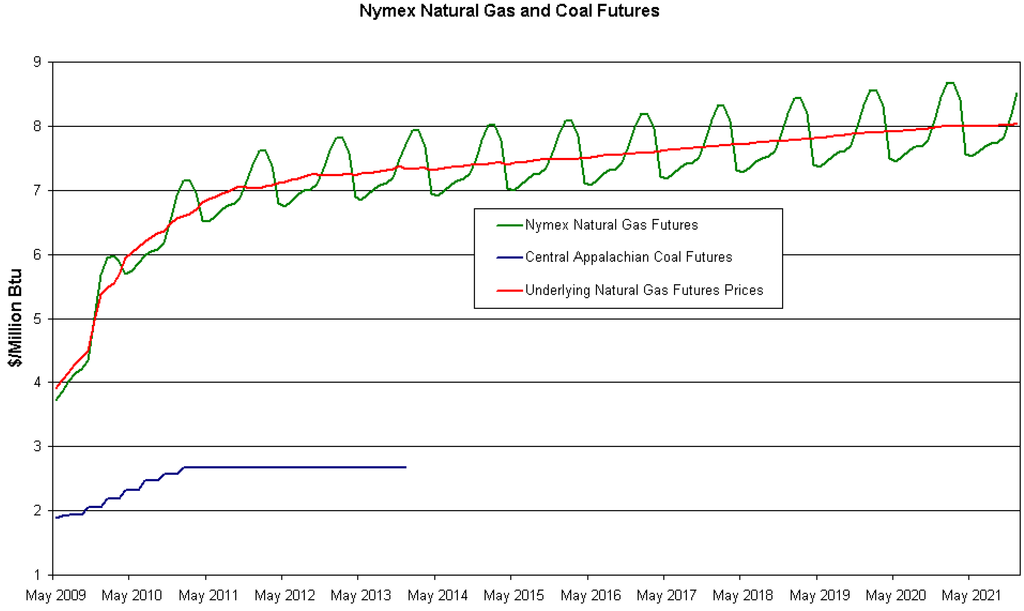
Figure 5.
Price of futures contracts on natural gas and coal. Source: NYMEX.
The information embedded in the prices of futures contracts on coal and natural gas can be used to assess the present value of energy costs. Thus, by using readily available futures prices and discounting them at the riskless rate, we can derive the present value of cumulative costs (or revenues) in a relatively simple manner, even graphically. Stated differently, we do not need to compute the actual price process nor to discount future values at a rate augmented by the risk premium.
In particular, we can fit a curve to the discrete futures prices available in the market for a set of maturities (say March, June, September, December, up to five years ahead)13. Let denote this curve, which shows the time-0 price of a unit of energy (conveyed in coal, or gas) to be delivered at time t in exchange for an amount of money . The curve on a given date (0) can be fitted by following several procedures14. This will allow us to compute the value V at that time (0) of future fuel costs15:
E denotes the thermal efficiency of the plant involved; it inversely affects the input consumption per unit of output. Depending on the particular type of plant (natural gas-fired, or coal-fired, or IGCC), E can take on the value . We are accordingly interested in the futures price of either natural gas or coal, i.e., . The time limits of the integral, and , comprise the useful life of the plant16. The integral stands for the (time-0) present value of the costs incurred by producing a unit of energy (e.g., one MWh/year) from natural gas or coal over the plant lifetime . Each futures price (of natural gas, or coal) paid at time t is discounted at the risk-free interest rate r over the time period stretching from now (time 0) until the contract’s maturity date (t)17. Several cases can be analysed within this framework.
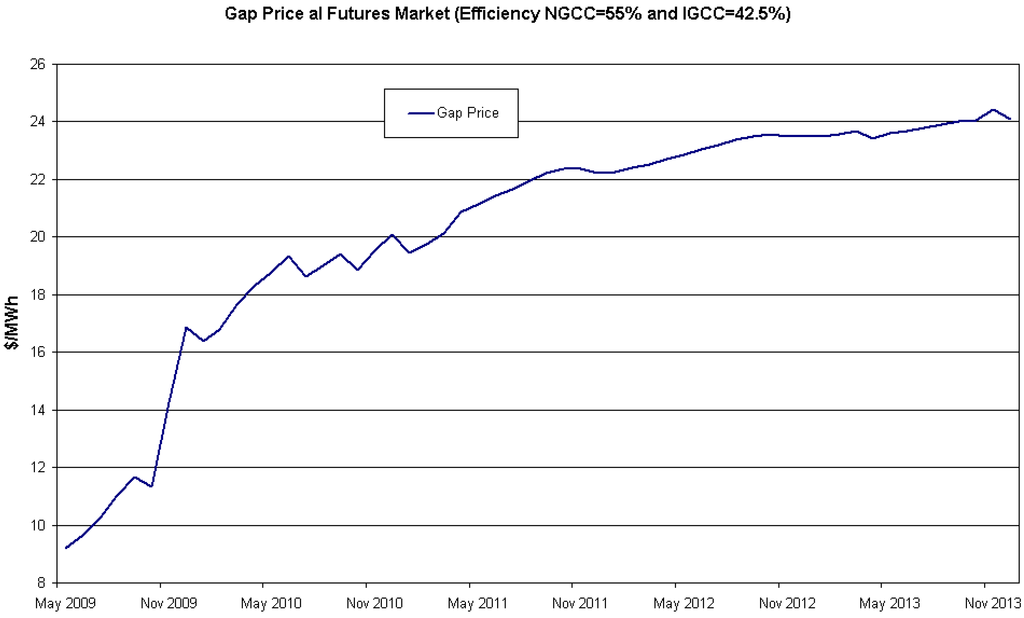
Figure 6.
Fuel price gap as implied by futures prices of natural gas and coal.
Case 1. Assume that a given design mix of fuel inputs is used every year in an IGCC plant. For example, each unit of black coal is accompanied by a fixed number α of units of petroleum coke. Our formula for the present value of future fuel costs would then become:
where stands for the futures price of petroleum coke to be delivered at t.
Case 2. In principle the above formula is also valid for computing the present value of a unit of electricity (one MWh) to be produced each period over the plant life . If there were a well-developed futures market for electricity then we could take the futures price on this market. The present value of future revenues from electricity would be:
Case 3. Let us consider two different power plants designed to produce the same yearly amount of electricity18. They are further assumed to have the same useful life, and to start operation at the same time. In this case, the above present value of revenues would not be a relevant input to the investment decision provided it is high enough to recover the investment costs and enjoy a reasonable profit. Instead, the relevant factor would be cost minimization across plants while taking into account investment risks.
4.2. Fuel flexibility in an IGCC power plant
In fact, not one but a wide variety of feedstocks is available to an IGCC station: coal, biomass, petroleum coke, crude oil, high sulfur fuel oil, other refinery residuals. Some of these feedstocks are not suitable for the use in combustion power generation cycles considering the potential pollution risks. This input flexibility is an intrinsic feature of IGCC plants as compared to other power generation technologies. For example, a flexible design for a PC plant to run on several types of coal would command a much higher price and entail a greater complexity of the plant.
We have just seen above the case without input flexibility. There were more than one input fuel on offer, but we were restricted to choose only one fuel type to be used as a feedstock from the opening of the plant to its closure. We have shown that in this case futures markets alone can allow us to compute the present values of alternative fuel costs. However, under input flexibility the true cost to be incurred will be somewhat lower, given that at some times we will be able to select another, cheaper fuel. In other words, the option to switch between fuels adds an economic value to the power station, since at every moment the cheapest alternative can be chosen. Note, though, that all the ensuing effects of any fuel switching must be duly taken into account. For instance, there may be a switching cost to fuel substitution, or the plant efficiency level may fall short of the design level. Nonetheless, it is an important option since, for installations with long life spans, the cost of the potential fuels may undergo significant changes over time.
Thus, let us consider a hypothetical scenario in which the plant managers can choose between using coal or petcoke19. The thermal efficiency changes accordingly ( or ). There are switching costs between fuels20: denotes the costs to switching from coal to petcoke, whereas is the cost to switching from petcoke to coal.
First let us focus on the revenue side. The power plant is designed to produce an annual electricity output A (in MWh). This value is a function of the installed capacity, M (in MW), and the fraction of the year that the plant is expected to be in operation, defined as capacity factor, C (with ):
If the capacity factor C changes over time, as it actually does, then we should use a sum over the whole year:
This electricity is assumed to be sold every year on the futures market at the current (exogenous) market price (in €/MWh). Once we have derived the yearly revenues, we can compute their cumulative value.
Next we focus on fuel costs. If the prices of both fuels are and (in €/MWh), then total fuel costs over a period would amount to if the plant is operated in coal mode, and if it is operated in petcoke mode. Now we address the minimization of the costs of running the plant over the whole time horizon by means of two bi-dimensional binomial lattices, one for each mode of operation. To understand what a (one-dimensional) binomial lattice is, we can think of a random variable (say, a price P) that begins at a known value (), and may increase (by a multiplicative factor u) with a given probability to or decrease with complementary probability to (where ) at the end of the period . This same process follows over successive periods. The term ’bi-dimensional’ just indicates that we are not dealing with one but two random prices at any moment. Thus, we have a given combination of prices ( and ) at the initial node. Each of the prices evolves on its own so there are four branches starting from the initial node. At the end of the period there are four possible nodes: (1) both prices have moved up, (2) the first one up and the second down, (3) the first one down and the second up, or (4) both prices have moved down.
Prior to the valuation of future costs we must know how fuel prices behave in a risk-neutral world (for example, by exploiting futures prices), along with their volatilities and correlations (these estimates must be consistent with futures market data). This all will allow us to compute the changes and in the log prices of both fuels (i.e., and ) and the risk-neutral probabilities , , , ; for one, is the probability (in the risk-neutral world) that after a short time lapse, , coal price has moved upwards while petcoke price has moved downwards.
The way to proceed in our case is by using not one but two binomial lattices, one for each of the two possible modes of operation. At any moment the manager of the plant must compare the value in a given node of one lattice (mode) with its counterpart in the other lattice (mode) after adjusting for any switching cost. In this way she can choose the optimal mode of operation at any time. Valuation proceeds backwards, from the end of the useful plant life to the moment when the investment decision is made (see Abadie and Chamorro [6]).
At expiration the IGCC plant ceases fuel consumption, so it incurs no fuel costs (), irrespective of whether it expires operating in coal mode or petcoke mode21. Therefore, when the plant reaches maturity:
In other words, the fuel costs at the final nodes in both the coal-mode lattice and the petcoke-mode lattice are zero.
In earlier periods production costs must be minimized by choosing between two alternatives:
- to continue operation in the current mode during the period :
- -
- paying for the fuel costs,
- -
- and accept the present value of the future costs that derive from starting the next period in the current mode, assuming that at any time in the future the best mode of operation will be chosen;
- to change the operation mode:
- -
- incurring the switching costs,
- -
- operate in the new mode during , paying for the fuel costs,
- -
- and accept the present value of the future costs that derive from starting the next period in the current mode, assuming that at any time in the future the best mode of operation will be chosen.
Analytically, when the starting state corresponds to operating with coal, the binomial lattice will take on the following value:
In words, starting in coal mode (hence ), fuel cost over the period will be the minimum of two quantities: (1) the cost to continue operation in the current (coal) mode during that period, paying for the fuel costs (), and accepting the present value of the future costs that derive from starting the next period in the current mode (i.e., the expected value of the four possible nodes discounted at a rate r over that period), and (2) the cost to change the operation mode (to petcoke), incurring the switching costs (), operate in the new mode during that period, paying for the fuel costs (), and accept the present value of the future costs that derive from starting the next period in the current mode (the last term with the discount factor).
Similarly, when the starting state corresponds to operating in petcoke mode, the binomial lattice will take on the following value:
Following this process backwards we arrive at the initial moment (time 0). Then we choose the cheapest alternative:
Thus we learn how to start operation of the plant, whether running on coal or petcoke. Besides, as fuel prices evolve over time, we can trace their movements on the two lattices. They already show when and where it is optimal to switch fuel, so we can react accordingly. In this way we minimize the fuel cost of running the plant over time.
Whether the “initial” least-cost fuel (as opposed to the alternative of using one single fuel forever) is coal or petcoke depends on several factors: (i) switching costs: the higher they are, the less valuable the option to switch; (ii) fuel prices volatilities: if there is no uncertainty, we are in a deterministic setting so the option to switch becomes worthless; (iii) fuel prices correlation: if they are highly unrelated, there is a greater chance that the option to switch to the cheaper fuel will be exercised at same time in the future; (iv) the (efficiency-adjusted) gap between both fuel prices: the lower it is, the higher the probability that price swings will entail changes in their relative cost and economic appeal.
4.3. Availability and reliability of the IGCC plant
Given that the IGCC plant commands a higher investment cost, the percentage of time over which the plant operates is particularly relevant from an economic point of view. According to Chen and Rubin [12], the assumed capacity factor contributes most to the total volatility of the cost of electricity in their analysis. An operating plant produces electricity and hence revenues that can meet both fixed and variable costs and also service the debt. Typically, funding needs will require the payment of an interest rate which is above the risk-free rate r.
Due to its characteristics, it would be sensible to design the IGCC plant as a base load plant. Thus, a 400 MW plant which operates 70% on average over the year would produce 2,452,800 MWh yearly. If, instead, the availability rises to 80%, then the production would rise to 2,803,200 MWh yearly. This is 350,400 MWh more over a year. A gross computation suffices to show the importance of the improvement. We just multiply this amount by the profit spread (per MWh) and the number of years of useful life. After discounting the resulting figure to the present, we would see that this present value is sizeable.
The higher complexity of the IGCC plant (relative to other power generation alternatives) involves a risk that the desired availability is not reached. This is why the time in operation is one of the features to look after carefully, so as to improve the plant’s profitability. Indeed, notwithstanding some successful experiments in IGCC power plants, the low number of operating plants showed a lot of problems, mostly concerning the availability (Franco and Diaz [8]). Indeed there are several reasons for concern. One is fluctuations of demand over time. At a higher level, there is a need to keep thermal plants running at some degree for various reasons (e.g., to provide greater reliability and stability of the whole system). Therefore, not all units in that system can be operated at full output. In sum, really high availabilities may not be possible in practice.
The importance of availability goes well beyond the amount of output electricity. It affects more fundamental parameters, among them the efficiency of the plant. Net design energy efficiency (also called name-plate efficiency) is a static energy efficiency and gives the energy efficiency if a plant operates at best performance. The operational energy efficiency is the year-round average efficiency of a plant and is usually a few percent points lower than the design efficiency. Capacity utilization is an important factor influencing the operational efficiency of a plant. According to Graus and Worrell [13], operational efficiency is typically 1–2% lower than the design energy efficiency if the plant operates at 85% capacity (7500 full load hours). If the power plant operates at 50% capacity the operational efficiency is typically 3–4% lower. Efficiency, in turn, affects fuel consumption (for a given output) and pollutant emissions.
4.4. Environmental costs of gasification technology
Here we restrict ourselves to emissions and their economic cost as perceived through the market for carbon emission allowances; other pollutants are considered in Section 5. Even though an IGCC plant may have been granted a number of free allowances initially, the very existence of this market implies that at some point in time selling (some or all of) them can be the best decision. Note, however, that the possibility of auctioning (as opposed to “grand-fathering”) the allowances beyond Kyoto (2013–2020) looks ever more likely. Under these circumstances, unless a temporary support to this technology is in place (e.g., because of its innovative profile), the cost of emission allowances should be taken into account.
Actual emissions will depend mainly on the plant efficiency. The first plants deployed reach efficiencies between 39% and 43%. Under current technology, however, efficiency can presumably reach 50%, with even 60% being possible in the future. For example, according to IPCC [14] a plant burning bituminous coal has an emission factor of 94.6 k under 100% efficiency conditions. Thus total emissions amount to 0.34056 t under full efficiency22. Therefore, emissions could change as a function of efficiency as shown in Table 4.

Table 4.
Carbon emissions (t as a function of efficiency (%).
| 35% | 40% | 45% | 50% | 55% | 60% | |
|---|---|---|---|---|---|---|
| Emissions from IGCC | 0.973 | 0.851 | 0.757 | 0.681 | 0.619 | 0.568 |
| Emissions from NGCC | - | - | - | 0.404 | 0.367 | 0.337 |
| Difference | - | - | - | +0.277 | +0.252 | +0.231 |
Higher efficiencies not only translate into fuel savings (and hence a weaker market demand for fuel), but lower emissions and spared allowances as well (i.e., lower environmental costs). Carbon emissions are certainly a relatively heavier burden for IGCC than for gas-fired combined cycles. Yet the difference narrows for higher efficiency levels23.
As long as NGCC plants continue to set the market price of electricity ever more frequently, they will eventually pass their costs on to this price. Since natural gas is more expensive than the fuels used in an IGCC plant, this is an advantage of the latter. And conversely, the IGCC plant may find it difficult to pass their carbon costs on to the electricity price; this is a comparative disadvantage. This handicap to the gasification technology can be lessened in two ways: a higher level of efficiency and, beyond some threshold level of carbon price, the construction of a carbon capture and storage (CCS) unit24.
Now the European Union Emissions-Trading Scheme (EU ETS) is a market for carbon permits. It commenced operation in 2005. The sectors covered by the system are power generation and energy-intensive manufacturing industry (from 2011/2012, also aviation). The cap on emission allowances will be cut by 21% in 2020 in comparison to 2005 levels (European Commission [15]).
Let be the time-0 curve in the market for futures contracts on emission allowances. Usually this curve shows an increasing profile over time (within a given trading period, e.g., the Kyoto commitment period 2008–2012). This is mainly due to a growing demand and a constant supply of permits. Future cuts in the total cap of allowances will probably entail a jump in prices. The futures curve would ideally reflect all these issues and it would fit neatly the market prices in place on the day we undertake the valuation.
Since every t emitted bust be met by one emission allowance, the present value of emitting one t yearly over the plant’s useful life is:
This cost must be multiplied by the total number of tonnes emitted yearly. For example, if the plant size is 400 MW and it operates 80% of the time (admittedly, a tall order), it will produce 2,803,200 MWh/year. Now, if it burns bituminous coal with an efficiency of 45% it will emit 0.757 t, or 2,122,022 tyear; this figure must multiplied by the above cost. Depending on the emission allowance price, the impact on the plant’s profitability can be significant. Figure 7 shows futures prices on the European Climate Exchange (ECX) on 04/17/200925. Futures contracts currently traded have maturities stretching until December 2014. Beyond this date, some extrapolation method must be used.
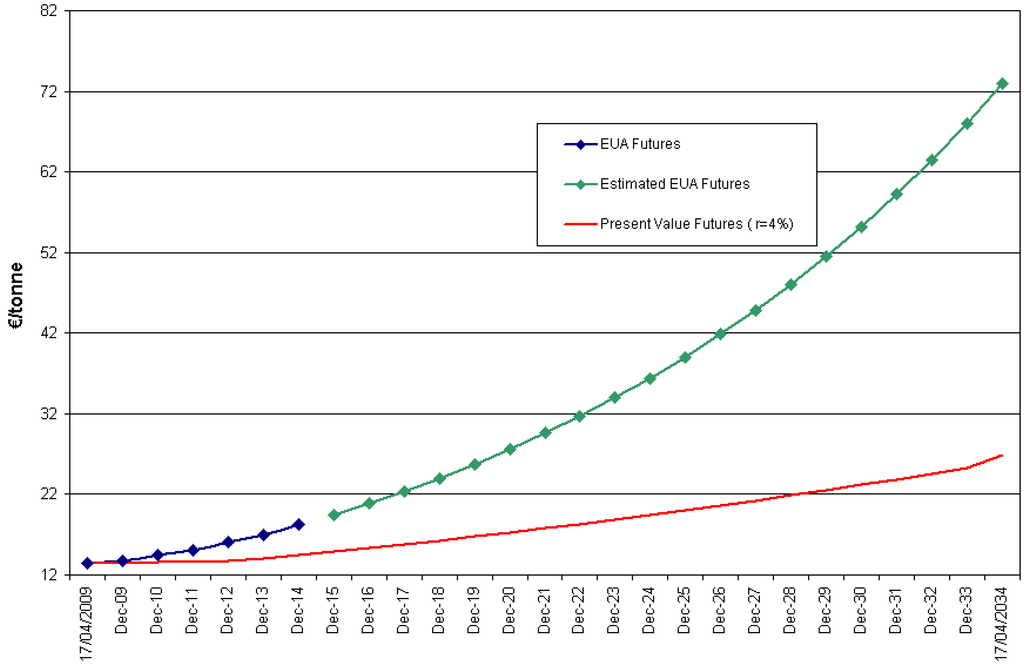
Figure 7.
Futures prices of European Union emission allowances (blue line), estimated prices for the distant future (green line), and futures prices discounted to the present (red line). Source of EUA prices: ECX.
On the other hand, increasing efficiency up to 50%, would take emissions down to 0.681 t/MWh, or 1,908,979 tyear. In this case 213,043 tyear have been avoided. This figure is not to be overlooked, since it amounts to savings of 10% in the bill of carbon permits, plus the simultaneous savings in fuel consumed.
A previous experience of emissions markets can be found in the U.S. Clean Air Act (the Acid Rain Program). Insley [16] addresses the effect of uncertainty in the price of emission permits on the decision to install a “scrubber”. To model this uncertainty, she proposes a geometric Brownian motion (GBM) for the changes in the permit price. At the same time, observation of Figure 7 suggests that, for the contracts available, futures prices of carbon allowances grow exponentially with the time to maturity; this is consistent with a GBM process. Therefore, if we want a simple estimation of carbon costs, we can assume that the allowance price follows a standard GBM; see Section 6 below for details. Then, the formula for the futures price reduces to:
where denotes the allowance price at time 0 (when the valuation is made), and is the drift rate of the allowance price process. It can easily be shown that beyond 2014 (the latest maturity now traded), assuming that the same GBM process as over 2008-2012 applies, the futures price is given by:
Computing the drift rate through the difference of the (log) prices for maturities December-2013 and December-2014, , the lower curve in Figure 7 results. This curve depicts for a (nominal) riskless interest rate % assumed in the long term. Therefore, the area below this curve over the next 25 years is:
The amount gives the present value of the cumulative cost of emitting one metric t each year over the next quarter century. The present value of total carbon costs equals times the total number of tonnes emitted yearly26.
4.5. Facilities’ cost
Estimating installation costs is not an easy task. In particular, it depends on the specific country in which the IGCC plant is built, because of the different costs of labor, capital, materials, taxes, potential subsidies or support measures, etc. Total cost is particularly sensitive to the evolution of the prices of the commodities used during construction (steel, cement, ...); these prices have been rising sharply until recently thus pushing costs to new heights. Note also that there could be economies of scale when building bigger gasification plants. These economies, though, must be weighed against the value of modularity.
There are distinct estimates of facility costs. In general they are not consistent with each other, given that they rest on very different assumptions. Yet it is worth noting that, in the medium term, the U.S. Department of Energy (DoE) sets a target capital cost of less than $1,000/kW for IGCC plants. Irrespective of the higher cost of the first IGCC stations, Table 5 shows some estimates for the mid term and compares them with those of alternative Super Critical PC plants and Ultra Super Critical PC plants.

Table 5.
Capital cost ($/kW) for different plants.
| IGCC | SCPC | USCPC | |
|---|---|---|---|
| DoE | 1,300 | 1,000-1,400 | - |
| Harvard | 1,400 | 1,200 | - |
| EPRI | 1,350 | - | 1,235 |
| Flour | 1,111 | - | - |
| Bechtel | 1,099 | 1,100 | - |
| Siemens | - | - | 1,000 |
According to Booras and Holt [17], if the Illinois # 6 coal is used, the capital costs for Sub-PC, USCPC and IGCC with spare are $1290, 1340 and 1440 per kW respectively (about $90/kW higher), without capture. Franco and Diaz [8] set the specific cost of a commercial IGCC plant at some 40–60% above that of a similar conventional PC plant.
5. Other Relevant Issues
The flexibility to produce several output goods with economic value. The set includes hydrogen, sulfur, sulfuric acid, and ammonia. They all are derived after cleaning and separation processes. Nonetheless, a massive deployment of IGCC plants could lead to an over-supply of these products and a downward pressure on the prices of some of these goods.
Maximizing the value of the plant in this respect goes along similar lines as maximization regarding input flexibility. Output prices and volatilities along with cross-correlations play an important role. Switching costs also cannot be forgotten.
The revenues from electricity. This is important when the gasifier syngas output is used to produce electricity in an IGCC power plant. Here a number of institutional issues come to the fore. Electricity prices are sensitive to market design, which changes across countries and over time.
To the extent that NGCC plants set the price of electricity, the profit margins of IGCC plants can be negatively affected (note the fuel price gap between coal and gas after adjusting for relative efficiencies). As natural gas price increases relative to that of coal, the IGCC technology becomes more competitive. And conversely, as the NGCC plant has lower carbon emissions, it passes a lower fraction of the allowance price on to electricity. If allowance prices are high, the IGCC plant turns less competitive at which point management should assess when it is the optimal time to build a CCS unit (provided it is technically feasible).
Transportation costs. The costs to deliver the fuel inputs must be computed. They affect the choice of the site for the gasification plant and the design fuel to be used. For example, areas close to working coal mines enjoy a comparative advantage as potential building sites for an IGCC plant. The advantage is greater in the case of coal seams with low extractions costs. The same applies for areas close to oil refineries if the plant uses oil by-products as feedstock.
The process efficiency. For example, what percentage of the thermal content of the syngas used in an IGCC power plant is finally transformed into electricity. The higher the efficiency, the lower the amount of fuel used and GHG emissions. If the plant is located in a country where carbon restrictions apply, lower emissions in turn imply lower costs of allowance purchases27.
According to U.S. DoE, the IGCC plant efficiency is close to 40%, but they could reach levels close to 60% with the deployment of advanced high-pressure solid oxide fuel cells28. However, it must be remembered that competing technologies can also improve their efficiency. In this regard, while the energy efficiency for gas fired-power plants in the 1980s was still below 50%, currently the most modern combined cycles can have efficiencies of nearly 60%, corresponding to an energy efficiency improvement for new plants of about 0.7% per year in the last 15 years. For coal-fired power generation, the efficiency increased from 34% in 1990 to 38% in 1995, corresponding to 0.6% per year.
In general, the IGCC plant efficiency compares favorably with conventional coal-fired station efficiency (between 33% and 40%), but construction costs are higher for the IGCC plant. Graus and Worrell [13] show current energy efficiency levels for new power plants by applying best available technology per type of fossil fuel source; see Table 629.

Table 6.
Energy efficiency of several state-of-the-art power plants.
| Technology | Fuel | Net efficiency | Best practice plant |
|---|---|---|---|
| PC steam cycle (USC) | coal | 46% | Denmark |
| PC steam cycle (USC) | lignite | 43% | Germany |
| IGCC | coal | 46% | Spain |
| NGCC | natural gas | 59-60% | UK |
Source: Graus and Worrell [13].
The continuous assessment of available technologies including economics and risks is a vital approach towards the adoption of viable system integrations. If efficiency is expected to increase sharply in the short term without a significant rise in cost, it may be optimal to delay investments in gasification technologies (given their long useful lives), unless this is offset with strong economic incentives. On the other hand, to ensure that new power plants are based on best available technology, high prices can give a further incentive. This is particularly true for technologies based on coal. Indeed they can act as an additional incentive to earlier adoption of cleaner technologies, thus counteracting the former temptation to wait.
The flexibility for adopting CCS relative to other alternative technologies. IGCC power plants fall within the so-called “clean coal technologies” (CCT), where good thermodynamic performances of power plant are joined with a control of pollutant emissions. Three different stages to achieve “clean coal” are available: (1) advanced technologies (the efficiency pathway); (2) long-term vision of capture and storage; and (3) control and reduction of pollutants , , mercury, and particle matter (excluding ) without structural modification of cycles.
We have already dealt with the plant’s energy efficiency. As for the second route, the possibility to complete construction of an IGCC plant in such a way as to enhance it later with a CCS unit should be valued. Now, a “call option” on an asset is a financial contract that gives the holder the right, with no obligation, to acquire the underlying asset by paying a prespecified price (the “exercise price”) on or before a given maturity (in the latter case it is called an American-type option); of course, this option can be purchased for a price or “premium”. Similarly, designing the plant to be “capture-ready” would be akin to paying the premium of an American option that gives its holder the possibility (with no obligation) to build a CCS unit at a lower cost in the future. The value of this option would mainly depend on the volatility of allowance prices. The option should be exercised as soon as the allowance price surpasses a certain threshold. Obviously the unexercised option would be worthless in the last years of the plant lifetime.
In a sense, the IGCC technology is particularly well suited to be accompanied by a CCS unit at a lower cost than other technologies. The reason is the higher concentration of reached during the process which allows for more efficient separation methods. Carbon capture technologies require great amounts of energy, with a great impact on the thermodynamic performance of the plant, seriously decreasing power generation efficiency, and increasing other environmental pollutants (ammonia, limestone). capture processes from power production fall into three general categories: (1) flue gas separation; (2) oxy-fuel combustion in power plants; and (3) pre-combustion separation30. As Herzog and Golomb [18] point out, each of these technologies carries both an energy and economic penalty.
An energy penalty can be calculated as , where x is the output of a reference power plant without capture and y is the output of the same plant with capture. The calculation requires that the same fuel input be used in both cases. For example, if the power plant output is reduced by 20% because of the capture process (), the process is said to have an energy penalty of 20%. The energy penalty for an NGCC plant is about 16%, whereas for a PC plant is 28%, and for an IGCC plant is 14%, actually less than for a PC plant despite its use of coal.
CCS costs can be considered in terms of four components: separation, compression, transport, and injection. Herzog and Golomb [18] consider costs associated with capture from fossil fuel-fired power plants with subsequent transport and storage. In this case, the cost of capture includes both separation and compression costs because both of these processes almost always occur at the power plant. CCS results in an increase in the cost of electricity of 1–2 $c/kWh for an NGCC plant, 1–3 $c/kWh for an IGCC plant, and 2–4 $c/kWh for a PC plant.
Chen and Rubin [12] study the effect of different capture efficiencies on the performance and cost of IGCC power plants. The energy penalty, the capital cost, and the cost of electricity increase more rapidly at high removal efficiency. In particular, the cost of electricity of the CCS plant with 90% removal (compared to the reference plant without capture) increases by 19% before compression, by 30% after compression, and by 45% with additional transport and storage costs.
Other environmental profits. The development of CCT is an objective not easy to be performed for different reasons. On the one hand, coal is not a uniform resource due to its extremely variable composition. This makes it difficult to reach a standardization of advanced technologies, which can be very sensitive to the fuel used. On the other hand, coal combustion produces structurally more pollutants than other fossil fuels.
In IGCC plants the pollutants in the syngas are removed before the syngas is combusted in the turbines (in contrast to conventional PC plants which extract them from the flue gas). The net volume of syngas being treated in an IGCC power plant operated in a pre-combustion mode is 1/100 (or less) of the exhaust gas volume that must be cleansed in a conventional coal-fired plant using a post-combustion system31. In addition, gasification units require less pollution control equipment because they generate fewer emissions, further reducing the plant operating costs. See Table 7 (Winters [19]).
A detailed description of the technologies and processes to control and reduce pollutants , , mercury, and particle matter (excluding ) can be found in Franco and Diaz [8]. According to them, IGCC is basically the cleanest coal technology with inherently lower , , and particle matter, the lowest collateral solid wastes and wastewater, potential for the lowest cost removal of mercury, and the cheapest route to separation. An additional benefit is the possibility to use municipal solid waste (MSW) in the gasifier. This can be a good solution relative to other alternative treatments of MSW, e.g., incineration. Since the plant also produces a certain amount of carbon monoxide (CO) as an intermediate product stringent safety measures need to be put into place.

Table 7.
Air pollutant comparisons (coal based).
| Technology | ||||
|---|---|---|---|---|
| Air pollutant | Existing coal | New SCPC | New IGCC | Co-Pro (power &F-T diesel) |
| (k/MWh) | 1.7 | 0.2 | 0.16 | 0.04 |
| (k/MWh) | 4.7 | 0.29 | 0.15 | 0.06 |
| Mercury (g/GWh) | 23.6 | 1.8 | 1.8 | 1.8 |
Source: Winters [19].
Support measures for gasification technologies. The cost of a gasifier is around 15% of the total capital cost of the IGCC plant, while the cleaning unit amounts to something between 10% and 12%. Thus potential measures to support these technologies could be justified as subsidies to their adoption and also as a measure to enhance security of supply in troubled times, given the world distribution of coal reserves.
6. Stochastic Price Models
Next we briefly discuss some stochastic models that can be appropriate for valuing investments related to the gasification technology, and IGCC power plants in particular.
6.1. The GBM model
This is a well-known model. It can be used to model the behavior of the emission allowance price, C, for example. In this case, C follows a non-stationary process (much like a common stock). In a risk-neutral setting:
where denotes carbon price at time t. This current value has an instantaneous drift rate . The instantaneous volatility of the price changes is , and stands for the increment to a standard Wiener process.
Let us consider a futures contract on the emission allowance. In this case, the formula for the futures price is:
which allows to easily estimate the parameter (as shown in Section 4.4). Upon knowledge of and the spot price on the market, it is possible to compute the present value of one t emitted (or one allowance surrendered) yearly between times and :
6.2. The Inhomogeneous geometric Brownian motion (IGBM)
Coal price or natural gas price, P, instead, can be assumed to be governed by a stationary process; in particular, there is an anchor value which may be somehow related to the marginal cost of extraction or the price of a substitute fuel. The IGBM model in a risk-neutral world is:
where denotes the speed of reversion towards the long-run equilibrium price , and stands for the risk premium related to gas price uncertainty. is the instantaneous volatility of fuel price changes, and is a standard Wiener process. Assuming that starts from an initial, known value and grows at a constant rate θ we have.
Let us consider a futures contract on a unit of fuel. The formula for the futures price in this case is:
And the present value of a unit of fuel consumed yearly between and is:
7. Concluding Remarks
This paper deals with the economics of gasification. We address this issue with the help of some financial concepts and instruments. As it is well known, time and uncertainty are major themes in finance. A number of markets allow firms and individuals to allocate assets through time and spread the risks they face. And wherever there is a market, there is a price. The informational content of prices can be seized to better assess potential investments in gasification plants. This is a great leap forward with respect to valuations that assume constant input or output prices. Focusing on IGCC power plants in particular, we have naturally watched fuel input prices. The analysis, though, can be further extended to the output electricity price and the price of emission allowances (where appropriate). Admittedly, some parameter values are not quite realistic. The main purpose is to show how the methodology works.
Clearly markets are sources of relevant information for inflexible technologies. Indeed, they are particularly important for flexible technologies such as gasification, since it is conveniently suited to adjust to market price swings by switching fuels, processes, final products, ancillary systems, and the like. These flexibilities (or options to switch) are valuable. Though the value of a given flexibility is not obvious, we have explained how to address this issue at the intake stage.
We have also commented upon the environmental benefits afforded by gasification. Note that some economic sectors and countries are not currently covered by climate regulations, but this situation can suddenly change. This is a regulatory risk, and it must be treated as such in investment decisions. In this respect, Citigroup, J.P. Morgan Chase, and Morgan Stanley developed a new system of environmental standards in 2008. The new, more stringent system is aimed at financing decisions regarding coal-fired power plants in the U.S. Their guess seems to be that there is a greater risk in this type of investments because of its higher emissions in case environmental restrictions are set in place. Under their “Carbon Principles”, these banks require investors in coal-fired stations to have previously assessed other options such as improvements in energy efficiency or renewable energies, and that these options have proven to be insufficient. In case a coal-based plant is to be financed, they require the plant to be built “capture-ready”, i.e., well suited to host a CCS system eventually. In addition, the owners must be able to collect electricity bills that allow them to pay for the emission allowances they could need in the future.
Overall, a myriad physical and technical parameters are involved in the assessment of any particular gasification project. But these facilities do not operate in an institutional vacuum. Like it or not, markets and regulations matter, and time and risk pervade the whole process of decision making. Fortunately, though, markets provide sizeable pieces of information to put a value on time and risk. Hopefully we have introduced some of these pieces in a friendly manner and shown how their power can be harnessed for valuation purposes in a particularly suitable setting, namely gasification.
Acknowledgements
We thank three anonymous referees for their thoughtful comments and useful suggestions. They have contributed to improve both the contents of the paper and its presentation. Any error remains our own.
Appendix: Futures Markets: A Primer
As stated at the beginning of Section 4 above, the price of the input fuels is a major issue when assessing the economic profitability of gasification technology. The same holds true for the price of the electricity output or those of other unintended byproducts such as polluting emissions (of sulfur, carbon, etc.). As it turns out, many of these commodities are customarily traded on futures markets. And we have shown that futures prices are a key ingredient to the valuation process. Therefore, for those unfamiliar with the raison d’etre of these markets or the way in which they operate, the following introduction may be welcome. Along the way we also explain the relation between futures prices and spot prices.
The standard explanation for the role of futures markets is that they help to spread and hence reduce risks, and to motivate the collection and dissemination of information relevant to the planning of consumption and production. Let us analyze these aspects in some detail.
A forward contract is an agreement whereby the seller currently agrees to deliver to the buyer a specific asset on a specified future date at a fixed price (K), to be paid on the delivery date (T). If the fixed price to be paid on the delivery date were sufficiently low, the buyer would have to pay a positive amount for the contract. If it were set high enough, the seller would have to pay the buyer to take the contract. Clearly, there is an intermediate price, known as the “forward price”, at which the current value of the contract would be zero. This is the fixed price that is customarily used for newly-written forward contracts. Consequently, a forward contract will have a value of zero when the contract is initiated (time 0). Of course, the value of an outstanding contract (f) will subsequently change as the value of the underlying asset changes.
One of the parties to a forward contract assumes a “long position” and agrees to buy the underlying asset on the delivery date for the delivery price. The other party assumes a “short position” and agrees to sell the asset on the same date for the same price. The forward price and the delivery price are equal at the time the contract is entered into. As time passes, the forward price is liable to change while the delivery price, of course, remains the same. A forward contract is settled at maturity. The holder of the short position delivers the asset to the holder of the long position in return for a cash amount equal to the delivery price.
Forward contracts are usually between two financial institutions or between a financial institution and one of its corporate clients. They are not normally traded on a exchange. No cash changes hand at the time of the agreement. However, either or both parties to the transaction often have to post some funds to guarantee fulfillment of the contract.
The easiest forward contract to value is one written on an asset that provides the holder with no income. Consider the following two portfolios at time t:
- Portfolio A: it consists of one long forward contract on the asset (worth f) plus an amount of cash equal to (or, equivalently, a bond that matures at the expiration date of the forward contract, T, and which at that date will have a value equal to the delivery price, K).
- Portfolio B: it consists of one unit of the asset (worth ).
In Portfolio A, the cash, assuming that it is invested at the risk-free rate (r), will grow to an amount K at time T, to be used to pay for the asset at the maturity of the forward contract. And the payoff from the long position in a forward contract on one unit of the asset will be at time T. Both portfolios will therefore consist of one unit of the asset at time T; see Table 8.

Table 8.
Values of alternative portfolios.
| Portfolio | Current date | Delivery date |
|---|---|---|
| A: long forward | f | |
| long cash | K | |
| B: long asset |
For there to be no arbitrage opportunities, they must be equally valuable at the earlier time t. It follows that, at time t, we have . Obviously, this equation can be arranged into , i.e., a portfolio consisting of one unit of the asset and one short forward contract would provide a certain amount of cash K at time T (regardless of whether the asset moves up or down in the meantime): (while of course . Through the ability to construct such a riskless hedge, risk can be effectively “squeezed out” of the problem, so that investors’ risk attitudes do not matter (Trigeorgis [2]). Therefore, for valuation purposes, we can equivalently—and more conveniently—pretend to be in a risk-neutral world where risk is irrelevant. In such a world, all assets (including stocks, options, forwards, futures, ...) would earn the risk-free return, and so expected cash flows (weighted by the risk-neutral probabilities) could be appropriately discounted at the risk-free rate.
Now similar to a forward contract, an individual who takes a long position in a futures contract nominally agrees to buy a designated good or asset on the delivery date (T) for the futures price prevailing at the time the contract is initiated (0). Hence, the futures price must also equal the spot price on the delivery date. Again, no money changes hands initially. Subsequently, however, as the futures price changes, the party in whose favor the price change occurred must immediately be paid the full amount of the change by the losing party. As a result, the payment required on the delivery date to buy the underlying good or asset is simply its spot price at that time. The difference between that amount and the initial futures price has been paid (or received) in installments throughout the life of the contract. Like the forward price, the equilibrium futures price must also continually change over time. It must do so in such a way that the remaining stream of future payments described above always has a value of zero32.
A futures contract may be defined as a highly standardized forward contract (Houthakker [20]). The standardization characteristic generally involves five elements: (1) Quantity: buyers and sellers can deal only in lots of fixed size (of course, they can buy or sell any number of such lots); (2) Quality: the commodity or asset is not usually completely specified, but can be anywhere in a range (e.g., all wheat of certain grades); (3) Delivery time: the lot can be delivered at any time within a specified period, say a month; (4) Location: the lot must be delivered in specified places in one or more specified cities; (5) Identity of contractors: after the initial contract is established, the buyer and seller normally have no further dealings with each other, thus eliminating credit risk. The execution is guaranteed by a clearing house, which acts as seller to all buyers and as buyer to all sellers. The clearing house can offer this guarantee by virtue of the security deposits, known as “margin”, it collects from its members.
The immediate purpose of this standardization is to minimize transaction costs and thereby to allow futures contracts to be traded on an organized exchange. Futures prices are regularly reported in the financial press. They are determined on the floor of the exchange in the same way as other prices (i.e., by the laws of supply and demand). For example, a risk-averse wheat farmer may hedge his future harvest by selling October wheat futures in January, in which case he is “long” in actuals and “short” in futures. A trader whose net position in the spot market is offset by his position in the futures market is called a hedger; in particular, he is a “short hedger” if he is long in the spot market and short in the futures market (and a “long hedger” if these positions are reversed). Traders who are net long or net short in the overall market (spot plus futures) are known as speculators.
The prices prevailing in the spot and futures markets at any time are not necessarily equal. However, there are two main links between these markets; one is provided by the delivery mechanism and the other by hedging. As to delivery, when a futures contract reaches maturity the remaining shorts have to deliver what they have sold, and the remaining longs have to accept and pay for what they have bought. Clearly, the shorts will not deliver anything that could be sold at a higher price in the spot market, nor will the longs take delivery of anything that they could buy more cheaply elsewhere. At delivery time, therefore, the futures price must be equal to the spot price of the items that are actually delivered. Since this ultimate equality is widely anticipated, it will also influence futures and spot prices prior to delivery time.
Hedging also serves to relate futures prices and spot prices. If a futures price is high compared to a spot price, hedgers will buy in the spot market and sell futures. They can do so without risk if the futures price exceeds the spot price by more than the “carrying charge”, which is the cost of holding physical inventories between the present and the maturity of the futures contract. The futures price therefore cannot exceed the current spot price by more than the prevailing carrying charge33.
If merchants can increase their profits by hedging, they must be willing to pay a risk premium for the opportunity to do so. It is conceivable that short hedging exactly offsets long hedging, in which case any premiums paid by hedgers would cancel out. There is considerable evidence, however, that in most markets short hedging exceeds long hedging at most times. Now if the hedgers are net short in futures, the speculators in futures must be net long (since there is a sale for every purchase). It can be argued that speculators will only be net long if they expect futures prices to rise. At any particular moment the speculators may of course be wrong, but on average they are right, and each futures price will tend to rise until, at the maturity of the contract, it equals the relevant spot price. The speculators’ gain is the hedgers’ loss; thus the speculators receive a risk premium proportionate to the amount of hedging they make possible. This risk premium is implicit in the hedgers’ willingness to sell futures contracts that have a tendency to appreciate. This, in brief, is the so-called theory of “normal backwardation”34.
It is also possible at times that hedgers are net long in futures while speculators are net short. Then the opposite pattern would result: futures prices will tend to fall. This situation is called “contango”. To be sure, the price of a futures contract will always reflect the combination of two elements: (1) the traders’ forecast of the future spot price of the asset, and (2) the traders’ risk aversion (in the form of the implicit risk premium for securing a fixed price today for future delivery).
Behavior towards risk can be easily defined in terms of simple gambles. Assume an individual is confronted with the following two lotteries: lottery A pays off $1 for sure, whereas lottery B has two possible payoffs, $2 and $0, each with equal probability of 50%. Note that the expected payoff from lottery B amounts to $1. If the individual is indifferent between lotteries A and B he is said to be risk neutral. It is possible that the individual strictly prefers the certain payment of $1 to the average payment of $1; if lottery A is strictly preferred to B, the individual is risk averse. The other possibility is that the individual strictly prefers B to A, in which case the individual is a risk lover.
In a risk-neutral context, all the individuals are assumed to be risk neutral. As such, they are only concerned with average or expected values (not with dispersion around these values): as long as all the available assets (or portfolio of assets) have the same expected returns, the individuals are indifferent among them. One particular asset is the risk-free asset (e.g., a Treasury bill, assuming its probability of default is null). Let r denote the (certain) rate of return on this asset. If all the individuals show risk neutrality, all the assets in the market must have the same expected rate of return, in particular the risk-free rate, r35. Further, it can be shown that the futures price , i.e., the value of the delivery price at time t such that the current value of the futures contract equals zero, is the expected spot price in a risk-neutral context. In this context, expected cash flows from any one asset can be discounted to the present at the riskless rate r in order to compute their present value.
References
- Gasification: Redefining clean energy; Gasification Technologies Council: Arlington, VA, USA, 2008; Available online: http://www.gasification.org (accessed August 21, 2009).
- Trigeorgis, L. Real Options - Managerial Flexibility and Strategy in Resource Allocation; The MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Dixit, A.K.; Pindyck, R.S. Investment under uncertainty; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Sick, G. Real Options. Handbooks in Operations Research and Management Science 1995, 9, 631–691. [Google Scholar] [CrossRef]
- Ronn, E.I. Real Options and Energy Management; Risk Books: London, UK, 2002. [Google Scholar]
- Abadie, L.M.; Chamorro, J.M. Valuing flexibility: The case of an integrated gasification combined cycle power plant. Energ. Econ. 2008, 30, 1850–1881. [Google Scholar] [CrossRef]
- Holt, N. Gasification process selection: Trade-offs and ironies. In Proceeding of the Gasification Technologies Conference, Washington, DC, USA; 2004. [Google Scholar]
- Franco, A.; Diaz, A.R. The future challenges for “clean coal technologies”: Joining efficiency increase and pollutant emission control. Energy 2009, 34, 348–354. [Google Scholar] [CrossRef]
- British Petroleum. Statiscal review of world energy 2009. Available online: http://www.bp.com (accessed August 21, 2009).
- World Energy Outlook 2007; International Energy Association: Paris, France.
- International energy outlook; Energy Information Administration, U.S. DoE: Washington, DC, USA, 2009.
- Chen, C.; Rubin, E.S. CO2 control technology effects on IGCC plant performance and cost. Energ. Policy 2009, 37, 915–924. [Google Scholar] [CrossRef]
- Graus, W.; Worrell, E. Trend in efficiency and capacity of fossil power generation in the EU. Energ. Policy 2009, 37, 2147–2160. [Google Scholar] [CrossRef]
- Guidelines for National Greenhouse Gases Inventory; IPCC: Geneva, Switzerland, 2006.
- EU action against climate change: Leading global action to 2020 and beyond; European Commission: Brussels, Belgium, 2008.
- Insley, M.C. On the option to invest in pollution control under a regime of tradable emissions allowances. Can. J. Econ. 2003, 36, 860–883. [Google Scholar] [CrossRef]
- Booras, G.; Holt, N. Pulverized coal and IGCC plant cost and performance estimates. In Proceedings of Gasification Technology Conference, Washington, DC, USA, October 2004; 2004. [Google Scholar]
- Herzog, H.; Golomb, D. Carbon Capture and Storage from Fossil Fuel Use. In Encyclopedia of Energy; Elsevier Science Inc.: New York, NY, USA, 2004; pp. 277–287. [Google Scholar]
- Winters, T. Should the U.S. coal option be preserved? IAEE Newsletter 2008, 13–16. [Google Scholar]
- Houthakker, H.S. Futures Trading. In The New Palgrave: Finance; Eatwell, J., Milgate, M., Newman, P., Eds.; The Macmillan Press Ltd.: New York, NY, USA, 1989; pp. 153–158. [Google Scholar]
- Khadse, A.; Qayyumi, M.; Mahajani, S.; Aghalayam, P. Underground coal gasification: A new clean coal utilization technique for India. Energy 2007, 32, 2061–2071. [Google Scholar] [CrossRef]
- Rardin, R.; Yu, Z.; Holland, F.; Oberbeck, J. Factors that affect the design and implementation of clean coal technologies in Indiana; Purdue University: West Lafayette, IN, USA, 2005; Available online: http://www.purdue.edu/dp/energy/pdf/Purdue-FinalReport-2005.pdf (accessed August 21, 2009).
- Rao, A.D. Integrated Gasification Combined Cycle (IGCC): Coal and biomass-based. In Encyclopedia of Energy Engineering and Technology; Capehart, B.L., Ed.; Taylor & Francis Group, LLC: Lilburn, GA, USA, 2007; pp. 906–913. [Google Scholar]
- Parker, G. Coal-to-Liquid Fuels. In Encyclopedia of Energy Engineering and Technology; Capehart, B.L., Ed.; Taylor & Francis Group, LLC: Lilburn, GA, USA, 2007; pp. 163–171. [Google Scholar]
- Cortazar, G.; Milla, C.; Severino, F. A multicommodity model of futures prices: Using futures prices of one commodity to estimate the stochastic process of another. J. Futures Markets 2008, 28, 537–560. [Google Scholar] [CrossRef]
- Abadie, L.M.; Chamorro, J.M. European CO2 prices and carbon capture investments. Energ. Econ. 2008, 30, 2992–3015. [Google Scholar] [CrossRef]
- 1We leave aside underground coal gasification. This is a combination of mining, exploitation and gasification. Typically it consists of two adjacent boreholes drilled into a coal seam and pressurized oxidant such as air or oxygen/steam are used for ignition of the coal seam. It eliminates the cost—and energy—of mining and transportation. Cooking the coal in place also leaves unwanted pollutants in the ground, and any stripped out during the chemical processing can be pumped right back where it came from. Thus the technique can be particularly useful where coal has a high ash content, or for exploiting deep coal deposits and steeply dipping coal seams. See Khadse et al. [21].
- 2See Rardin et al. [22] for a description of the gasification technology and the major types of gasifiers.
- 3Small scale fixed bed gasifiers in particular are widely used in India and other developing countries.
- 4This information and related materials can be accessed at http://www.gasification.org.
- 5World Gasification Database, available in www.gasification.org.
- 6Rao [23] describes the case of an IGCC plant that burns coal and biomass.
- 7More information is available in Parker [24] and in the web site http://www.fischer-tropsch.org/site_map.htm.
- 8Sources: United States: Energy Information Administration. Based on EIA, Annual Coal Report 2006, Table 15 and Unpublished File Data of the Coal Reserves Data Base (April 2007). All Other Data: World Energy Council, 2007 Survey of Energy Resources.
- 9For those unfamiliar with futures markets perhaps some basic preliminaries may be in order; see the Appendix.
- 10If construction costs are high and the time lapse is long, investments will have to be financed presumably at a high rate, and several years will pass before the first revenues allow to start serving the debt and repaying the investment.
- 11A possible qualification to this statement involves transport costs incurred by each type of fuel. In some instances, physical proximity to the supply source can be a relevant factor for investment decision making on coal-based technologies.
- 12However, despite lower costs related to fuel consumption, the IGCC plant will incur higher operation and maintenance costs due to its greater complexity.
- 13Since these investments have very long useful lives (several decades), organised markets might lack contracts maturing beyond some future date. In this case, we could resort to over-the-counter (OTC) markets, or infer an estimate consistent with the available prices, especially those for the longest maturities. Cortazar et al. [25] undertake the estimation in one market through its correlation with another market for which a higher number of prices for longer maturities are available.
- 14For example, we can draw a cubic spline through the futures prices for discrete expiration dates. Alternatively, if we propose a stochastic process for the spot price, we can try to derive the corresponding formula for the futures price; we develop this approach below.
- 15This is somewhat similar to using the zero-coupon curve in the interbank market on a given day to value fixed-income contracts that are traded on that market.
- 16Assuming we are at time 0, different plants with distinct construction periods are characterized by different values of . Similarly, different useful lives can be represented by distinct differences .
- 17It can be shown that by using the prices on futures markets we are able to solve the problem of risk and the appropriate discount rate for future cash flows.
- 18This could be the case when a given expected increase in demand is to be met.
- 19This model would remain valid between a design fuel and an alternative one.
- 20If there were no switching costs, it would suffice to equate them to zero in our model. However, there would be a more straightforward way to implement this situation.
- 21The plant could have a positive residual or terminal value, perhaps as a potential site for a new plant, or an alternative use. This possibility can be easily added to the model.
- 22One kWh amounts to 3600 kilo joules (kJ), and one Giga joule (GJ) is a million kJ.
- 23The average -intensity for gas-fired power generation decreased by 32%, from 600 g/kWh in 1990 to 410 g/kWh in 2005. For the period 2005-2015 another decrease is expected of 10% to 370 g/kWh (Graus and Worrell [13]). The average -intensity for coal-fired power generation decreased by 9%, from 1,000 g/kWh in 1990 to 910 g/kWh in 2005 and is expected to further reduce by 7% to 840 g/kWh by 2015.
- 24Abadie and Chamorro [26] assess the case for building a CCS unit given the allowance prices observed in the EU ETS.
- 25In anticipation of the establishment of the ETS, beginning in 2004, a futures market in allowances developed. Contracts on emission allowances are traded on different platforms (in addition to over-the-counter markets). Due to its volume of operations and liquidity, the European Climate Exchange (ECX, London UK) stands apart.
- 26For instance, in the above example of the 400 MW plant operating 80% of the time at an efficiency level of 45%, emissions were 2,122,022 tyear.
- 27Even if carbon restrictions are not currently in place in a given country, decision makers should take potential regulatory changes into account when assessing new investments. This is due to the very long useful lives of gasification plants.
- 29The efficiencies are net design efficiencies based on net calorific value.
- 30Pre-combustion capture is usually applied in IGCC power plants. In gasification facilities that do not generate electricity, is separated after the gasification stage from other gases, such as methane, hydrogen or a mix of carbon monoxide and hydrogen.
- 31Gasification Technologies Council [1].
- 32If interest rates are non-stochastic and there are no arbitrage opportunities, it can be shown that futures prices are equal to forward prices.
- 33It does not follow, however, that a futures price must always exceed the spot price by the relevant carrying charge. Positive inventories may be held even if the spot price is above the futures price. This is because inventories have a “convenience yield”, derived from their availability when buyers need them.
- 34The empirical validity of this theory remains in dispute.
- 35If one particular asset had a higher expected return, then all the agents would chase it. But every purchase requires that there is someone willing to sell, which is not the case. The same holds true if a particular asset has an expected rate of return lower than r: everyone tries to sell it but nobody is willing to buy it. Market equilibrium in a risk-neutral setting requires that the expected return is just the same across all the assets.
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).