Unbalanced Magnetic Pull Calculation in Ironless Axial Flux Motors
Abstract
1. Introduction
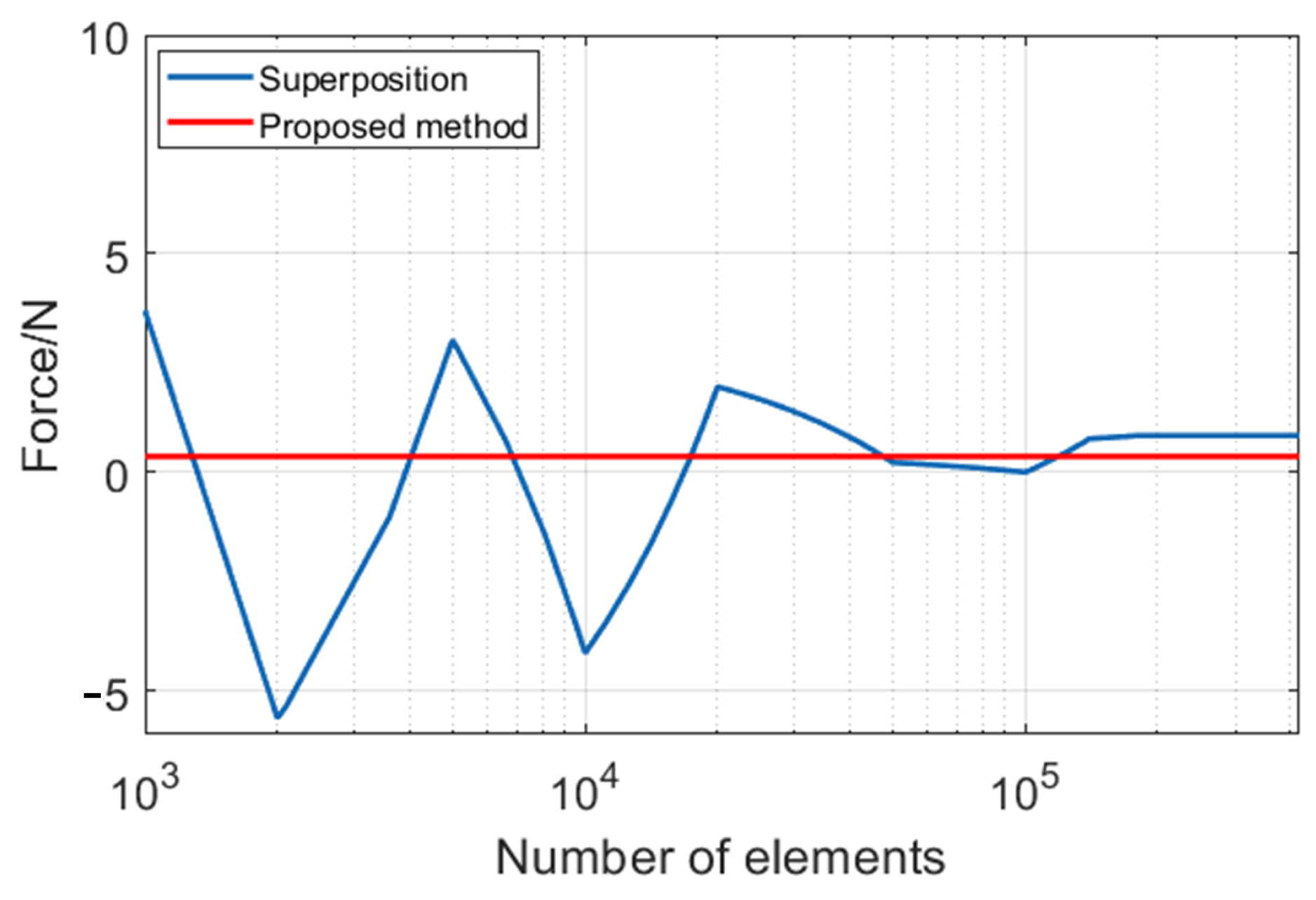
2. Catastrophic Cancellation
3. Theoretical Derivation
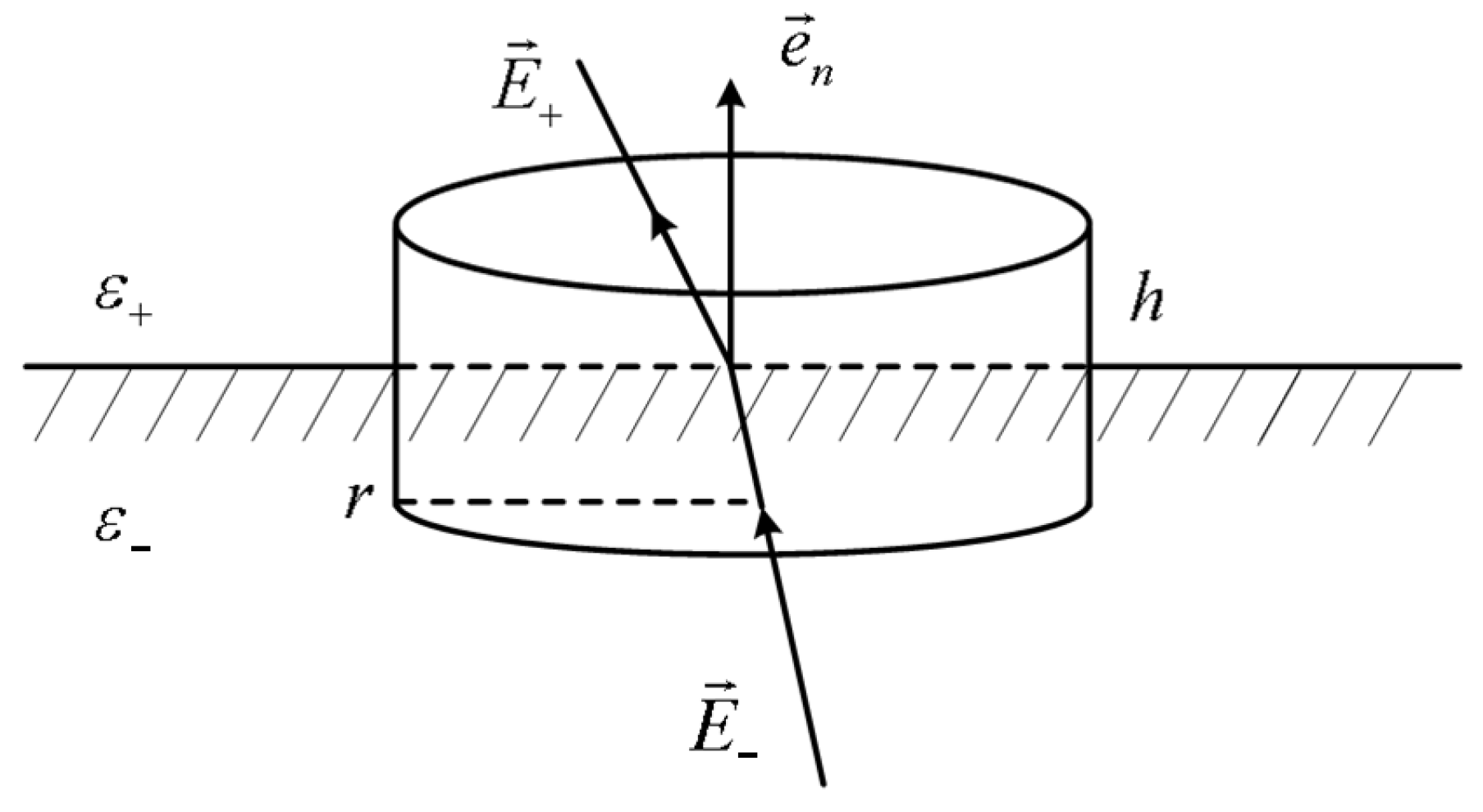
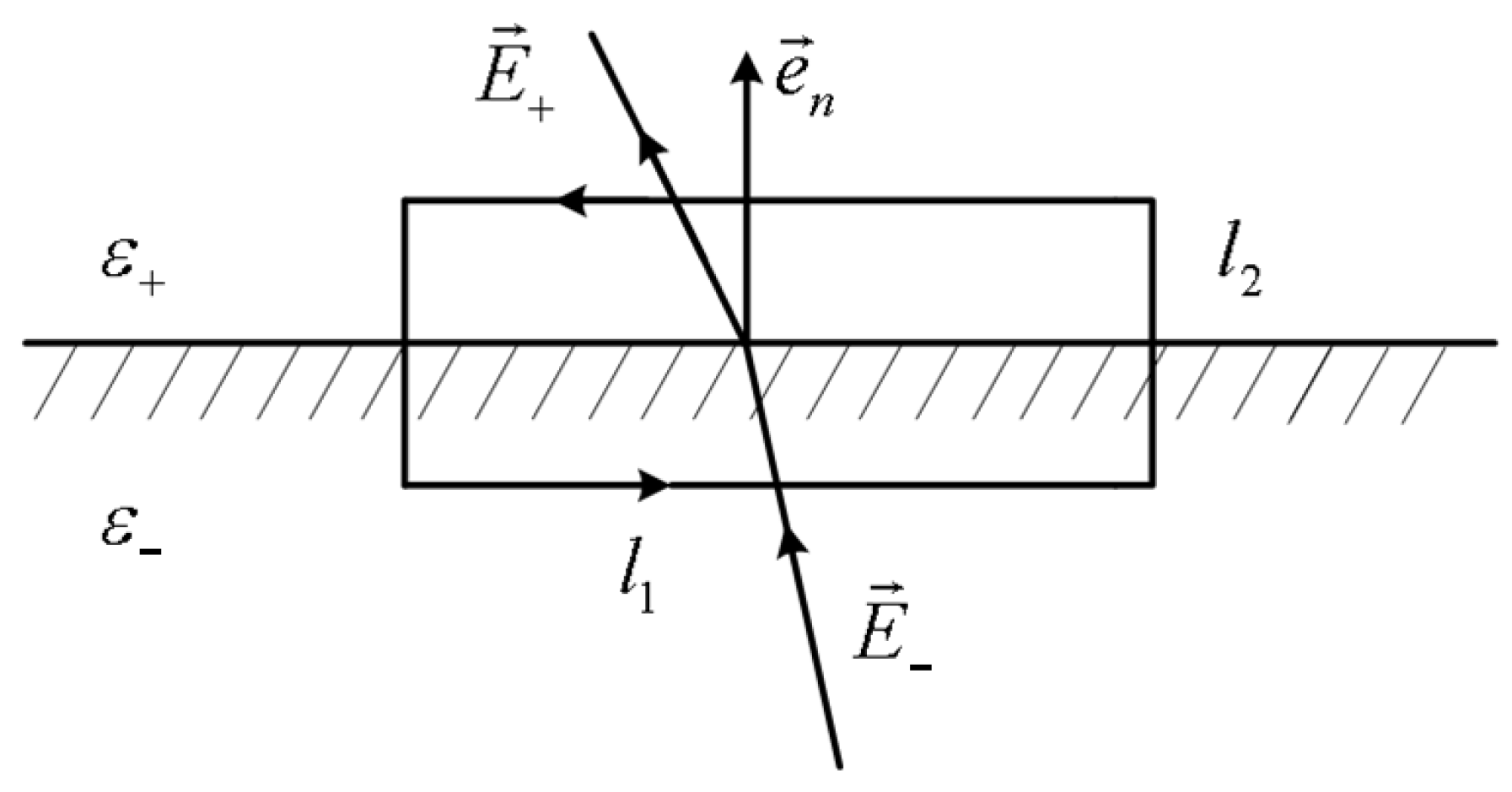
3.1. Maxwell Stress Tensor
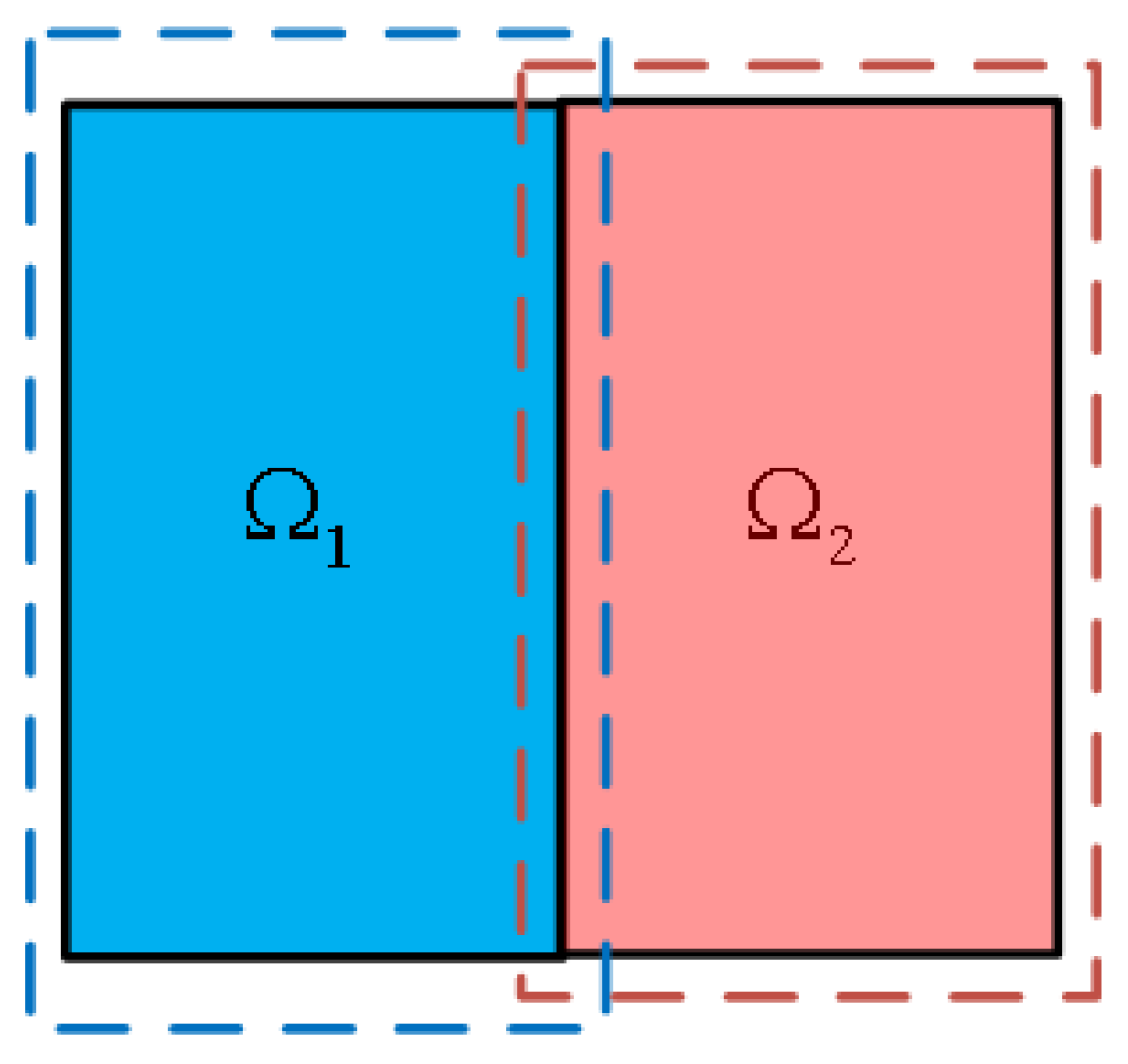
3.2. Determination and Merging of Integral Regions
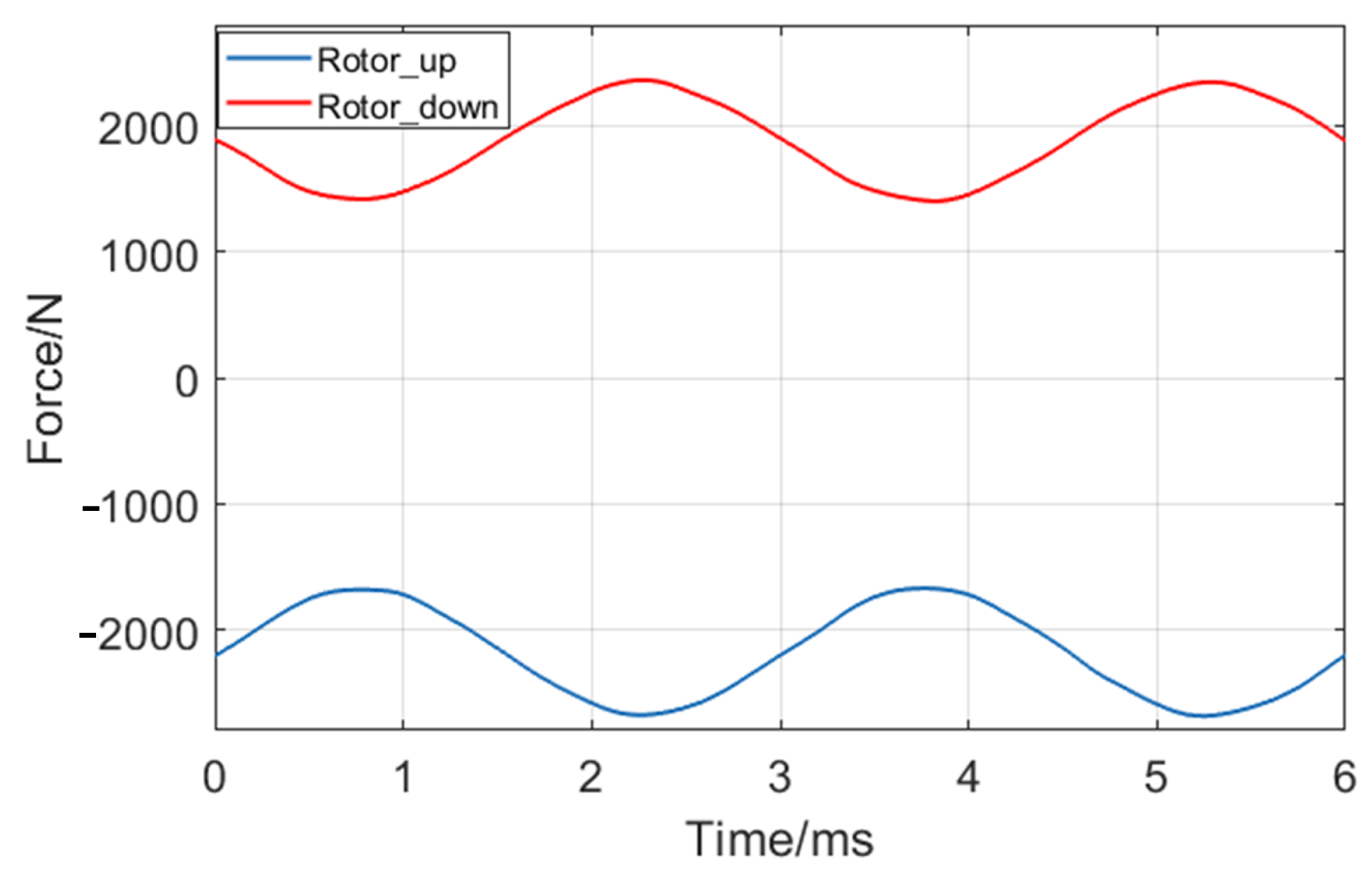
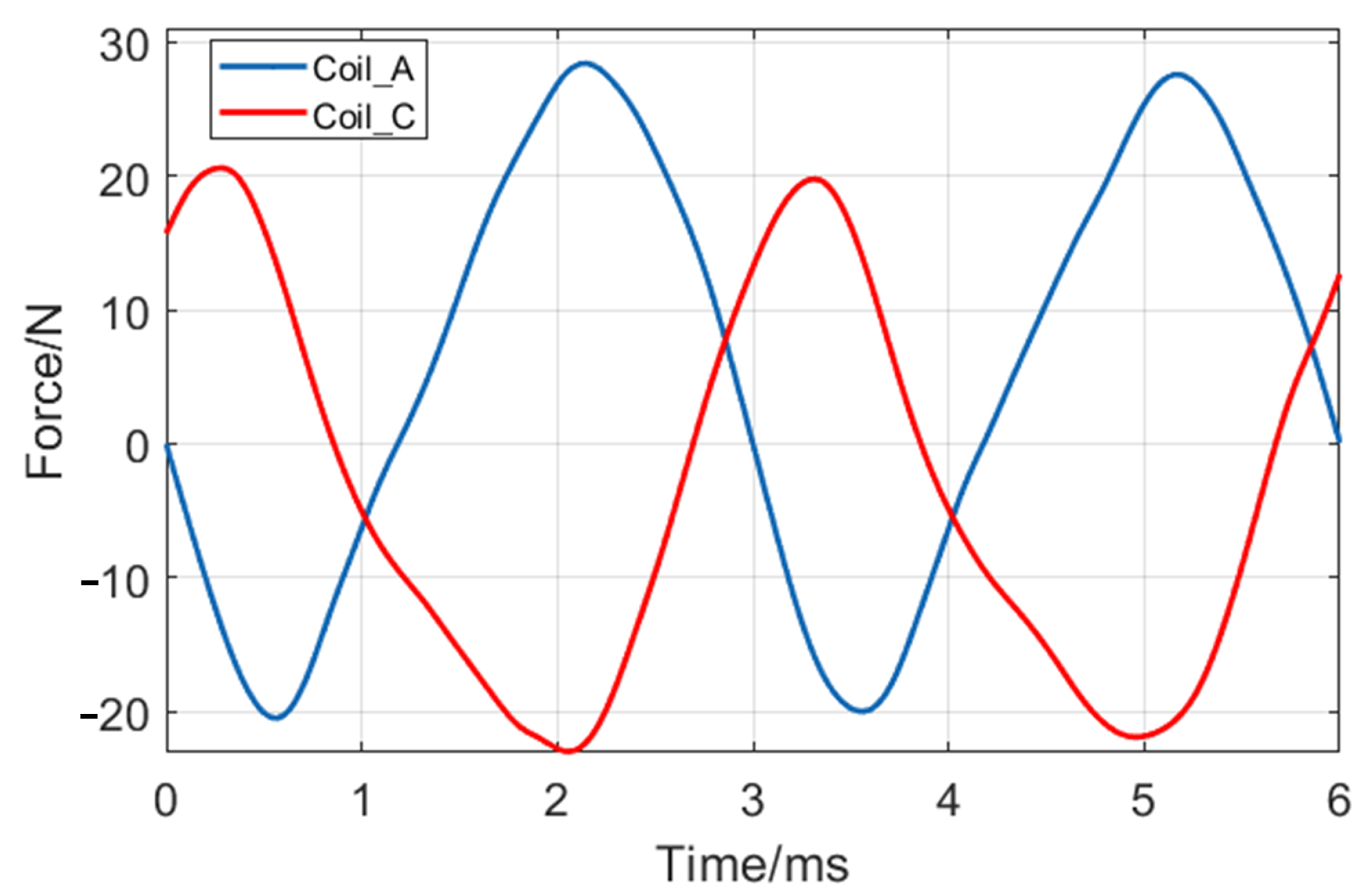
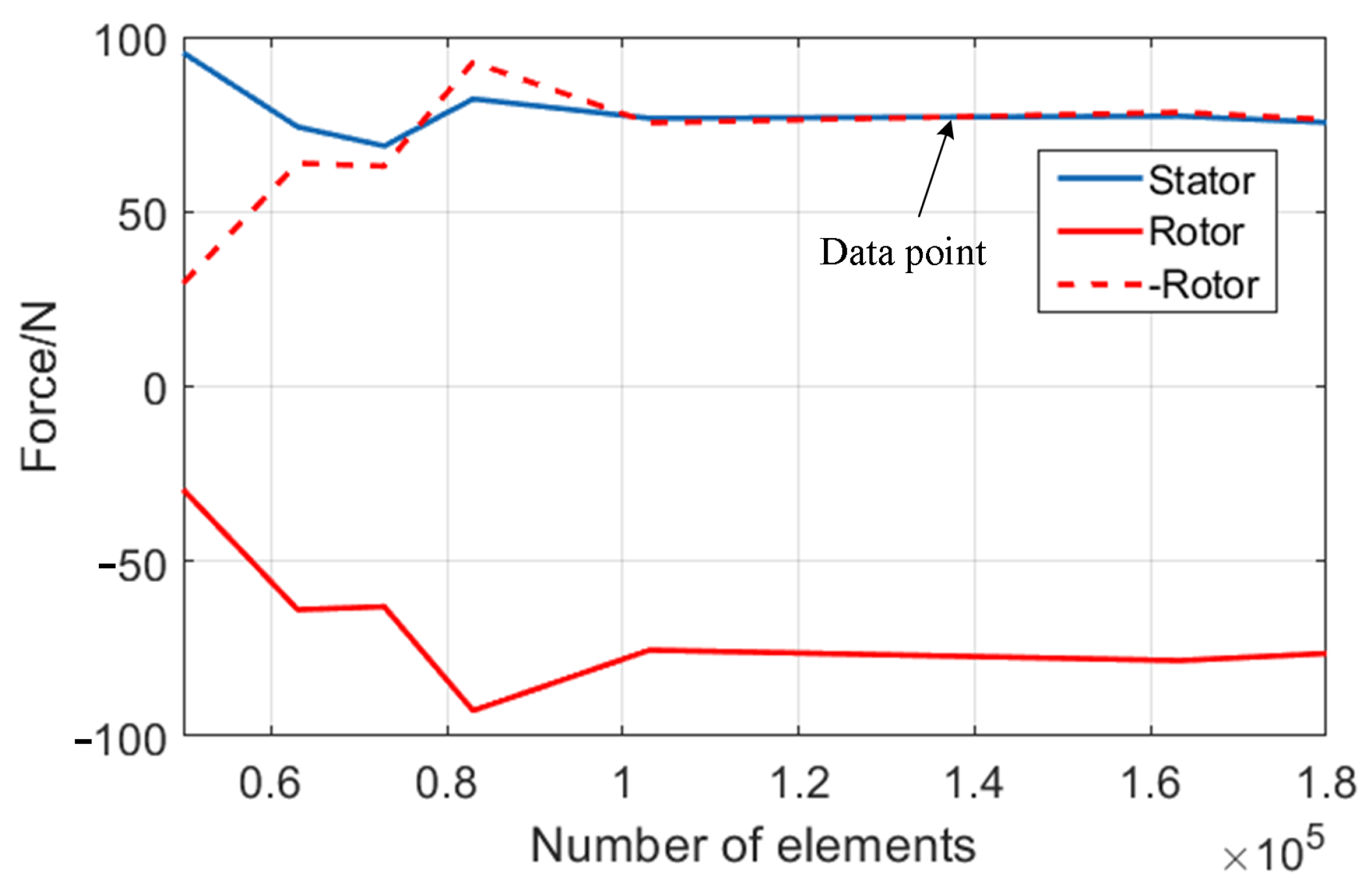
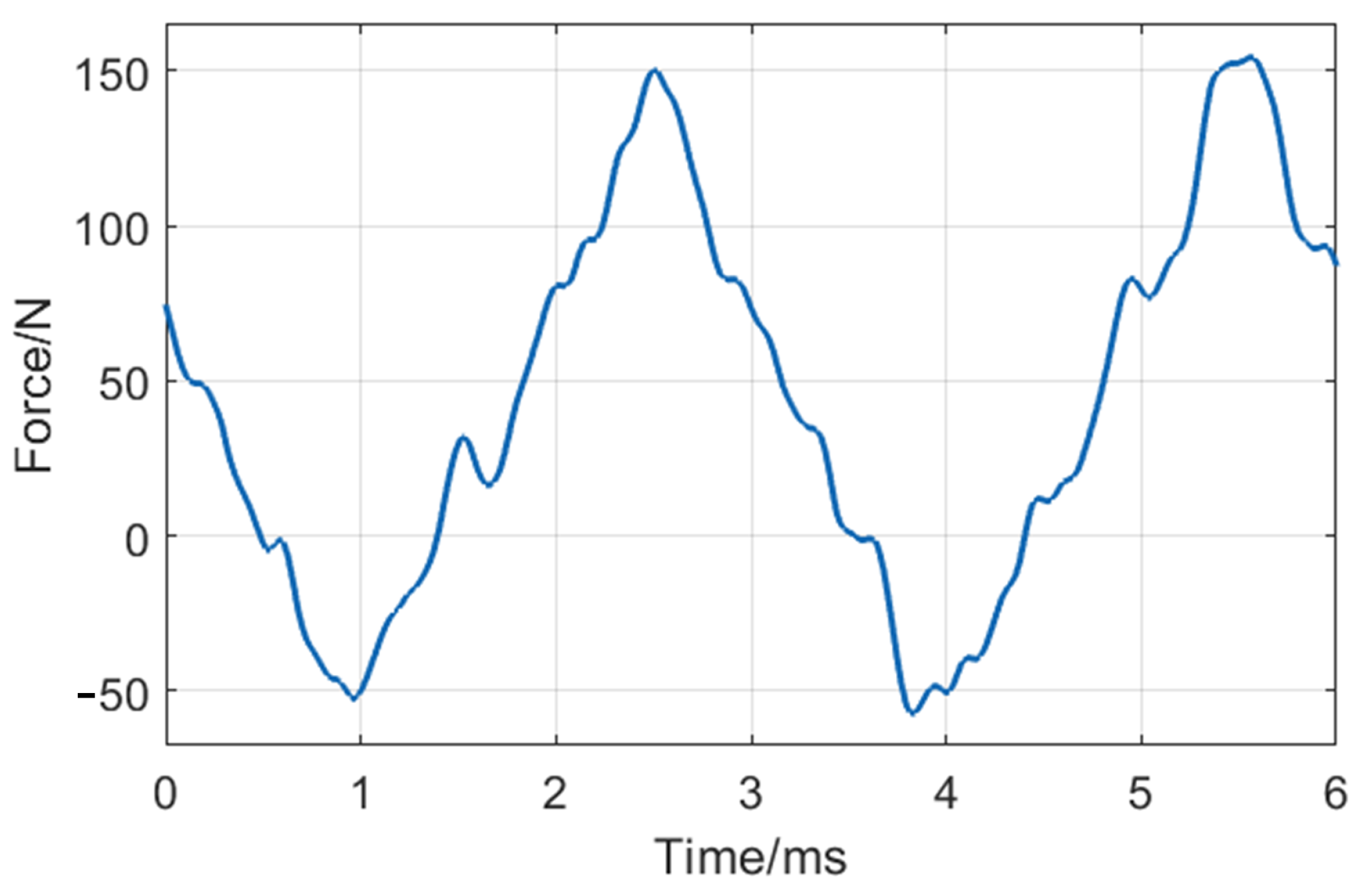
4. Calculation of Unbalanced Magnetic Pull
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Electromagnetic energy | |
| x | Displacement |
| Force density tensor | |
| Virtual displacement | |
| Maxwell stress tensor | |
| Virtual strain tensor | |
| Force density of free current | |
| Free current | |
| Magnetic induction intensity | |
| Magnetic field strength | |
| Electric field intensity | |
| Magnetization intensity | |
| Polarization intensity | |
| Equivalent magnetizing current | |
| Equivalent polarization current | |
| Displacement current | |
| Charge density | |
| Electric field intensity | |
| Electric displacement field | |
| Dielectric constant | |
| External electric field | |
| o | Infinitesimal in meters |
| Equivalent polarized charge | |
| Dielectric constant | |
| External magnetic field strength | |
| Electric field intensity on the inner surfaces of the interface | |
| Electric field intensity on the outer surfaces of the interface | |
| Magnetic induction intensity on the inner surfaces of the interface | |
| Magnetic induction intensity on the outer surfaces of the interface | |
| Force density of the surface current and surface charge | |
| Force density of the volume current and volume charge | |
| The surface Maxwell stress tensor | |
| The Maxwell stress tensor | |
| The total Maxwell stress tensor |
Appendix A

| Attribute | Parameter |
|---|---|
| Permanent magnet | N48H |
| Size of PMs/mm | 30 × 30 × 16 |
| Distance between PMs/mm | 24 |
| Diameter of copper wire/mm | 0.5 |
| Length of copper wire/mm | 30 |
| Current/A | 100 |
References
- Wang, H.; Zeng, X.; Eastham, J.F.; Pei, X. Axial Flux Permanent Magnet Motor Topologies Magnetic Performance Comparison. Energies 2024, 17, 401. [Google Scholar] [CrossRef]
- Wang, X.; Xu, S.; Li, C.; Li, X. Field-Weakening Performance Improvement of the Yokeless and Segmented Armature Axial Flux Motor for Electric Vehicles. Energies 2017, 10, 1492. [Google Scholar] [CrossRef]
- Yang, Y.P.; Shih, G.Y. Optimal Design of an Axial-Flux Permanent-Magnet Motor for an Electric Vehicle Based on Driving Scenarios. Energies 2016, 9, 285. [Google Scholar] [CrossRef]
- Wang, G.; Jiang, T.; Han, Q.; Zhu, R.; Wu, B.; Bai, W.; Wang, S. Rotor-bearing system dynamics under dynamic air gap eccentricity. J. Mech. Sci. Technol. 2024, 38, 6461–6470. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Liu, J.; Liu, J.; Shi, Z. An estimation method of bearing frictional power losses in a propulsion shaft through a tribo-dynamic model. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2024, 238, 1495–1511. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Q.; Guan, H. Vibration characteristics of a rotating flywheel-flexible coupling system with misalignment fault: Experiment and simulation. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2024, 238, 9840–9855. [Google Scholar] [CrossRef]
- Novak, M.; Kosek, M. Unbalanced magnetic pull induced by the uneven rotor magnetization of permanent magnet synchronous motor. In Proceedings of the 2014 ELEKTRO, Rajecke Teplice, Slovakia, 19–20 May 2014. [Google Scholar]
- Wu, Y.C.; Li, Y.G.; Feng, W.Z.; Zhang, W.J. Analysis on unbalanced magnetic pull generated by turn-to-turn short circuit of rotor windings within turbine generator. Electr. Mach. Control 2015, 19, 37–44. [Google Scholar]
- Perers, R.; Lundin, U.; Leijon, M. Saturation Effects on Unbalanced Magnetic Pull in a Hydroelectric Generator With an Eccentric Rotor. IEEE Trans. Magn. 2007, 43, 3884–3890. [Google Scholar] [CrossRef]
- Zhu, R.; Tong, X.; Han, Q.; He, K.; Wang, X.; Wang, X. Calculation and Analysis of Unbalanced Magnetic Pull of Rotor under Motor Air Gap Eccentricity Fault. Sustainability 2023, 15, 8537. [Google Scholar] [CrossRef]
- Jastrzebski, R.P.; Pilat, A.K. Analysis of Unbalanced Magnetic Pull of a Solid Rotor Induction Motor in a Waste Heat Recovery Generator. IEEE Trans. Energy Convers. 2022, 38, 1208–1218. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, X.; Ma, M.; Wang, C. Calculation and analysis of unbalanced magnetic pulls of different stator winding setups in static eccentric induction motor. Chin. Phys. B 2019, 27, 088401. [Google Scholar] [CrossRef]
- Dorrell, D.G. Calculation of unbalanced magnetic pull in small cage induction motors with skewed rotors and dynamic rotor eccentricity. IEEE Trans. Energy Convers. 1996, 11, 483–488. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, X.; Wang, Z. Study of Unsymmetrical Magnetic Pulling Force and Magnetic Moment in 1000 MW Hydrogenerator Based on Finite Element Analysis. Symmetry 2024, 16, 1351. [Google Scholar] [CrossRef]
- Wen, X.; Fang, H.; Li, R.; Liu, Z.; Zhou, J.; Li, D.; Qu, R. Research on Sensitivity of Slot-Pole Combination to Unbalanced Magnetic Pull Induced by Rotor Eccentricity. IEEE Trans. Ind. Appl. 2024, 60, 6186–6196. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Yu, Y.; Liu, J. Research on unbalanced characteristics of axial-varying eccentric rotor based on signal demodulation. Mech. Syst. Signal Process. 2024, 220, 111647. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, B. Analysis of Magnetic Forces in Axial-Flux Permanent-Magnet Motors with Rotor Eccentricity. Math. Probl. Eng. 2021, 2021, 7683715. [Google Scholar] [CrossRef]
- Mirimani, S.M.; Vahedi, A.; Marignetti, F.; De Santis, E. Effect of Inclined Static Eccentricity Fault in Single Stator-Single Rotor Axial Flux Permanent Magnet Machines. IEEE Trans. Magn. 2012, 48, 143–149. [Google Scholar] [CrossRef]
- Mirimani, S.M.; Vahedi, A.; Marignetti, F.; Di Stefano, R. An online eccentricity fault detection method for Axial Flux machines. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 18–20 June 2014; pp. 285–289. [Google Scholar]
- Mirimani, S.M.; Vahedi, A.; Marignetti, F.; De Santis, E. Static Eccentricity Fault Detection in Single-Stator–Single-Rotor Axial-Flux Permanent-Magnet Machines. IEEE Trans. Ind. Appl. 2012, 48, 1838–1845. [Google Scholar] [CrossRef]
- Park, Y.; Fernandez, D.; Lee, S.B.; Hyun, D.; Jeong, M.; Kommuri, S.K.; Cho, C.; Reigosa, D.; Briz, F. On-line detection of rotor eccentricity for PMSMs based on hall-effect field sensor measurements. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4678–4685. [Google Scholar]
- Böcker, J. Some reflections on electromagnetic force in matter. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 1433–1440. [Google Scholar]
- Grandia, R.S.; Galindo, V.A.; Galve, A.U.; Fos, R.V. General Formulation for Magnetic Forces in Linear Materials and Permanent Magnets. IEEE Trans. Magn. 2008, 44, 2134–2140. [Google Scholar] [CrossRef]
- Adamiak, K.; Mizia, J.; Dawson, G.; Eastham, A. Finite element force calculation in linear induction machines. IEEE Trans. Magn. 1987, 23, 3005–3007. [Google Scholar] [CrossRef]
- Mizia, J.; Adamiak, K.; Eastham, A.R.; Dawson, G.E. Finite element force calculation: Comparison of methods for electric machines. IEEE Trans. Magn. 1988, 24, 447–450. [Google Scholar] [CrossRef]
- Ito, M.; Tajima, F.; Kanazawa, H. Evaluation of force calculating methods. IEEE Trans. Magn. 1990, 26, 1035–1038. [Google Scholar] [CrossRef]
- Sadowski, N.; Lefevre, Y.; Lajoie-Mazenc, M.; Cros, J. Finite element torque calculation in electrical machines while considering the movement. IEEE Trans. Magn. 1992, 28, 1410–1413. [Google Scholar] [CrossRef]
- Ghosh, M.K.; Gao, Y.; Dozono, H.; Muramatsu, K.; Guan, W.; Yuan, J.; Tian, C.; Chen, B. Proposal of Maxwell Stress Tensor for Local Force Calculation in Magnetic Body. IEEE Trans. Magn. 2018, 54, 7206204. [Google Scholar] [CrossRef]
- Bermúdez, A.; Rodríguez, A.L.; Villar, I. Extended Formulas to Compute Resultant and Contact Electromagnetic Force and Torque From Maxwell Stress Tensors. IEEE Trans. Magn. 2017, 53, 7200409. [Google Scholar] [CrossRef]
- Sugai, I. Maxwell stress tensors in isotropic linear media. Proc. IEEE 1965, 53, 1250–1251. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 3rd ed.; Pearson Education Asia Limited: Singapore, 2006. [Google Scholar]
- Güemes, J.A.; Iraolagoitia, A.M.; Del Hoyo, J.I.; Fernandez, P. Torque Analysis in Permanent-Magnet Synchronous Motors: A Comparative Study. IEEE Trans. Energy Convers. 2011, 26, 55–63. [Google Scholar] [CrossRef]
- de Alvarenga, B.P.; de Paula, G.T. On-Load Apparent Inductance Derivative of IPMSM: Assessment Method and Torque Estimation. IEEE Trans. Magn. 2020, 56, 8100610. [Google Scholar]
- Lee, S.; Lee, J.; Cho, S. Isogeometric Shape Optimization of Ferromagnetic Materials in Magnetic Actuators. IEEE Trans. Magn. 2016, 52, 7200208. [Google Scholar] [CrossRef]
- Silveyra, J.M.; Garrido, J.M.C. Torque calculation method for axial-flux electrical machines in finite element analysis. Finite Elem. Anal. Des. 2023, 227, 104042. [Google Scholar] [CrossRef]
- Wang, C.; Han, J.; Zhang, Z.; Hua, Y.; Gao, H. Design and Optimization Analysis of Coreless Stator Axial-Flux Permanent Magnet In-Wheel Motor for Unmanned Ground Vehicle. IEEE Trans. Transp. Electrif. 2022, 8, 1053–1062. [Google Scholar] [CrossRef]
- Zhu, G.; Hu, H.; Guo, W.; Zhang, K.; Chen, Y.; Chen, X. Magnetic Force Calculation in Reluctance Force Launcher. IEEE Trans. Magn. 2022, 58, 8001409. [Google Scholar] [CrossRef]
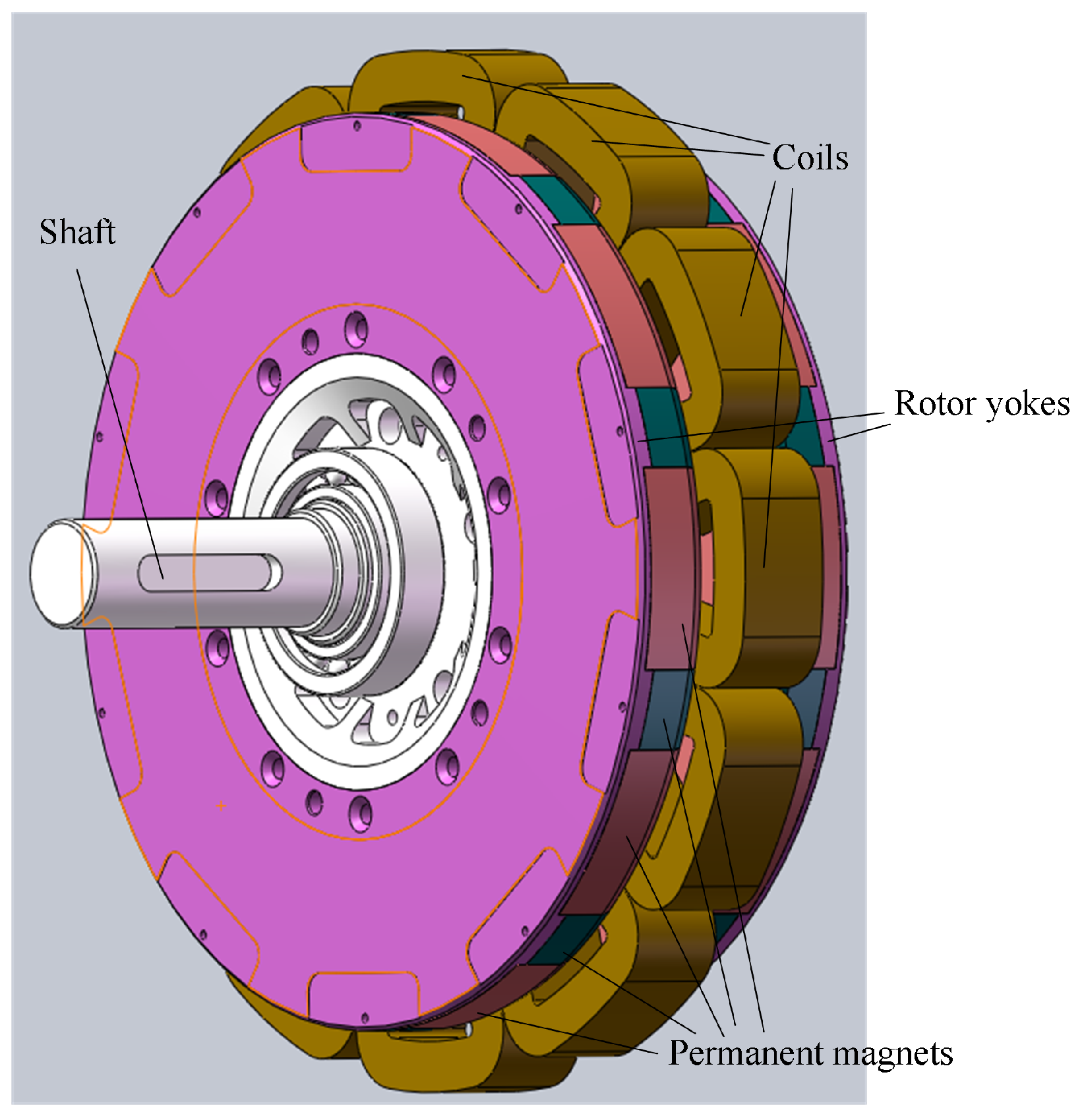
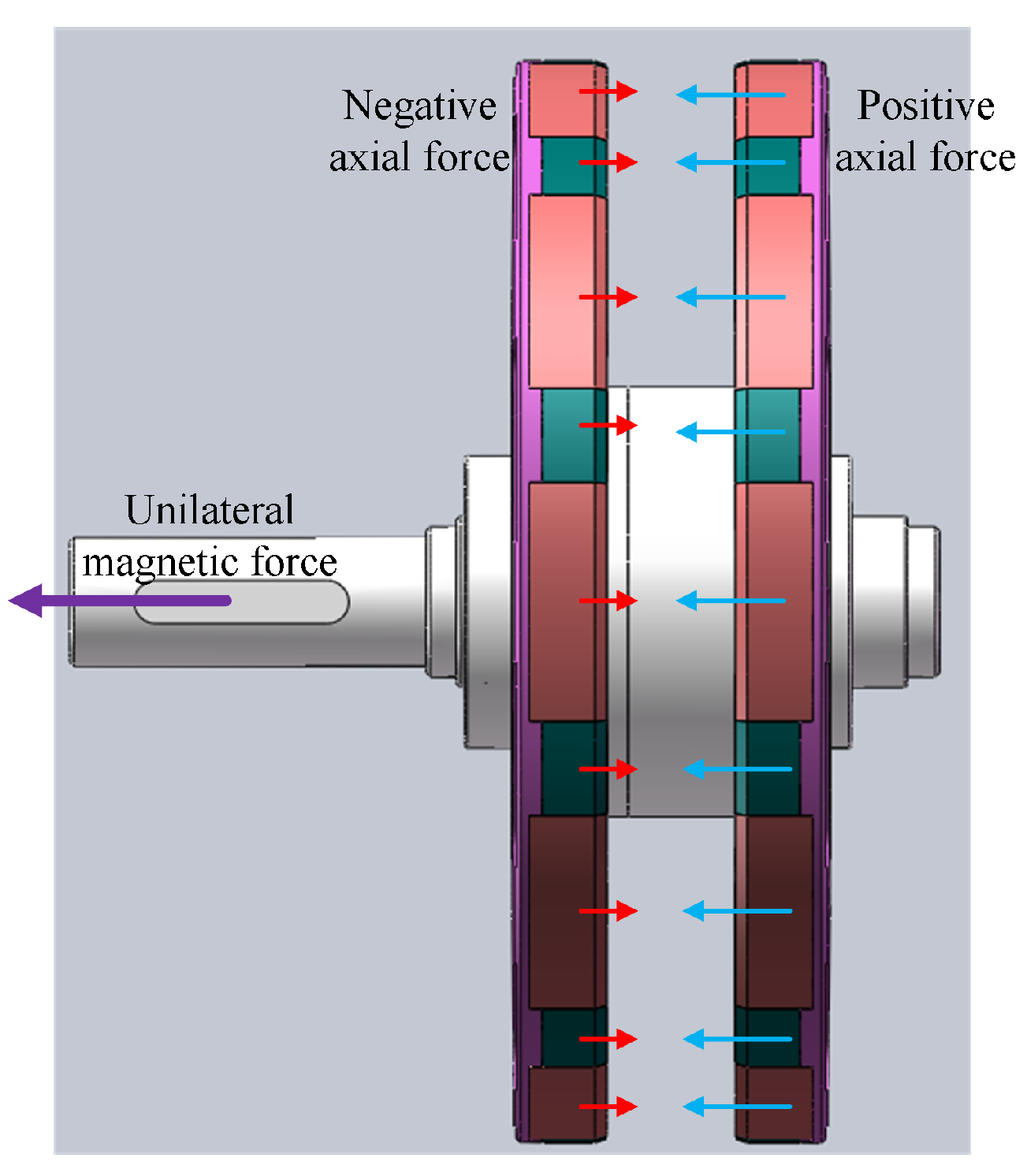
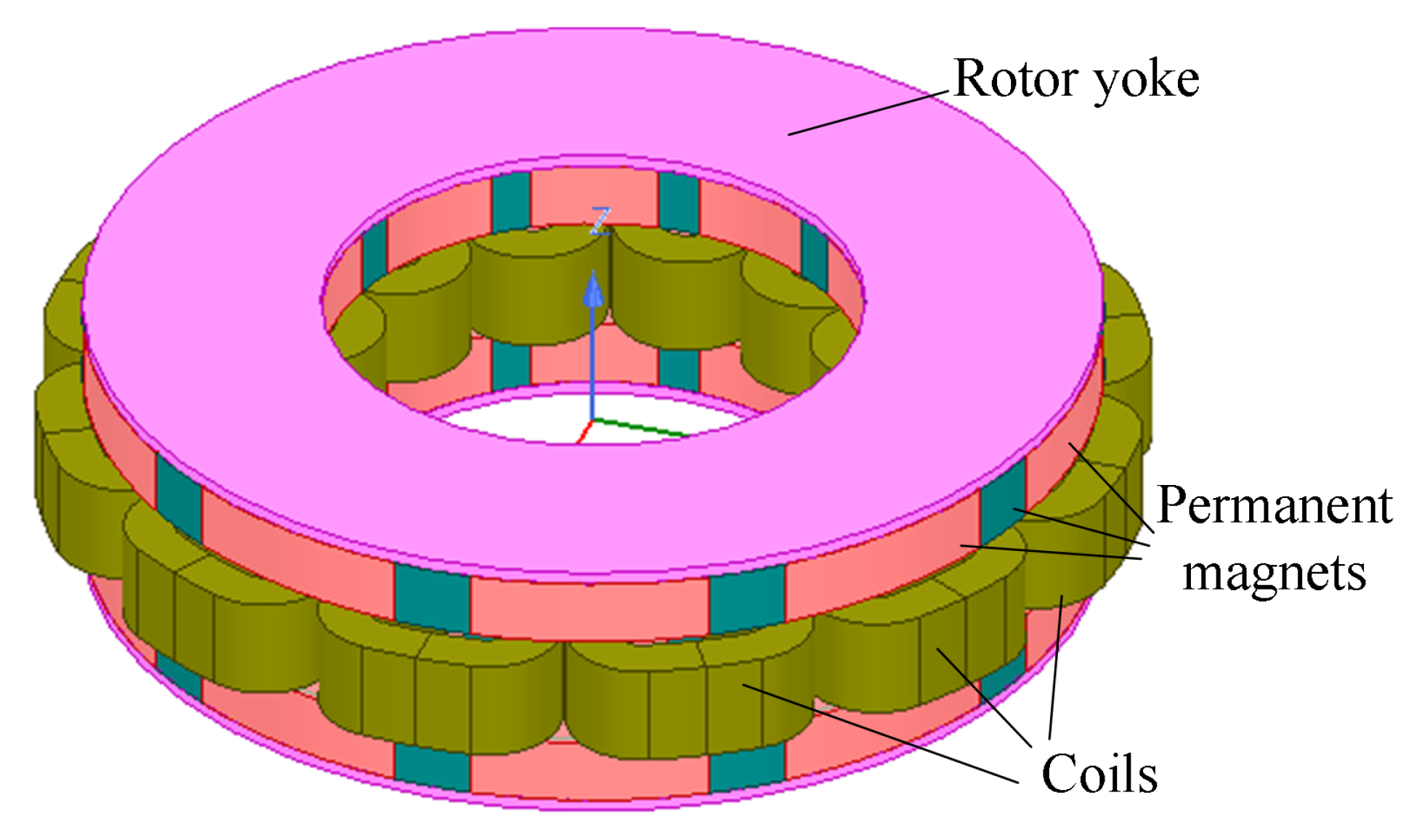





| Attribute | Parameter |
|---|---|
| Maximum torque/Nm | 500 |
| Maximum speed/rpm | 2000 |
| Number of phase | 3 |
| Outer radius of PM/mm | 120 |
| Inner radius of PM/mm | 64 |
| Attribute | Parameter |
|---|---|
| Rotor topology | Double outer rotor NS topology |
| Permanent magnet | N48H |
| Slot-pole combination | 10-pole-12-slot |
| Phase current amplitude/A | 720 |
| Turns of coil | 24 |
| Air gap thickness/mm | 1.75 |
| Axial thickness of coil/mm | 24 |
| Main PM thickness/mm | 16 |
| Auxiliary PM thickness/mm | 16 |
| Main PM pole-arc coefficient | 0.75 |
| Rotor yoke thickness/mm | 3 |
| Stator axial offset/mm | +0.5 |
| Method | Stator | Rotor |
|---|---|---|
| Proposed method | 76.7 N | 75.4 N |
| Virtual work principle | 238.2 N | 100.8 N |
| Superposition method | 252.8 N | 100.8 N |
| Simulation | 170.1 N | 76.6 N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, G.; Luo, J. Unbalanced Magnetic Pull Calculation in Ironless Axial Flux Motors. Energies 2025, 18, 2397. https://doi.org/10.3390/en18092397
Zhu G, Luo J. Unbalanced Magnetic Pull Calculation in Ironless Axial Flux Motors. Energies. 2025; 18(9):2397. https://doi.org/10.3390/en18092397
Chicago/Turabian StyleZhu, Guoqing, and Jian Luo. 2025. "Unbalanced Magnetic Pull Calculation in Ironless Axial Flux Motors" Energies 18, no. 9: 2397. https://doi.org/10.3390/en18092397
APA StyleZhu, G., & Luo, J. (2025). Unbalanced Magnetic Pull Calculation in Ironless Axial Flux Motors. Energies, 18(9), 2397. https://doi.org/10.3390/en18092397





