1. Introduction
The wound-rotor synchronous generator (WRSG), a crucial device in power systems, delivers electrical energy to consumers. Despite its high reliability, WRSG are not immune to faults, which can disrupt the power supply. Therefore, the reliability of WRSG is a notable concern in power systems, leading to the development of various methods aimed at enhancing system reliability. It is of significant importance in the realm of various engineering systems to establish a fault detection and isolation (FDI) algorithm with both high accuracy and reliability for incipient stage fault detection and estimation objectives [
1,
2,
3,
4,
5,
6,
7,
8].
In the WRSG, stator winding faults account for a substantial 60% of total faults, and the most common generator fault is the turn-to-turn/inter-turn short-circuit (TTSC) due to coil insulation failure [
9,
10,
11]. Although stator phase-to-phase and phase-to-ground faults are more severe compared with inter-turn winding faults, they are more readily detected by protection relays quite rapidly. Conversely, the identification of stator TTSC faults in their incipient stage presents a greater challenge as they exert a negligible influence on terminal currents. It is widely believed that many phase-to-ground, phase-to-phase, and other severe faults originate as an undetected stator TTSC, which progressively escalate until catastrophic failure ensues [
12]. In practice, the stator TTSC that occurs in the winding of the generator induces a significant current flow in the shorted loops, leading to potential winding failures [
13]. Consequently, condition monitoring (CM) has become a critical necessity for early-stage stator TTSC fault detection, facilitating timely diagnosis and the prevention of subsequent anomalies, issues, and malfunctions [
9,
11].
The CM approaches for stator TTSC faults are classified into two categories, namely flux linkage and current/voltage signature [
14,
15]. The authors in [
14] and [
16] provided a comprehensive review of these two CM categories. The malfunction of the stator winding results in a reduction in the flux linkage in the vicinity of the fault region, while the stray flux correspondingly experiences an adverse increase. Consequently, flux monitoring has emerged as a potentially effective method for fault diagnosis [
17,
18]. The authors in [
17] employed an array of 24 sensitive tunneling magneto-resistive sensors to measure the distribution of stray magnetic fields for detecting stator TTSC faults in synchronous machines.
In the study conducted by Kim et al. [
19], a novel detection coil was introduced, specifically designed to detect fluctuations in flux linkage induced by the TTSC. The authors in [
20] utilized dual search coils (SC) to measure the flux linkage across diverse air-gap regions of the generator. This method enables detection of the asymmetric distribution of the rotating magnetic field, which further aids in identification of the TTSC and the pinpointing of the defect-prone area. Despite the flux linkage sensor being predominantly cost-effective, reliable, and sensitive, it is primarily hindered by practical installation limitations.
Due to their accessibility through electrical measuring elements, utilizing the voltage and current characteristics induced by TTSC faults for fault diagnosis is the most prevalent approach in the field [
21,
22,
23]. Contrary to the methods based on flux linkage, those based on current/voltage do not necessitate additional sensors [
24]. They are more readily obtainable and reliable, making them the preferred choice in the aviation industry.
The authors in [
25] proposed a model-based approach for the detection and diagnosis of stator winding faults in the brushless wound-field synchronous generator (BWFSG) utilized in the aviation industry. The authors in [
26] utilized a residual current vector derived from the discrepancy between the measured stator currents and stator currents projected by a state observer for TTSC fault diagnosis. The authors in [
27] proposed a robust method for TTSC fault detection that addressed the issue of harmonics in machine currents and voltages being affected by the bandwidths of dual-loop controllers. This interference often leads to failures in the TTSC fault detection methods when based solely on current or voltage signature analysis. The authors in [
28] proposed a model-based approach using the extended Kalman filter (EKF) and unscented Kalman filter (UKF) for the FDI of stator inter-turn faults in synchronous generators.
The authors in [
29] used a long short-term memory (LSTM) machine learning network along with conventional signal processing tools to detect incipient TTSC faults in an induction generator. Employing the phasor method, the author in [
30] illustrated that under linear and steady-state conditions, the two stator TTSC parameters, specifically the short-circuit turn ratio and the short-circuit branch resistance, could not be distinctively determined based on the voltage and current measurements due to their multiple solutions. The author in [
30] introduced a TTSC severity index anchored on the generator stator winding resistance and fault circuit winding resistance. This pioneering research delved into the determinants of current and voltage dynamics during stator TTSC faults [
10,
31]. However, the theory in [
30] is limited to linear and steady-state scenarios. Moreover, the stator TTSC severity index proposed includes specific generator parameters, limiting its wide applicability and universality.
Here, we summarize the mainstream method categories for stator TTSC faults, the typical methods in each category as well as their corresponding advantages, disadvantages, and references to relevant research, as shown in
Table 1.
The research framework of this paper is shown in
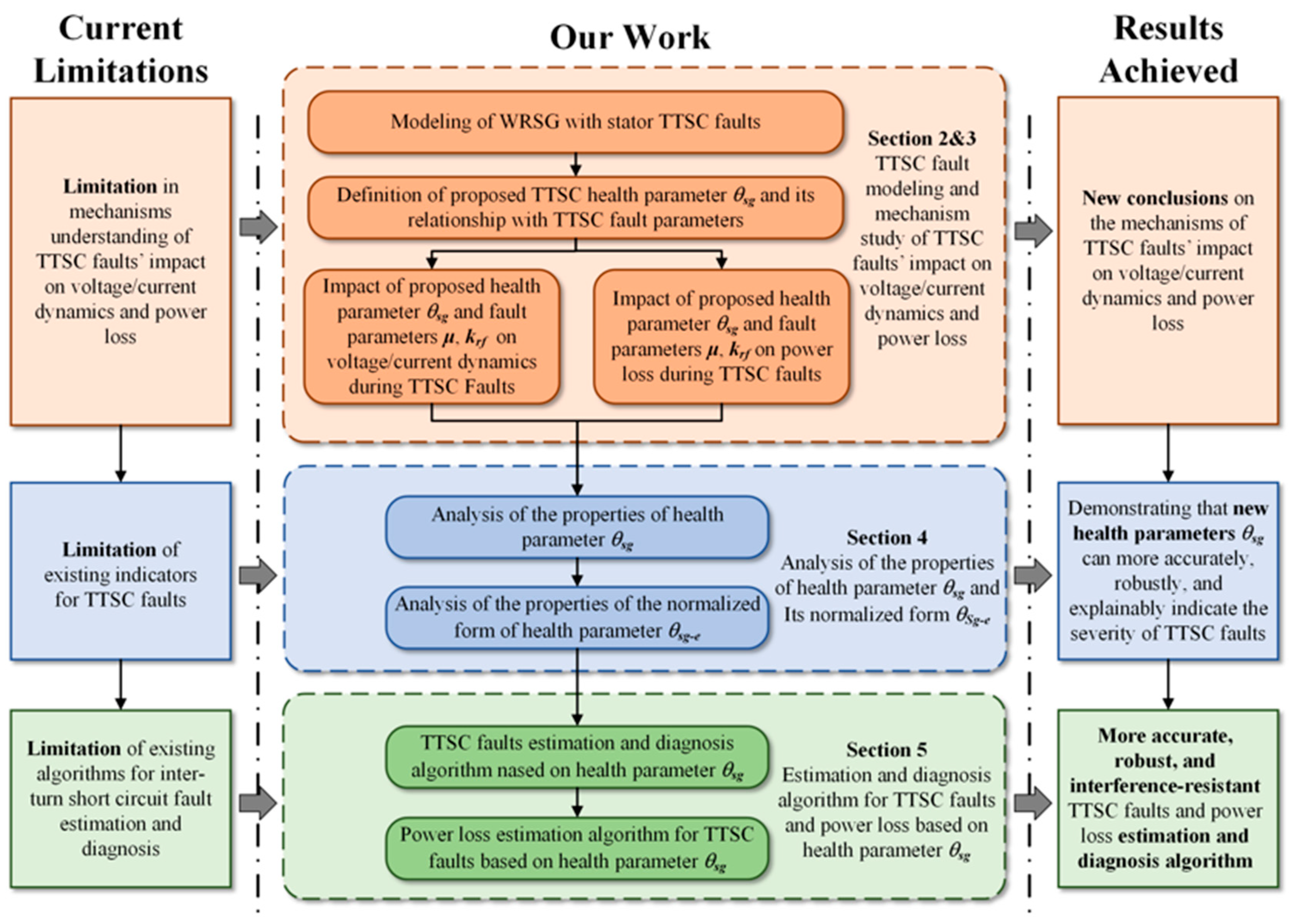
Figure 1, which introduces the main research problems addressed, the work conducted, the innovations implemented, and the achievements obtained in this study. Currently, research on the analysis, estimation, and diagnosis of generator stator TTSC faults has three major limitations. (1) A limited understanding of the TTSC fault mechanisms, manifested as an insufficient comprehension of how fault parameters affect the voltage, current, and the mechanisms of power loss caused by faults. (2) The limitations of existing TTSC fault indicators. Due to the aforementioned insufficient understanding, fault indicator parameters developed based on this cognition (such as zero-sequence voltage, negative-sequence voltage, and second harmonics) are susceptible to external interference and cannot accurately assess the severity of faults. (3) Limitations of the existing TTSC fault estimation and diagnostic algorithms. Since these algorithms are built upon the above-mentioned easily-interfered indicators, they generally suffer from poor accuracy, low stability, and weak anti-interference capabilities.
To address these three limitations, this paper systematically conducted the following three targeted research efforts in sequence, yielding three innovative achievements. First, to resolve the insufficient understanding of fault influence mechanisms,
Section 2 and
Section 3 deeply analyze the relationship between the fault parameters and fault voltage/current dynamics as well as the relationship between the fault parameters and power loss. We propose a new TTSC fault health parameter and thoroughly explore the correlation between the health parameter and voltage/current dynamics and power loss, thereby gaining new insights into how TTSC faults affect the voltage and current characteristics. Second, regarding the limitations of the existing fault indicators,
Section 4 presents an in-depth theoretical analysis of the properties of the proposed health parameter and its normalized forms, demonstrating that the parameters offer greater accuracy, robustness, and interpretability compared with traditional fault indicators. (3) Based on the above research findings,
Section 5 focuses on addressing the limitations of the existing fault estimation and diagnostic algorithms. Building upon the proposed health parameters, we designed TTSC fault and power loss estimation and diagnostic algorithms with higher accuracy, stronger robustness, and superior anti-interference capabilities.
These systematic research efforts, along with the resulting new understanding of fault mechanisms, new health parameter, fault evaluation systems, and new fault and power loss estimation and diagnostic algorithms, effectively address the deficiencies and limitations in the current research. Finally, in
Section 6, we validate the above conclusions and achievements through extensive Monte Carlo simulations.
2. Model of WRSG with Stator TTSC Faults
In this section, we present a generic model of the WRSG capable of representing stator winding TTSC faults. The structure of the WRSG is shown in
Figure 2, consisting of a main generator, load, exciter, and an automatic voltage regulator (AVR). The main generator is responsible for supplying three-phase AC power to the load. The exciter provides excitation voltage to the field winding of the main generator rotor, thereby generating the magnetic field. The AVR acts as a controller to ensure that the output voltage remains within a specified range by controlling the excitation voltage of the exciter. Given that this study focused on stator TTSC faults in the main generator, we did not explicitly specify the structure and type of the AVR and exciter. Instead, the AVR and exciter were considered equivalent to an AC5A excitation voltage controller [
4,
47,
48], and it was assumed that the output excitation voltage could be measured or estimated. We further assumed that the faults were incipient and that the generator possessed a degree of redundancy; consequently, the effects of the magnetic saturation were not taken into consideration [
25]. These assumptions simplify the modeling complexity and enhance its generalizability. It is worth noting that due to these assumptions, our approach is primarily applicable for early-stage TTSC detection in generators operating within linear regimes, where nonlinear behaviors remain minimal.
We assumed that the main generator stator had three phases, namely
, and
, which were used to output the three-phase alternating voltage/current, as depicted in
Figure 2. The TTSC faults were assumed to occur in phase
of the main generator, where the short-circuit branch had a resistance of
and a current of
. The ratio of the number of turns in the short-circuited section to the total number of turns
is denoted by
. The short-circuited section in phase
is referred to as
, while the healthy section is referred to as
. The directions of the respective currents are illustrated in
Figure 3. We introduced the parameter
, which signifies the ratio of the resistance of the short-circuit branch to that of the short-circuit part of the coil, to compute
, where
. Consequently, the fault in the TTSC can be characterized by the fault parameters
and
.
The main generator was modeled by using a widely adopted and validated multi-loop theory [
25,
49,
50]. This approach assumes that the TTSC fault results in the formation of a new current path, as depicted in
Figure 3, causing a diversion of current, and thus reducing the current flowing through the original turns. During this process, the number of turns in the faulty phase does not decrease. Based on this assumption, the multi-loop theory treats the short-circuit branch formed during a TTSC fault as a fault loop. Subsequently, by computing the coupling effects of the fault current in this loop with other parts of the generator, the operational state of the generator under this fault condition can be deduced. This methodology enables the representation of both normal scenarios (where the short-circuit branch resistance is near-infinite) and faulty scenarios (where the short-circuit branch resistance is relatively low).
Furthermore, the dq0 rotor reference frame was employed to reduce the complexity of the inductance matrix involved in the conversion of flux linkage and current, thus minimizing the utilization of computational resources. Furthermore, the orientation of coordinate axes and the directionality of various quantities are available in the reference to the IEEE standards [
51]. In the following, we present the key governing expressions to characterize the dynamics of the generator.
The relationship between the voltage, current, and flux linkage of the armature winding of the main generator can be described by
where
denote the voltage of the stator winding in the dq0 rotating reference frame;
denote the flux linkage of the stator winding in the dq0 rotating reference frame;
denote the current of the stator winding in the dq0 rotating reference frame;
denotes the transformation matrix from the abc frame to the dq0 frame;
denotes the stator phase winding resistance;
denotes the generator speed;
denotes the noise indicating uncertainty.
The rotor of the main generator can be classified into two types, namely salient and round. Our research focused on the salient-pole rotor for subsequent investigation. It should be noted that the subsequent theoretical analysis and conclusions also held for the round structure. However, due to space limitations, we do not provide a separate demonstration for the round structure.
The relationship between the voltage, current, and flux linkage of the rotor winding in the generator is described by
where
denote the voltage of the rotor field winding, damper bars on the d-axis and q-axis;
denote the flux linkage of rotor field winding, damper bars on the d-axis and q-axis;
denote the current of rotor field winding, damper bars on the d-axis and q-axis;
denote the resistance of rotor field winding, damper bars on the d-axis and q-axis;
denotes the noise indicating uncertainty.
The relationship between the flux linkage and current in the generator can be expressed by
where
is the first column of the matrix T, and
Equations (1)–(3) determine the voltage–current relationship of the generator. It should be noted that as this study focused on the initial stages of the TTSC malfunction, the inductance matrix did not take into account the effects of distortion in the space harmonics and air-gap flux density disturbance, among others that are caused by the TTSC [
14,
25,
52]. However, our theory is applicable to any form of inductance matrix, and hence is capable of being extended. This suggests that, if necessary, more accurate results that consider the effects of distortion and air-gap flux density disturbances can be obtained by integrating other analytical methods, such as the winding function approach (WFA), to refine the inductance matrix [
4]. However, while our method has extension potential, this paper specifically focused on the current assumptions, namely ignoring the aforementioned effects and concentrating on early-stage TTSC faults.
Due to presence of stator TTSC faults, the above equations contain parameters that are related to the fault. To investigate the above equation, it is necessary to introduce the following equations to describe the fault circuit, namely
where
denotes the flux linkage of the faulty winding
in phase
.
Equations (1)–(4) determine the current–voltage dynamics of the main generator. Subsequently, to model the voltage–current characteristics of general electrical loads, rather than focusing on specific load structures, a state-space approach was employed here to represent various types of electrical loads and their voltage–current characteristics, as shown in Equation (5) [
53,
54], where
represents the load state variables, which may include voltage, current, and other load-specific states depending on the particular load characteristics. The corresponding generator terminal measurements of voltage and current can be expressed by using Equation (6). By simultaneously solving Equations (1)–(6), the voltage–current dynamics and measurements of the entire system can be obtained.
where
, .
is the characteristic equation of the electrical load and its state variables;
denote the terminal voltage of the three-phase;
denote the terminal current of the three-phase;
denote the uncertainty associated with current and voltage measurements, respectively;
~ is the superscript of the measured values.
Equations (1)–(5) provide and define the system, where the solutions to these equations represent the dynamic voltage and current of the system. Equation (6), on the other hand, provides the relationship between the measured values and the true values of the voltage and current. Based on these equations, we constructed a WRSG model in MATLAB/Simulink to solve these equations and simulate the TTSC faults.
4. Characteristics and Normalized Form of the Health Parameter θsg
In this section, we describe and present the three beneficial characteristics of the proposed health parameter . Subsequently, we introduce the normalized form of this parameter and discuss its functionality.
4.1. Characteristics of the Health Parameter θsg
Specificity and Robustness: Under the condition that all other factors remain unchanged, the health parameter value is specific, with each health parameter value corresponding to a determined terminal voltage/current response. There is no identical health parameter that corresponds to different terminal voltage/current dynamics and impacts. Furthermore, the proposed health parameter exhibits robustness and a high degree of resistance to extraneous factors. Furthermore, it reliably indicates the degree of stator TTSC faults across a variety of conditions.
Quantifiability and Monotonicity: The health parameter is quantifiable and monotonic in nature to allow for an objective and quantitative assessment of the system health and performance. This quantification and monotonicity enable an effective comparison between different levels of the fault severity. For instance, as the severity of the fault increases (or decreases), the corresponding value of the health parameter also increases (or decreases).
Universality and Interpretability: The health parameter is universalizable, implying that it can be applied to the WRSG of different sizes or configurations. The health parameter is also easily interpretable, providing information with clear physical significance regarding the condition of the generator, thereby facilitating relevant decision-making processes for health monitoring and diagnosis.
Next, we demonstrate that the proposed health parameter possesses the above characteristics. Based on Theorem 1, one can substantiate that the proposed health parameter is capable of uniquely determining the terminal current and voltage dynamic responses. Therefore, our health parameter exhibits specificity. Given that the proposed health parameter is derived solely from the fault parameters, its values are not influenced by external factors. Consequently, these parameters provide a consistent and stable indication of the severity of the TTSC fault under various operational conditions, exhibiting exceptional robustness.
In order to substantiate that our health parameter exhibited quantifiability and monotonicity, it was necessary to define the criteria to evaluate the severity of two TTSC faults. We assumed that for two TTSC faults, and , their severity levels were and , respectively, and the associated fault parameters were and , respectively. The power losses and occurred under the same fault output voltage and current . Subsequently, we conducted comparisons under four different scenarios.
Scenarios 1: If , , it was assumed that .
Scenarios 2: If , , it was assumed that when . Conversely, when , then .
Scenarios 3: If , , it was assumed that when . Conversely, when , then .
Scenarios 4: If , , it was assumed that when , then and when , then and when , then .
The reasons for choosing the above comparison criteria were as follows. In the first three scenarios, we could directly compare them based on our intuitive understanding of the TTSC faults. When the ratio of the short-circuit turns and ratio of the short-circuit branch resistance was the same, the fault parameters were completely identical, resulting in the same severity of the fault. When the ratio of the short-circuit turns was fixed, the fault with a lower ratio of the short-circuit branch resistance was more severe. When the ratio of the short-circuit branch resistance was the same, the fault with a higher ratio of short-circuit turns was more severe. However, in the fourth scenario, where both the short-circuit turns and short-circuit branch resistance were different, a direct comparison was not possible. Therefore, one needs to choose a metric to evaluate, and in this scenario, we chose the power loss caused by the TTSC.
The above reasoning was based on the fact that power loss directly affects the efficiency of the generator, which in turn affects the operation of the system. Additionally, the power loss also leads to extra heat generated by the fault. The significant increase in this heat poses a severe challenge to the safe operation of the generator. Therefore, power loss is an excellent reference value for measuring the impact and severity of the fault [
30,
55]. It follows that under the same fault voltage and current conditions, a fault with a higher power loss is more severe, while faults with the same power loss have the same severity.
Subsequently, we will demonstrate that the proposed health parameter satisfied the requirements of quantifiability and monotonicity under the above comparison rules. Upon examining the definition of , it was evident that the first three scenarios all met the criteria of quantifiability and monotonicity. Therefore, we will now proceed to show that the quantifiability and monotonicity still held for scenario 4.
Upon analysis of the health parameter , it was observed that it decreased with the increase in the short-circuit range , and with the decrease in the short-circuit resistance . This suggests that as the severity of TTSC faults increases, the value of the health parameter consistently declines. The maximum value of the health parameter is achieved when the short-circuit range approaches zero and the short-circuit resistance approaches infinity, representing an ideal state of health with a maximum value of . Conversely, the minimum value of the health parameter occurs when the short-circuit range , indicating a full-phase short circuit, and when the resistance is 0, this represents an ideal state of the maximum fault with a minimum value of 1. Therefore, the health parameter ranges within the interval , where 1 designates an ideal state of a complete short circuit, and represents an ideal state of the complete health.
Upon substituting Equation (11) into Equation (13), one is able to derive the following expression:
From Equation (14), it follows that under the same voltage and current , the power progressively increases as the health parameter decreases from to . Thus, in conjunction with the above analysis and evaluation criteria, one can conclude that the severity of a fault escalates with the decrease in the health parameter . As the fault phase progresses from a healthy state to a complete short circuit, indicating an escalating severity, the health parameter correspondingly decreases from to . Consequently, we were able to validate that our proposed health parameter adheres to quantifiability and monotonicity.
Based on the observations and conclusions above, an additional benefit of using the power loss as an assessment metric became evident, namely it aligned with the criteria corresponding to the other three scenarios. Specifically, for higher severe faults occurring within these scenarios, there was a corresponding increase in the power loss.
As demonstrated in
Section 2 and
Section 3, our proposed health parameter can be applied to various types of loads, exciters, and AVR, thereby exhibiting strong universality. Moreover, an observation of
revealed that this health parameter is independent of any other generator parameter and relies solely on the fault branch resistance ratio
and the short-circuit turns ratio
. These parameters are universal for TTSC faults, hence,
displays a high degree of universality, can be applied in generators with different parameters, and exhibits broad representativeness. An identical health parameter
value corresponds to a similar degree of TTSC faults, which demonstrates its universality. As previously illustrated,
is a value that gradually changes from
to 1 as the fault severity increases, thereby making
have direct physical meanings that are clear and interpretable. Consequently, we validated that
possesses both universality and interpretability.
The above properties endowed our proposed health parameter with superior capabilities for assessing stator TTSC faults in the WRSG compared with traditional fault indication signals such as the zero-sequence voltage [
14,
39]. These assertions will also be validated in
Section 6.
4.2. Normalized Form of the Health Parameter θsg
In the realm of fault diagnosis technology, the aim is to make health parameters more intuitive. Consequently, we proposed a normalized form, denoted by
, of the health parameter
. Unlike
,
is a parameter ranging from 0 to 1. The corresponding normalized form for the proposed health parameter is now given as follows:
where
denotes a scaling coefficient.
Given that the health parameter and its normalized counterpart have a monotonic and bijective mapping, it can be inferred that the normalized form of the health parameter also adheres to all previously identified characteristics pertaining to .
When equals 1, it signifies an healthy state, with no short-circuit occurrence. As decreases, the magnitude of the TTSC fault progressively increases. When diminishes to 0, it indicates a complete short-circuit fault in the phase (i.e., the short-circuit turns ratio is 1, and the short-circuit branch resistance ratio is 0). Consequently, compared with , its normalized form is more intuitive.
The scaling factor in is utilized to adjust the sensitivity of to incipient faults. A larger increases the sensitivity of to incipient faults, resulting in a faster decay during early faults. Conversely, a smaller reduces the sensitivity of to incipient faults, requiring a more significant fault to cause a noticeable decrease in . In this study, was .
In summary, when we aim to express the fault degree more intuitively, can replace . This normalized health parameter can be used to describe TTSC faults in WRSG, offering superior interpretability and intuitiveness.
Here, we would like to provide a more intuitive explanation of the physical meaning behind our health parameters and . can be understood as an abstract-level short-circuit resistance obtained by weighting the short-circuit branch resistance with the shorted turn ratio . The larger this abstract-level short-circuit resistance, the smaller the short-circuit magnitude. When this short-circuit resistance approaches infinity, there is naturally no short circuit; when it equals zero, it indicates a complete short circuit. Meanwhile, can be viewed as a normalized form of , designed for easier practical use. A value of 1 represents complete health, while a value of 0 represents a complete short circuit—the worst health condition. This approach is similar to various health parameters used in the industry, making it more intuitive to understand and implement.
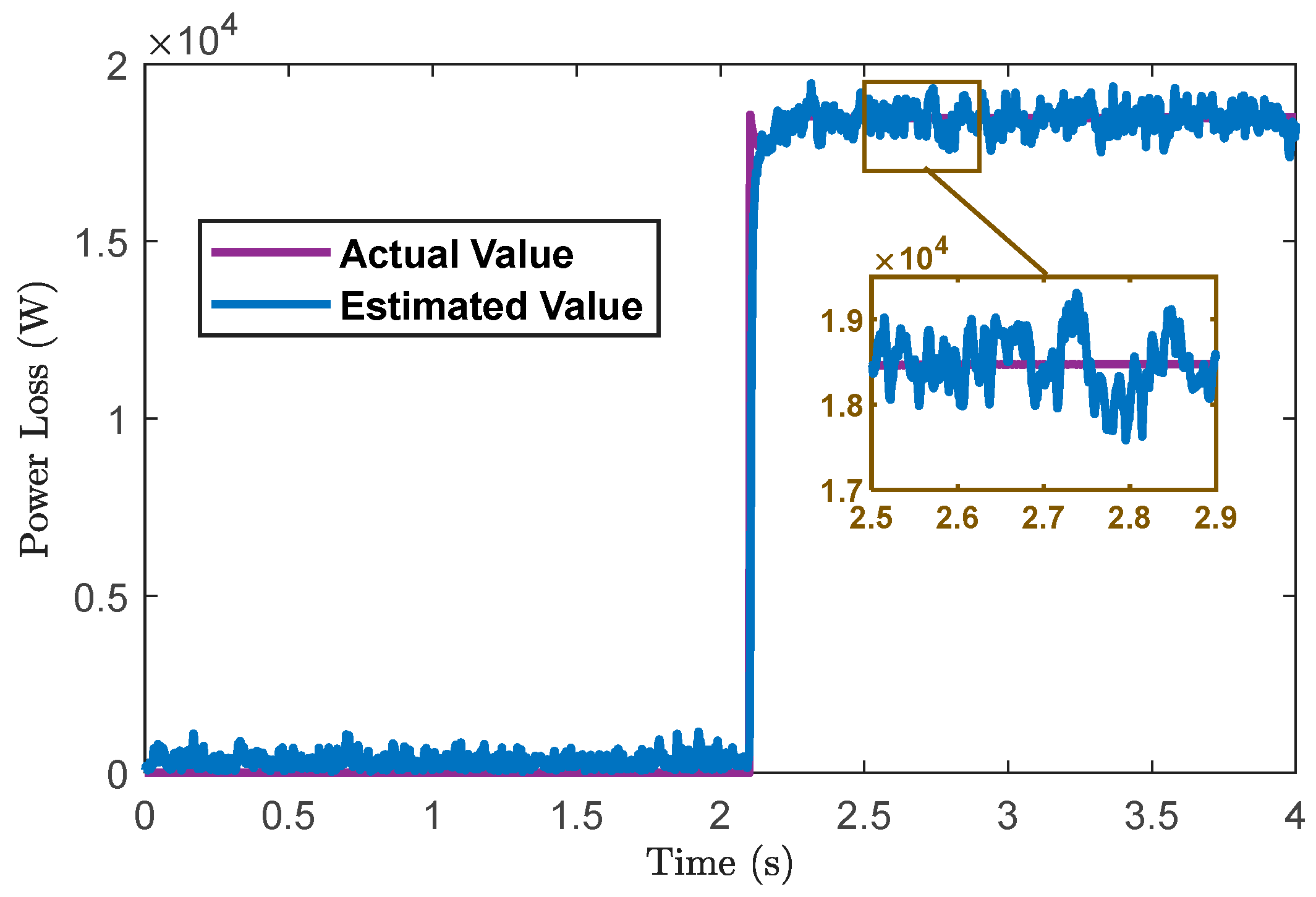
5. Estimation Algorithm for the Health Parameter θsg and Power Loss Ploss
In this section, we present the proposed estimation method based on the Kalman filter (KF) for estimating the proposed health parameter and power loss, followed by an analysis of their associated errors.
Let us express the current–voltage characteristic Equations (1)–(3) of the generator as follows:
By treating the measured voltage in Equation (6) as the input and the measured current as the output and substituting them into Equations (15) and (16), with the flux linkage considered as the state variable, the current–voltage characteristic equation of the generator can be expressed in the state-space representation given by Equations (17) and (18) after some algebraic manipulation, as follows:
where
and
.
Upon substituting
in Equation (18) with Equation (11), one can derive the following:
By considering
as an augmented state variable
, the state-space Equations (17) and (18) can be further expressed in the following form:
where
In the above system, the only nonlinear component is denoted by
. Given the assumption that the fault was not excessively severe and that the magnetic saturation effects were absent, it was evident that
<< 1. The term
represents noise, which is also a relatively low magnitude quantity. Consequently, the impact of this nonlinear component on the system was considered negligible. For the sake of reducing the computational cost and complexity of proposed algorithms, we opted to disregard this nonlinearity. Hence, the system can be represented in the following linearized form in Equations (22) and (23):
Subsequently, for a continuous generator system, one can employ a KF to estimate the augmented state,
, of the system. The KF algorithm utilized for estimating
involves the following update Equations (24)–(26) for the covariance matrix, the KF gain, and the state estimate
[
56], namely
where
and
are matrices representing the intensity of noise for
and
, respectively, where the superscript ^ denotes the estimated value.
Upon obtaining the estimate of
through the application of the KF, we are then able to derive the estimate of
. Subsequently, an estimate of the parameter
and the power loss
can be ascertained by using the following equations.
The complete estimation algorithm is outlined in Algorithm, as shown in
Figure 4. It must be noted that due to the characteristics of probability distributions, the estimates of
and
derived from
using Equations (26) and (27) are not unbiased and are subject to error. However, the simplicity and computational efficiency of the above method for estimating
and the power loss
from
make it a viable option, particularly when the estimation error of
remains small. Consequently, this method was retained for subsequent use in this study. For more precise estimates and to understand the distribution of these estimates, Monte Carlo sampling techniques can be employed to derive more reliable estimates of
and the power loss from
[
57].
It is important to further note that, as mentioned in
Section 2, the excellent properties of our proposed health parameters and the algorithm developed for estimating TTSC fault severity and power loss are based on the assumption that the TTSC fault is in its early, low-magnitude stage, and that the generator possesses a degree of redundancy. Consequently, the effects of magnetic saturation were not taken into consideration [
25], and we also ignored the space harmonics and air-gap flux density disturbance, among other factors caused by the TTSC [
14,
25,
52]. Therefore, if the TTSC fault becomes more severe, this method cannot be directly applied and would require further research and adjustments.