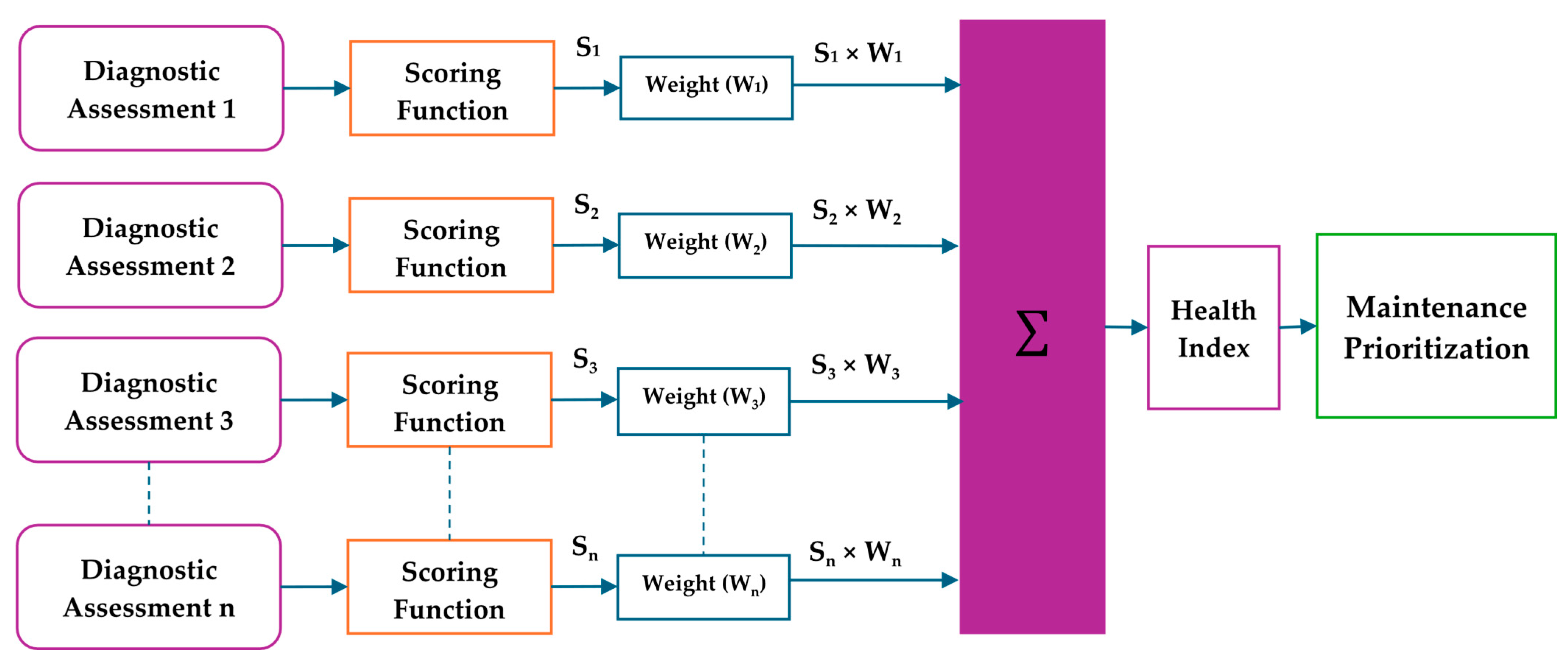
Figure 1.
Schematics for scoring–weighting Health Index prediction.
Figure 1.
Schematics for scoring–weighting Health Index prediction.
Figure 2.
Schematics for non-conventional Health Index prediction.
Figure 2.
Schematics for non-conventional Health Index prediction.
Figure 3.
Histogram of the oil quality parameter.
Figure 3.
Histogram of the oil quality parameter.
Figure 4.
Histogram of the dissolved gas analysis parameter.
Figure 4.
Histogram of the dissolved gas analysis parameter.
Figure 5.
Histogram of the paper condition parameter.
Figure 5.
Histogram of the paper condition parameter.
Figure 6.
Oversampling and undersampling process.
Figure 6.
Oversampling and undersampling process.
Figure 7.
Hybrid method process.
Figure 7.
Hybrid method process.
Figure 8.
Flowchart for generating synthetic data using SMOTE.
Figure 8.
Flowchart for generating synthetic data using SMOTE.
Figure 9.
Generated synthetic data using SMOTE.
Figure 9.
Generated synthetic data using SMOTE.
Figure 10.
Generated synthetic data using Borderline-SMOTE.
Figure 10.
Generated synthetic data using Borderline-SMOTE.
Figure 11.
Generated synthetic data using SMOTE-Tomek.
Figure 11.
Generated synthetic data using SMOTE-Tomek.
Figure 12.
Generated synthetic data using SMOTE-ENN.
Figure 12.
Generated synthetic data using SMOTE-ENN.
Figure 13.
Distribution of the class on the Health Index dataset.
Figure 13.
Distribution of the class on the Health Index dataset.
Figure 14.
Class imbalance ratio for the original dataset.
Figure 14.
Class imbalance ratio for the original dataset.
Figure 15.
Metric performance for the regression and classification model (normalization based on standard).
Figure 15.
Metric performance for the regression and classification model (normalization based on standard).
Figure 16.
Metric performance for the regression and classification model (hybrid normalization).
Figure 16.
Metric performance for the regression and classification model (hybrid normalization).
Figure 17.
Distribution of the class on original Health Index dataset and modified dataset.
Figure 17.
Distribution of the class on original Health Index dataset and modified dataset.
Figure 18.
Random Forest performance for various oversampling ratio.
Figure 18.
Random Forest performance for various oversampling ratio.
Figure 19.
Neural Network performance for various oversampling ratios.
Figure 19.
Neural Network performance for various oversampling ratios.
Figure 20.
SVM performance for various oversampling ratios.
Figure 20.
SVM performance for various oversampling ratios.
Figure 21.
Naïve Bayes performance for various oversampling ratios.
Figure 21.
Naïve Bayes performance for various oversampling ratios.
Figure 22.
Comparison of VG class recall for various datasets.
Figure 22.
Comparison of VG class recall for various datasets.
Figure 23.
Comparison of G class recall for various datasets.
Figure 23.
Comparison of G class recall for various datasets.
Figure 24.
Comparison of C class recall for various datasets.
Figure 24.
Comparison of C class recall for various datasets.
Figure 25.
Comparison of P class recall for various datasets.
Figure 25.
Comparison of P class recall for various datasets.
Figure 26.
Comparison of VP class recall for various datasets.
Figure 26.
Comparison of VP class recall for various datasets.
Figure 27.
p-value for F1-scores of various methods.
Figure 27.
p-value for F1-scores of various methods.
Figure 28.
Boxplot of classification accuracy for various datasets.
Figure 28.
Boxplot of classification accuracy for various datasets.
Figure 29.
Boxplot of precision for various datasets.
Figure 29.
Boxplot of precision for various datasets.
Figure 30.
Boxplot of recall for various datasets.
Figure 30.
Boxplot of recall for various datasets.
Figure 31.
Boxplot of F1-score for various datasets.
Figure 31.
Boxplot of F1-score for various datasets.
Table 1.
Distribution of transformer data.
Table 1.
Distribution of transformer data.
| Parameter | N | Mean | Min | Q1 | Median | Q3 | Max |
|---|
| Oil Quality Factor |
| BDV | 3073 | 71.316 | 11.100 | 62.00 | 74.40 | 84.20 | 100.2 |
| Water | 3098 | 8.337 | 0.00 | 3.654 | 5.809 | 10.225 | 93.57 |
| Acid | 3065 | 0.06276 | 0.00 | 0.020 | 0.030 | 0.070 | 3.600 |
| IFT | 2726 | 29.192 | 0.00 | 29.20 | 31.80 | 33.40 | 48.70 |
| Color | 3064 | 1.3914 | 0.00 | 0.490 | 0.800 | 2.20 | 8.00 |
| Faults Factor |
| H2 | 3820 | 56.29 | 0.00 | 0.00 | 17.00 | 41.14 | 4616.78 |
| CH4 | 3839 | 64.31 | 0.00 | 5.07 | 20.00 | 66.10 | 2111.70 |
| C2H2 | 3828 | 4.190 | 0.00 | 0.00 | 0.00 | 0.00 | 927.00 |
| C2H4 | 3829 | 36.38 | 0.00 | 0.00 | 4.00 | 16.61 | 2533.81 |
| C2H6 | 3839 | 107.46 | 0.00 | 3.00 | 30.00 | 142.02 | 1354.67 |
| Paper Condition Factor |
| Age | 3797 | 16.55 | 0.00 | 7.00 | 16.00 | 24.00 | 53.00 |
| CO | 3666 | 287.6 | 0.78 | 40.9 | 137.0 | 339.0 | 12,914.0 |
| CO2 | 3733 | 1660.3 | 0.00 | 348.5 | 922.0 | 2094.4 | 48,837.0 |
| DP | 309 | 774.5 | 40.2 | 564.9 | 744.8 | 972.2 | 1553.4 |
Table 2.
Research on the scoring–weighting method for the Health Index.
Table 2.
Research on the scoring–weighting method for the Health Index.
| Ref. | Scoring–Weighting |
|---|
| [25] | |
| The Health Index assessment is based on four Health Index components, namely main Health Index HIm, insulating paper Health Index HIiso, Health Index based on DGA HICH, and Health Index for Oil Quality HIoil. |
|
| Obtain the main Health Index by looking at the value of the Health Index decreasing exponentially based on year. |
|
| w1 and w2 are weightings with values of 0.3 and 0.7. Fco is the carbon–oxygen factor, and Cfur is the furan content. |
|
| FCH is a function of the hydrocarbon factor. |
|
| Foil is an Oil Quality factor based on acidity levels, breakdown voltage, water content, and dielectric losses. |
| [9] | |
| The HI value consists of a combination of 24 test parameters, with 40% weighting from LTC and 60% from transformer parameters. |
| [8] | |
|
| HI1 is the theoretical Health Index value, B is the aging coefficient, T is the operating age, fL is the loading factor, fe is the environmental factor based on pollution. |
|
| HIF1 is the dissolved gas index, HIF2 is the oil quality index, HIF3 is the furan index, HIF4 is the dielectric loss index, HIF5 is the absorption ratio index, HIF6 is the DC resistance index, and HIF7 is the partial discharge index. |
| [10] | |
| The final Health Index (HIfinal) consists of factor scores (SFj) and factor weighting (Wj), factor scores can be calculated from the Health Index results for each factor. |
|
| This reference uses factors namely Oil Quality Factor (Breakdown voltage, water content, acidity, interfacial tension, and color scale), Faults Factor (Based on DGA test results), and Paper Condition Factor (CO & CO2, Age, and 2FAL). |
Table 3.
Scoring for transformer parameters.
Table 3.
Scoring for transformer parameters.
| Parameter | Score |
|---|
| 1 | 2 | 3 | 4 | 5 |
|---|
| Oil Quality Factor |
| BDV (2.5 mm kV) | >170 kV | >55 | 40–55 | 30–40 | - | <30 |
| 72.5–170 kV | >60 | 60–50 | 50–40 | - | <40 |
| <72.5 kV | >60 | 60 | 50–60 | - | <50 |
| Water (ppm) | >170 kV | <20 | 20–30 | 30–40 | - | >40 |
| 72.5–170 kV | <10 | 10–20 | 20–30 | - | >30 |
| <72.5 kV | <10 | 10–15 | 15–20 | - | >20 |
| Acid (mgKOH/g) | >170 kV | <0.03 | 0.03–0.15 | 0.15–0.3 | | >0.3 |
| 72.5–170 kV | <0.03 | 0.03–0.1 | 0.1–0.2 | - | >0.2 |
| <72.5 kV | <0.03 | 0.03–0.1 | 0.1–0.15 | | >0.15 |
| IFT (mN/m) | Inhibited | >35 | 28–35 | 22–28 | - | <22 |
| Uninhibited | >35 | 35–25 | 25–20 | - | <20 |
| Color | <0.5 | 0.5–1.0 | 1.0–2.5 | 2.5–4 | >4 |
| Faults Factor |
| H2 (ppm) | <80 | 80–200 | 200–320 | >320 | - |
| CH4 (ppm) | <90 | 90–150 | 150–210 | >210 | - |
| C2H2 (ppm) | <1 | 1–2 | 2–3 | >3 | - |
| C2H4 (ppm) | <50 | 50–100 | 100–150 | >150 | - |
| C2H6 (ppm) | <90 | 90–170 | 170–250 | >250 | - |
| Paper Condition Factor |
| AGE (year) | <20 | 20–30 | 30–40 | 40–60 | >60 |
| DP estimated (2FAL) | >800 | 700–800 | 500–700 | 300–500 | <300 |
| CO (ppm) | <350 | 351–570 | 571–1400 | 1401–2500 | >2500 |
| CO2 (ppm) | <2500 | 2500–4000 | 4001–10,000 | 10,000–17,500 | >17,500 |
Table 4.
Distribution of Health Index parameter data.
Table 4.
Distribution of Health Index parameter data.
| Parameter | N | Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum |
|---|
| BDV | 3073 | 71.31 | 17.65 | 11.10 | 62.00 | 74.40 | 84.20 | 100.20 |
| Water | 3098 | 8.33 | 7.92 | 0.00 | 3.65 | 5.81 | 10.22 | 93.57 |
| Acid | 3065 | 0.0627 | 0.1519 | 0.00 | 0.020 | 0.03 | 0.07 | 3.60 |
| IFT | 2726 | 29.19 | 8.77 | 13.00 | 29.20 | 31.80 | 33.40 | 48.70 |
| Color | 3064 | 1.391 | 1.44 | 0.00 | 0.49 | 0.80 | 2.20 | 8.00 |
| H2 | 3820 | 56.29 | 183.12 | 0.00 | 0.00 | 17.00 | 41.14 | 4616.78 |
| CH4 | 3839 | 64.31 | 150.36 | 0.00 | 5.07 | 20.00 | 66.10 | 2111.70 |
| C2H2 | 3828 | 4.19 | 29.59 | 0.00 | 0.00 | 0.00 | 0.00 | 927.00 |
| C2H4 | 3829 | 36.38 | 156.16 | 0.00 | 0.00 | 4.00 | 16.61 | 2533.81 |
| C2H6 | 3839 | 107.46 | 169.68 | 0.00 | 3.00 | 30.00 | 142.02 | 1354.67 |
| Age | 3797 | 16.55 | 10.83 | 0.00 | 7.00 | 16.00 | 24.00 | 53.00 |
| CO | 3666 | 287.60 | 587.60 | 0.78 | 40.90 | 137.00 | 339.00 | 12,914.00 |
| CO2 | 3733 | 1660.30 | 2705.80 | 0.00 | 348.50 | 922.00 | 2094.40 | 48,837.00 |
| DP | 309 | 774.50 | 312.10 | 40.2 | 564.90 | 744.80 | 972.20 | 1553.40 |
Table 5.
Metrics of performance to evaluate ML model.
Table 5.
Metrics of performance to evaluate ML model.
| Metrics | Description |
|---|
| Area Under the ROC Curve (AUC) | AUC measures the ability of the model to distinguish between different classes. It provides a value between 0 and 1, where a higher value indicates better performance in distinguishing classes. |
| Classification Accuracy (CA) | This metric calculates the proportion of correctly classified instances over the total number of instances. While useful, accuracy alone might not be sufficient for imbalanced datasets, as it can be biased towards the majority class. |
|
TP = Number of correct positive predictions
TN = Number of correct negative predictions
FP = Number of false positive predictions
FN = Number of false negative predictions |
| Precision | Precision measures the proportion of correctly predicted positive observations to the total predicted positives. It is crucial when the cost of false positives is high. |
|
| Recall | Also known as Sensitivity, Recall calculates the proportion of correctly predicted positive observations to all actual positives. It is vital when the cost of false negatives is high. |
|
| F1 Score | The F1-score is the harmonic mean of Precision and Recall. It provides a balanced measure of the two metrics, especially useful for imbalanced datasets. |
|
Table 6.
Remarks on several ML algorithms.
Table 6.
Remarks on several ML algorithms.
| Algorithms | Advantage | Disadvantage |
|---|
| Neural Network | Captures complex patterns effectively, flexible, adaptable to various datasets. | Prone to bias towards the majority class, susceptible to overfitting. |
| SVM | Optimal for small datasets, effective when class margins are clearly defined. | Inefficient for large datasets, sensitive to noise in the data. |
| Random Forest | Resilient to overfitting, highly flexible in handling various types of data. | Requires parameter tuning for optimal performance, may perform suboptimal on highly imbalanced datasets. |
| Fuzzy Logic | Handling uncertainty effectively can be easily modified. | High subjectivity in rule and membership function definition, limited performance on large datasets. |
Table 7.
Regression–classification comparison.
Table 7.
Regression–classification comparison.
| Metric | Scoring Table 4 + Min–Max | Scoring Table 4 |
|---|
| Random Forest | SVM | Neural Network | Random Forest | SVM | Neural Network |
|---|
| RMSE | 4.975 | 10.356 | 5.242 | 5.012 | 11.226 | 5.972 |
| R2 | 0.986 | 0.681 | 0.931 | 0.986 | 0.614 | 0.920 |
| F1-score | 0.873 | 0.843 | 0.863 | 0.872 | 0.801 | 0.852 |
| AUC-ROC | 0.968 | 0.957 | 0.968 | 0.967 | 0.950 | 0.959 |
Table 8.
Performance of various ML algorithms for the prediction of the Health Index.
Table 8.
Performance of various ML algorithms for the prediction of the Health Index.
| Algorithm | AUC | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest (n = 50) | 0.9767 | 0.8623 | 0.8615 | 0.8623 | 0.8594 |
| Random Forest (n = 200) | 0.9778 | 0.8675 | 0.8646 | 0.8675 | 0.8643 |
| Random Forest (n = 500) | 0.9784 | 0.8701 | 0.8675 | 0.8701 | 0.8669 |
| Random Forest (Grid Search) | 0.9784 | 0.8701 | 0.8676 | 0.8701 | 0.8672 |
| Neural Network (100), iter = 1000 | 0.9804 | 0.8623 | 0.8597 | 0.8623 | 0.8597 |
| Neural Network (100,100), iter = 1000 | 0.9719 | 0.8532 | 0.8554 | 0.8532 | 0.8486 |
| Neural Network (100,100,100), iter = 1000 | 0.9787 | 0.8740 | 0.8706 | 0.8740 | 0.8704 |
| Neural Network (Grid Search) | 0.9787 | 0.8545 | 0.8509 | 0.8545 | 0.8505 |
| Support Vector Machine | 0.9685 | 0.8195 | 0.8027 | 0.8195 | 0.8092 |
| Naïve Bayes | 0.7714 | 0.6026 | 0.6041 | 0.6026 | 0.5857 |
Table 9.
Cross-validation results for the (5-Fold) original dataset.
Table 9.
Cross-validation results for the (5-Fold) original dataset.
| Algorithms | | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest optimized | Mean | 0.8646 | 0.8648 | 0.8646 | 0.8616 |
| | Std Dev | 0.0035 | 0.0039 | 0.0035 | 0.0033 |
| Neural Network optimized | Mean | 0.8636 | 0.8627 | 0.8636 | 0.8620 |
| | Std Dev | 0.0069 | 0.0073 | 0.0069 | 0.0074 |
| Support Vector Machine | Mean | 0.8013 | 0.7906 | 0.8013 | 0.7915 |
| | Std Dev | 0.0163 | 0.0198 | 0.0163 | 0.0171 |
| Naïve Bayes | Mean | 0.6068 | 0.6100 | 0.6068 | 0.5939 |
| | Std Dev | 0.0121 | 0.0095 | 0.0121 | 0.0129 |
| 1D-CNN | Mean | 0.8521 | 0.8533 | 0.8521 | 0.8527 |
| | Std Dev | 0.0071 | 0.0079 | 0.0071 | 0.0075 |
| LSTM | Mean | 0.8641 | 0.8627 | 0.8641 | 0.8634 |
| | Std Dev | 0.0046 | 0.0053 | 0.0046 | 0.0049 |
Table 10.
Confusion matrix of Random Forest.
Table 10.
Confusion matrix of Random Forest.
| | | Prediction |
|---|
| | | Random Forest 1 | Random Forest 2 | Random Forest 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 3.0% | 89.4% | 5.1% | 2.5% | 0.0% | 3.0% | 89.8% | 5.1% | 2.1% | 0.0% | 2.5% | 90.3% | 5.5% | 1.7% | 0.0% |
| C | 0.0% | 12.8% | 74.5% | 12.2% | 0.5% | 0.0% | 12.2% | 77.1% | 10.1% | 0.5% | 0.0% | 11.7% | 76.6% | 11.2% | 0.5% |
| P | 0.0% | 2.5% | 12.4% | 85.1% | 0.0% | 0.0% | 2.5% | 12.4% | 84.5% | 0.6% | 0.0% | 2.5% | 11.2% | 85.7% | 0.6% |
| VP | 0.0% | 0.0% | 0.0% | 64.3% | 35.7% | 0.0% | 0.0% | 0.0% | 71.4% | 28.6% | 0.0% | 0.0% | 0.0% | 71.4% | 28.6% |
Table 11.
Confusion matrix of Neural Network.
Table 11.
Confusion matrix of Neural Network.
| | | Prediction |
|---|
| | | Neural Network 1 | Neural Network 2 | Neural Network 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 98.8% | 1.2% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 2.5% | 90.3% | 5.9% | 1.3% | 0.0% | 3.4% | 88.1% | 7.2% | 1.3% | 0.0% | 3.0% | 89.4% | 6.4% | 1.3% | 0.0% |
| C | 0.0% | 9.0% | 75.5% | 14.9% | 0.5% | 0.0% | 12.2% | 73.4% | 14.4% | 0.0% | 0.0% | 10.1% | 79.8% | 10.1% | 0.0% |
| P | 0.0% | 2.5% | 13.0% | 83.2% | 1.2% | 0.6% | 3.7% | 9.3% | 86.3% | 0.0% | 0.0% | 1.9% | 11.2% | 85.7% | 1.2% |
| VP | 0.0% | 0.0% | 7.1% | 64.3% | 28.6% | 0.0% | 0.0% | 0.0% | 78.6% | 21.4% | 0.0% | 0.0% | 7.1% | 71.4% | 21.4% |
Table 12.
Confusion matrix of RF and NN with Grid Search optimization.
Table 12.
Confusion matrix of RF and NN with Grid Search optimization.
| | | Prediction |
|---|
| | | Random Forest Optimized | Neural Network Optimized |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 98.8% | 1.2% | 0.0% | 0.0% | 0.0% |
| G | 2.5% | 89.4% | 6.4% | 1.7% | 0.0% | 3.4% | 89.0% | 6.4% | 1.3% | 0.0% |
| C | 0.0% | 11.2% | 78.2% | 10.1% | 0.5% | 0.0% | 11.7% | 75.0% | 12.8% | 0.5% |
| P | 0.0% | 1.9% | 12.4% | 85.1% | 0.6% | 0.6% | 3.1% | 11.8% | 83.9% | 0.6% |
| VP | 0.0% | 0.0% | 0.0% | 71.4% | 28.6% | 0.0% | 0.0% | 0.0% | 78.6% | 21.4% |
Table 13.
Confusion matrix of SVM and NB.
Table 13.
Confusion matrix of SVM and NB.
| | | Prediction |
|---|
| | | SVM | NB |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 3.0% | 89.8% | 7.2% | 0.0% | 0.0% | 15.3% | 67.8% | 10.2% | 5.5% | 1.3% |
| C | 0.0% | 16.0% | 72.9% | 11.2% | 0.0% | 0.0% | 41.5% | 36.7% | 17.0% | 4.8% |
| P | 1.2% | 16.1% | 13.7% | 68.9% | 0.0% | 0.0% | 47.8% | 11.8% | 35.4% | 5.0% |
| VP | 0.0% | 7.1% | 14.3% | 78.6% | 0.0% | 0.0% | 7.1% | 0.0% | 42.9% | 50.0% |
Table 14.
Performance of ML + RUS.
Table 14.
Performance of ML + RUS.
| Algorithm + RUS | AUC | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest (n = 50) | 0.9492 | 0.7681 | 0.7681 | 0.7681 | 0.7651 |
| Random Forest (n = 200) | 0.9499 | 0.7536 | 0.7672 | 0.7536 | 0.7519 |
| Random Forest (n = 500) | 0.9402 | 0.7536 | 0.7672 | 0.7536 | 0.7519 |
| Random Forest (Grid Search) | 0.9402 | 0.7826 | 0.7929 | 0.7826 | 0.7795 |
| Neural Network (100), iter = 1000 | 0.9602 | 0.7391 | 0.7510 | 0.7391 | 0.7349 |
| Neural Network (100,100), iter = 1000 | 0.9602 | 0.7826 | 0.7905 | 0.7826 | 0.7743 |
| Neural Network (100,100,100), iter = 1000 | 0.9615 | 0.7536 | 0.7539 | 0.7536 | 0.7455 |
| Neural Network (Grid Search) | 0.9615 | 0.7681 | 0.7691 | 0.7681 | 0.7643 |
| Support Vector Machine | 0.9423 | 0.7101 | 0.6934 | 0.7101 | 0.6930 |
| Naïve Bayes | 0.7624 | 0.6232 | 0.6116 | 0.6232 | 0.6146 |
Table 15.
Cross-validation results (5-Fold).
Table 15.
Cross-validation results (5-Fold).
| Algorithms | | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest optimized | Mean | 0.6809 | 0.6881 | 0.6809 | 0.6667 |
| | Std Dev | 0.0390 | 0.0389 | 0.0390 | 0.0397 |
| Neural Network optimized | Mean | 0.7395 | 0.7437 | 0.7395 | 0.7320 |
| | Std Dev | 0.0652 | 0.0719 | 0.0652 | 0.0741 |
| Support Vector Machine | Mean | 0.6851 | 0.6835 | 0.6851 | 0.6664 |
| | Std Dev | 0.0458 | 0.0635 | 0.0458 | 0.0488 |
| Naïve Bayes | Mean | 0.6703 | 0.6778 | 0.6703 | 0.6618 |
| | Std Dev | 0.0467 | 0.0500 | 0.0467 | 0.0482 |
Table 16.
Confusion matrix of Random Forest + RUS.
Table 16.
Confusion matrix of Random Forest + RUS.
| | | Prediction |
|---|
| | | Random Forest 1 | Random Forest 2 | Random Forest 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 7.7% | 76.9% | 7.7% | 7.7% | 0.0% | 15.4% | 69.2% | 7.7% | 7.7% | 0.0% | 15.4% | 69.2% | 7.7% | 7.7% | 0.0% |
| C | 0.0% | 7.1% | 57.1% | 21.4% | 14.3% | 0.0% | 0.0% | 57.1% | 28.6% | 14.3% | 0.0% | 0.0% | 57.1% | 28.6% | 14.3% |
| P | 7.1% | 0.0% | 21.4% | 64.3% | 7.1% | 7.1% | 0.0% | 21.4% | 64.3% | 7.1% | 7.1% | 0.0% | 21.4% | 64.3% | 7.1% |
| VP | 0.0% | 0.0% | 0.0% | 14.3% | 85.7% | 0.0% | 0.0% | 0.0% | 14.3% | 85.7% | 0.0% | 0.0% | 0.0% | 14.3% | 85.7% |
Table 17.
Confusion matrix of Neural Network + RUS.
Table 17.
Confusion matrix of Neural Network + RUS.
| | | Prediction |
|---|
| | | Neural Network 1 | Neural Network 2 | Neural Network 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 15.4% | 69.2% | 7.7% | 0.0% | 7.7% | 7.7% | 84.6% | 0.0% | 0.0% | 7.7% | 15.4% | 76.9% | 0.0% | 0.0% | 7.7% |
| C | 0.0% | 14.3% | 50.0% | 35.7% | 0.0% | 0.0% | 21.4% | 50.0% | 21.4% | 7.1% | 0.0% | 21.4% | 50.0% | 28.6% | 0.0% |
| P | 0.0% | 0.0% | 7.1% | 71.4% | 21.4% | 7.1% | 0.0% | 7.1% | 71.4% | 14.3% | 7.1% | 0.0% | 14.3% | 64.3% | 14.3% |
| VP | 0.0% | 0.0% | 0.0% | 21.4% | 78.6% | 0.0% | 0.0% | 0.0% | 14.3% | 85.7% | 0.0% | 0.0% | 0.0% | 14.3% | 85.7% |
Table 18.
Confusion matrix of RF and NN with Grid Search optimization + RUS.
Table 18.
Confusion matrix of RF and NN with Grid Search optimization + RUS.
| | | Prediction |
|---|
| | | Random Forest Optimized | Neural Network Optimized |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 15.4% | 69.2% | 7.7% | 7.7% | 0.0% | 7.7% | 92.3% | 0.0% | 0.0% | 0.0% |
| C | 0.0% | 0.0% | 57.1% | 28.6% | 14.3% | 0.0% | 7.1% | 50.0% | 42.9% | 0.0% |
| P | 0.0% | 0.0% | 21.4% | 71.4% | 7.1% | 0.0% | 0.0% | 21.4% | 57.1% | 21.4% |
| VP | 0.0% | 0.0% | 0.0% | 7.1% | 92.9% | 0.0% | 0.0% | 0.0% | 14.3% | 85.7% |
Table 19.
Confusion matrix of (SVM and Naïve Bayes) + RUS.
Table 19.
Confusion matrix of (SVM and Naïve Bayes) + RUS.
| | | Prediction |
|---|
| | | SVM | NB |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 15.4% | 69.2% | 7.7% | 0.0% | 7.7% | 23.1% | 61.5% | 15.4% | 0.0% | 0.0% |
| C | 7.1% | 14.3% | 57.1% | 21.4% | 0.0% | 0.0% | 14.3% | 50.0% | 28.6% | 7.1% |
| P | 14.3% | 14.3% | 28.6% | 35.7% | 7.1% | 0.0% | 21.4% | 21.4% | 35.7% | 21.4% |
| VP | 0.0% | 0.0% | 0.0% | 7.1% | 92.9% | 0.0% | 7.1% | 0.0% | 28.6% | 64.3% |
Table 20.
Performance of ML + SMOTE.
Table 20.
Performance of ML + SMOTE.
| Algorithm + SMOTE | AUC | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest (n = 50) | 0.9731 | 0.8831 | 0.8819 | 0.8831 | 0.8821 |
| Random Forest (n = 200) | 0.9736 | 0.8890 | 0.8879 | 0.8890 | 0.8881 |
| Random Forest (n = 500) | 0.9736 | 0.8864 | 0.8852 | 0.8864 | 0.8855 |
| Neural Network (100), iter = 1000 | 0.9717 | 0.8847 | 0.8840 | 0.8847 | 0.8842 |
| Neural Network (100,100), iter = 1000 | 0.9726 | 0.8814 | 0.8803 | 0.8814 | 0.8807 |
| Neural Network (100,100,100), iter = 1000 | 0.9743 | 0.8814 | 0.8800 | 0.8814 | 0.8805 |
| Support Vector Machine | 0.9699 | 0.8610 | 0.8604 | 0.8610 | 0.8582 |
| Naïve Bayes | 0.7833 | 0.6475 | 0.6431 | 0.6475 | 0.6252 |
Table 21.
Cross-validation results (5-Fold) SMOTE dataset.
Table 21.
Cross-validation results (5-Fold) SMOTE dataset.
| Algorithms | | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest optimized | Mean | 0.8919 | 0.8912 | 0.8919 | 0.8908 |
| | Std Dev | 0.0045 | 0.0042 | 0.0045 | 0.0048 |
| Neural Network optimized | Mean | 0.8856 | 0.8846 | 0.8856 | 0.8846 |
| | Std Dev | 0.0091 | 0.0095 | 0.0091 | 0.0092 |
| Support Vector Machine | Mean | 0.8540 | 0.8529 | 0.8540 | 0.8512 |
| | Std Dev | 0.0060 | 0.0065 | 0.0060 | 0.0063 |
| Naïve Bayes | Mean | 0.6415 | 0.6372 | 0.6415 | 0.6204 |
| | Std Dev | 0.0121 | 0.0130 | 0.0121 | 0.0144 |
Table 22.
Confusion matrix of Random Forest + SMOTE.
Table 22.
Confusion matrix of Random Forest + SMOTE.
| | | Prediction |
|---|
| | | Random Forest 1 | Random Forest 2 | Random Forest 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% |
| G | 3.0% | 85.6% | 5.9% | 3.8% | 1.7% | 2.5% | 85.2% | 6.4% | 4.2% | 1.7% | 3.0% | 83.5% | 8.1% | 3.8% | 1.7% |
| C | 0.0% | 8.5% | 80.5% | 7.6% | 3.4% | 0.0% | 8.1% | 82.2% | 6.8% | 3.0% | 0.0% | 8.1% | 81.8% | 6.8% | 3.4% |
| P | 0.8% | 7.6% | 7.2% | 80.9% | 3.4% | 0.8% | 6.8% | 6.4% | 81.8% | 4.2% | 0.8% | 6.8% | 5.5% | 82.6% | 4.2% |
| VP | 0.0% | 0.8% | 1.3% | 3.0% | 94.9% | 0.0% | 0.8% | 1.3% | 2.1% | 95.8% | 0.0% | 0.8% | 1.3% | 2.1% | 95.8% |
Table 23.
Confusion matrix of Neural Network + SMOTE.
Table 23.
Confusion matrix of Neural Network + SMOTE.
| | | Prediction |
|---|
| | | Neural Network 1 | Neural Network 2 | Neural Network 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% | 99.2% | 0.4% | 0.0% | 0.4% | 0.0% | 98.7% | 0.4% | 0.0% | 0.8% | 0.0% |
| G | 2.5% | 85.2% | 8.5% | 2.5% | 1.3% | 2.5% | 85.6% | 6.4% | 4.7% | 0.8% | 2.1% | 84.7% | 8.9% | 3.8% | 0.4% |
| C | 0.0% | 6.4% | 81.4% | 8.5% | 3.8% | 0.4% | 6.8% | 79.7% | 8.9% | 4.2% | 0.0% | 7.6% | 78.8% | 8.9% | 4.7% |
| P | 0.8% | 5.5% | 10.6% | 81.4% | 1.7% | 0.8% | 4.2% | 10.6% | 81.4% | 3.0% | 0.8% | 4.7% | 9.7% | 81.8% | 3.0% |
| VP | 0.0% | 1.3% | 1.3% | 2.5% | 94.9% | 0.0% | 0.8% | 3.0% | 1.3% | 94.9% | 0.0% | 1.3% | 0.0% | 2.1% | 96.6% |
Table 24.
Confusion matrix of RF and NN with Grid Search optimization + SMOTE.
Table 24.
Confusion matrix of RF and NN with Grid Search optimization + SMOTE.
| | | Prediction |
|---|
| | | Random Forest Optimized | Neural Network Optimized |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 99.2% | 0.8% | 0.0% | 0.0% | 0.0% | 99.2% | 0.0% | 0.0% | 0.8% | 0.0% |
| G | 3.0% | 86.0% | 5.9% | 3.4% | 1.7% | 3.0% | 82.6% | 9.7% | 3.8% | 0.8% |
| C | 0.0% | 7.2% | 81.8% | 7.6% | 3.4% | 0.4% | 4.7% | 80.9% | 10.2% | 3.8% |
| P | 0.8% | 6.8% | 6.4% | 81.8% | 4.2% | 0.8% | 4.7% | 9.3% | 82.2% | 3.0% |
| VP | 0.0% | 0.8% | 1.3% | 2.1% | 95.8% | 0.0% | 2.1% | 3.4% | 1.7% | 92.8% |
Table 25.
Confusion matrix of (SVM and Naïve Bayes) + SMOTE.
Table 25.
Confusion matrix of (SVM and Naïve Bayes) + SMOTE.
| | | Prediction |
|---|
| | | SVM | NB |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 4.2% | 82.6% | 7.2% | 2.1% | 3.8% | 15.7% | 60.2% | 11.4% | 4.7% | 8.1% |
| C | 0.8% | 8.5% | 74.6% | 8.1% | 8.1% | 0.0% | 33.1% | 41.9% | 14.4% | 10.6% |
| P | 0.8% | 6.4% | 10.2% | 75.4% | 7.2% | 2.5% | 41.1% | 9.3% | 28.8% | 18.2% |
| VP | 0.0% | 0.8% | 0.0% | 0.8% | 98.3% | 0.0% | 2.1% | 0.0% | 5.1% | 92.8% |
Table 26.
Performance of ML + Borderline-SMOTE.
Table 26.
Performance of ML + Borderline-SMOTE.
| Algorithm + Borderline-SMOTE | AUC | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest (n = 50) | 0.9699 | 0.8890 | 0.8873 | 0.8890 | 0.8879 |
| Random Forest (n = 200) | 0.9720 | 0.8898 | 0.8883 | 0.8898 | 0.8888 |
| Random Forest (n = 500) | 0.9721 | 0.8941 | 0.8926 | 0.8941 | 0.8932 |
| Random Forest (Grid Search) | 0.9721 | 0.8924 | 0.8909 | 0.8924 | 0.8915 |
| Neural Network (100), iter = 1000 | 0.9747 | 0.8746 | 0.8721 | 0.8746 | 0.8728 |
| Neural Network (100,100), iter = 1000 | 0.9678 | 0.8864 | 0.8851 | 0.8864 | 0.8851 |
| Neural Network (100,100,100), iter = 1000 | 0.9738 | 0.8737 | 0.8714 | 0.8737 | 0.8719 |
| Neural Network (Grid Search) | 0.9738 | 0.8873 | 0.8862 | 0.8873 | 0.8860 |
| Support Vector Machine | 0.9702 | 0.8542 | 0.8509 | 0.8542 | 0.8509 |
| Naïve Bayes | 0.7587 | 0.6407 | 0.6327 | 0.6407 | 0.6147 |
Table 27.
Cross-validation results (5-Fold) Borderline-SMOTE dataset.
Table 27.
Cross-validation results (5-Fold) Borderline-SMOTE dataset.
| Algorithms | | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest optimized | Mean | 0.8922 | 0.8918 | 0.8922 | 0.8914 |
| | Std Dev | 0.0107 | 0.0104 | 0.0107 | 0.0108 |
| Neural Network optimized | Mean | 0.8852 | 0.8847 | 0.8852 | 0.8844 |
| | Std Dev | 0.0101 | 0.0101 | 0.0101 | 0.0103 |
| Support Vector Machine | Mean | 0.8544 | 0.8519 | 0.8544 | 0.8514 |
| | Std Dev | 0.0026 | 0.0029 | 0.0026 | 0.0026 |
| Naïve Bayes | Mean | 0.6307 | 0.6207 | 0.6307 | 0.6027 |
| | Std Dev | 0.0078 | 0.0084 | 0.0078 | 0.0064 |
Table 28.
Confusion matrix of Random Forest + Borderline-SMOTE.
Table 28.
Confusion matrix of Random Forest + Borderline-SMOTE.
| | | Prediction |
|---|
| | | Random Forest 1 | Random Forest 2 | Random Forest 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% |
| G | 3.8% | 83.9% | 6.8% | 5.5% | 0.0% | 3.0% | 83.9% | 7.6% | 5.5% | 0.0% | 3.0% | 83.1% | 8.5% | 5.5% | 0.0% |
| C | 0.0% | 8.5% | 80.5% | 7.6% | 3.4% | 0.0% | 9.7% | 78.8% | 8.9% | 2.5% | 0.0% | 9.3% | 80.9% | 7.2% | 2.5% |
| P | 0.8% | 6.4% | 7.6% | 82.6% | 2.5% | 0.8% | 5.9% | 6.8% | 84.3% | 2.1% | 0.8% | 5.5% | 6.4% | 85.2% | 2.1% |
| VP | 0.0% | 0.0% | 0.8% | 1.3% | 97.9% | 0.0% | 0.0% | 0.4% | 1.3% | 98.3% | 0.0% | 0.0% | 0.4% | 1.3% | 98.3% |
Table 29.
Confusion matrix of Neural Network + Borderline-SMOTE.
Table 29.
Confusion matrix of Neural Network + Borderline-SMOTE.
| | | Prediction |
|---|
| | | Neural Network 1 | Neural Network 2 | Neural Network 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 99.6% | 0.0% | 0.0% | 0.4% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 2.1% | 84.7% | 8.5% | 3.8% | 0.8% | 2.1% | 86.9% | 6.4% | 4.7% | 0.0% | 3.4% | 83.9% | 7.6% | 4.7% | 0.4% |
| C | 0.4% | 11.0% | 72.9% | 11.4% | 4.2% | 0.0% | 11.0% | 76.3% | 8.9% | 3.8% | 0.0% | 11.4% | 72.5% | 11.9% | 4.2% |
| P | 0.8% | 5.1% | 8.9% | 82.2% | 3.0% | 0.8% | 5.9% | 6.4% | 83.1% | 3.8% | 0.8% | 5.9% | 7.2% | 83.5% | 2.5% |
| VP | 0.0% | 0.4% | 0.8% | 1.3% | 97.5% | 0.0% | 0.0% | 0.8% | 1.7% | 97.5% | 0.0% | 0.0% | 1.7% | 1.3% | 97.0% |
Table 30.
Confusion matrix of RF and NN with Grid Search optimization + Borderline-SMOTE.
Table 30.
Confusion matrix of RF and NN with Grid Search optimization + Borderline-SMOTE.
| | | Prediction |
|---|
| | | Random Forest Optimized | Neural Network Optimized |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 99.6% | 0.4% | 0.0% | 0.0% | 0.0% | 99.2% | 0.0% | 0.0% | 0.8% | 0.0% |
| G | 3.0% | 83.9% | 7.6% | 5.5% | 0.0% | 1.7% | 86.9% | 6.8% | 4.7% | 0.0% |
| C | 0.0% | 8.9% | 80.5% | 8.1% | 2.5% | 0.4% | 9.7% | 75.4% | 11.0% | 3.4% |
| P | 0.8% | 5.5% | 7.6% | 83.9% | 2.1% | 0.4% | 5.5% | 6.4% | 84.3% | 3.4% |
| VP | 0.0% | 0.0% | 0.4% | 1.3% | 98.3% | 0.0% | 0.0% | 0.4% | 1.7% | 97.9% |
Table 31.
Confusion matrix of (SVM and Naïve Bayes) + Borderline-SMOTE.
Table 31.
Confusion matrix of (SVM and Naïve Bayes) + Borderline-SMOTE.
| | | Prediction |
|---|
| | | SVM | NB |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 5.1% | 81.4% | 9.7% | 2.1% | 1.7% | 19.1% | 59.7% | 11.4% | 3.4% | 6.4% |
| C | 1.3% | 10.6% | 69.5% | 10.6% | 8.1% | 0.0% | 31.4% | 40.7% | 14.4% | 13.6% |
| P | 1.3% | 4.2% | 11.4% | 78.0% | 5.1% | 3.0% | 43.2% | 11.4% | 26.3% | 16.1% |
| VP | 0.0% | 0.0% | 0.0% | 1.7% | 98.3% | 0.0% | 2.1% | 0.0% | 4.2% | 93.6% |
Table 32.
Performance of ML + SMOTE-Tomek.
Table 32.
Performance of ML + SMOTE-Tomek.
| Algorithm + SMOTE-Tomek | AUC | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest (n = 50) | 0.9815 | 0.9134 | 0.9136 | 0.9134 | 0.9126 |
| Random Forest (n = 200) | 0.9811 | 0.9108 | 0.9108 | 0.9108 | 0.9100 |
| Random Forest (n = 500) | 0.9808 | 0.9082 | 0.9081 | 0.9082 | 0.9073 |
| Random Forest (Grid Search) | 0.9811 | 0.9108 | 0.9108 | 0.9108 | 0.9100 |
| Neural Network (100), iter = 1000 | 0.9820 | 0.8970 | 0.8978 | 0.8970 | 0.8955 |
| Neural Network (100,100), iter = 1000 | 0.9867 | 0.9030 | 0.9021 | 0.9030 | 0.9021 |
| Neural Network (100,100,100), iter = 1000 | 0.9790 | 0.8970 | 0.8958 | 0.8970 | 0.8958 |
| Neural Network (Grid Search) | 0.9867 | 0.9065 | 0.9061 | 0.9065 | 0.9060 |
| Support Vector Machine | 0.9770 | 0.8857 | 0.8868 | 0.8857 | 0.8839 |
| Naïve Bayes | 0.7718 | 0.6528 | 0.6545 | 0.6528 | 0.6298 |
Table 33.
Cross-validation results for the (5-Fold) SMOTE-Tomek dataset.
Table 33.
Cross-validation results for the (5-Fold) SMOTE-Tomek dataset.
| Algorithms | | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest optimized | Mean | 0.8974 | 0.8965 | 0.8974 | 0.8963 |
| | Std Dev | 0.0121 | 0.0120 | 0.0121 | 0.0123 |
| Neural Network optimized | Mean | 0.8954 | 0.8946 | 0.8954 | 0.8944 |
| | Std Dev | 0.0111 | 0.0113 | 0.0111 | 0.0111 |
| Support Vector Machine | Mean | 0.8580 | 0.8570 | 0.8580 | 0.8553 |
| | Std Dev | 0.0103 | 0.0110 | 0.0103 | 0.0105 |
| Naïve Bayes | Mean | 0.6478 | 0.6445 | 0.6478 | 0.6261 |
| | Std Dev | 0.0074 | 0.0112 | 0.0074 | 0.0089 |
Table 34.
Confusion matrix of Random Forest + SMOTE-Tomek.
Table 34.
Confusion matrix of Random Forest + SMOTE-Tomek.
| | | Prediction |
|---|
| | | Random Forest 1 | Random Forest 2 | Random Forest 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 98.7% | 0.4% | 0.0% | 0.8% | 0.0% | 98.7% | 0.4% | 0.0% | 0.8% | 0.0% | 98.7% | 0.4% | 0.0% | 0.8% | 0.0% |
| G | 1.3% | 88.2% | 4.4% | 3.1% | 3.1% | 1.7% | 87.8% | 4.8% | 2.6% | 3.1% | 2.2% | 87.8% | 4.4% | 2.6% | 3.1% |
| C | 0.4% | 5.7% | 81.1% | 7.9% | 4.8% | 0.4% | 5.3% | 80.6% | 9.3% | 4.4% | 0.4% | 5.3% | 80.6% | 8.8% | 4.8% |
| P | 0.0% | 2.2% | 3.9% | 90.8% | 3.1% | 0.0% | 3.1% | 3.9% | 90.4% | 2.6% | 0.0% | 3.9% | 4.4% | 89.0% | 2.6% |
| VP | 0.0% | 1.7% | 0.0% | 0.9% | 97.4% | 0.0% | 1.7% | 0.0% | 0.9% | 97.4% | 0.0% | 1.7% | 0.0% | 0.9% | 97.4% |
Table 35.
Confusion matrix of Neural Network + SMOTE-Tomek.
Table 35.
Confusion matrix of Neural Network + SMOTE-Tomek.
| | | Prediction |
|---|
| | | Neural Network 1 | Neural Network 2 | Neural Network 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 98.7% | 0.8% | 0.0% | 0.4% | 0.0% | 98.7% | 0.4% | 0.0% | 0.8% | 0.0% | 99.2% | 0.4% | 0.0% | 0.4% | 0.0% |
| G | 0.9% | 90.8% | 2.6% | 3.5% | 2.2% | 0.9% | 87.8% | 7.9% | 2.6% | 0.9% | 1.3% | 89.5% | 3.9% | 3.9% | 1.3% |
| C | 0.4% | 9.3% | 74.9% | 9.7% | 5.7% | 0.4% | 6.2% | 77.5% | 10.6% | 5.3% | 0.4% | 9.7% | 77.1% | 7.9% | 4.8% |
| P | 0.0% | 3.5% | 5.7% | 86.4% | 4.4% | 0.0% | 3.1% | 5.7% | 89.0% | 2.2% | 0.0% | 2.6% | 9.6% | 84.6% | 3.1% |
| VP | 0.0% | 2.1% | 0.0% | 0.9% | 97.0% | 0.0% | 0.9% | 0.9% | 0.4% | 97.9% | 0.0% | 1.3% | 0.4% | 0.9% | 97.4% |
Table 36.
Confusion matrix of RF and NN with Grid Search optimization + SMOTE-Tomek.
Table 36.
Confusion matrix of RF and NN with Grid Search optimization + SMOTE-Tomek.
| | | Prediction |
|---|
| | | Random Forest Optimized | Neural Network Optimized |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 98.7% | 0.4% | 0.0% | 0.8% | 0.0% | 98.7% | 0.4% | 0.0% | 0.8% | 0.0% |
| G | 1.7% | 87.8% | 4.8% | 2.6% | 3.1% | 0.9% | 88.2% | 8.3% | 1.7% | 0.9% |
| C | 0.4% | 5.3% | 80.6% | 9.3% | 4.4% | 0.4% | 5.7% | 78.0% | 10.6% | 5.3% |
| P | 0.0% | 3.1% | 3.9% | 90.4% | 2.6% | 0.0% | 3.1% | 7.5% | 88.2% | 1.3% |
| VP | 0.0% | 1.7% | 0.0% | 0.9% | 97.4% | 0.0% | 0.9% | 0.9% | 0.4% | 97.9% |
Table 37.
Confusion matrix of (SVM and Naïve Bayes) + SMOTE-Tomek.
Table 37.
Confusion matrix of (SVM and Naïve Bayes) + SMOTE-Tomek.
| | | Prediction |
|---|
| | | SVM | NB |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 3.1% | 84.3% | 4.8% | 1.7% | 6.1% | 16.6% | 61.6% | 11.4% | 2.6% | 7.9% |
| C | 0.4% | 6.2% | 77.1% | 9.7% | 6.6% | 0.4% | 36.1% | 41.4% | 12.3% | 9.7% |
| P | 0.9% | 2.6% | 6.6% | 82.0% | 7.9% | 0.9% | 40.4% | 7.9% | 28.5% | 22.4% |
| VP | 0.0% | 0.4% | 0.0% | 0.9% | 98.7% | 0.0% | 2.1% | 0.0% | 5.1% | 92.8% |
Table 38.
Performance of ML + SMOTE-ENN.
Table 38.
Performance of ML + SMOTE-ENN.
| Algorithm + SMOTE-ENN | AUC | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest (n = 50) | 0.9988 | 0.9834 | 0.9834 | 0.9834 | 0.9833 |
| Random Forest (n = 200) | 0.9993 | 0.9822 | 0.9823 | 0.9822 | 0.9822 |
| Random Forest (n = 500) | 0.9992 | 0.9822 | 0.9823 | 0.9822 | 0.9822 |
| Random Forest (Grid Search) | 0.9992 | 0.9822 | 0.9823 | 0.9822 | 0.9822 |
| Neural Network (100), iter = 1000 | 0.9940 | 0.9751 | 0.9752 | 0.9751 | 0.9750 |
| Neural Network (100,100), iter = 1000 | 0.9941 | 0.9763 | 0.9762 | 0.9763 | 0.9761 |
| Neural Network (100,100,100), iter = 1000 | 0.9961 | 0.9763 | 0.9763 | 0.9763 | 0.9761 |
| Neural Network (Grid Search) | 0.9961 | 0.9786 | 0.9787 | 0.9786 | 0.9785 |
| Support Vector Machine | 0.9926 | 0.9537 | 0.9542 | 0.9537 | 0.9534 |
| Naïve Bayes | 0.8927 | 0.7295 | 0.7282 | 0.7295 | 0.7113 |
Table 39.
Cross-validation results for the (5-Fold) SMOTE-ENN dataset.
Table 39.
Cross-validation results for the (5-Fold) SMOTE-ENN dataset.
| Algorithms | | Classification Accuracy | Precision | Recall | F1-Score |
|---|
| Random Forest optimized | Mean | 0.9831 | 0.9832 | 0.9831 | 0.9830 |
| | Std Dev | 0.0055 | 0.0054 | 0.0055 | 0.0056 |
| Neural Network optimized | Mean | 0.9855 | 0.9856 | 0.9855 | 0.9854 |
| | Std Dev | 0.0046 | 0.0046 | 0.0046 | 0.0047 |
| Support Vector Machine | Mean | 0.9656 | 0.9663 | 0.9656 | 0.9652 |
| | Std Dev | 0.0094 | 0.0090 | 0.0094 | 0.0096 |
| Naïve Bayes | Mean | 0.7429 | 0.7503 | 0.7429 | 0.7302 |
| | Std Dev | 0.0129 | 0.0190 | 0.0129 | 0.0140 |
Table 40.
Confusion matrix of Random Forest + SMOTE-ENN.
Table 40.
Confusion matrix of Random Forest + SMOTE-ENN.
| | | Prediction |
|---|
| | | Random Forest 1 | Random Forest 2 | Random Forest 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 0.0% | 98.7% | 0.0% | 0.0% | 1.3% | 0.0% | 98.0% | 0.0% | 0.0% | 2.0% | 0.0% | 98.0% | 0.0% | 0.0% | 2.0% |
| C | 0.0% | 0.8% | 95.4% | 1.5% | 2.3% | 0.0% | 0.0% | 96.2% | 2.3% | 1.5% | 0.0% | 0.0% | 96.2% | 2.3% | 1.5% |
| P | 0.8% | 0.0% | 3.9% | 95.3% | 0.0% | 0.8% | 0.0% | 4.7% | 94.5% | 0.0% | 0.8% | 0.0% | 4.7% | 94.5% | 0.0% |
| VP | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% |
Table 41.
Confusion matrix of Neural Network + SMOTE-ENN.
Table 41.
Confusion matrix of Neural Network + SMOTE-ENN.
| | | Prediction |
|---|
| | | Neural Network 1 | Neural Network 2 | Neural Network 3 |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 0.0% | 98.0% | 0.7% | 0.0% | 1.3% | 0.0% | 98.0% | 0.7% | 0.0% | 1.3% | 0.0% | 98.7% | 0.0% | 0.0% | 1.3% |
| C | 0.0% | 0.0% | 91.6% | 4.6% | 3.8% | 0.0% | 0.8% | 91.6% | 5.3% | 2.3% | 0.0% | 0.0% | 92.4% | 4.6% | 3.1% |
| P | 0.0% | 0.0% | 3.9% | 94.5% | 1.6% | 0.0% | 0.0% | 3.9% | 95.3% | 0.8% | 0.0% | 0.0% | 4.7% | 93.7% | 1.6% |
| VP | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% |
Table 42.
Confusion matrix of RF and NN with Grid Search optimization + SMOTE-ENN.
Table 42.
Confusion matrix of RF and NN with Grid Search optimization + SMOTE-ENN.
| | | Prediction |
|---|
| | | Random Forest Optimized | Neural Network Optimized |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 0.0% | 98.0% | 0.0% | 0.0% | 2.0% | 0.0% | 98.0% | 0.7% | 0.0% | 1.3% |
| C | 0.0% | 0.0% | 96.2% | 2.3% | 1.5% | 0.0% | 0.8% | 93.1% | 3.8% | 2.3% |
| P | 0.8% | 0.0% | 4.7% | 94.5% | 0.0% | 0.0% | 0.0% | 3.1% | 95.3% | 1.6% |
| VP | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% |
Table 43.
Confusion matrix of (SVM and Naïve Bayes) + SMOTE-ENN.
Table 43.
Confusion matrix of (SVM and Naïve Bayes) + SMOTE-ENN.
| | | Prediction |
|---|
| | | Random Forest Optimized | Neural Network Optimized |
|---|
| | | VG | G | C | P | VP | VG | G | C | P | VP |
|---|
| Actual | VG | 100% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% | 0.0% | 0.0% |
| G | 1.3% | 91.5% | 3.9% | 0.7% | 2.6% | 9.8% | 77.1% | 8.5% | 1.3% | 3.3% |
| C | 0.0% | 1.5% | 90.8% | 5.3% | 2.3% | 0.0% | 42.0% | 38.2% | 16.8% | 3.1% |
| P | 0.8% | 0.0% | 4.7% | 89.0% | 5.5% | 0.0% | 40.2% | 7.9% | 28.3% | 23.6% |
| VP | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 5.2% | 0.0% | 4.7% | 90.1% |
Table 44.
Validation model RF and NN using ten actual transformer data.
Table 44.
Validation model RF and NN using ten actual transformer data.
| TRF | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| BDV | 90 | 83.6 | 91.4 | 97.9 | 93.6 | 90 | 93.5 | 91 | 49.1 | 29.6 |
| Water | 7 | 8.9 | 20.35 | 16.71 | 14.59 | 10.18 | 14.9 | 9.54 | 34.97 | 19.1 |
| Acid | 0.005 | 0.0276 | 0.0827 | 0.0223 | 0.0294 | 0.031 | 0.086 | 0.0071 | 0.1948 | 0.1755 |
| IFT | 25.2 | 36.6 | 17.2 | 33.1 | 27.1 | 25.4 | 18.4 | 28.5 | 16.8 | 20.1 |
| Color | 0.2 | 2.2 | 2.5 | 0.2 | 2.2 | 0.5 | 3.5 | 2.3 | 7.4 | 2.2 |
| H2 | 0 | 33 | 65 | 32 | 15 | 314 | 22 | 0 | 92 | 31 |
| CH4 | 0 | 19 | 28 | 410 | 146 | 226 | 183 | 112 | 113 | 132 |
| C2H2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C2H4 | 0 | 0 | 5 | 427 | 179 | 238 | 9 | 0 | 27 | 8 |
| C2H6 | 4 | 64 | 23 | 315 | 230 | 221 | 1045 | 150 | 59 | 283 |
| CO | 613 | 76 | 580 | 55 | 71 | 85 | 238 | 285 | 1133 | 245 |
| CO2 | 1483 | 2660 | 3221 | 1618 | 1209 | 2067 | 5275 | 9327 | 6280 | 3900 |
| DP | - | - | - | - | - | - | 434.602 | - | - | - |
| Age | 2 | 36 | 17 | 28 | 7 | 7 | 22 | 37 | 29 | 23 |
| Actual Condition | VG | G | G | C | C | C | P | P | VP | VP |
| RF + SMOTE | VG | G | G | G | G | C | P | P | VP | C |
| RF + BSMOTE | VG | G | G | G | G | G | P | P | VP | C |
| RF + SMOTE-Tomek | VG | G | G | G | G | G | P | P | VP | VP |
| RF + SMOTE-ENN | VG | G | G | C | C | C | P | P | VP | VP |
| NN + SMOTE | VG | G | VP | C | C | G | P | VP | VP | P |
| NN + BSMOTE | G | G | C | C | C | G | P | VP | VP | P |
| NN + SMOTE-Tomek | VG | G | VP | C | G | G | P | P | VP | P |
| NN + SMOTE-ENN | VG | G | G | C | C | C | P | P | VP | VP |