Evaporative Condensation Air-Conditioning Unit with Microchannel Heat Exchanger: An Experimental Study
Abstract
1. Introduction
2. Introduction of the Unit
3. Discussion of the Experimental Results
3.1. Experimental Conditions and Test Contents
3.2. Uncertainty Analysis of the Experimental Data
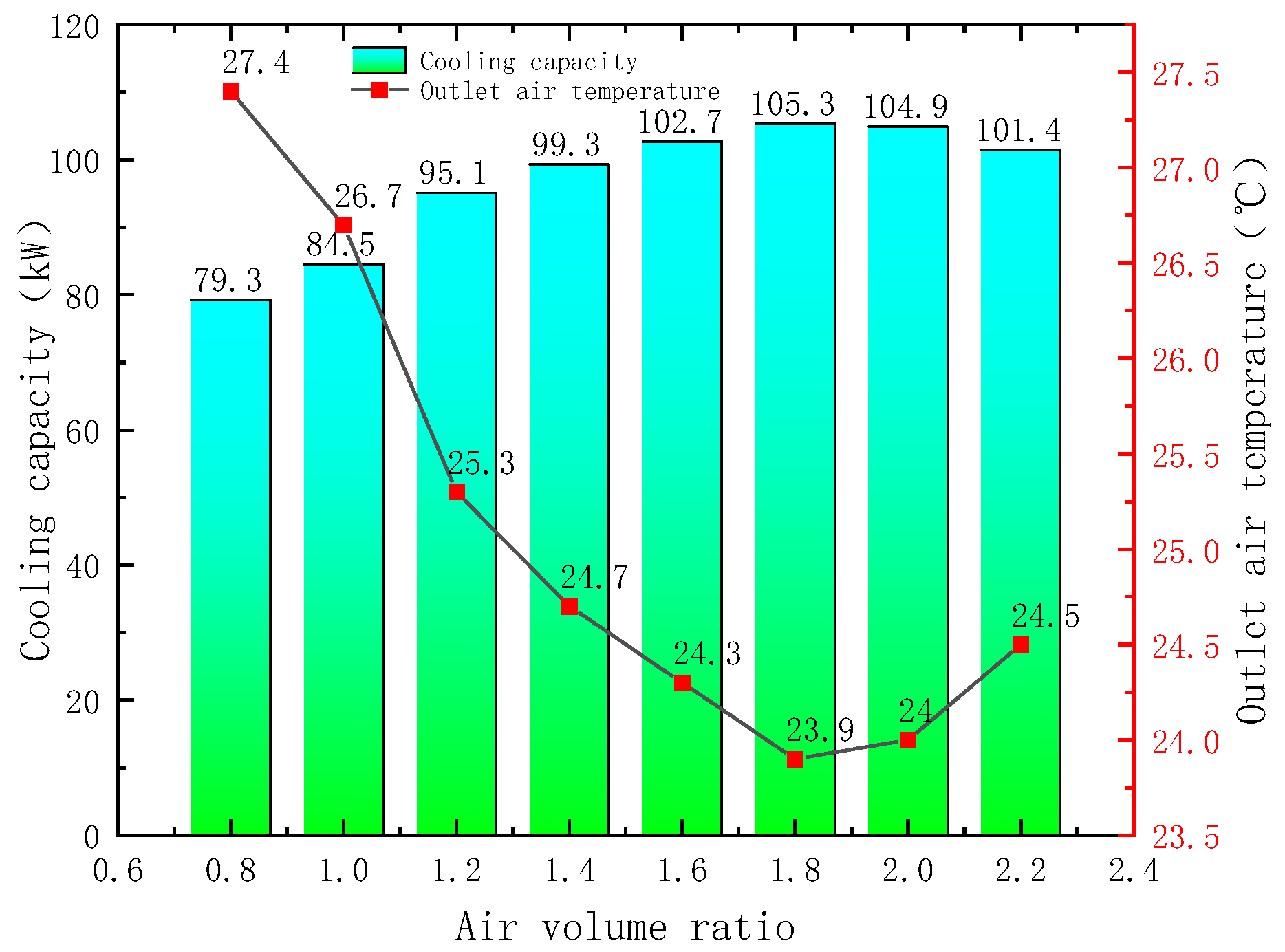
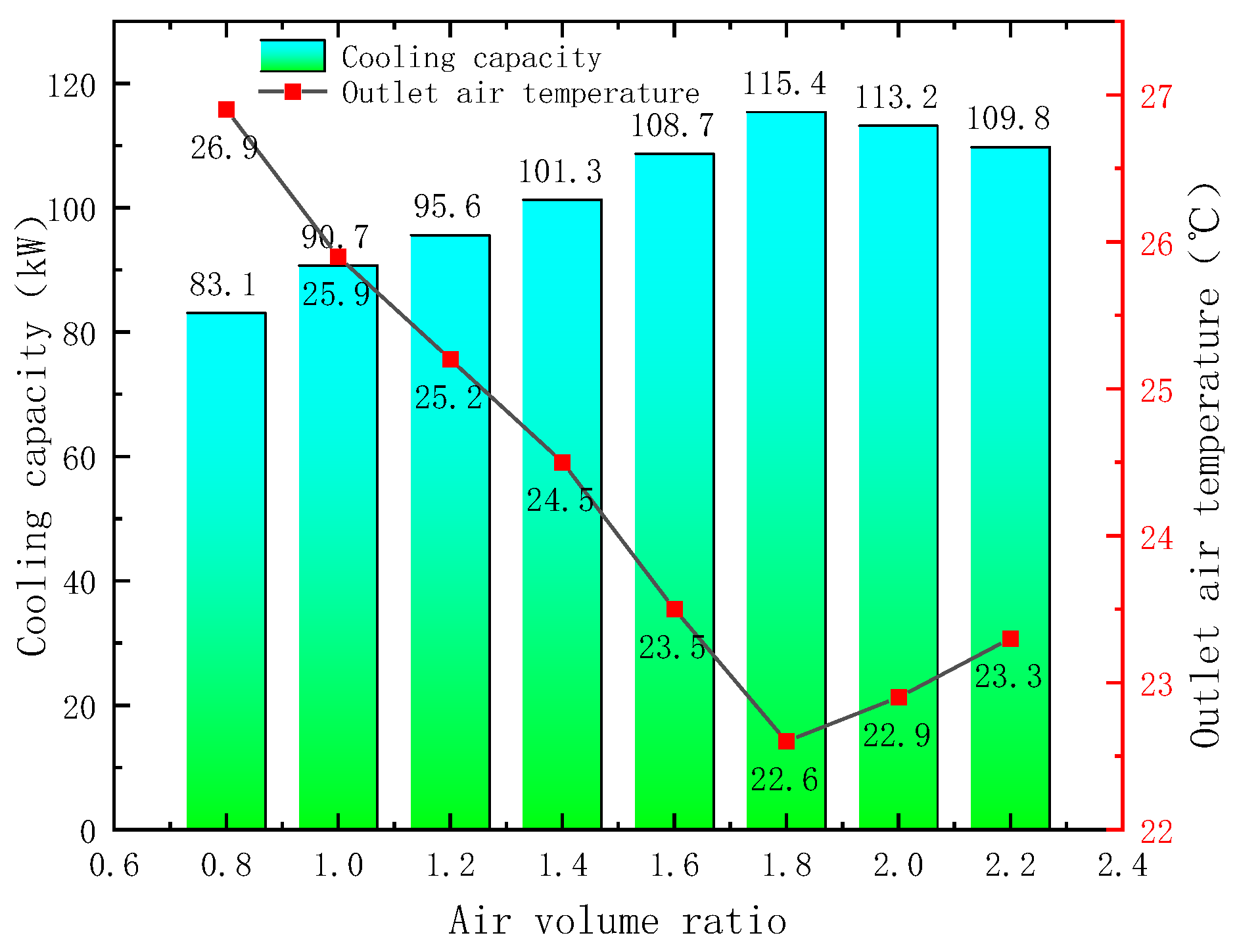
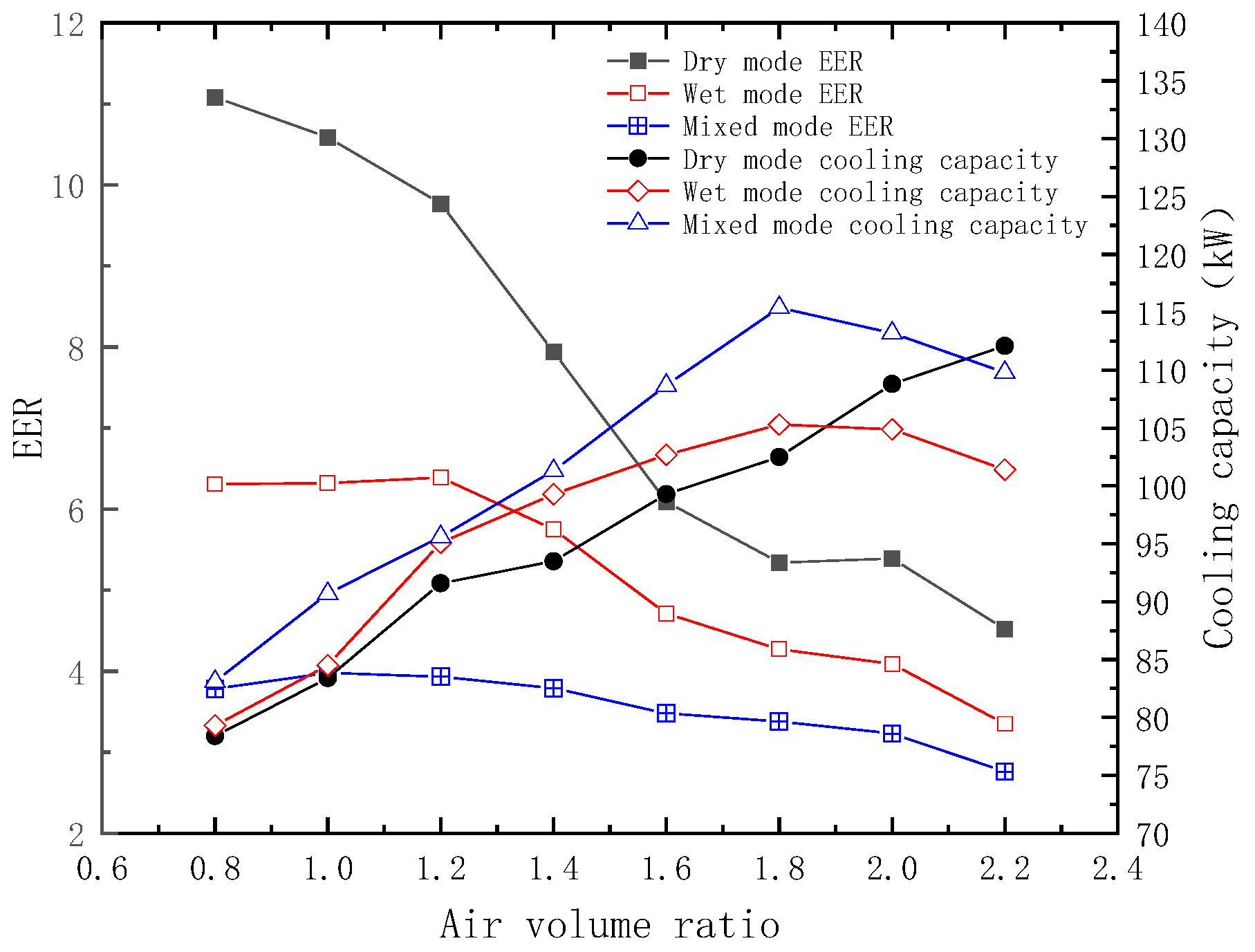
3.3. Experiment of the Optimal Airflow Ratio
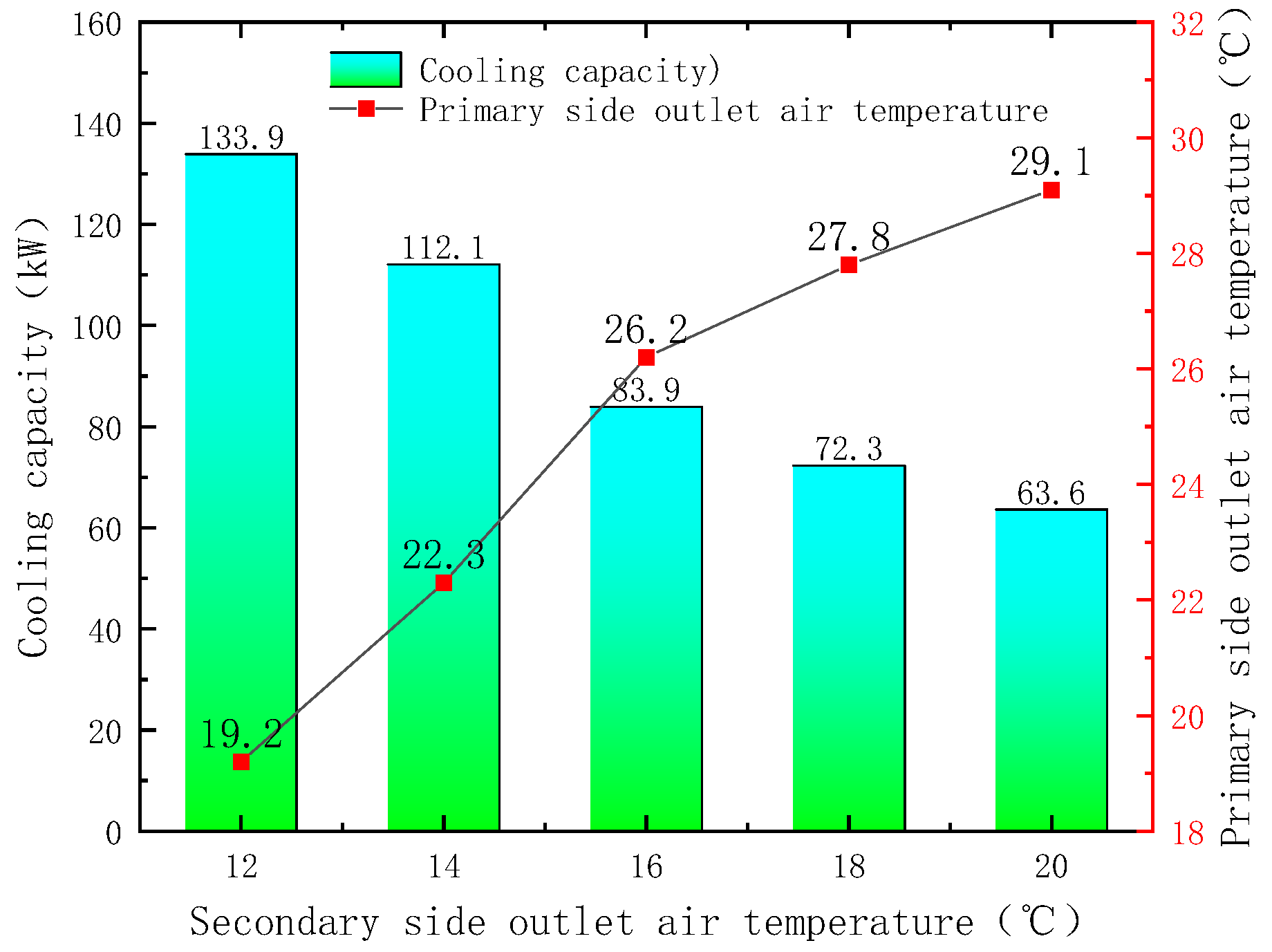
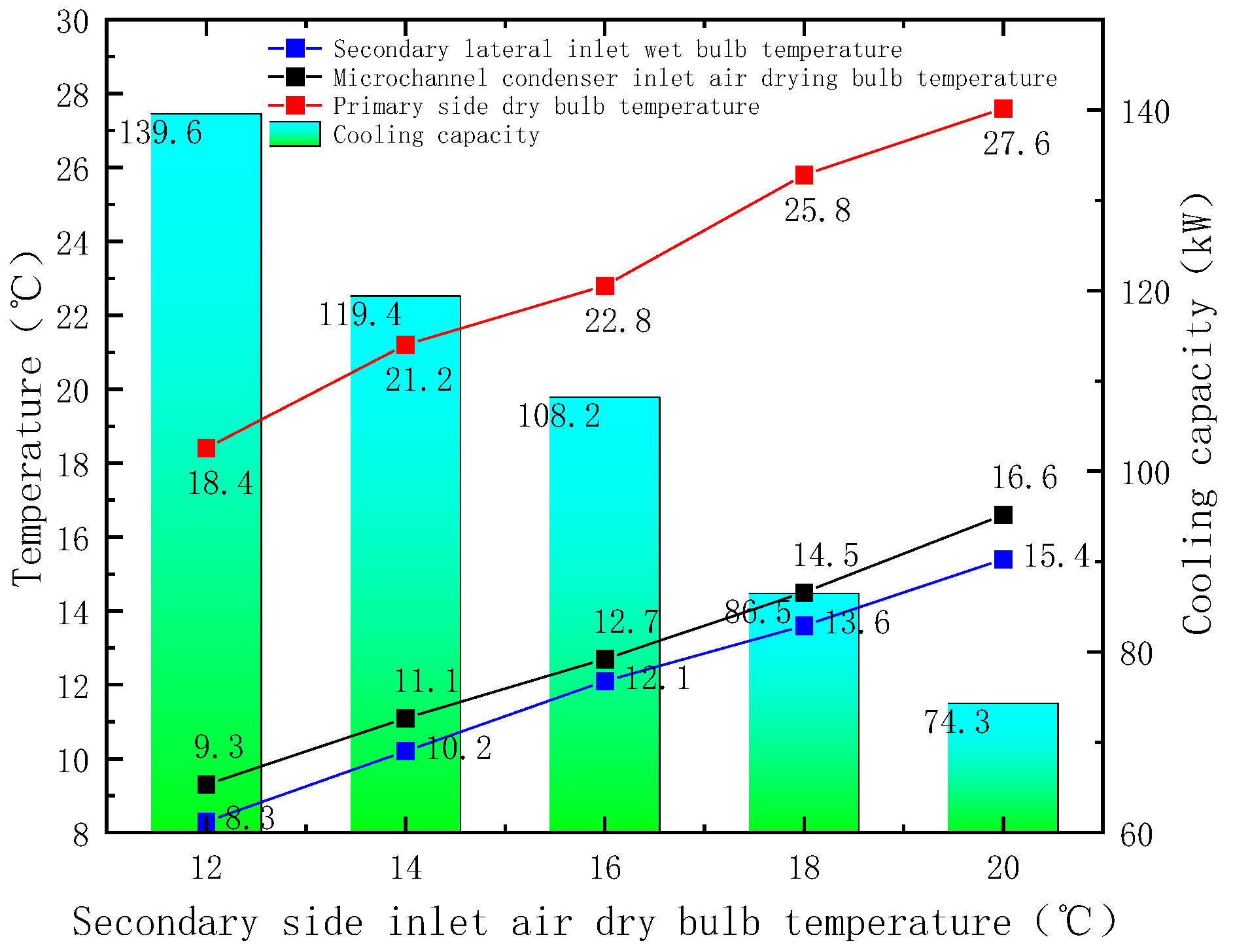
3.4. Inlet Air Temperature Test
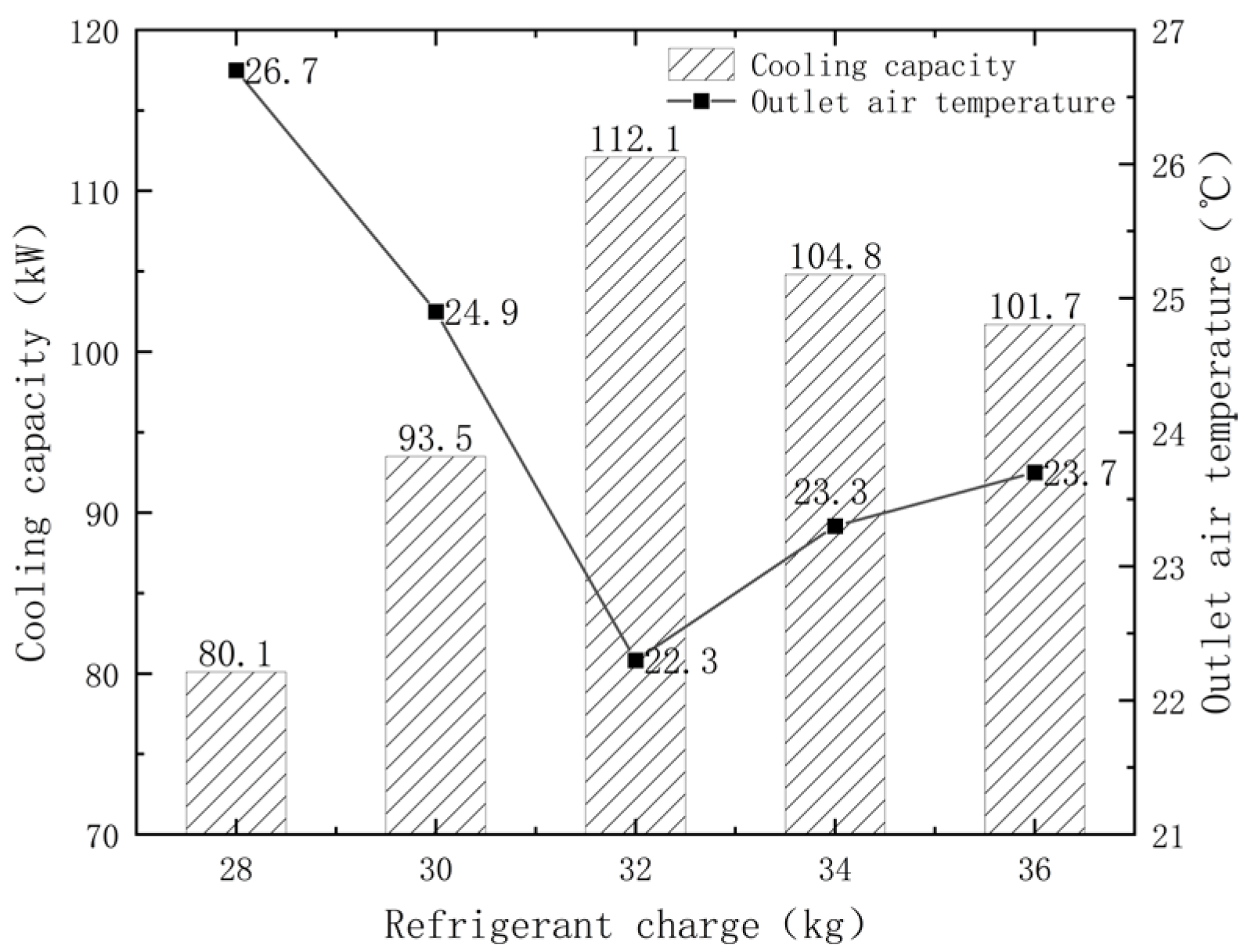
4. Exploration of the Refrigerant Charge
4.1. Method 1
- ①
- Liquid filling volume in the evaporation section
- ②
- The intratracheal fluid filling volume can be obtained by Equation (5):
- ③
- The condensing section charge can be determined by applying the Nusselt theory of condensation heat transfer, as expressed in Equation (6):
- ④
- The fluid filling volume in the liquid tube is determined with Equation (7):
4.2. Method 2
- ①
- On the evaporation side, Equation (9) applies the following:
- ②
- The amount of vapor in the rising tube can be obtained by Equation (10):
- ③
- On the condenser side, refer to Equation (11):
- ④
- The volume of the liquid in the drop tube can be calculated by Equation (12):
- ⑤
- The volume of liquid missing on the evaporation side is determined via Equation (13):
- ⑥
- For the fluid charge needed for heat pipe startup,
- ⑦
- The separate heat pipe system’s charging volume is determined with Equation (14):
4.3. Method 3
5. Conclusions
- (1)
- The maximum refrigeration capacity of the unit in the dry, wet, and mixed modes was 112.1, 105.8, and 115.4 kW, respectively, and the primary-side air outlet temperatures were 22.3, 23.9, and 22.6 °C, respectively. The optimal air volume ratios were 2.2, 1.8, and 1.8, respectively. The energy efficiency of the unit was assessed, yielding the order of dry mode > wet mode > mixed mode, and the energy efficiency of the unit gradually decreased with the increasing air volume ratio.
- (2)
- As the outdoor dry- and wet-bulb temperatures increased, the cooling capacity of the unit gradually decreased. The dry-bulb temperature of the air on the secondary side impacted the cooling capacity in the dry mode, and the wet-bulb temperature of the air on the secondary side influenced the cooling capacity in the wet mode. When the dry-bulb temperature of the air on the secondary side was 12~20 °C, the EER in the wet mode was better than that in the dry mode, and in areas with a sufficient water supply, the duration of the wet mode could be extended at temperatures ranging from 10 to around 14 °C to improve the energy efficiency of the unit.
- (3)
- The optimal refrigerant charge of the refrigerant pump heat pipe system of the unit was 32 kg, at which point the cooling capacity of the unit was the highest, measuring 112.1 kW, and the primary-side air outlet temperature was the lowest, at 22.3 °C, which was essentially consistent with the value of 32.37 kg calculated by the proposed simple algorithm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q. Competitive Landscape and Market Share of China’s Data Center Industry. Data Cent. Constr. 2021, 8, 4. [Google Scholar]
- Jiang, L.-L.; Tang, Y.; Zhou, W.; Jiang, L.-Z.; Xiao, T.; Li, Y.; Gao, J.-W. Design and fabrication of sintered wick for miniature cylindrical heat pipe. Trans. Nonferr. Met. Soc. China 2014, 24, 292–301. [Google Scholar] [CrossRef]
- Liu, C.; Chen, Y.; Feng, D.; Zhang, H.; Miao, J.; Feng, Y.; Yan, Y.; Zhang, X. Experimental study on temperature uniformity and heat transfer performance of nitrogen loop heat pipe with large area and multi-heat source. Appl. Therm. Eng. Des. Process. Equip. Econ. 2022, 210, 118344. [Google Scholar] [CrossRef]
- Ma, G.Y.; Wei, C.C.; Zhang, S.; Zhou, F. Application of a pumped loop heat pipe heat exchanger unit for a small data center. Beijing Gongye Daxue Xuebao/J. Beijing Univ. Technol. 2015, 41, 439–445. [Google Scholar]
- Dong, J.; Lin, Y.; Deng, S.; Shen, C.; Zhang, Z. Experimental investigation of an integrated cooling system driven by both liquid refrigerant pump and vapor compressor. Energy Build. 2017, 154, 560–568. [Google Scholar] [CrossRef]
- Yan, G.; Feng, Y.; Peng, L. Experimental analysis of a novel cooling system driven by liquid refrigerant pump and vapor compressor. Int. J. Refrig. 2015, 49, 11–18. [Google Scholar] [CrossRef]
- Liu, S.; Ma, G.; Jiao, X.; Xu, S.; Wu, G. Performance of a mechanically-driven loop heat pipe heat recovery system. Appl. Therm. Eng. 2022, 207, 118066. [Google Scholar]
- Chen, F.; Zhou, X.; Liao, S. Energy Saving Model and Calculation Example of Three Cooling Schemes for Data Center in Hot Summer and Cold Winter Area. J. Power Energy Eng. 2022, 9, 1–20. [Google Scholar]
- Ohadi, M.M.; Dessiatoun, S.V.; Choo, K.; Pecht, M.; Lawler, J.V. A comparison analysis of air, liquid, and two-phase cooling of data centers. In Proceedings of the 2012 28th Annual IEEE Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM), San Jose, CA, USA, 18–22 March 2012; pp. 58–63. [Google Scholar]
- Wei, A.; Ren, X.; Lin, S.; Zhang, X. CFD analysis on flow and heat transfer mechanism of a microchannel Ω-shape heat pipe under zero gravity condition. Int. J. Heat Mass Transf. 2020, 163, 120448. [Google Scholar] [CrossRef]
- Han, Z.; Xue, D.; Wei, H.; Ji, Q.; Sun, X.; Li, X. Study on operation strategy of evaporative cooling composite air-conditioning system in data center. Renew. Energy 2021, 177, 1147–1160. [Google Scholar] [CrossRef]
- Yue, Z.; Shu, X.; Guo, Y.; Zhang, S. Characteristic Analysis and Experimental Study on a Hybrid System with Magnetic Pump-driven Two Phase Cooling System. J. Refrig. 2016, 37, 1–5. [Google Scholar]
- Lin, Y.; Liu, J.; Xu, X.; Liu, Z.; Li, G. Experimental Research on Air Conditioning System of a Computer Room Based on Refrigerant Pump Pressurization. J. Refrig. 2020, 41, 83–88. [Google Scholar]
- Xue, L.; Ma, G.; Zhou, F.; Li, F.; Yan, X.; Jiang, M. Performance Analysis of Gas-Pump-Driven Free-cooling Unit in a Small Data Center. J. Refrig. 2019, 40, 1–9. [Google Scholar]
- Bai, K.; Ma, G.; Zhou, F.; Zhang, S. Performance characteristics of pump-driven mechanical refrigeration and thermosyphon integrated system. Heat. Vent. Air Cond. 2016, 46, 109–115. [Google Scholar]
- Liu, Z.; Huang, X.; Chang, J.; Chang, J. Design and test analysis of evaporative cooling(condensation) air conditioning unit data center. Refrig. Air-Cond. 2020, 20, 6. (In Chinese) [Google Scholar]
- GB 50174-2017; Code for Design of Data Centers. China Planning Press: Beijing, China, 2017. (In Chinese)
- T/DZJN 27-2021; Evaporative Cooling Iir—Conditioning Equipment of Data Centers. China Planning Press: Beijing, China, 2021. (In Chinese)
- Wang, W.; Xiong, R.; Tu, C. Analysis of the Filling Quantity for Separated Type Heat Pipe. Power Eng. 1997, 03, 67–69 +73. (In Chinese) [Google Scholar]
- Zhang, H. Inverstigation on the optimized working status of separated type heat pipe heat exchangers. Petrochem. Equip. Technol. 1996, 3, 13–17+65. (In Chinese) [Google Scholar]
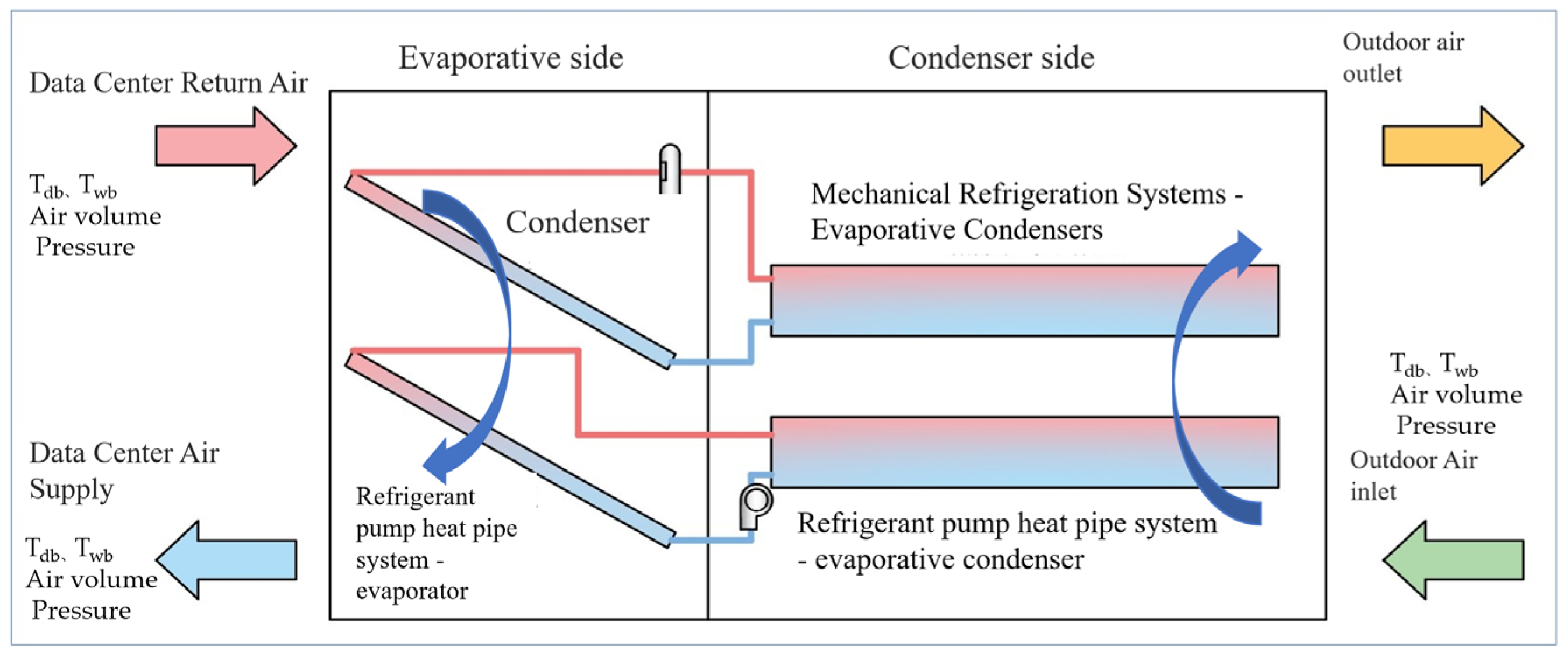

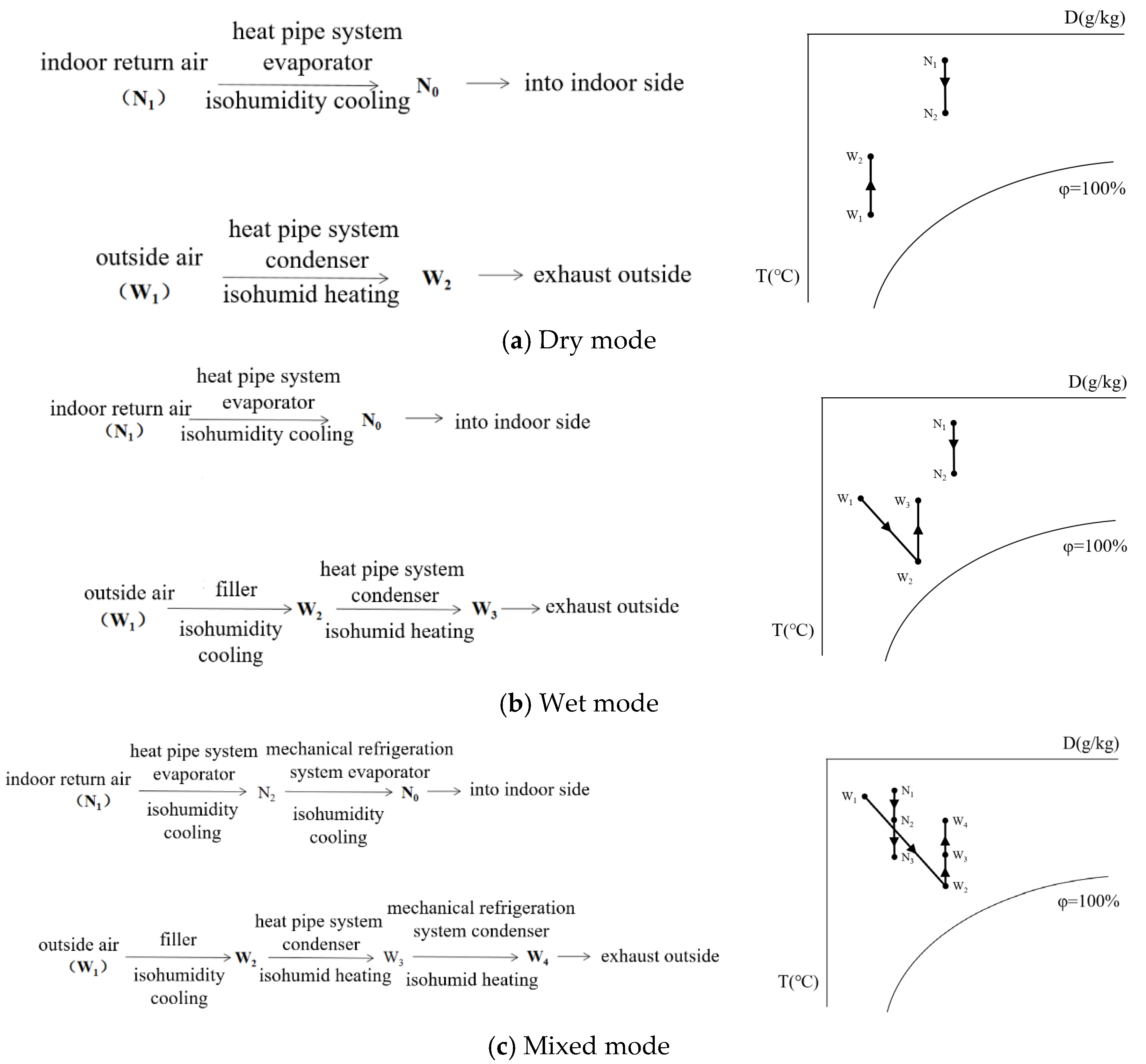






| Mode | Ambient Air Parameters | Fan | Water Pump | Refrigerant Pump | Compressor |
|---|---|---|---|---|---|
| Dry mode | Tdb ≤ 14 °C | ON | OFF | ON | OFF |
| Wet mode | Tdb > 14 °C, Twb ≤ 14 °C | ON | ON | ON | OFF |
| Mixed mode | Twb > 14 °C | ON | ON | ON | ON |
| Parameters | Value | Unit |
|---|---|---|
| Cooling capacity | 120 | kW |
| Primary air volume | 30,000 | m3/h |
| Secondary air volume | 66,000 | m3/h |
| Primary air temperature | 25 | °C |
| Primary air return temperature | 38 | °C |
| Air velocity | 2.24 | m/s |
| Area | 3.72 | m2 |
| Value | Unit | |
|---|---|---|
| Refrigerant | R410a | |
| Cooling capacity | 60 | kW |
| Primary air volume | 30,000 | m3/h |
| Secondary air volume | 66,000 | m3/h |
| Evaporation temperature | 17 | °C |
| Condensation temperature | 50 | °C |
| Mode | Outdoor Side | Indoor Side | ||||||
|---|---|---|---|---|---|---|---|---|
| Air Inlet State | Air Inlet State | |||||||
| Dry Bulb (°C) | Wet Bulb (°C) | Dew Point (°C) | Air Volume (m3/h) | Dry Bulb (°C) | Wet Bulb (°C) | Dew Point (°C) | Air Volume (m3/h) | |
| Dry mode | 35.0 | 19.5 | 10.6 | 30,000 | 38.0 | 22 | Not lower than the tap water temperature | 66,000 |
| Wet mode | 17 | 13 | 10 | 38.0 | 22 | Not lower than the tap water temperature | ||
| Mixed mode | 14 | / | / | 38.0 | 22 | / | ||
| Equipment | Test Content | Measuring Range | Accuracy Requirement |
|---|---|---|---|
| Testo 174H Temperature and Humidity Recorder (Titisee-Neustadt, Germany) | Dry-bulb temperature Relative humidity | 0~100 °C; 0~100% | ±0.5 °C/±3% |
| Testo 410-1 Impeller Anemometer (Titisee-Neustadt, Germany) | Wind speed | 0.40~20.0 m/s | ±(0.2 m/s + 2% measured value) |
| Testo 869 Infrared Thermal Imager (Titisee-Neustadt, Germany) | Infrared thermal imaging | −20~ + 280 °C | Thermal sensitivity < 0.12 °C |
| Air Volume Ratio | Secondary Air Volume (m3/h) | Secondary Air Velocity (m/s) | Percentage of Fan Input (%) |
|---|---|---|---|
| 0.8 | 24,000 | 2.2 | 40 |
| 1 | 30,000 | 2.8 | 55 |
| 1.2 | 36,000 | 3.3 | 63 |
| 1.4 | 42,000 | 3.9 | 70 |
| 1.6 | 48,000 | 4.4 | 82 |
| 1.8 | 54,000 | 5.0 | 88 |
| 2 | 60,000 | 5.5 | 90 |
| 2.2 | 66,000 | 6.1 | 100 |
| Component | Volume (m3) | Refrigerant Charge (kg) |
|---|---|---|
| Evaporator | 0.0123 | 11.07 |
| Condenser | 0.0167 | 3.01 |
| Reservoir | 0.0135 | 13.77 |
| Gas–liquid separator | 0.0106 | 1.908 |
| Liquid lines | 0.000147 | 0.18 |
| Gas lines | 0.000161 | 0.0066 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, J.; Huang, X.; Chu, H.; Yang, L.; Lv, W.; Tang, X.; Tian, J. Evaporative Condensation Air-Conditioning Unit with Microchannel Heat Exchanger: An Experimental Study. Energies 2025, 18, 2356. https://doi.org/10.3390/en18092356
Chu J, Huang X, Chu H, Yang L, Lv W, Tang X, Tian J. Evaporative Condensation Air-Conditioning Unit with Microchannel Heat Exchanger: An Experimental Study. Energies. 2025; 18(9):2356. https://doi.org/10.3390/en18092356
Chicago/Turabian StyleChu, Junjie, Xiang Huang, Hongxu Chu, Liu Yang, Weihua Lv, Xing Tang, and Jinxing Tian. 2025. "Evaporative Condensation Air-Conditioning Unit with Microchannel Heat Exchanger: An Experimental Study" Energies 18, no. 9: 2356. https://doi.org/10.3390/en18092356
APA StyleChu, J., Huang, X., Chu, H., Yang, L., Lv, W., Tang, X., & Tian, J. (2025). Evaporative Condensation Air-Conditioning Unit with Microchannel Heat Exchanger: An Experimental Study. Energies, 18(9), 2356. https://doi.org/10.3390/en18092356






