Techno-Economic Comparison of a Large-Scale Nuclear Power Plant, Small Modular Reactors, and Wind and Solar Power Plant Deployment
Abstract
:1. Introduction
2. Methods
- —net operating income in year t (USD);
- —investments and other expenses in year t (USD);
- —discount rate (-);
- —construction period in years;
- projected exploitation lifetime in years;
- —discrete time in years.
- —electricity generation in year t (MWh);
- —electricity price (USD/MWh);
- —discount rate (-);
- —discrete time in years;
- —plant lifetime in years;
- —investment (capital) costs in year t (USD);
- —operations and maintenance costs in year t (USD);
- —fuel costs in year t (USD);
- —carbon costs in year t (USD);
- —decommissioning costs in year t (USD).
- -
- The discount rate at which costs and benefits are discounted is stable and the same for all considered technologies and does not change its value during the lifetime of the project under consideration. Capital costs and the relevant discount rate may vary from technology to technology. Assuming that these costs are identical allows comparison of calculated LCOE values for different technologies and regions;
- -
- Electricity price is stable and does not change in time during the project’s lifetime. All electricity produced, with adopted capacity factors, was sold at this price.
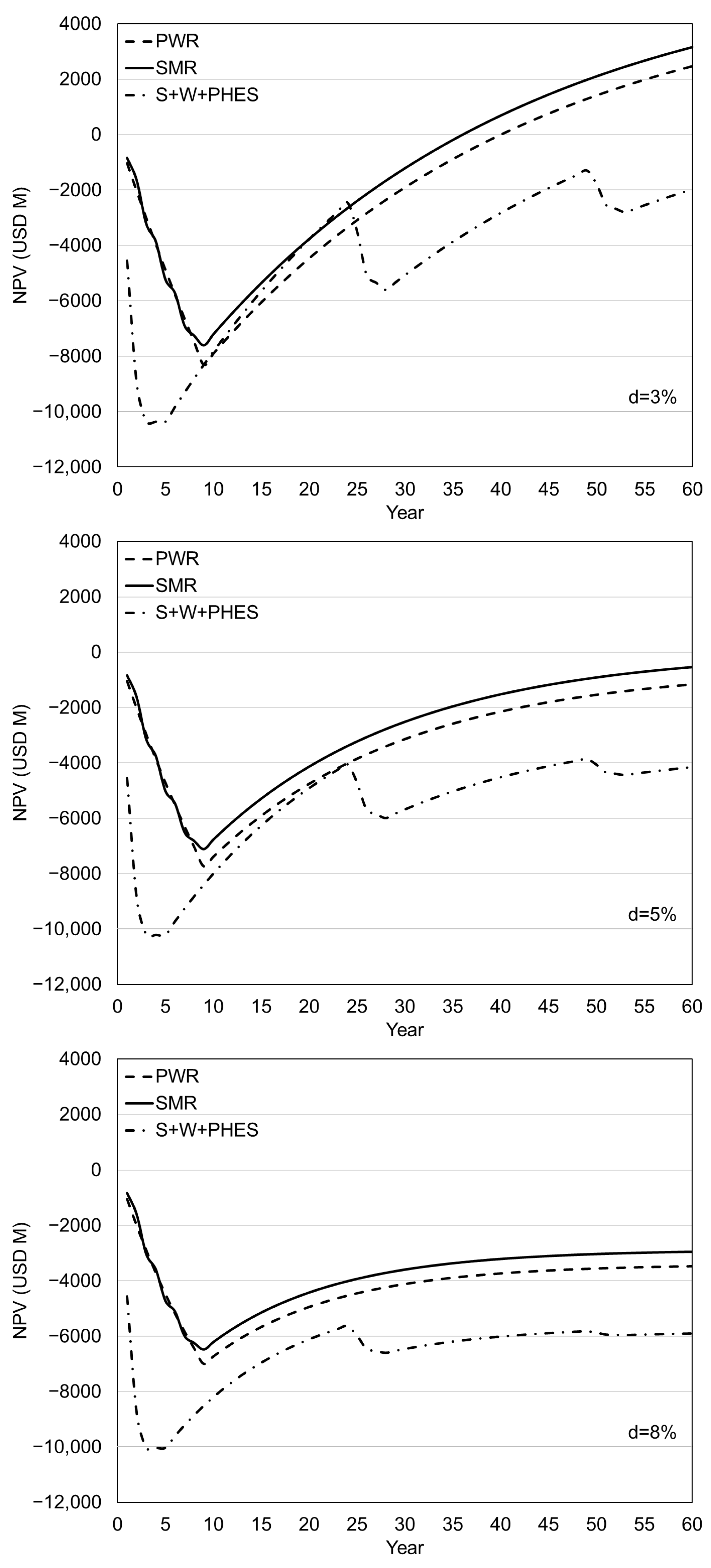
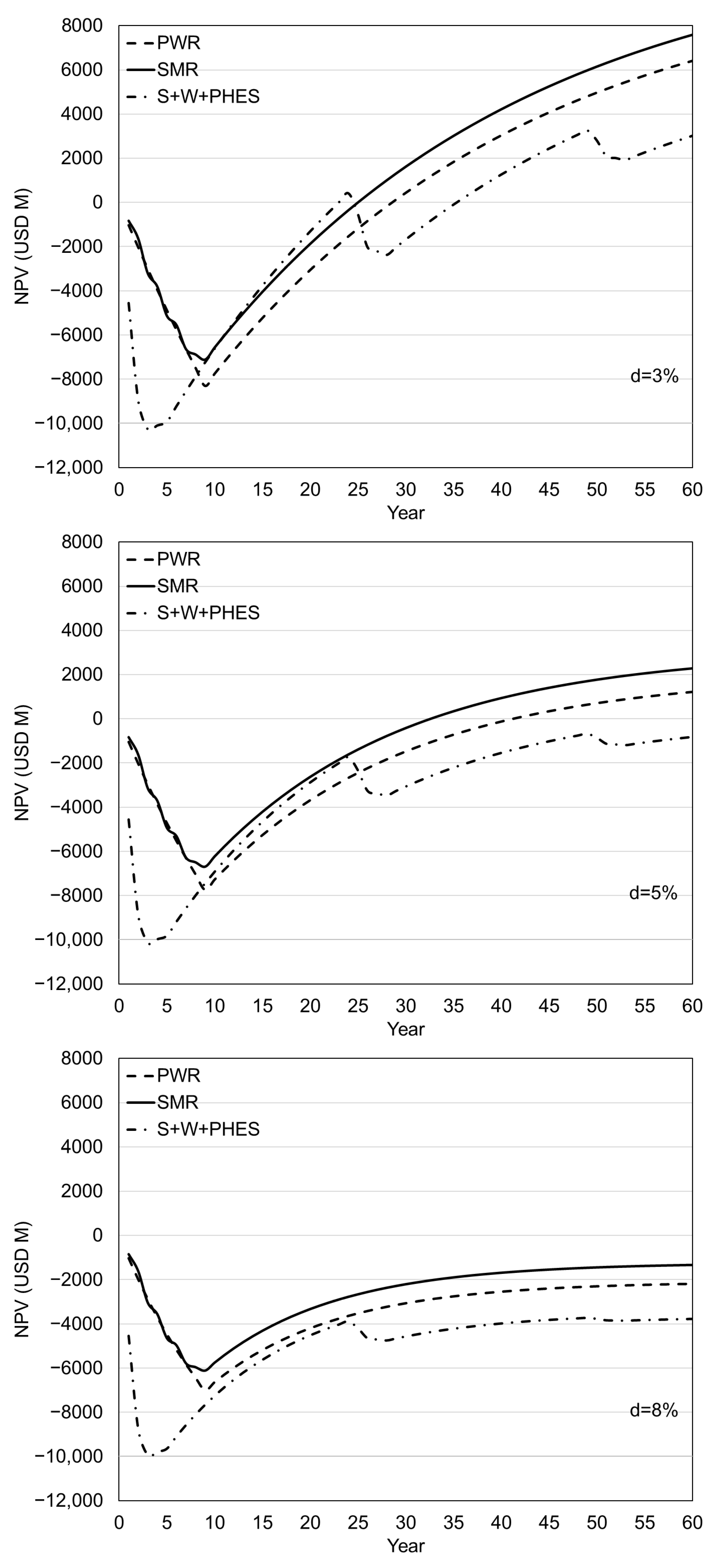
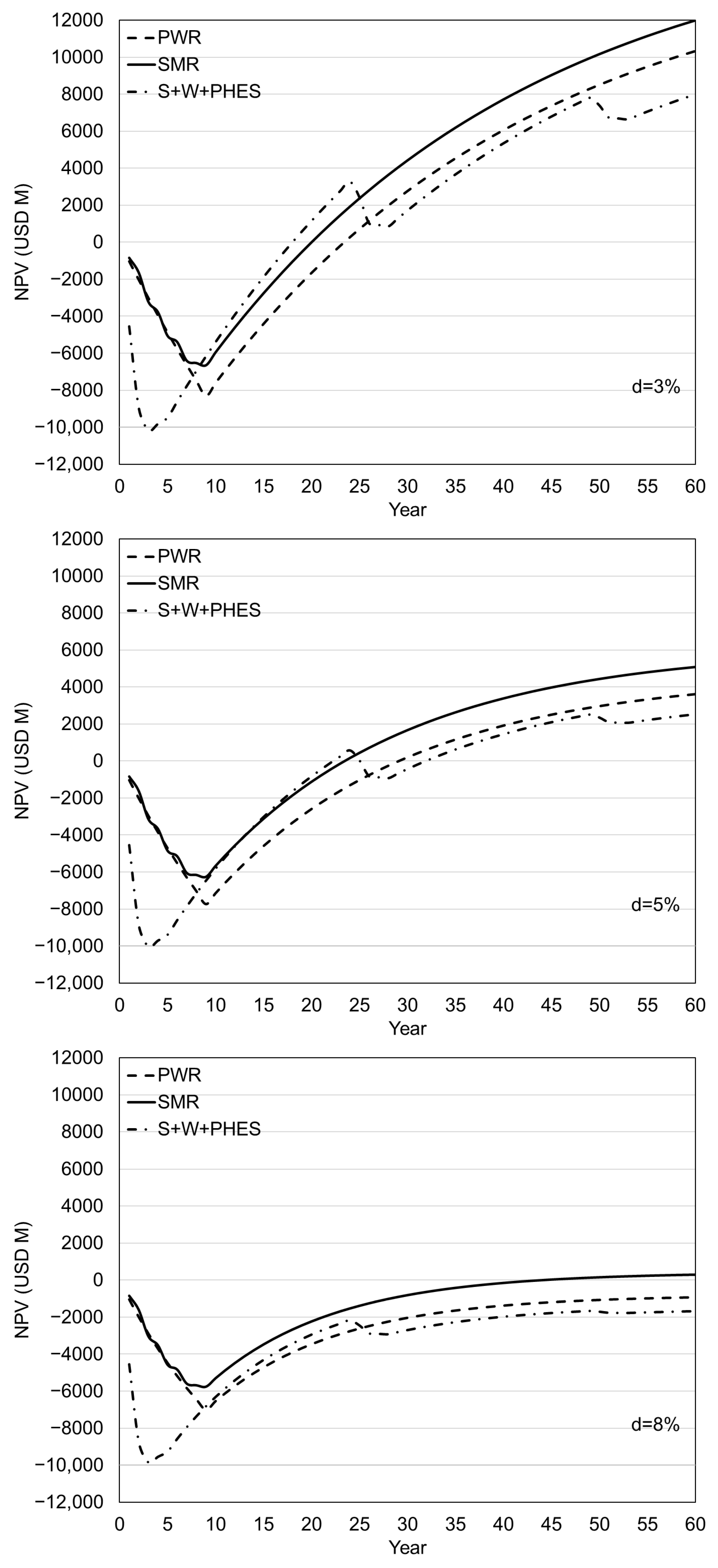
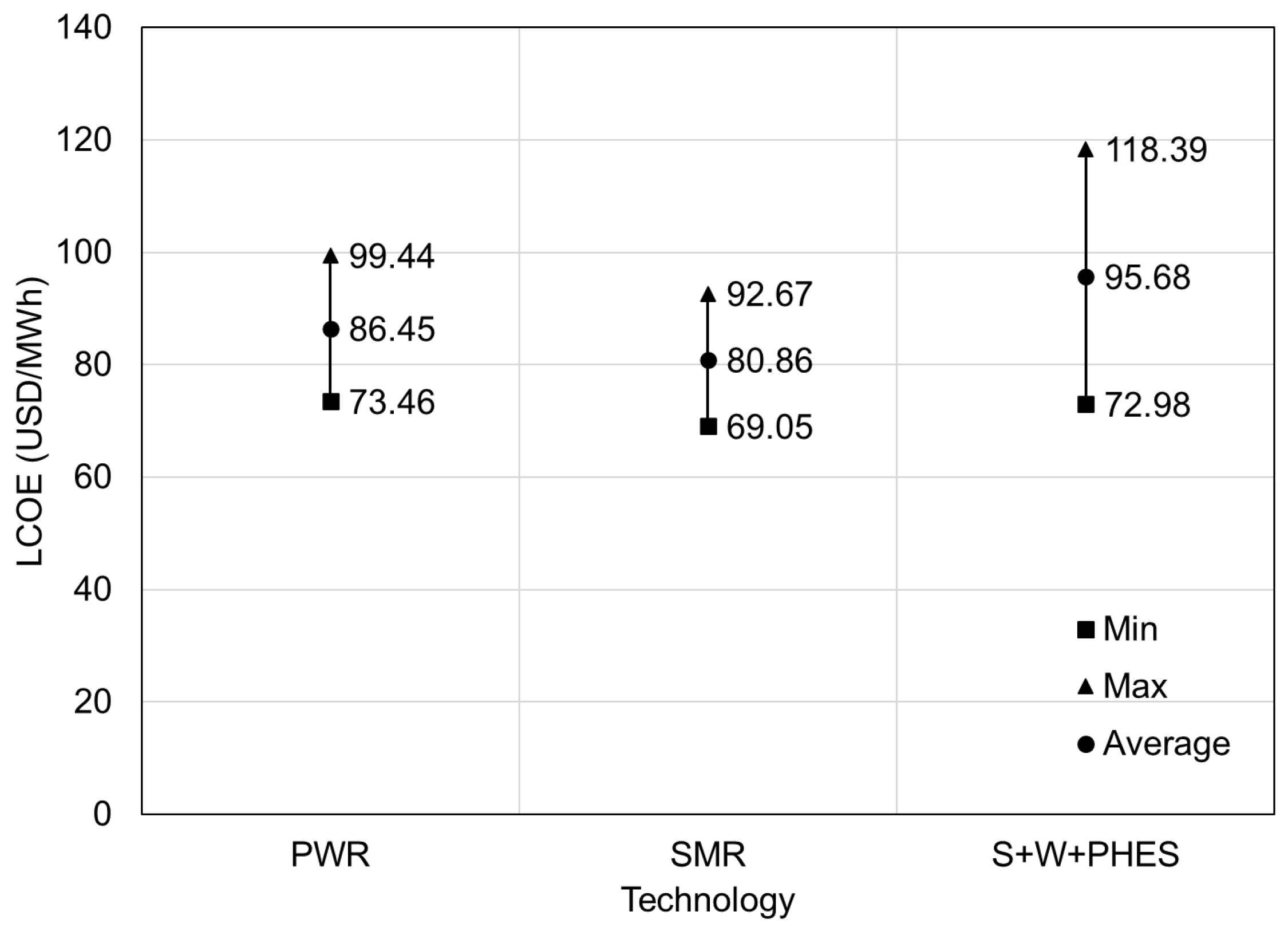
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| electricity price (USD/MWh) | |
| carbon costs in year t (USD) | |
| discount rate (-) | |
| net operating income in year t (USD) in Equation (1) decommissioning costs in year t (USD) in Equation (2) | |
| electricity generation in year t (MWh) | |
| fuel costs in year t (USD) | |
| investment (capital) costs in year t (USD) | |
| LCOE | levelized cost of electricity (USD/MWh) |
| n | plant lifetime (year) |
| NPV | net present value (USD) |
| operations and maintenance costs in year t (USD) | |
| investments and other expenses in year t (USD) | |
| discrete time (year) | |
| construction period (year) | |
| projected exploitation lifetime (year) |
Abbreviations
| CBAM | Carbon Border Adjustment Mechanism |
| DC | direct current |
| EPR | European Pressurised Reactor |
| EU | European Union |
| LCOE | levelized cost of electricity |
| LS | large-scale |
| USD M | million dollars |
| NPP | nuclear power plant |
| NPV | net present value |
| OECD | Organisation for Economic Co-operation and Development |
| O&M | operations and maintenance |
| PB | payback |
| PHES | pumped hydroelectric energy storage |
| PV | photovoltaic |
| PWR | pressurized water reactor |
| SMR | small modular reactor |
| VVER | In Russian: Водо-Водяной Энергетический Реактор; romanized: Vodo-Vodyanoi Enyergeticheskiy Reaktor; in English: water–water power reactor |
References
- Republic of Serbia. Law on the Ratification of the Energy Community Treaty Between the European Community and the Republic of Albania, the Republic of Bulgaria, Bosnia and Herzegovina, the Republic of Croatia, the Former Yugoslav Republic of Macedonia, the Republic of Montenegro, Romania, the Republic of Serbia and the United Nations Interim Administration Mission in Kosovo in Accordance with Security Council Resolution 1244 of the United Nations. Official Gazette of the Republic of Serbia. No. 62. 19 July 2006. Available online: https://reg.pravno-informacioni-sistem.rs/api/Attachment/prilozi/418158/Ugovor_o_osnivanju_Energetske_zajednice.htm (accessed on 11 April 2025).
- Decision of the Ministerial Council of the Energy Community No 2022/02/MC-EnC. Available online: https://www.energy-community.org/legal/acquis.html (accessed on 13 February 2025).
- Statistical Office of the Republic of Serbia, Renewable Energy Share in the Total Final Energy Consumption. Available online: https://data.stat.gov.rs/Home/Result/SDGUN070201?caller=SDGUN&languageCode=sr-Latn (accessed on 13 February 2025).
- Energy Balance of the Republic of Serbia for 2022. Available online: https://www.mre.gov.rs/extfile/sr/1144/energetski_bilans_rs_za_2022__0.pdf (accessed on 13 February 2025).
- European Parliament and Council. Regulation (EU) 2023/956 of the European Parliament and of the Council of 10 May 2023 Establishing a Carbon Border Adjustment Mechanism. Official Journal of the European Union. L 130, 16 May 2023, 52–104. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32023R0956 (accessed on 11 April 2025).
- Li, X.; Hu, C.; Luo, S.; Lu, H.; Piao, Z.; Jing, L. Distributed Hybrid-Triggered Observer-Based Secondary Control of Multi-Bus DC Microgrids Over Directed Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 1–14. [Google Scholar] [CrossRef]
- Li, W.; Zou, Y.; Yang, H.; Fu, X.; Xiang, S.; Li, Z. Two-Stage Stochastic Energy Scheduling for Multi-Energy Rural Microgrids With Irrigation Systems and Biomass Fermentation. IEEE Trans. Smart Grid 2024, 16, 1075–1087. [Google Scholar] [CrossRef]
- Rehmani, A.M.; Kazmi, S.A.A.; Altamimi, A.; Khan, Z.A.; Awais, M. Techno-Economic Environmental Assessment of an Isolated Rural Micro-Grid from a Mid-Career Repowering Perspective. Sustainability 2023, 15, 2137. [Google Scholar] [CrossRef]
- Development of the Electric Power Industry of the Republic of Serbia Up to the Year 2050, Serbian Academy of Sciences and Arts Department of Technical Sciences; Academy Board for Energy: Belgrade, Serbia, 2023. (In Serbian)
- Leading the Energy Transition Factbook—Electricity Storage; SBC Energy Institute: Gravenhage, TX, USA, 2013; Available online: https://wecanfigurethisout.org/ENERGY/Web_notes/Round_Pegs/Power_Cycles_and_Energy_Storage_Supporting_Files/Electricity%20Storage%20-%20SBC%20Energy%20Institute%202013.pdf (accessed on 13 February 2025).
- Federal Aviation Administration, Lithium Battery Incidents. Available online: https://www.faa.gov/hazmat/resources/lithium_batteries/incidents (accessed on 18 February 2025).
- Olabi, A.G.; Onumaegbu, C.; Wilberforce, T.; Ramadan, M. Mohammad Ali Abdelkareem, Abdul Hai Al -Alami, Critical review of energy storage systems. Energy 2021, 214, 118987. [Google Scholar] [CrossRef]
- Stanimirovic, A.; Djordjevic, V. JSC EPS—Overview & Serbian Nuclear Energy, Electric Power Industry of Serbia. In Proceedings of the Foundational Infrastructure for the Responsible Use of Small Modular Reactor Technology—FIRST, Belgrade, Serbia, 17–19 December 2024. [Google Scholar]
- Stevanovic, V. Program for the introduction of nuclear energy and the development of organizational, institutional and technical technological infrastructure, Nuclear Power Plants in Serbian Energy, Serbian Academy of Sciences and Arts, Belgrade, November 2022. (In Serbian). Available online: https://www.sanu.ac.rs/wp-content/uploads/2022/11/Nuklearna-energija.pdf (accessed on 11 April 2025).
- Đorđević, A.; Đurišić, Ž. Mathematical model for the optimal determination of voltage level and PCC for large wind farms connection to transmission network. IET Renew. Power Gener. 2019, 13, 2240–2250. [Google Scholar] [CrossRef]
- Projected Costs of Generating Electricity, 2020 ed.; International Energy Agency, Nuclear Energy Agency Organisation for Economic Co-operation and Development: Paris, France, 2020; Available online: https://iea.blob.core.windows.net/assets/ae17da3d-e8a5-4163-a3ec-2e6fb0b5677d/Projected-Costs-of-Generating-Electricity-2020.pdf (accessed on 13 February 2025).
- Small Modular Reactors, Catalogue 2024, International Atomic Energy Agency. 2024. Available online: https://aris.iaea.org/Publications/SMR_catalogue_2024.pdf (accessed on 13 February 2025).
- U.S. Energy Information Administration (EIA). Nuclear Explained-Nuclear Power Plants. Available online: www.eia.gov/outlooks/aeo/assumptions/pdf/elec_cost_perf.pdf (accessed on 2 December 2024).
- Ferreira, H.L.; Garde, R.; Fulli, G.; Kling, W.; Lopes, J.P. Characterisation of electrical energy storage technologies. Energy 2013, 53, 288–298. [Google Scholar] [CrossRef]
- Koivunen, T.; Hirvijoki, E. Effect of investment cost on technology preference in a flexible, low-carbon Finnish power system. Nucl. Energy Des. 2024, 417, 112854. [Google Scholar] [CrossRef]
- Deline, C.; Muller, M.; White, R.; Perry, K.; Springer, M.; Deceglie, M.; Jordan, D. Availability and Performance Loss Factors for U.S. PV Fleet Systems, National Renewable Energy Laboratory, Technical Report NREL/TP-5K00-88769. February 2024. Available online: https://www.nrel.gov/docs/fy24osti/88769.pdf (accessed on 28 April 2025).
- Lillo-Sánchez, L.; López-Lara, G.; Vera-Medina, J.; Pérez-Aparicio, E.; Lillo-Bravo, I. Degradation analysis of photovoltaic modules after operating for 22 years. A case study with comparisons. Sol. Energy 2021, 222, 84–94. [Google Scholar] [CrossRef]
- Staffell, I.; Green, R. How does wind farm performance decline with age? Renew. Energy 2014, 66, 775–786. [Google Scholar] [CrossRef]
- Astolfi, D.; Pandit, R. Wind Turbine Performance Decline with Age. Energies 2022, 15, 5225. [Google Scholar] [CrossRef]
- Westinghouse Electric Company LLC. Uprating Programs Technology. Available online: https://westinghousenuclear.com/media/rpolsxfb/uprating-programs-technology.pdf (accessed on 28 April 2025).
- International Atomic Energy Agency (IAEA). Power Reactor Information System (PRIS). Available online: https://pris.iaea.org/pris/CountryStatistics/ReactorDetails.aspx?current=531 (accessed on 28 April 2025).
- Gumber, A.; Riccardo, Z.; Steffen, B. A global analysis of renewable energy project commissioning timelines. Appl. Energy 2024, 358, 122563. [Google Scholar] [CrossRef]
- World Nuclear Association, Nuclear Fuel Cycle, Decommissioning Nuclear Facilities. Available online: https://world-nuclear.org/information-library/nuclear-fuel-cycle/nuclear-waste/decommissioning-nuclear-facilities (accessed on 19 February 2025).
- Thunder Said Energy, Solar Power: Decommissioning Costs. Available online: https://thundersaidenergy.com/downloads/solar-power-decommissioning-costs/ (accessed on 19 February 2025).
- The Institute for Energy Research, The Cost of Decommissioning Wind Turbines Is Huge. Available online: https://www.instituteforenergyresearch.org/renewable/wind/the-cost-of-decommissioning-wind-turbines-is-huge/ (accessed on 19 February 2025).
- Palmer’s Creek Wind Farm Site Permit Application Chippewa County, Minnesota. Available online: https://www.edockets.state.mn.us/documents/%7B29950B36-761E-4C68-B259-F0FBF90842F4%7D/download (accessed on 19 February 2025).
- U.S. Energy Information Administration (EIA). Capital Cost and Performance Characteristic Estimates for Utility Scale Electric Power Generating Technologies. Available online: https://www.eia.gov/analysis/studies/powerplants/capitalcost/pdf/capital_cost_aeo2020.pdf (accessed on 19 February 2025).
- Larsen, L.M.; Guaita, N.; Lantgios, I.; Zhou, J.; Abou-Jaoude, A.; Stauff, N. Nuclear Energy Cost Estimates for Net Zero World Initiative—2024 Update, Idaho National Laboratory, INL/RPT-24-80552. 2024. Available online: https://inldigitallibrary.inl.gov/sites/sti/sti/Sort_130016.pdf (accessed on 19 February 2025).
- Nøland, J.K.; Hjelmeland, M.; Korpås, M. Cost Projections of Small Modular Reactors: A Model-Based Analysis. IAEA-CN-123/45. Preprint 2024, 1–7. [Google Scholar] [CrossRef]
- Kindra, V.; Maksimov, I.; Zlyvko, O.; Rogalev, A.; Rogalev, N. Thermodynamic Analysis and Comparison of Power Cycles for Small Modular Reactors. Energies 2024, 17, 1650. [Google Scholar] [CrossRef]
- Rahmanta, M.A.; Harto, A.W.; Agung, A.; Ridwan, M.K. Nuclear Power Plant to Support Indonesia’s Net Zero Emissions: A Case Study of Small Modular Reactor Technology Selection Using Technology Readiness Level and Levelized Cost of Electricity Comparing Method. Energies 2023, 16, 3752. [Google Scholar] [CrossRef]
- Mignacca, B.; Locatelli, G. Economics and finance of Small Modular Reactors: A systematic review and research agenda. Renew. Sustain. Energy Rev. 2020, 118, 109519. [Google Scholar] [CrossRef]
- Steffen, B.; Beuse, M.; Tautorat, P.; Schmidt, T.S. Experience Curves for Operations and Maintenance Costs of Renewable Energy Technologies. Joule 2019, 4, 359–375. [Google Scholar] [CrossRef]
- Vartiainen, E.; Masson, G.; Breyer, C.; Moser, D.; Medina, E.R. Impact of weighted average cost of capital, capital expenditure, and other parameters on future utility-scale PV levelised cost of electricity. Prog. Photovolt. 2019, 28, 439–453. [Google Scholar] [CrossRef]
- Ivkovic, B. Wind Power Plants, Profitability of Investments in Distributed Sources of Electricity. 2014. Available online: https://www.ho-cired.hr/wp-content/uploads/2014/12/Ivkovic_-Vjetroelektrane_1.pdf (accessed on 19 February 2025). (In Croatian).
- International Renewable Energy Agency. Renewable Power Generation Costs in 2023. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2024/Sep/IRENA_Renewable_power_generation_costs_in_2023.pdf (accessed on 19 February 2025).


| Large-Scale NPP with PWR | Modular NPP with SMR | Solar and Wind Power Plants + PHES | |||
|---|---|---|---|---|---|
| Solar | Wind | PHES | |||
| Net capacity (MWel) | 1200 | 4x300 | 3033 | 1706 | - |
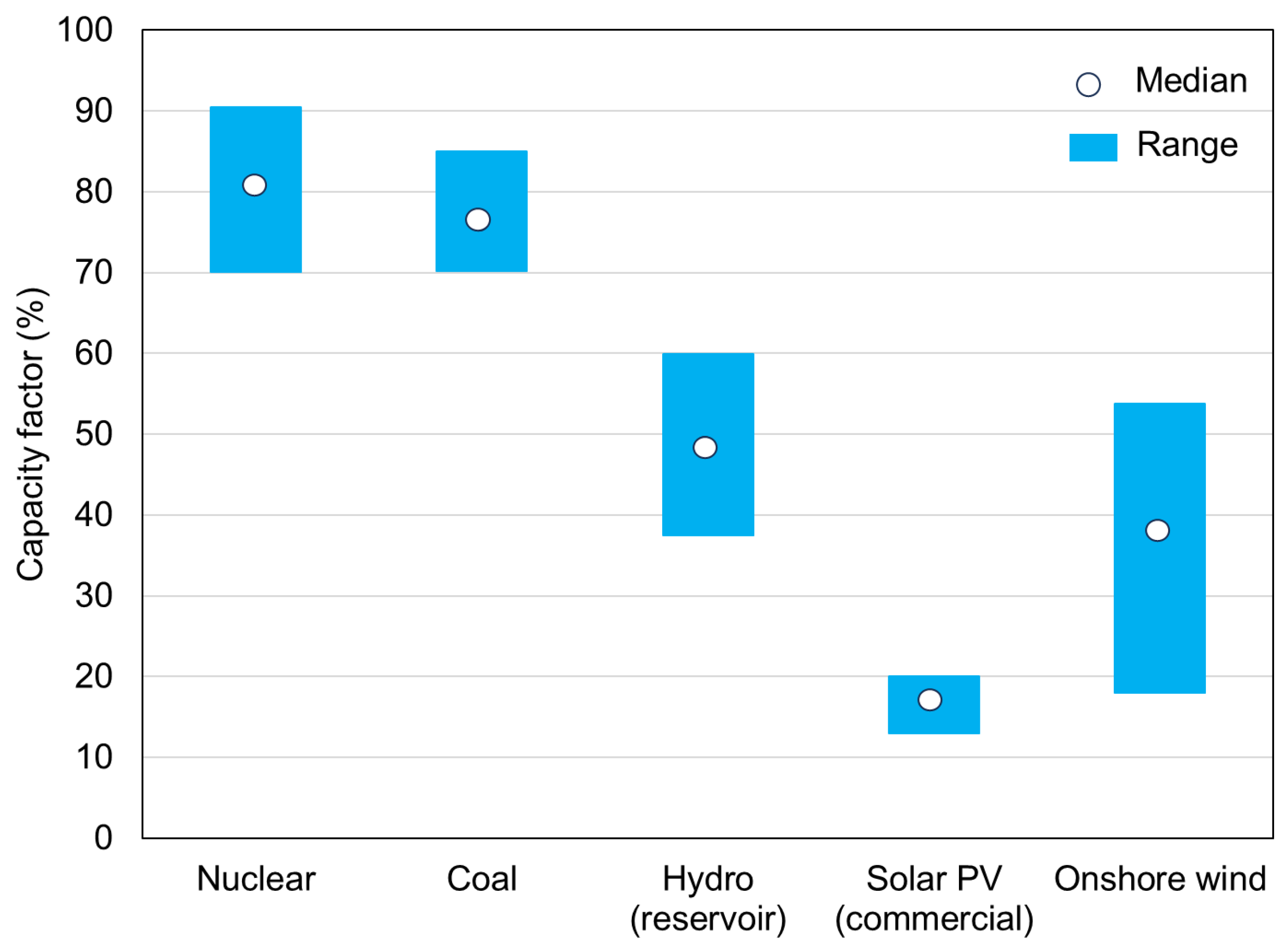
| Capacity factor (%) | 91 | 91 | 18 | 32 | - |
| Total overnight cost (USD/kW) | 7777 | 8349 | 1808 | 2098 | - |
| Total investment cost (USD M) | 9332 | 4x2505 | 5484 | 3579 | 3100 |
| The period of exploitation (year) | 60 | 60 | 25 | 25 | - |
| The construction period (year) | 9 | 3 (per one module) | 2 | 3 | 5 |
| The fuel costs (USD/MWh) | 9.33 | 9.33 | - | - | - |
| The decommissioning costs (USD M) | 1500 | 1500 | 303 | 256 | - |
| The O&M costs (USD/MWh) | 15 | 15 | 6.34 | 22 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milivojevic, S.; Petrovic, M.M.; Stevanovic, V.D.; Riznic, J.; Lazarevic, M. Techno-Economic Comparison of a Large-Scale Nuclear Power Plant, Small Modular Reactors, and Wind and Solar Power Plant Deployment. Energies 2025, 18, 2355. https://doi.org/10.3390/en18092355
Milivojevic S, Petrovic MM, Stevanovic VD, Riznic J, Lazarevic M. Techno-Economic Comparison of a Large-Scale Nuclear Power Plant, Small Modular Reactors, and Wind and Solar Power Plant Deployment. Energies. 2025; 18(9):2355. https://doi.org/10.3390/en18092355
Chicago/Turabian StyleMilivojevic, Sanja, Milan M. Petrovic, Vladimir D. Stevanovic, Jovica Riznic, and Milos Lazarevic. 2025. "Techno-Economic Comparison of a Large-Scale Nuclear Power Plant, Small Modular Reactors, and Wind and Solar Power Plant Deployment" Energies 18, no. 9: 2355. https://doi.org/10.3390/en18092355
APA StyleMilivojevic, S., Petrovic, M. M., Stevanovic, V. D., Riznic, J., & Lazarevic, M. (2025). Techno-Economic Comparison of a Large-Scale Nuclear Power Plant, Small Modular Reactors, and Wind and Solar Power Plant Deployment. Energies, 18(9), 2355. https://doi.org/10.3390/en18092355






