Research on Coordinated Control of Dynamic Reactive Power Sources of DC Blocking and Commutation Failure Transient Overvoltage in New Energy Transmission
Abstract
1. Introduction
2. Causes of Transient Overvoltage
2.1. DC Blocking
2.2. Commutation Failure
3. Dynamic Reactive Power Source Device Analysis
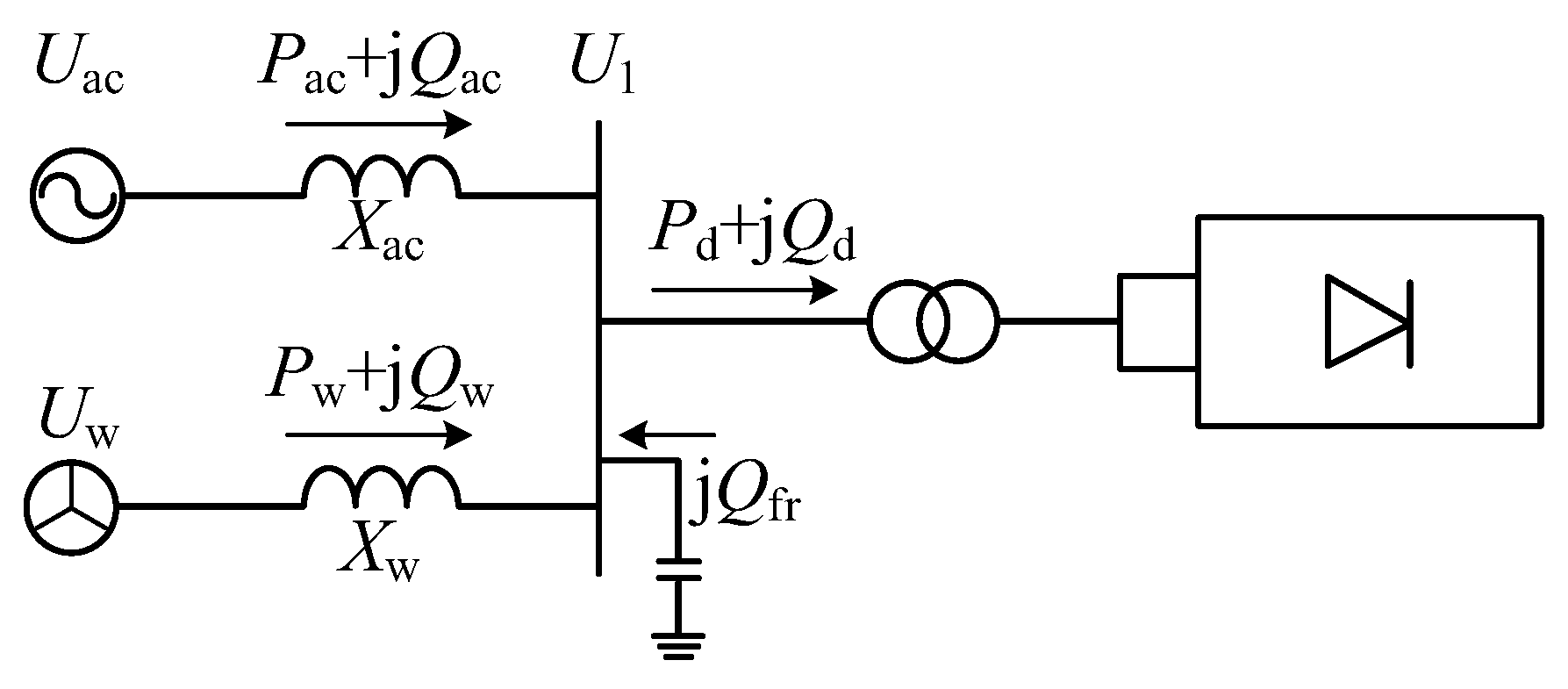
3.1. Basic Model of Dynamic Reactive Power Source Devices
3.2. Sensitivity Analysis of Dynamic Reactive Power Source Control Parameters
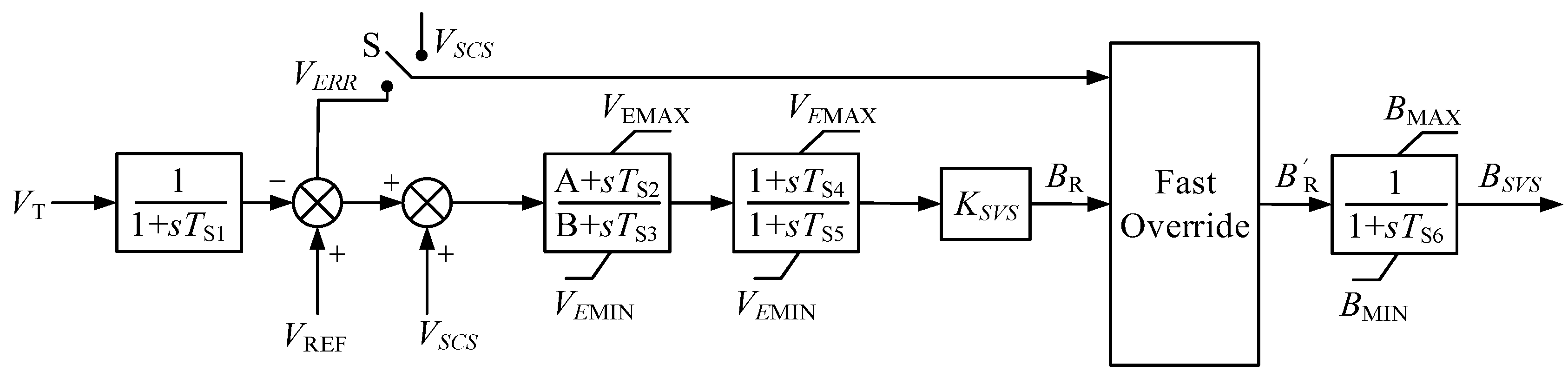
3.2.1. SVC Parameter Sensitivity Analysis
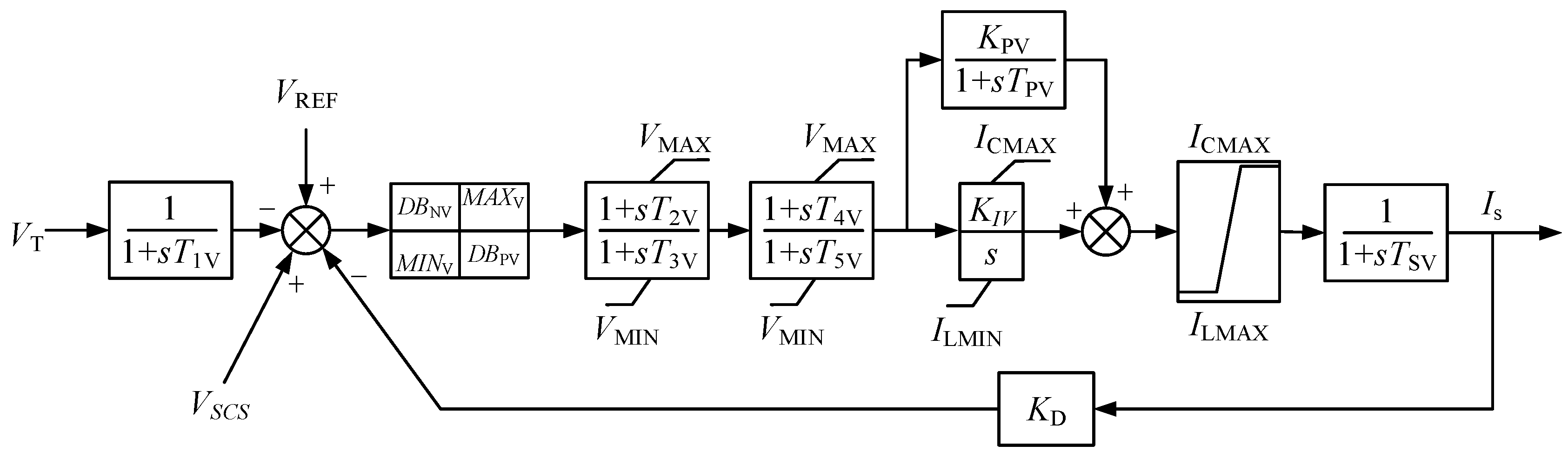
3.2.2. STATCOM Parameter Sensitivity Analysis
3.2.3. Synchronous Condenser Parameter Sensitivity Analysis
4. Multi-Objective Collaborative Control Strategy for Dynamic Reactive Power Sources
4.1. Collaborative Optimization Control Model for Transient Overvoltage Suppression
4.1.1. Objective Function
4.1.2. Constraints
- System Power Balance Constraint
- System State Variable Constraints
- Control Parameter Range Constraints
4.2. Collaborative Optimization Control Solution Method
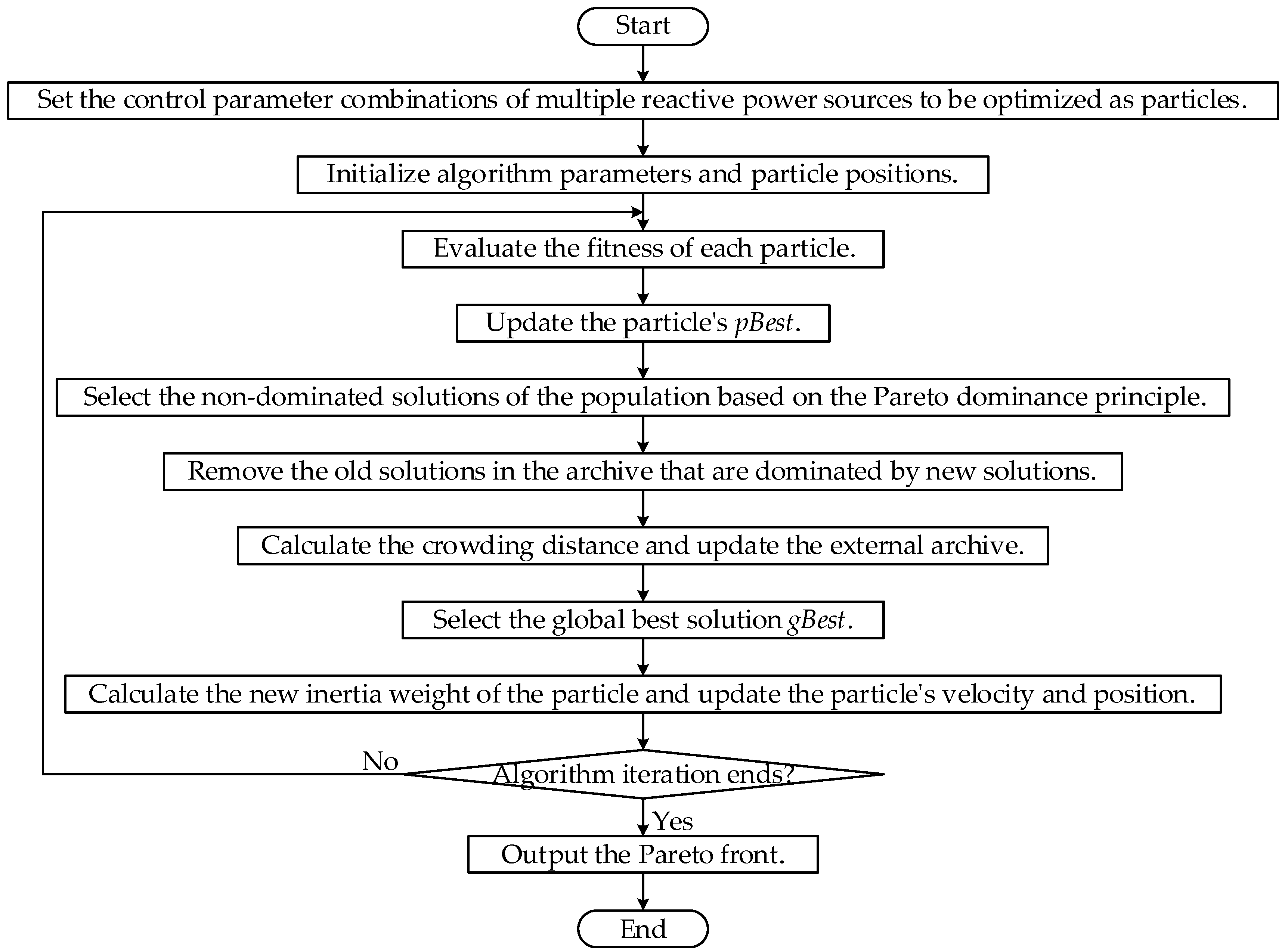
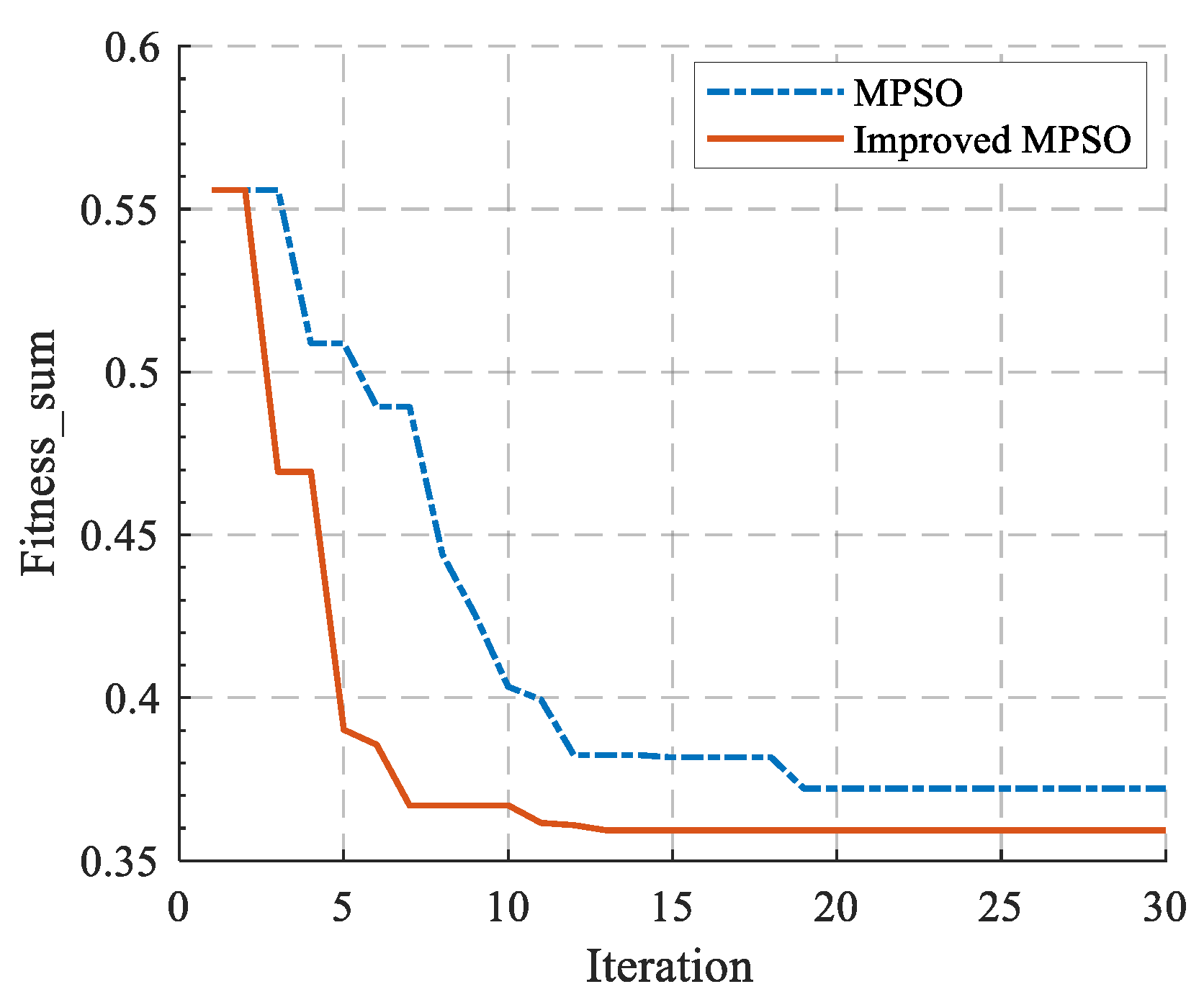
4.2.1. Particle Swarm Optimization Algorithm
4.2.2. Dynamic Inertia Weight Considering Comprehensive Trajectory Sensitivity
4.2.3. Multi-Objective Optimization and Pareto Front
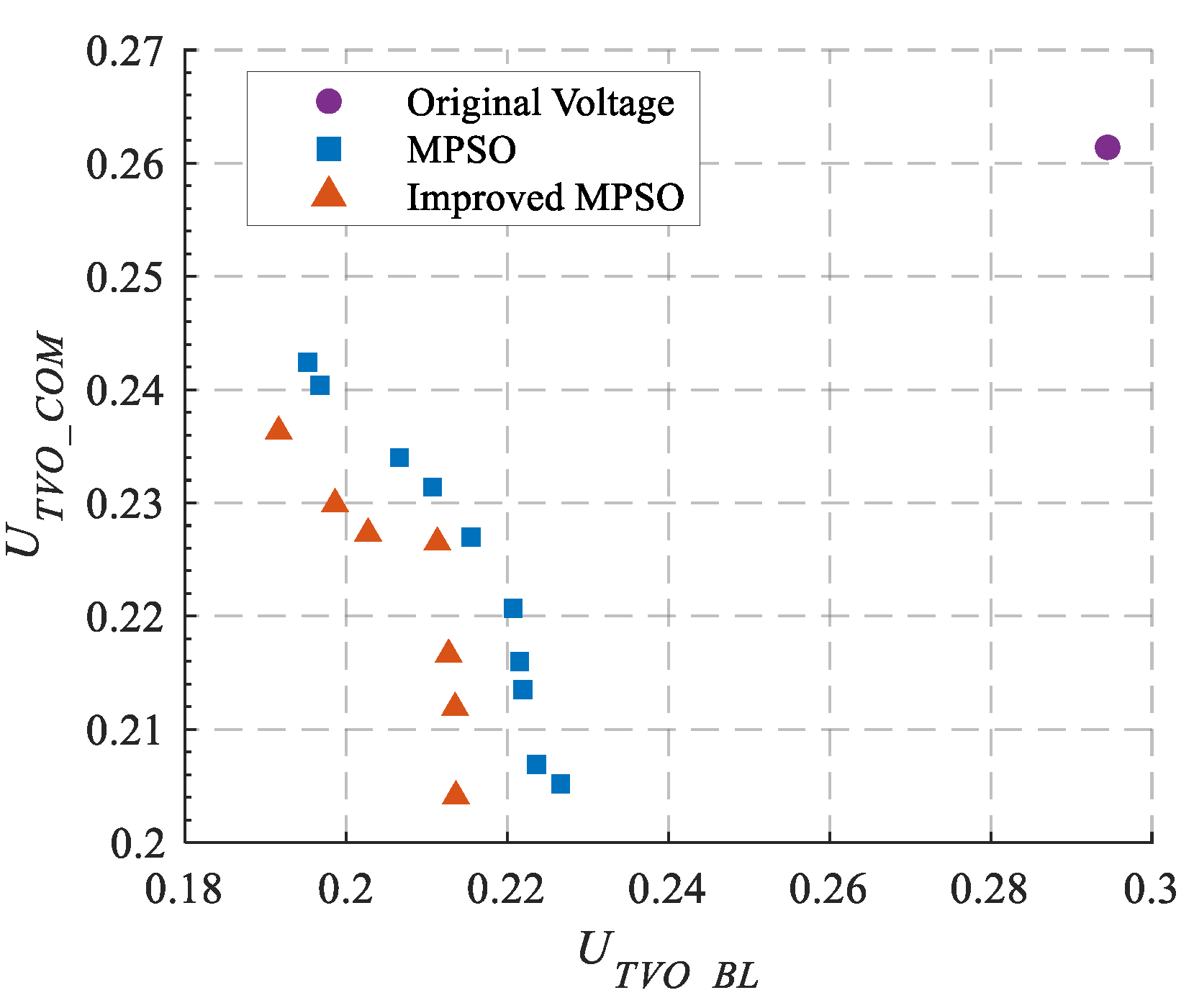
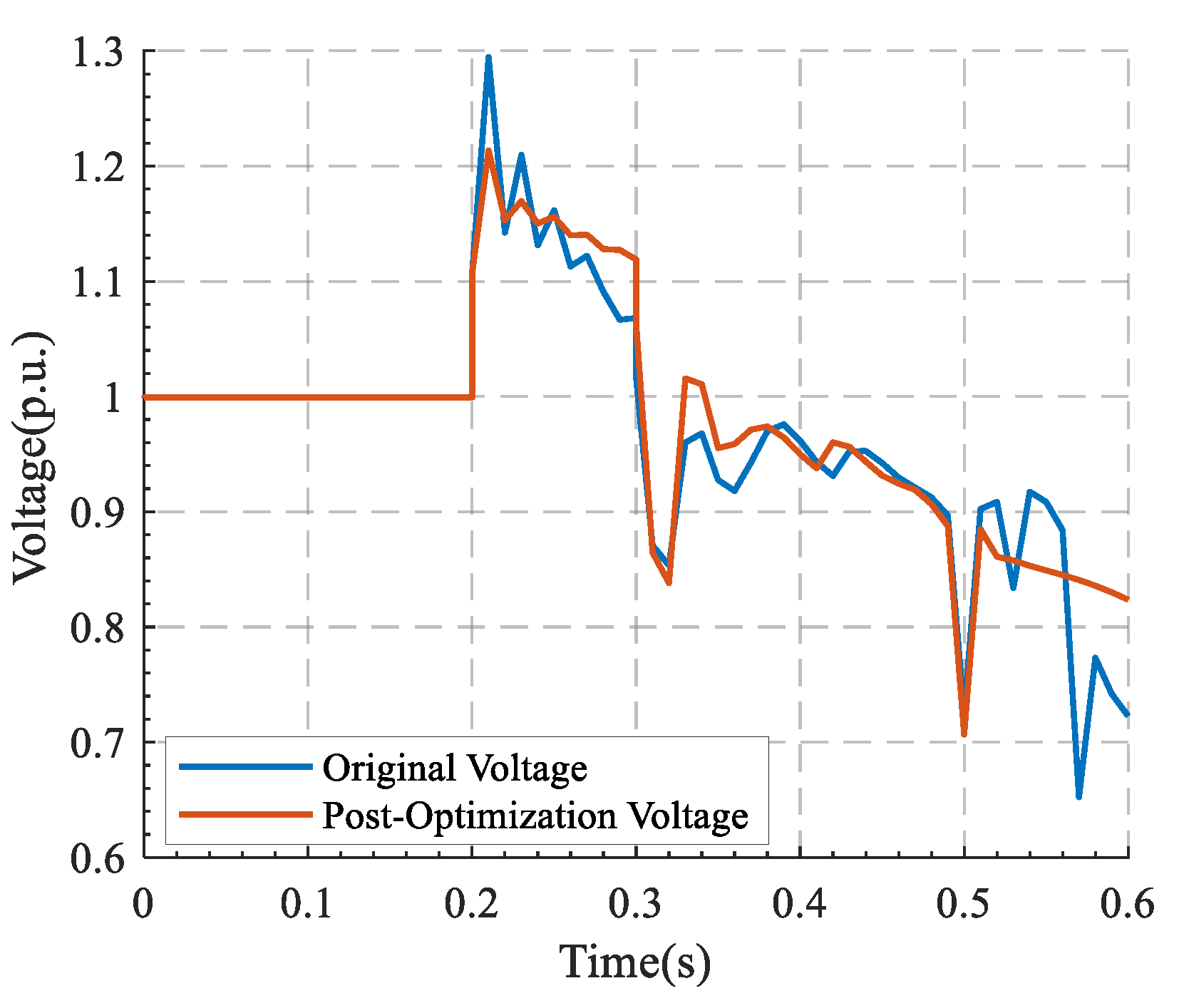
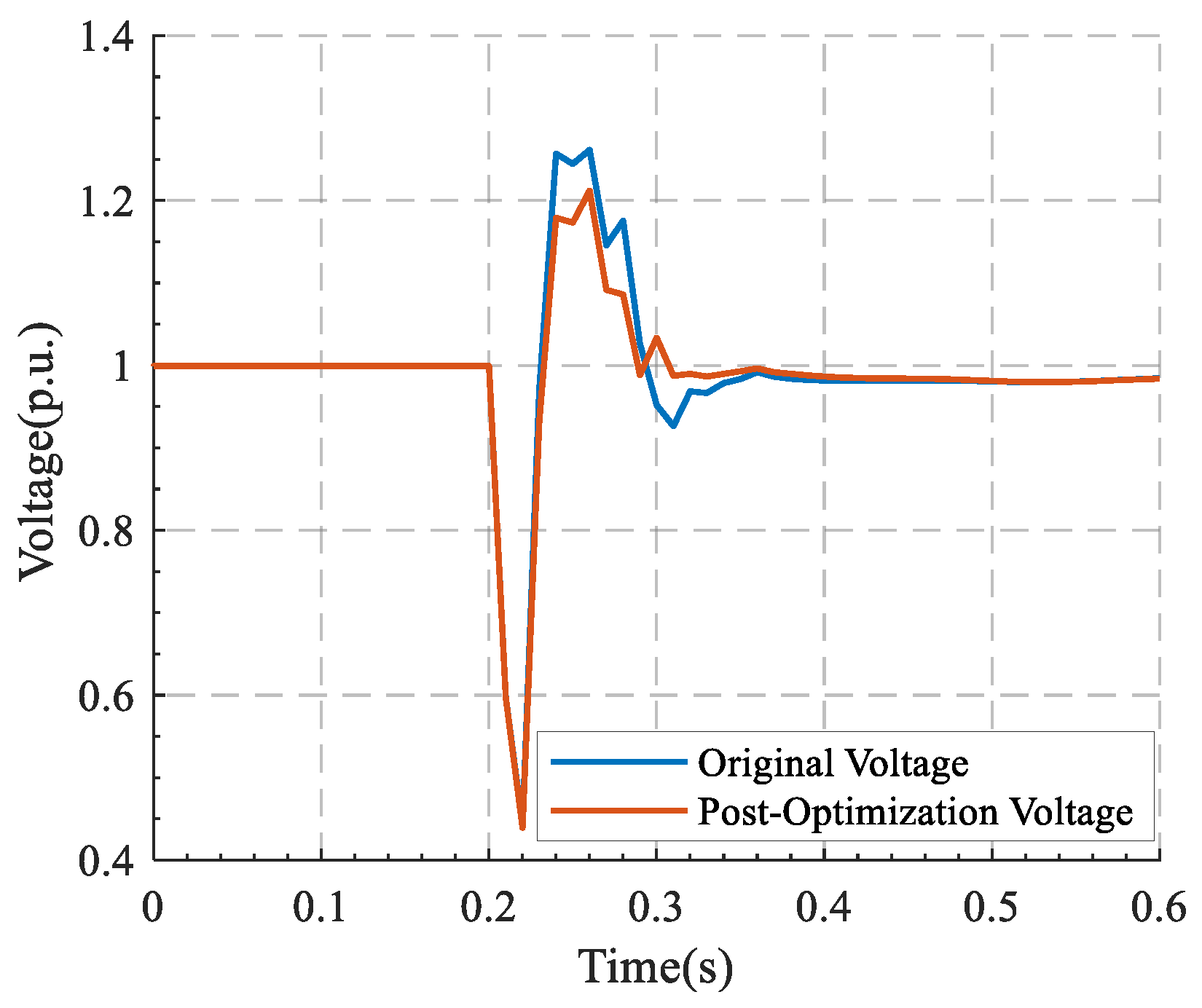
4.3. Case Study Analysis
4.3.1. Equivalent Three-Machine System
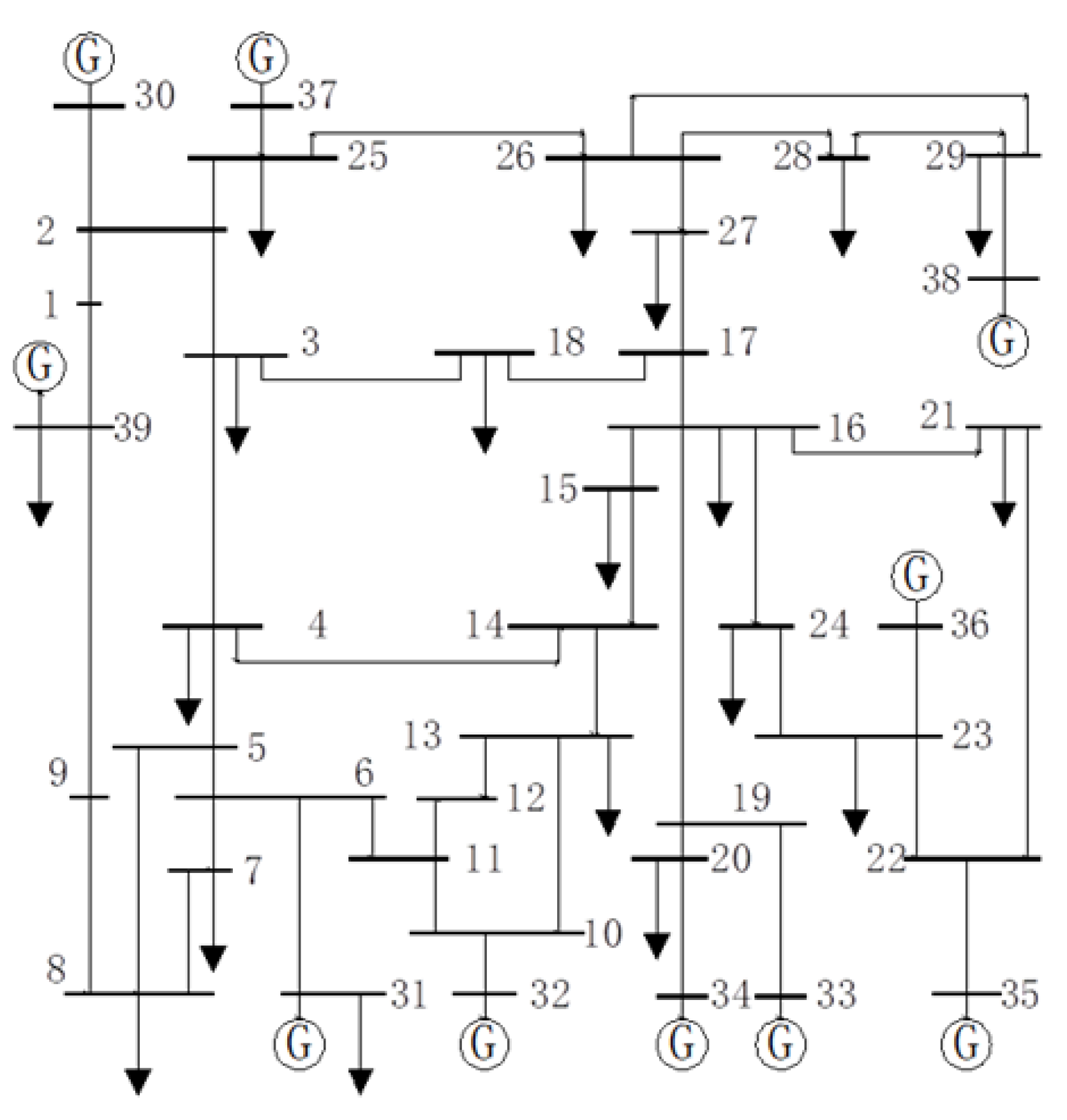
4.3.2. Dual IEEE 39-Bus Hybrid System
5. Conclusions
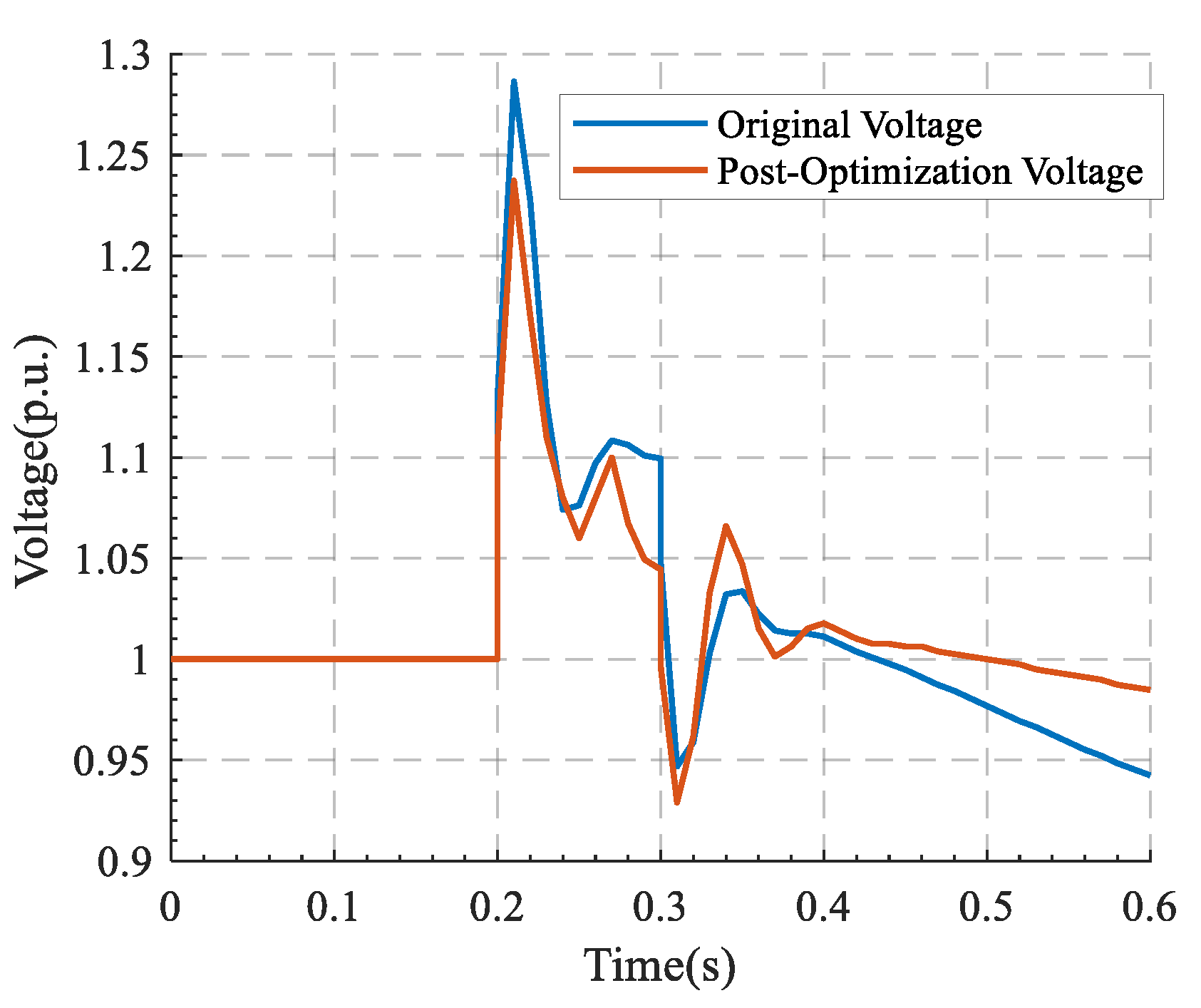
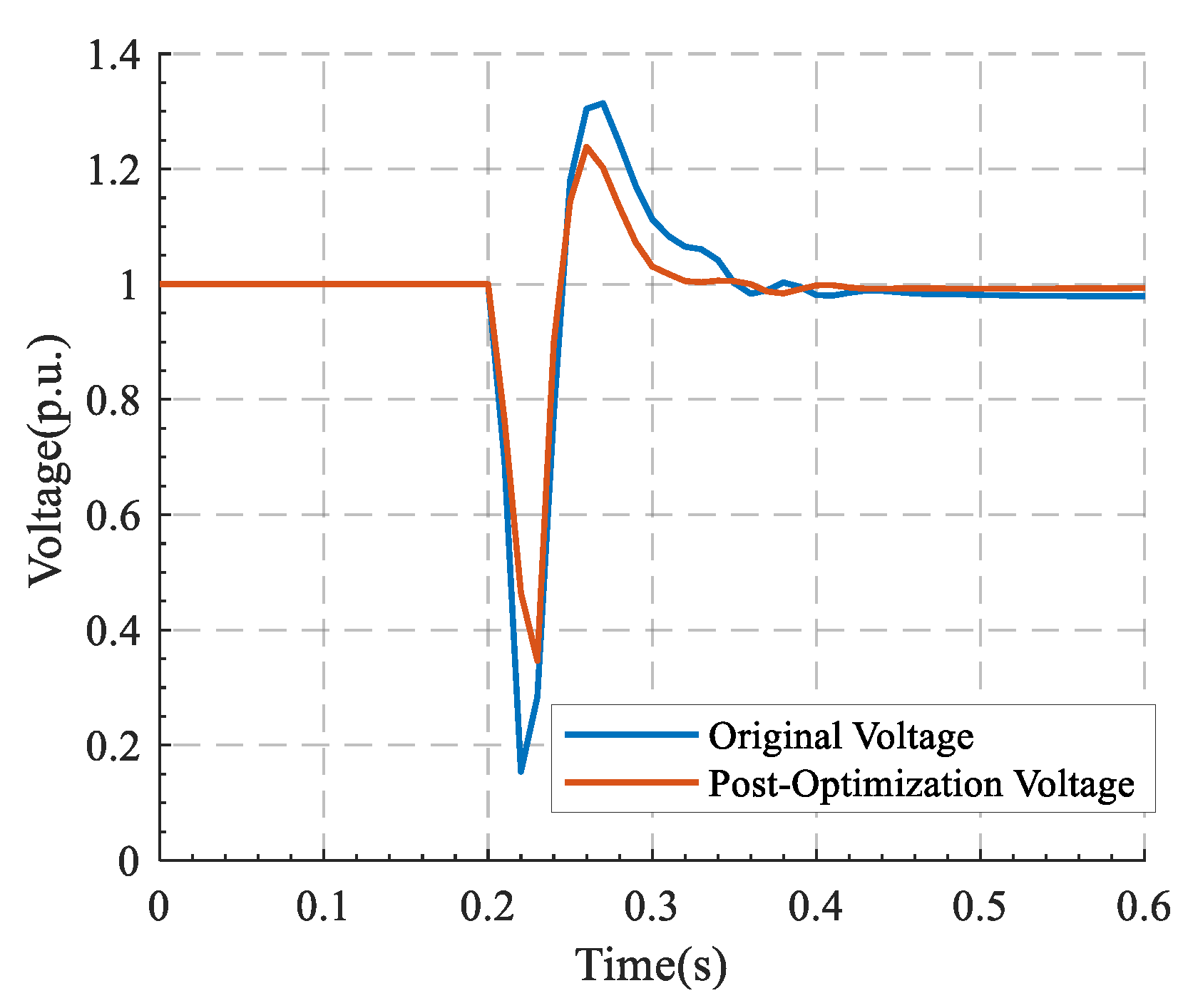
- A typical system model for renewable energy transmission via DC lines is established. The formation process of transient overvoltages under DC blocking and commutation failure faults is analyzed, and the influence of dynamic reactive power imbalance on voltage evolution is elucidated.
- Based on trajectory sensitivity analysis and parameter perturbation methods, the impacts of key control parameters of dynamic reactive power devices on transient overvoltages under different faults are systematically quantified. Highly sensitive parameters under multiple fault conditions are identified, leading to a parameter prioritization framework that provides a solid theoretical basis for fine-grained, coordinated control of multiple devices.
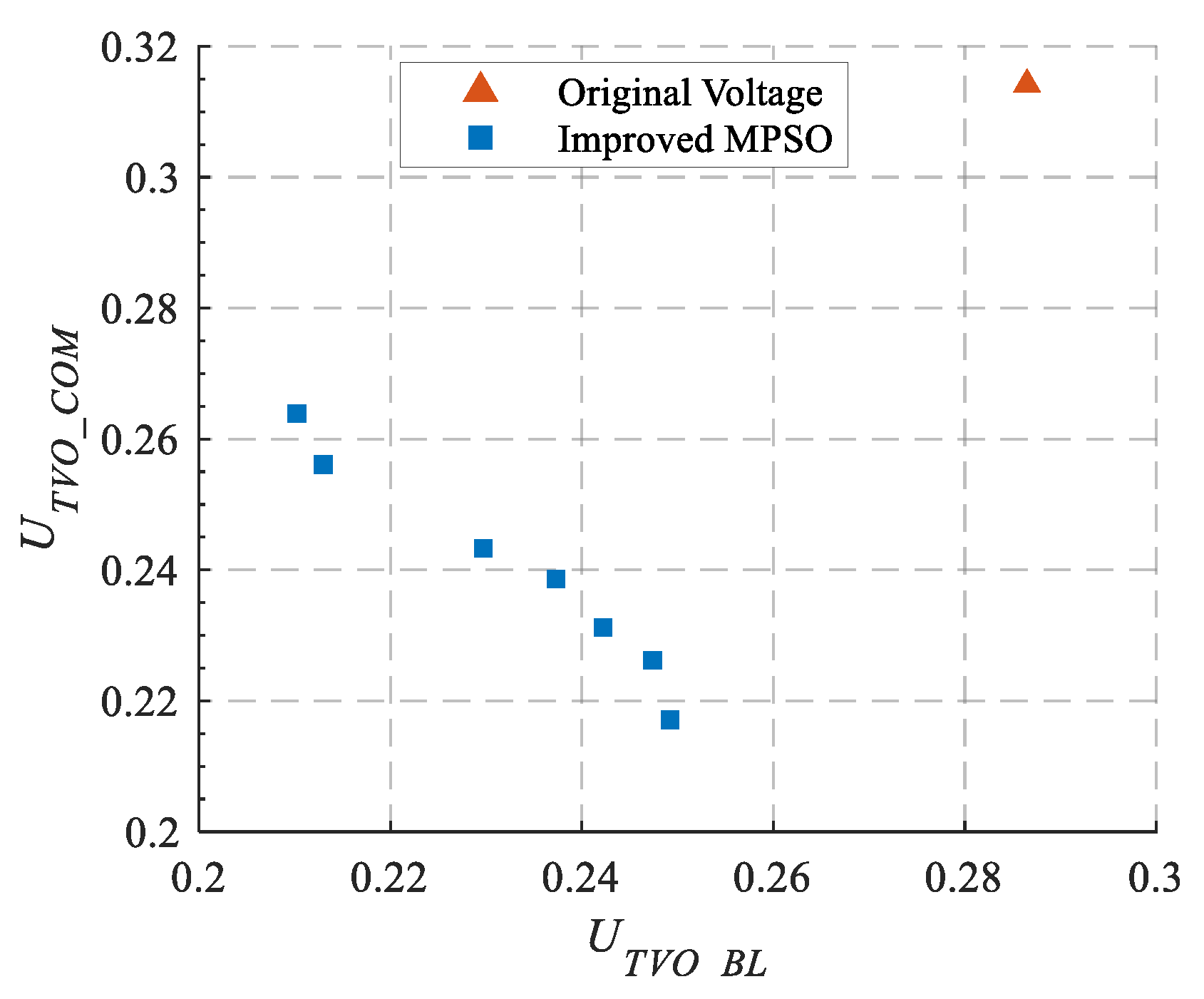
- A multi-objective coordinated optimization model for multiple reactive power devices is constructed to simultaneously address the suppression requirements of different fault types. A novel optimization algorithm integrating comprehensive trajectory sensitivity with a dynamic inertia weight particle swarm optimization method is proposed, which is combined with Pareto front theory to achieve global optimization of control parameters and coordination among multiple objectives. This significantly enhances the overall dynamic response capabilities of reactive power devices and improves system voltage stability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harrison, A.; Alombah, N.H.; Kamel, S.; Ghoneim, S.S.M.; El Myasse, I.; Kotb, H. Towards a Simple and Efficient Implementation of Solar Photovoltaic Emulator: An Explicit PV Model Based Approach. Eng. Proc. 2023, 56, 261. [Google Scholar] [CrossRef]
- El Myasse, I.; El Magri, A.; Watil, A.; Mansouri, A.; Kissaoui, M.; Ouabi, H.; Blouh, F.E. Enhancing Wind Power Plant Integration Using a T-NPC Converter with DR-HVDC Transmission Systems. IFAC-PapersOnLine 2024, 58, 472–477. [Google Scholar] [CrossRef]
- Feng, N.; Feng, Y.; Su, Y.; Zhang, Y.; Niu, T. Dynamic Reactive Power Optimization Strategy for AC/DC Hybrid Power Grid Considering Different Wind Power Penetration Levels. IEEE Access 2024, 12, 187471–187482. [Google Scholar] [CrossRef]
- Adireddy, R.; Deepak, B.S.; Ravindra, M.; Ramachandra Murthy, K.V.S. Study of Different Techniques to Mitigate Temporary Overvoltage in Photovoltaic System. Mater. Today Proc. 2022, 56, 3222–3226. [Google Scholar] [CrossRef]
- Mohseni, M.; Masoum, M.A.S.; Islam, S.M. Low Voltage Ride-through of DFIG Wind Turbines Complying with Western-Power Grid Code in Australia. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Amin, M.; Molinas, M. Understanding the Origin of Oscillatory Phenomena Observed Between Wind Farms and HVdc Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 378–392. [Google Scholar] [CrossRef]
- Liang, W.; Shen, C.; Sun, H.; Xu, S. Overvoltage Mechanism and Suppression Method for LCC-HVDC Rectifier Station Caused by Sending End AC Faults. IEEE Trans. Power Deliv. 2024, 39, 1299–1302. [Google Scholar] [CrossRef]
- Yin, C.; Li, F. Reactive Power Control Strategy for Inhibiting Transient Overvoltage Caused by Commutation Failure. IEEE Trans. Power Syst. 2021, 36, 4764–4777. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Li, Y.; Hu, J.; Ma, S.; Wang, T. Transient Overvoltage Suppression of LCC-HVDC Sending-end System Based on DC Current Control Optimisation. IET Energy Syst. Integr. 2024, 6, 182–195. [Google Scholar] [CrossRef]
- Mannen, T.; Wada, K. Overvoltage Suppression in Initial Charge Control for DC Capacitor Using Multiple Leg Short-Circuits with SiC-MOSFETs in Power Converters. IEEE Open J. Power Electron. 2023, 4, 703–715. [Google Scholar] [CrossRef]
- Maruta, H.; Hoshino, D. Transient Response Improvement of Repetitive-Trained Neural Network Controlled DC-DC Converter with Overcompensation Suppression. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 2088–2093. [Google Scholar]
- Hamdan, I.; Ibrahim, A.; Noureldeen, O. Modified STATCOM Control Strategy for Fault Ride-through Capability Enhancement of Grid-Connected PV/Wind Hybrid Power System during Voltage Sag. SN Appl. Sci. 2020, 2, 364. [Google Scholar] [CrossRef]
- Guo, C.; Wang, Z.; Mu, Z.; Yin, H. Research on Power Frequency Overvoltage and Reactive Power Compensation of Transmission Lines Considering New Energy Access. In Proceedings of the 2024 9th Asia Conference on Power and Electrical Engineering (ACPEE), Shanghai, China, 11–13 April 2024; pp. 1888–1892. [Google Scholar] [CrossRef]
- Wu, D.; Ma, B.; Du, Y.; Zhao, T.; Jia, Z. Dynamic Reactive Power Allocation with Multi-Source Coordination in the AC Collecting System of the Large Scale Renewable Energy Base. In Proceedings of the 2024 4th Power System and Green Energy Conference (PSGEC), Shanghai, China, 22–24 August 2024; pp. 581–585. [Google Scholar] [CrossRef]
- Manuela Monteiro Pereira, R.; Manuel Machado Ferreira, C.; Maciel Barbosa, F. Comparative Study of STATCOM and SVC Performance on Dynamic Voltage Collapse of an Electric Power System with Wind Generation. IEEE Lat. Am. Trans. 2014, 12, 138–145. [Google Scholar] [CrossRef]
- Pathak, A.K.; Sharma, M.P.; Gupta, M. Effect on Static and Dynamic Reactive Power in High Penetration Wind Power System with Altering SVC Location. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Xu, Y.; Dong, Z.Y.; Zhao, J.; Xue, Y.; Hill, D.J. Trajectory Sensitivity Analysis on the Equivalent One-Machine-Infinite-Bus of Multi-Machine Systems for Preventive Transient Stability Control. IET Gener. Transm. Distrib. 2015, 9, 276–286. [Google Scholar] [CrossRef]
- Umer, M.; Olejnik, P. Approximate Analytical Approaches to Nonlinear Differential Equations: A Review of Perturbation, Decomposition and Coefficient Methods in Engineering. Arch. Computat. Methods Eng. 2025, in press. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Zdiri, S.; Chrouta, J.; Zaafouri, A. Cooperative Multi-Swarm Particle Swarm Optimization Based on Adaptive and Time-Varying Inertia Weights. In Proceedings of the 2021 IEEE 2nd International Conference on Signal, Control and Communication (SCC), Tunis, Tunisia, 20–22 December 2021; pp. 200–207. [Google Scholar]
- Giagkiozis, I.; Fleming, P.J. Pareto Front Estimation for Decision Making. Evol. Comput. 2014, 22, 651–678. [Google Scholar] [CrossRef] [PubMed]
- Tušar, T.; Filipič, B. Visualization of Pareto Front Approximations in Evolutionary Multiobjective Optimization: A Critical Review and the Prosection Method. IEEE Trans. Evol. Comput. 2015, 19, 225–245. [Google Scholar] [CrossRef]
- Honghai, K.; Fuqing, S.; Yurui, C.; Kai, W.; Zhiyi, H. Reactive Power Optimization for Distribution Network System with Wind Power Based on Improved Multi-Objective Particle Swarm Optimization Algorithm. Electr. Power Syst. Res. 2022, 213, 108731. [Google Scholar] [CrossRef]
- Raquel, C.R.; Naval, P.C. An Effective Use of Crowding Distance in Multiobjective Particle Swarm Optimization. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, Washington, DC, USA, 25–29 June 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 257–264. [Google Scholar]


| Parameter Name | Initial Value | Range |
|---|---|---|
| Ts1 Filter Time Constant (s) | 0.02 | (0.00, 0.20) |
| VEMAX Maximum Voltage Deviation (p.u.) | 1.16 | (0.70, 1.30) |
| Ts2 First Stage Lead Time Constant (s) | 0.10 | (0.00, 1.40) |
| Ts3 First Stage Lag Time Constant (s) | 0.10 | (0.01, 1.50) |
| Ts4 Second Stage Lead Time Constant (s) | 1.00 | (0.00, 8.00) |
| Ts5 Second Stage Lag Time Constant (s) | 1.00 | (0.10, 4.90) |
| Ksvs Continuous Control Gain | 4.46 | (0.50, 9.50) |
| DV Voltage Deviation (p.u.) | 0.10 | (0.01, 0.40) |
| Parameter Name | BL TSTVO_pa | BL ITSTVO_pa | COM TSTVO_pa | COM ITSTVO_pa |
|---|---|---|---|---|
| Ts1 | −9.40 | −6.67 | −38.40 | −6.55 |
| VEMAX | 0.00 | 0.58 | 0.00 | −0.58 |
| Ts2 | 1.60 | 0.41 | 9.90 | 1.00 |
| Ts3 | −8.50 | −3.42 | −4.30 | −7.00 |
| Ts4 | 2.20 | 0.71 | 7.20 | 0.99 |
| Ts5 | −2.00 | −1.08 | 1.00 | −1.69 |
| Ksvs | 2.68 | 2.68 | −1.78 | −1.49 |
| DV | −26.75 | −7.49 | 4.25 | 6.85 |
| Parameter Name | Initial Value | Range |
|---|---|---|
| VOL_REFH | 1.10 | (0.80, 1.30) |
| SETDATAH | 5.00 | (0.00, 20.00) |
| VOL_HIGH | 1.10 | (1.00, 1.30) |
| VOL_HIGH_RET | 1.1 | (1.00, 1.30) |
| VOL_HIGH_DELAY | 0 | (0.00, 5.00) |
| Parameter Name | BL TSTVO_pa | BL ITSTVO_pa | COM TSTVO_pa | COM ITSTVO_pa |
|---|---|---|---|---|
| VOL_REFH | −314.60 | −450.56 | 0.00 | −125.40 |
| SETDATAH | 14.50 | 29.13 | 0.00 | 14.25 |
| VOL_HIGH | −88.00 | −50.60 | 0.00 | −30.80 |
| VOL_HIGH_RET | / | / | 0.00 | 0.00 |
| VOL_HIGH_DELAY | −3.20 | −0.32 | −16.80 | −1.68 |
| Parameter Name | Initial Value | Range |
|---|---|---|
| TR Regulator Input Filter Time Constant (s) | 0.02 | (0.01, 2.00) |
| K Regulator Gain | 56.25 | (1.00, 70.00) |
| KV Proportional Integral | 1.00 | (0.00, 10.00) |
| T1 First Stage Lead Time Constant (s) | 1.00 | (0.10, 10.00) |
| T2 First Stage Lag Time Constant (s) | 10.00 | (0.20, 20.00) |
| T3 Second Stage Lead Time Constant (s) | 0.04 | (0.01, 1.00) |
| T4 Second Stage Lag Time Constant (s) | 0.03 | (0.01, 1.00) |
| KA Voltage Regulator Gain | 14.20 | (1.00, 20.00) |
| TA Voltage Regulator Amplifier Time Constant (s) | 0.02 | (0.01, 1.00) |
| Parameter Name | BL TSTVO_pa | BL ITSTVO_pa | COM TSTVO_pa | COM ITSTVO_pa |
|---|---|---|---|---|
| TR | 0.00 | 0.00 | −96.00 | −16.38 |
| K | 0.00 | 2.53 | −2.25 | −28.04 |
| KV | 0.00 | 0.00 | 0.10 | 0.03 |
| T1 | 0.00 | 0.12 | −1.50 | −2.75 |
| T2 | 0.00 | 0.10 | 2.50 | 2.12 |
| T3 | 0.00 | 0.01 | 2.40 | 0.26 |
| T4 | 0.00 | −0.07 | 0.00 | 0.43 |
| KA | 0.00 | 1.20 | −2.13 | −23.02 |
| TA | 0.00 | −0.05 | −0.20 | 0.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Yuan, Z.; Chen, D.; Li, Z.; Tang, X.; Song, Y.; Zhou, G. Research on Coordinated Control of Dynamic Reactive Power Sources of DC Blocking and Commutation Failure Transient Overvoltage in New Energy Transmission. Energies 2025, 18, 2349. https://doi.org/10.3390/en18092349
Sun S, Yuan Z, Chen D, Li Z, Tang X, Song Y, Zhou G. Research on Coordinated Control of Dynamic Reactive Power Sources of DC Blocking and Commutation Failure Transient Overvoltage in New Energy Transmission. Energies. 2025; 18(9):2349. https://doi.org/10.3390/en18092349
Chicago/Turabian StyleSun, Shuqin, Zhenghai Yuan, Dezhi Chen, Zaihua Li, Xiaojun Tang, Yunting Song, and Guanghao Zhou. 2025. "Research on Coordinated Control of Dynamic Reactive Power Sources of DC Blocking and Commutation Failure Transient Overvoltage in New Energy Transmission" Energies 18, no. 9: 2349. https://doi.org/10.3390/en18092349
APA StyleSun, S., Yuan, Z., Chen, D., Li, Z., Tang, X., Song, Y., & Zhou, G. (2025). Research on Coordinated Control of Dynamic Reactive Power Sources of DC Blocking and Commutation Failure Transient Overvoltage in New Energy Transmission. Energies, 18(9), 2349. https://doi.org/10.3390/en18092349





