Compressed Air Energy Storage in Salt Caverns Optimization in Southern Ontario, Canada
Abstract
1. Introduction
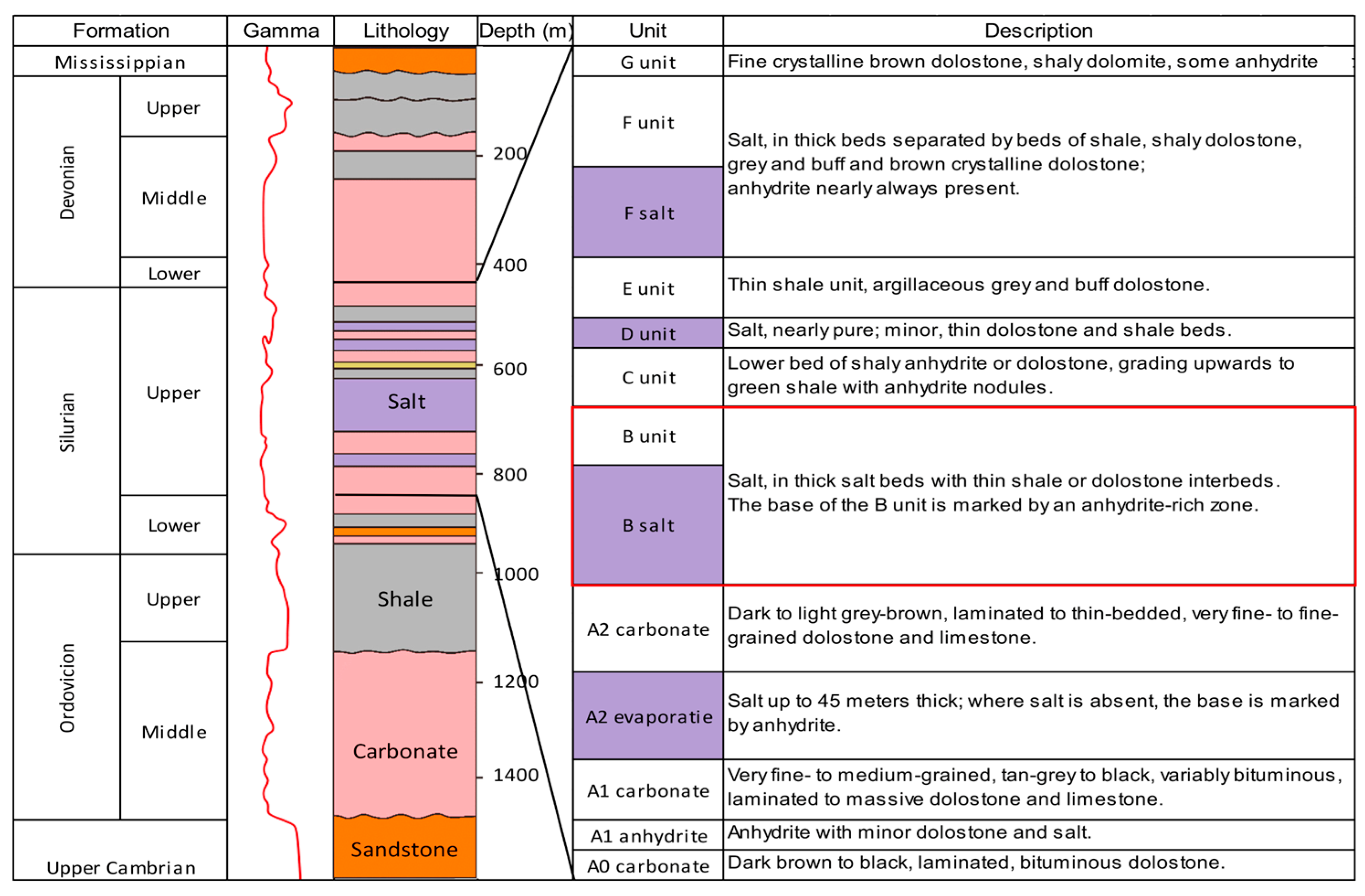
2. Geological Setting
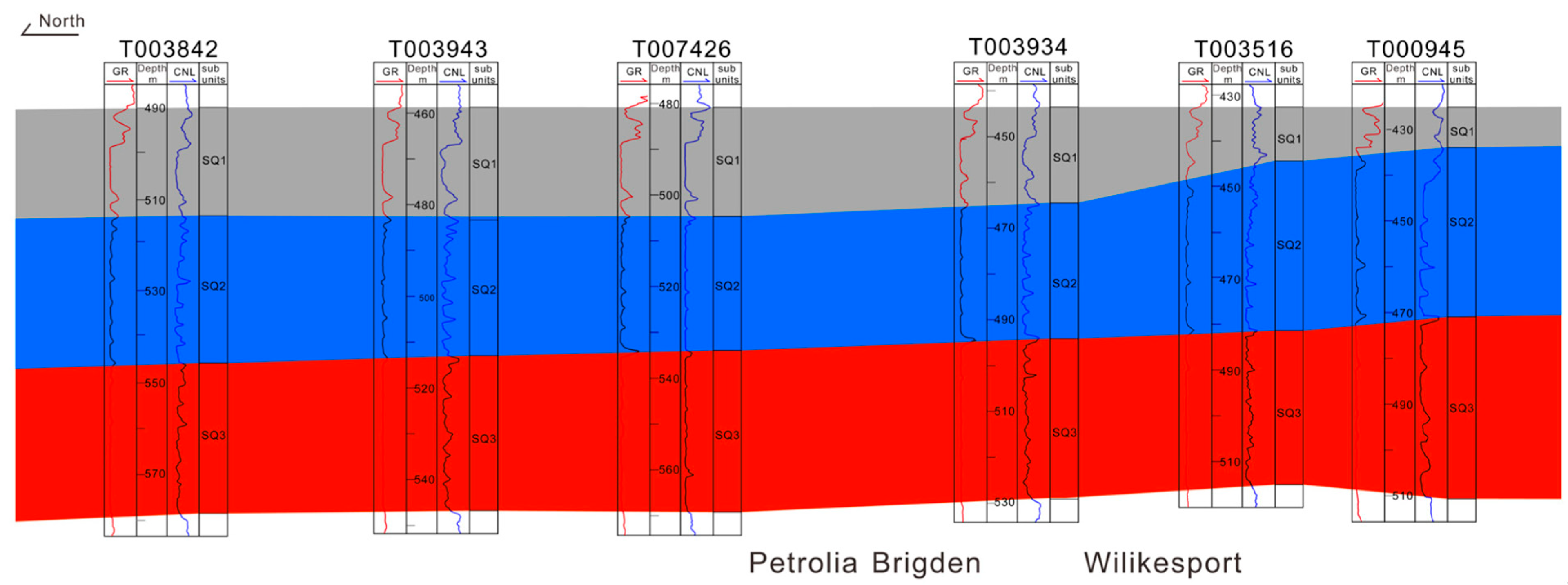
- The SQ1 subunit is characterized by high GR and CNL values, corresponding to interbedded halite and limestone;
- The SQ2 subunit consists of dark, laminated halite with pronounced fluctuations in the logging curves;
- The SQ3 subunit exhibits relatively stable and lower curve values, indicative of massive halite deposits.
3. Constitutive Model
3.1. Elastoplastic Constitutive Model
3.2. Creep Constitutive Model
3.3. Evaluation Model of Tightness
4. Numerical Model
4.1. Cavern Design
- Cylinder
- 2.
- Ellipsoid
4.2. Operating Pressure Design and Leakage Evaluation
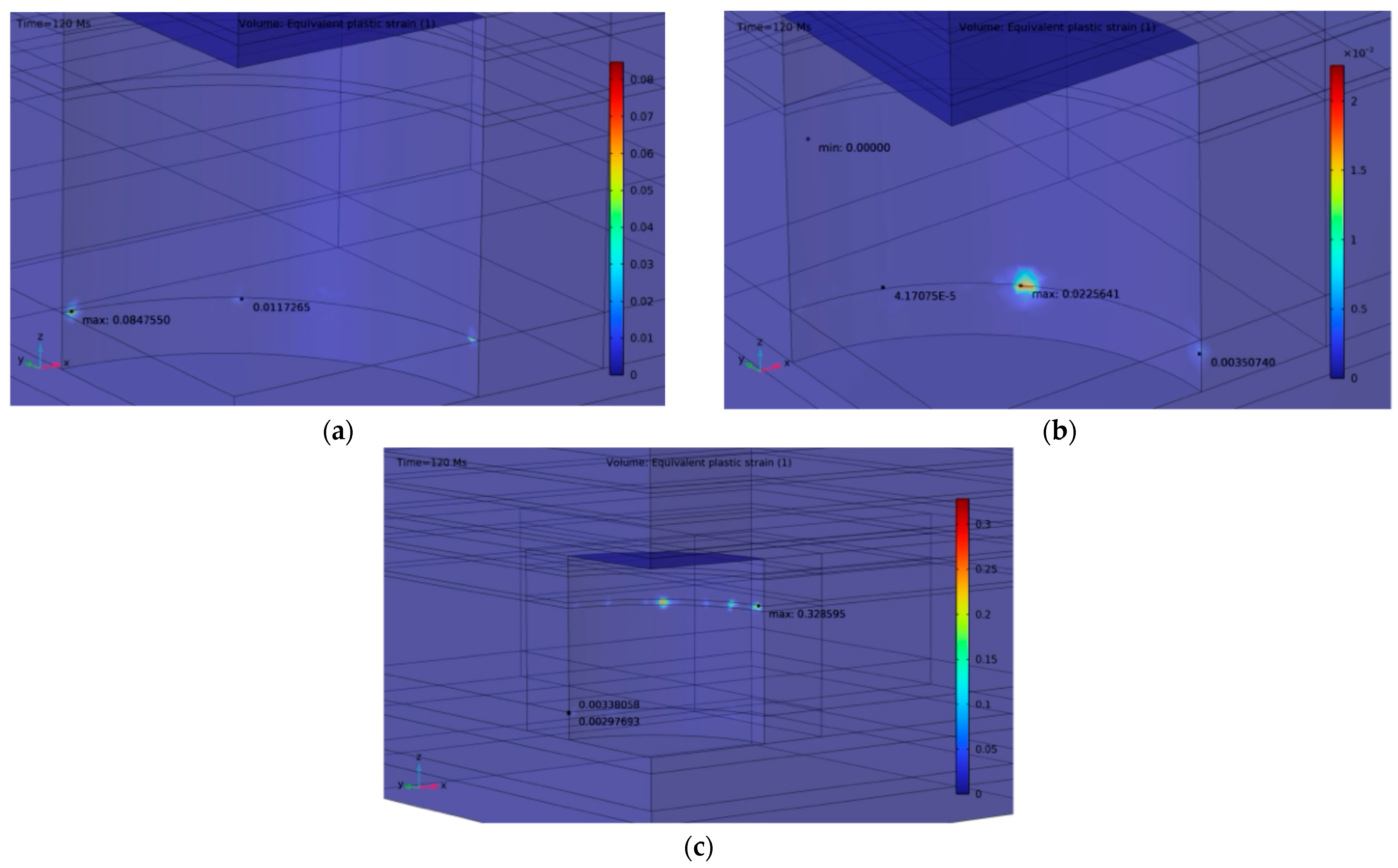
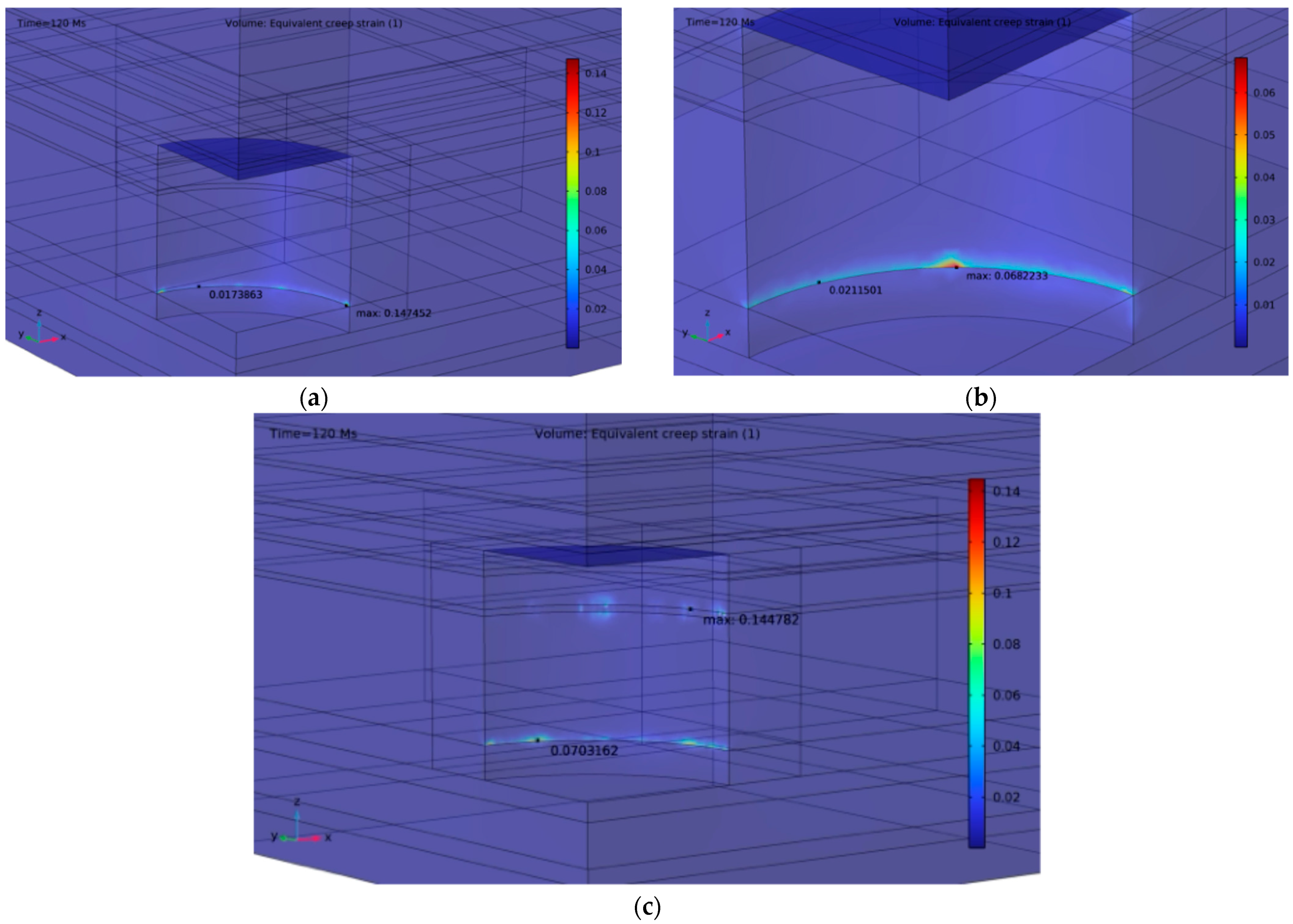
5. Modeling Results
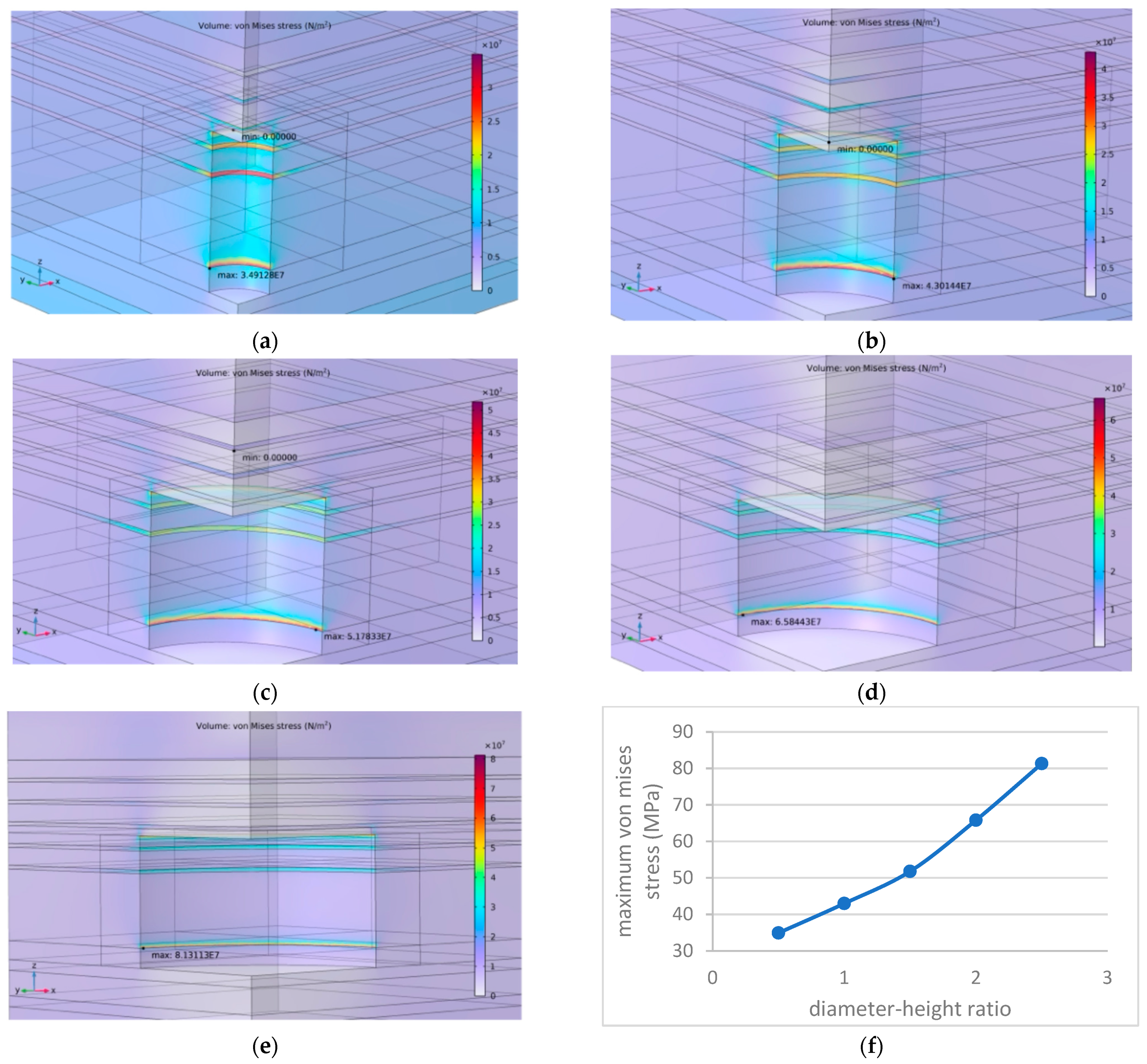
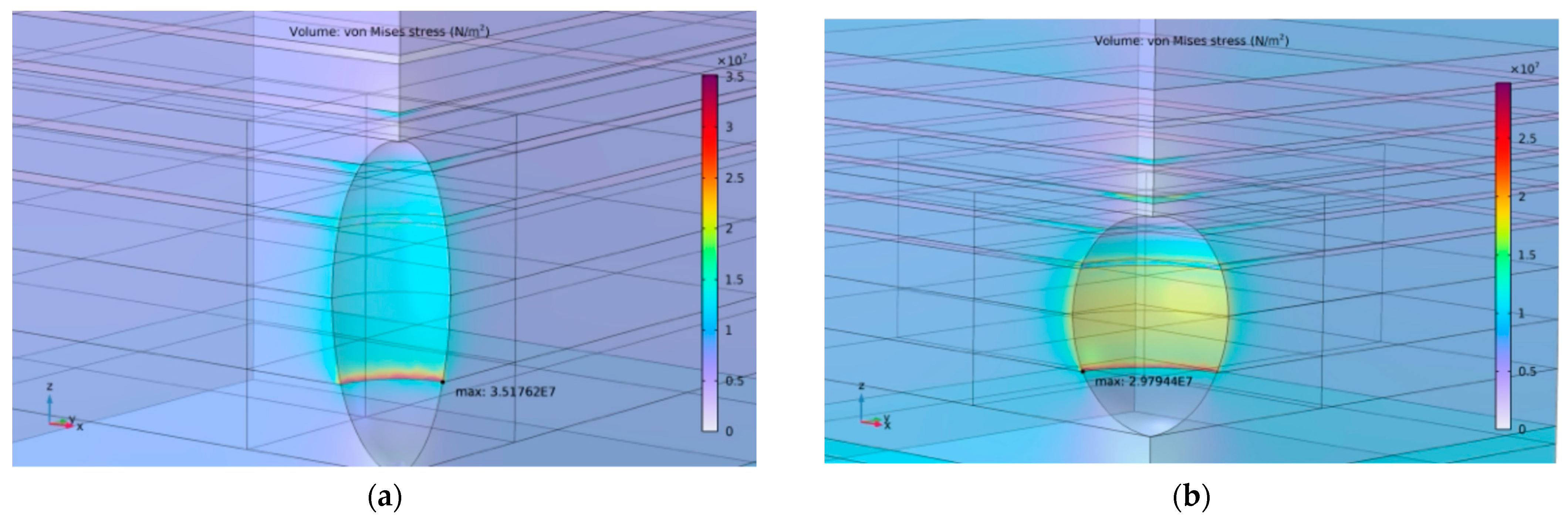
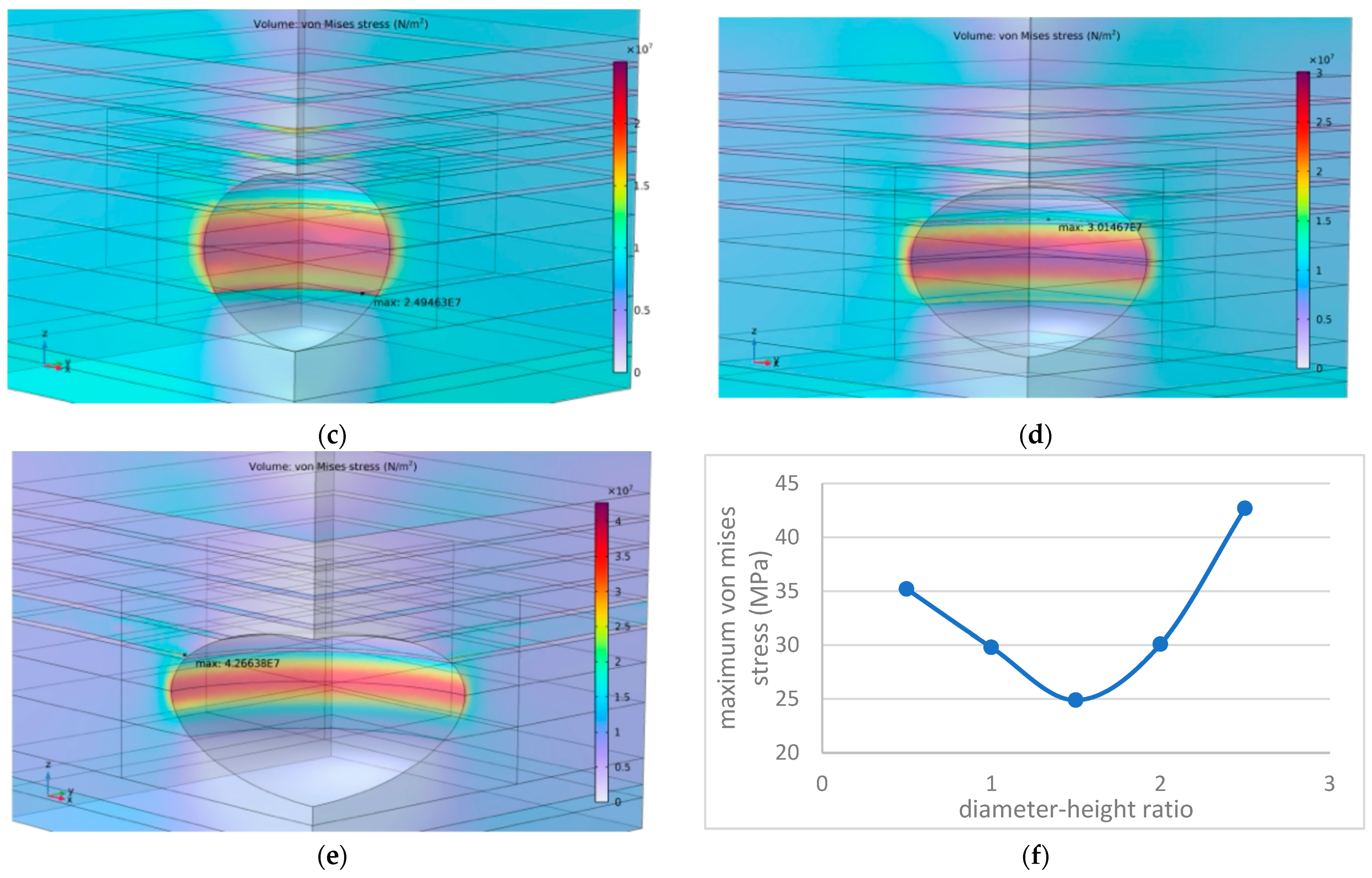
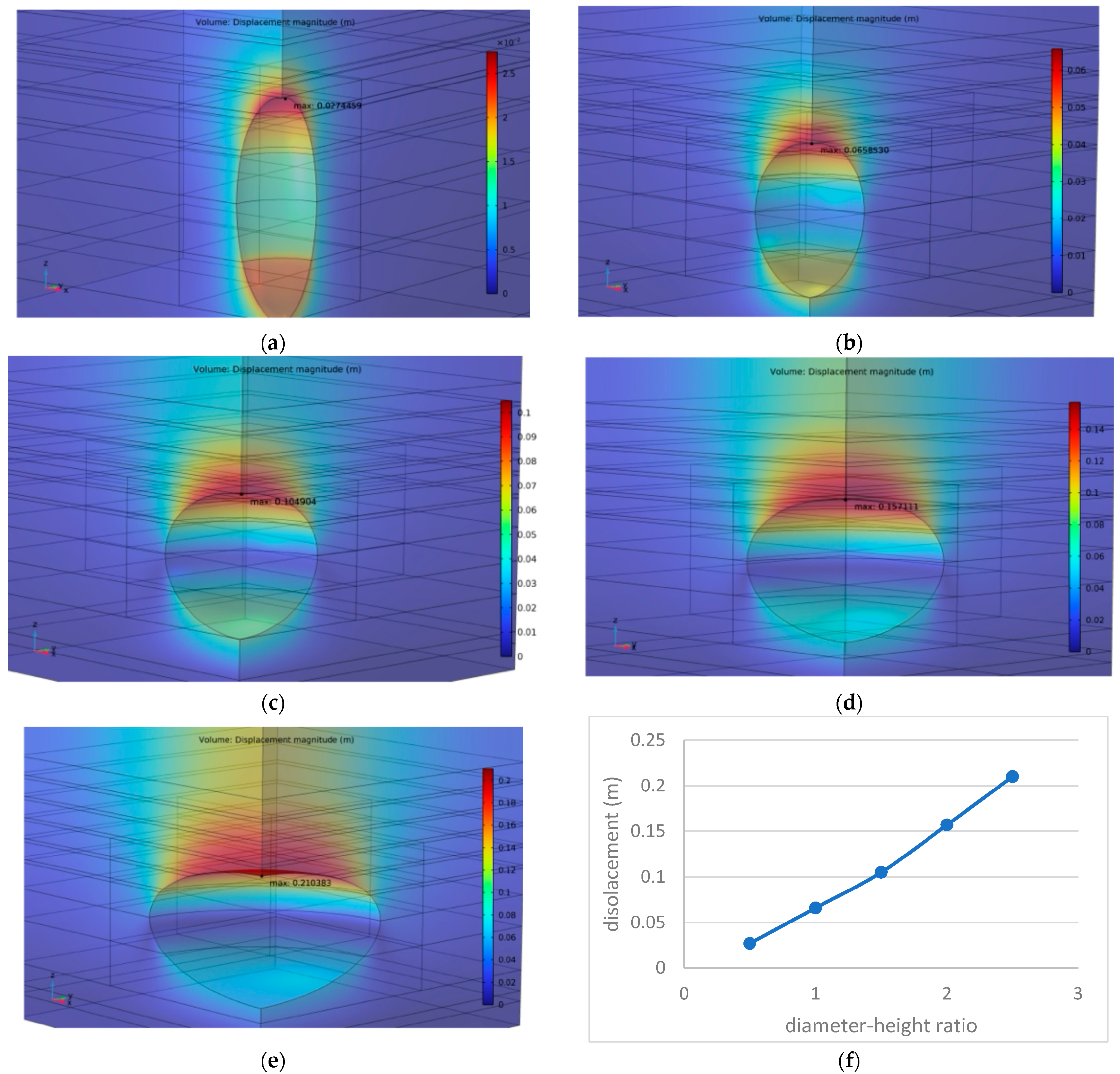
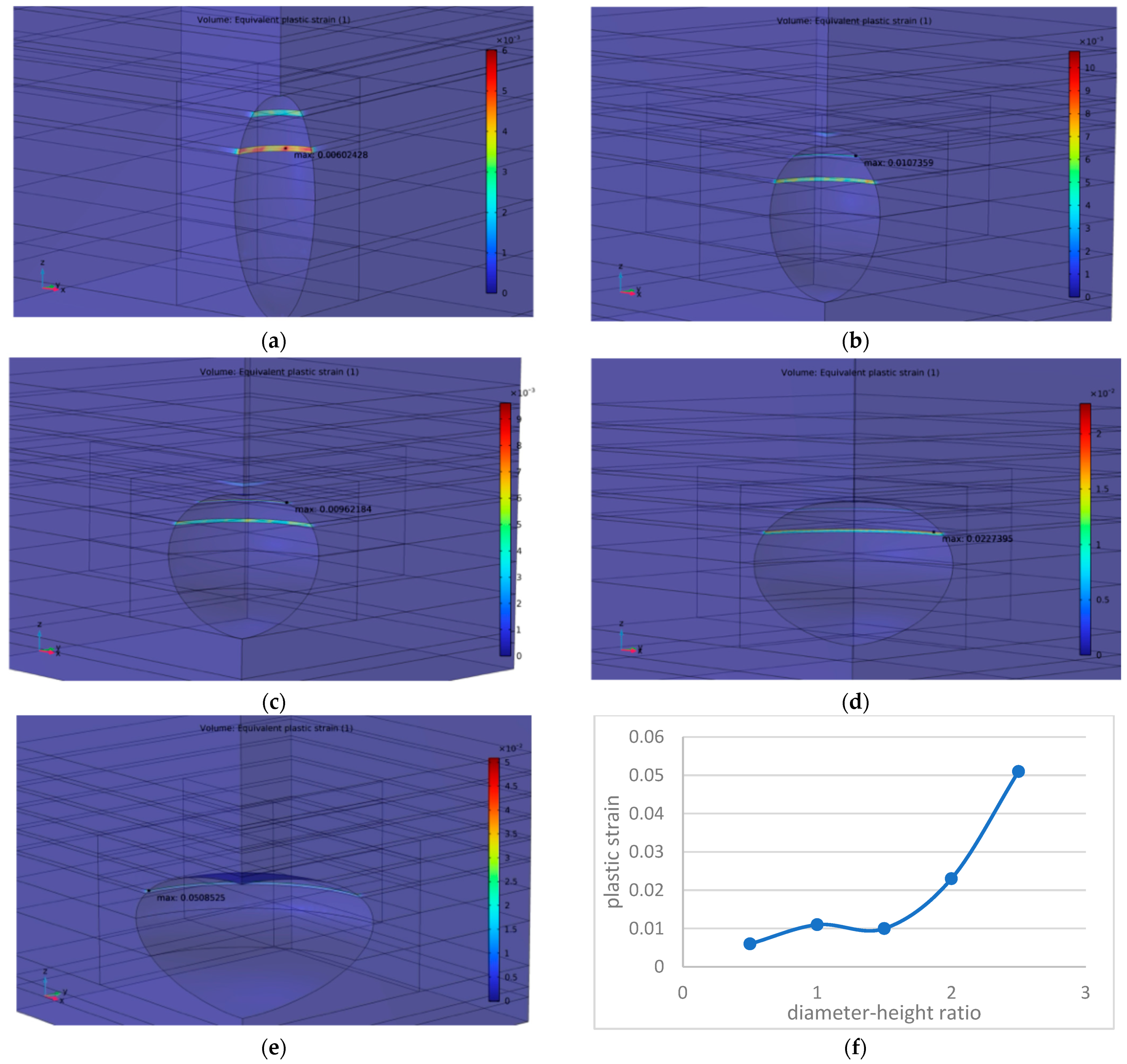
5.1. Cavern Shape and Parameter Optimization
- Cylinder
- Ellipsoid
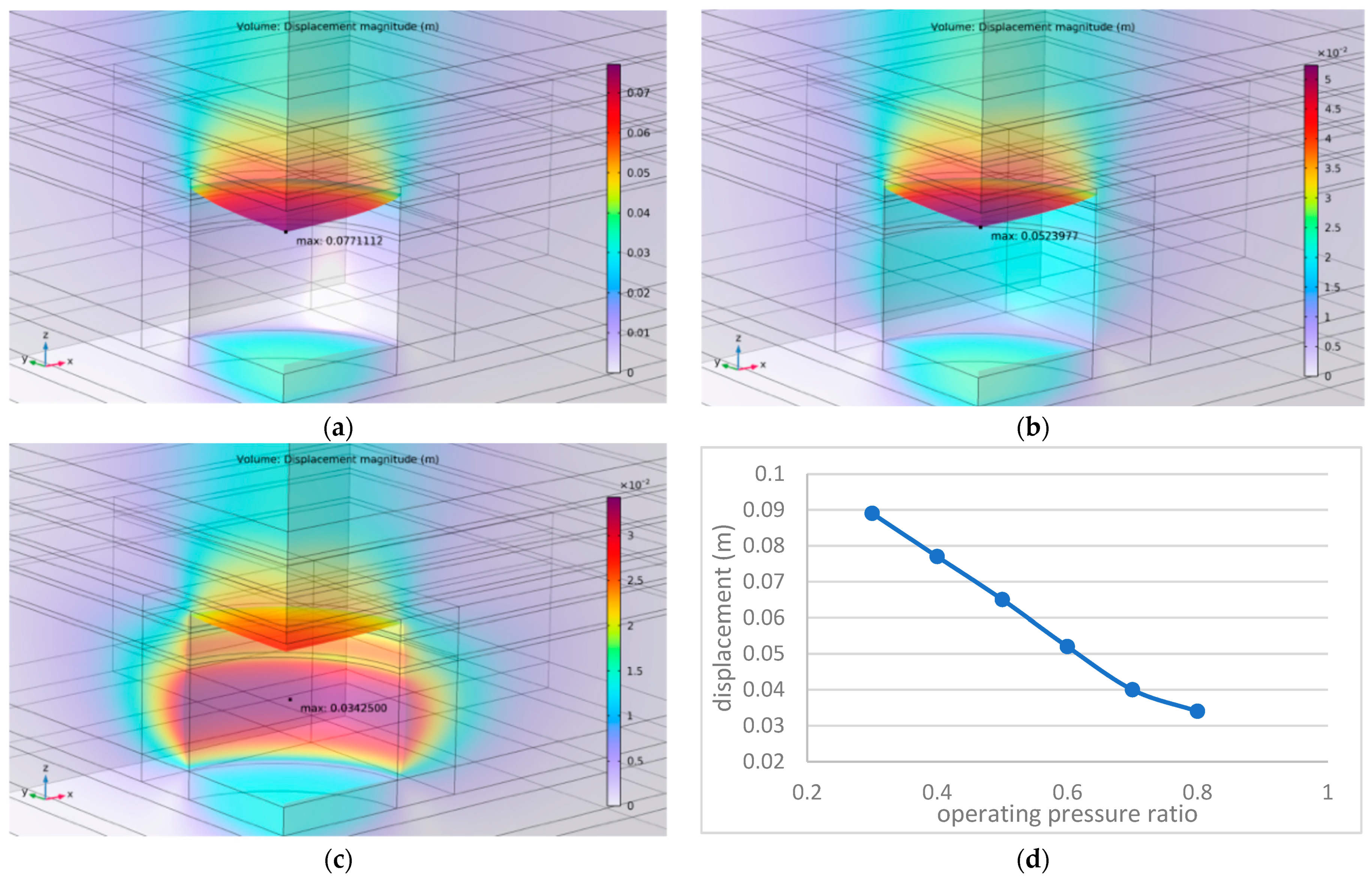
5.2. Operating Pressure Optimization
5.2.1. Stational Analysis for Initial Selection of Operating Pressure
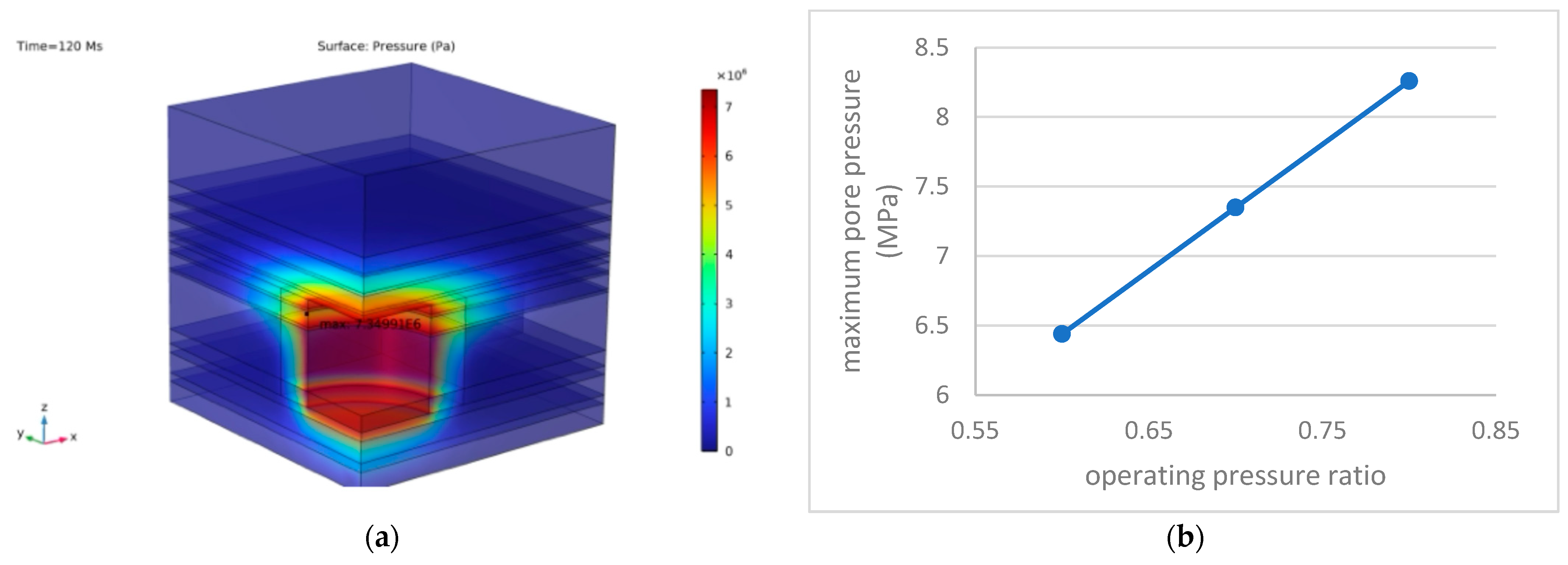
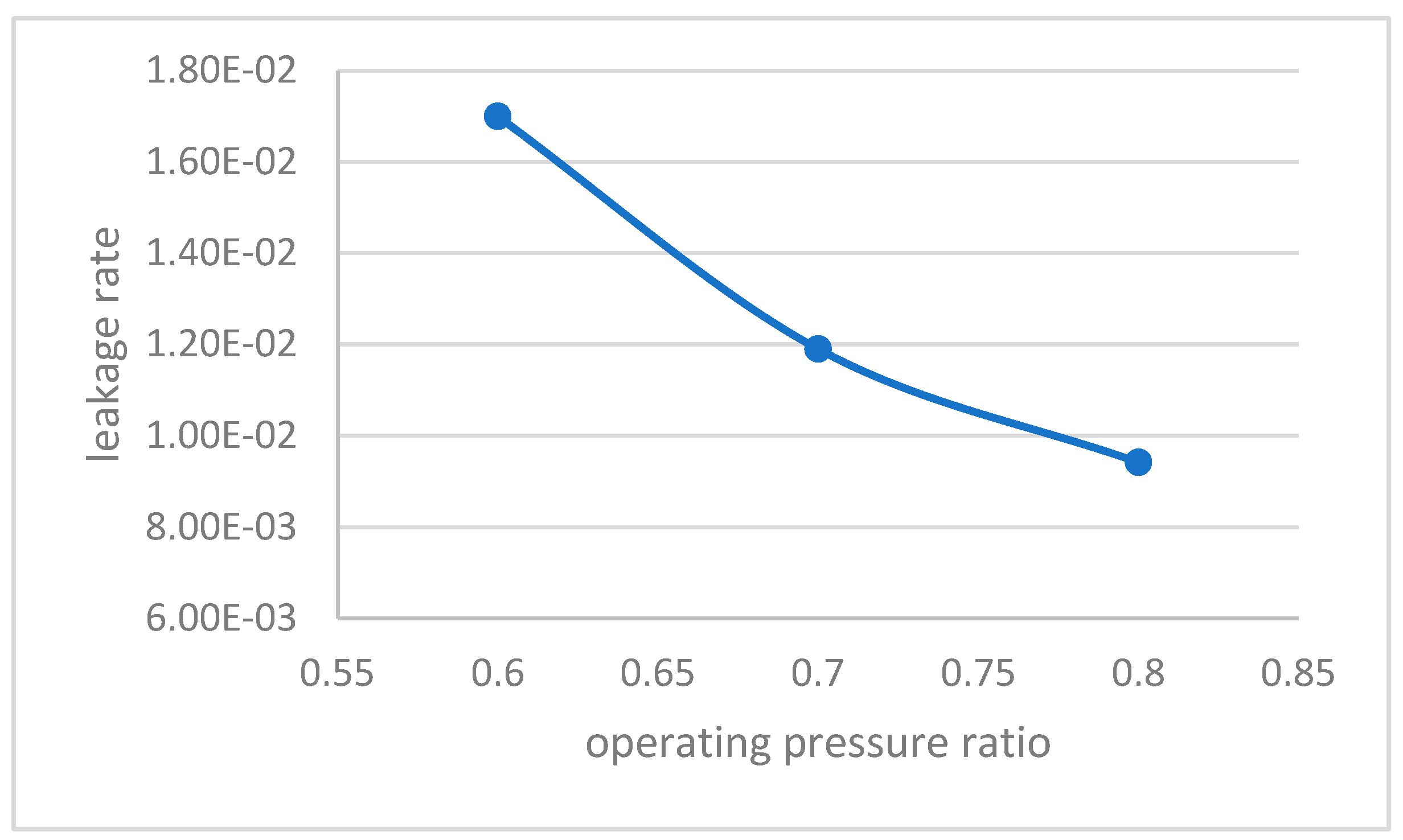
5.2.2. Tightness Evaluation
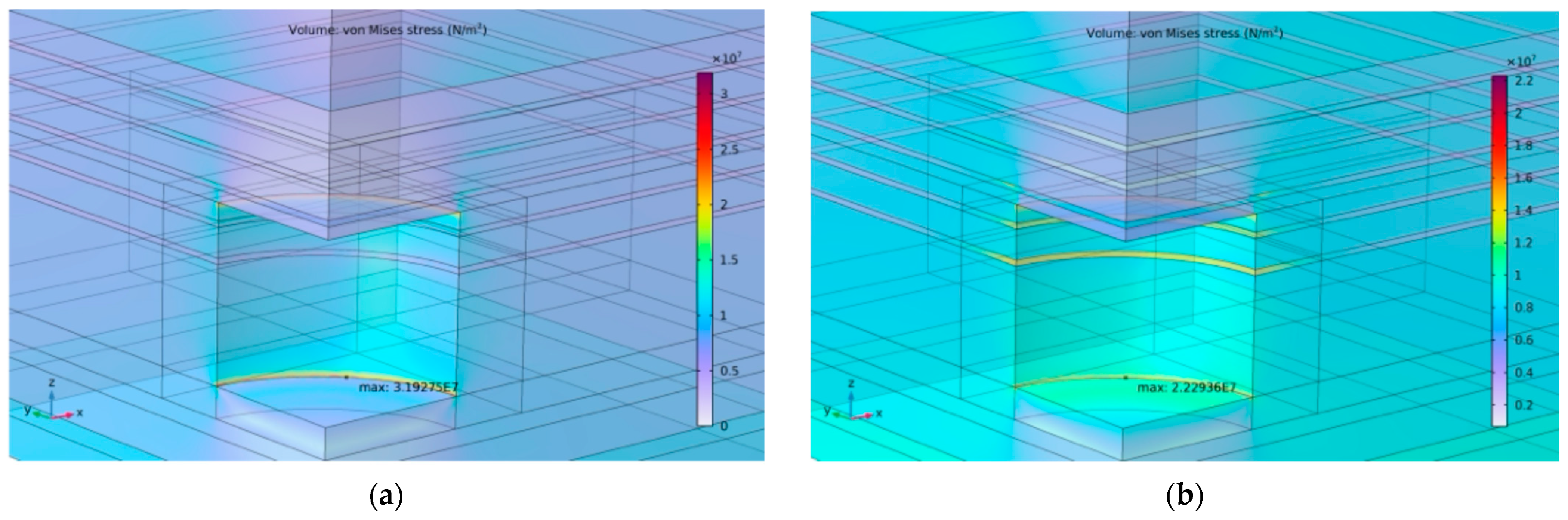
5.2.3. Long-Term Stability Evaluation
6. Conclusions
7. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hansen, J.E.; Sato, M.; Simons, L.; Nazarenko, L.S.; Sangha, I.; Kharecha, P.; Zachos, J.C.; von Schuckmann, K.; Loeb, N.G.; Osman, M.B.; et al. Global Warming in the Pipeline. Oxf. Open Clim. Change 2023, 3, kgad008. [Google Scholar] [CrossRef]
- NICR 2013-05 US Nat Resources 2020, 2030 2040.Pdf. Available online: https://www.dni.gov/files/documents/NICR%202013-05%20US%20Nat%20Resources%202020%2C%202030%202040.pdf?utm_source=chatgpt.com (accessed on 18 February 2025).
- Global Overview—Renewables 2024—Analysis. IEA. Available online: https://www.iea.org/reports/renewables-2024/global-overview (accessed on 18 February 2025).
- Japan Adopts New Carbon Reduction Targets as It Plans to Boost Nuclear and Renewable Energy by 2040|AP News. Available online: https://apnews.com/article/japan-climate-energy-decarbonization-targets-nuclear-carbon-7006f2dd241e30a3129a00da5bf707dd (accessed on 18 February 2025).
- Europe Posts Record Year for Clean Energy Use as Trump Pulls US Toward Fossil Fuels. AP News. Available online: https://apnews.com/article/europe-renewables-climate-change-solar-wind-fossil-fuels-4a6ff96bbde3251cb42109e1d9d4b399 (accessed on 18 February 2025).
- Fariza, I. Cold Without Wind: German ‘Dunkelflaute’ Brings Electricity Prices to Crisis Levels and Depletes Gas Reserves. EL PAÍS English. Available online: https://english.elpais.com/international/2024-12-12/cold-without-wind-german-dunkelflaute-brings-electricity-prices-to-crisis-levels-and-depletes-gas-reserves.html (accessed on 19 February 2025).
- Malka, L.; Daci, A.; Kuriqi, A.; Bartocci, P.; Rrapaj, E. Energy Storage Benefits Assessment Using Multiple-Choice Criteria: The Case of Drini River Cascade, Albania. Energies 2022, 15, 4032. [Google Scholar] [CrossRef]
- Zou, P.; Chen, Q.; Yu, Y.; Xia, Q.; Kang, C. Electricity Markets Evolution with the Changing Generation Mix: An Empirical Analysis Based on China 2050 High Renewable Energy Penetration Roadmap. Appl. Energy 2017, 185, 56–67. [Google Scholar] [CrossRef]
- Evans, A.; Strezov, V.; Evans, T.J. Assessment of Utility Energy Storage Options for Increased Renewable Energy Penetration. Renew. Sustain. Energy Rev. 2012, 16, 4141–4147. [Google Scholar] [CrossRef]
- Li, H.; Ma, H.; Zhao, K.; Zhu, S.; Yang, K.; Zeng, Z.; Zheng, Z.; Yang, C. Parameter Design of the Compressed Air Energy Storage Salt Cavern in Highly Impure Rock Salt Formations. Energy 2024, 286, 129520. [Google Scholar] [CrossRef]
- Nikolaos, P.C.; Marios, F.; Dimitris, K. A Review of Pumped Hydro Storage Systems. Energies 2023, 16, 4516. [Google Scholar] [CrossRef]
- Shah, M.; Prajapati, M.; Yadav, K.; Sircar, A. A Comprehensive Review of Geothermal Energy Storage: Methods and Applications. J. Energy Storage 2024, 98, 113019. [Google Scholar] [CrossRef]
- Takach, M.; Sarajlić, M.; Peters, D.; Kroener, M.; Schuldt, F.; von Maydell, K. Review of Hydrogen Production Techniques from Water Using Renewable Energy Sources and Its Storage in Salt Caverns. Energies 2022, 15, 1415. [Google Scholar] [CrossRef]
- Rabi, A.M.; Radulovic, J.; Buick, J.M. Comprehensive Review of Compressed Air Energy Storage (CAES) Technologies. Thermo 2023, 3, 104–126. [Google Scholar] [CrossRef]
- Li, L.; Liang, W.; Lian, H.; Yang, J.; Dusseault, M. Compressed Air Energy Storage: Characteristics, Basic Principles, and Geological Considerations. Adv. Geo-Energy Res. 2018, 2, 135–147. [Google Scholar] [CrossRef]
- Tarkowski, R. Underground Hydrogen Storage: Characteristics and Prospects. Renew. Sustain. Energy Rev. 2019, 105, 86–94. [Google Scholar] [CrossRef]
- Wan, J.; Sun, Y.; He, Y.; Ji, W.; Li, J.; Jiang, L.; Jurado, M.J. Development and Technology Status of Energy Storage in Depleted Gas Reservoirs. Int. J. Coal. Sci. Technol. 2024, 11, 29. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, G.; Yang, C.; Ma, H.; Yin, L.; Liao, Y.; Zhao, K.; Zeng, Z.; Li, H.; Han, Y. A Novel Nano-Grade Organosilicon Polymer: Improving Airtightness of Compressed Air Energy Storage in Hard Rock Formations. Int. J. Min. Sci. Technol. 2024, 34, 305–321. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, K.; Pan, L.; Cai, Z.; Li, C.; Li, Y. Numerical Investigation of a Joint Approach to Thermal Energy Storage and Compressed Air Energy Storage in Aquifers. Appl. Energy 2017, 203, 948–958. [Google Scholar] [CrossRef]
- Donadei, S.; Schneider, G.-S. Compressed Air Energy Storage in Underground Formations. In Storing Energy; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- King, M.; Jain, A.; Bhakar, R.; Mathur, J.; Wang, J. Overview of Current Compressed Air Energy Storage Projects and Analysis of the Potential Underground Storage Capacity in India and the UK. Renew. Sustain. Energy Rev. 2021, 139, 110705. [Google Scholar] [CrossRef]
- Fertig, E.; Apt, J. Economics of Compressed Air Energy Storage to Integrate Wind Power: A Case Study in ERCOT. Energy Policy 2011, 39, 2330–2342. [Google Scholar] [CrossRef]
- Yin, J.; Zhan, X. Impact of Bias-Correction Methods on Effectiveness of Assimilating SMAP Soil Moisture Data into NCEP Global Forecast System Using the Ensemble Kalman Filter. IEEE Geosci. Remote Sens. Lett. 2018, 15, 659–663. [Google Scholar] [CrossRef]
- Mou, J.; Shang, H.; Ji, W.; Wan, J.; Xing, T.; Ma, H.; Peng, W. Feasibility Analysis of Compressed Air Energy Storage in Salt Caverns in the Yunying Area. Energies 2023, 16, 7171. [Google Scholar] [CrossRef]
- Zhao, H.; Hao, X. Risk Assessment of Zero-Carbon Salt Cavern Compressed Air Energy Storage Power Station. J. Clean. Prod. 2024, 468, 143002. [Google Scholar] [CrossRef]
- Dooner, M.; Wang, J. Potential Exergy Storage Capacity of Salt Caverns in the Cheshire Basin Using Adiabatic Compressed Air Energy Storage. Entropy 2019, 21, 1065. [Google Scholar] [CrossRef]
- Lemieux, A.; Shkarupin, A.; Sharp, K. Geologic Feasibility of Underground Hydrogen Storage in Canada. Int. J. Hydrogen Energy 2020, 45, 32243–32259. [Google Scholar] [CrossRef]
- Li, L.; Yin, S.; Wang, Z. A Preliminary Assessment of Underground Space Resources for Hydrogen Storage in Salt Caverns in Lambton County, Southern Ontario, Canada. Mining 2024, 4, 530–545. [Google Scholar] [CrossRef]
- Rine, M.J.; McLaughlin, P.I.; Bancroft, A.M.; Harrison, W.B.; Kuglitsch, J.; Caruthers, A.H.; Ramezani, J.; Kaczmarek, S.E.; Emsbo, P. Linked Silurian Carbon Cycle Perturbations, Bursts of Pinnacle Reef Growth, Extreme Sea-Level Oscillations, and Evaporite Deposition (Michigan Basin, USA). Palaeogeogr. Palaeoclimatol. Palaeoecol. 2020, 554, 109806. [Google Scholar] [CrossRef]
- Carter, T. Bedded Salt in Ontario: Geology, Solution Mining and Cavern Storage. Available online: https://www.ogsrlibrary.com/downloads/Salt-Geology-and-Cavern-Storage-OPI-2009.pdf (accessed on 4 November 2024).
- Drucker-Prager Criterion—ProQuest. Available online: https://www.proquest.com/docview/1114283355?accountid=14906&parentSessionId=0O9lmQYtpEmaQrytQSxrvu%2BeWyUhsFF82rIAZqnZ%2FQw%3D&pq-origsite=primo&sourcetype=Scholarly%20Journals (accessed on 4 November 2024).
- Liu, W.; Dong, Y.; Zhang, Z.; Li, L.; Jiang, D.; Fan, J.; Chen, J.; Zhang, X.; Wan, J.; Li, Z. Optimization of Operating Pressure of Hydrogen Storage Salt Cavern in Bedded Salt Rock with Multi-Interlayers. Int. J. Hydrogen Energy 2024, 58, 974–986. [Google Scholar] [CrossRef]
- Chromik, M.; Korzeniowski, W. A Method to Increase the Leaching Progress of Salt Caverns with the Use of the Hydro-Jet Technique. Energies 2021, 14, 5833. [Google Scholar] [CrossRef]
- Cyran, K. Insight Into a Shape of Salt Storage Caverns. Arch. Min. Sci. 2020, 65, 363–398. [Google Scholar] [CrossRef]
- Małachowska, A.; Łukasik, N.; Mioduska, J.; Gębicki, J. Hydrogen Storage in Geological Formations—The Potential of Salt Caverns. Energies 2022, 15, 5038. [Google Scholar] [CrossRef]
- Caglayan, D.G.; Weber, N.; Heinrichs, H.U.; Linßen, J.; Robinius, M.; Kukla, P.A.; Stolten, D. Technical Potential of Salt Caverns for Hydrogen Storage in Europe. Int. J. Hydrogen Energy 2020, 45, 6793–6805. [Google Scholar] [CrossRef]
- Parkes, D.; Evans, D.J.; Williamson, P.; Williams, J.D.O. Estimating Available Salt Volume for Potential CAES Development: A Case Study Using the Northwich Halite of the Cheshire Basin. J. Energy Storage 2018, 18, 50–61. [Google Scholar] [CrossRef]
- Williams, J.D.O.; Williamson, J.P.; Parkes, D.; Evans, D.J.; Kirk, K.L.; Sunny, N.; Hough, E.; Vosper, H.; Akhurst, M.C. Does the United Kingdom Have Sufficient Geological Storage Capacity to Support a Hydrogen Economy? Estimating the Salt Cavern Storage Potential of Bedded Halite Formations. J. Energy Storage 2022, 53, 105109. [Google Scholar] [CrossRef]
- Ma, L.; Wang, M.; Zhang, N.; Fan, P.; Li, J. A Variable-Parameter Creep Damage Model Incorporating the Effects of Loading Frequency for Rock Salt and Its Application in a Bedded Storage Cavern. Rock Mech. Rock Eng. 2017, 50, 2495–2509. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, C.; Zhao, H.; Mei, S.; Zhou, S. An Iterative Method for Evaluating Air Leakage from Unlined Compressed Air Energy Storage (CAES) Caverns. Renew. Energy 2018, 120, 434–445. [Google Scholar] [CrossRef]
- Zhao, K.; Liu, Y.; Li, Y.; Ma, H.; Hou, W.; Yu, C.; Liu, H.; Feng, C.; Yang, C. Feasibility Analysis of Salt Cavern Gas Storage in Extremely Deep Formation: A Case Study in China. J. Energy Storage 2022, 47, 103649. [Google Scholar] [CrossRef]
- Ozarslan, A. Large-Scale Hydrogen Energy Storage in Salt Caverns. Int. J. Hydrogen Energy 2012, 37, 14265–14277. [Google Scholar] [CrossRef]




| Lithology | Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | Cohesion (MPa) | Angle of Internal Friction (deg) |
|---|---|---|---|---|---|
| Shale | 25 | 0.35 | 2500 | 1.5 | 25 |
| Salt | 2.26 | 0.28 | 2200 | 5.76 | 31.6 |
| Anhydrite | 12.9 | 0.22 | 3000 | 3.2 | 35 |
| Limestone | 20 | 0.23 | 2700 | 15.9 | 36 |
| Lithology | Permeability (m2) | Porosity | Compressibility (Pa−1) | Diffusion Coefficient (m2/s) |
|---|---|---|---|---|
| Shale | 1 × 10−19 | 0.07 | 3.6 × 10−11 | 1 × 10−8 |
| Salt | 1 × 10−21 | 0.01 | 5.84 ×10−10 | 1 × 10−9 |
| Anhydrite | 1 × 10−19 | 0.04 | 1.3 × 10−10 | 1 × 10−8 |
| Limestone | 1 × 10−18 | 0.01 | 1 × 10−10 | 1 × 10−8 |
| Operating Pressure (MPa) | Capacity (kg) | Total Mass of Leaked Air (kg) | Leakage Rate (%) |
|---|---|---|---|
| 4.8–9.6 | 1.44 × 108 | 1.36 × 106 | 0.94 |
| 4.8–8.4 | 1.11 × 108 | 1.32 × 106 | 1.19 |
| 4.8–7.2 | 7.59 × 107 | 1.29 × 106 | 1.70 |
| Lithology | Creep Rate Coefficient (1/s) | Stress Exponent | Reference Stress (MPa) |
|---|---|---|---|
| Shale | 5 × 10−15 | 3.24 | 1.0 |
| Salt | 1.415 × 10−14 | 3.52 | 1.0 |
| Anhydrite | 3.3 × 10−15 | 3.16 | 1.0 |
| Limestone | 4.8 × 10−15 | 4 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Yin, S. Compressed Air Energy Storage in Salt Caverns Optimization in Southern Ontario, Canada. Energies 2025, 18, 2258. https://doi.org/10.3390/en18092258
Huang J, Yin S. Compressed Air Energy Storage in Salt Caverns Optimization in Southern Ontario, Canada. Energies. 2025; 18(9):2258. https://doi.org/10.3390/en18092258
Chicago/Turabian StyleHuang, Jingyu, and Shunde Yin. 2025. "Compressed Air Energy Storage in Salt Caverns Optimization in Southern Ontario, Canada" Energies 18, no. 9: 2258. https://doi.org/10.3390/en18092258
APA StyleHuang, J., & Yin, S. (2025). Compressed Air Energy Storage in Salt Caverns Optimization in Southern Ontario, Canada. Energies, 18(9), 2258. https://doi.org/10.3390/en18092258






