Optimal Configuration of Flywheel–Battery Hybrid Energy Storage System for Smoothing Wind–Solar Power Generating Fluctuation
Abstract
1. Introduction
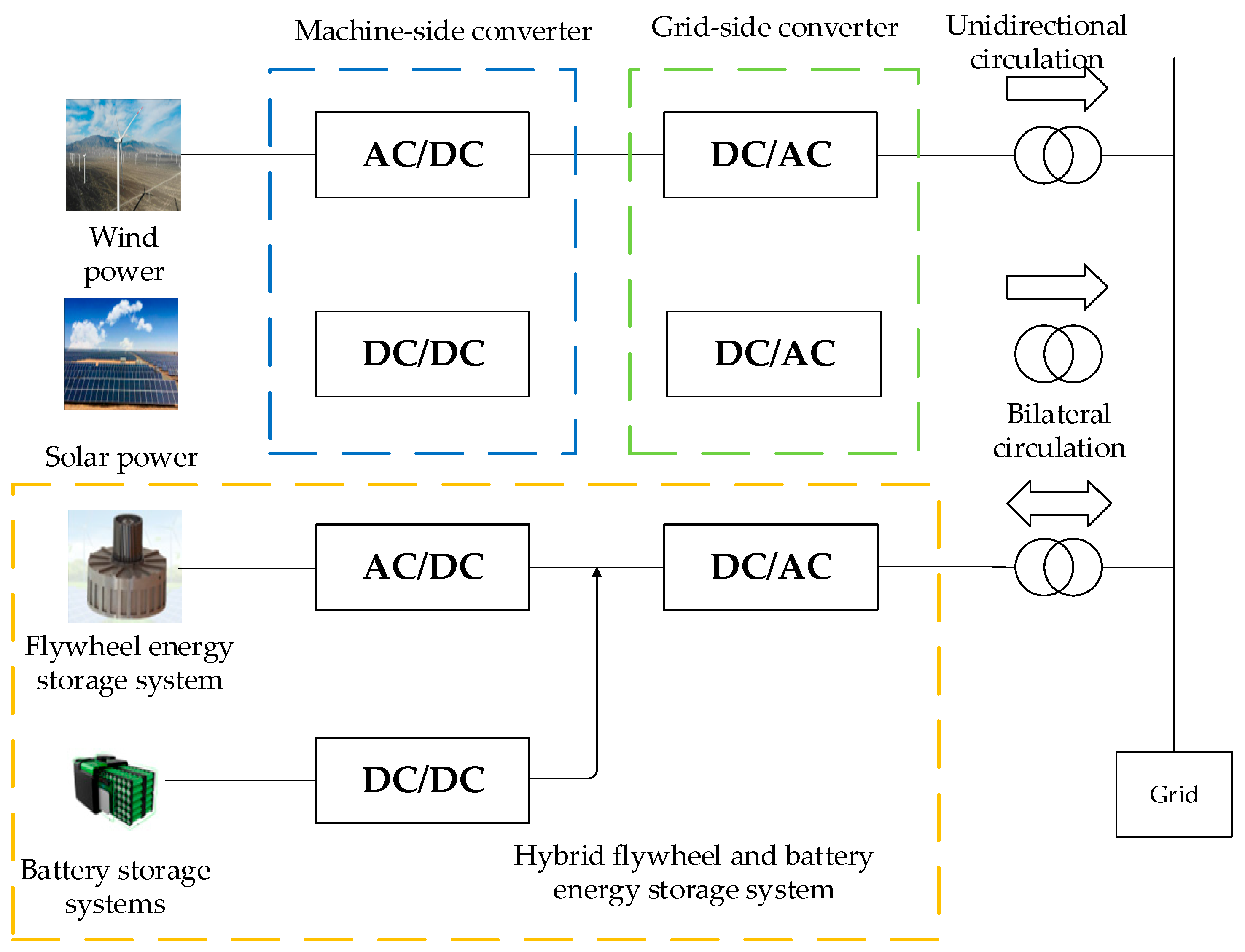
2. Grid-Connected Wind–Solar Power and Flywheel–Battery HESS
2.1. Subsection
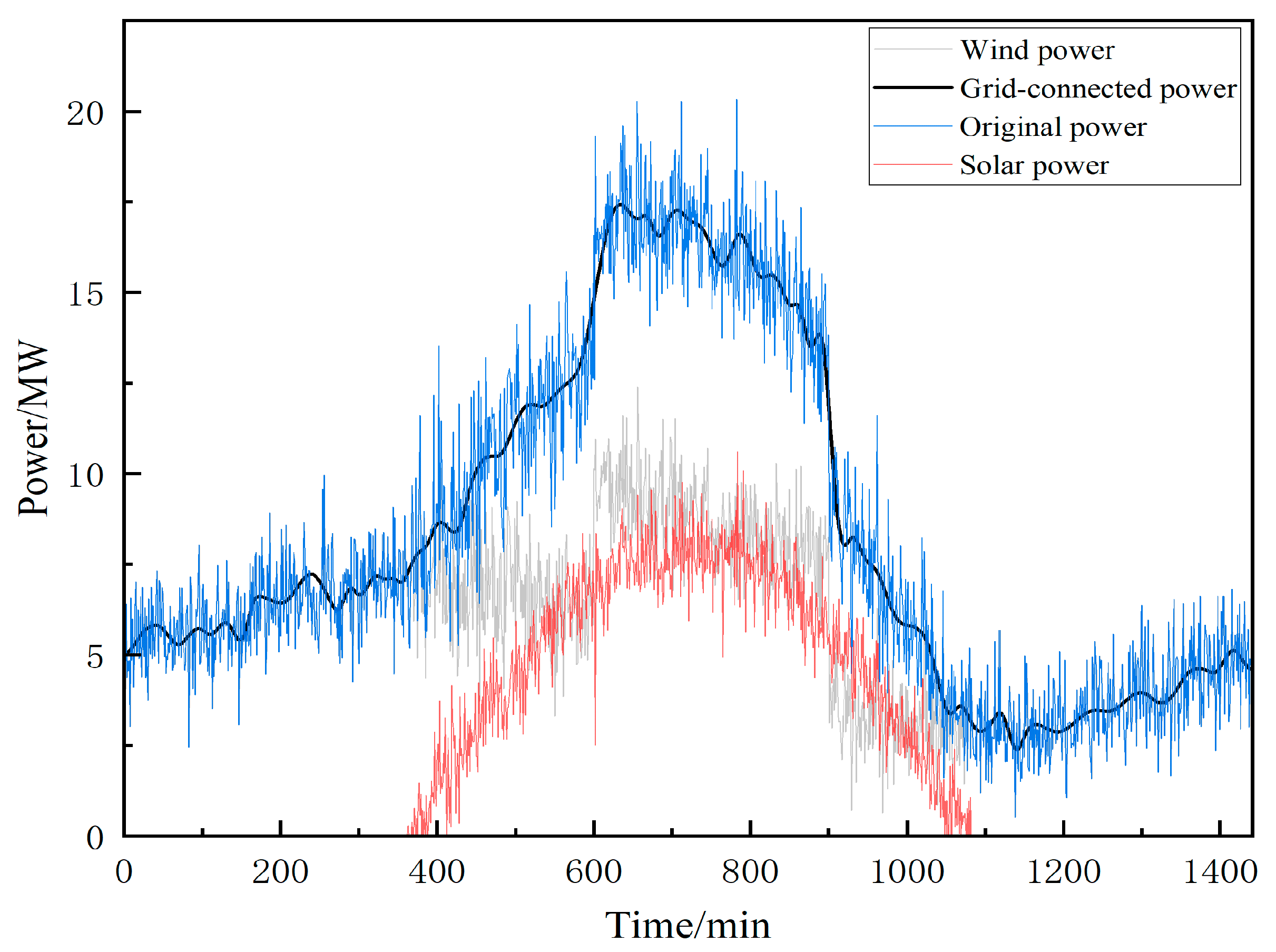
2.2. Fluctuation in Wind–Solar Power Grid Connection
3. Power Allocation of Flywheel–Battery HESS
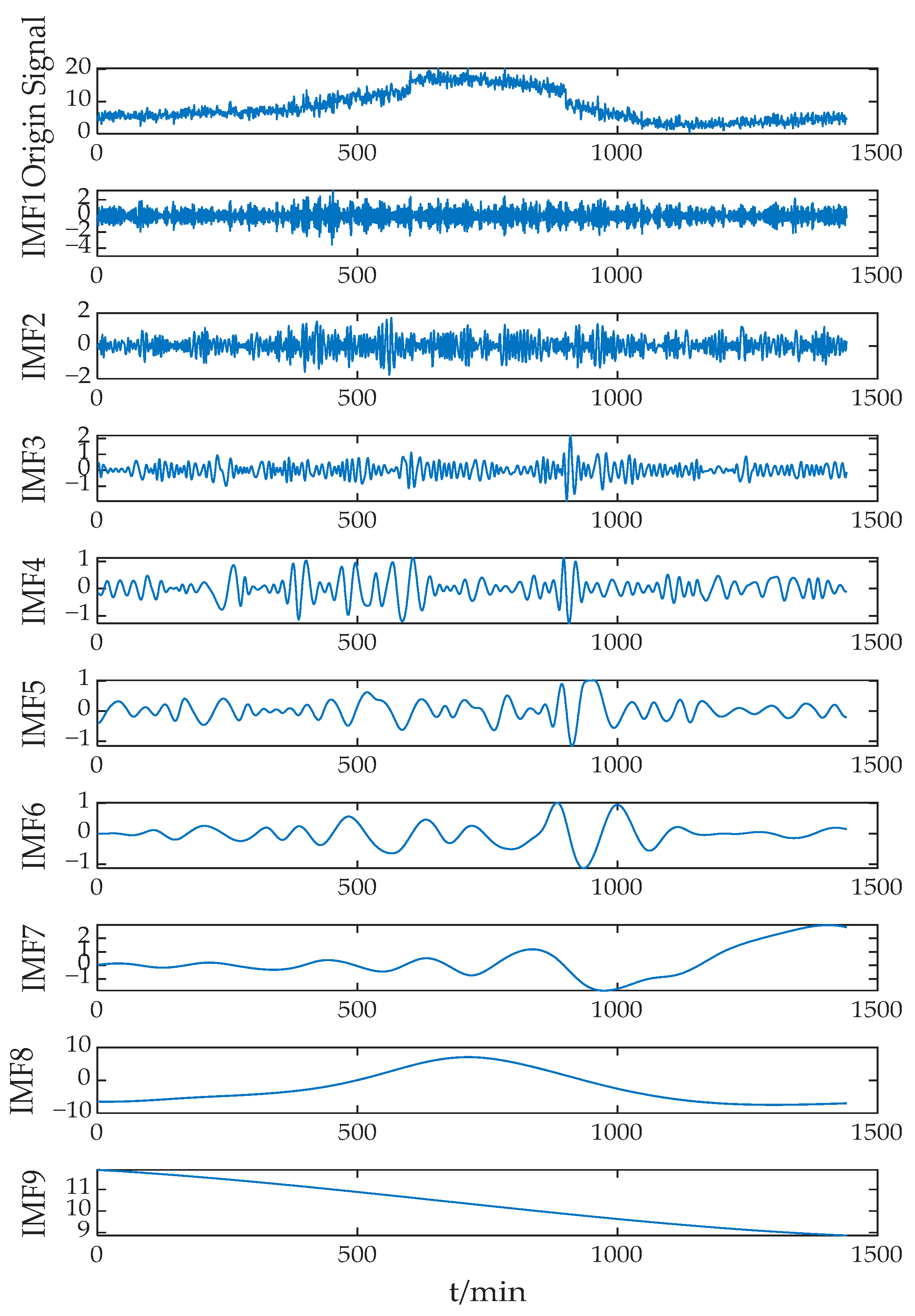
3.1. ICEEMDAN-Based Power Allocation for HESS
3.2. Secondary Power Allocation Based on Low-Pass Filtering
4. Mathematical Model for Optimal Allocation of Energy Storage
4.1. Objective Function
4.2. Constraints
4.2.1. Power Constraints
4.2.2. SOC Constraints
4.2.3. Capacity Constraint
4.2.4. Considering the Economic Constraints of the Full Lifecycle of the Battery
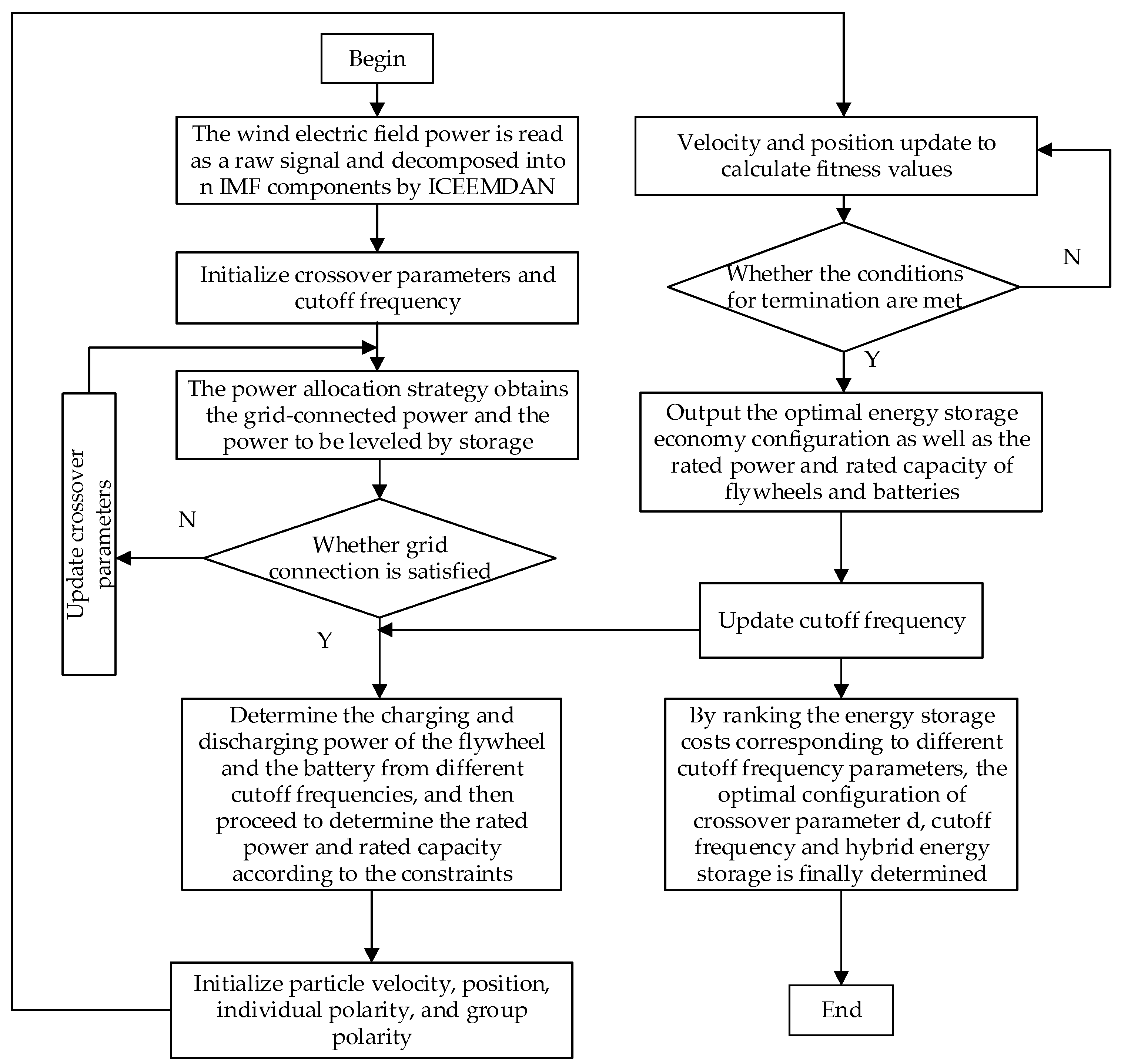
5. Improved PSO
- Read the power of the wind–solar generating station as the original signal, obtaining the grid-connected signal and the suppression command signal by the ICEEMDAN decomposition method and initializing the crossover parameter and the cutoff frequency.
- According to the power distribution strategy, the grid-connected signal and the energy storage to be stabilized signal are obtained to determine whether the grid-connected signal meets the conditions. If not, update the crossover frequency parameters; if the conditions are met, determine the charging and discharging power of the flywheel and the battery based on the cutoff frequency, and then determine the initial power and capacity.
- Initialize the particle velocity, position, individual polarity, and group polarity by taking the initial power and capacity of the flywheel and battery as the minimum value of the rated power and rated capacity.
- Update the particle velocity, position, individual extreme value, and group extreme value, and process the boundary constraints.
- Interpret whether the termination conditions are met and determine the optimal energy storage economy configuration as well as the rated power and rated capacity of the flywheel and battery.
6. Calculation Example Analysis
7. Discussion
8. Conclusions
- (1)
- The ICEEMDAN method is employed to decompose the original wind–solar power signal into a grid-connected power signal and a leveling command signal. A low-pass filter is then applied to separate the leveling command signal by frequency, allocating the appropriate components to the flywheel and battery within the HESS.
- (2)
- To optimize capacity allocation, a hybrid flywheel–battery storage model is established, considering the impact of different cutoff frequencies on power allocation, as well as the effects of the depth of discharge and cycle count on battery lifespan over its entire lifecycle. The PSO (particle swarm optimization) algorithm is employed to solve this model and determine the optimal energy storage capacity configuration.
- (3)
- A simulation analysis was conducted on a microgrid consisting of 10 MW wind power generation, 10 MW solar power generation, and the flywheel–battery HESS. The results showed that the use of hybrid energy storage had a significant power smoothing effect, with a maximum power fluctuation rate of 3.2% within 1-min intervals. The maximum power fluctuation within 1-min intervals was mostly below 8%. Under the same stabilizing effect, the HESS achieved a 45.1% reduction in costs compared to single-battery energy storage. This demonstrated the wind–solar power leveling capability and economic value of the flywheel–battery HESS.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, P.; Liu, F.; Jiang, Q.R.; Mao, H.Y. Stability of large disturbances in “double-high” power systems: Problems, challenges and prospects. J. Tsinghua Univ. (Sci. Technol.) 2021, 61, 403–414. [Google Scholar]
- Sayed, E.T.; Olabi, A.G.; Alami, A.H.; Radwan, A.; Mdallal, A.; Rezk, A.; Abdelkareem, M.A. Renewable Energy and Energy Storage Systems. Energies 2023, 16, 1415. [Google Scholar] [CrossRef]
- Notton, G.; Nivet, M.-L.; Voyant, C.; Paoli, C.; Darras, C.; Motte, F.; Fouilloy, A. Intermittent and stochastic character of renewable energy sources: Consequences, cost of intermittence and benefit of forecasting. Renew. Sustain. Energy Rev. 2018, 87, 96–105. [Google Scholar] [CrossRef]
- Rajah, I.; Sowe, J.; Schimpe, M.; Barreras, J.V. Degradation-Aware Derating of Lithium-Ion Battery Energy Storage Systems in the UK Power Market. Electronics 2024, 13, 3817. [Google Scholar] [CrossRef]
- Chang, H.; Xing, Y.; Miao, B.; Li, L.; Liu, C.; Xiang, K.; Chi, Y.; Liu, Y. A Quantitative Method of Carbon Emission Reduction for Electrochemical Energy Storage Based on the Clean Development Mechanism. Processes 2024, 12, 2472. [Google Scholar] [CrossRef]
- Kouba, N.E.Y.; Sadoudi, S. Optimal Power Management and Control of Hybrid Solar–Wind Microgrid Including Storage System. Proceedings 2024, 105, 3. [Google Scholar] [CrossRef]
- Ministry of Finance of China. New Guidelines for the Management of Special Funds for Clean Energy Development. Available online: https://www.china5e.com/rule/news-878267-1.html (accessed on 22 March 2025).
- Dongyang Municipal Government. Local Energy Storage Subsidy Policy. Available online: https://www.china5e.com/news/news-1184001-1.html (accessed on 22 March 2025).
- Australian Renewable Energy Agency (ARENA). Funding Support for Battery Storage Projects. Available online: https://www.china5e.com/news/news-1184001-1.html (accessed on 22 March 2025).
- Politico. World’s Largest Battery Plant on Fire in Central California. Politico. 2025. Available online: https://www.politico.com/news/2025/01/17/worlds-largest-battery-plant-on-fire-in-central-california-00198914 (accessed on 23 March 2025).
- Hang, X.; Ruan, P.; Zhang, L.; Li, J.; Tian, G.; Hu, D.; Zhu, B. Application analysis of flywheel energy storage in thermal power frequency modulation in central China. Energy Storage Sci. Technol. 2021, 10, 1694–1700. [Google Scholar]
- Mousavig, S.M.; Faraji, F.; Majazi, A.; Al-Haddad, K. A comprehensive review of flywheel energy storage system technology. Renew. Sustain. Energy Rev. 2017, 67, 477–490. [Google Scholar] [CrossRef]
- Sharma, P.; Kumar, V. Current technology of supercapacitors: A review. J. Electron. Mater. 2020, 49, 3520–3532. [Google Scholar] [CrossRef]
- Hong, F.; Liang, L.; Pang, Y.L.; Jia, X.Y.; Fang, F. Adaptive cooperative sag-based primary FM control strategy for flywheel energy storage combined thermal power units. Therm. Power Gener. 2023, 52, 36–44. [Google Scholar]
- Leclanche; S4 Energy. Flywheel-Lithium Battery Hybrid Energy Storage System in The Netherlands. Polaris Power News Network. Available online: https://www.china5e.com/news/news-1099175-1.html (accessed on 22 March 2025).
- State Grid Shanxi Electric Power Research Institute. Hybrid Energy Storage Frequency Regulation Experiment in Youyu Laoqianshan Wind Farm. Polaris Power News Network. Available online: https://www.china5e.com/news/news-1184001-1.html (accessed on 23 March 2025).
- Yan, Q.M.; Liu, Y.C.; Dong, X.Z.; Ma, Y.X. Optimal allocation of hybrid energy storage capacity based on CEEMDAN-HT for smoothing PV output. Power Syst. Prot. Control 2022, 50, 43–53. [Google Scholar]
- Teng, W.; Xu, Q.X.; Wang, Y.J.; Qin, R.; Wu, X.; Liu, Y.B. Economic configuration of flywheel cooperative battery hybrid energy storage system for smoothing wind power fluctuation. J. Chin. Soc. Power Eng. 2024, 44, 1101–1108. [Google Scholar]
- Wang, J.J.; Gou, K.J.; Chen, H.; Chen, H.G.; Xue, G.; Zhang, G.Q. Optimal allocation of flywheel-electrochemical hybrid energy storage capacity for smoothing wind power fluctuation. J. Chin. Soc. Power Eng. 2024, 44, 439–446. [Google Scholar]
- Hao, X.W. Application Study of Hybrid Energy Storage for Smoothing Wind Power Output Fluctuation; North China Electric Power University: Beijing, China, 2023. [Google Scholar]
- Wang, S. Research on Hybrid Energy Storage Capacity Allocation Method for Photovoltaic Power Levelling; North China Electric Power University: Beijing, China, 2023. [Google Scholar]
- Lu, Q.Y.; Yang, Y.G.; Chen, J.S.; Liu, Y.; Liu, N.; Cao, F. Capacity optimization of hybrid energy storage systems for offshore wind power volatility smoothing. Energy Rep. 2023, 9, 575–583. [Google Scholar] [CrossRef]
- Li, H.Z.; Sun, D.Y.; Li, B.K.; Wang, X.; Zhao, Y.; Wei, M.; Dang, X. Collaborative optimization of VRB-PS hybrid energy storage system for large-scale wind power grid integration. Energy 2023, 265, 126292. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.J.; Guo, H.; Zhang, X.; Guo, C.; Chen, H. A hybrid energy storage system with optimized operating strategy for mitigating wind power fluctuations. Renew. Energy 2018, 125, 121–132. [Google Scholar] [CrossRef]
- He, B.; Ren, Y.F.; Jia, W.Q.; Xue, Y.; Yang, P.W.; Ren, Z. Study on the strategy of energy storage MPC for smoothing the power fluctuation of decentralized wind power. Acta Energiae Solaris Sin. 2024, 45, 132–139. [Google Scholar]
- Sun, Z.L.; Chen, J.; Yan, Y.L.; Zhang, B.M.; Wang, Z.D.; Jiao, D.D. Coordinated control of dual-stack self-cycling based on hybrid energy storage for smoothing wind power fluctuations. Acta Energiae Solaris Sin. 2021, 42, 125–132. [Google Scholar]
- Zhang, Y.; Wu, Y.; Li, L.; Liu, Z. A Hybrid Energy Storage System Strategy for Smoothing Photovoltaic Power Fluctuation Based on Improved HHO-VMD. Int. J. Photoenergy 2023, 2023, 9633843. [Google Scholar] [CrossRef]
- Mehrdad, G.; Omkolsoom, S.; Navid, R.; Hassan, B. Optimum storage sizing in a hybrid wind-battery energy system considering power fluctuation characteristics. J. Energy Storage 2022, 52, 104634. [Google Scholar]
- Villa-Ávila, E.; Arévalo, P.; Ochoa-Correa, D.; Iñiguez-Morán, V.; Jurado, F. A New Adaptive Strategy for Enhancing the Stability of Isolated Grids through the Integration of Renewable Energy and V2G Management. Appl. Sci. 2024, 14, 6380. [Google Scholar] [CrossRef]
- Tang, X.S.; Sun, Y.S.; Zhou, G.P.; Miao, F.F. Coordinated control of multi-type energy storage for wind power fluctuation suppression. Energies 2017, 10, 1212. [Google Scholar] [CrossRef]
- Li, C.; Qin, L.J. Capacity optimization of hybrid energy storage with independent frequency regulation based on improved particle swarm algorithm. Acta Energiae Solaris Sin. 2023, 44, 426–434. [Google Scholar]
- Li, X.; Wan, G.J.; Qiu, Y.; Hou, Y.C.; Zhou, Q. Optimal allocation of hybrid energy storage capacity based on VMD. Acta Energiae Solaris Sin. 2022, 43, 88–96. [Google Scholar]
- Song, J.; Geng, L.X.; San, Y.F.; Wen, Y.B.; Sun, P.; Gong, L.J. Hybrid energy storage assisted thermal power unit primary FM capacity planning based on EMD decomposition. Energy Storage Sci. Technol. 2023, 12, 496–503. [Google Scholar]
- Xu, Q.X.; Teng, W.; Wu, X.; Liu, Y.B.; Liang, S.Y. Capacity allocation method of flywheel energy storage system for smoothing wind power fluctuation. Energy Storage Sci. Technol. 2022, 11, 3906–3914. [Google Scholar]
- Hong, F.; Liang, B.Y.; Sun, F.D.; Liang, L.; Wang, W.; Fang, F. Frequency regulation control strategy of flywheel energy storage coupled with thermal power units in multiple operation stages. Power Gener. Technol. 2024; in press. Available online: http://kns.cnki.net/kcms/detail/33.1405.tk.20241111.1419.002.html (accessed on 22 March 2025).
- Wang, J.Y.; Yang, K.; Song, Z.X.; Wu, C.Y.; Bai, Y.L. Primary frequency regulation control strategy for battery-flywheel hybrid energy storage based on adaptive SOC. Power Eng. Technol. 2024, 43, 122–130. [Google Scholar]
- Syed, M.M.; Hansen, P.; Morrison, G.M. Performance of a shared solar and battery storage system in an Australian apartment building. Energy Build. 2020, 225, 110321. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, N.; Kang, C.; Kirschen, D.; Xia, Q. Cloud energy storage for residential and small commercial consumers: A business case study. Appl. Energy 2017, 188, 226–236. [Google Scholar] [CrossRef]
- Sun, L.; Qiu, J.; Han, X.; Yin, X.; Dong, Z.Y. Capacity and energy sharing platform with hybrid energy storage system: An example of hospitality industry. Appl. Energy 2020, 280, 115897. [Google Scholar] [CrossRef]



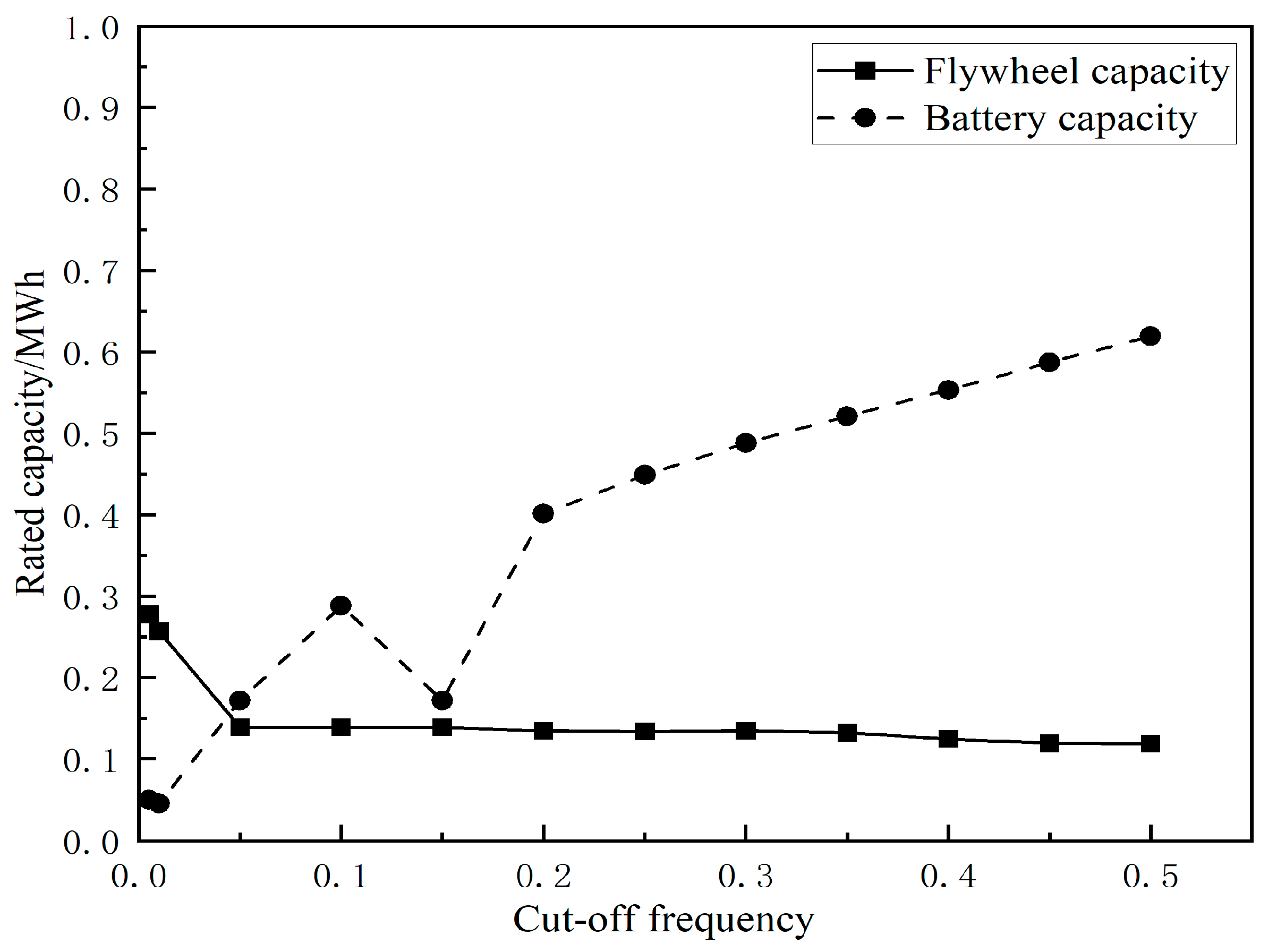


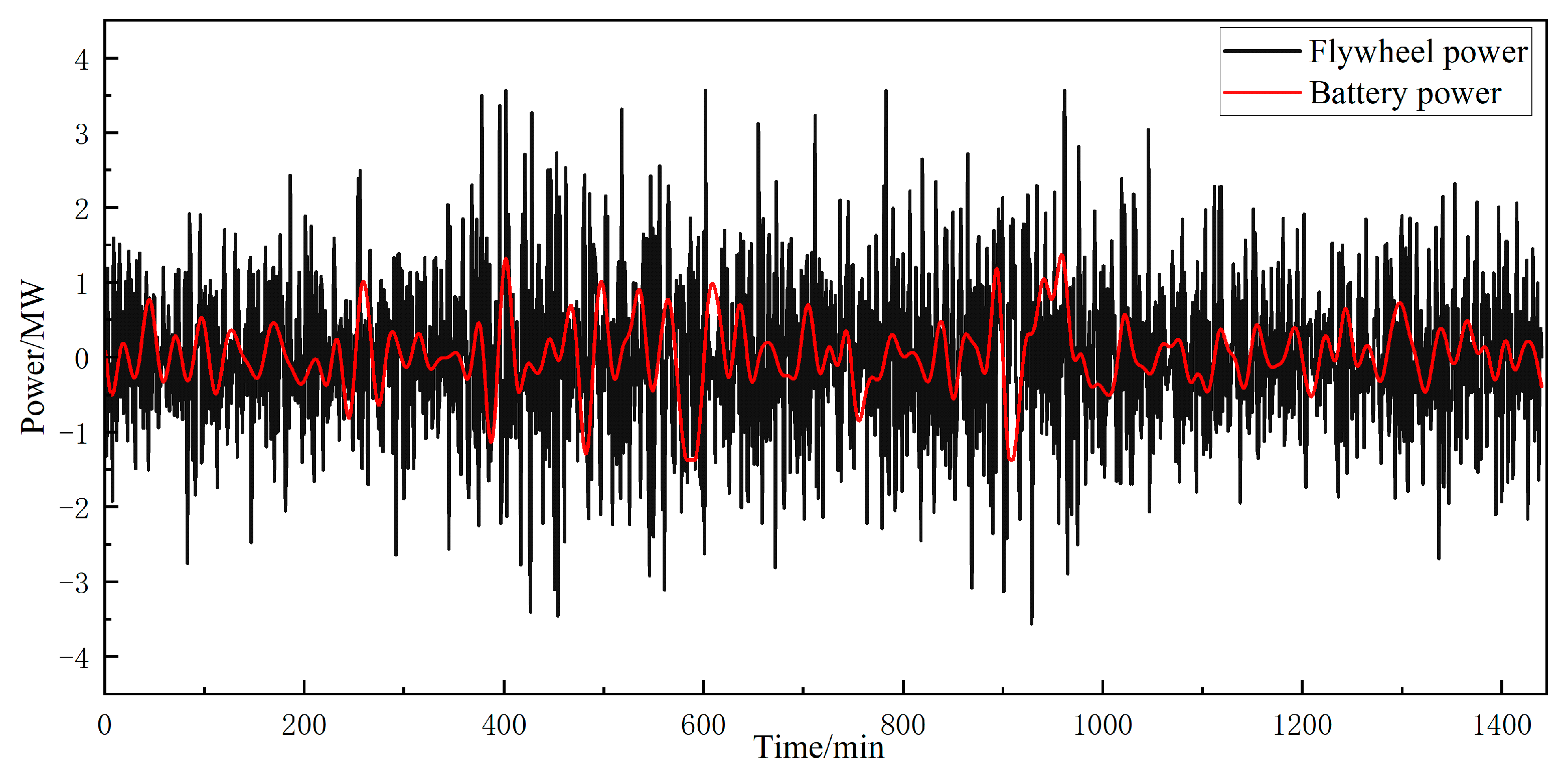
| Installed Wind and Solar Power Capacity (MW) | Maximum Variation in Active Power (MW) | |
|---|---|---|
| <30 | 3 | 10 |
| 30–150 | installed capacity/10 | installed capacity/3 |
| >150 | 15 | 50 |
| Parameters | Battery | Flywheel |
|---|---|---|
| Energy storage charge/discharge efficiency/% | 90 | 95 |
| SOC upper and lower limits | (0.2, 0.8) | (0.1, 0.9) |
| SOC initial value | 0.5 | 0.5 |
| Unit power cost of energy storage investment/ | 200 | 300 |
| Unit capacity cost of energy storage investment/ | 150 | 3000 |
| Energy storage O&M unit power cost/ | 40 | 20 |
| Energy storage unit replacement power cost/ | 100 | |
| Energy storage unit replacement capacity cost/ | 75 |
| Type of Energy Storage | Rated Power/MW | Rated Capacity/MWh | Replacement Times | Y/ 104 CNY | |
|---|---|---|---|---|---|
| Single-battery energy storage | Battery storage | 4.6794 | 0.1843 | 6 | 4169.87 |
| Hybrid energy storage | Flywheel energy storage | 3.9205 | 0.1388 | - | 2388.52 |
| Battery storage | 1.6423 | 0.288 | 1 | ||
| Energy Storage Type | |||
|---|---|---|---|
| Flywheel Energy Storage | 0.9067 | 0.13531 | 0.0820 |
| Battery Energy Storage | 0.3310 | 0.00635 | 0.0150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, S.; Gong, Y.; Mu, X.; Zhao, S.; Wang, C. Optimal Configuration of Flywheel–Battery Hybrid Energy Storage System for Smoothing Wind–Solar Power Generating Fluctuation. Energies 2025, 18, 2055. https://doi.org/10.3390/en18082055
Wen S, Gong Y, Mu X, Zhao S, Wang C. Optimal Configuration of Flywheel–Battery Hybrid Energy Storage System for Smoothing Wind–Solar Power Generating Fluctuation. Energies. 2025; 18(8):2055. https://doi.org/10.3390/en18082055
Chicago/Turabian StyleWen, Shaobo, Yipeng Gong, Xiufeng Mu, Sufang Zhao, and Chuanjun Wang. 2025. "Optimal Configuration of Flywheel–Battery Hybrid Energy Storage System for Smoothing Wind–Solar Power Generating Fluctuation" Energies 18, no. 8: 2055. https://doi.org/10.3390/en18082055
APA StyleWen, S., Gong, Y., Mu, X., Zhao, S., & Wang, C. (2025). Optimal Configuration of Flywheel–Battery Hybrid Energy Storage System for Smoothing Wind–Solar Power Generating Fluctuation. Energies, 18(8), 2055. https://doi.org/10.3390/en18082055






