Coordinated Interaction Strategy of User-Side EV Charging Piles for Distribution Network Power Stability
Abstract
1. Introduction
- High-precision charging load prediction: By constructing a complete travel chain model for EVs, dynamic simulation operation of vehicles in the road network can be achieved, and a spatiotemporal distribution prediction model that integrates dynamic road network state analysis can be developed to provide reliable data support for regulation strategies.
- Systematically resolving conflicts among multiple stakeholders: Propose a multi-objective optimization framework aimed at balancing the interests of charging station operators, EV users, and the power grid, effectively alleviating the economic and safety contradictions caused by disorderly charging.
- Road–Grid Deep Coupling Modeling: A co-simulation framework integrating dynamic road network and distribution grid models is developed, with charging stations as interactive nodes, to quantify the spatiotemporal correlations among traffic flow, user travel behavior, and grid load. This approach overcomes the limitations of traditional research that overemphasizes grid-side modeling while neglecting road network dynamics.
2. “Vehicle–Road Network” Interaction-Related Modeling
2.1. Traffic Model
2.1.1. Road Network Topology
2.1.2. Related Traffic Data
2.2. Grid Model
2.3. Coupled Model
2.4. Tariff Response Model
3. Charging Load Spatiotemporal Distribution Forecasting
3.1. Analysis of EV Driving Characteristics
3.2. Energy Consumption Model Considering Environmental Temperature
4. Multi-Objective Charging/Discharging Optimization Control Model
4.1. Objective Functions
4.1.1. User Charging Cost
4.1.2. Charging Station Revenue Model
4.1.3. Constraints
4.2. Model Solution
5. Case Studies
5.1. Relevant Settings
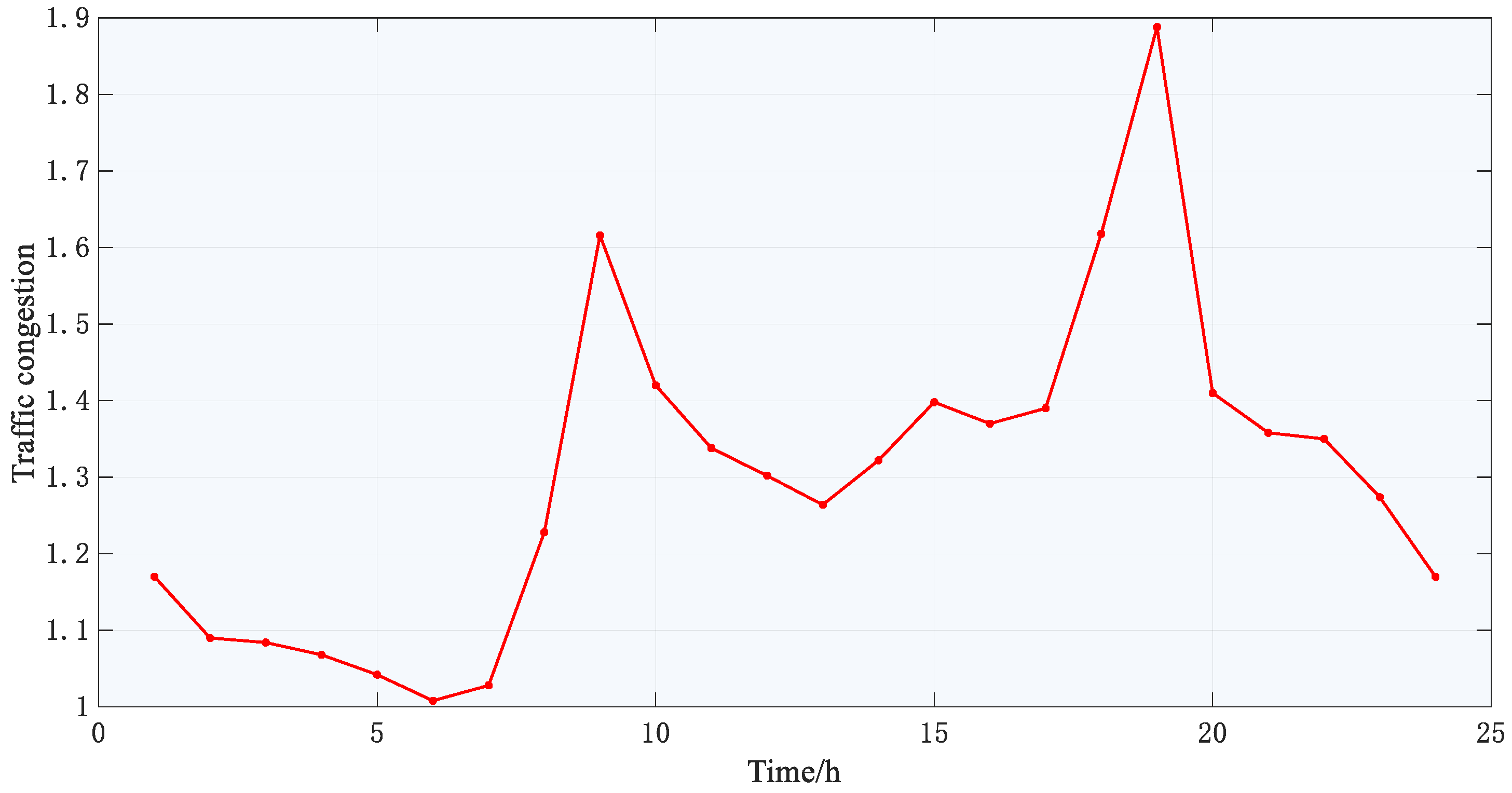
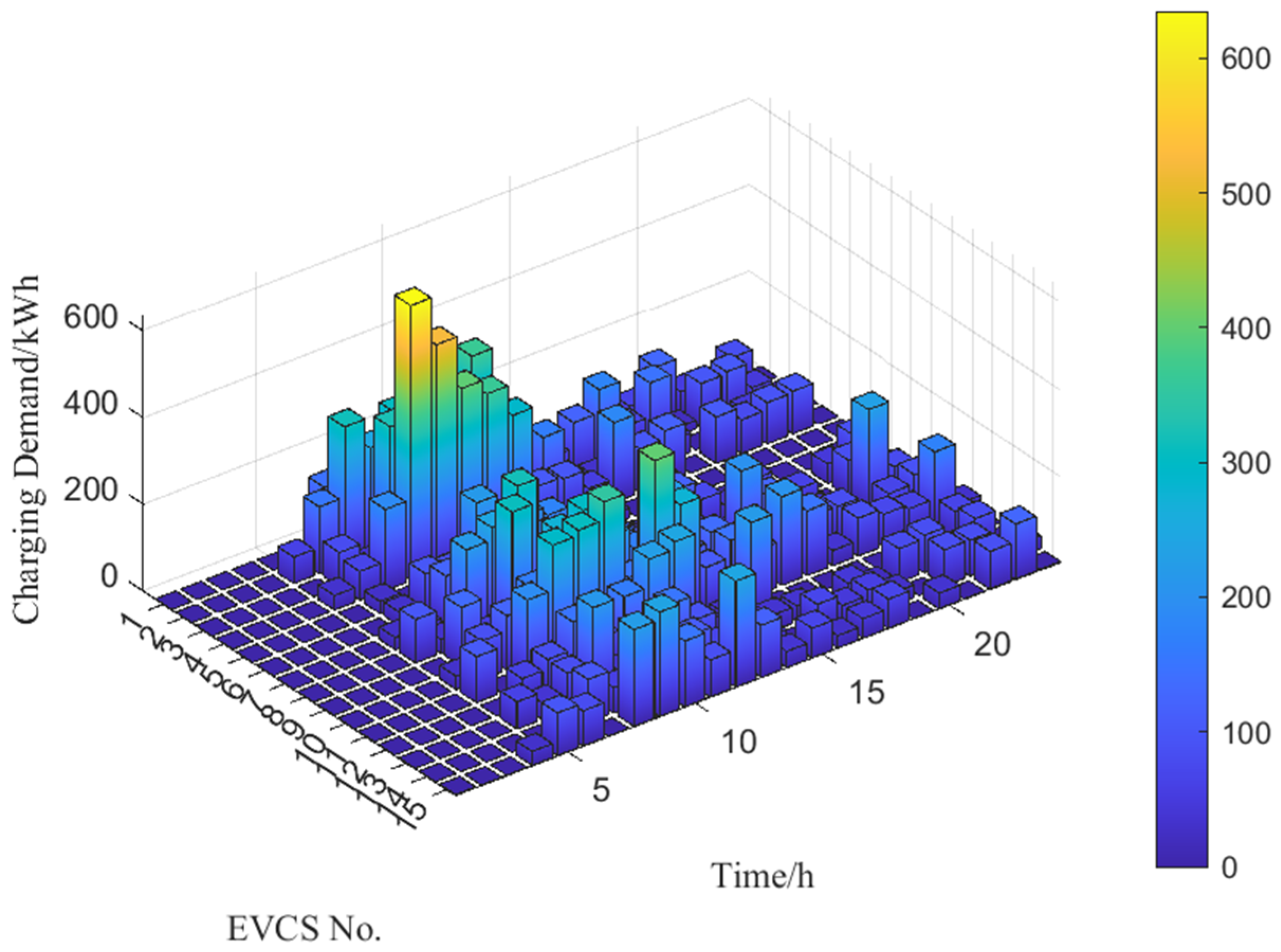
5.2. Analysis of Prediction Results
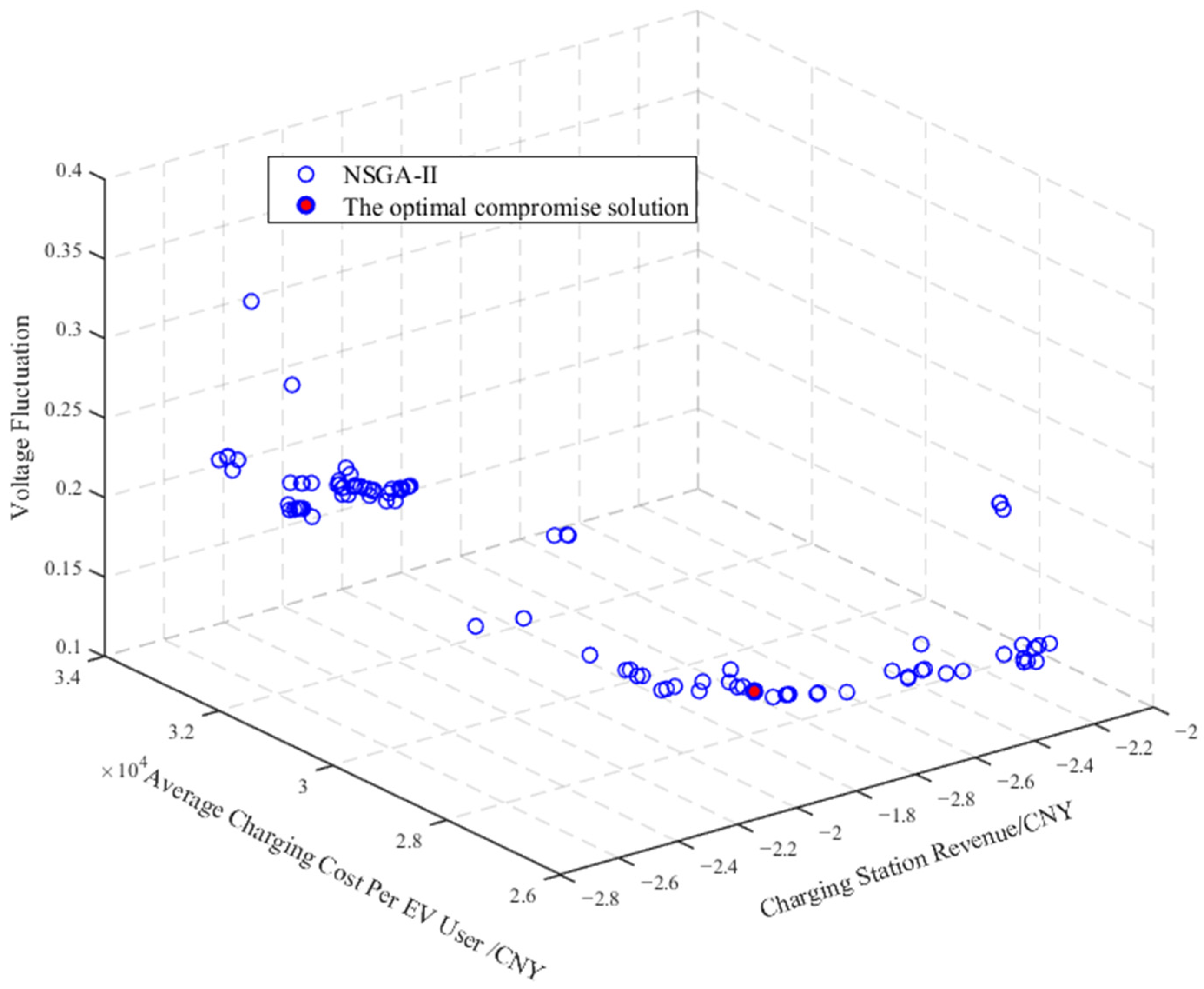
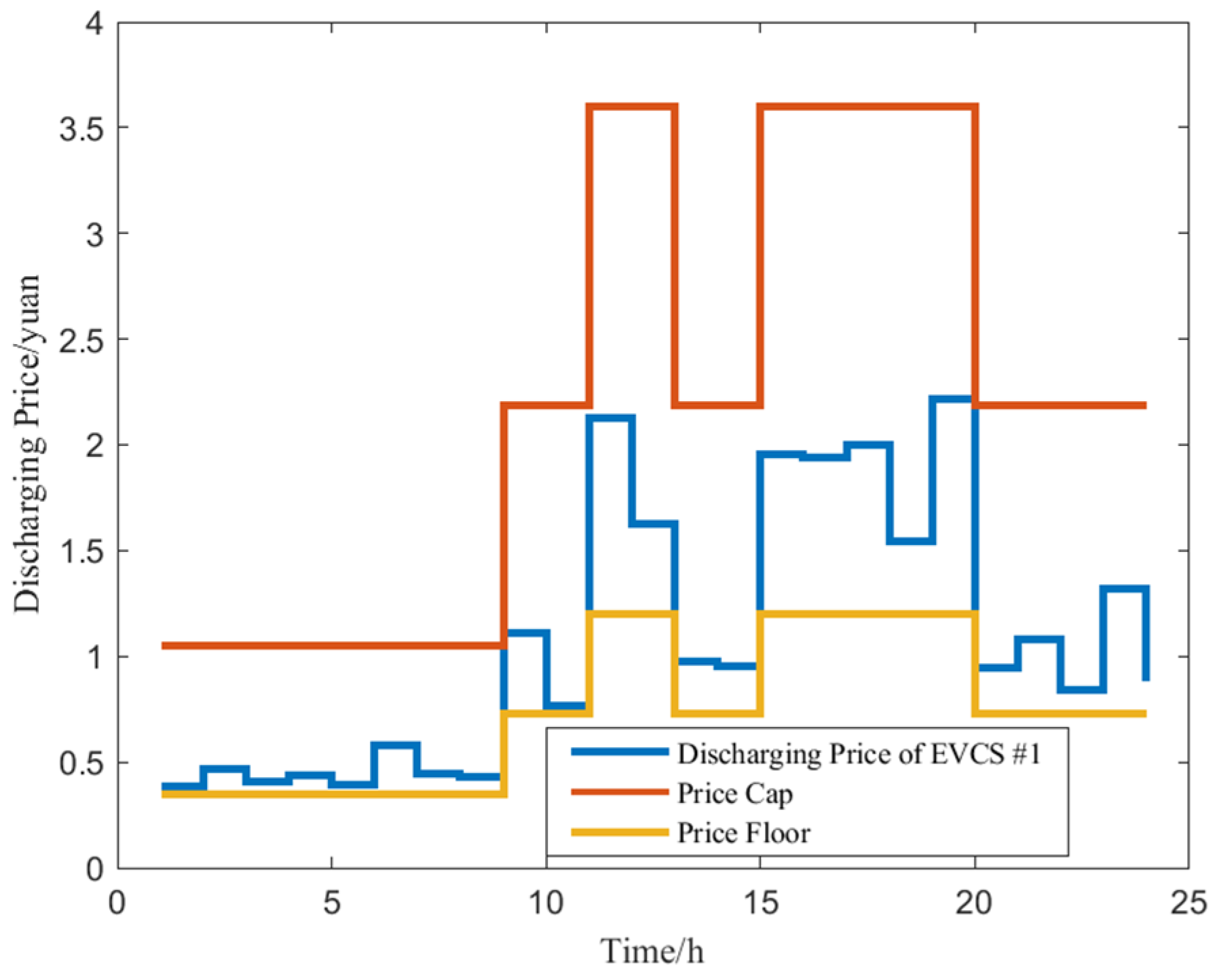
5.3. Analysis of Optimization Results
6. Conclusions
7. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | traffic congestion index | ||
| AC | air conditioning | saturation level | |
| EVs | electric vehicles | traffic flow on road segment i at time t | |
| MOPSO | multi-objective particle swarm optimization | basic capacity | |
| MOSPO | multi-objective stochastic paint optimization | road weight | |
| NHTS | National Household Travel Survey | node voltage | |
| NSGA-II | non-dominated sorting genetic algorithm II | active power | |
| POI | point of interest | reactive power | |
| QGIS | quantum geographic information system | price sensitivity function | |
| V2G | vehicle-to-grid | price difference | |
| Model parameters | cooling power unit | ||
| the output voltage of cell | time penalty coefficient | ||
| road segment identifier | travel time delay | ||
| instantaneous vehicle speed | real-time charging price | ||
| free-flow speed | |||
References
- Manoharan, Y.; Hosseini, S.E.; Butler, B.; Alzhahrani, H.; Senior, B.T.F.; Ashuri, T.; Krohn, J. Hydrogen fuel cell vehicles; current status and future prospect. Appl. Sci. 2019, 9, 2296. [Google Scholar] [CrossRef]
- Yang, B.; Li, J.; Shu, H.; Cai, Z.; Tang, B.; Huang, X.; Zhu, M. Recent advances of optimal sizing and location of charging stations: A critical overview. Int. J. Energy Res. 2022, 46, 17899–17925. [Google Scholar] [CrossRef]
- Sun, L.M.; Yang, B. Optimal planning of electric vehicle charging station based on spatio-temporal distribution prediction of charging demand. Power Gener. Technol. 2024, 1–12. Available online: http://kns.cnki.net/kcms/detail/33.1405.TK.20240914.1014.002.html (accessed on 1 March 2025).
- Hu, Y.W.J.; Yang, B.; Wu, P.Y.; Wang, X.; Li, J.; Huang, Y.; Su, R.; He, G.; Yang, J.; Su, S.; et al. Optimal planning of electric-heating integrated energy system in low-carbon park with energy storage system. J. Energy Storage 2024, 99, 113327. [Google Scholar] [CrossRef]
- Alaee, P.; Shao, J.; Bemš, J.; Guerrero, J.M. Coordinated routing optimization and charging scheduling in a multiple-charging station system: A strategic bilevel multi-objective programming. Sustain. Energy Grids Netw. 2025, 42, 101659. [Google Scholar] [CrossRef]
- Shin, J.; Hwang, W.S.; Choi, H. Can hydrogen fuel vehicles be a sustainable alternative on vehicle market?: Comparison of electric and hydrogen fuel cell vehicles. Technol. Forecast. Soc. Change 2019, 143, 239–248. [Google Scholar] [CrossRef]
- Wang, Z.H. Research on electric vehicle orderly charging and vehicle-network interaction technology under the dual carbon goal. Electr. Power Eng. Technol. 2021, 40, 1. [Google Scholar]
- Zhang, H.; Moura, S.J.; Hu, Z.; Song, Y. PEV fast-charging station siting and sizing on coupled transportation and power networks. IEEE Trans. Smart Grid 2016, 9, 2595–2605. [Google Scholar] [CrossRef]
- Chen, K.Y.; Niu, Y.G. Real-time scheduling strategy of electric vehicle based on vehicle-to-grid application. Power Syst. Prot. Control 2019, 47, 1–9. [Google Scholar]
- Hu, W.P.; He, L.F.; Chen, J.J. A bi-layer optimization based schedule considering large-scale electric vehicles. Power Syst. Prot. Control 2016, 44, 22–28. [Google Scholar]
- Luo, X.; Cheng, J.; Wang, L.X. Spatio-temporal optimal scheduling of electric vehicles based on equivalent load real-time tariff and node real-time tariff guidance. Power Syst. Technol. 2025, 1–17. [Google Scholar] [CrossRef]
- Xu, J.J.; Cheng, Y.L.; Zheng, T.F.; Liu, H.J.; Zhu, S.L.; Wu, Z.J. Optimal scheduling of electric vehicle clusters considering characteristics and adjust ability of charging behavior. Autom. Electr. Power Syst. 2023, 47, 23–32. [Google Scholar]
- Pang, X.F.; Fang, X.; Yu, Y.; Zheng, Z.; Li, H. Optimal scheduling method for electric vehicle charging and discharging via Q-learning-based particle swarm optimization. Energy 2025, 316, 134611. [Google Scholar] [CrossRef]
- Li, Y.J.; Zhang, Z.S.; Xing, Q. Real-time online charging control of electric vehicle charging station based on a multi-agent deep reinforcement learning. Energy 2025, 319, 135095. [Google Scholar] [CrossRef]
- Liu, N.; Chen, Q.F.; Liu, J.; Lu, X.; Li, P.; Lei, J.; Zhang, J. A heuristic operation strategy for commercial building microgrids containing Evs and PV system. IEEE Trans Ind. Electron. 2015, 62, 2570. [Google Scholar] [CrossRef]
- Jia, R.D.; Pan, H.X.; Zhang, S.L.; Hu, Y. Charging scheduling strategy for electric vehicles in residential areas based on offline reinforcement learning. J. Energy Storage 2024, 103, 114319. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, X.D.; Li, L.Y.; Zhang, H.; Pan, R.; Su, Y. Two-stage game collaborative scheduling optimization of EV shared charging based on electricity-carbon joint mechanism. Power Syst. Technol. 2024, 48, 3584–3594. [Google Scholar]
- Sun, X.; Jiang, H.L.; Xie, J.D.; Wang, S.M.; Wang, S. Charging and discharging scheduling mechanism of electric vehicles in park based on user credit index. J. Shanghai Jiaotong Univ. 2025, 59, 1–17. [Google Scholar] [CrossRef]
- Yan, L.M.; Zeng, J.W.; Xu, J.J.; Peng, C.; Zhao, S.Q.; Jia, Y. Scheduling strategy of distribution grid with electric vehicles and photolatic based on evolutionary dynamics game. Acta Energiae Solaris Sin. 2024, 45, 316–323. [Google Scholar]
- Wang, S.Q.; Liu, B.; Hua, Y.P.; Li, Q.; Zhou, J.; Xiang, Y.; Tang, B. Dispatchable capability of aggregated electric vehicle charging in distribution systems. Energy Eng. 2024, 122, 129–152. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, Y.H.; Zhang, T.; Song, W.Y.; Wang, P.; Xi, L. Multi-microgrid system optimization scheduling including electric vehicle coordinated charging and reward and punishment ladder carbon trading. Electr. Power Constr. 2025, 46, 174–188. [Google Scholar]
- Ran, Y.Z.; Liao, H.H.; Liang, H.J.; Lu, L.; Zhong, J. Optimal scheduling strategies for EV charging and discharging in a coupled power-transportation network with V2G scheduling and dynamic pricing. Energies 2024, 17, 6167. [Google Scholar] [CrossRef]
- Liu, Z.J.; Dai, J.; Yang, L.R. Flexibility mining and optimal scheduling for electric vehicle clusters considering dynamic coordination of power-transportation coupling network. Autom. Electr. Power Syst. 2024, 48, 127–137. [Google Scholar]
- Zheng, Y.S.; Li, F.; Dong, J.L.; Luo, J.T.; Zhang, M.; Yang, X.L. Optimal dispatch strategy of spatio-temporal flexibility for electric vehicle charging and discharging in vehicle-road-grid mode. Autom. Electr. Power Syst. 2022, 46, 88–97. [Google Scholar]
- Zhang, C. A robust optimization scheduling strategy for “vehicle-road-network” systems considering dual uncertainty. Sustain. Energy Grids Netw. 2025, 42, 101654. [Google Scholar] [CrossRef]
- Jiang, X.F.; Wei, W.; Wang, Y.C.; Chen, G.; Zhang, R.T.; Liao, K.; Xiao, Q. Orderly charging guidance strategies for electric vehicles under EVs-traffic-distribution collaborative optimization. J. Electr. Power Sci. Technol. 2023, 38, 44–56. [Google Scholar]
- Lakshmikanthi, V.P.; Rao, M.D. Applications of QGIS and machine learning for road crash spot identification. Earth Sci. Inform. 2024, 17, 2331–2346. [Google Scholar]
- He, B.; Yang, B.; Han, Y.; Zhou, Y.; Hu, Y.; Shu, H.; Su, S.; Yang, J.; Huang, Y.; Li, J.; et al. Optimal EVCS planning via spatial-temporal distribution of charging demand forecasting and traffic-grid coupling. Energy 2024, 313, 133885. [Google Scholar] [CrossRef]
- Zhang, H.; Du, Q.; Zhang, S.; Yang, R. A semantically enhanced label prediction method for imbalanced POI data category distribution. ISPRS Int. J. Geo-Inf. 2024, 13, 364. [Google Scholar] [CrossRef]
- Deng, Y.X.; Huang, Y.P.; Huang, Z.C. Charging and discharging capacity forecasting of electric vehicles based on random forest algorithm. Autom. Electr. Power Syst. 2021, 45, 181–188. [Google Scholar]
- Wei, Y.; Sze, C.; Viswanathan, N.; Li, Z.; Alpert, C.J.; Reddy, L.; Huber, A.D.; Tellez, G.E.; Keller, D.; Sapatnekar, S.S. Techniques for scalable and effective routability evaluation. ACM Trans. Des. Autom. Electron. Syst. 2014, 19, 1–37. [Google Scholar] [CrossRef]
- Xie, X.Y.; Liu, X.X.; Li, C.; Hu, Z.P.; Liu, K.; Chen, T. Distribution network reconfiguration considering distributed generation and electric vehicle cluster scheduling. Electr. Power 2023, 56, 119–125. [Google Scholar]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radialdistribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Wang, Y. Dynamic coupling model for vehicle-road-power grid interaction: A multi-agent-based optimization framework for EV charging and grid services. Renew. Sustain. Energy Rev. 2024, 210, 114731. [Google Scholar]
- Li, D.S.; Adama, z.; Liao, J.T.; Yang, H. An energy management strategy with renewable energy and energy storage system for a large electric vehicle charging station. eTransportation 2020, 6, 100076. [Google Scholar] [CrossRef]
- Han, Y.M.; He, B.; Yang, B.; Li, J.L. Optimal planning of electric vehicle charging stations combined with battery energy storage systems considering driving characteristics. J. Shanghai Jiaotong Univ. 2024, 1–29. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. Inst. Electr. Electron. Eng. 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Li, J.L.; Yang, B.; Hu, Y.W.J.; Zhang, R. Location and capacity planning of electricity hydrogen hybrid energy storage system considering demand response. Power Syst. Technol. 2023, 47, 3698–3714. [Google Scholar]
- Li, X.; Zhang, Y.; Wang, H.; Liu, Z. A grey target-based multi-objective optimization framework for EV charging scheduling considering grid flexibility and user preferences. IEEE Trans. Sustain. Energy 2023, 1, 512–525. [Google Scholar]
- Qiu, Z.Y.; Mo, Y.B. CHP system ED optimization based on improved snow geese algorithm. Mod. Electron. Tech. 2025, 48, 127–135. [Google Scholar]
- Li, W.; Xiao, Y.; Feng, H. Multi-objective real-time scheduling optimization study of multi-energy supply system based on improved flower pollination algorithm. J. Harbin Eng. Univ. 2025, 1–8. Available online: http://kns.cnki.net/kcms/detail/23.1390.U.20250313.1201.004.html (accessed on 26 March 2025).
- Li, L.B.; Gao, Y.B.; Dai, L.L.; Gao, G.Q. Multi-strategy improved white shark algorithm for wind and hydrogen storage microgrids optimal Scheduling. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2025, 1–7. [Google Scholar] [CrossRef]
- Lu, C. Research on the optimization of new energy vehicle marketing strategies: A case study of BYD. Mod. Mark. 2025, 55–57. [Google Scholar]
- Wu, D. Electric Charging Pile Time-Slot Price, Which Time-Slot Electricity Is the Cheapest. Wu Di Electric. 2022. Available online: https://www.modiauto.com.cn/bk/53133.html (accessed on 26 March 2025).
- Pacific Auto. How Much Does It Cost to Charge at ZEEKR Super Charging Station? Pacific Auto. 2024. Available online: https://www.pcauto.com.cn/jxwd/4382/43828413.html (accessed on 26 March 2025).
- Sohu. Evening Charging at Half-Price! Tesla Launches “Off-Peak Supercharging” in China: As Low as 1.2 CNY per kWh During Off-Peak Hours. Sohu. 2022. Available online: https://www.sohu.com/a/562838243_120960892# (accessed on 26 March 2025).









| Driving Characteristic | Node Type | Distribution Model | Fitting Parameters |
|---|---|---|---|
| Initial Driving Time | - | Weibull Distribution | = 7.986 6.696 |
| Initial SOC | - | Normal Distribution | 0.2 0.5 |
| Parking Duration | Residential Area | Log-normal Distribution | |
| Work Area | Weibull Distribution | 3032.83 1.043 | |
| Other Areas | Generalized Extreme Value Distribution | = 0.765 35.419 63.477 | |
| Driving Distance | - | Normal Distribution | 0.88 3.3 |
| Step 1: | ) |
| Step 2: | Initialize population with random solutions |
| Step 3: | FOR1 DO |
| Step 4: | Evaluate objective functions for all solutions |
| Step 5: | Perform Fast Non-Dominated Sorting to identify Pareto fronts ) |
| Step 6: | FORDO |
| Step 7: | |
| Step 8: | END FOR2 |
| Step 9: | Select parents using Binary Tournament:
|
| Step 10: | Apply genetic operators:
|
| Step 11: | Combine parent and offspring populations |
| Step 12: | Perform Environmental Selection:
|
| Step 13: | END FOR1 |
| Step 14: | ) |
| Algorithm | NSGA-II | ABMSG [40] | IFP [41] | DWSO [42] | MOPSO | MOSPO |
|---|---|---|---|---|---|---|
| Key Features | Fast non-dominated sorting | Dynamic Brownian motion perturbation | Multi-objective fusion function | Split problem decomposition architecture | Pareto dominance and repository maintenance | Color theory-inspired search mechanism |
| Computational Efficiency | High | High | Medium | Medium | High | High |
| Diversity | High | Medium | High | Medium | High | High |
| Year | 2002 | 2024 | 2024 | 2020 | 2021 | 2022 |
| Parameters | Value |
|---|---|
| Weight of EV/(kg) | 1900 |
| Battery Capacity of EV/(k·Wh) | 60 |
| Transmission Efficiency | 0.92 |
| Motor Efficiency | 0.91 |
| Algorithm | Parameters | Value |
|---|---|---|
| NSGA-II | Crossover Percentage | 0.5 |
| Mutation Percentage | 0.5 | |
| Mutation Rate | 0.02 | |
| MOPSO | Inertia Weight | 0.5 |
| Intertia Weight Damping Rate | 0.99 | |
| Personal Learning Coefficient | 1 | |
| Global Learning Coefficient | 2 | |
| Mutation Rate | 0.1 | |
| MOSPO | Grid Inflation Parameter | 0.1 |
| Number of Grids per each Dimension | 30 | |
| Leader Selection Pressure Parameter | 4 | |
| Extra (to be deleted) Repository Member Selection Pressure | 2 |
| Algorithm | Charging Station Revenue/(CNY) | Average Charging Cost Per EV User/(CNY) | Voltage Fluctuation |
|---|---|---|---|
| Initial State | 17,384.14 | 56.72 | 0.45 |
| NSGA-II | 23,195.97 | 46.07 | 0.14 |
| MOPSO | 14,418.34 | 44.52 | 0.20 |
| MOSPO | 19,926.46 | 87.43 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, J.; Huang, M.; Sun, X.; Chen, Z.; Zhang, Z.; Li, Y.; Zhang, Y.; Ai, Q. Coordinated Interaction Strategy of User-Side EV Charging Piles for Distribution Network Power Stability. Energies 2025, 18, 1944. https://doi.org/10.3390/en18081944
Zhan J, Huang M, Sun X, Chen Z, Zhang Z, Li Y, Zhang Y, Ai Q. Coordinated Interaction Strategy of User-Side EV Charging Piles for Distribution Network Power Stability. Energies. 2025; 18(8):1944. https://doi.org/10.3390/en18081944
Chicago/Turabian StyleZhan, Juan, Mei Huang, Xiaojia Sun, Zuowei Chen, Zhihan Zhang, Yang Li, Yubo Zhang, and Qian Ai. 2025. "Coordinated Interaction Strategy of User-Side EV Charging Piles for Distribution Network Power Stability" Energies 18, no. 8: 1944. https://doi.org/10.3390/en18081944
APA StyleZhan, J., Huang, M., Sun, X., Chen, Z., Zhang, Z., Li, Y., Zhang, Y., & Ai, Q. (2025). Coordinated Interaction Strategy of User-Side EV Charging Piles for Distribution Network Power Stability. Energies, 18(8), 1944. https://doi.org/10.3390/en18081944






