Multichannel Attention-Based TCN-GRU Network for Remaining Useful Life Prediction of Aero-Engines
Abstract
1. Introduction
- A temporal convolutional network (TCN) is utilized. In the field of time series data modeling, TCN’s dilated convolution allows it to extract long-term dependencies into sequences.
- We designed an attention mechanism applied to multiple temporal resolutions and multiple features. For the output data from multiple TCN networks, an attention framework is designed to combine data from several time scales and channels. Consequently, multichannel attention fusion is formed, and the newly formed model is labeled MCA-TCN.
- The prediction of RUL is accomplished by gated cycle units. A layer of the GRU network is passed after all networks to further filter the effective information and achieve a high accuracy prediction.
2. Related Work
3. Methodology
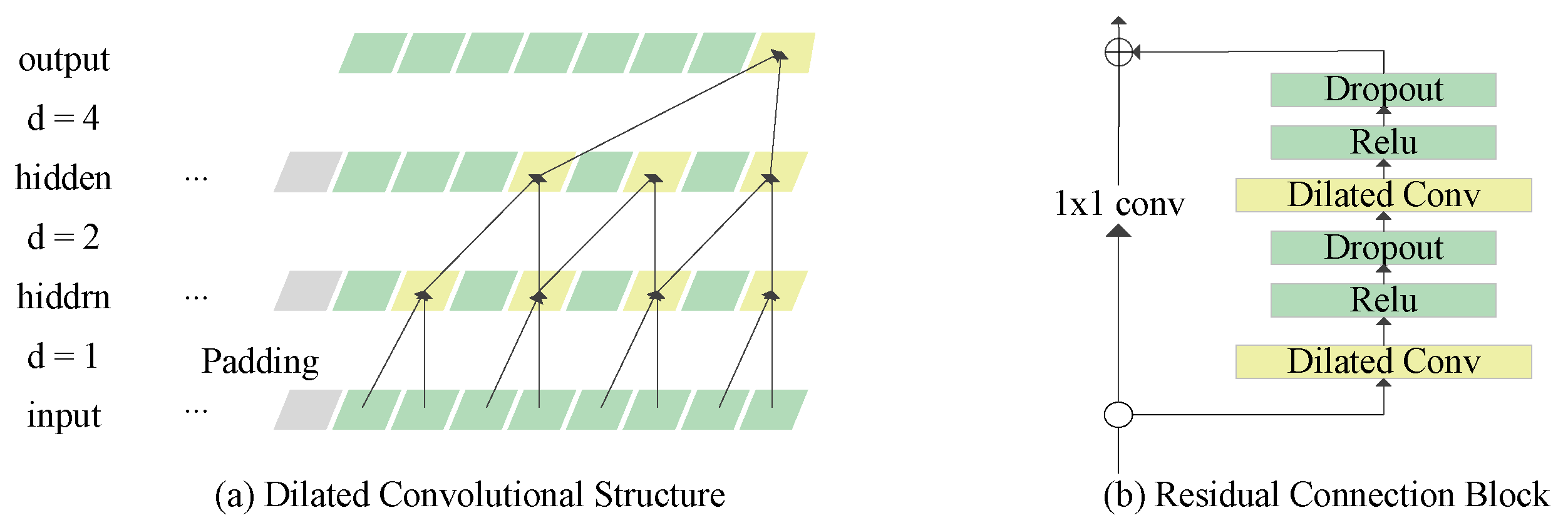
3.1. Temporal Convolutional Network
3.1.1. Dilated Convolutions
3.1.2. Residual Connections
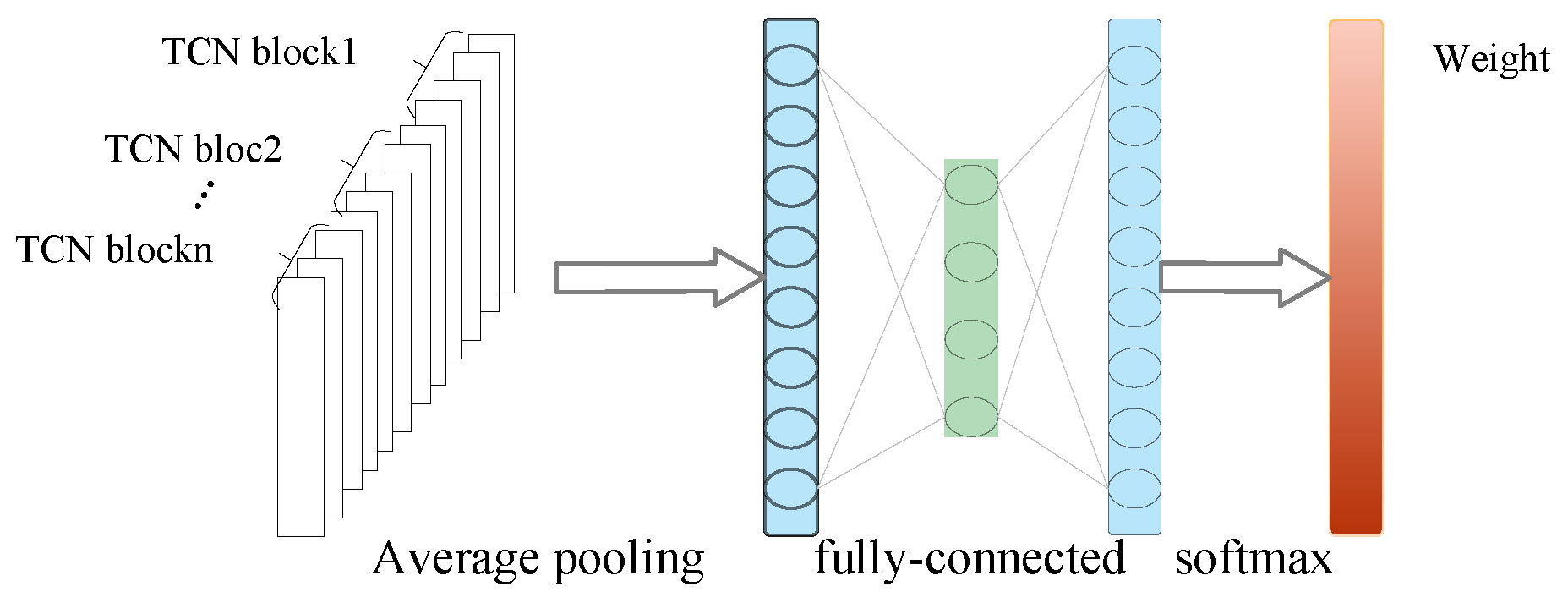
3.2. Multi-Temporal Feature Attention Mechanism
- (1)
- For 1-D input data , input the TCN block and obtain the output ;
- (2)
- After inputting n blocks, the connection data become ; then, after average pooling and 1-D convolution, the data become ;
- (3)
- Pooled information is transformed into less informative representations through the application of a fully-connected layer, and the dimensionality of the data is reduced through a second fully-connected layer;
- (4)
- Input sigmoid function to obtain the weight , then multiply by elements, obtain weighted data , and the Softmax function is calculated as (3);
- (5)
- To reduce the amount of data, reshape the weighted data and sum in axis 1 to make the data and block output data the same size as one TCN block.
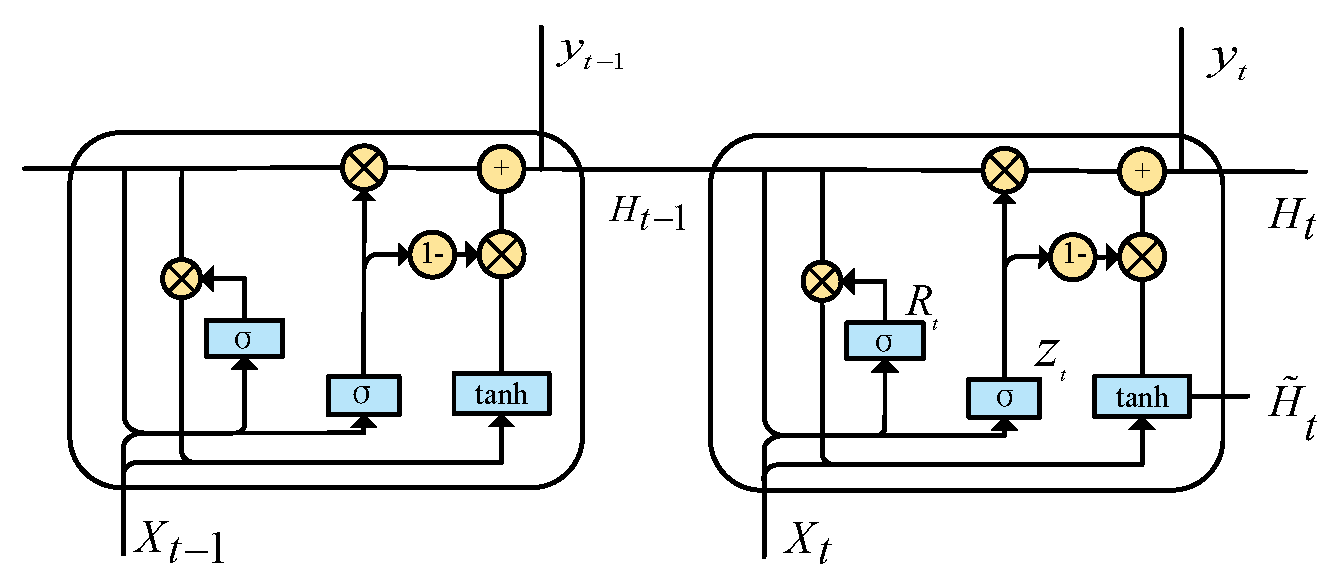
3.3. Gated Recurrent Unit
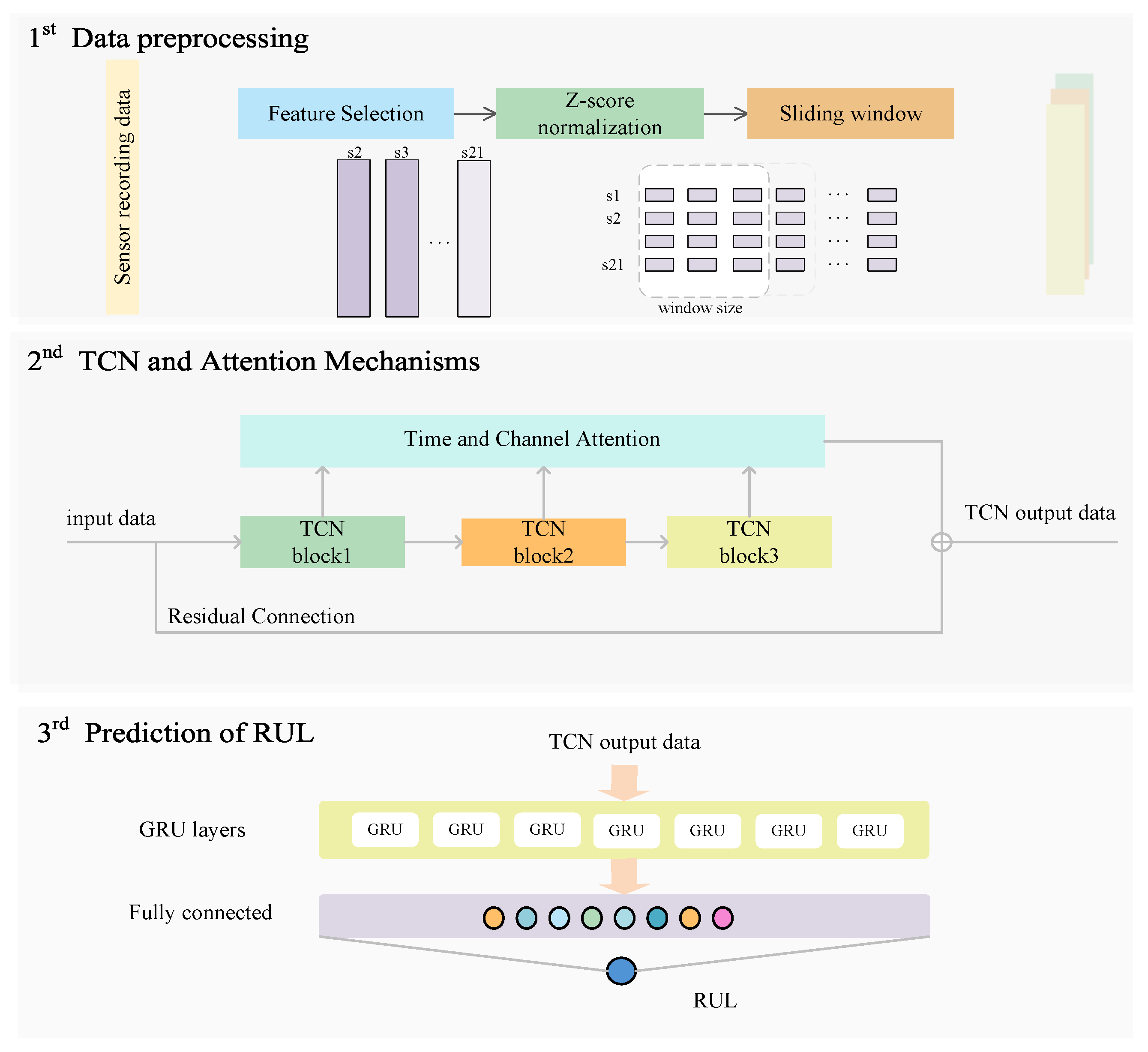
3.4. Proposed Methodology
4. Experiment and Discussion
4.1. CMAPSS Datasets Description
4.2. Data Pre-Processing
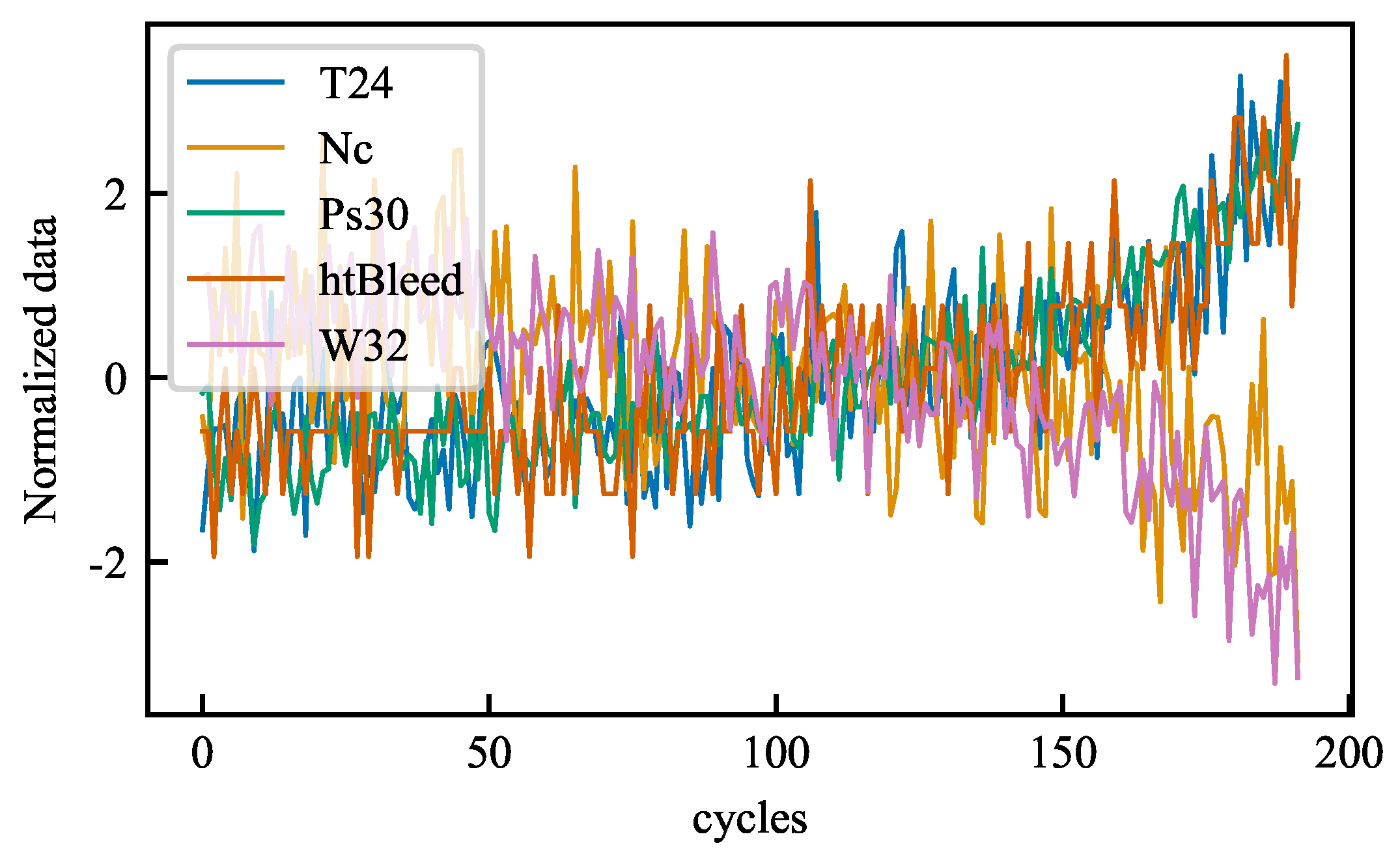
4.2.1. Z-Score Normalization
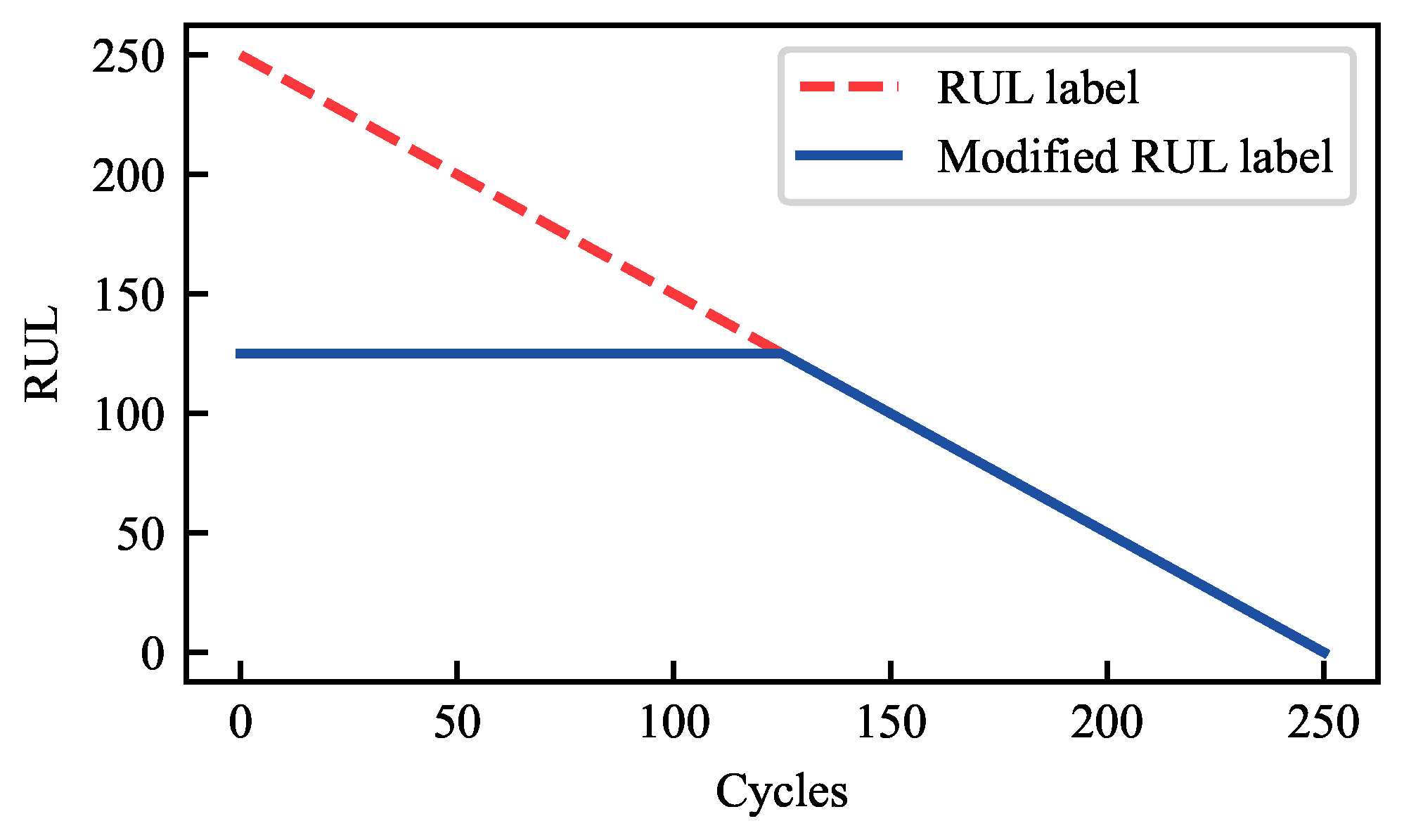
4.2.2. Two-Stage Degradation
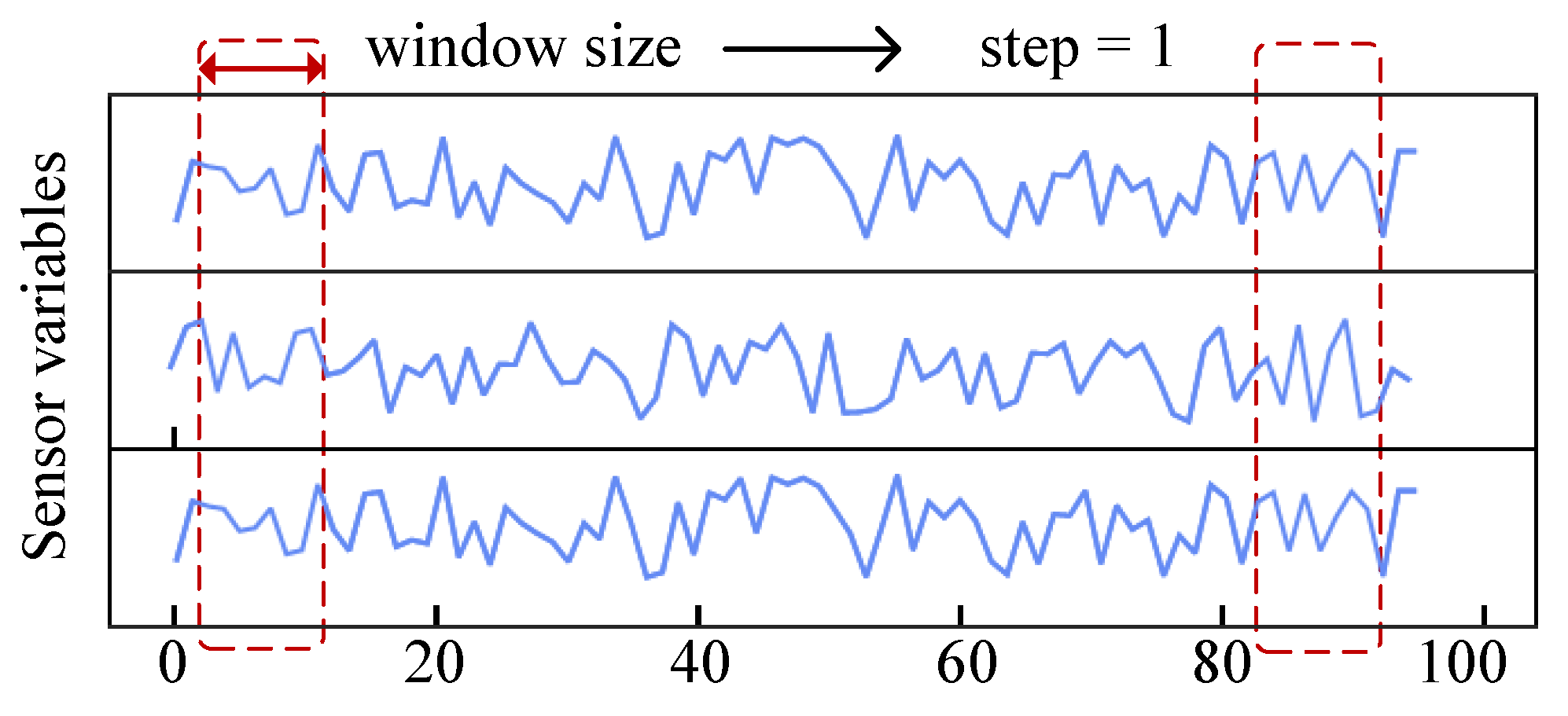
4.2.3. Sliding Window
4.3. Model Evaluation
4.3.1. Root Mean Square Error
4.3.2. Score Function
4.4. Experimental Setup
4.5. Experimental Results
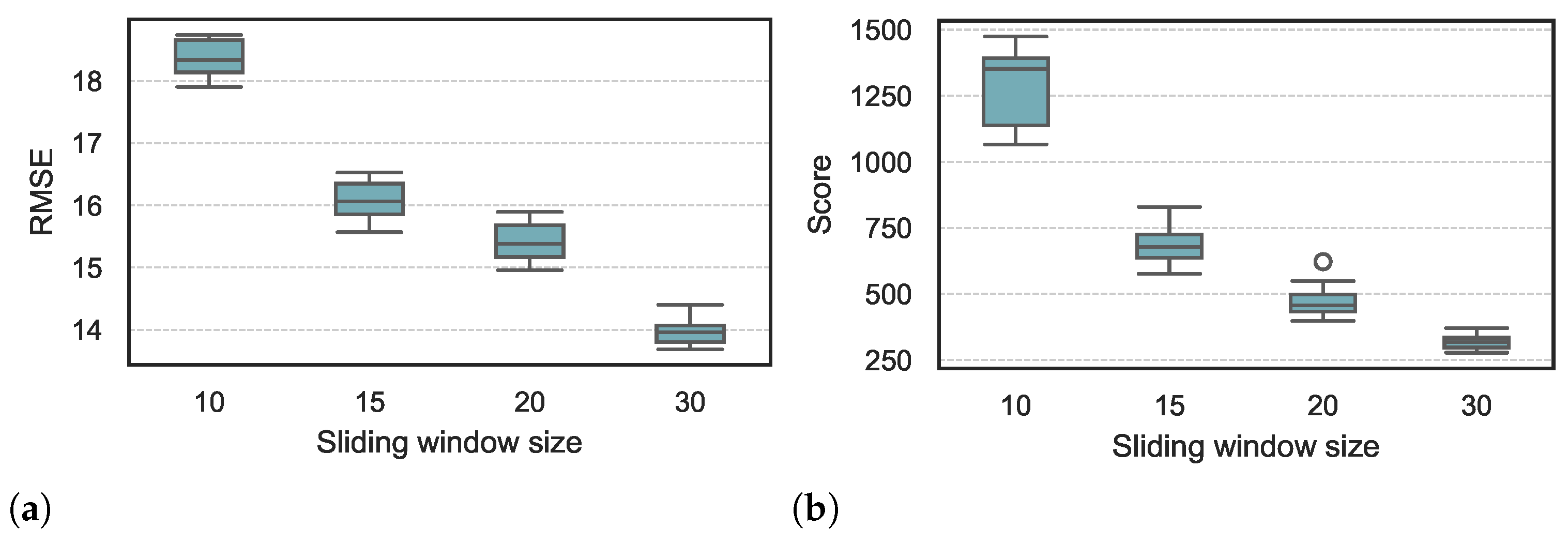
4.5.1. The Effect of Sliding Time Windows
4.5.2. Ablation Experiments of the Proposed Method
4.5.3. Comparison of the Proposed Methodology with Previous Methodologies
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dangut, M.D.; Jennions, I.K.; King, S.; Skaf, Z. Application of deep reinforcement learning for extremely rare failure prediction in aircraft maintenance. Mech. Syst. Signal Process. 2022, 171, 108873. [Google Scholar] [CrossRef]
- Ren, H.; Chen, X.; Chen, Y. Reliability Based Aircraft Maintenance Optimization and Applications; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Kordestani, M.; Orchard, M.E.; Khorasani, K.; Saif, M. An overview of the state of the art in aircraft prognostic and health management strategies. IEEE Trans. Instrum. Meas. 2023, 72, 3505215. [Google Scholar] [CrossRef]
- De Pater, I.; Reijns, A.; Mitici, M. Alarm-based predictive maintenance scheduling for aircraft engines with imperfect Remaining Useful Life prognostics. Reliab. Eng. Syst. Saf. 2022, 221, 108341. [Google Scholar]
- Ordóñez, C.; Lasheras, F.S.; Roca-Pardiñas, J.; de Cos Juez, F.J. A hybrid ARIMA–SVM model for the study of the remaining useful life of aircraft engines. J. Comput. Appl. Math. 2019, 346, 184–191. [Google Scholar]
- Dong, R.; Li, W.; Ai, F.; Wan, M. Design of PHM test verification method and system for aviation electrical system. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021; pp. 1–5. [Google Scholar]
- Raouf, I.; Kumar, P.; Cheon, Y.; Tanveer, M.; Jo, S.H.; Kim, H.S. Advances in prognostics and health management for aircraft landing gear—progress, challenges, and future possibilities. Int. J. Precis. Eng. Manuf.-Green Technol. 2025, 12, 301–320. [Google Scholar]
- Li, C.; Li, S.; Feng, Y.; Gryllias, K.; Gu, F.; Pecht, M. Small data challenges for intelligent prognostics and health management: A review. Artif. Intell. Rev. 2024, 57, 214. [Google Scholar] [CrossRef]
- Zio, E. Prognostics and Health Management (PHM): Where are we and where do we (need to) go in theory and practice. Reliab. Eng. Syst. Saf. 2022, 218, 108119. [Google Scholar]
- Zhang, Y.; Fang, L.; Qi, Z.; Deng, H. A review of remaining useful life prediction approaches for mechanical equipment. IEEE Sens. J. 2023, 23, 29991–30006. [Google Scholar]
- Hesabi, H.; Nourelfath, M.; Hajji, A. A deep learning predictive model for selective maintenance optimization. Reliab. Eng. Syst. Saf. 2022, 219, 108191. [Google Scholar] [CrossRef]
- Deepika, J.; Reddy, P.M.; Murari, K.; Rahul, B. Predictive Maintenance of Aircraft Engines: Machine Learning Approaches for Remaining Useful Life Estimation. In Proceedings of the 2025 6th International Conference on Mobile Computing and Sustainable Informatics (ICMCSI), Morang, Nepal, 7–8 January 2025; pp. 1679–1686. [Google Scholar]
- Dangut, M.D.; Skaf, Z.; Jennions, I.K. Handling imbalanced data for aircraft predictive maintenance using the BACHE algorithm. Appl. Soft Comput. 2022, 123, 108924. [Google Scholar]
- Jia, W.; Haimin, L.; Xiao, W. Application and design of PHM in aircraft’s integrated modular mission system. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Qingdao), Qingdao, China, 25–27 October 2019; pp. 1–6. [Google Scholar]
- Kiakojoori, S.; Khorasani, K. Dynamic neural networks for gas turbine engine degradation prediction, health monitoring and prognosis. Neural Comput. Appl. 2016, 27, 2157–2192. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, virtually, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Fang, X.; Xie, L.; Dimarogonas, D.V. Simultaneous distributed localization and formation tracking control via matrix-weighted position constraints. Automatica 2025, 175, 112188. [Google Scholar]
- El-Brawany, M.A.; Ibrahim, D.A.; Elminir, H.K.; Elattar, H.M.; Ramadan, E. Artificial intelligence-based data-driven prognostics in industry: A survey. Comput. Ind. Eng. 2023, 184, 109605. [Google Scholar] [CrossRef]
- Gawde, S.; Patil, S.; Kumar, S.; Kamat, P.; Kotecha, K.; Abraham, A. Multi-fault diagnosis of Industrial Rotating Machines using Data-driven approach: A review of two decades of research. Eng. Appl. Artif. Intell. 2023, 123, 106139. [Google Scholar]
- Li, X.; Ding, Q.; Sun, J.Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar]
- Li, H.; Zhao, W.; Zhang, Y.; Zio, E. Remaining useful life prediction using multi-scale deep convolutional neural network. Appl. Soft Comput. 2020, 89, 106113. [Google Scholar]
- Shi, Z.; Chehade, A. A dual-LSTM framework combining change point detection and remaining useful life prediction. Reliab. Eng. Syst. Saf. 2021, 205, 107257. [Google Scholar]
- Yan, J.; He, Z.; He, S. Multitask learning of health state assessment and remaining useful life prediction for sensor-equipped machines. Reliab. Eng. Syst. Saf. 2023, 234, 109141. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Wang, Z.; Li, Z. Remaining useful life prediction of aero-engine based on PCA-LSTM. In Proceedings of the 2021 7th International Conference on Condition Monitoring of Machinery in Non-Stationary Operations (CMMNO), Guangzhou, China, 11–13 June 2021; pp. 63–66. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Lin, L.; Wu, J.; Fu, S.; Zhang, S.; Tong, C.; Zu, L. Channel attention & temporal attention based temporal convolutional network: A dual attention framework for remaining useful life prediction of the aircraft engines. Adv. Eng. Inform. 2024, 60, 102372. [Google Scholar]
- Liu, H.; Liu, Z.; Jia, W.; Lin, X. Remaining useful life prediction using a novel feature-attention-based end-to-end approach. IEEE Trans. Ind. Inform. 2020, 17, 1197–1207. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Mao, R.; Li, Y.; Lu, W.; Zhang, J. TPANet: A novel triple parallel attention network approach for remaining useful life prediction of lithium-ion batteries. Energy 2024, 309, 132890. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar]
- Heimes, F.O. Recurrent neural networks for remaining useful life estimation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–6. [Google Scholar]
- Miao, H.; Li, B.; Sun, C.; Liu, J. Joint learning of degradation assessment and RUL prediction for aeroengines via dual-task deep LSTM networks. IEEE Trans. Ind. Inform. 2019, 15, 5023–5032. [Google Scholar] [CrossRef]
- Chen, W.; Liu, C.; Chen, Q.; Wu, P. Multi-scale memory-enhanced method for predicting the remaining useful life of aircraft engines. Neural Comput. Appl. 2023, 35, 2225–2241. [Google Scholar] [CrossRef]
- Zhao, K.; Jia, Z.; Jia, F.; Shao, H. Multi-scale integrated deep self-attention network for predicting remaining useful life of aero-engine. Eng. Appl. Artif. Intell. 2023, 120, 105860. [Google Scholar] [CrossRef]
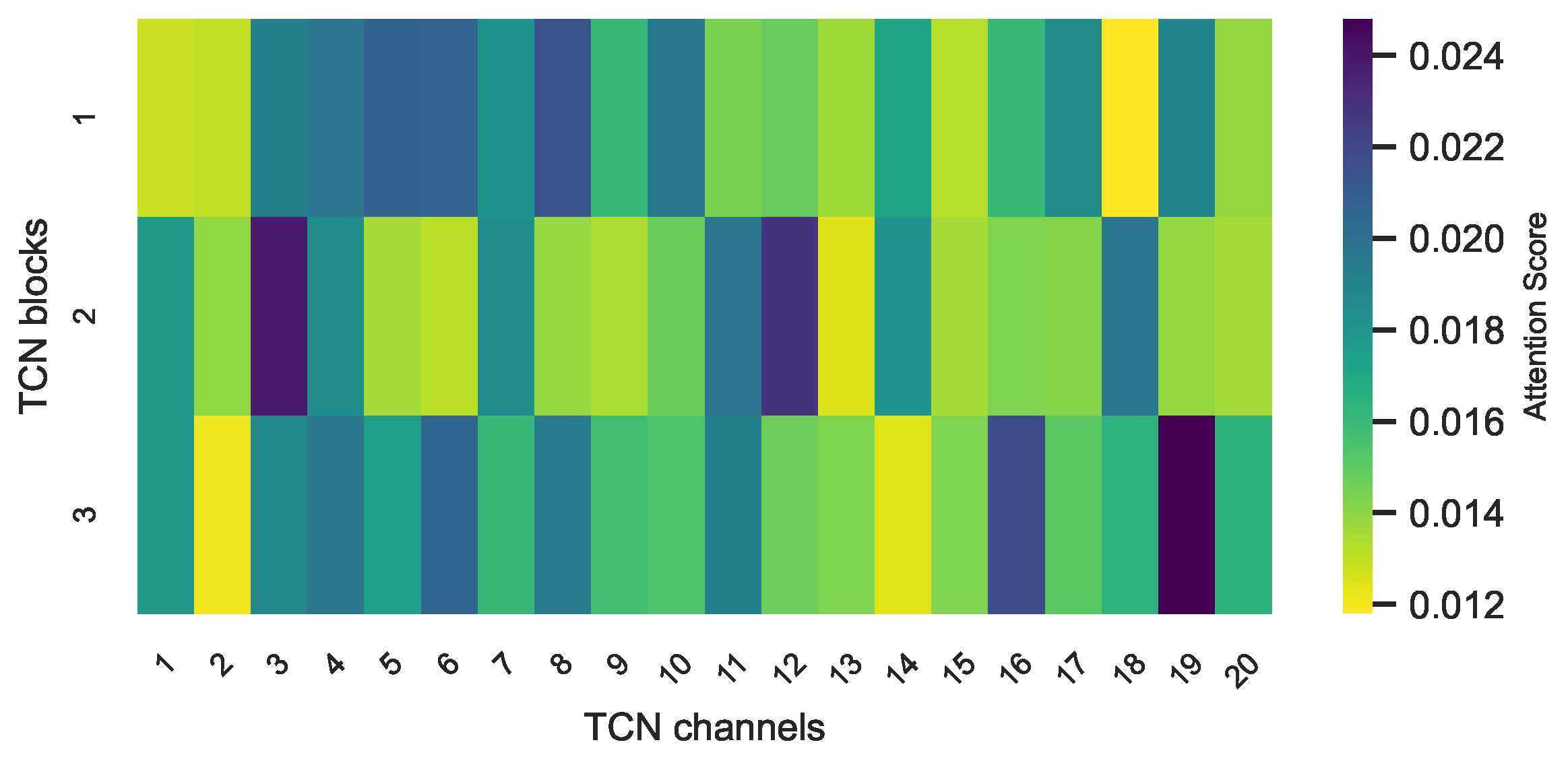
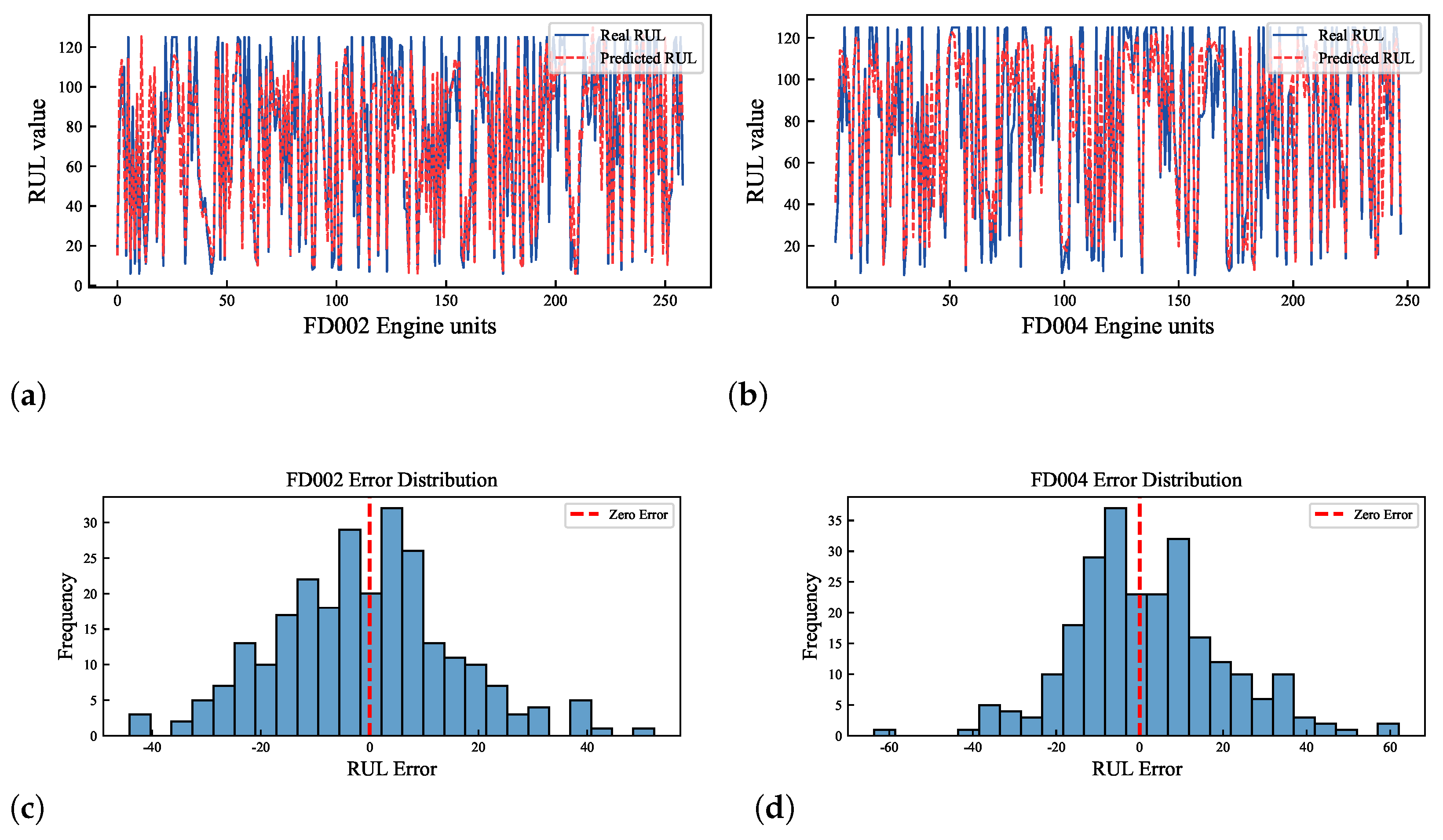
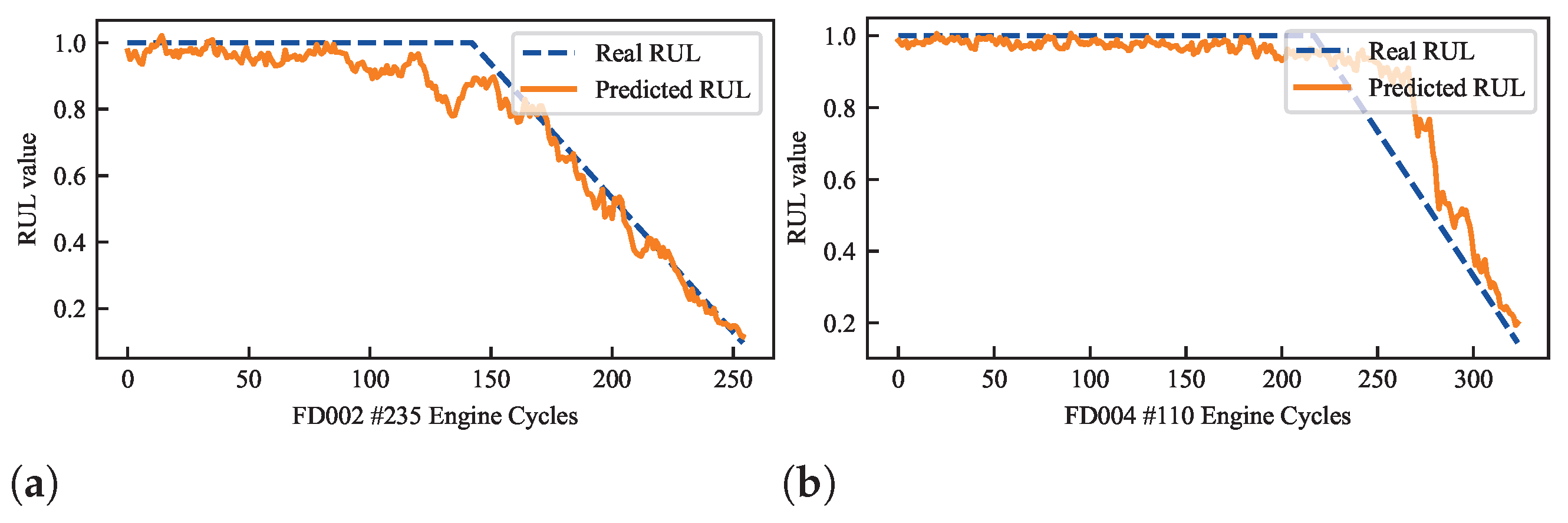
| Sub-Datasets | FD001 | FD002 | FD003 | FD004 |
|---|---|---|---|---|
| train engines | 100 | 260 | 100 | 249 |
| test engines | 100 | 259 | 100 | 248 |
| conditions | 1 | 6 | 1 | 6 |
| failure model | 1 | 1 | 2 | 2 |
| Minimum RC | 31 | 21 | 38 | 19 |
| Sensor Variables | Units | Description |
|---|---|---|
| T2 | °R | Total temperature at fan inlet |
| T24 | °R | Total temperature at LPC outlet |
| T30 | °R | Total temperature at HPC outlet |
| P2 | psia | Pressure at fan inlet |
| T50 | °R | Total temperature at LPT outlet |
| Nf | rpm | Physical fan speed |
| P15 | psia | Total pressure in bypass-duct |
| P30 | psia | Total pressure at HPC outlet |
| Nc | rpm | Physical core speed |
| epr | – | Engine pressure ratio (P50/P2) |
| BPR | – | Bypass Ratio |
| farB | – | Burner fuel-air ratio |
| htBleed | – | Bleed Enthalpy |
| Ps30 | psia | Static pressure at HPC outlet |
| phi | pps/psi | Ratio of fuel flow to Ps30 |
| NRf | rpm | Corrected fan speed |
| NRc | rpm | Corrected core spee |
| Nf_dmd | rpm | Demanded fan speed |
| PCNfR_dmd | rpm | Demanded corrected fan speed |
| W31 | lbm/s | HPT coolant bleed |
| W32 | lbm/s | LPT coolant bleed |
| Hyperparameter | Descriptions | Value |
|---|---|---|
| Batch size | Samples per update step | 512 |
| Epoch | Complete training cycles | 60 |
| Lr | Initial learning rate | 0.001 |
| Dropout rate | The proportion of neurons randomly deactivated | 0.25 |
| TCN channels | The number of channels in one TCN block | 20 |
| TCN BLOCKS | The total number of TCN blocks | 3 |
| GRU size | The number of GRU units | 18 |
| Methods | FD002 | FD004 | ||
|---|---|---|---|---|
| RMSE | Score | RMSE | Score | |
| Without attention | 16.72 | 1361.8 | 20.50 | 3502.93 |
| With attention | 16.19 | 1189.4 | 18.33 | 2091.27 |
| Methods | Year | FD002 | FD004 | ||
|---|---|---|---|---|---|
| RMSE | Score | RMSE | Score | ||
| DCNN [20] | 2018 | 24.86 | \ | 29.44 | \ |
| Dt-LSTM [35] | 2019 | 17.87 | \ | 21.81 | \ |
| AGCNN [28] | 2020 | 19.43 | 1492 | 21.50 | 3392 |
| MS-DCNN [21] | 2020 | 19.35 | 3747 | 22.22 | 4844 |
| MSDCNN-LSTM [36] | 2023 | 18.70 | 1873.86 | 21.57 | 2699.34 |
| MSIDSN [37] | 2023 | 18.26 | 2046.65 | 22.48 | 2910.73 |
| CATA-TCN [27] | 2024 | 17.61 | 1361.23 | 21.04 | 2303.42 |
| proposed model | - | 16.19 | 1189.4 | 18.33 | 2091.27 |
| Methods | Main Contributions |
|---|---|
| DCNN | A deep convolutional network without prior knowledge and signal processing |
| Dt-LSTM | Proposes a dual-task deep LSTM network |
| AGCNN | An attention mechanism that dynamically adjusts weights |
| MS-DCNN | A multi-scale deep convolutional network |
| MSDCNN-LSTM | Combines deep convolutional networks and LSTM networks |
| MSIDSN | Self-attentive mechanism and parallel BiGRU to improve prediction performance |
| CATA-TCN | Combination of channel and temporal attention to capture key information |
| Proposed model | Proposing a novel attention mechanism for fusing multilayer networks |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, J.; Lin, P. Multichannel Attention-Based TCN-GRU Network for Remaining Useful Life Prediction of Aero-Engines. Energies 2025, 18, 1899. https://doi.org/10.3390/en18081899
Zou J, Lin P. Multichannel Attention-Based TCN-GRU Network for Remaining Useful Life Prediction of Aero-Engines. Energies. 2025; 18(8):1899. https://doi.org/10.3390/en18081899
Chicago/Turabian StyleZou, Jiabao, and Ping Lin. 2025. "Multichannel Attention-Based TCN-GRU Network for Remaining Useful Life Prediction of Aero-Engines" Energies 18, no. 8: 1899. https://doi.org/10.3390/en18081899
APA StyleZou, J., & Lin, P. (2025). Multichannel Attention-Based TCN-GRU Network for Remaining Useful Life Prediction of Aero-Engines. Energies, 18(8), 1899. https://doi.org/10.3390/en18081899






